Transient current balancing modulation for seamless load step response in a dual-active-bridge converter with triple phase-shift control

Abstract

With the load step demands, the dual-active-bridge dc–dc converter might be arsing a temporal dc offset and overshoot current in the inductor and transformer due to improper direct modulation. The dc offset and overshoot current often causes a series of complex electromagnetic problems and bring up extra conduction loss into the system. In this paper, a dedicated transient current balancing (TCB) modulation for seamless transient response is proposed. The triple phase-shift (TPS) control, a three dimensional gating signal scheme is selected as the research target. The proposed TCB modulation are checked for all transition cases between different TPS steady state modes. To minimize the dc offset, the TCB modulation adjusts the selected phase-shift by referring a floating reference. Consequently, a fast transient response without dc bias current of TPS control can be obtained. And, the proposed TCB modulation can easily determined by a uniformed solution which is irrespective of steady state. All theoretical works have been validated by both simulation and actual experimental test.

Introduction

Most recently, among power electronics systems, the high-frequency (HF) isolated bidirectional dc–dc converter (IBDC) has received wide attention, and it has been widely implemented as an interface in renewable generation applications for bidirectional power delivery^1,2. IBDC has many competitive advantages such as galvanic isolation, high power density, high conversion efficiency and simple control. The dual-active-bridge (DAB) dc–dc converter is a typical topology of IBDC, which is featured with bidirectional power flow, soft-switching capability, low control complexity and high conversion efficiency³. The scenarios particularly suited for DAB converter include renewable energy generation and storage system. The phase-shifted modulation (PSM) was proposed to be controlled DAB converter by an outer phase-shift⁴. However, with conventional PSM or single phase-shift (SPS) control, DAB would suffer from switching loss and conduction loss, which arises from hard-switching operation, circulating current and backow power respectively. To overcome conventional modulation apparently drawbacks, advanced phase-shift modulation include extended phase-shift (EPS) control⁵, dual-phase-shift (DPS) control⁶ and triple-phase-shift (TPS) control^7,8 are investigated step by step. All of these advanced phase-shift modulation are adopted one or more inner-bridge phase shifts, which is the inherent feature of the DAB structure. Thus, the cost of these improvements are increasing complexity level of control. In the present work, the main focus is put on evaluating the impact of the implemented modifications on the conversion efficiency of a DAB converter.

The modeling and closed-loop control of a DAB converter has gained considerable attention in research area since it ensures transmission stability^9,10,11. Although the DAB converter conversion performance has been apparently enhanced, these modified system still suffered from substantial dc bias current during load step changing process. The dc bias current might lead to the bias magnetic saturation and loud noise, overheating, vibration and even breakdown of HF transformers⁹. However, there are only a few previous reported focusing the transient response performance of the DAB converter, especially the step load changing with advanced phase-shift modulation. To depress the circulating current, a dynamic current matching modulation for paralleled switches in drive circuit was studied, which is matching dynamic current in particular time intervals¹². The instantaneous current matching modulation was proposed for SPS control during transient state^13,15. With improper direct modulation in DAB resonant converter, the transient process tends to oscillate. In¹⁶, a dedicated transient modulation for DAB resonant converter was investigated. Based on SPS control, a fast transient response modulation for transient switching performance was discussed in detail¹⁷. And, a similar dc offset depression solution was given for EPS control and DPS control in^14,18. These two similar modulation were distributed the optimized variable on different phase-shift, so that the transition can avoid dc bias current¹⁹. There will be more different transition cases, and the complexity level to adjust multi-phase-shift together increases. To enhance the conversion performance, a boundary current transition progress with no dc bias current and no backflow power was proposed in²⁰. The seamless transient response in three-level DAB converter was discussed too²¹. However, all of these transition improving modulation has one or more control restrictions, which are the inherent limitations of the conventional transient modulation. To overcome above-mentioned restrictions, the DAB converter can be controlled up to TPS control, which are powerful to achieve better performance. Therefore, it is meaningful to explore how to obtain a fast and dc-bias-free transient response in a DAB converter with TPS control.

In this paper, a transient current balancing (TCB) modulation based on TPS control is proposed for the fast load step process. Referring to floating reference gating signals, the TCB modulation will be modified the partial gating signal to eliminate dc bias current. The TCB modulation would solve a uniformed solution for any possible cases of TPS control, which is simple and easy to implement. All theoretical works have been discussed and validated by both simulation and a series of actual experimental test. Finally, a conclusions are drawn in last section.

Transient current balancing modulation for load step transient state

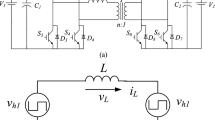
The DAB converter topology schematic is illustrated in Fig. 1. $V_{in}$ is a DC sources. $C_1$ and $C_2$ are high frequency filter capacitors. $S_1 - S_8$ are the eight active switches on primary side and secondary side. $D_{S1} - D_{S8}$ are eight parasitic diodes of each switches. $C_{S1} - C_{S8}$ are eight junction capacitors or snubber. Those parasitic diodes and junction capacitors are parallel connected with active switches. $L_k$ is inductor which is connected on the primary side as the main energy transfer device. $i_{L}$ is the current across the inductor $L_k$. $r_k$ is the sum value of the equivalent resistance of $L_k$ and the winding resistance of the HF transformer. $v_{p}$ and $v_{s}$ are HF output voltages on the primary side and the secondary side respectively. The turn ratio of HF transformer is defined as $n_t : 1$. The voltage gain of the DAB converter is defined as $M = n_tV_{out} / V_{in}$.

Fig. 1

Circuit schematic of DAB converter.

TPS control has two independent inner phase-shift $D_1T$, $D_3T$ in two full bridges $S_1$ and $S_4$, $S_5$ and $S_8$. An outer phase-shift $D_2T$ exists between the gating signal of $S_1$ and $S_5$. All phase shifts are referred to the $S_1$ turn-on instant. All the switch duty cycle are set at 50% with a fixed switching frequency $f_s$. The high frequency period is $T=\pi$. The DAB converter operation mode are regulated in TPS control, which composed of various phase-shift $D_1T$, $D_2T$ and $D_3T$ combination. In this work, all the examples were performed in the forward power mode(power flowing from $V_{in}$ to $V_{out}$). The range of phase-shift ratio are $D_1,D_2,D_3 \in [0,1)$. Hence, both $v_{p}$ and $v_{s}$ are became three-level square wave voltages. And, the reverse power mode(power flowing from $V_{out}$ to $V_{in}$) can be concluded as similar method as forward power mode.

Table 1 The output power and mode conditions of TPS.

With the TPS control, the DAB converter has five typical steady-state operation modes for buck operation ($M < 1$), where the converter voltage gain is defined as $M=\frac{n_tV_{out}}{V_{in}}$. In Table 1, the calculation characteristics for each typical mode including mode conditions, output power $P_o$ and normalized peak current $I_{peak}$ are concluded in detail.

Fig. 2

The mode A steady-state waveform of TPS.

Fig. 3

The mode B steady-state waveform of TPS.

According to the peak current $I_{peak}$, these five modes can be categorized into two groups. As shown in Fig. 2, the feature of mode A can be described as $D_2+D_3\leqslant 1$, which contain mode 1,2,3. The mode A has gained considerable attention in TPS control due to soft-switching capability and conversion efficiency performance. The steady-state waveform of mode B are presented in Fig. 3 with feature $D_2+D_3 > 1$, which is typically found in the light-load region⁷. In any mode, there are eight distinctive time intervals in one switching period, in which the on/off state of switches and the polarities of voltages/currents are different.

A general differential equation instantaneous currents of DAB converter in each steady-state time interval can be obtained as (1).

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{rcl} i_1& & = i_0 + \frac{\Delta V}{L_k}(t_1-t_0)T \\ i_2& & = i_1 + \frac{\Delta V}{L_k}(t_2-t_1)T \\ i_3& & = i_2 + \frac{\Delta V}{L_k}(t_3-t_2)T \\ i_4& & = i_3 + \frac{\Delta V}{L_k}(t_4-t_3)T = -i_0. \end{array} \right. \end{aligned} \end{aligned}$$

(1)

where the $\Delta V$ is interval voltage difference.

Load transient problem for direct modulation

The major problem of direct modulation is substantial dc offset and overshoot current during step load response. With the step load change commands, the phase-shift are directly regulated always leads to dc bias current in DAB converter. A typical example of such a direct modulation applied in mode A is shown in Fig. 4. Under the TPS control, when a step load change in a DAB converter happens, the phase-shift are directly modulated from $D_1T$, $D_2T$, $D_3T$ to $(D_1+d_1)T$,$(D_2+d_2)T$,$(D_3+d_3)T$. It can be seen that $S_3$ (rising edge of $v_p$ from 0 to $V_{in}$), $S_6$ (rising edge of $v_s$ from $-n_tV_{out}$ to 0), $S_7$ (rising edge of $v_s$ from 0 to $n_tV_{out}$) turn-on duration are delayed directly in the same time. The duty cycle are extended in this HF period which $DT > \pi$. The initial transient current is same as before. While, the peak transient current is much higher than the theoretical new peak current due to unbalance duty cycle. Thus, the average voltage $V_{ave}$ are unbalance during this HF period. Regarding (1), the inductor average current ${I_{ave}}$ can be obtained as (2) which value is non-zero. The non-zero average current is the dc bias current. Similar to mode A, with direct modulation, mode B would lead to the dc bias current too.

$$\begin{aligned} \begin{aligned} I_{ave} = \frac{(-V_{in}d_1 + n_tV_{out}(2d_2T+d_3))T}{2f_sL_k}. \end{aligned} \end{aligned}$$

(2)

Fig. 4

Transient waveform of DAB converter using direct transient current control with TPS control in mode A.

Fig. 5

Direct modulation Simulation of DAB converter with TPS control in mode A.

Fig. 6

Direct modulation Simulation of DAB converter with TPS control in mode B.

The transient response simulation results of mode A and mode B with direct modulation were presented in Figs. 5 and 6 which illustrate the waveform of $i_L$. With direct modulation, the vertical asymmetry of the current waveform reveals the existence of a dc bias current. While, this drawbacks would brings up extra conduction loss, and this unexpected offset may cause the magnetic saturation, out of switch safe operation region and even a breakdown of HF transformers⁹. Hence, the temporal dc bias current are expected to be zero. It is important to depress the dc bias current generated for a stable transition progress.

TCB modulation for inner mode

In this section, a new transient current balancing (TCB) modulation for the step load response was proposed. A seamless and fast transient response with TCB modulation can be realized. The basic principle of TCB modulation for TPS control is to balance the transient instantaneous current by referring dynamic phase-shift ratio d which is a uniformed solution for all the possible transition cases in TPS control. At initial state, a gating signal is selected as floating reference. During the transient state, the instantaneous currents between transient state and steady state are maintained. And, the dynamic phase-shift ratio d can be solved. Referring to the floating reference, the corresponding gating signals are regulated by dynamic phase-shift dT. Thus, with TCB modulation, in any transient state would turn into steady state immediately. The DAB converter are operated without the dc bias current in any transition of TPS control.

The inner mode is those transition process, in which the initial mode and the final mode are the same, classing into this category. The mode A to mode A was taken as a first example in detail to explain the inner mode transient state with TCB modulation.

Fig. 7

Transient waveform using TCB modulation with TPS control inside mode A.

In TPS control, mode A is most typical forward power mode with features $D_2+D_3\leqslant 1$ (as shown in Fig. 2). The instantaneous currents of DAB converter in the initial mode A steady state can be obtained as (3).

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{rcl} i_1& & = i_0 + \frac{n_tV_{out}}{L_k}D_1T \\ i_2& & = i_1 + \frac{V_{in} + n_tV_{out}}{L_k}(D_2-D_1)T \\ i_3& & = i_2 + \frac{V_{in}}{L_k}D_3T \\ i_4& & = i_3 + \frac{V_{in} - n_tV_{out}}{L_k} (1-D_2-D_3)T. \end{array} \right. \end{aligned} \end{aligned}$$

(3)

Letting $i_0 = -i_4$, the $i_4$ can be found as (4)

$$\begin{aligned} \begin{aligned} i_4 = \frac{(V_{in}(1-D_1) + n_tV_{out}(2D_2+D_3-1))}{2f_sL_k}. \end{aligned} \end{aligned}$$

(4)

Same as direct modulation, the same transient conditions are applied in the proposed TCB modulation too (As Fig. 7 shown). Compared with the direct modulation, the TCB modulation would set a gating signal as floating reference. Referring to the reference signal, the switches $S_1, S_3, S_6, S_7$ turn on duration would modified by phase-shift dT to $(1 + d_1 - d) T$, $(1 + d_2 - d) T$, $(1 +d_2 + d_3 - d) T$, $(1 - d) T$ respectively. According to the TCB modulation, the operation on gating signal during transient state can be concluded as:

• 1. The $S_2$ turn-off moment is selected as floating reference position. And, all the gating signal are optimized by dynamic phase-shift ratio d.

• 2. The $S_3$ turn-off moment is delayed by $(d_1-d)T$. The duration of the on state of $S_3$ is changed from T to $(1 + d_1 - d) T$, which shift the rising edge of $v_p$ (from 0 to $V_{in}$).

• 3. The $S_6$ turn-off moment is delayed by $(d_2-d)T$. The duration of the on state of $S_6$ is changed from T to $(1 + d_2 - d) T$, which shift the rising edge of $v_s$ (from $-n_tV_{out}$ to 0).

• 4. The $S_7$ turn-off moment is delayed by $(d_2+d_3-d)T$. The duration of the on state of $S_7$ is changed from T to $(1 +d_2 + d_3 - d) T$, which shift the rising edge of $v_s$ (from 0 to $n_tV_{out}$).

• 5. The $S_1$ turn-off moment is shifted by $-dT$ to offset overshoot current. The duration of the on state of $S_1$ is changed from T to $(1 - d) T$, which shift the falling edge of $v_p$ (from $V_{in}$ to 0).

• 6. Except for these change, the high frequency period of other switches are still kept at T.

Hence, the instantaneous currents of transient state can be represented as (5).

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{rcl} i'_1 &= i'_0 &+ \frac{n_tV_{out}}{L_k}(D_1 + d_1 - d)T \\ i'_2 &= i'_1 &+ \frac{V_{in} + n_tV_{out}}{L_k}(D_2 + d_2 - D_1 - d_1)T \\ i'_3 &= i'_2 &+ \frac{V_{in}}{L_k}(D_3 + d_3)T \\ i' _4 &= i'_3 & + \frac{V_{in} - n_tV_{out}}{L_k}(1-D_2 - d_2 - D_3 - d_3) T \end{array} \right. \end{aligned} \end{aligned}$$

(5)

As the end of steady state 1 is the beginning of transient state, which the initial transient current is $i'_0=i_0$. Thus, the peak transient current $i'_4$ can be obtained as (6).

$$\begin{aligned} \begin{aligned} i'_4 &=\frac{1}{2f_sL_k} (V_{in}(1 - D_1 - 2d_1) \\&\quad + n_tV_{out}(2 D_2+4 d_2+D_3+2 d_3-1-2d)). \end{aligned} \end{aligned}$$

(6)

From (3) and (4), the steady state 2 peak current ${i''_{4}}$ can be calculated as (7).

$$\begin{aligned} \begin{aligned} i_4&''=\frac{1}{2f_sL_k} (V_{in}(1 - D_1 - d_1) \\&\quad + n_tV_{out}(D_2+2 d_2+D_3+ d_3-1)). \end{aligned} \end{aligned}$$

(7)

To avoid the dc offset, the transient state demands an instantaneous transition to the steady state 2. So, the current between these two state needs to match which is letting $i'_4 = i''_4$. Then, the dynamic phase-shift ratio d can be obtained as (8).

$$\begin{aligned} \begin{aligned} d = d_2+\frac{Md_3-d_1}{2M} \end{aligned} \end{aligned}$$

(8)

As (8) shown, the dynamic phase shift ratio d is only determined by $d_1, d_2, d_3$ and M. Compared with direct modulation, the transient state with TCB modulation only has four time interval (from $t({i'_0})$ to $t({i'_4})$ ) in theoretically.

Similar to mode A, mode B in inner mode can applied TCB modulation in transient state too. Mode B is discontinuous current mode with features $D_2+D_3>1$, which usually exists on light low region⁷. As shown in Fig. 8, the steady state 1 to steady state 2 of mode B can achieve a seamless transition.

Fig. 8

Transient waveform using TCB modulation with TPS control inside mode B.

The instantaneous currents of DAB in the mode B steady state can be obtained as (9).

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{rcl} i_1& & = i_0 \\ i_2& & = i_0 + \frac{ n_tV_{out}}{L_k}(1+D_2)T \\ i_3& & = i_2 + \frac{V_{in}+n_tV_{out}}{L_k}(D_2-D_3)T \\ i_4& & = i_3 + \frac{V_{in} }{L_k} (1-D_2)T = -i_0. \end{array} \right. \end{aligned} \end{aligned}$$

(9)

The steady state 1 peak current $i_4$ of mode B can be get as (10).

$$\begin{aligned} \begin{aligned} i_4 = \frac{(V_{in}(1-D_1) + n_tV_{out}(1-D_3))}{2f_sL_k}. \end{aligned} \end{aligned}$$

(10)

As inner mode of mode A, the $S_2$ turn-off moment is selected as floating reference position. And, the switches $S_1, S_3, S_6, S_7$ turn on duration would be extended by referring the floating reference. According to the dynamic phase-shift dT, all the phase shift were shifted by $( d_1 - d) T$, $( d_2 - d) T$, $(d_2 + d_3 - d) T$, $- d T$ respectively. Except for these changes, other switches still keeps the 50% duty cycle operation. With similar operation on gating signal during transient state, the edge of HF voltages $v_p$ and $v_s$ are shifted correspondingly during the transient state. Thus, the instantaneous currents in transient state of mode B can be calculated easily as (11).

$$\begin{aligned} \begin{aligned} \left\{ \begin{array}{rcl} i'_1 & = i'_0& \\ i'_2& = i'_0& + \frac{ n_tV_{out}}{L_k}(1-D_2-d_1-d)T \\ i'_3& = i'_2& + \frac{V_{in}+n_tV_{out}}{L_k}(D_2+d_2-D_3-d_3)T \\ i'_4& = i'_3 & + \frac{V_{in} }{L_k} (1-D_2-d_2)T. \end{array} \right. \end{aligned} \end{aligned}$$

(11)

The transient current $i_4=-i'_0$ since there no sudden change in transient initial current. So that, the $i'_4$ can be solve as (12).

$$\begin{aligned} i'_4& =\frac{(V_{in}(1 - D_1 - 2d_1) + n_tV_{out}(1-D_3+2 d_2-2d))}{2f_sL_k}. \end{aligned}$$

(12)

And, the mode B steady state 2 peak current ${i_{4}}$ can be calculated as (13).

$$\begin{aligned} i'_4 & =\frac{(V_{in}(1 - D_1 - d_1) + n_tV_{out}(1-D_3-d_3))}{2f_sL_k}. \end{aligned}$$

(13)

To achieve balancing in the inductor current such that $i'_4 = i''_4$, the dynamic phase-shift ratio $d$ can be derived as shown in (8) which is the same solution for the TCB modulation. Meanwhile, the transient state of mode B begins at $t({i'_0})$ and ends at $t({i'_4})$ which contains 4 time interval too.

Although the calculation processes are not same, the TCB solution expression of dynamic ratio d is always same as (8). Thus, the TCB modulation can obtain a uniformed solution for the inner mode.

TCB modulation for inter mode

Generally, the inter mode which the transitions between two different mode, were more complicated than inner mode. However, a smooth inter mode transient response can be realized with TCB modulation. After determined the floating reference, the general operation on gating signal during inter mode transient state are similar to inner mode. So, the result of dynamic phase shift ratio d are unified in inter mode too.

The transient period from mode A to mode B was presented in Fig. 9. The turn-off instant of $S_2$ is determined as the floating reference. The switches $S_1, S_3, S_6, S_7$ turn-on duration over four time intervals with TCB modulation are became to $(1+d_1-d)T$, $(1+d_2-d)T$, $(1+d_2+d_3-d)T$ and $(1-dT)$, respectively. The other switches kept the 50% duty cycle. Also, the rising edge of $v_p$, the rising edge of $v_s$ and falling edge of $v_p$ are manipulated step by step. Then, the transient state starts at $t(i'_0)$ and ends with $t(i'_4)$ with four independent time intervals, indicating that steady state 2 can begin by $t(i'_4)$.

From mode A to mode B, the $i_4$ of initial steady state is same as mode A which is represented as (3) and (4). Then, the transient state current $i'_4$ can be obtained as (12) by solving (11). In the steady state 2 (mode B), the current $i''_4$ is same as (13). With TCB modulation, the dynamic phase shift dT can be found by balancing transient current between mode A and mode B ($i'_0=-i''_4$). Hence, the dynamic phase shift ratio $d =d_2 +\frac{Md_3-d_1}{2M}$, which only represent by $d_1, d_2, d_3$ and M too.

Fig. 9

Transient waveform using TCB modulation with TPS control form mode A to mode B.

To provide more detail of TCB modulation for inter mode, a transition process from mode B to mode A was displayed in Fig. 10. The transient period is from $t(i'_0)$ to $t(i'_4)$, which includes four time intervals as in each above-mentioning examples. The turn-on duration of $S_1, S_3, S_6, S_7$ are altered with dynamic phase-shift dT to $(1 + d_1 - d) T$, $(1 + d_2 - d) T$, $(1 +d_2 + d_3 - d) T$, $(1 - d) T$ respectively. The rising and falling edge of $v_p$ are delayed by $(d_1-d)T$ and dT. The $v_s$ rising edge are delayed by $(d_2-d)T$ and $(d_2+d_3-d)T$.

With TCB modulation, the transient current $i'_4$ is intended to be equal as the post steady state peak current $-i''_0$. Hence, the steady state 2 of this mode begins with $i'_4$ as expected. Regarding (6) and (7), the expression of dynamic phase shift ratio d remains the same as (8).

Fig. 10

Transient waveform using TCB modulation with TPS control form mode B to mode A.

Based on the analysis on this section, some features of the proposed TCB modulation can be concluded as follows. The TCB modulation is a universal method for all the transient response of TPS control which with consistent solution. The dynamic phase shift ratio d is applied on the gating signals of selected switches which based solely on $d_1, d_2, d_3$ and M. The modification of these gating signals affects on the two HF voltages $v_p$ and $v_s$. The rising edge or falling edge of $v_p$ and $v_s$ are altered to eliminate the dc bias current. Meanwhile, the duration of the transient state always encompasses four time intervals.

Validation by experimental results

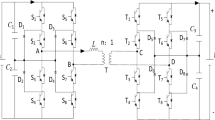
A lab prototype of a DAB converter was built and tested for validation of the proposed TCB modulation. The layout was presented as Fig. 11. Two dc sources $V_{in}$ = 120 V and $V_{out}$ = 72 V. The voltage gain $M=0.6$. EA 8360-15T bench power supply is used as the input DC source, while the load is provided with a BK 8510 programmable DC electronics load. The HF transformer is made of an ETD49 ferrite core with a material type of N97. The actual turn ratio of windings is 18:18 ($n_t=1:1$) and the resulted magnetizing inductance is 4 mH. The series inductor $L_k=53.84 \mu$H. The switching frequency $f_s=100 k$Hz. The high frequency period $T = 5\mu$s. EP4CE115F23I7N FPGA board from Altera is applied as the PWM generator to generate the gating signals of DAB converter. All the switches on H-Bridge are implemented with IPP320N20N (200 V, 34 A, $R_{ds}$=60 $m\Omega$) from Infineon. The detail specifications of prototype is listed in Table 2.

Table 2 Detial specification of prototype.

Fig. 11

The experimental prototype.

The implementation of the proposed TCB modulation is shown in Fig. 12. The I/O interface of FPGA checks and confirm the load step commands. Once the load step command is confirmed, the new demand load level $P^*$ can be evaluated, and the current phase-shift $D_1*$, $D_2*$, $D_3*$ can be updated based on $P^*$. With the difference between $D_1*$, $D_2*$, $D_3*$ and initial phase-shift $D_1$, $D_2$, $D_3$, the $d_1$, $d_2$, $d_3$ can be calculated and dynamic phase-shift ratio d can be solved which would sent to PWM generator. After PWM generator arrangement, the gating signals of transient response are applied on DAB converter.

Fig. 12

The implementation of the proposed TCB modulation.

The direct modulation of mode A is presented as Figs. 13 and 14. The transient current are apparently decreased with a long transient period where more than 30 HF periods. The initial phase-shifts are $D_1 = 24^\circ$, $D_2=42^\circ$, $D_3=12^\circ$ at 100 W. And, new steady state is $D_1^* = 36^\circ$, $D_2^*=72^\circ$, $D_3^*=24^\circ$ at 130 W. The switch $S_3$, $S_6$, $S_7$ turn on duration are directly expanded according to $d_1=12^\circ$, $d_2=30^\circ$, $d_3=12^\circ$. The phase-shift command is effects on the rising edge of $v_p$ (0 to $V_{in}$)and the rising edge of $v_s$ ($-n_tV_{out}$ to 0, 0 to $n_tV_{out}$). During the transient state, the peak current $i_L$ jump from 0.97A to 1.92A then back to 1.45A, which indicates a non-zero transient current. It would results in a temporal DC bias current at 0.45A. Similar dc offset phenomena also exists in other TPS transient processes with direct modulation.

Fig. 13

Experimental waveform using direct modulation.

Fig. 14

Experimental waveform using direct modulation.

The experimental waveform of inner mode with proposed TCB modulation is displayed in Figs. 15 and 16. Experimental waveform using TCB modulation in mode A as shown in Fig. 15, the initial steady state conditions is same as direct modulation $D_1 = 24^\circ$, $D_2=42^\circ$, $D_3=12^\circ$. When the power level rise from 100 W to 130 W, the post steady state conditions $D_1+d_1 = 36^\circ$, $D_2+d_2=72^\circ$, $D_3+d_3=24^\circ$. So, the $d_1=12^\circ$, $d_2=30^\circ$, $d_3=12^\circ$ and dynamic phase-shift ratio $d=26^\circ$. $S_2$ is set as floating reference, and the turn on duration of $S_1$, $S_3$, $S_6$, $S_7$ is expended. The rising and falling edge of $v_p$, the rising edge of $v_s$ are manipulated with $14^\circ$, $-4^\circ$, $14^\circ$, $26^\circ$ step by step. When proposed TCB modulation is adopted, the transient peak current instantly step from 0.95A to 1.45A. The current $i_L$ is always symmetric about the x-axis, which indicates zero bias current. The experimental result illustrate that a fast and seamless transition within mode A. Thus, the transient response is completed instantly without overshoot current and dc offset.

Fig. 15

Experimental waveform using TCB modulation inner mode A.

The inner mode experimental waveform using TCB modulation in mode B is given in Fig. 16, where a decline in the power level from 75 W to 40 W. The initial steady state conditions are $D_1 = 120^\circ$, $D_2=135^\circ$, $D_3=110^\circ$. The post steady state conditions $D_1+d_1 = 135^\circ$, $D_2+d_2=140^\circ$, $D_3+d_3=120^\circ$. So, the $d_1=15^\circ$, $d_2=5^\circ$, $d_3=10^\circ$ and dynamic phase-shift ratio $d=-5.5^\circ$. Since d is negative, the turn on duration of switches are extended. Referring to the floating reference, the rising and falling edge of $v_p$, the rising edge of $v_s$ are shifted according to the dynamic phase-shift ratio d by $10^\circ$, $-0.5^\circ$, $5^\circ$, $-5^\circ$, respectively. The transient peak current instantly reduces from 1.12 A to 0.93 A, indicating the dc offset free transient operation. Thus, TCB modulation effectively completes the seamless transition in mode B as predicted.

Fig. 16

Experimental waveform using TCB modulation inner mode B.

The Experimental plots shown in Fig. 17 is experimental waveform using TCB modulation from mode A to mode B. At the initial Mode A operating at 95 W, the phase-shifts are $D_1 = 60^\circ$, $D_2=45^\circ$, $D_3=60^\circ$. The post steady state is mode B at 130 W which $D_1^* = 90^\circ$, $D_2^*= 135^\circ$, $D_3^*=80^\circ$. Then, the differences in phase-shifts are $d_1=30^\circ$, $d_2=90^\circ$, $d_3=20^\circ$. Thus, the dynamic phase-shift ratio $d=75^\circ$. The $S_2$ turn off moment is set as floating reference position. Furthermore, the switches $S_1, S_3, S_6, S_7$ turn-on duration are extended with phase-shift dT to $\frac{7}{12}T$, $\frac{3}{4}T$, $\frac{13}{12}T$, $\frac{43}{36}T$ respectively. Other switches turn-on duration are maintained. The current amplitude jumps from 1.15A to 1.40A immediately without overshoot current or dc bias current.

Fig. 17

Experimental waveform using TCB modulation from mode A to mode B.

Experimental plots of transient response from mode B to mode A is presented in Fig. 18. The phase-shifts at initial mode B at 110 W are $D_1 = 60^\circ$, $D_2=135^\circ$, $D_3=60^\circ$. The new steady state is mode A at 160 W with $D_1^* = 30^\circ$, $D_2^*= 90^\circ$, $D_3^*=45^\circ$. So the adjustments parameter is $d_1=-30^\circ$, $d_2=-45^\circ$, $d_3=-15^\circ$. Then, the dynamic phase-shift ratio $d=-27.5^\circ$ where causing the edge of $v_p$ and $v_s$ are delayed with $2.5^\circ$, $17.5^\circ$, $-12.5^\circ$, $27.5^\circ$ respectively. The transient current amplitude instantly increases from 1.25A to 1.78A. From mode B to mode A, there no noticeable dc bias current can be observed on the current waveform at the transient response.

Fig. 18

Experimental waveform using TCB modulation from mode B to mode A.

According to the experimental results in this section, the proposed TCB modulation of TPS control can realize a fast load step transition. The TCB modulation would not bring up extra conduction loss since it eliminate dc offset and overshoot current. The TPS transient state with TCB modulation is smooth and seamless. Meanwhile, the TCB modulation has a unified solution in TPS control, which is simple and easy to apply. Thus, compared with conventional modulation, the TCB modulation offers overall improved transition performance.

Table 3 Comparison between previous works.

Finally, the TCB modulation proposed in this work is compared with previous research. The comparison results are presented in Table 3. It is evident from the table that there are significant advantages in aspects such as computational complexity, unified solution and control complexity.

Conclusion

This work has mainly proposed a transient current balancing modulation for a DAB converter with TPS control during the load step response. By adjusting corresponding gating signals with TCB modulation, a seamless transient response and dc-bias-free system can be implemented. Through theoretical analysis, the TCB modulation can be applied to all transition situations of TPS control with an unified solution. Compared with the traditional direct modulation, TCB modulation only demands to adjust the required phase-shift in each PWM module. The results of experimental test show the transient state of direct modulation and TCB modulation in different situations, demonstrating that TCB modulation can minimize response duration and eliminate dc offset successfully. Therefore, the TCB modulation is an effective method to depress the dc offset, while ensuring a satisfactory and faster transient response performance of DAB converter.