A novel EWMA-based adaptive control chart for industrial application by using hastings approximation

Abstract

Control charts are commonly used for process monitoring under the assumption that the variable of interest follows a normal distribution. However, this assumption is frequently violated in real-world applications. In this study, we develop an adaptive control chart based on the exponentially weighted moving average (EWMA) statistic to monitor irregular variations in the mean of the Truncated Transmuted Burr-II (TTB-II) distribution, employing Hastings approximation for normalization. We propose a continuous function for the adaptation of the smoothing constant. The performance of the proposed TTB-II distribution is compared with multiple existing distributions, including TB-II, TB-III, TB-XII, B-II, B-III, and B-XII, to demonstrate its competitive advantages. The run-length profiles, including the average run-length (ARL) and the standard deviation of run-length (SDRL), are computed under various parameter settings. The effectiveness of the proposed chart is evaluated using Monte Carlo (MC) simulations in terms of run-length profiles. The practical implementation of the proposed chart is demonstrated with a real dataset, illustrating the design and application procedures.

Introduction

Statistical process control (SPC) is a process enhancement method broadly utilized by recent industrial and service organizations. This methodology is founded on the utilization of control charts and quality characteristics data. Communal and well-established control charts include the Shewhart control chart that was proposed by W. A. Shewhart¹. Control charting is an important tool to observe the quality of a process. The utilization of a control chart is to control continuous process by recognizing and remedying issues as they happen, foreseeing the regular scope of results produced by the process, determining if a process is steady, investigating patterns of process discrepancy from common causes, non-routine events, or special causes, incorporated into the process. The control charts recognize the perfect opportunity for activity when the process has a deviation. Subsequently, a control chart identifies the ideal restorative move time. Roberts² proposed EWMA chart to monitor mean which was distributed as normal. The EWMA statistic-based control charts perform considerably better as compared to the Shewhart control chart in recognizing a small to moderate magnitude of the shift in a process. In SPC literature, the competence of EWMA statistic-based control charts, in recognizing the small to moderate magnitude of shifts in process and expecting the process level at the accompanying time frame, attracts various scholars and professionals. Added details can be seen in Lucas & Saccucci³, Lowry et al.⁴, and Zhao et al.⁵. Some new amendments in the EWMA chart with quantified shifts are considered by Riaz et al.⁶.

Although the eminence of these control charts, they are viable when the quality analyst is concerned with planning a control chart for a particular shift. Nonetheless, the situation is extremely phenomenal; the magnitude of shift is known in advance. So, lately, analysts have begun zeroing in on the design of adaptive control charts which provide more developed affirmation against various magnitudes of shift sizes in the process. In an adaptive EWMA (AEWMA) control charting scheme we generally adapt any of the parameter of control charts based on sample information. The basic idea is to work on error size, $\:{y}_{t}-{x}_{t-1}$, to recognize, in a further cleared path, different shift sizes while diminishing the inertia issue. Capizzi & Masarotto⁷ designed an AEWMA chart for mean. The AEWMA chart was intended to consolidate the provision of EWMA chart by utilizing the Huber score function. Zhao et al.⁵, utilize the adaptable computation, to analyze the dynamic noticing arrangement of the voltage departure provisions or difference shortcomings in energy putting away systems on specific grounds. Sarwar, M.A. & Noor-ul-Amin⁸ proposed AEWMA chart constructed on a continuous function.

Shafqat et al.⁹ presented an attribute chart based on the Burr X by incorporating a Moving Average (MA) scheme. They calculated ARLs considering varying sample sizes, MA statistics, and parameter values. Results show that the new MA control chart is better than existing chart. Similarly, Tan & Liu¹⁰ introduced an EWMA control chart based on the Truncated Normal distribution to monitor process mean in the presence of outliers. Their results indicate that this chart remains robust with standard normally distributed data, and the control limits are unaffected by both the quantity and magnitude of outliers. Under the normality assumption, a control chart might mislead manufacturing engineers to notice a process shift. For studying system failure data, Burr¹¹ proposed a family of distributions that contain twelve different forms of Cumulative Distribution Function (CDF). The corresponding distribution functions have a variety of shapes that help this system the use in extensive areas of application. Type I contains the uniform distribution, and types II, III, X, and XII have a variety of shapes that enable this system to approximate histograms of various kinds of data. Although some properties of Burr type II distribution have been examined Tadlkamalla¹² and Ragab, A¹³. but some dimensions still need consideration. So, we consider this type of Burr family in the present manuscript.

Let X follows the Burr type II distribution with cdf given as

$$\:G\left(x;k\right)={\left({e}^{-x}+1\right)}^{-k}\:,\:$$

(1)

with respective probability density function (pdf) given as,

$$\:g\left(x;k\right)=k{\left({e}^{-x}+1\right)}^{-k-1}{e}^{-x},\:\forall\:\:x\in\:\left(-\infty\:,+\infty\:\right)\:\wedge\:\:k>0$$

(2)

where shape parameter k defines different shapes of the model. Various fields of science used the Burr type II distribution. In reliability engineering, the truncated transmuted Burr-II distribution can be effectively applied to model the lifespan of mechanical or electronic components. Often, these components exhibit lifetimes that are right-skewed, with most failing within a predictable period but a few lasting exceptionally longer. However, lifetimes are naturally bounded by physical constraints or practical limits, such as warranty periods or operational caps. By using this distribution, engineers can accurately model both the common failure times and rare, extended lifespans within a defined range, helping to optimize maintenance schedules and anticipate long-term performance. Some other real-life data sets exhibited by the Burr type II distribution are actuarial, finance, environment, survival analysis, failure data, metrology, flood levels, and risk insurance. The transformation or addition of parameter(s) to well-known distributions are commonly used methods in literature to obtain newly modified, extended, and generalized distributions. These recently evolved models give a superior fit to the data over the sub and contending models.

Several distributions can be utilized to observe the production process, and in this manuscript, the control chart has been derived using the proposed left Truncated Transmuted Burr type II (TTB-II) distribution to monitor process. The outline of the remaining manuscript is coordinated as follows: Sect. 2 provides an intensive portrayal of TTB-II distribution, in Sect. 3, a detailed design of the proposed chart for TTB-II distribution is given. Section 4 provides the performance of the proposed AEWMA chart. For illustration purposes, the working of the proposed AEWMA control chart using a real-life data set example is presented in Sect. 5. At last, Sect. 6 précises the key disclosures and closes the manuscript.

Description of TTB-II distribution

In distribution theory, the distribution having heavy-tailed and can be significantly skewed are quite good to explain many real-life situations. The transmutation map method is viewed as a helpful approach to developing new distributions. Shaw & Buckley¹⁴ proposed quadratic rank transmutation map method (QRTMM) through which we can get a new extended model that would be added flexible by introducing a transmuted parameter to an existing distribution. Added details about the QRTMM can be seen in Shaw & Buckley¹⁴, . The new extended model describes better properties of the tail and also improves the goodness of fit statistics. For modeling the life testing problems, here we generalize the Burr type II distribution using the QRTMM. In literature many distributions based on the QRTMM are available for modeling lifetime data; for illustration, Nofal et al.¹⁵, Khan et al.¹⁶, and Afify et al.¹⁷.

Definition 1

Let the continuous random variable Y of the base distribution have cdf G(y). Now, the QRTM distribution of Y is given as

$$\:F\left(y\right)=-\:\lambda\:{G}^{2}\left(y\right)+\lambda\:G\left(y\right)+G\left(y\right),\:\:\:\:\:\:\:\forall\:\:\lambda\:\in\:\left[-1,+1\right],$$

(3)

also, the respective pdf is

$$\:f\left(y\right)=g\left(y\right)\left[-2\:\lambda\:G\left(y\right)+\lambda\:+1\right],\:\:\:\:\:\:\:\:\:\:\:\forall\:\:\lambda\:\in\:\left[-1,+1\right],$$

(4)

where f(y) is the pdf QRTM distribution and g(y) is the pdf of the base distribution. For $\:\lambda\:$ = 0, the QRTM distribution of Y reduces to the base distribution of Y.

Definition 2

Let denote a left truncated random variable with a threshold is defined as Its cdf is as follows

$$\:{F}_{l}\left(y\right)=\frac{F\left(y\right)-F\left(l\right)}{1-F\left(l\right)},$$

(5)

where F(y) is the cdf of the base distribution.

Proposition 1

Let be the vector of parameters of a continuous random variable Z which follows the transmuted Burr type II (TB-II) distribution, also the cdf of Z is given as

$$\:F\left(z;\varvec{\omega\:}\right)={\left(1+{e}^{-z}\right)}^{-k}\left[\lambda\:-\:\lambda\:{\left({e}^{-z}+1\right)}^{-k}+1\right],$$

(6)

where $\:{\uplambda\:}$ and k are the transmuted and shape parameters of the TB-II distribution correspondingly.

Proof

Consider the pdf and cdf introduced in Eqs. (1) and (2) which relate, correspondingly, to g(x) and G(x) in Eqs. (4) and (3) of Definition 1. Now we can easily affirm this by applying Definition 1 to the considered pdf and cdf. Then, at that point, in like manner, the respective pdf of the TB-II distribution is as under

$$\:f\left(z;\varvec{\omega\:}\right)=k{\left({e}^{-z}+1\right)}^{-k-1}{e}^{-z}\left[\lambda\:-2\:\lambda\:{\left({e}^{-z}+1\right)}^{-k}+1\right],$$

(7)

The idea of a truncated distribution plays a substantial role in analyzing process optimization, quality improvement, and in many production processes. To truncate a distribution is to limit its values to some defined interval and then normalize this density so that the integral over that interval is one. Truncated distributions emerge in situations where the occurrence of the event is restricted to values that lie above or under a given threshold or inside a predetermined range.

Proposition 2

Let Y be a random variable and be the vector of parameters. If Y follows the TTB-II distribution, then the cdf of Y is as follows

$$\:F\left(y;\varvec{\omega\:}\right)=\frac{\left[\left\{{\left({e}^{-y}+1\right)}^{-k}-{2}^{-k}\right\}\lambda\:-\:\left\{{\left({e}^{-y}+1\right)}^{-2k}-{2}^{-2k}\right\}\lambda\:+1\right]}{{4}^{-k}\left({2}^{k}-1\right)\left({2}^{k}-\lambda\:\right)},\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:y\in\:\left(0,\infty\:\right),$$

(8)

or

$$\:F\left(y;\varvec{\omega\:}\right)=\frac{\left(1+\lambda\:\right)\left\{\sum\:_{i=0}^{\infty\:}\left(\genfrac{}{}{0pt}{}{i+k}{i}\right){e}^{-yi}{\left(-1\right)}^{i}-{2}^{-k}\right\}-\lambda\:\left\{\sum\:_{i=0}^{\infty\:}\left(\genfrac{}{}{0pt}{}{2k+i}{i}\right){\left(-1\right)}^{i}{e}^{-yi}-{4}^{-k}\right\}}{A},\:\:\:\:\:y\in\:\left(0,\infty\:\right),$$

(9)

where $\:{A=4}^{-k}\left({2}^{k}-1\right)\left({2}^{k}-\lambda\:\right).$ Also $\:{\uplambda\:}$, and k are transmuted and shape parameters of the TTB-II distribution correspondingly.

Proof

Consider the cdf introduced in Eq. (6) which relates, correspondingly, to F(x) in Eq. (5) of Definition 2. Now we can easily affirm this by applying Definition 2 to the considered cdf. Then, at that point, in like manner, the respective pdf of the TB-II distribution is as under

$$\:f\left(y;\varvec{\omega\:}\right)={A}^{-1}k{{e}^{-y}\left({e}^{-y}+1\right)}^{-k-1}\left[-\:2\lambda\:{\left({e}^{-y}+1\right)}^{-k}+\lambda\:+1\right],\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:y\in\:\left(0,\infty\:\right),$$

(10)

or

$$\:f\left(y;\varvec{\omega\:}\right)=\frac{\left(1+\lambda\:\right)k\sum\:_{m=0}^{\infty\:}\left(\genfrac{}{}{0pt}{}{k+m}{m}\right){\left(-1\right)}^{m}{e}^{-y(m+1)}-2k\lambda\:\sum\:_{m=0}^{\infty\:}\left(\genfrac{}{}{0pt}{}{2k+m}{m}\right){\left(-1\right)}^{m}{e}^{-y(m+1)}}{A},\:\:\:\:\forall\:\:y\in\:\left(0,\infty\:\right)$$

(11)

where $\:{A=4}^{-k}\left({2}^{k}-1\right)\left({2}^{k}-\lambda\:\right).$ Also $\:{\uplambda\:}$, and k are transmuted and shape parameters of the TTB-II distribution correspondingly. The fact that approaches various distributions makes the proposed TTB-II model a truly adaptable model. The different properties of TTB-II are discussed in supplementary Appendix A and some important graphs can be visualized in supplementary Appendix B.

Fig. 1

(a) pdf plots for selected values of λ of TTB-II distribution. (b) pdf plots for selected parameter values of TTB-II distribution

Figure 1(a), (b) present the pdf plots of TTB-II distribution at different parametric settings.

Design of the proposed AEWMA chart

In this section, we explain the design of the proposed AEWMA chart to monitor the process which follows the proposed TTB-II (a positively skewed) distribution. Let $\:\left\{{U}_{t}\right\}$ be an identically independent sequence of two-parameter TTB-II distributed random variables with shape and transmute parameters k, λ respectively i.e., $\:U\sim$TTB-II (k, λ). The respective cdf of U is as under

$$\:H\left(u\right)=\frac{\left[\lambda\:\left\{{\left({e}^{-u}+1\right)}^{-k}-{2}^{-k}\right\}-\:\lambda\:\left\{{\left({e}^{-u}+1\right)}^{-2k}-{2}^{-2k}\right\}+1\right]}{{4}^{-k}\left({2}^{k}-1\right)\left({2}^{k}-\lambda\:\right)}\:\:\:\:\:\:u\in\:\left(0,\infty\:\right),\:\:k\in\:\left(0,\infty\:\right)\:\wedge\:\:\lambda\:\in\:\left[-1,+1\right],\:$$

(12)

To normalize the $\:{U}_{t},\:$we used the algebraic approximation proposed by Hastings¹⁸.

$$\:Z=-\left(x-\frac{{c}_{0}+{c}_{1}x+{c}_{2}{x}^{2}}{{d}_{0}+{d}_{1}x+{d}_{2}{x}^{2}+{d}_{3}{x}^{3}}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:H\left(u\right)\in\:(0,\:0.5]$$

(13)

$$\:Z=+\left(x-\frac{{c}_{0}+{c}_{1}x+{c}_{2}{x}^{2}}{{d}_{0}+{d}_{1}x+{d}_{2}{x}^{2}+{d}_{3}{x}^{3}}\right)\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:H\left(u\right)\in\:(0.5,\:1.0)$$

(14)

where:

$$\:x=\left\{\begin{array}{c}\sqrt{ln\left(\frac{1}{{\left(H\left(u\right)\right)}^{2}}\right)}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:H\left(u\right)\in\:\left(0,\:0.5\right]\\\:\sqrt{ln\left(\frac{1}{{\left(1-H\left(u\right)\right)}^{2}}\right)}\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:H\left(u\right)\in\:(0.5,\:1.0)\end{array}\right.$$

(15)

$$\:{c}_{0}=2.515517\:\:\:\:\:\:\:\:\:\:\:{c}_{1}=0.802853\:\:\:\:\:\:\:\:\:\:\:\:{c}_{2}=0.010328$$

$$\:{d}_{0}=1.000000\:\:\:\:\:\:\:\:\:\:{d}_{1}=1.432788\:\:\:\:\:\:\:\:\:\:\:{d}_{2}=0.189269\:\:\:\:\:\:\:\:\:\:\:{d}_{3}=0.001308$$

Now,

For the in-control process, $\:{Z}_{t}$ is standard normal variable, i.e., $Z_{t} \sim N\left( {{\text{0,1}}} \right)$.

The literature has recommended that the shift magnitude of the process $\:{\delta\:}_{t},\:$which cannot be known in advance practically, can be estimated using some estimator. Here we estimate $\:{\delta\:}_{t}$ using the estimator proposed by Haq et al.¹⁹ given as

$$\:{{\widehat{\delta\:}}^{*}}_{t}=\:{{\widehat{\delta\:}}^{*}}_{t-1}+\varphi\:\left({Z}_{t}-{{\widehat{\delta\:}}^{*}}_{t-1}\right)$$

(16)

$$\:{{\widehat{\delta\:}}_{t}}^{**}=\:\frac{{{\widehat{\delta\:}}_{t}}^{*}}{1-{\left(1-\varphi\:\right)}^{t}}$$

(17)

where$\:\:\varphi\:\in\:\left(\text{0,1}\right]$, $\:{{\widehat{\delta\:}}_{0}}^{*}=0$. Taking absolute value of $\:{{\widehat{\delta\:}}_{t}}^{**}$ as $\:{\widehat{\delta\:}}_{t}$ (estimate for $\:{\delta\:}_{t}$). Now the plotting statistic of the proposed chart by using the sequence$\:\:\left\{{Z}_{t}\right\}$ is given as

$$\:{F}_{t}=\:g\left({\widehat{\delta\:}}_{t}\right){Z}_{t}+\left(1-g\left({\widehat{\delta\:}}_{t}\right)\right){F}_{t-1}$$

(18)

where $\:{F}_{0}=0$ and $\:g\left({\widehat{\delta\:}}_{t}\right)\in\:\left(\text{0,1}\right]$ such that

$$\:g\left({\widehat{\delta\:}}_{t}\right)=\left\{\begin{array}{c}\begin{array}{c}\frac{1}{24\left[1+{\left({\widehat{\delta\:}}_{t}\right)}^{-2}\right]}\:\:\:\:\:\:\forall\:\:{\widehat{\delta\:}}_{t}\in\:\left(\text{0.0,1.0}\right]\\\:\frac{1}{19\left[1+{\left({\widehat{\delta\:}}_{t}\right)}^{-1}\right]}\:\:\:\:\:\:\forall\:\:{\widehat{\delta\:}}_{t}\in\:\left(\text{1.0,2.7}\right]\end{array}\\\:1\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\forall\:\:{\widehat{\delta\:}}_{t}\in\:(2.7,\infty\:)\end{array}\right.$$

(19)

These values of constants are suggested for which the given continuous function is overall better as far as run-length profiles. The $\:{F}_{t}$ is obtained by using$\:\:g\left({\widehat{\delta\:}}_{t}\right)$ in such a way that the chart becomes optimal in the early recognition of shifts in the process mean. The working of the proposed chart is similar to the control chart suggested by Sarwar, M.A. & Noor-ul-Amin⁸.

Decision rule. The proposed statistic $\:\left|{F}_{t}\right|$ gives an out-of-control warning whenever it is more than the threshold L (always supposed to be positive) if a one-sided AEWMA control chart. Likewise, the proposed statistic $\:\left|{F}_{t}\right|$ produces an out-of-control signal whenever $\:{F}_{t}$ > L or $\:{F}_{t}$ < -L if two-sided chart is taken.

When $\:\psi\:$ and n are given, the value of L (L > 0) is a threshold. The threshold is chosen so that $\:\left|{F}_{t}\right|$ is ensured at some chosen fixed level (say ARL0). For specific values of n and $\:\:\psi\:$, the value of L is determined independently. The $\:L$ value is utilized to compute the ARL0 (fixed in-control ARL); threshold by selecting the recommended adaptive functional methodology.

Performance assessment

Run-length profiles such as the mean, and the standard deviation of run-lengths are good measures to evaluate the efficiency of a control chart. The Markov chain method, the probability method, the MC simulations method, and the method of Integral equations are well-known available methods in SPC literature. Here we leaned toward the MC simulation method. The run-length profiles are computed using 100,000 iterations with ARL₀ = 370, and$\:\:\psi\:=$ 0.15, 0.20.

Algorithm

For the data distributed as TTB-II distribution the run length matrices are quantified in the following steps:

• Step 1 Specify the parameters of TTB-II distribution and fix the smoothing constant .

• Step 2 Randomly generate sample value at time t and compute value by using Eq. (12).

• Step 3 Normalize the TTB-II data using Eqs. (13), (14).

• Step 4 Estimate shift estimator (say) by using and according to this estimated, the function will determine (smoothing constant) and then the plotting statistic is computed using (Sect. 3 contains the detail of the design).

Determine the ARL₀

Decide on the desired ARL₀ value (e.g., 370) to ensure the process behaves as expected when in control.

• i. Choose the control limit value, L, such that ARL₀ converges to the desired value (e.g., 370). This is achieved by performing simulations with 100,000 replicates under the in-control state.

• ii. Before using the chart to detect out-of-control state at a specified shift level δ, perform similar simulations to identify appropriate combinations of parameters (e.g., smoothing constants, sample sizes) that work effectively for the shifted process.

For out-of-control situation

• i. If$\:\:\left|{F}_{t}\right|>L,\:$called out-of-control, becomes run-length, save iteration number as run-length. Else, repeat steps 2–4.

• ii. Continue selection of sampling units from to complete hundred thousand replications.

• iii. The run-length profiles at different specified $\:\delta\:$ are assessed through respective simulations.

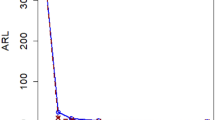
From the analysis of Tables 1 and 2, the general lead of the results of a short conversation is given by.

• At fixed $\:\psi\:$ and k, both the ARL and SDRL increases, as the transmuted parameter λ increases and vice versa. From Table 1 with λ = 0.90, 0.95 at $\:\psi\:\:$= 0.15 with k = 0.25 the respective ARL = 44.32, 80.72, and SDRL = 35.41, 66.79. A similar result can be seen in Table 2.

• At fixed $\:\psi\:$ and λ, both the ARL and SDRL increases, as the shape parameter k increases and vice versa. For illustration, from Table 1 with k = 0.25, 1.50 at $\:\psi\:\:$= 0.15 with λ = 0.80 the respective ARL = 26.48, 71.59, and SDRL = 20.94, 58.57. A similar result can be seen in Table 2.

• At fixed k and λ, both the ARL and SDRL incline to increase, as the smoothing constant $\:\psi\:$ decreases and vice versa. For illustration, from Tables 1 and 2 with k = 0.25 at $\:\psi\:\:$= 0.15, 0.20 with λ = 0.95 the corresponding ARL = 174.16, 173.40, and SDRL = 155.85, 149.81.

• For a monitoring system where the understudy variable is sensitive, the small value of $\:\psi\:$ can increase the responsiveness of the proposed AEWMA chart.

Table 1 Results of the AEWMA chart for ARL₀ = 370, $\:\psi\:$ = 0.15, and L = 0.1689.

Table 2 Results of the AEWMA chart for ARL₀ = 370, $\:\psi\:$ = 0.20, and L = 0.2039.

Illustrative example

Using simulated data and real data sets the proposed control charts has been trailed by many researchers in SPC literature. Here, we study a real-life data to present the application and working of the suggested AEWMA control chart. For this purpose, the real data set prior utilized by Abdul-Moniem²⁰ is considered. The data set is regarding the life of fatigue fracture of Kelvar 373/epoxy. Constant pressure at the 90% stress level is applied till all had failed on this data so there is no censoring and we have a complete data set. The data is listed as: 0.0251, 0.0886, 0.0891, 0.2501, 0.3113, 0.3451, 0.4763, 0.5650, 0.5671, 0.6566, 0.6748, 0.6751, 0.6753, 0.7696, 0.8375, 0.8391, 0.8425, 0.8645, 0.8851, 0.9113, 0.9120, 0.9836, 1.0483, 1.0596, 1.0773, 1.1733, 1.2570, 1.2766, 1.2985, 1.3211, 1.3503, 1.3551, 1.4595, 1.4880, 1.5728, 1.5733, 1.7083, 1.7263, 1.7460, 1.7630, 1.7746, 1.8275, 1.8375, 1.8503, 1.8808, 1.8878, 1.8881, 1.9316, 1.9558, 2.0048, 2.0408, 2.0903, 2.1093, 2.1330, 2.2100, 2.2460, 2.2878, 2.3203, 2.3470, 2.3513, 2.4951, 2.5260, 2.9911, 3.0256, 3.2678, 3.4045, 3.4846, 3.7433, 3.7455, 3.9143, 4.8073, 5.4005, 5.4435, 5.5295, 6.5541, 9.0960. The summary statistics are presented in Table 3. We compare the TTB-II distribution with those of its competitive distributions, namely: the Transmuted Burr II (TB-II) (New), Transmuted Burr III (TB-III) Abdul-Moniem²⁰, Transmuted Burr XII (TB-XII) Afify et al.¹⁷, Burr II (B-II), Burr III (B-III) and Burr XII (B-XII) Burr¹¹, distributions with densities given in supplementary Appendix A. -2log likelihood (-2$\:\widehat{l}$), AIC, CAIC, and BIC are the four different statistics of fit as the selection criterion for the optimal model. Further, four different renowned goodness of fits (GOF) statistics named Cramer-von Mises (C), Kolmogorov-Smirnov (K), Anderson Darling (A), and Chi-square ($\:{\chi\:}^{2}$) statistics along with their p-values are calculated for the TTB-II, TB-II, TB-III, TB-XII, B-II, B-III, and B-XII models. To assess how closely the cdf of a given distribution fits the empirical distribution for the given data set, these statistics and criteria are extensively used in literature. The parameters of all distributions are estimated through the maximum likelihood estimation (MLE) method.

Table 3 The descriptive summary of the life of fatigue fracture data.

Table 4 MLEs, and a, C, K, $\:{\chi\:}^{2}$ with (p-values) for the life of fatigue fracture data.

Table 5 −2$\:\widehat{l}$, AIC, BIC, and CAIC for the life of fatigue fracture data.

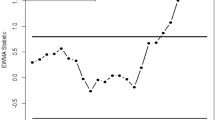
From Tables 4 and 5, since the proposed model has the smallest GOF and maximum p-value so it can be considered the best-fitted model. The closeness of the proposed model fit can also be seen in Figs. 2 and 3 for the life of fatigue fracture data. We assume that the data set follows the TTB-II distribution with transmuted parameter (λ = 0.2056) and shape parameter (k = 4.0431). The first 30 samples are taken as Phase 1 and the remaining 36 samples as the Phase II data set. The parametric choice for the proposed chart is ($\:\psi\:$ = 0.15, L = 0.2239). Figure 4 demonstrates the proposed chart following the design given in Sect. 3.

Fig. 2

Fitted (a) pdf (b) PP plot for the TTB-II distribution for the fatigue fracture data.

Fig. 3

(a) pdf (b) Boxplot for the TTB-II distribution for the fatigue fracture.

Fig. 4

AEWMA chart for the life of the fatigue fracture.

Conclusion

The generalization of standard distributions gives more flexible distributions for the analysis of real-life data’s legitimate concept of generalization. Because of the wide use of the Burr family in real-life data analysis, the generalization of Burr type II distribution becomes the motivation for the truncated transmuted Burr type II (TTB-II) distribution. Different properties of TTB-II distribution are analyzed. Three applications delineate that the new proposed model gives a steadily good fit. The pdf shapes and hazard function plots of the TTB-II model establish that TTB-II is more flexible and accommodates several shapes for the hazard function. Further, utilizing the AEWMA chart to screen the TTB-II distributed data is examined. At that point, the AEWMA chart can be set up as per our strategies. The ARL computation are done via simulations. A real-life data-based numerical example is used to illustrate the application of the AEWMA chart.