Safety risk assessment of weak tunnel construction with rich groundwater using an improved weighting cloud model

Abstract

Many tunnels in Western China are excavated through soft and water-rich rocks. Tunnel excavation in such regions is highly susceptible to disasters such as collapses and water and mud inrush. To control the risks associated with tunneling, this paper proposes a risk evaluation model applicable to soft and water-rich tunnels. First, geological data corresponding to typical soft and water-rich tunnels and related cases were analyzed. By analyzing the natural geology, tunnel characteristics, and construction management, ten influencing factors were selected as the risk evaluation indicators, and a risk evaluation hierarchy was established. Second, the improved combination weight method was applied to obtain the optimal weights of each indicator. A cloud model was then used to visualize the final risk level and establish an evaluation system for soft and water-rich surrounding rocks. Finally, the developed evaluation model was practically applied to a railway tunnel in Western China. The results were highly consistent with the actual situation and could play a guiding role in the construction process. This confirmed the reliability and applicability of the proposed model, which can also be used as a reference for other similar tunnels.

Introduction

Since the turn of the 21st century, an increasing number of tunnels have been constructed worldwide. These tunnels can be characterized by their long distance, large buried depth, high pressure groundwater-rich, high in-situ stress, frequent disasters, and complex structure¹. In particular, the high-pressure water-rich tunnels in the western mountainous regions of China, such as Yunnan, Guizhou, and Sichuan, are often associated with disasters such as large deformation, landslides, and water and mud inrush². The Dayaoshan Tunnel on the Beijing–Guangzhou Line has frequently been caught by accidents such as gushing mud and landslides, resulting in huge economic losses. The old Tanna Tunnel in Japan had a maximum surge of 28.8 × 10³ m³/d, and it had taken 16 years to construct³. Hence, it is important to mitigate the construction risks associated with tunneling in soft and water-rich rocks and to promote the safety and efficiency of construction.

The main causes of disaster in soft water-rich tunnels are the high water enrichment and high in-situ stress. Ou et al.⁴ analyzed data pertaining to accidents in deep tunnels. Accidents with the highest probability of occurrence were found to be collapses, large deformations, water and mud inrush, and leakage of hazardous gases. The proportion of water and mud inrush accidents was up to 45%, whereas collapses and large deformations accounted for 35% of the accidents⁵. Li et al.¹ analyzed the mechanism of the occurrence of water and mud inrush disasters in terms of the disaster source, water-surge channel, and water-isolating layer. The main reason for the occurrence of a water surge is believed to be the interaction between the movement of the front-end hazard source and the disturbance due to tunnel construction. Li² performed a risk assessment of the Ganzhuang Tunnel by studying the breakage mechanism of carbonaceous rock. The thickness of the safe water barrier was proposed through the cusp mutation theory. Qin et al.⁶ analyzed the disaster-causing mechanisms of excavation disturbance and heavy rainfall on tunnel collapse by analyzing typical soil layers. Excavation disturbances caused the soil shear stresses to drop, and the heavy rainfall induced the collapse of the penetration surface above the tunnel. Shi et al.⁷ categorized coal mine water inrush accidents into four types by analyzing water inrush events in Chinese coal mines: 92.3% of the gushing water was from the limestone aquifer, 4.9% from surface water, and 1.4% each from the sandstone aquifer and impact water. Wu et al.⁸ found a relationship between the surrounding rock and surge water through geological investigation and mineral experimental analysis. When the surrounding rock contains more soluble minerals and has a poor lithology, excavation disturbance can easily trigger a sudden water disaster. For the large deformation of soft rocks, Jeon et al.⁹ analyzed the effects of faults, surrounding rock, and grouting on tunnel stability through equal scaling experiments on tunnel faults. He et al.¹⁰ pointed out that common mountain tunnel boring methods can cause large deformation, soft rock sinking near tunnel vaults, and cracks in the lining. The idea of risk compensation was applied to the Muzhailing and Changning Tunnel projects to study the control mechanism under the large deformation of soft rocks.

In most of the current catastrophic accidents, debris flow, landslides, and large deformations have been studied more often, and the effects of hazardous gases are seldom considered. Leakage of hazardous gases in plateau tunnels occurs from time to time, such as in the Longquanshan and Wushaoling tunnels, where a hazardous gas leakage had occurred, causing scheduled delays¹¹. A gas explosion in the Zipingpu Tunnel caused 44 deaths and 11 injuries, with economic losses amounting to $20.35 million¹². Therefore, in this study, a risk assessment model was constructed under actual engineering conditions to consider characteristic indicators such as hazardous gases.

The use of risk modeling has grown rapidly since its application to engineering evaluation. The concept of quantitative risk assessment was introduced by Kaplan in 1981¹³. In 2014, Aven et al.¹⁴ developed a new risk assessment model by adding the k dimension, which introduced the concept of an iterative risk response system¹⁵. The purpose of risk evaluation is to balance the level of risk with the cost and to control the risk in a reasonable interval¹⁶. This idea enhances the practical application of risk evaluation. Eskesen et al.¹⁷ put forth “Guidelines for Risk Management in Tunnels,” where seven risk evaluation models for road and undersea tunnels have been proposed. Later, Browne et al. developed a systematic organization structure for risk evaluation systems and management norms¹⁸.

Model construction strongly depends on the choice of data and algorithms. Fu et al.¹⁹ established a risk assessment system for deep foundation pits using the Apriori algorithm to mine the correlation weights among the influencing factors. Zhao et al.²⁰ combined the multi-risk decision analysis method with complex networks and applied it to the risk evaluation of underground spaces. Xu²¹ employed a k-value clustering algorithm to evaluate the risk of urban flooding (k is the number of clusters in the cluster, and k = 5). Gorsevski et al.²² used a clustering algorithm for the risk assessment of large deformations in landslides. Papadopoulou et al.²³ used a logistic regression algorithm to assess the risk of karst tunnel collapse. However, some of the algorithms require high quality and large amounts of data and are not very generalizable; in addition, most of the risk studies based on objective assignment algorithms ignore the coupling relationship between risks^24,25,26. Chen et al.²⁷ explored the coupling relationship of the risks during subway construction using a small amount of data through an improved empowerment method and achieved remarkable results. Improved combinatorial weight algorithms have received increasing attention²⁸. Lin et al.²⁹ analyzed data through a combination weight algorithms and constructed a risk evaluation model for water and mud inrush in karst tunnels based on a cloud model. Zhang et al.³⁰ established a risk evaluation system for urban flood disasters through a game theory combination weighting algorithm. However, most of the current portfolio empowerment models only consider the overall risk during tunnel construction; research on the dynamic risks in each section of the tunnel during the construction process is lacking. Hai et al.³¹ realized the dynamic evolution of the risk during road tunnel construction through the Dirichlet al.location algorithm and the NK model. Xue et al.²⁶ utilized convolutional neural network layers for the dynamic risk assessment of data collected from 13 highway tunnels in Beijing and pointed out the inadequacies of the dynamic analysis in risk assessments. Risk evaluation is temporal and spatial: as a project progresses, the original risk evaluation system does not receive good feedback³².

In this study, a risk evaluation model was constructed for soft and water-rich surrounding rock plateau tunnels, transforming qualitative indicators into quantitative ones to assess the dynamic risk level in complex environments. The model can help a construction unit to understand the risks in the construction area in time and accordingly optimize the construction plan. Three main evaluation objects are considered in the model: natural geological factors, tunnel design parameters, and construction safety management. The special geological formations, hazardous gases, and other characteristics of western tunnels were considered in conjunction with project characteristics. Ten evaluation indicators were used to determine the optimal dynamic weights of each indicator in different intervals using an improved combinatorial weight method. Finally, the risk level in each tunnel section was established through the cloud modeling method. The model was applied to a tunnel located in the western region of China, and its feasibility and accuracy were demonstrated through the results.

Overview of the tunnel project

The tunnel is located in Ganzi Prefecture, Sichuan Province, China, which is situated on the Western Sichuan Plateau, with an absolute altitude of more than 4000 m. The tunnel mileage is from D1K470 + 908 to D1K480 + 874, and its length is 9975 m, with one side uphill. The maximum buried depth is approximately 500 m, and the tunnel arrangement is a single hole with double lines plus an inclined shaft. The entrance is in a steep hillside with poor slope stability and is prone to collapsing downhill during the rainy season. The construction environment is poor due to the development of adverse geology along the entire route and the distribution of electric towers and other structures around the import and export stacking yard. Figure 1 shows the construction topography.

Fig. 1

Topographic map of tunnel construction.

The surface is covered by Quaternary residual soil, pebble soil, and coarse rounded gravel soil of the Upper Pleistocene floodplain. The overburden has a small thickness, and the bedrock is exposed sporadically. The tunnel area is covered by Quaternary soil and underlying Triassic soil layer. The surrounding rock is mainly of grades IV–V, with an overall poor lithology. The tunnel crosses multiple faults and folds. The terrain is deeply cut, showing tectonic denudation of alpine landforms, with large ups and downs, a relative height difference of 400–900 m, and a natural slope of 30°–50°. The tunnel mainly passes through unequal-thickness interbedded layers of carbonaceous slate and sandstone, with pore water and bedrock fissure water developing in the loose stockpile layer below the tunnel area. Figure 2 shows the geological profile.

Fig. 2

Geological map of the tunnel area.

Fig. 3

Cross-section of the tunnel.

The tunnel is constructed in a horseshoe shape, primarily utilizing the micro-step method for excavation, with additional support from full section excavation and other techniques. The micro-step excavation method involves dividing the excavation process into several smaller steps. Each step has a relatively small excavation volume and area, and corresponding support or reinforcement measures are implemented following each excavation. This approach allows for a gradual advancement of the excavation while maintaining the highest safety factor. A cross-section of the tunnel is illustrated in Fig. 3.

Construction risk in the project area

The tunnel is a typical high-risk water-rich deep-buried plateau tunnel. The tunnel area crosses several folds and fractures, and the terrain is deeply cut. Passing through many streams and accompanied by torrential rains in summer, the tunnel has poor air circulation conditions, and construction workers have frequently suffered from high altitude sickness and sunburn. The winters here are cold with frozen water and frozen equipment. The exit D1K480 + 874 section is close to Donglai Village Bridge, with complicated construction conditions. The tunnel passes through water-rich carbonaceous slate and sandstone interlaced with interlayers of unequal thickness, which are prone to landslides, large soft-rock variations, water and mud inrush, and other disasters.

Collapes: The risk of landslide is at the entrance and exit sections of the tunnel. The entrance section D1K470 + 908 is covered with gravel soil, and the exit section D1K480 + 874 is covered with gravel soil and pebble soil. The tunnel is thinly overburdened with sporadic bedrock outcrops. The terrain is heavily biased. Heavy rains are frequent from June to September each year, and the probability of landslides during excavation is high. Landslide risk was in the entire tunnel dark hole section, especially the fracture zone section of the fault, the shallow buried section of the tunnel entrance and the V level surrounding rocks section. During the construction of the entrance section D1K470 in the tunnel area, a small landslide occurred, see Fig. 4.

Fig. 4

Construction site slip and fall diagram.

Water and mud inrush: The climate in the tunnel area is between continental monsoon plateau climate and sub-cold humid climate. As the tunnel area is located in a narrow riverbed with a small drop in the water level, it is prone to waterlogging. The stratigraphy is a water-rich peripheral rock, and groundwater collection is dominated by pore water from loose rocks and bedrock fissure water. The terrain crosses several geological zones. The risk of sudden mud and water surges is in the fault fracture zone section of the entire tunnel. Surges and seepages are common during construction in the tunnel area, see Fig. 5.

Fig. 5

(a) Surging water. (b) Seepage and surge water.

Large deformations in soft rock: Soft rock large deformation refers to the phenomena observed in tunnel or underground engineering within soft rock geological conditions. Due to the inherent characteristics of the rock mass, as well as factors such as ground stress conditions and construction disturbances, the surrounding rock may experience significant plastic deformation or creep. This deformation can exceed 20 cm. The large deformation is mainly in the soft rock section under high stress. The length of the medium-large deformation of the entire tunnel reaches 690 m, accounting for 6.9%, and the slight large deformation reaches 750 m, accounting for 7.5%. Groundwater and fractured surrounding rock are the main factors causing the large deformation of the soft rock. Based on geological investigation data, a preliminary prediction of the large deformation level of the entire tunnel was made, as shown in Table 1.

Table 1 Prediction of large deformation classes in soft rocks.

Risk evaluation indicators

By identifying and analyzing the causes of the major risk events in this tunnel, the risk evaluation indicators were divided into three main categories: natural geological conditions, tunnel characteristic parameters, and construction safety management, as shown in Fig. 6.

Fig. 6

Risk evaluation indicator.

Natural geological conditions

(a) Classification of surrounding rock B1: The self-stability of rock mass is mainly affected by their strength and integrity. The higher the grade of the surrounding rock, the worse its self-stability, the more broken the rock mass, and the greater the likelihood of disasters such as collapse and water surge. All of the indicators below are from geological survey reports. The formula for calculating BQ, which is the basic quality index of the rock mass, is as follows³³.

$$\:BQ=100+3{\sigma\:}_{c}+250{K}_{v}$$

(1)

Where σ_c is the uniaxial compressive strength (UCS) of the rock mass in MPa, and K_v is the integrity factor. The index is widely utilized in geotechnical engineering and rock mechanics to assess the integrity of a rock mass. It indicates the extent to which structural defects, such as joints, cracks, and voids, affect the overall quality of the rock mass.

The groundwater and orientation of the structure plane influence the stability of a tunnel project, which requires a modification of the BQ, and the correction formula is as follows:

$$\:\left[BQ\right]=BQ - 100\, ({K}_{1}+{K}_{2}+{K}_{3})$$

(2)

Where K₁ is the groundwater influence coefficient, K₂ is the influence coefficient of the orientation of the structure plane, and K₃ is the influence coefficient of the initial ground stress state.

From Eqs. (1) and (2), it can be seen that the [BQ] value is a comprehensive index reflecting the performance of the surrounding rock. According to the relevant specification³⁴, the geotechnical quality class is graded according to Table 2.

Table 2 Classification of surrounding rock B1.

(b) Groundwater abundance B2: Groundwater, as an extremely dynamic factor causing surrounding rock collapse and large soft rock deformation^35,36, relies on the inflow of underground streams, pore and fissure water pooling, and heavy rainfall through the surface. Groundwater action has three forms, i.e., physical action (erosion, softening), chemical action (dissolution, reduction, etc.), and mechanical action (mechanical erosion, dynamic water pressure, etc.)³⁷. Under these actions, the self-stability of the surrounding rock is affected, resulting in disasters such as water and mud surges in the tunnel area. Therefore, groundwater abundance is categorized into five classes in terms of the degree of groundwater enrichment, as shown in Table 3.

(c) Fault width B3: The development of faults is a typical feature of tunnels in the western plateau, and it is a typical geological formation that affects groundwater development and causes collapses. The rock mass is fragmented within the faults and their influence zones. The groundwater dynamic conditions are abundant. The erosion of underground chambers influences the stability of a part of the tunnel area that crosses the fault and is highly susceptible to collapse due to excavation disturbances and other impacts. In this study, the grading method of the faults proposed by Zhang et al.³⁸ is referred, as shown in Table 4.

(d) Fold width B4: The fold structure is a typical geological formation. The degree of erosion in the core of the fold is higher, and the probability of deformation and destruction of the rock mass is higher. Under the effect of extrusion and excavation disturbance at the wing of the fold structure, the tunnel area is prone to stress concentration. Under high in-situ stresses, the development of joints between rock layers provides channels for groundwater flow, which may pose a greater construction risk^39,40. It is graded in Table 5.

(e) Hazardous gas B5: Low-oxygen and high-nitrogen hazards are often present in highland tunnels. During construction, the confined air environment with nitrogen in the bedrock lithology, which has a certain hydrocarbon-generating capacity, has an unstable distribution and is difficult to measure and eliminate. It poses a significant threat to the safety of construction workers. According to the national standard⁴¹ and Kang et al.’s¹² study on tunnels rich in gas and other harmful gases, the harmful gas pressure as a grading standard is shown in Table 6.

Table 3 Classification of groundwater abundance B2.

Table 4 Classification of fault widths B3.

Table 5 Classification of fold widths B4.

Table 6 Classification of hazardous gas B5.

Tunnel design parameters

(f) Excavation span B6: The wider the excavation span, the lower the self-stability of the surrounding rock and the higher the risk probability of large deformation and collapse. According to the relevant literature⁴² the excavation spans are categorized, as in Table 7.

Table 7 Classification of excavation span B6.

(g) Tunnel buried depth ratio B7: Generally, when a tunnel is excavated, a natural arch structure is formed above it, which can take up a part of the load. The arch structure is strongly influenced by the tunnel buried depth ratio (L₀/L, where L₀ is the tunnel buried depth, and L is the maximum tunnel excavation height). When the tunnel is located in the entrance section or when the tunnel depth ratio ≤ 5, the unloading stress will spread directly to the ground, resulting in an unstable surrounding rock and the inability to form a natural arch. If the tunnel is not supported promptly, the risk of tunnel collapse will increase dramatically. Therefore, the risk of tunnels at shallow burials is higher. According to relevant literature and construction experience⁴³, the classification criteria are selected as in Table 8.

Table 8 Classification of tunnel buried depth ratio B7.

(h) Excavation method B8: The excavation method is an important influencing factor of tunneling and plays a decisive role in the outcome of the construction. Different construction methods have different safety factors, economic benefits, and construction times under different geological conditions. For soft water-rich surrounding rock tunnels, the micro-step method is mainly adopted as the main method, supplemented by open cut and full-section excavation. Therefore, based on field reports and relevant experience⁴⁴, the classification of excavation methods is shown in Table 9.

Table 9 Classification of excavation method B8.

Construction safety management

(i) Support measure B9: The support structure is one of the most effective means of controlling tunnel deformation and ensuring construction safety. The support process encompasses advancing support, initial support, and secondary lining. Different grades of surrounding rock require distinct support methods. In the case of weak surrounding rock, reinforcement should be achieved through curtain grouting, advancing support, and anchors^45,46. This is illustrated in Table 10.

Table 10 Different surrounding rock support methods.

Combined with the actual site and engineering experience, the classification of the support measures is shown in Table 11.

(j) Safety management B10: The quality of the safety management determines the quality of the project and encompasses a combination of worker occupational skill levels, site management, and site monitoring⁴⁷. A scientific construction plan, complete organizational structure, and reasonable on-site management will directly influence the construction efficiency⁴⁸. Poor management and a low level of professionalism can often lead to errors in site handovers, triggering risks such as tunnel collapses^49,50. Therefore, efficient safety management is necessary. To simplify the analysis, site management and frequency of site monitoring are used as graded indicators, as shown in Table 12.

Table 11 Classification of support measures B9.

Table 12 Classification of safety management B10.

Evaluation model

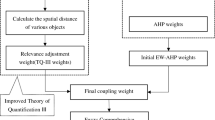
Through the above analysis of the tunnel risk factors, ten indicators were selected to construct a risk evaluation system for soft and water-rich surrounding rock tunnels. The improved game theory combination weighting-cloud model algorithm was introduced to determine the optimal weights of each evaluation index. Based on the principle of maximum membership, a comprehensive risk evaluation model was established. Figure 7 shows the flowchart of the risk evaluation system.

Fig. 7

Risk evaluation flowchart.

The soft and water-rich peripheral rock tunnel is a type of tunnel with typical characteristics located on the plateau in Western China. In this study, the engineering background and risk of the tunnel area were analyzed. The risk evaluation indices are determined in Sect. 2. In general, multiple evaluation indicators have different ranges of values and meanings. In order to make the results reasonable and scientific, all data were dimensionless using the maximum-minimum-value method. Positive normalization was used when a large indicator was more advantageous for data evaluation:

$${Y_{ij}}=\frac{{{x_{ij}} - {x_{i\hbox{min} }}}}{{{x_{i\hbox{max} }} - {x_{i\hbox{min} }}}}$$

(3)

Reverse normalization was used when small indicators were more advantageous for data evaluation:

$${Y_{ij}}=\frac{{{X_{i\hbox{max} }} - {X_{ij}}}}{{{X_{i\hbox{max} }} - {X_{i\hbox{min} }}}}$$

(4)

Where Y_ij denotes the normalized data, x_ij denotes the original data, and x_{i max} and x_{i min} denote the maximum and minimum values of row i of data, respectively. The establishment of optimal weights mainly relies on the subjective weighting method, i.e., the analytic hierarchy process (AHP), and the objective weighting method, i.e., the entropy weight method.

The AHP is a method for qualitative and quantitative analyses of complex problems between multiple objectives. It was proposed by American mathematician Thomas Saaty⁵¹ in 1977. A hierarchical structural model that stratifies decision goals, considerations, and decision objects according to their interrelationships is one of the most popular tools in multi-criteria decision-making (MCDM)^52,53. Kim et al.⁵⁴ performed a risk evaluation of tunnel collapse using the AHP method.

The entropy weight method is based on Shannon’s information entropy formula in information theory:

$$H(x)=\sum\limits_{{i=1}}^{n} {p({x_i})\log (p({x_i}))}$$

(5)

A higher information entropy indicates higher information complexity. The formula can be optimized as follows:

$${H_j}= - 1/\ln (n)\sum\limits_{{i=1}}^{n} {{P_{ij}}} \ln ({p_{ij}})$$

(6)

Where H_j is the entropy value, and P_ij is the probability of occurrence of the evaluation indicator.

The entropy weight method uses the laws of the data to determine the weights of the indicators, thus avoiding the subjective influence on the data of subjective weighting methods such as the AHP method. The score of each evaluation index is weighted using the following mathematical formula to obtain the weights of each evaluation index, and finally, the final degree of certainty is obtained by multiplying the score and weight of each evaluation index. This determines the final grade of the subject of this evaluation⁵⁵.

$$Pij=\frac{{Yij}}{{\sum\limits_{{i=1}}^{n} {Yij} }},i=1,2.n;j=1,2.m$$

(7)

$$Ej= - \ln {(n)^{ - 1}}\sum\limits_{{i=1}}^{n} {Pij\ln Pij}$$

(8)

$$Wj=\frac{{1 - Ej}}{{k - \sum {Ej} }}(j=1,2,.,m)$$

(9)

Where E_j is the information entropy value, and W_j is the weight value. The two results are linearly fitted to obtain the optimal weights.

Combination weighting: n weights are obtained based on n weighting methods, and a set of basic weight vectors W_j {w₁, w₂…, w_n} was constructed. A possible set of weights comprising n vectors combined in an arbitrary linear combination can be expressed as follows.

$$\:W=\sum\:_{k=1}^{n}{\alpha\:}_{k}{\omega\:}_{k}^{T}({\alpha\:}_{k}>0)$$

(10)

Where w is the optimal possible weight value, and α_k is the weight coefficient.

The optimal weights can be thought of as a compromise between n weights, and such a compromise can be viewed as an optimization of the weights. Optimization aims to minimize the sum of deviations between W and W_k. The basic idea is similar to the least-squares method⁵³. Therefore, in this study, a polynomial regression was fitted to the optimal weights to note the most dangerous indicators in different stages.

$$\:min\parallel \sum\:_{j=1}^{n}{\alpha\:}_{j}{\omega\:}_{j}^{T}-{\omega\:}_{i}^{T}\parallel \:(i\:=\hspace{0.17em}1,\:2\dots\:,\:n)$$

(11)

A first-order derivative of the above equation gives:

$$\:{\sum\:}_{j=n}^{n}{\alpha\:}_{j}{\omega\:}_{i}{\omega\:}_{j}^{T}={\omega\:}_{i}{\omega\:}_{i}^{T}\:(i\:=\hspace{0.17em}1,\:2\dots\:,\:n)\:\:$$

(12)

The corresponding matrix equation is:

$$\left[ {\begin{array}{*{20}c} {\omega _{1} \omega _{1}^{T} } & \cdots & {\omega _{1} \omega _{n}^{T} } \\ \vdots & \ddots & \vdots \\ {\omega _{n} \omega _{1}^{T} } & \cdots & {\omega _{n} \omega _{n}^{T} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\alpha _{1} } \\ {\alpha _{2} } \\ \ldots \\ \end{array} } \\ {\alpha _{n} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\omega _{1} \omega _{1}^{T} } \\ {\omega _{2} \omega _{2}^{T} } \\ \ldots \\ {\omega _{n} \omega _{n}^{T} } \\ \end{array} } \right]$$

(13)

The corresponding weight coefficients are obtained and then normalized.

$$\:{\alpha\:}_{k}^{*}=\frac{{\alpha\:}_{k}}{\sum\:_{k=1}^{n}{\alpha\:}_{k}}$$

(14)

Ultimately, the optimal weight value $\:{\omega\:}^{*}$ is:

$$\:{\omega\:}^{*}=\sum\:_{k=1}^{n}{\alpha\:}_{k}{\omega\:}_{k}^{T}$$

(15)

Cloud model: Cloud model is a mathematical tool used for transforming qualitative concepts into quantitative data for uncertainty analyses. Using the three mathematical indicators of expectation E_x, entropy E_n, and hyper-entropy H_e to represent the qualitative concepts, a mutual transformation between the qualitative and quantitative indices is simply and directly accomplished⁵⁶. Definition of cloud model: let U be a quantitative domain represented by exact numerical values, with a corresponding quantitative concept A, x ∈U. For any x in the domain U, there is an membership certainty Ct(x) corresponding to it, Ct(x) ∈ [0, 1]. The distribution of x on U is called a cloud model theory.

In the cloud model theory, the expectation E_x is used to represent the expectation of the spatial distribution of the cloud droplet domain, which is the point that represents the qualitative concepts and is the most typical sample of concept quantification in the model. The entropy E_n can measure the fuzzy range of qualitative concepts and react to the uncertainty of qualitative concepts in an integrated manner. The hyper-entropy H_e is used to measure the uncertainty in the entropy, which is used to reflect the discrete degree of cloud droplets in the theoretical space. The greater the hyper-entropy, the thicker the cloud droplets.

$$E_{x}^{p}=\frac{{{C_{\hbox{max} }}+{C_{\hbox{min} }}}}{2}$$

(16)

$$\:{E}_{n}^{p}=\frac{{C}_{max}-{C}_{min}}{6}$$

(17)

$${H_e}=\beta$$

(18)

Where$E_{x}^{p}$ is the expected value of the corresponding p-level indicator; $E_{n}^{p}$ is the entropy of the corresponding p-level indicator. According to the fuzzy theory, in this study, β = 0.01 is uniformly adopted, and C_max and C_min are the maximum and minimum values of the boundary of the corresponding p-level, respectively. Figure 8 shows the cloud model metrics.

Fig. 8

Diagram of the cloud model metrics.

Figure 9 shows the main process of the cloud model computation.

Fig. 9

Flowchart of cloud model computation.

Step 1

Generate normal random numbers En* with En as the expectation and He as the standard deviation.

Step 2

Generate a normal random number x with Ex as the expectation and absolute value of En* as the standard deviation, x being a cloud droplet in the domain of the argument.

Step 3

Calculate ${C_t}(x)={e^{\frac{{ - {{(x - Ex)}^2}}}{{{e^{2{{(En)}^2}}}}}}}$, where C_t(x) is the membership certainty of x in the qualitative concept A.

The degree of membershipe is the value of the function that has a correspondence with x in the cloud model, taking a value between 0 and 1. The degree of membership corresponding to the measured indicators can be found for each evaluation indicator, and the final risk level can be assessed using the integrated degree of certainty⁵⁷.

The final degree of certainty is the magnitude of the value of each evaluation indicator multiplied by the weight of the corresponding indicator, with the following formula:

$$Si=\sum\limits_{{j=1}}^{m} {Wj*Pij}$$

(19)

Spearman’s rank correlation coefficient: Spearman’s rank correlation coefficient is a statistical measure employed to evaluate the strength and direction of the monotonic relationship between two variables. Unlike Pearson’s correlation coefficient, which necessitates that the data be linearly related and normally distributed, Spearman’s rank correlation is applicable to ordinal or non-linear relationships⁵⁸. The formula for its calculation is as follows.

$$\rho =1 - \frac{{6\sum {d_{i}^{2}} }}{{n({n^2} - 1)}}$$

(20)

where ρ is the Spearman rank correlation coefficient, and $d_{i}^{2}$ is the rank difference for the iii-th data point, and n is the number of data points.

Sobol Indics: Sobol’ indices serve as a robust sensitivity analysis tool designed to quantify the contribution of each input variable to the uncertainty associated with model outputs. This method assesses the impact of individual input variables, as well as their combinations, on variations in the output variable by decomposing the variance of the model output⁵⁹. The formula for calculation is as follows.

$$Var(Y)=E[{Y^2}] - {(E[Y])^2}\;Var(Y)=E[{Y^2}] - {(E[Y])^2}$$

(21)

$${S^i}=\frac{{Var(Y|{X_{ - i}})}}{{Var(Y)}}$$

(22)

where $Var(Y)$ is the the total variance of the output Y, and $E[Y]$ is the expected value (mean) of the output, and ${(E[Y])^2}$ is the expected value of the squared output. $Var(Y|{X_{ - i}})$is the conditional variance of the output Y, given that the input variable ${X_i}$ is fixed. ${S^i}$ is the Sobol indics.

Case study

Based on the engineering investigation report and expert advices, the six most dangerous sections in the tunnel area were evaluated. Each section has certain risk characteristics: the entrance section from D1K470 + 908 to D1K470 + 913.35 and the exit section from D1K480 + 860 to D1K480 + 874 have the highest risk of collapse. The section D1K473 + 755 is rich in groundwater, and it was in the rainy season when construction was in progress. The D1K475 + 800 section passes through a fault. The D1K477 + 028 section is excavated with full-section excavation. The D1K478 + 663 section exhibits fold development. Therefore, the above six segments were selected, and the cloud model was used to react to the final risk level of each segment. Table 13 presents the monitoring indicators of each section.

Table 13 Monitoring and measurement indicators for monitoring sectors.

The AHP method determines the subjective weights, and the subjective weights were obtained by constructing the judgment matrix. Figure 10; Table 14 present the judgment matrix and subjective weights, which are in line with the consistency test results. Table 14(a) presents the judgment matrix of the three types of evaluation objects. Table 14(b), (c), and (d) present the judgment matrices of the evaluation indicators of the three evaluation objects, respectively. The corresponding subjective weight values of each evaluation indicator were obtained from Eqs. (3)–(7). Figure 10 presents the subjective weights of each evaluation indicator.

Table 14 Judgement matrix for evaluation objects.

Fig. 10

Subjective weights of evaluation subjects.

The objective weights were determined in conjunction with the entropy weighting method with the following parameters in Table 15:

Table 15 Table of weighting parameters.

According to Eqs. (13)–(17), the optimal weights were obtained based on the objective and subjective weights of the different monitoring intervals listed in Table 15, and the dynamic weight changes in the different intervals were obtained by polynomial regression, as shown in Fig. 11.

Fig. 11

Dynamic weight change curve.

The blue curve in the above figure shows the risk evaluation weights of the D1K470 section. The red curve shows the risk evaluation weights of the D1K480 section, and the rest of the curves represent the weights at the time of construction to a certain section. The change in the curves indicates that the weight values of the evaluation indices change in the different construction stages, and the risk during construction also changes accordingly. Table 16 presents the optimal weight values for each zone.

Table 16 Optimal weight values for each zone.

The above optimal weight values are inputted to the cloud model. Taking the first evaluation index surrounding rock grade as an example, the quantitative value of the corresponding index is inputted to the x-conditional cloud generator in the cloud model for calculation (number of cloud droplets: 3000), and the cloud model is obtained, as shown in Fig. 12.

Fig. 12

Cloud model diagram.

The final risk level is determined based on Eq. (19) and the cloud model of the ten evaluation indicators. In different construction stages, the weights change dynamically, and the risk level of each section changes accordingly. Figure 13 shows the dynamic risk level of tunnel construction. Figure 13(a) shows the risk cloud diagram of the D1K470 section. Figure 13(b) shows the risk cloud diagram of the D1K473 section. Due to the change in the weights, the risk level of the D1K470 section changes accordingly. Figures 13(c)–(f) show the risk level cloud for each monitoring segment. Figure 14 presents the final certainty cloud for the D1K480 section.

Fig. 13

Cloud map of the dynamic risk level of the tunnel area.

Fig. 14

Maximum certainty percentile of the risk for the tunnel area.

Analysis and validation of results: Comparing the actual construction situation of each section with the risk assessment results, the D1K470 section is at the entrance and reaches grade IV risk. This zone has a low buried depth ratio and cannot form a natural arch. During the construction on 5th March 2022, a small landslide occurred during heavy rainfall on-site, as shown in Fig. 4. During the construction of the D1K473–D1K475 section, there was a common phenomenon of water and mud inrush, which is in line with the grade III risk. On 8th July 2022, the maximum gushing volume of water reached 140 m³/h, see Fig. 15 below. After construction, a combination of plugging, diversion, and drainage was adopted, which significantly reduced the risk level. After construction, the risk level was significantly reduced by the combination of plugging, diversion, and drainage.

Fig. 15

Mud surge incident map of the D1K475 + 609 section.

The main construction risks of the water-rich surrounding rock tunnels in this project are: (1) The tunnel area passes through special geological formations, such as folded faults, and the fracture zones cause the rock layers to be broken and the rock properties to be weak, which significant influence the mechanical properties of the surrounding rocks and make the construction extremely difficult. (2) The broken rock layer provides a channel for the circulation of underground water, and the large area of the water-rich surrounding rock makes it easy to produce a sudden water inrush in the excavation process, thus triggering landslides and other disasters. (3) The tunnel section is large, the construction environment is complicated, and it is located on the plateau. The natural geographical conditions cause transport difficulties as well as delayed feedback on event handling. (4) The overall construction period in the tunnel area is long, and there are weaknesses in safety management. There is a lag in the monitoring and management response and a lack of emergency treatment capability. Therefore, in the subsequent project, measures should be taken to improve the excavation environment where the surrounding rock lithology is poor, such as conduit-induced drainage, grouting, tarpaulin laying, and other measures. In high-risk sections, an emergency response team should be set up, the monitoring frequency should be increased, and means such as high-intensity lining should be used.

Discussion

In order to verify the proposed approach in this model. Given that the weights in this article are variable, we select the weights from the final section for comparison. The changes in these weights are evaluated against those derived from the traditional analytic hierarchy process and the entropy weight method to assess the model’s efficiency, As shown in Table 17 below.

Table 17 Sepearman coefficient between factors.

The analysis presented in the table illustrates that, within the Analytic Hierarchy Process (AHP) method, the weight of index B7 exhibits the most significant variability. This is primarily due to the omission of the importance of the buried depth ratio of index B7 in the judgment inverse matrix of the AHP. In practical engineering scenarios, accurately measuring the stress variations resulting from changes in the buried depth ratio poses challenges, necessitating a data-driven approach for analysis. Conversely, in the entropy weight method, index B9 demonstrates the most considerable weight fluctuation. The analysis indicates that the scores for support measures are relatively uniform, making it difficult to derive direct insights from the data. Nevertheless, implementing support measures is essential for effectively managing risks and adjusting risk levels. Regarding index B6, which pertains to the excavation span, the weight is assigned a value of 0 due to the constancy of the excavation span in the design data. However, it is important to note that variations in the excavation span can significantly impact the risk associated with tunnel excavation. Excessively large excavation spans can lead to issues such as collapses. The changes observed in the other indicators remain within acceptable limits. Consequently, it can be concluded that the improved combinatorial weighting method addresses the shortcomings of the AHP, which overly relies on expert judgment and may neglect critical data. This method also resolves the issue of minimal index changes that are inadequately represented in the entropy weight method. Overall, this model demonstrates superior evaluation capabilities compared to traditional single models.

Global sensitivity analysis is a methodological approach used to investigate how variations in input parameters affect the state or output changes of a model. To assess the impact of various indicators on the model, this paper employs the Spearman correlation coefficient method, with the corresponding index coefficients presented in Table 18 below.

Table 18 Sepearman coefficient between factors.

The table above illustrates the Spearman coefficient, which primarily indicates two states: positive and negative correlation. A positive correlation means that as one indicator increases, the other also increases. Conversely, a negative correlation indicates that as one indicator increases, the other decreases. Notably, there is a strong positive correlation between indicators B5 and B10, as well as B6 and B9, suggesting the possibility of shared dependent variables upon further analysis. In practical engineering applications, these indicators are typically analyzed separately for statistical purposes. Additionally, a strong negative correlation exists between B3 and B9, which aligns with established engineering practices. Furthermore, the Spearman correlation coefficients among the remaining indicators reveal a lack of strong correlations, suggesting that the selection of indices for the model is appropriate and that the model exhibits good robustness.

We used Sobol to analyze the sensitivity of each indicator, as shown in Fig. 16.

Fig. 16

Sobol sensitivity index.

The Sobol index reveals that the model exhibits significant sensitivity to the abundance of underground water in B2 and the buried depth ratio of the B7 tunnel. These factors should be prioritized as critical indicators for monitoring and control. By enhancing monitoring efforts and implementing timely, targeted interventions, the overall risk can be effectively mitigated. In contrast, the excavation span represented by Index B6 and the safety management associated with Index B10 contribute minimally to the model, suggesting that these indices can be streamlined in future iterations. Nevertheless, it is important to acknowledge that they may still interact with other indicators discussed in this paper.

Conclusions

Soft and water-rich surrounding rock tunnels in the western plateau are characterized by complex construction influencing factors and high social impact, making them high-risk projects. To reduce the construction risk and improve project efficiency, this study used a cloud model to determine the risk level based on the game theory combination weighting principle, which dynamically shows the changes in the risk during the construction period. A risk assessment model was proposed for the construction of soft and water-rich surrounding rock tunnels by analyzing the natural geological conditions, tunnel design parameters, and construction safety management of tunnel construction in soft and water-rich surrounding rocks, and combining domestic and international research and actual engineering cases. The model analysis process is clear and reproducible, and the results obtained are reliable, instructive, and can be of some reference value for similar projects. The main conclusions drawn from this research are as follows:

(1) The risk level could be classified into five grades: extremely low risk (Grade I), low risk (Grade II), medium risk (Grade III), high risk (Grade IV), and extremely high risk (Grade V).

(2) The disadvantage of the AHP as a subjective weighting method is that it is too subjective. The entropy weight method, which is an objective weighting method, has a drawback in that it overemphasizes the feedback of the data, thus ignoring the coupling relationship between indicators. By combining the two, the advantages of each method are complemented, and the conversion between qualitative and quantitative indices is achieved, thus significantly eliminating the subjectivity and increasing the accuracy.

(3) Based on combinatorial weighting and combining the AHP method and entropy weight method, a new weight fusion model was proposed to fit polynomials to the optimal weights, and a weight change curve was obtained. It can dynamically analyze the dynamic changes in the risks corresponding to different construction periods.

(4) The EAHP cloud model applied to the risk evaluation of soft and water-rich surrounding rocks can deal with the ambiguity and uncertainty in the engineering evaluation, provide an effective method for similar projects, and ensure reliable decision support for constructors.

(5) We compared the enhanced model with the traditional model and confirmed its superior performance. To assess the model’s sensitivity, we utilized the Spearman rank correlation coefficient and Sobol indices. The results demonstrated that the model displayed increased sensitivity to the B2 groundwater abundance index and the buried depth of the B7 tunnel. Therefore, it is crucial to strengthen the management of these two indices in practical engineering applications.