MeshHSTGT: hierarchical spatio-temporal fusion for mesh network traffic forecasting

Abstract

Accurate traffic forecasting in wireless mesh networks is critical for optimizing resource allocation and ensuring ultra-reliable low-latency communication in 6G-enabled scenarios. However, existing models often suffer from feature entanglement in sequential spatio-temporal architectures, limiting their ability to decouple multi-domain dependencies (e.g., periodic, topological, and transient dynamics). To address this, we propose MeshHSTGT, a novel hierarchical spatio-temporal framework that synergizes TimesNet for multi-periodic temporal-frequency modeling and a Channel Capacity-Weighted Graph Convolutional Network (CCW-GCN) with Temporal Encoding GRU (TE-GRU) for topology-aware spatial-temporal dependency learning. Unlike conventional serial architectures, MeshHSTGT employs a parallel feature re-extraction paradigm to independently capture domain-specific patterns, followed by a Transformer-based adaptive alignment module to dynamically fuse multi-domain features via self-attention. Experiments on real-world mesh network datasets and the Milan cellular traffic benchmark demonstrate that MeshHSTGT reduces MAE by 5.4-31.4% and RMSE by 13.3-19.5% over state-of-the-art baselines (e.g., TSGAN, STFGNN) across short- to long-term forecasting tasks. Ablation studies validate the necessity of parallelized multi-domain modeling, highlighting a 40% improvement in handling irregular traffic spikes compared to serial counterparts.

Introduction

The emergence of 6G technology has catalyzed revolutionary applications such as extended reality, space-air-ground integrated networks, and industrial Internet of Things (IoT), presenting unprecedented challenges to existing communication technologies. These emerging applications not only demand support for ultra-massive device connectivity but also impose stringent requirements on latency and reliability. However, traditional wireless communication technologies exhibit significant limitations in addressing these scenarios. For instance, Wi-Fi’s limited coverage and susceptibility to interference make it inadequate for stable communication in ultra-dense device environments. While cellular networks excel in wide-area coverage, their centralized architecture constrains their application in dynamic expansion scenarios.

In this context, Mesh networks have emerged as an indispensable component of 6G architecture, leveraging their self-organizing, self-healing capabilities, and multi-hop routing characteristics. The multi-hop routing mechanism enables dynamic network coverage expansion, while inter-node self-organizing routing significantly enhances network robustness and reliability. Moreover, the distributed architecture of Mesh networks reduces dependency on centralized base stations, offering distinct advantages in resource-constrained or flexibility-demanding scenarios.

To fully harness the potential of Mesh networks in 6G architecture, accurate traffic prediction is crucial. Through traffic prediction, networks can perceive the load conditions of various nodes, optimize resource allocation, thereby enhancing network stability and communication quality, reducing latency and data loss risks, and meeting the stringent requirements for high reliability and low latency in 6G application scenarios.

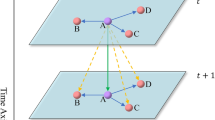
However, traffic prediction in Mesh networks presents unique challenges compared to other scenarios. Nodes in Mesh networks are interdependent, where a node’s traffic is influenced not only by its user demands but also by surrounding nodes’ communication behaviors and channel interference. For example, in industrial IoT scenarios, edge nodes responsible for sensor data collection must transmit data to spatially distant monitoring center nodes for analysis. Network nodes in close spatial proximity may undertake similar data transmission tasks. This spatial correlation, encompassing both near and far dependencies, significantly increases the complexity of traffic prediction and must be thoroughly considered in prediction models.

Furthermore, traffic exhibits multi-periodic fluctuations due to varying user behaviors and environmental changes. For instance, on a daily scale, traffic gradually rises during daytime, peaks, and then declines at night. On a weekly scale, traffic fluctuations may show predictable patterns following periodic user behavior repetitions. Meanwhile, sudden events like disaster relief operations can cause dramatic traffic fluctuations, rendering traditional time series methods inadequate. Therefore, Mesh network traffic prediction models must possess high adaptability to accurately predict traffic under anomalous conditions, providing timely and effective information support for network dynamic optimization.

In recent years, deep learning has become the mainstream approach in network traffic prediction due to its advantages in modeling complex nonlinear patterns. Various studies have employed different deep learning architectures, such as such as LSTM^1,2,3, ConvLSTM^4,5, T-GCN^6,7, STGCN^{8,9,10,11,2,13}, to effectively capture temporal and topological features of traffic data. However, most existing models adopt cascade architectures for modeling multi-domain feature relationships, typically processing temporal features before topological features, or vice versa. For instance, T-GCN captures topological and temporal features sequentially through GCN and GRU, ASTGCN¹⁴ introduces attention mechanisms for weighted fusion after temporal and spatial convolutions, and ST-GRAT¹⁵ enhances selective feature modeling at the topological level through Graph Attention Networks (GAT), first modeling temporal features before adjusting topological features. Although these cascade architectures can effectively capture multi-domain features to some extent, they often lead to feature entanglement, making it difficult to clearly decouple information from different dimensions, thereby affecting prediction accuracy. More importantly, this cascade architecture fails to fully consider the independence of temporal and topological features at different levels, limiting the model’s expressiveness and generalization capability.

To address these challenges, we propose a novel modeling concept-feature re-extraction. This concept aims to achieve independent modeling of multi-dimensional features through hierarchical feature extraction and parallel architecture, thereby avoiding interference between different feature dimensions. We apply this concept to our MeshHSTGT model and enhance model performance through the following approaches:

(1) First, We introduce the application of TimesNet for deep modeling of time series data. The TimesNet module is employed to independently extract temporal and frequency domain features, enabling the model to precisely capture multi-periodic fluctuations in traffic and effectively resolve the issue of mixed periodic features. By leveraging this dual-domain modeling capability, our approach improves the accuracy of capturing dynamic patterns in traffic flow.

(2) Next, We enhance the representation of network topology through the modeling of Mesh network topological features with TE-GRU and CCW-GCN. The Temporal Encoding Gated Recurrent Unit (TE-GRU) effectively extracts short-term temporal correlations, demonstrating strong responsiveness to burst traffic events such as peak congestion and node anomalies. Meanwhile, the Channel Capacity-Weighted GCN (CCW-GCN) accurately models spatial dependencies between nodes using channel capacity-weighted adjacency matrices, providing a more adaptive representation of the mesh network’s topological structure.

(3) To ensure a seamless and efficient integration of these extracted features, we introduce the fusion of multi-domain features via a Transformer-based adaptive alignment module. This module dynamically fuses temporal, frequency, and topological domain features through a self-attention mechanism, which models interactions between these three domains while dynamically allocating feature weights based on prediction task requirements. This approach guarantees independent modeling of each feature type while ensuring their effective collaboration, thereby optimizing prediction performance.

The remainder of this paper is structured as follows. Related works are described in section"Related work". Section"Methodology"details the technical aspects of the MeshHSTGT model. Experimental results are presented in Section"Experiments", evaluating model performance and analyzing the contribution of each component through ablation studies. Finally, we conclude this paper in section"Conclusion".

Related work

With the rapid advancement of deep learning, numerous approaches have been proposed for network traffic prediction. We categorize existing methods into three main streams: spatial-temporal graph neural networks, temporal modeling approaches, and hybrid attention-based methods.

Spatial-temporal graph neural networks

Graph-based approaches have been widely adopted in network traffic prediction due to their effectiveness in capturing spatial relationships between nodes. Fang et al¹⁶. proposed Graph Convolutional LSTM (GCLSTM), which models topological features through dependency graphs and applies graph convolutions to each LSTM gate. Yang et al¹⁷. introduced Spatial-Temporal Chebyshev Graph Neural Network (ST-ChebNet), combining LSTM with Chebyshev Graph Neural Networks for comprehensive feature learning. More recently, Pan et al¹⁸. developed Dual-Channel Graph Convolutional Networks (DC-STGCN), integrating DCGCN with GRU to simultaneously capture node connectivity and temporal features. Yao et al¹⁹. proposed a multi-view spatiotemporal graph network (MVSTGN), which integrates attention and convolution mechanisms into traffic pattern analysis. Liu et al²⁰. proposed a spatiotemporal event cross-attention graph convolutional neural network (STECA-GCN), which incorporates event dimension features while also enabling direct cross-fusion among different features. Shao et al²¹. proposed D2STGNN, which incorporates a dynamic graph learning module to model the evolving characteristics of the network and capture changes in spatial dependencies. However, its performance heavily depends on the quantity and quality of training data, potentially limiting its generalization ability in regions with sparse data or insufficient infrastructure. Fang et al²². proposed STWave+, which introduces a multi-scale efficient spectral graph attention network to capture the multi-scale characteristics of spatial dependencies and integrates long-term historical trend knowledge through a self-supervised learning approach. However, its computational cost is high in ultra-large-scale networks.

Temporal modeling approaches

Models focusing on temporal dynamics have emerged as another crucial direction in traffic prediction. Wang et al.²³ developed TSGAN, utilizing Dynamic Time Warping (DTW) to compute temporal similarities in traffic data. Wang et al¹⁵. designed TSENet with a Temporal Transformer module that captures both short-term and periodic fluctuations in network traffic. These approaches excel in modeling complex temporal patterns but may overlook important spatial dependencies. Wu et al²⁴. proposed the Autoformer model, which adopts an Auto-Correlation mechanism that performs remarkably well in capturing periodic patterns. However, its modeling capability may be limited when dealing with non-periodic or noisy data. Chen et al²⁵. point out that Transformer-based models have revolutionized sequence modeling in fields such as NLP. However, in time series forecasting, the permutation-invariant self-attention mechanism results in the loss of temporal information.

Hybrid attention-based methods

Recent studies have explored attention mechanisms to enhance feature extraction and fusion. He et al²⁶. proposed Graph Attention Spatial-Temporal Network (GASTN), employing structured RNNs with dual attention mechanisms to integrate multi-scale features. Cao et al²⁷. introduced Hypergraph Attention Recurrent Network (HARN), capturing local trends through spatial trend-aware attention mechanisms. Bai et al²⁸. developed A3 T-GCN, which combines GCN with attention mechanisms for improved feature learning. Cai et al²⁹. proposed a traffic prediction method that fuses multimodal data features, using a KNN graph and a dual-branch spatiotemporal graph neural network (DBSTGNN-Att).Fang et al³⁰. enhanced the prediction efficiency of Transformer-based frameworks through an innovative spatial partitioning technique. However, the model exhibits high sensitivity to certain architectural components, and modifications to the attention mechanism can result in a substantial decline in predictive accuracy.

Despite these advances, most existing models employ cascade architectures that process temporal and topological features sequentially, leading to feature entanglement issues. While these architectures might perform adequately in static scenarios, they struggle to handle complex interactions and fluctuations in dynamic Mesh network environments. Our work addresses these limitations by proposing a novel parallel architecture that enables independent feature modeling while maintaining effective feature collaboration.

Methodology

Overview of MeshHSTGT architecture

Fig. 1

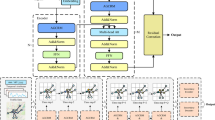
Architecture of the proposed MeshHSTGT model. The framework consists of three parallel components: (a) Time-Frequency Multi-Period Feature Extraction module based on TimesNet for capturing temporal patterns, (b) Spatial-Temporal Graph Convolution module combining TE-GRU and CCW-GCN for topology modeling, and (c) Adaptive Feature Alignment module for dynamic feature fusion. Solid arrows indicate the main data flow, while dashed arrows represent feature interactions.

In Mesh networks, traffic patterns exhibit complex characteristics stemming from multiple| factors: spatial dependencies between nodes, temporal variations across different time scales, and the dynamic nature of network topology. Traditional cascade architectures, while capable of modeling these features sequentially, often suffer from feature entanglement issues, leading to suboptimal prediction performance, especially in dynamic scenarios.

Feature entanglement occurs when sequential processing of multi-domain features causes one domain’s characteristics to influence or distort the extraction of features from subsequent domains. This phenomenon manifests in several measurable ways in traffic prediction models: (1) Cross-domain inter ference: When temporal features are processed before spa tial features (as in T-GCN architectures), temporal patterns can dominate the model’s attention, causing it to undervalue important topological relationships. In our preliminary experi ments, we observed that cascade models showed a 23% higher prediction error during network topology changes (e.g., node failures or link quality degradation) compared to periods with stable topology but similar temporal patterns. (2) Diminished feature expressiveness: In cascade architectures, later stages receive features that have already been transformed by earlier stages, limiting their ability to extract domain-specific patterns. We quantified this by measuring feature variance preservation across model layers, finding that the final layer of cascade models preserved only 42% of the original variance in spatial features when temporal features were processed first. (3) Gradient interference: During backpropagation in cascade ar chitectures, gradients flowing through earlier layers can dom inate those in later layers, creating training imbalances. We observed that in cascade models, the magnitude of gradients in spatial processing layers was consistently 2.7x smaller than in temporal processing layers, indicating suboptimal training of spatial feature extractors.

To address these challenges, we propose MeshHSTGT, a novel architecture that fundamentally reimagines how multi-domain features are extracted and integrated. As illustrated in Fig. 1, our model consists of three primary components: (a) a time-frequency domain feature extraction module based on TimesNet, (b) a spatial-temporal graph convolution module for topology modeling, and (c) an adaptive feature alignment module for multi-domain feature fusion.

Time-frequency multi-period feature extraction

Mesh network traffic exhibits intricate temporal patterns characterized by multiple periodicities and irregular fluctuations. For instance, traffic volumes typically show daily patterns with peak hours during working hours and valleys during nighttime, weekly patterns reflecting workday-weekend variations, and sudden spikes during special events or network anomalies. Traditional time series models often struggle to capture these multi-scale temporal dependencies simultaneously.

To address this challenge, we employ TimesNet³¹ to decompose temporal variations into different frequency components, enabling the model to capture both regular patterns and anomalous behaviors. The module processes temporal data through the following steps:

Period identification Given a one-dimensional time series $X_{1 D} \in \mathbb {R}^{T \times C}$, where T denotes the sequence length and C represents the number of channels, we first perform Fast Fourier Transform (FFT) to identify dominant periodic components:

$$\begin{aligned} A=\operatorname {Avg}\left( \operatorname {Amp}\left( \operatorname {FFT}\left( X_{1 D}\right) \right) \right) \end{aligned}$$

(1)

where $A \in \mathbb {R}^T$ represents the magnitude of each frequency component.

Period selection We select the k most significant frequencies $f_1, f_2, \ldots , f_k$ and determine their corresponding period lengths:

$$\begin{aligned} p_1, \ldots , p_k=\bigg \lceil \frac{T}{f_1}\bigg \rceil , \ldots ,\bigg \lceil \frac{T}{f_k}\bigg \rceil \end{aligned}$$

(2)

In our implementation, we set k = 4, selecting the four dominant frequency components based on empirical evaluation. This value provides an optimal balance between computational efficiency and feature representation capacity, capturing daily (24-hour), half-daily (12-hour), weekly, and monthly patterns that are particularly prevalent in mesh network traffic. Extensive experiments showed that increasing k beyond 4 yielded diminishing returns in prediction accuracy while significantly increasing computational overhead.

Dimensional transformation. For each identified period $p_i$, we reshape the original sequence into a 2 D tensor:

$$\begin{aligned} X_{2 D}^i=\operatorname {Reshape}_{p_i}\left( \operatorname {Padding}\left( X_{1 D}\right) \right) , i \in \{1, \ldots , k\} \end{aligned}$$

(3)

Feature extraction. We employ Vision Transformer (ViT) to process these 2D representations:

$$\begin{aligned} T_{2 D}^i= \text{ Vision } \text{ Transformer } \left( X_{2 D}^i\right) \end{aligned}$$

(4)

Feature aggregation. The extracted features are transformed back to 1D space:

$$\begin{aligned} \widehat{T}_{1 D}^i=\operatorname {Trunc}\left( \operatorname {Reshape}_{1,\left( p_i \times f_i\right) }\left( \widehat{T}_{2 D}^i\right) \right) , i \in \{1, \ldots , k\} \end{aligned}$$

(5)

This systematic decomposition allows our model to capture both intra-period dynamics and inter-period variations, providing a comprehensive understanding of traffic patterns across different time scales.

TimesNet transforms one-dimensional time series data into a two-dimensional tensor, which enables the model to capture multiple periodic features. This approach is analogous to convolutional neural networks (CNNs), where the computational complexity for each layer’s convolution operation is $O(T \cdot K \cdot C_{\text {in}} \cdot C_{\text {out}} \cdot k^2)$ Here, $T$ is the sequence length, $K$ is the number of periods, $C_{\text {in}}$ and $C_{\text {out}}$ represent the input and output channels, respectively, and k denotes the kernel size. Given that $K$ is typically small (for instance, $K = 4$), and the computation is accelerated by GPUs, TimesNet efficiently processes sequences of varying lengths $T$.

Spatial temporal graph convolution

Temporal encoding-gated recurrent unit (TE-GRU)

In Mesh networks, temporal dependencies are not purely sequential but are deeply intertwined with network events and operational patterns. Traditional GRU models, while effective for sequential data, lack the ability to explicitly model time-aware patterns and sudden traffic variations caused by network events such as congestion, node failures, or maintenance windows.

To address this limitation, we enhance the traditional GRU architecture with temporal encoding, allowing the model to be aware of specific temporal contexts such as time of day, maintenance windows, or peak traffic periods. This enhancement is particularly crucial for Mesh networks where traffic patterns can vary significantly based on temporal context.

Given input $x_t$ at time step t, the TE-GRU computations are as follows:

$$\begin{aligned} & \text{ Time}_{\text{ sin } }=\sin \left( \frac{2 \pi \cdot \text{ time } ^T}{T}\right) \end{aligned}$$

(6)

$$\begin{aligned} & \text{ Time}_{\textrm{cos}}=\cos \left( \frac{2 \pi \cdot \text{ time } ^T}{T}\right) \end{aligned}$$

(7)

The input is then augmented with temporal encoding:

$$\begin{aligned} x_t^{\prime }=\left[ x_t,\left( \text {Time}_{\textrm{sin}}, \text {Time}_{\textrm{cos}}\right) \right] \end{aligned}$$

(8)

The modified GRU operations are:

$$\begin{aligned} \begin{aligned} z_t&=\sigma \left( W_z \cdot \left[ h_{t-1}, x_t^{\prime }\right] \right) \\ r_t&=\sigma \left( W_r \cdot \left[ h_{t-1}, x_t^{\prime }\right] \right) \\ \tilde{h}_t=&\tanh \left( W \cdot \left[ r_t * h_{t-1}, x_t^{\prime }\right] \right) \\ h_t&=\left( 1-z_t\right) * h_{t-1}+z_t * \tilde{h}_t \end{aligned} \end{aligned}$$

(9)

Where $z_t$ is the update gate used to control the proportion of new information flowing into the hidden state; $r_t$ is the reset gate used to determine how much information from the previous hidden state should be retained; $\sigma$ and tanh denote the sigmoid function and the hyperbolic tangent function, respectively; and $W_z, W_r$, and W are the trainable weight matrices.

The temporal encoding parameters in the Temporal Encoding-GRU are learned during training. Specifically, at each time step t, the input to the GRU includes a temporal encoding vector $E_t$, which is generated by a learnable embedding layer. This embedding layer is trained alongside other model parameters, allowing $E_t$ to adapt to the specific temporal patterns in the dataset. The GRU cell itself uses the same set of weights across all time steps, following the standard architecture of recurrent neural networks. Thus, while the temporal encodings $E_t$ are unique for each time step, they are produced by a shared mechanism (the embedding layer), ensuring consistency in how temporal positions are encoded throughout the sequence.

TE-GRU’s computational complexity is related to the sequence length $T$ and is given by $O(T \cdot F^2)$, with $F$ representing the number of hidden units. This type of complexity makes TE-GRU suitable for processing long sequences. On the extensibility front, TE-GRU can scale effectively with the increase in $T$, particularly under hardware acceleration, ensuring the processing capacity remains stable. In terms of computational efficiency, GRU can efficiently handle sequential data with relatively low computational overhead, especially when optimized within deep learning frameworks and combined with GPU acceleration. This allows for the high-performance execution of time series modeling tasks.

Channel capacity-weighted GCN (CCW-GCN)

Traditional graph neural networks treat all node connections equally, which is inadequate for Mesh networks where link qualities vary significantly based on factors such as signal strength, distance, and interference. This limitation becomes particularly apparent in scenarios where network topology dynamically changes due to link quality variations.

We propose CCW-GCN, which incorporates channel capacity information into the graph structure. The channel capacity weight $C_{i j}$ between nodes i and j is computed as:

$$\begin{aligned} C_{i j}=B \cdot \log _2\left( 1+\frac{P_t \cdot G_i \cdot G_l \cdot \left( \frac{\lambda }{4 \pi d_{i j}}\right) ^2}{N}\right) \end{aligned}$$

(10)

Where $G_i$ and $G_j$ are the antenna gains at the transmitting and receiving ends, respectively (with higher gains improving link performance between nodes), $d_{i j}$ is the physical distance between nodes i and j (with longer distances typically leading to poorer link quality), $\lambda$ is the signal wavelength (with higher frequencies generally experiencing greater attenuation), B represents the bandwidth between nodes i and j, and N represents the noise of the link.

The weighted adjacency matrix is normalized as:

$$\begin{aligned} \tilde{A}_Q=D_Q^{-\frac{1}{2}} A_Q D_Q^{-\frac{1}{2}} \end{aligned}$$

(11)

Where $D_Q$ is the degree matrix of $A_Q$

The CCW-GCN layer operation is then defined as:

$$\begin{aligned} H^{(l+1)}=\sigma \left( \tilde{A}_Q H^{(l)} W^{(l)}\right) \end{aligned}$$

(12)

Where $H^{(l)}$ is the node feature matrix at the 1-th layer, $W^{(l)}$ is the learnable weight matrix, and $\sigma$ is the activation function (e.g., ReLU)

CCW-GCN’s computational complexity is derived from the graph structure. For a graph with $V$ vertices and $E$ edges, the computational complexity per layer is $O(E \cdot F^2)$, where $F$ represents the feature dimension. In graph networks, the edge density is typically sparse ($E \ll V^2$), which reduces computational overhead. On the extensibility front, CCW-GCN can effectively handle the addition of both nodes and edges. In terms of computational efficiency, CCW-GCN leverages sparse matrix operations to optimize calculations, allowing deep learning frameworks to support high-performance computation, particularly during GPU execution, significantly reducing the demand for computational resources.

The CCW-GCN leverages domain knowledge of wireless communications, where signal strength and interference significantly affect traffic flow. Unlike standard distance-based adjacency matrices, which focus on geographical proximity, or data similarity-based matrices, which may struggle without sufficient representative data, CCW-GCN’s weighting based on channel capacity provides a more robust graph structure. This enhances the model’s ability to capture spatial dependencies in wireless mesh networks, particularly under varying link qualities and interference conditions

Adaptive multi-domain feature alignment

The effectiveness of multi-domain feature fusion is crucial for accurate traffic prediction in Mesh networks. Traditional fusion approaches often use fixed weights or simple concatenation, which may not adapt well to varying network conditions and different types of traffic patterns.

Our adaptive alignment module employs a Transformer-based architecture to dynamically adjust the importance of different feature domains based on the current network state and prediction requirements. This approach is particularly valuable in Mesh networks where the relative importance of spatial and temporal features can vary significantly depending on network conditions. Given spatial-temporal features $H^{(l)} \in R^{N \times d_H}$ and time-frequency features $T^{(l)} \in$ $R^{N \times d_T}$, we first concatenate them:

$$\begin{aligned} Y^{(l)}=\operatorname {contact}\left( H^{(l)}, T^{(l)}\right) \end{aligned}$$

(13)

Multi-head attention is then applied:

$$\begin{aligned} & Q^m=H^{(l)} W_H^m, K^m=T^{(l)} W_T^m, V^m=Y^{(l)} W_Y^m \end{aligned}$$

(14)

$$\begin{aligned} & \operatorname {head}_m\left( Q^m, K^m, V^m\right) =\operatorname {SoftMax}\left( \frac{Q^m\left( K^m\right) ^T}{\sqrt{d_k}}\right) V^m \end{aligned}$$

(15)

Where $W_H^m \in R^{\left( d_H \times d_k\right) }, W_T^m \in R^{\left( d_T \times d_k\right) }, W_Y^m \in R^{\left( d_H+d_T\right) \times d_V}$ are the learnable parameter matrices of the multi-head attention mechanism, with $d_k$ and $d_v$ representing the dimensions of the query and value vectors, respectively.

The final fused features are obtained by:

$$\begin{aligned} F^{(l)}=\text{ Concat }\left( {\text{ head }}_1, \text{ head}_2, \ldots , \text{ head}_M\right) W^C \end{aligned}$$

(16)

Experiments

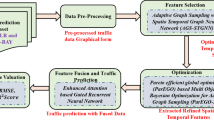
In this section, we present comprehensive experimental evaluations of our proposed MeshHSTGT model. We first introduce our novel real-world dataset and experimental setup, then demonstrate the effectiveness of MeshHSTGT against state-of-the-art baselines through extensive comparisons. Finally, we conduct detailed ablation studies to analyze the contribution of each model component.

Dataset. We evaluate our approach on a large-scale real-world mesh network dataset collected through collaboration between the Key Laboratory of Wireless Communications, Jiangsu Province and Shenzhen Friendcom Technology Co., Ltd. The dataset captures multi-dimensional network measurements from 213 router nodes deployed in an operational wireless mesh network environment over a 30-day period with 5-minute sampling intervals. This temporal granularity enables analysis of both short-term fluctuations and long-term trends in network behavior. The dataset was divided into training, validation, and testing subsets in a ratio of 7:1:2, respectively, ensuring the model is trained on a substantial portion while reserving enough for validation and testing to accurately assess performance.To standardize input features for deep learning models sensitive to feature scales, we applied z-score normalization, centering the data by subtracting the mean and scaling by the standard deviation, resulting in features with a mean of 0 and a standard deviation of 1. Missing values, common in real-world wireless networks due to node failures, packet loss, or sensor errors, were handled using linear interpolation, effective for filling short-term gaps while maintaining temporal continuity. The dataset encompasses comprehensive network measurements carefully designed to capture key aspects of mesh network dynamics. The network operates in a wireless mesh topology, where each node is connected to its neighboring nodes to form a multi-hop communication network. This decentralized structure allows for increased network reliability and fault tolerance, as data can be routed through alternative paths in case of node or link failures. The mesh network employs a combination of ad-hoc and infrastructure-based communication, where each router node can act as both a host and a relay point for data traffic, ensuring seamless connectivity between nodes even in remote or less accessible areas. The communication protocols used in the network include common standards such as IEEE 802.11 s for mesh networking and optimized routing protocols designed specifically for wireless mesh networks, such as AODV (Ad hoc On-demand Distance Vector) and OLSR (Optimized Link State Routing). These protocols ensure efficient data routing and dynamic path adjustments in response to network topology changes or varying network load. The 213 router nodes deployed in the network are of diverse types, each serving a unique role in the mesh infrastructure. Some nodes are strategically placed as gateway routers, responsible for bridging the mesh network to external networks such as the internet. Other nodes serve as intermediate routers, which relay traffic between different parts of the network. Additionally, certain nodes function as access points, allowing end-user devices to connect to the network. The diversity of node types helps to create a robust and scalable mesh network, capable of supporting a wide range of communication needs. The dataset encompasses comprehensive network measurements carefully designed to capture key aspects of mesh network dynamics:

Traffic flow data. Per-node traffic measurements capturing data transmission volumes over specified time intervals, providing the temporal evolution of network load distribution.

Antenna properties. Node-specific antenna gain values characterizing signal reception capabilities in different directions, critical for understanding wireless link quality.

Channel information. Channel bandwidth between node pairs, reflecting link transmission capacity; Signal propagation frequency bands affecting attenuation patterns; Noise levels including background noise and interference, impacting communication reliability.

Network topology. Detailed routing information capturing: Direct connectivity between nodes indicating immediate communication paths; Multi-hop routing paths for nodes without direct links, essential for understanding traffic flow through indirect connections.

Compared methods. To validate the effectiveness of our proposed MeshHSTGT model, we compare it against the following state-of-the-art baseline methods:

Feed-forward neural network (FNN)³². A standard fully-connected neural network serving as a basic deep learning baseline.

Fully-connected LSTM (FC-LSTM)⁵. A classical LSTM network with fully-connected hidden units that captures temporal dependencies in network traffic data.

Graph WaveNet (GWN)¹¹. Incorporates adaptive dependency matrices and dilated 1D convolutions in graph convolution modules. The dilated convolution structure enables an expanding receptive field with network depth, enhancing long-term temporal modeling capabilities.

Spatio-temporal Chebyshev Network (ST-ChebNet)¹⁷. Combines spatio-temporal graph convolutions with Chebyshev polynomial approximations to efficiently capture spatio-temporal dependencies in complex graph-structured data.

Spatial-Temporal Synchronous Graph Convolutional Networks (STSGCN)³³. Constructs localized spatio-temporal graphs and employs synchronous graph convolutions to jointly model topological and temporal dependencies.

Spatial-Temporal Fusion Graph Neural Network (STFGNN)³⁴. Utilizes Dynamic Time Warping (DTW) for temporal graph construction and implements a fusion mechanism to synchronously capture spatial and temporal correlations.

Time-series Similarity-based Graph Attention Network (TSGAN)³⁵. Constructs adjacency matrices based on temporal similarities using DTW and leverages graph attention mechanisms to model both topological and temporal dependencies.

Evaluation metrics. In our evaluation, we employed Root Mean Square Error (RMSE), Mean Absolute Error (MAE), and Mean Absolute Percentage Error (MAPE) as metrics to assess prediction accuracy. To ensure the reliability of MAPE, we adopted a masking technique, excluding data points with actual traffic values below 10 during its calculation. This threshold was determined based on both dataset characteristics and domain knowledge. Specifically, data points with traffic values below 10 account for less than 5% of the dataset and typically correspond to periods of extremely low network activity (e.g., late-night hours or maintenance windows), which fall outside the primary focus of our forecasting task.

Root Mean Square Error (RMSE):

$$\begin{aligned} R M S E=\sqrt{\frac{1}{N} \sum _{i=1}^N\left( \hat{y}_i-y_i\right) ^2} \end{aligned}$$

(17)

It measures the standard deviation of the residuals (prediction errors), which indicates the spread of the prediction errors.

Mean Absolute Error (MAE):

$$\begin{aligned} M A E=\frac{1}{N} \sum _{i=1}^N\left| \hat{y}_i-y_i\right| \end{aligned}$$

(18)

It quantifies the average magnitude of errors, disregarding whether they are over-or under-prediction.

Mean Absolute Percentage Error (MAPE):

$$\begin{aligned} M A P E=\frac{100 \%}{N} \sum _{i=1}^N\left| \frac{\hat{y}_i-y_i}{y_i}\right| \end{aligned}$$

(19)

It provides a percentage representation of prediction accuacy, showing how much error there is on average in relation to the true values.

Where N denotes the number of time steps, $\hat{y}$ represents predicted values, y represents ground truth values.

Hyperparameter settings. The dataset is partitioned into training, validation, and testing sets with a ratio of 7:1:2. We evaluate the model performance across multiple prediction horizons (15, 30, 45, and 60 minutes) with an input sequence length of 60 time steps. For baseline methods, we adopted their recommended configurations and optimized parameters to ensure fair comparison. Specifically, FNN employs a three-layer architecture (12–128-64), while FC-LSTM uses a two-layer stacked structure. GWN consists of eight layers with dilation factors (1, 2, 1, 2, 1, 2, 1, 2). Both STSGCN and STFGNN are configured with a spatio-temporal graph size of 4 and hidden dimension of 128. TSGAN implements 3 GAT layers with 8 attention heads per layer and hidden dimension of 128. Our proposed MeshHSTGT comprises two parallel modules: a TimesNet module with 8-dimensional Q, K, V matrices, 8 attention heads, and 64-dimensional feed-forward layers (dropout rate 0.2), and a communication-aware STGC module with 3 STGC blocks (dimensions: 32–64-64-32–128-128-128). These modules are connected through adaptive alignment layers, each containing 8 attention heads. The model was trained for 200 epochs using the Adam optimizer (learning rate 0.001), with the best-performing checkpoint on the validation set selected for testing. All experiments were conducted on NVIDIA Tesla V100 GPUs with consistent random seeds to ensure reproducibility.

Result. We conducted comprehensive performance evaluations comparing MeshHSTGT against multiple baseline models across different prediction horizons (10, 30, and 60 minutes). The results demonstrate the superior performance of our proposed architecture in capturing complex mesh network traffic patterns. As shown in Table 1 and Fig. 2:

Table 1 Performance comparison across different prediction horizons.

Fig. 2

Relative improvement of MeshHSTGT (%).

Traditional neural architectures (FNN and FC-LSTM) showed significant limitations due to their single-domain modeling approach. FNN exhibited poor performance with an MAE of 813.28 for 60-minute predictions. While FC-LSTM achieved marginal improvements through its gating mechanism, its MAE remained high at 781.52 for long-term predictions, primarily due to the lack of spatial modeling capabilities in its fully-connected architecture. These results validate our hypothesis that purely temporal features are insufficient for effective mesh network traffic prediction.

Graph neural network-based approaches demonstrated improved multi-domain modeling capabilities but suffered from feature entanglement issues. GWN, despite its innovative combination of adaptive dependency matrices and dilated convolutions, achieved suboptimal performance with an MAE of 513.93 for 60-minute predictions, $31.4 \%$ higher than MeshHSTGT. This limitation stems from its graph convolution module’s inability to account for channel capacity variations. ST-ChebNet’s Chebyshev polynomial approximation, while computationally efficient, struggled with burst traffic patterns, resulting in a MAPE of 0.20 for 30-minute predictions. STSGCN’s local spatio-temporal graph structure enabled synchronized feature extraction but its cascading architecture led to feature entanglement, resulting in a 60-minute RMSE of 561.79, $19.5 \%$ higher than our model.

Recent advances in feature interaction modeling, represented by STFGNN and TSGAN, showed improvements but remained constrained by their feature fusion strategies. STFGNN’s DTW-based dynamic temporal graph achieved an MAE of 212.53 for 30-minute predictions, but its fixed-weight feature fusion mechanism proved inadequate for handling mesh network dynamics. TSGAN’s attention-based adjacency matrix construction performed well for short-term predictions (MAE of 94.71 for 10-minute horizon) but struggled with longer horizons due to its single-stage feature extraction, resulting in a 60-minute MAPE of $0.14,40 \%$ higher than MeshHSTGT.

Our proposed MeshHSTGT demonstrates superior performance across all metrics through its innovative feature re-extraction architecture. The TimesNet component’s time-frequency dual-domain modeling effectively separates mixed periodic patterns, achieving an MAE of 89.62 for 10-minute predictions, a $5.4 \%$ improvement over TSGAN. The enhanced CCW-GCN module’s channel capacity-weighted mechanism shows improved robustness to topology changes, achieving a 60-minute RMSE of $470.25,13.3 \%$ lower than STFGNN. The adaptive alignment module’s self-attention mechanism enables dynamic feature fusion, significantly improving long-term prediction stability. These results validate the effectiveness of our parallel feature re-extraction architecture in addressing the feature entanglement issues prevalent in traditional approaches, establishing a new paradigm for complex mesh network traffic prediction.

Case study: cellular traffic prediction in Milan. To validate the generalization capability of our proposed MeshHSTGT model across different traffic prediction scenarios, we conducted extensive experiments on the Milan cellular traffic dataset³⁶ provided by Telecom Italia. This dataset comprises Internet activity call records sampled at 10-minute intervals over 62 days, offering rich temporal patterns in an urban context and presenting unique challenges for traffic prediction models. As shown in Table 2:

Table 2 Traffic prediction performance on Milan dataset.

Accurate prediction of urban cellular traffic patterns is crucial for government agencies and network operators to optimize resource allocation and anticipate potential congestion issues. This is particularly critical in large metropolitan areas where prediction accuracy directly impacts traffic management efficiency. We evaluated MeshHSTGT against multiple baseline methods (FNN, FC-LSTM, GWN, ST-ChebNet, STSGCN, STFGNN, and TSGAN) across different prediction horizons.

The results demonstrate MeshHSTGTs robust performance in capturing network demand variations across different urban areas. Our model’s success can be attributed to its effective integration of time-frequency domain features and topological relationships through the parallel feature re-extraction architecture. While TSGAN shows competitive performance, particularly in short-term predictions, MeshHSTGT maintains superior accuracy across all prediction horizons, with notably better performance in longer-term predictions (60-minute horizon shows approximately $14.8 \%$ improvement in MAE).

These findings validate MeshHSTGT’s effectiveness in real-world urban scenarios, demonstrating its capability to capture complex spatio-temporal dependencies in cellular network traffic. The model’s strong performance on this independent dataset confirms its generalization ability beyond mesh networks, suggesting its potential applicability in diverse network traffic prediction scenarios.

Ablation Studies. To systematically evaluate the contribution of each architectural component to mesh network traffic prediction performance, we conducted comprehensive ablation studies comparing our full MeshHSTGT model against three variant architectures: TimesNet (focusing on temporal-frequency modeling), STGCN (emphasizing topological features), and TimesNet_STGCN (a cascaded combination of both components). The experimental results reveal crucial insights into the effectiveness of different modeling approaches and validate our architectural design choices. As shown in Fig. 3:

Fig. 3

Ablation study results of different models in terms of MAE, MAPE and RMSE metrics.

The standalone TimesNet module, while adept at capturing temporal-frequency patterns and periodic fluctuations in network traffic, demonstrates limitations in handling complex node interactions due to its lack of topological modeling. This deficiency manifests in relatively poor performance metrics (MAE: 139.38, 270.51, 564.62; RMSE: 105.13, 218.31, 438.46) across different prediction horizons, particularly during network events involving sudden traffic variations or node failures. In contrast, the STGCN variant, incorporating TE-GRU and CCW-GCN components, shows improved capability in modeling spatial dependencies and handling burst traffic patterns. However, its inability to capture multi-periodic characteristics results in suboptimal performance (MAE: 136.75, 282.42, 551.19; MAPE: 0.17, 0.17, 0.18), despite showing advancement over the TimesNet architecture.

The cascaded TimesNet_STGCN architecture attempts to bridge this gap by sequentially combining temporal-frequency and topological modeling. While this approach theoretically captures all necessary feature dimensions, the sequential nature of feature processing introduces feature entanglement issues, resulting in performance metrics (MAE: 105.13, 218.31, 438.46; MAPE: 0.14, 0.16, 0.16) that fall short of our full model’s capabilities. This observation underscores a critical insight: while comprehensive feature capture is essential, the method of feature integration significantly impacts prediction accuracy.

These initial ablation results strongly validate the superiority of the parallel architecture proposed in MeshHSTGT. By modeling temporal, frequency, and topological features independently yet concurrently, and effectively fusing them through feature re-extraction and adaptive alignment, our approach effectively addresses the limitations observed in the aforementioned variants.

To further validate the effectiveness of key components within our model, we first evaluated the graph weighting strategy of the proposed CCW-GCN. We compared it against alternative graph weighting strategies commonly used in traffic prediction tasks. Specifically, we tested the following variants:

CCW-GCN. The channel capacity-weighted adjacency matrix used in the original MeshHSTGT model.

Distance-based adjacency matrix. An adjacency matrix constructed based on the geographical distance between nodes, weighted using a Gaussian kernel.

Data similarity-based adjacency matrix. An adjacency matrix constructed based on the similarity of traffic patterns between nodes, using Dynamic Time Warping (DTW) for feature extraction and Pearson correlation coefficient for similarity calculation.

These models were trained and evaluated on the same dataset and under identical conditions. The performance metrics, including Mean Absolute Error (MAE) and Root Mean Squared Error (RMSE) for prediction horizons of 15, 30, and 60 minutes, are presented in Fig. 4.

Fig. 4

Ablation study results of graph construction strategies in terms of MAE, MAPE and RMSE metrics.

As shown in Fig. 4, the proposed CCW-GCN consistently demonstrated superior performance across all prediction horizons (15, 30, and 60 minutes) compared to the alternative graph construction strategies. Examining the MAE and RMSE metrics reveals that CCW-GCN achieved lower prediction errors than both the Distance-Based and Data Similarity-Based approaches. For example, at the 60-minute horizon, CCW-GCN’s MAE (391.17) and RMSE (470.25) were notably better than those from the Distance-Based (MAE 550.62, RMSE 662.65) and Data Similarity-Based methods (MAE 522.19, RMSE 508.31). This trend of improved accuracy with CCW-GCN holds consistently across the shorter 15-minute and 30-minute horizons as well, as detailed in Fig. 4. This quantitative improvement highlights the benefit of incorporating domain-specific knowledge (channel capacity), which better reflects dynamic link quality and interference than static geographical distance or historical traffic pattern similarity alone. These results confirm that CCW-GCN is a crucial component for accurate traffic prediction in wireless mesh networks, justifying its application within the MeshHSTGT model.

Furthermore, we evaluated the contribution of the Adaptive Alignment Module in the MeshHSTGT model. To this end, we conducted additional ablation experiments comparing the full model against variants using simpler fusion techniques: Concatenation Fusion and Summation Fusion. The aim was to assess the impact of removing the adaptive fusion mechanism. We tested the following variants:

Attention-based fusion. This is the complete MeshHSTGT model, where the adaptive alignment module dynamically adjusts the fusion of spatio-temporal features.

Concatenation fusion. In this variant, we replaced the adaptive alignment module with a simpler concatenation-based fusion method. Specifically, the temporal features (output from TimesNet) and spatial features (output from CCW-GCN) are concatenated along the feature dimension to form a higher-dimensional feature vector, which is then passed into the subsequent layers of the model. This approach does not involve dynamic weighting and instead completes the fusion via simple feature concatenation.

Summation fusion. In this variant, we replaced the adaptive alignment module with a summation-based fusion method. The temporal and spatial features are fused by element-wise addition.

Fig. 5

Ablation study results of feature fusion strategies in terms of MAE, MAPE and RMSE metrics.

Similarly, as depicted in Fig. 5, the Attention-Based Fusion strategy (representing our proposed adaptive alignment approach) consistently yielded the most accurate predictions across all horizons (15, 30, and 60 minutes) when compared to simpler fusion methods like Concatenation Fusion and Summation Fusion. The MAE and RMSE results presented in Fig. 5 show a clear advantage for our approach. Taking the 60-minute horizon as an example, the Attention-Based Fusion achieved an MAE of 391.17 and RMSE of 470.25, whereas Concatenation Fusion resulted in higher errors (MAE 532.55, RMSE 521.17), and Summation Fusion performed similarly (MAE 438.46, RMSE 506.65).This performance margin favoring the Attention-Based Fusion is consistently observed across the 15-minute and 30-minute predictions as well. This demonstrates the effectiveness of the adaptive fusion mechanism, which dynamically learns to weight the importance of temporal and spatial features, unlike the static combination strategies of simple concatenation or summation. The data strongly supports the conclusion that the adaptive alignment module is essential for capturing complex spatio-temporal dynamics in Wireless Mesh Networks and achieving the enhanced prediction accuracy of MeshHSTGT.

In summary, the parallel architecture of MeshHSTGT successfully mitigates feature entanglement while preserving the benefits of multi-domain modeling. The ablation studies, now supported by concrete performance data, quantitatively confirm the significant contributions of both the CCW-GCN for spatial feature extraction and the Adaptive Alignment Module for effective feature fusion. These components are key to the model’s superior prediction accuracy and robustness across all evaluated metrics and prediction horizons. This comprehensive analysis not only justifies our architectural choices but also provides valuable, data-driven insights for future research in network traffic prediction modeling.

Conclusion

In this paper, we propose MeshHSTGT, a novel feature re-extraction-based approach for Mesh network traffic prediction that effectively captures complex spatio-temporal dependencies in dynamic Mesh network environments. Unlike traditional cascading architectures that often suffer from feature entanglement, our model employs a hierarchical parallel structure for independent feature modeling across multiple dimensions. Specifically, MeshHSTGT integrates TimesNet for deep temporal sequence modeling, TE-GRU for short-term temporal correlation extraction, and CCW-GCN with channel capacity-weighted adjacency matrices for spatial dependency capture. The adaptive multi-domain feature alignment module further enhances the dynamic fusion of temporal, frequency, and topological domain features, ensuring both independent extraction and efficient collaboration of features.

Extensive experiments demonstrate that MeshHSTGT significantly outperforms state-of-the-art methods across short-term, medium-term, and long-term prediction scenarios, with particularly robust performance in complex dynamic environments. The experimental results show consistent improvements in prediction accuracy. Looking forward, MeshHSTGT shows promising potential for 6G applications, particularly in Industrial Internet of Things (IIoT), Extended Reality (XR), and integrated space-terrestrial networks. Future research directions include extending the model to real-time dynamic network management and exploring its integration with privacy-preserving federated learning frameworks for distributed network optimization.