Robust parameter inversion of coal mining subsidence based on the combination of RANSAC and DE algorithms

Abstract

Underground mining operations may lead to extensive surface environmental issues such as ground subsidence, cracks, and water accumulation. Obtaining high-precision mining subsidence prediction parameters in advance allows for accurate prediction of ground subsidence, which is of great significance for protecting the ecological environment and preventing geological disasters in mines. Currently, methods for obtaining subsidence prediction parameters based on surface measurement data primarily rely on inversion algorithms. However, these algorithms are often susceptible to outliers, resulting in low robustness and consequently limiting the accuracy of the predicted results. To address this issue, this study presents the RANSAC-DE algorithm, which integrates the high precision, efficiency, and global search capabilities of the Differential Evolution (DE) algorithm with the high robustness of the Random Sample Consensus (RANSAC) algorithm. The comparison of simulation experiments shows that the RANSAC-DE algorithm can effectively identify and eliminate the interference of outliers, and its anti-outlier interference performance is much better than DE and Huber-DE. In addition, the RANSAC-DE algorithm inherits the advantages of the DE algorithm, such as high inversion accuracy, strong global search capability, robustness against missing observation points interference, and Gaussian noise interference. The measured data of the 1312 working face of Guqiao Mine was used for case verification. The root mean square error (RMSE) of the subsidence fitting obtained by the RANSAC-DE method is 33.2 mm, much better than the 62.2 mm and 67.6 mm obtained by the DE and Huber-DE methods, respectively. Furthermore, ML06, ML07, and ML09 are correctly identified as outliers, verifying the robustness of the RANSAC-DE algorithm.

Introduction

Mining subsidence poses a serious threat to the ecological environment, and accurately predicting the impact of surface subsidence caused by mining is significant for controlling mining subsidence disasters. Polish scholar Litvinishen¹ proposed the prediction method of mining subsidence based on random medium theory, and Liu et al.² subsequently developed this theory into the probability integral method (PIM). This method is also one of China’s primary methods of mining subsidence prediction³. The accuracy of the predicted results of this method directly depends on the accuracy of the PIM parameters⁴. Regarding the issue of accurately obtaining PIM parameters, the current primary method is to establish surface movement observation stations and use the measured subsidence data from these stations for inversion⁵.

Many scholars have conducted extensive research on how to use measured data to calculate PIM parameters. Traditional parameter inversion methods include the characteristic point method⁶, least squares method⁷, etc. Although these methods are simple in form, they have significant limitations in application and low reliability of calculation results⁸. In recent years, many scholars have introduced intelligent optimization algorithms to invert PIM parameters, such as patterns search⁶, genetic algorithm⁹, particle swarm optimization algorithm¹⁰, Wolf pack algorithm¹¹, etc. Comparative studies have shown that these methods can all invert the correct parameters, but they may also fall into the problem of local optima and weak robustness to some extent⁸. As an efficient heuristic global search algorithm, the DE algorithm¹² has the characteristics of strong global search ability, simple method structure, and easy programming implementation. It can effectively handle optimization problems with nonlinear, non-convex, multimodal, high-dimensional, and discontinuous characteristics. Therefore, it is widely used in mathematics, computer engineering, and other fields. However, the traditional DE algorithm is also sensitive to outliers and is not very effective under many outliers.

To reduce the effect of the outliers in the measured data on the parameter inversion results, many scholars have conducted studies from the two aspects of parameter robust estimation and outlier identification^13,14. Guo et al.¹⁵ and Wang et al.¹⁶ respectively used the minimum norm method and Huber function method for parameter robustness estimation. Yang et al.¹⁷ compared the robustness of the minimum norm method and Huber function combined with the genetic algorithm for parameter inversion. Wang et al.¹⁸ introduced the IGGIII scheme to alleviate the adverse effects of outliers in parameter inversion of the CA-rPSO algorithm. Fischler M.A et al.¹⁹ proposed the RANSAC algorithm for the graph fitting problem. Later, the algorithm has been improved many times^20,21,22 and has been widely used in computer vision. This method estimates model parameters by randomly selecting a subset of data multiple times and chooses the set of parameter solutions with the most inliers in the estimated model as the optimal solution. It is robust in dealing with high-rate outlier data inversion problems. Duan et al.^23,24 proposed combining RANSAC with PSO and grid search algorithms to invert seismic fault parameters and verified the robustness of the algorithm.

This paper aims to address the problem of robust inversion of subsidence prediction parameters. Considering the outstanding advantages of the DE algorithm in terms of high efficiency, high precision, and strong global search capability during parameter inversion, as well as its sensitivity to outliers, and the high robustness of the RANSAC algorithm, which cannot be directly applied to the parameter inversion of complex nonlinear models, this study proposes the RANSAC-DE algorithm, which combines both algorithms to achieve complementary advantages in inversion problem of subsidence prediction parameters. It can effectively identify outliers and eliminate their interference, thereby enhancing the robustness of the algorithm’s inversion results.

Robust inversion method for mining subsidence parameters

The subsidence prediction method of the probability integral model (PIM)

Fig. 1

Model of surface subsidence caused by mining of small units.^1,2.

According to the random medium theory¹, the surface subsidence caused by unit mining presents a normal distribution characteristic on the profile. Based on this theory, the prediction formula of surface subsidence caused by working face mining can be obtained, as shown in Fig. 1.

$$\begin{aligned} W(x,y)=\int \limits _{0}^{l} \int \limits _{0}^{d} W_{0}W_{e}(x,y) \,ds\,dt=\int \limits _{0}^{l} \int \limits _{0}^{d} \frac{W_{0}}{r^2}e^{-\pi \frac{(x-s)^2+(y-t+\Delta l)^2}{r^2}} \,ds\,dt \end{aligned}$$

(1)

Where W(x, y) is the subsidence value of the ground point (x, y), and (s, t) is the coordinate of the small unit mining center. $W_{0}$ is the maximum subsidence value of the surface. Its formula is $W_{0}=mqcos\alpha$, in which m is the mining thickness of the working face, q is the subsidence coefficient, and $\alpha$ represents the dip in the coal seam. r represents the main influence radius, its formula is $r=H/tan\beta$ , H represents the mining depth of the working face, and $tan\beta$ represents the tangent value of the main influencing angle $\beta$. $\Delta l=Hcot\theta$, in which $\theta$ is the maximum subsidence angle. $l=L-S_l-S_r$, $d=D-S_u-S_d$, L and D represent the strike length and the inclination length of the working face, respectively. $S_{l}$, $S_{r}$, $S_{u}$, and $S_{d}$ represent the offset values of left, right, upper, and lower inflection points, respectively. Above is the subsidence calculation model in the PIM.

Robust inversion of PIM parameters

From formula (1), it can be seen that among the PIM parameters, the parameters related to subsidence include the subsidence coefficient q, the main influence angle tangent $tan\beta$, the maximum subsidence angle $\theta$, and in addition, there are four inflection point offsets $S_{l}$, $S_{r}$, $S_{u}$, and $S_{d}$. Since the PIM is a complex nonlinear model, it is difficult to calculate the PIM parameter value directly based on the measured data. Therefore, the optimization algorithm is mainly used to invert the PIM parameters.

Parameter inversion algorithm based on DE

Differential evolution algorithm(DE) is an evolutionary algorithm proposed by Storn.R.¹² based on the basic laws of biological evolution in nature. For the inversion problem of the PIM parameters, the general steps of PIM parameters inversion based on the DE algorithm are as follows:

Step 1: Determine the PIM parameters and their ranges to be inverted. The number of parameters is set to $D=7$, namely q, $tan\beta$, $\theta$, $S_{l}$, $S_{r}$, $S_{u}$, and $S_{d}$. The parameter range can be set based on experience.

Step 2: Combining the conclusion of Storn.R.¹² on the parameter value selection of DE algorithm, set the population size $N_{p}=50$, iteration number $G_{m}=100$, mutation factor $F_{0}=0.4$, and crossover factor $cr=0.4$ of the DE algorithm.

Step 3: Generate the genes of all individuals in the initial population according to the PIM parameters and their ranges.

Step 4: Calculate the cost function value of all individuals in the initial population. Currently, the residual sum of squares between the estimated and measured subsidence values is mainly used as the fitting effect evaluation criterion²⁵. Therefore, the cost function is selected as shown in formula (2):

$$\begin{aligned} f=\sum _{i=1}^{n} V_{i}^{T}V_{i}=\sum _{i=1}^{n}(W_{i}-W_{i}^{0})^2 \end{aligned}$$

(2)

Where f is the individual cost function value, $W_{i}$ and $W_{i}^{0}$ are the estimated and measured subsidence values of point i, respectively. $V_{i}$ is the difference value between $W_{i}$ and $W_{i}^{0}$, and n is the number of all ground observation stations.

Step 5: Perform the mutation operation. Randomly select three parent individuals $X_{r1}$, $X_{r2}$, and $X_{r3}$, and use formula (3) to generate the mutation vector.

$$\begin{aligned} v=X_{r1}+F(X_{r3}-X_{r2}) \end{aligned}$$

(3)

Where v is the calculated mutation vector. $F=F_{0}\cdot 2^\lambda$, $\lambda =\exp (1-G_{m}/(G_{m}+1-G)) )$. G represents the current number of iterations.

Step 6: Perform the crossover operation. Generate a random number rand between 0 and 1, determine the crossover behavior of each gene of the parent target vector X and the mutation vector v by comparing the random number rand with the crossover factor cr, and finally generate a trial vector u. As shown in formula (4):

$$\begin{aligned} u_{j}={\left\{ \begin{array}{ll} v_{j}\quad (rand\le cr\quad or \quad rand= jrand) \\ X_{j}\quad (rand> cr\quad and \quad rand\ne jrand) \end{array}\right. } \end{aligned}$$

(4)

Where $u_{j}$, $v_{j}$, and $X_{j}$ are the gene values with subscript j in the trial vector, mutation vector, and target vector, respectively. jrand is an integer in [0, D], which ensures that at least one gene in the trial vector u comes from the mutation vector v, increasing the perturbation effect of the genes, as shown in Fig. 2.

Fig. 2

The crossover process of mutation vector and target vector.

Step 7: Perform the selection operation. Formula (2) calculates the individual cost function values of the trial vector u and the target vector X. A greedy strategy compares the cost function value. If the cost function value of the trial vector u is lower than the parent target vector X, then the trial vector u is accepted as the new generation individual to replace the original parent target vector X.

Step 8: Repeat steps (5) to (7) to continue the population mutation, crossover, and selection operations. When the iteration termination condition is met, the algorithm ends. The current optimal individual $X_{best}$ is output, which is the optimal parameter combination.

Iteratively reweighted least squares

The cost function formula (2) can somewhat reduce the impact of random errors. Still, it is susceptible to outliers and may cause significant deviations in the parameter inversion results¹⁵. In actual projects, due to the complexity of the observation environment, geological environment, or the inadaptability of the prediction model, mining subsidence monitoring data sometimes has many outliers, which seriously interferes with the accuracy of the inversion parameter results¹⁶.

The iterative reweighted least squares method (IRLS) is a commonly used robust estimate method²⁶, which can effectively weaken the impact of outliers. Basic ideas are based on formula (2), which recalculates the weight $P_{i}$ according to the residues of each observation point to reduce the weight of outliers and weaken the impact of outliers, as formula (5).

$$\begin{aligned} f=\sum _{i=1}^{n} V_{i}^{T}P_{i}V_{i}=\sum _{i=1}^{n}P_{i}(W_{i}-W_{i}^{0})^2 \end{aligned}$$

(5)

Usually, the general calculation steps are as follows: Firstly, assuming that the initial weight $p_{i}^{1}$ of each observation point is 1, calculate the optimal parameter solution and the estimated subsidence value $W_{i}^{1}$ of each observation point. Then, calculate the residual $V_{i}^{1}$ of estimates and measured values. Use the residual value $V_{i}^{1}$ to recalculate the weight of the next iteration $p_{i}^{2}$. Repeat the above process until a satisfactory parameter is obtained.

The Huber weight function²⁷ is a function of computing weights commonly used in a stable estimation method. It is especially suitable for processing data containing outliers. It can reduce the impact of significant errors while maintaining sensitivity to minor errors. Therefore, this paper uses the Huber function to calculate the weight.

$$\begin{aligned} P_{i}^{k+1}=\left\{ \begin{array}{cl} 1 & \left| V_{i}^{k}\right| \le \delta \\ \frac{\delta }{\left| V_{i}^{k}\right| } & \left| V_{i}^{k}\right| >\delta \end{array}\right. \end{aligned}$$

(6)

Where $P_{i}^{k+1}$ presents the calculated weight value of observation point i during the $k+1$ iteration, $\delta$ is the set residual threshold, and $V_{i}^{k}$ is the residual value of observation point i calculated after the k iteration.

Parameter inversion algorithms based on RANSAC-DE

Random sampling consistency algorithms (RANSAC) are commonly used in image feature point matching. As shown in Fig. 3, compared with the least squares method (LSM), since the RANSAC method divides the measured values into inliers and outliers, it can effectively identify and eliminate the interference of outliers. It can find the most reasonable parameters under many outliers with high reliability and robustness²².

Fig. 3

Comparison of line fitting effects between RANSAC and LSM.

Fig. 4

Partition random sampling method for subsidence.

Aiming at the problem of PIM parameter inversion in measured subsidence data with outliers, this paper proposes the RANSAC-DE method that combines the RANSAC algorithm with the DE algorithm. This method can realize the automatic identification and elimination of outliers in the observed data and improve the accuracy of the parameter inversion results. The general steps of the RANSAC-DE algorithm are as follows:

Step 1: Determine the relevant parameters required by the RANSAC algorithm. It includes the minimum number of samples $N_{s}$ and the inliers’ point judgment threshold T. The minimum number of samples can be determined using the PIM prior model and the partition uniform acquisition method, thereby increasing the rationality of the parameter inversion results. As shown in Fig. 4, the observation line is divided into five sampling parts from A to E according to the subsidence boundary, inflection point, and maximum subsidence point. Therefore, 5 sample points are selected on each strike and inclination observation line, and the minimum number of randomly selected samples $N_{S}=10$. The inlier judgment threshold T is determined according to the value of inliers and outliers, ensuring that the RANSAC method can effectively identify inliers and outliers. In this example, We set $T=100$ mm.

Step 2: Construct random samples from all observation points, then use the DE algorithm to invert the PIM parameters based on the random sample points.

Step 3: Using the PIM parameters obtained by the DE algorithm, calculate the estimated subsidence values $W_{i}$ at all observation points. Calculate the absolute residual $\left| V_{i} \right|$ based on the estimated subsidence values $W_{i}$ and the measured subsidence value $W_{i}^{0}$, and compare the value $\left| V_{i} \right|$ with the threshold T. If $\left| V_{i} \right|$ is less than the threshold T, the observation point is marked as an inlier. Otherwise, the observation point is marked as an outlier. Finally, we recorded the number of inliers $N_{i}$.

Step 4: Compare $N_{i}$ with the current maximum number of inliers $Max\_N_{i}$. If $N_{i}$ is greater than $Max\_N_{i}$, then update $Max\_N_{i}$ and corresponding parameter solution $param\_best$, recalculate the inliers ratio $P=N_{i}/n$, and use P to calculate and update the maximum number of iterations $N_{r}=\log (1-0.99) / \log \left( 1-P^{N_{s}}\right)$ of the RANSAC.

Step 5: Determine whether the current iteration count $n_{r}$ is less than $N_{r}$; if so, continue iterating through steps (2) to (4). Otherwise, end the iteration process and output the current maximum number of inliers $Max\_N_{i}$ along with its optimal parameter $param\_best$.

A flowchart depicting the RANSAC-DE inversion model is illustrated in Fig. 5.

Fig. 5

Flowchart of the RANSAC-DE solving the PIM parameters.

The execution process of the RANSAC-DE algorithm requires a certain amount of time and computational resources. Its time complexity is $O(N_p*G_m*N_r)$, and the running time will significantly increase when the proportion of outliers is high. With the widespread application of emerging monitoring technologies such as remote sensing, the large volumes of monitoring data can pose challenges to the algorithm’s processing efficiency. Fortunately, the requirements for real-time processing in the subsidence parameter inversion problem are not stringent, and it’s also well-suited for data processing methods that utilize parallel computing, ensuring that the computational efficiency meets practical engineering needs.

Simulation experiment

It is an effective method to verify the performance of the inversion algorithm using simulated working face and observation station data. The information regarding the simulated working face is the following: the average mining depth of the coal seam measured H=400 m, with a mining thickness of m=3.0 m and a coal seam dip of $\alpha =10^{\circ }$. The strike length of the working face L=800 m, while the inclination length D=500 m. The roof management technique employed involved a caving method. In the subsidence basin above the working face, 54 observation points (E1-E54) and 44 observation points (S1-S44) were arranged along the strike and inclination, respectively, with a spacing of 30 m between each observation point. The schematic diagram of the working face and observation station location is shown in Fig. 6. The parameter values and the parameter search ranges are designed in Table. 1.

Fig. 6

The schematic diagram of the working face and observation station location.

Table 1 Designed parameter values and parameter search ranges of simulated working face.

Analysis of the accuracy of the inversion results

We used the design values of PIM parameters and the working face’s geological and mining data to predict each observation point’s subsidence value. Then, the subsidence value and parameters search range are used to invert the PIM parameters of the working face. Since the evolution process is random, five inversions are averaged as the final result. The parameter inversion results are shown in Table 2.

Table 2 Comparison of the inversion results.

The data in Table 2 show that the relative errors of the q, $tan\beta$, and $\theta$ parameters inverted by the DE, Huber-DE, and RANSAC-DE algorithms are all less than 0.5%, and the errors of the inflection point offset are all less than 3%. It indicates that these three methods can all accurately invert the PIM parameters.

Based on the above parameter inversion results and the geological and mining data of the working face, the subsidence fitting effect of surface strike observation line E and the dip observation line S is shown in Fig.7.

Fig. 7

Comparison of subsidence fitting effects of the DE, Huber-DE, and RANSAC-DE algorithms.

The subsidence values of the strike and dip observation lines inverted by the three algorithms of DE, Huber-DE, and RANSAC-DE are consistent with the measured subsidence values, with the maximum absolute errors of 17 mm, 15 mm, and 17 mm, respectively, and the RMSE of the fitting point mean errors of 6.2 mm, 5.5 mm, and 5.8 mm, respectively.

Fig. 8

The values of parameters q and $tan\beta$ obtained from the inversion of five experiments.

Figure 8 shows the distribution of the values of parameter q and $tan\beta$ obtained from five inversions. In the five experiments, the maximum value of q is 0.8036, the minimum value is 0.7962, and the difference is 0.0074; the maximum value of $tan\beta$ is 2.0109, the minimum value is 1.9805, and the difference is 0.0304. The parameters q and $tan\beta$ inverted by the DE, Huber-DE, and RANSAC-DE algorithms are all close to the designed values, which verifies the stability of the inversion results of the three algorithms.

The inversion results of the DE, Huber-DE, and RANSAC-DE algorithms were not significantly different in the experiment. It is because the threshold $\delta =100$ mm set by the Huber-DE algorithm, and the residual between the estimated and measured values of all points is less than $\delta$, so according to formula (6), the weights of all points are 1. Hence, the Huber-DE algorithm degenerates into the traditional DE algorithm. In the RANSAC-DE algorithm, since there is no measured subsidence error in all observation points, it can be considered that the randomly selected sample points are all inliers. At this time, the RANSAC-DE algorithm also degenerates into the traditional DE algorithm. Therefore, the DE, Huber-DE, and RANSAC-DE methods show the same stability and accuracy and can fully meet the parameter inversion accuracy requirements.

Analysis of the robustness of the inversion results

Global search performance

The PIM parameters inversion process uses the geological and mining data of the mining face, combines experience to determine the parameter search ranges, and uses an optimization algorithm to calculate the final parameter value. Differences in parameter values in different regions make it challenging to decide on the range of estimated values for the PIM parameters during the inversion process. The general solution is to appropriately enlarge the parameter search range when inverting PIM parameters in unfamiliar geological regions, giving the optimization algorithm a more extensive parameter search space. However, this approach may also cause the optimization algorithm to find a local optimal solution rather than a global one²⁸.

In this paper, to verify the global search capability of the RANSAC-DE algorithm, the parameter search ranges were modified, and three groups of parameter combinations in different ranges were designed for comparative experiments, as shown in Table 3. The parameter values obtained after inversion experiments are shown in Table 4.

Table 3 Parameter search ranges.

Table 4 The RANSAC-DE inversion results in different parameter search ranges.

The data in Table 4 shows that as the parameter ranges change, the obtained parameter values remain close to the set parameter values, and the result accuracy does not change much. The relative errors of the parameters q, $tan\beta$, and $\theta$ are all less than 0.6%, and the errors of the inflection point offset are all less than 3%. The RMSE of the subsidence fitting of the observation points is 5.4 mm, 6.5 mm, and 6.8 mm, respectively. The RMSE has increased slightly but still meets the general accuracy engineering needs.

When no error exists in the measured data, the RANSAC-DE algorithm will degenerate into the traditional DE algorithm. Using the DE algorithm, the distribution changes of the parameters q and $tan\beta$ at the initial, 10th, 20th, and 40th iterations are plotted, as shown in Fig. 9.

Fig. 9

Changes in the distribution of parameters q and $tan\beta$ caused by iterative evolution of the population.

It can be seen that the population distribution at the initial is relatively uniform, distributed in the entire search space. With the continuous iteration of the algorithm, the parameters q and $tan\beta$ gradually approach the design values. Therefore, intuitively, the DE model has an excellent global search capability, and in the later iterations, the individuals in the population continue to gather, and a higher-precision parameter solution can also be obtained.

Anti-missing observation point interference performance

In actual engineering applications, observation of ground subsidence takes a long time. Due to interference from natural factors and human factors during this period, some of the initially designed surface observation points may be missing. Experiments were conducted with 30 observation points randomly missing to verify the ability to anti-missing observation point interference of the DE, Huber-DE, and RANSAC-DE algorithms. The inversion results are shown in Table 5 and Fig. 10.

Table 5 The experiment results of anti-missing observation point interference.

Fig. 10

Comparison of subsidence fitting effects when 30 observation points were missed.

It can be seen that the relative errors of the main parameters q, $tan\beta$, and $\theta$ inverted by the three methods of DE, Huber-DE, and RANSAC-DE are all lower than 0.8%, and the inflection point offset are all less than 6%. The absolute errors of fitting subsidence value are all less than 30 mm, and the RMSE of the subsidence fitting is 6.4 mm, 10.2 mm, and 7.3 mm, respectively. The experimental results show that the DE, Huber-DE, and RANSAC-DE inversion algorithms can all resist the interference from the observation point missing.

Anti-Gaussian noise interference performance

In the actual observation process, random noise is inevitable. These random noises are concentrated and symmetrical. These random noises are concentrated and symmetrical. It conforms to the fundamental law of Gaussian normal distribution. In this paper, to study the algorithm’s ability to anti-Gaussian noise error interference, the random error following a normal distribution N(0,40) was added to the measured data to verify the robustness of the DE, Huber-DE, and RANSAC-DE algorithms. The parameter inversion results are shown in Table 6 and Fig. 11.

Table 6 The experiment results of anti-Gaussian noise interference.

Fig. 11

Comparison of subsidence fitting effects under Gaussian noise interference.

It can be seen that the relative errors of the main parameters q, $tan\beta$, and $\theta$ inverted by the DE, Huber-DE, and RANSAC-DE algorithms are all less than 0.8%, and the inflection point offset are all less than 5%. The absolute errors of fitting subsidence value are all less than 100 mm, and the RMSE of the subsidence fitting is 44.6 mm, 43.2 mm, and 39.7 mm, respectively. The experimental results show that the DE, Huber-DE, and RANSAC-DE inversion algorithms can all anti-Gaussian noise interference.

The analysis shows that since the Gaussian noise error N(0, 40) is set to be less than the threshold $\delta =T=100$ mm, the Huber-DE and RANSAC-DE methods will degenerate into the traditional DE algorithm. Due to the symmetry and compensability of Gaussian noise errors, when the sum of squared residuals between the estimated and measured subsidence is used as the evaluation method for the subsidence fitting effect, the inversion method can still accurately fit the measured subsidence curve and inverse the PIM parameters.

Anti-outliers interference performance

In the actual monitoring process, due to the carelessness of the observers, measurement errors or instrument operation mistakes may occur, resulting in incorrect monitoring data. In addition, the unique geological structure and stress in local surface areas also make the monitoring data unable to reflect the surface movement caused by underground mining activities¹⁶. These abnormal data will directly affect the accuracy of the inversion results. In this paper, to verify the algorithm’s ability to anti-outliers interference, 20 observation points were randomly selected, and outliers with absolute errors ranging from 200 mm to 400 mm were added to the measured subsidence data at these points. The inversion of PIM parameters was conducted using subsidence data with outliers, and the inversion results are shown in Table 7 and Fig. 12.

Table 7 The experiment results of anti-outliers interference.

Fig. 12

Comparison of subsidence fitting effects under outliers interference.

For the traditional DE algorithm, the relative error of the parameter q inverted by the traditional DE algorithm reaches 3.78%, and the maximum relative error of the inflection point offset reaches 11.02%. The RMSE of the subsidence fitting of the observation points is 121.0 mm. Near the maximum subsidence point, due to the influence of outliers, the estimated maximum subsidence value is about 75 mm larger than the theoretical value, resulting in a significantly larger parameter q obtained through inversion by the DE algorithm.

For the Huber-DE algorithm, the relative error of the parameter q inverted by the Huber-DE algorithm reaches 2.64%, and the maximum relative error of the inflection point offset reaches 8.15%. The RMSE of the subsidence fitting of the observation points is 121.2 mm. The weight of all inliers is 1, and the weight of outliers is between 0.28 and 0.57. Near the maximum subsidence point, due to the influence of outliers, the estimated maximum subsidence value is about 54 mm larger than the theoretical value. Our analysis shows that although the Huber-DE algorithm can somewhat reduce the weight of outliers in the overall evaluation of fitting performance, it cannot eliminate the influence of outliers completely, causing the overall fitting subsidence curve to shift towards the side of outliers.

For the RANSAC-DE algorithm, the relative error of the parameter q inverted by the RANSAC-DE algorithm is only 0.28%, and the maximum relative error of the inflection point offset is only 5.5%. After removing the identified outliers, the RMSE of the subsidence fitting of the observation points is 7.1 mm. All design outliers were identified and eliminated successfully. The residuals of fitting subsidence of outliers are significant, and others are minimal. The residuals between the estimated maximum subsidence value and the theoretical value were less than 5 mm, and the fitted subsidence curve was consistent with the theoretical subsidence curve.

The comparison shows that the RANSAC-DE algorithm performs much better in resisting the influence of outliers than the traditional DE and the Huber-DE algorithm. It can not only accurately invert the PIM parameters but also accurately identify outliers. This feature will promote the analysis of the causes of outliers and the study of the laws of surface movement.

Engineering applications

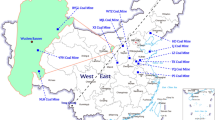
The algorithm robustness is verified using measured data from the surface observation point of the 1312 working face of Gubei Coal Mine, located in Huainan City, Anhui Province. The geological and mining information of the working face is as follows: the average mining depth of the coal seam measured 528 m, with a mining thickness of 3.3 m and a coal seam dip of $5^{\circ }$. The strike length of the working face L = 620 m, while the inclination length D = 205 m. The roof management technique employed involved a caving method. The surface observation stations are designed along the strike direction at intervals of 30 m. Due to interference from ground terrain and buildings, the actual location of the observation point is slightly different from the designed location. Some points were missing during the monitoring process, and the actual available observation point locations are shown in Fig. 13. Twenty leveling measurements were conducted to obtain the final subsidence values of the observation points.

Combined with the measured subsidence data of observation points, We used the DE, Huber-DE, and RANSAC-DE algorithms to invert the PIM parameters of the 1312 working face. The inversion results are shown in Table 8 and Fig. 14.

Fig. 13

Location of the 1312 working face and observation stations. (The map was generated by the authors with the help of ArcGIS 10.6 (https://support.esri.com/en/download/7583) and does not require any permission from anywhere).

Table 8 The inversion results of 1312 working face. ($\delta =T=50$ mm).

Fig. 14

Comparison of robust inversion results of the subsidence curve of the 1312 working face.

The comparison of the results shows that the RMSE of the subsidence fitting obtained by the DE, Huber-DE, and RANSAC-DE algorithms are 62.2 mm, 67.6 mm, and 33.2 mm, respectively. The overall fitting trend between the estimated and measured subsidence curves is consistent, indicating that these methods can all be used to convert PIM parameters in mining areas.

From the overall measured subsidence curve shape, the measured subsidence values for points ML06, ML07, and ML09 in the data significantly deviate from the shape of the overall subsidence curve. It can be inferred that these points are outliers. By comparing the curves in the local graph, it is found that to minimize the sum of squares of the overall subsidence fitting residuals, the DE and the Huber-DE algorithms are disturbed by local outliers, which makes the estimated subsidence values of ML49$\sim$MS23 smaller but reduces the overall fitting effect. The RANSAC-DE algorithm automatically identifies ML06, ML07, and ML09 as outliers, eliminating the influence of outliers on the overall subsidence fitting effect and ensuring the robustness of this algorithm.

Fig. 15

The surface subsidence basin and subsidence contour map caused by 1312 working face mining.

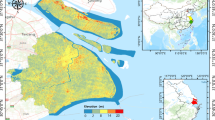
Using the PIM parameters obtained by the RANSAC-DE algorithm, the surface subsidence basin and subsidence contour map of the 1312 working face mining were calculated, as shown in Fig. 15. It can be seen that the prediction effect is consistent with the measured subsidence curve, which intuitively verifies the reliability and robustness of the parameters obtained by the RANSAC-DE algorithm.

Discussion

Currently, some intelligent optimization algorithms are being applied to the problem of inverting subsidence prediction parameters. However, due to the influence of various factors, a single inversion method often fails to achieve satisfactory application results. Numerous factors affect the inversion results of subsidence prediction parameters, such as errors and outliers in monitoring data, human disturbances affecting ground monitoring points, environmental factors like frozen soil and groundwater flow impacting monitoring data, and the presence of local faults or special geological structures underground. These can cause a small number of surface monitoring point data to deviate from the general subsidence patterns described by the Probability Integral Model (PIM), limiting the accuracy of the algorithm’s parameter inversion results. Manual identification and removal of these anomalous data points can effectively enhance the accuracy of the parameter inversion results. However, this approach also encounters challenges, such as the substantial workload of manual data preprocessing or the inability to identify certain outliers that do not exhibit significant differences.

The RANSAC algorithm continuously adjusts a randomly selected set of monitoring points and uses the inverted subsidence curve/surface to reassess the number of inliers among the monitoring points until it obtains a parameter solution with the maximum number of inliers. Since the small proportion of outliers among all monitoring points, the optimal parameter solution will fit the subsidence curve/surface around the normal points, allowing for the identification and removal of outliers, thereby enhancing the robustness of the algorithm. By combining the advantages of the DE algorithm, such as high precision and strong global search capability, the resulting RANSAC-DE algorithm forms a complementary synergy between the two algorithms, consistently achieving highly robust and high-precision parameter solutions.

With the application of remote sensing and other ground monitoring technologies, the surface subsidence data obtained often contains disturbances from vegetation and water surfaces, resulting in the presence of outlier interference in the data. In such cases, traditional inversion methods may face difficulties. However, the RANSAC-DE algorithm can effectively eliminate these outliers and produce robust parameter results. Additionally, the algorithm can also identify the regions where these outliers are distributed, which can be helpful for further analyzing the causes and patterns of abnormal phenomena (such as underground faults, surface vegetation growth conditions, etc.).

Since RANSAC operates by continuously randomly selecting a set of monitoring data for subsequent inversion, it involves repeated tasks of random selection, parameter inversion, and outlier count statistics. When the proportion of outliers is high, this repetitive process can consume a significant amount of runtime. Additionally, the setting of the inlier evaluation threshold T in the RANSAC algorithm is also crucial, as it affects the identification and differentiation between inliers and outliers. In the future, the practical application capability of the algorithm can be enhanced through further code optimization and algorithm innovation by utilizing parallel computing methods, adaptive thresholds, and adaptive parameter range adjustment techniques.

Conclusions

Aiming to address the problem of weak robustness of the traditional PIM parameter inversion algorithm, this paper proposes combining the RANSAC algorithm with the DE algorithm to improve its robustness. The simulation experiment and the actual engineering case verify the robustness of the algorithm. The main results are as follows:

(1)Under ideal measurement data, in the inversion results of the DE, Huber-DE, and RANSAC-DE algorithms, the relative errors of parameters q, $tan\beta$, and $\theta$ are all less than 0.5%, and the relative errors of inflection point offset are all less than 3% . All three algorithms can invert PIM parameters accurately and are feasible for application.

(2)All three algorithms have strong capabilities in global search, anti-missing observation points, and anti-Gaussian noise interference. In the anti-outliers interference performance, the RANSAC-DE inversion effect is much better than the traditional DE and Huber-DE, and it can effectively identify and eliminate the interference of outliers.

(3)The PIM parameters of the 1312 working face of Gubei Mine were inverted using the DE, Huber-DE, and RANSAC-DE algorithms. The comparison of the inversion results shows that the RMSE of the subsidence fitting of the RANSAC-DE algorithm is 33.2mm, which is much better than 62.2mm and 67.6mm of the DE and Huber-DE algorithms, and ML06, ML07, and ML09 are identified as outliers automatically. The RANSAC-DE method has excellent robust performance and has broad application prospects in the problem of robust inversion of PIM parameters.