Classification of Indian classical dances using MnasNet architecture with advanced polar fox optimization for hyperparameter optimization

Abstract

Indian classical dances represent a significant aspect of the nation’s cultural heritage, with each dance form characterized by its distinct style, posture, and movement. The automatic classification and recognition of these dances present considerable challenges due to differences in their postures, movements, and costumes. Recent advancements in deep learning techniques have yielded hopeful results in image classification tasks, including the classification of dance forms. In this study, a deep learning methodology using the MnasNet architecture is introduced for the classification of Indian classical dances. To enhance performance accuracy, the advanced polar fox optimization (APFO) algorithm is applied to optimize the hyperparameters of the MnasNet architecture. The experimental results are applied to Bharatnatyam Dance Poses dataset and its results have been compared with deferent state of the art similar models. Final results illustrate the efficacy of the proposed method in achieving elevated classification accuracy.

Introduction

Indian classical dances (ICD) are a significant part of the nation’s extensive cultural heritage, with origins that trace back thousands of years¹. These forms of dance help not only as a medium for artistic expression but also as a means of storytelling, conveying emotions, and safeguarding cultural traditions². As digital media continues to gain traction, there is a growing demand for automated classification of Indian classical dances³. This necessity arises from the fact that manual annotation and analysis of dance videos or images can be labor-intensive and subjective, often requiring a deep understanding of the various dance forms and their intricacies⁴.

Many individuals meet challenges in retrieving the expertise of knowledgeable dance instructors, primarily due to time limitations⁵. Traditional methods of dance education, such as attending in-person classes, may not adequately address the needs of differently abled individuals, including those who are Deaf or have speech impairments, as well as those who prefer self-directed learning⁶.

While there is an excess of online videos showing classical dance forms, they often lack the depth required for comprehensive understanding, underscoring the necessity for more robust educational resources⁷. Current technological initiatives have sought to use Indian Classical Dance forms through various techniques, including image processing and machine learning to identify Bharatanatyam mudras⁸.

Jain et al.⁹ developed a model to thoroughly classify forms of dance into 8 classes. A Deep Convolutional Neural Network (DCNN) has been suggested to classify the data while employing ResNet50 and outperformed other methods. The input data of the suggested model has been preprocessed while employing the sampling and thresholding of the image. After that, the suggested model was employed to the preprocessed instances. In the end, the accuracy value of 91% was achieved by the suggested model.

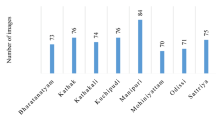
Rani and Devarakonda¹⁰ utilized a dataset that included 8 various classes of dance, including kathak, kathakali, sattriya, mohiniyattam, kuchipudi, Manipuri, odissi, and Bharatnatyam. To overcome the problem of overfitting and achieving less accurate results, transfer learning was suggested. The model was good at reducing space and time complexity, while employing a previously trained model called VGG16. Ultimately, the accuracy value of 85.4% was achieved, and this model could perform better than other models proposed previously.

Challapalli and Devarakonda¹¹ introduced CNN model that was optimized by Hybrid Particle Swarm Grey Wolf (HPSGW). This optimizer has been utilized to find the optimum variables of the CNN, such as number of epochs, filters’ size, number of hidden layers, and size of batch. There are three datasets, called MNIST, CIFAR, and Indian Classical Dance (ICD) that evaluated the suggested model. The suggested model could achieve the accuracy values of 97.3, 91.1%, and 99.4% while employing ICD, CIFAR, and MNIST, respectively.

In the following, another approach was developed by Reshma et al.¹² that classified various forms of Indian classical dance. There are several usages offered by the dance, such as online learning, even remedial treatment, cultural conservation, and entertainment. Due to the fact that the dataset is not that big, transfer leaning models and deep neural networks have been, in turn, employed for feature extraction and classification. The suggested approach illustrated a notable accuracy level of 97.05%.

Jhansi Rani and Devarakonda¹³ recommended the Indian Classical Dance Generative Adversarial Network (ICD-GAN) and Quantum-based Convolutional Neural Network (QCNN) to augment and classify data. There were 3 various stage in the present study, namely GAN-based augmentation, traditional augmentation, and the integration of them. The suggested QCNN has been suggested to decrease the calculation time. The findings revealed that augmentation based on GAN could perform superior to other traditional approaches. Also, QCNN could reduce the calculation complexity while enhancing accuracy of forecast. The suggested technique could accomplish the precision value of 98.7% that was validated by quantitative and qualitative analysis. The outcomes illustrated that this model was more efficacious in comparison with other approach designed for classifying Indian dance.

Nevertheless, these methods have their limitations, indicating a pressing need for more effective and accessible solutions to enhance the learning experience of Indian Classical Dance forms.

Recent developments in deep learning have demonstrated encouraging outcomes in image classification tasks, including the classification of dance¹⁴. Deep learning architectures, particularly convolutional neural networks (CNNs), have been effectively utilized in a range of image classification applications, such as object detection, facial recognition, and image segmentation. Nevertheless, the efficacy of these models can be enhanced further through the optimization of their hyperparameters, a task that presents its own set of challenges¹⁵.

The MnasNet architecture represents a lightweight and efficient neural network framework custom-made for mobile and embedded vision applications. Its design makes it particularly well-suited for dance classification tasks, as it can effectively learn robust features from images while operating within limited computational resources. Yet, the performance of the MnasNet architecture can be enhanced through the fine-tuning of its hyperparameters.

Nature-inspired optimization algorithms have demonstrated success in addressing various optimization challenges, including the hyperparameter optimization of deep learning models. In this study, we propose an advanced version of Polar Fox Optimization (APFO) algorithm for fine-tuning of the MnasNet architecture for the classification of Indian classical dances. The approach is evaluated using a dataset of Indian classical dances.

Dataset preparation

This study uses Bharatnatyam Dance Poses dataset as a publicly available dataset on Kaggle for the evaluating the model¹⁶. The dataset contains a classical dance form from southern India, divided into nine classes: “Ardhamandalam”, “Bramha”, “Garuda”, “Muzhumandi”, “Nagabandham”, “Nataraj”, “Prenkhana”, “Samapadam” and “Swastika” contains images of Bharatnatyam dancers in various dance poses.

In Bharatanatyam, a variety of postures are employed to express a range of emotions and narrate stories. Among the significant postures is Ardhamandalam, also referred to as Araimandi or Ayatham, which entails positioning the feet sideways to enhance the body’s stability. Muzhumandi is considered by a complete sitting position where the thighs are extended in opposite directions while the heels remain together. Additional postures include Garuda, a demanding stance that utilizes both hands and feet to demonstrate bravery, and Nagabandham, where the hands and legs are intertwined to represent serpents.

The Nataraj pose signifies the capacity to transcend ignorance and achieve salvation, whereas the Prenkhana posture consists of bending one knee while extending the other leg. The Samapadam, or Swastika, is the most basic form of Bharatanatyam posture, maintaining a straight body with slightly bent knees and apart toes, creating a harmonious appearance. These postures are essential to Bharatanatyam to convey various emotions and tell stories through the art of dance.

The dataset has the following characteristics: 1

.731 images, image size of 224 × 224 pixels, and JPEG format, sourced from Kaggle (https://www.kaggle.com/datasets/pranavmanoj/bharatnatyam-dance-poses). Table 1 illustrates the distribution of these classes in the dataset.

Table 1 The distribution of classes in the dataset.

Figure 1 indicates some samples of the Bharatnatyam Dance Poses dataset.

Fig. 1

Some samples of the Bharatnatyam Dance Poses dataset.

The Bharatanatyam Dance Poses dataset presents a rich assortment of images that feature a variety of dancers, costumes, and settings, contributing to the reduction of bias and enhancing the robustness of machine learning models. The images are of high quality, showcasing clear and distinct features, and portray dancers in numerous static poses, emphasizing the intricate hand and body movements characteristic of Bharatanatyam.

Importantly, the dataset encompasses a range of hand mudras, diverse static poses, and images captured under different lighting conditions, rendering it an invaluable asset for the development of machine learning models aimed at recognizing and classifying Bharatanatyam dance poses, with potential uses in dance analysis, recognition, and generation.

Preprocessing stage

Image preprocessing is a process to improve the quality of the input raw images into images that can be processed more precisely with minimum errors^17,18,19,20. The application of methods such as data segmentation, rescaling, and noise reduction highlights the importance of important features required for accurate dance classification. This research explores various preprocessing techniques that are frequently utilized to prepare dance images for classification objectives.

Standardizing image sizes

Standardizing image sizes is important for ensuring consistency, efficiency, and accuracy during the training of deep learning models, as it allows the model to process images of a consistent size and facilitates the recognition of features at a uniform scale.

To achieve uniformity in image dimensions, all images were resized to a standard size of 224 × 224 pixels, which is widely utilized in various deep learning frameworks, including the MnasNet model employed in this study. This resizing procedure required the computation of a scaling factor derived from the original dimensions $(H, W)$ and the desired dimensions $(h, w)$, leading to a new image size of:

$$\left({h}{^\prime}, {w}{^\prime}\right)=\left({H}_{r}, {W}_{r}\right)$$

(1)

where:

$$r=\text{ min}\left(\frac{\text{h}}{\text{H}},\frac{\text{w}}{\text{W}}\right)$$

(2)

The resized image was produced through Nearest Neighbor interpolation, Bilinear, or Bicubic Interpolation. We selected Bilinear Interpolation for its effective balance between precision and performance, as it computes a weighted average of the four closest pixels from the original image (Fig. 2).

Fig. 2

Some samples of the images rescaling in this study.

The resized images demonstrated a proper level of quality, exhibiting negligible loss of detail or distortion. This suggests that the selected rescaling Bilinear Interpolation technique has successfully maintained the original characteristics of the images. This process is significant for preparing the dataset for the training and evaluation of deep learning models, as it allows the models to learn from a uniform and high-quality collection of images.

Median filtering

Median filtering is known as one of the widely-used techniques in preprocessing stage for removing or reducing the percent of the noise in the images. The median filter is a non-linear filtering technique to replaces each pixel value with the median value of neighboring pixels. By considering the resized image as ${I}_{r}(x, y)$ and the median filtered image as ${I}_{r}{^\prime}(x, y)$. The median filtering process can be formulated as follows:

$${I}_{r}{^\prime}\left(x, y\right)=median\left({I}_{r}\left(x-k, y-k\right),\dots , {I}_{r}\left(x+k, y+k\right)\right)$$

(3)

where, $k$ defines the size of the neighborhood, and the median is calculated over the values of the neighboring pixels.

The median filtering kernel is a 2D array of size $(2k+1)\times (2k+1)$ that slides over the image, calculating the median value of the neighboring pixels at positions.

Median filtering is effective in removing salt and pepper noise, which is a common type of noise in digital images while preserving the edges of the images, unlike linear filters that can blur the edges. Figure 3 shows a sample image for a noisy ICD by salt and pepper and its results after median filtering.

Fig. 3

Sample example of applying the median filtering on an example ICD noisy image with histogram.

The image on the left exhibits significant degradation due to salt and pepper noise, a prevalent form of distortion in digital imagery. The histogram corresponding to this noisy image reveals a broad spectrum of pixel values, signifying the presence of noise. In contrast, the image on the right, which has undergone median filtering, demonstrates a marked decrease in noise levels.

The histograms of the filtered images under them are notably more concentrated, suggesting that the noise has been effectively mitigated. Furthermore, the median filtering technique has successfully maintained the edges and intricate details of the image, resulting in a cleaner and more aesthetically pleasing output. The comparing of the noisy and filtered images underscores the efficacy of median filtering in eliminating noise and enhancing image quality, thereby establishing it as a valuable method for pre-processing images in various fields, including image analysis and recognition tasks.

Images augmentation

To enhance the training dataset and strengthen the reliability of the proposed ICD classification model, a variety of data augmentation techniques, applying multiple transformations have been implemented to the resized images. This approach included horizontally and vertically flipping the images to represent different knee joint orientations, converting them to grayscale to emphasize structural details, and utilizing sharpening and smoothing filters to highlight fine features and minimize noise.

Furthermore, we introduced random rotations within a ± 10° range to replicate various viewpoints, scaled the images between 85 and 115% of their original dimensions to capture tears at different scales, and made random modifications to brightness and contrast to reflect a range of imaging conditions. Figure 4 indicates some samples of ICD images augmentation.

Fig. 4

Some samples of ICD images augmentation.

These modifications successfully replicate a variety of dance poses, orientations, lighting scenarios, and distances, thereby enriching and strengthening the training dataset. The augmented images maintain a high quality, with the transformations retaining the fundamental characteristics of the ICD poses, indicating that the data augmentation methods have been successful in improving the model’s capacity to identify and categorize ICD poses.

MnasNet

MnasNet was created using neural architecture search to develop an efficacious and lightweight CNN framework. Its goal is to find a balance between model size and accuracy, allowing it to be used on mobile devices and in resource-limited environments²¹. The discovery of efficient network frameworks can be automated through a process known as NAS (Neural Architecture Search). MnasNet utilizes NAS to navigate a wide range of network configurations, with the goal of identifying architectures that strike a good balance between computational efficacy and accuracy.

The MnasNet solution space encompasses several building modules, such as convolutional layers, squeeze-and-excitation operations, and depthwise separable convolutions, which are combined into a hierarchical framework to create the ultimate architecture. This solution space is specifically crafted to include a broad spectrum of possible architectures, enabling the creation of various and effective models.

MnasNet utilizes RL (Reinforcement Learning) to efficiently navigate the extensive solution space. The agent of RL views the framework search as a step-by-step decision-making procedure, learning to choose the most effective building modules for constructing the network²². The agent has been trained using a proxy dataset and assessed on the basis of predetermined metrics, including model size and accuracy.

MnasNet integrates DARTS (Differentiable Architecture Search), which frames architecture search as a constant optimality challenge. DARTS replaces the discrete selections of operations within the solution space with optimization based on gradient, enabling efficacious exploration of the solution space and aiding the discovery of high-performing structures.

MnasNet takes into account several goals when conducting the architecture solution process. Besides striving to maximize accuracy, it seeks to reduce computational demands and model size to the least amount. The current multi-objective optimization has been accomplished by employing Pareto fronts, which help identify architectures that offer varying trade-offs between efficiency and accuracy.

MnasNet integrates resource-conscious design to guarantee that the identified structures are appropriate for use on mobile devices. This includes taking into account factors like inference speed, memory usage, and consumption of power while conducting the solution process. Resource-conscious design assists in recognizing structures that not only show good performance but also meet the limitations of mobile platforms.

MnasNet utilizes transfer learning to improve the efficacy of the identified frameworks. Utilizing pre-trained networks like EfficientNet or MobileNet provides initial weights for the searched frameworks. This knowledge transfer accelerates the training procedure and enhances the ultimate accuracy.

The final MnasNet framework consists of several mobile inverted bottleneck modules (MBConv modules), each containing a sequence of operations selected by the NAS process. These blocks efficiently take hierarchical representation, allowing the network to gain great accuracy with a limited quantity of parameters. Figure 5 shows the architecture of the MnasNet.

Fig. 5

Architecture of MnasNet.

The MBConv module serves as a key element in the MnasNet structure. It comprises a series of functions, such as squeeze-and-excitation, depthwise convolution, expansion, addition, and projection. The formulas that govern the MBConv block have been expressed below:

- Expansion:

$${x}_{e}={W}_{e}\times x+{b}_{e}$$

(4)

where, the tensor of input has been demonstrated via $x$, the biases and weights of the expansion have been, in turn, demonstrated via ${b}_{e}$ and ${W}_{e}$, and the expanded tensor has been displayed via ${x}_{e}$.

- Depthwise convolution:

$${x}_{dw}={W}_{dw}\times {x}_{e}+{b}_{dw}$$

(5)

where, biases and weights of depthwise convolution have been, in turn, demonstrated via ${b}_{dw}$ and ${W}_{dw}$, and the depthwise convolved tensor has been depicted via ${x}_{dw}$.

- Squeeze-and-excitation:

$${x}_{se}={F}_{se}\left({x}_{dw}\right)=\sigma ({W}_{2}\times \delta \left({W}_{1}\times {x}_{dw}+{b}_{1}\right)+{b}_{2})\odot {x}_{dw}$$

(6)

where, the squeeze-and-excitation procedure has been indicated via ${F}_{se}$, the activation function of sigmoid has been displayed via $\sigma$, the activation function of ReLU has been demonstrated by $\delta$, and the component-wise multiplication has been represented via $\odot$. Moreover, the biases and weights of the squeeze-and-excitation layers have been, in turn, depicted via ${W}_{1}$, ${W}_{2}$, ${b}_{2}$, and ${b}_{1}$.

- Projection:

$${x}_{p}={W}_{P}\times {x}_{se}+{b}_{p}$$

(7)

where, the biases and weights of the projection have been, in turn, illustrated via ${b}_{p}$ and ${W}_{p}$, and the tensor of projection has been demonstrated via ${x}_{p}$.

- Addition:

$${x}_{out}={x}_{p}+x$$

(8)

where, MBConv block’s tensor of output has been demonstrated via ${x}_{out}$.

To optimize MnasNet, an integration efficiency and accuracy metrics have been utilized as the fitness function. Particularly, the negative log-likelihood loss for weighted total number of model size and accuracy were employed, and the inference latency is employed as the efficacy measurement.

The performance of the model was measured by accuracy of the fitness function employing validation dataset. The negative log-likelihood loss will be employed, which has been typically employed for tasks of classification. The accuracy of the fitness function can be illustrated in the following way:

$${L}_{acc}=-\frac{1}{N}\sum_{i=1}^{N}\sum_{c=1}^{C}{y}_{ic}\text{log}({p}_{ic})$$

(9)

where, the accuracy of the fitness function has been displayed via ${L}_{acc}$, the entire quantity of the instances within the validation dataset has been depicted via $N$, the quantity of classes has been indicated via $C$, the true label of class $c$ and instance $i$ has been represented via ${y}_{ic}$ that has the value of 1 when instance $i$ is in class $c$, else it has the value of 0.

The forecasted possibility value has been displayed via ${p}_{ic}$. The efficacy of the fitness function catches the inference latency and model size, which have been found to be highly critical to deploy MnasNet on devices that are resource-constrained. The efficacy of the fitness function has been expressed as a weighted total number of inference latency and model size in the following way:

$${L}_{eff}={\lambda }_{1}\times {C}_{size}+{\lambda }_{2}\times {C}_{latency}$$

(10)

where, the efficacy of the fitness function has been demonstrated via ${L}_{eff}$, the model size has been indicated via ${C}_{size}$ that can be evaluated regarding the entire quantity of variables or the footprint of the memory. The latency of inference has been indicated via ${C}_{latency}$ that has been assessed regarding the mean time taken for processing a single input. ${\lambda }_{1}$ and ${\lambda }_{2}$ have been found to be some hyperparameters, controlling the proportional significance of inference latency and model size in the entire efficacy metric,

Once utilizing cross-entropy loss, there are numerous important hyperparameters to take into account. These include learning rate, weight decay, number of epochs, batch size, learning rate decay, weight initialization, and momentum. Weight decay, referred to as L2 regularization, serves to prevent overfitting via penalizing massive weights. It is governed by the hyperparameter $\lambda$, which can determine the intensity of regularization. The rate of learning, denoted by $\alpha$, sets the magnitude of the updates of optimizer. Higher rates lead to quicker convergence but may overshoot optimum solutions, whereas lower rates might necessitate more training times but permit more precise updates.

The size of the batch, denoted as $N$, impacts the stability and level of noise in the gradient estimate. Larger batches lead to more stable estimates but require more memory, while smaller batches are more computationally efficacious but introduce noisier gradient. The quantity of epochs can determine number of times the dataset is passed through the model. More epochs can improve convergence but also pose the risk of overfitting. Momentum, represented by $\beta$, has been utilized in optimization algorithms such as metaheuristics.

It suggests a velocity term that can accumulate updates in a previously determined direction, enabling the optimizer to make momentum and quicken convergence. Decay of learning rate includes decreasing the rate of learning after a while to strike a balance between exploitation and exploration. This can be accomplished by approaches like exponential decay, learning rate schedules, or step decay. Weight initialization, such as He initialization or Xavier initialization, determines the initial weights of the model and is able to influence the optimization procedure and the speed at which convergence occurs. This can help prevent exploding or vanishing gradients and contribute to faster convergence.

In this study, an advanced version of Polar Fox Optimization (APFO) has been designed for minimizing the objective function and optimal selection of the hyperparameters. This algorithm is explained in details in the next section.

Advanced polar fox optimization (APFO)

The polar fox inhabits some of the coldest regions on earth. Its ability to endure the extreme cold is supported by its thick and deep fur, a specialized system for regulating body heat in its paws, and a substantial layer of body fat. The fox’s furry paws enable it to walk on ice while searching for food. Remarkably, the polar fox possesses exceptional hearing, allowing it to accurately pinpoint the situation of its prey even under layers of snow²³. Once it detects target, the fox leaps and breaks through the snow to catch its meal.

To solve meta-heuristic algorithms, it is crucial to consider the social structure and hunting techniques of groups of polar foxes. Each individual can exhibit various types of hunting behavior, including free, hardworking, experience-dependent and leader-dependent hunting manners. These behaviors are represented as behavioral matrices in the hunting procedure of the individuals ([PF, LF, a, b, and m]). Additionally, important concepts in this context include the mutation factor, groups, and population size.

Polar fox leash generation

The group of these individuals are named “leash” or “skulk”, representing a social unit comprising a mating pair, a few assisting female individuals, and litter. In spring, the focus of the candidates shifts towards a home and reproduction for their potential young. To model the group of individuals, the optimizer starts with an initial population of foxes distributed randomly within the search space, and then utilize the following equations.

$$X=\left[\begin{array}{ccc}{x}_{1}^{1}& {x}_{2}^{1}& \begin{array}{cc}\cdots & {x}_{d}^{1}\end{array}\\ {x}_{1}^{2}& {x}_{2}^{2}& \begin{array}{cc}\cdots & {x}_{d}^{2}\end{array}\\ \begin{array}{c}\vdots \\ {x}_{1}^{k}\end{array}& \begin{array}{c}\vdots \\ {x}_{2}^{k}\end{array}& \begin{array}{c}\begin{array}{cc}\ddots & \vdots \end{array}\\ \begin{array}{cc}\cdots & {x}_{d}^{k}\end{array}\end{array}\end{array}\right]$$

(11)

$${x}_{j}^{i}=LB+\overrightarrow{{r}_{1}}\times (UB-LB)$$

(12)

$$LB=[l{b}_{1} l{b}_{2} \cdots l{b}_{d}]$$

(13)

$$UB=[u{b}_{1} u{b}_{2} \cdots u{b}_{d}]$$

(14)

where, the situation matrix of the individuals have been displayed via $X$, the individual $i$ that has the ${j}^{th}$ value has been depicted via ${x}_{j}^{i}$, the quantity of individuals has been illustrated via $k$, a stochastic vector has been demonstrated via $\overrightarrow{{r}_{1}}$ that is between 0 and 1, the quantity of dimensions has been indicated via $d$. Moreover, the upper and lower boundaries have been, in turn, represented via $UB$ and $LB$.

Grouping polar fox

Each individual within the group has its own distinct hunting method. Some are willing to track the leader, some trust their experience, some freely explore their nearby, and some are extremely hardworking. As a result, the individuals are divided into 4 distinct groups that each one has been represented by behavior matrices G1, G2, G3, and G4. These matrices are initially defined as G1i, G2i, G3i, and G4i, respectively.

At first, there is an equal number of members in the groups.

However, in accordance with the calculated weight for the groups, which depends on the failure or success of the groups, the quantity of individuals changes during the leader motivation and mutation phase. Nonetheless, the groups retain one member as a minimum. After catching the preys successfully, the weights of the groups get adjusted using Eq. (15).

$${W}_{i}^{new}={W}_{i}+\frac{{t}^{2}}{N{G}_{i}}$$

(15)

where, the weight of ${i}^{th}$ group has been displayed via ${W}_{i}$, the number of individuals in group $i$ has been represented by $N{G}_{i}$, and the present iteration has been depicted by $t$. The weight of each group owns an initial value that can decrease the changing proportion.

Experience-based phase

The candidates do not hibernate in winter and instead display an integration of communal and nomadic manner, often forming small groups to forage. Here, Eqs. (16) and (17) have been suggested to replicate the jumping manner of the individuals while hunting. It has variables $P$ and $D$ which, in turn, stand for jumping power and imping direction. These variables have the ability to alter the situation of individuals from ${x}^{i}(t)$ to new situation ${x}^{i}(t+1)$. This procedure can be computed employing the subsequent formula:

$$\begin{aligned} & x^{i} \left( {t + 1} \right) = x^{i} \left( t \right) + P \times D \\ & PF_{i} = PF \times a^{z - 1} \\ & P = \overrightarrow {{r_{2} }} \times PF_{i} \\ & D = {\text{cos}}\left( {\overrightarrow {{r_{3} }} } \right) \\ \end{aligned}$$

(16)

where, the experimental strength factor of the individual $i$ has been illustrated via $P{F}_{i}$, the quantity of reports in stages on the basis of experience has been displayed via $z$, the present iteration has been depicted via $t$, the stochastic vectors of the individuals that are in the interval [0, 180] and [0, 1] have been, in turn, illustrated by $\overrightarrow{{r}_{3}}$ and $\overrightarrow{{r}_{2}}$. This procedure gets iterated by the time the subsequent criteria have been met; the individuals’ energy is lower than the previously determined level, and once a superior fitness value has been gained.

$$\left\{\begin{array}{c}P{F}_{i}<m\times PF \\ f(t)<f(t-1)\end{array}\right.$$

(17)

where, fitness has been depicted by $f$.

Leader-based stage

There is leader determined for each group for accomplishing the purpose. In the suggested network, the situation of the leader $(L)$ has been taken into account as the best fitness value; moreover, the individuals alter their situation ${x}^{i}(t)$ by chasing the situation of the leader to move to the novel situation ${x}^{i}(t+1)$. The current procedure has been calculated in the following way:

$$\begin{aligned} & x^{i} \left( {t + 1} \right) = x^{i} \left( t \right) + \overrightarrow {{r_{4} }} \times \left( {x^{i} \left( t \right) - L} \right) \times LF_{i} \\ & LF_{i} = LF \times b^{y - 1} \\ \end{aligned}$$

(18)

where, the strength element of the leader has been indicated via $L{F}_{i}$, the quantity of iterations within the current stage has been represented via $y$, and the random element has been displayed via $\overrightarrow{{r}_{4}}$ that is between − 1 and 1

The current procedure gets repeated by when the criteria mentioned in the following are met; when the leader’s energy is lower than the previously determined level, and when a superior outcome has been gained. The aforementioned conditions have been illustrated as follows:

$$\left\{\begin{array}{c}L{F}_{i}<m\times LF\\ f(t)<f(t-1)\end{array}\right.$$

(19)

Leader motivation phase

When polar foxes are unable to find prey, the leader encourages them, and the individuals switch their situation stochastically, and establish G1m, G2m, G3m and G4m as matrices of behavior (G1, G2, G3 and G4). This results in increased efforts in constrained numbers (MLR). After that, merely the individuals alter their location. The criterion for identifying a situation like this has been represented in Eq. (20).

$$critical=\left(NLM>MLM\right) or (t>0.8\times NI)$$

(20)

here, $critical$ has been considered an indicator that can determine if the algorithm has been stuck in local optima.

Mutation stage

The populations of these individuals have a high mortality rate. Often, parents abandon their pups, and some aggressive kits may kill their family members. Rabies, a fatal illness, damages up to 20 percent of the individuals in a population, especially during times of weakened immune systems due to starvation. During this stage, some weaker (less profitable) individuals have been replaced with new individuals in order to establish a stronger group using Eqs. (11) and (12).

$${x}^{i}=LB+\overrightarrow{{r}_{5}}\times \left(UB-LB\right), i=[1, 2, . . . NM]$$

(21)

$$NM=\left\{\begin{array}{c}NP-1 if critical\\ MF\times NP\end{array}\right.$$

(22)

where $\overrightarrow{{r}_{5}}$ has been considered a random vector that is between 0 and 1.

Fatigue simulation

After receiving motivation from the leader, the individuals experience a slight tiredness after each iteration, as indicated by G1r, G2r, G3r, and G4r. Eventually, the behavior matrix reaches G1i, G2i, G3i, and G4i. Additionally, if the quantity of candidates in a group is lower than 10% of the entire population, level of their energy increases. Equations (13) and (14) are utilized to simulate these locations.

$$\left\{\begin{array}{c}G1=\text{min}\left(G1-G1r, G1i\right)\\ G2=\text{min}\left(G2-G2r, G2i\right)\\ \begin{array}{c}G3=\text{min}\left(G3-G3r, G3i\right)\\ G4=\text{min}\left(G4-G4r, G4i\right)\end{array}\end{array}\right.$$

(23)

$$\left\{\begin{array}{c}G1=G1m\\ G2=G2m\\ \begin{array}{c}G3=G3m\\ G4=G4m\end{array}\end{array}\right.$$

(24)

Advanced polar fox optimization (APFO)

The Polar Fox Optimization begins its procedure from a randomly selected initial location. This initial location may be considerably distant from the optimal solution, and in the worst-case scenario, it might even move in a completely erroneous direction. Consequently, this leads to a search duration that is often longer than anticipated. In contrast, the Opposite-Based Learning (OBL) algorithm creates a mirrored position next to the original location within the initial population, following this methodology.

$${x}_{op}^{i}\left(t\right)=\underline{x}+\overline{x}-{x}^{i}\left(t\right)$$

(25)

where, ${x}_{op}^{i}\left(t\right)$ specifies the opposite location of the ${x}^{i}\left(t\right)$, and $\underline{x}$ and $\overline{x}$ describe the minimum and the maximum values of ${x}^{i}\left(t\right)$, respectively.

As a result, if vector ${x}_{op}^{i}\left(t\right)$ occupies a more favorable position than vector ${x}^{i}\left(t\right)$, it will be substituted. Furthermore, this research incorporates chaotic mapping as an additional modification.

Chaos theory suggests that small changes can produce significant impacts in highly sensitive dynamic systems. Its use as a modification term in metaheuristic approaches is becoming more prevalent. By leveraging chaos theory, simpler and more widely spread points are generated, which enhances the distribution of solutions within the solution space. This leads to an improved convergence rate for the PFO algorithm. Presented below is a standard definition of the chaotic mechanism.

$${x}^{i}\left(t+1\right)=f\left({x}^{i}\left(t\right)\right), i=\text{1,2},\dots ,N$$

(26)

The dimension of the map is indicated by $N$, while the generator function of the mechanism is represented as $f\left({x}^{i}\left(t\right)\right)$. To alter the algorithm, the Chebyshev chaotic map, recognized as a prominent type of chaotic mechanism, has been employed.

$$\overrightarrow{{r}_{5}}(i)=\mathit{cos}\left(\beta \times co{s}^{-1}({r}_{4}^{j})\right),$$

(27)

where $\beta$ equals 0.8, and $\overrightarrow{{r}_{5}}(0)$ has a value between − 1 and 1.

The APFO employs adaptive parameters including learning rate and exploration–exploitation balance by enabling it to adaptively adjust to multiple problem environments:

- Adaptive Learning Rate: Unlike GD (Gradient descent), which suffers from carefully manual tuning of the learning rate, APFO automatically tunes its parameters to achieve necessary convergence behavior.

Keeping a balance between Exploration (Globally search for new solutions) and Exploitation (Locally refine the known solution): APFO is able to balance global exploration and local exploitation and effectively escaping this premature convergence.

With this being aforementioned as limitations of standard approaches like GD which are sensitive to setting of hyperparameters and lead to heavy experimentation to reach optimal performance, APFO becomes more flexible than traditional approaches.

In this paper, we justified the choice of APFO as hyperparameter optimization due its better equilibrium between exploration–exploitation, adaptivity, absence from local optimal, computational overhead, and competence with MnasNet structure. These capabilities allow APFO to explore for the optimal hyperparameter settings to maximize the performance of the proposed model, which is reflected in its impressive results classifying Indian classical dance poses.

Simulation results

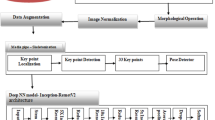
The proposed approach for recognizing poses in Indian classical dance follows a systematic methodology that commences with data acquisition. This involves gathering a dataset comprising images of various Indian classical dance forms, including Bharatanatyam, Kathak, Kathakali, Kuchipudi, Manipuri, Mohiniyattam, Odissi, and Sattriya. Subsequently, the collected images undergo preprocessing, which includes resizing them to a standardized dimension of 224 × 224 pixels, applying median filtering to eliminate noise, and normalizing pixel values to a range between 0 and 1. Figure 6 shows the step-by-step designing of the proposed methodology.

Fig. 6

The step-by-step designing of the proposed methodology.

Following this, a convolutional neural network (CNN) is employed to extract features from the preprocessed images, specifically utilizing the MnasNet architecture, known for its lightweight and efficient design suitable for mobile and embedded vision applications. The hyperparameters of the MnasNet model are fine-tuned through the Advanced Polar Fox Optimization (APFO) algorithm, a nature-inspired optimization technique that mimics the hunting strategies of polar foxes.

The experiments were conducted on Microsoft Windows 11 using Matlab R2019b, supported by an Intel® Core ™ i7-9750H CPU operating at 2.60GHz, with 16.0 GB of RAM, and an Nvidia 8 GB RTX 2070 GPU. The evaluation of the model was carried out using the Bharatnatyam Dance Poses dataset. In this research, a comprehensive evaluation framework was established to assess the effectiveness of the MnasNet/APFO model in the context of ICD classification.

The dataset was methodically divided into training and testing subsets, allocating 80% for training and the remaining 20% for testing. This intentional partitioning enabled a detailed assessment of the model’s performance. To enhance the reliability of our findings, the evaluation was repeated 20 times, providing a broader perspective on the model’s accuracy.

The accuracy of the MnasNet/APFO model was determined by calculating the mean accuracy across all iterations. This iterative approach yielded significant insights into the model’s consistency and reliability.

The models chosen for comparison comprised Transfer Learning¹², Deep Convolutional Neural Network (DCNN)⁹, VGG16¹⁰, CNN model that was optimized by Hybrid Particle Swarm Grey Wolf (CNN/HPSGW)¹¹, and Quantum-based Convolutional Neural Network (QCNN)¹³ This diverse array of models represented a range of methodologies, each offering unique benefits to the field. Subsequently, an assessment of the efficiency of the proposed MnasNet/APFO model is presented.

Evaluation measurements

The proposed MnasNet/APFO model experienced a thorough performance assessment using a range of statistical metrics, including Accuracy (ACC), Precision (PR), F-beta (F_β), Recall (RC), Kappa-score (κ_sc), Specificity (SPC), Fl Score (F1), and AUC. The mathematical expressions for the specified indices are presented below.

$${\kappa }_{sc}=\frac{{P}_{o(w)}-{P}_{e(w)}}{1-{P}_{e(w)}}$$

(28)

$$PR=\frac{TP}{TP+FP}\times 100$$

(29)

$$RC=\frac{TP}{TP+FN}\times 100$$

(30)

$$SPC=\frac{TN}{TN+FP}\times 100$$

(31)

$$ACC=\frac{TP+TN}{TP+TN+FP+FN}\times 100$$

(32)

$$F1=2\times \frac{Precision\times Sensitivity}{Precision+Sensitivity}\times 100$$

(33)

$${F}_{\beta }=\left(1+{\beta }^{2}\right)\times \frac{\left(1+{\beta }^{2}\right)\times TP}{\left(1+{\beta }^{2}\right)\times TP+{\beta }^{2}\times FN+FP}$$

(34)

where,

$${P}_{o(w)}=\frac{1}{N}{\sum }_{i=1}^{k}{\sum }_{j=1}^{k}{w}_{ij}{f}_{ij}$$

(35)

$${P}_{e(w)}=\frac{1}{{N}^{2}}{\sum }_{i=1}^{k}{\sum }_{j=1}^{k}{w}_{ij}{r}_{i}{c}_{j}$$

(36)

where $n$ indicates the number of observers, $N$ denotes the total number of observations, and $k$ signifies the number of classes, $\beta$ defines assigned a value of 2, while ${r}_{i}$ represents the sums of the rows, and c_j refers to the sums of the columns.

$${w}_{ij}=1-\frac{\left|i-j\right|}{k-1}$$

(37)

where FP, TN, FN, TP and represent false positive, true negative, false negative, and true positive, respectively.

Authentication of the APFO

The effectiveness of the proposed Advanced Polar Fox Optimization was evaluated using the CEC-BC-2019 test suite including a set of 10 varied benchmark functions, definitely made for different problem environments. The software package was developed for an annual optimization competition known as “The 100-Digit Challenge”. The main purpose of this competition is to identify the global optimum of each function with a precision of 100 decimal digits. Comprehensive details regarding the tasks are elaborated in the referenced document²⁴.

During all benchmark functions, CEC01, CEC02, and CEC03 exhibit varying dimensionalities of two, three, and five dimensions, respectively. The other functions are characterized by a dimensionality of 100. These functions are in four classes: unimodal, multimodal, hybrid, and composition functions. For example, CEC01 and CEC02 are Unimodal functions that has a single global optimum with no local optima.

In contrast, CEC03 and CEC04 are multimodal functions that include multiple local optima alongside a single global optimum. In contrast, CEC05 and CEC06 as Hybrid functions combine two/more unimodal or multimodal functions. At last, CEC07 to CEC10 as composition functions have been formed from multiple elementary functions through weighted sums.

To guarantee the dependability of the findings, the experiment was performed 15 times for each function, resulting in a distinct and randomized population on each occasion. The performance of the algorithm was evaluated using two primary metrics: Standard Deviation (SD) fitness value and Mean Fitness (MF) value. A population size of 50 was selected, with the maximum number of iterations capped at 200.

The effectiveness of the algorithm was compared against five advanced metaheuristic algorithms: Pelican Optimization Algorithm (POA)²⁵, Sine Cosine Algorithm (SCA)²⁶, Pigeon-inspired Optimization Algorithm (PIO)²⁷, Billiard-based Optimization Algorithm (BOA)²⁸, Wildebeest herd optimization (WHO)²⁹. The configuration parameters for these optimizers are detailed in Table 2.

Table 2 The configuration parameters for the analyzed optimizers.

The results of the comparison between the proposed optimizer and various examined optimizers are displayed in Table 3.

Table 3 The results of the comparison between the proposed optimizer and various examined optimizers.

The results in Table 3 indicate that APFO surpasses the performance of five other advanced metaheuristic algorithms on the majority of the benchmark functions, highlighting its superior capabilities. This advantage can be attributed to several factors, including its consistency, optimization precision, scalability, robustness against local optima, and overall efficiency. APFO demonstrates reliable performance across all 10 benchmark functions, as evidenced by its low SD values, which reflect its robustness and dependability.

It also achieves the lowest MF values on most functions, signifying enhanced optimization accuracy relative to the other algorithms. Moreover, APFO exhibits strong performance on both low-dimensional and high-dimensional functions, showing its scalability, and effectively avoids local optima while converging to the global optimum in multimodal scenarios.

Moreover, APFO requires fewer function evaluations to reach optimality compared to its counterparts, as indicated by its lower MF values. A comparative analysis reveals that APFO consistently outperforms POA, SCA, PIO, BOA, and WHO across most functions, with significantly reduced MF and SD values. The superiority of APFO can be linked to its innovative optimization strategy, which integrates the advantages of polar coordinates and fox optimization, facilitating efficient exploration of the search space and convergence to the global optimum.

Furthermore, APFO’s adaptive parameters, including the learning rate and the exploration–exploitation balance, allow it to adjust to various problem environments and enhance its performance. Lastly, the mechanism for preserving diversity within APFO ensures a varied population, thereby preventing premature convergence and promoting thorough exploration of the search space.

Optimized MnasNet

MnasNet is naturally good for extracting stronger features from the images, but by tuning its hyperparameters, the performance can be boosted. APFO is responsible for optimizing these hyperparameters to ensure that the model runs as efficiently as possible without wasting computational resources. Optimization Process is as follows:

Initialization: The algorithm initializes a population of candidate solutions (i.e., hyperparameter configurations) in the defined search space.

Evaluation: Every candidate solution is evaluated using the fitness function, which measures how the model performed on metrics such as validation accuracy and loss.

Exploration and Exploitation: APFO is an iterative search mechanism for finding values in the search space, as such it explores the search space to find promising regions (Exploration), and then focuses local search for finding solutions in that region (Exploitation).

Convergence: Through quickening exploration and exploitation, guided by adaptive parameters, concise chaos model, and opposite-based learning you will find the approximation of the optimal answer.

As the best-performing hyperparameter configuration is selected and realized on the MnasNet model after training and testing.

The outcomes of optimizing for the optimum selection of hyperparameters employing the suggested algorithm and two distinct metaheuristic optimizers, including Gradient Descent (GD)³⁰, and Polar Fox Optimization (PFO) have been illustrated below. Every algorithm undergoes several runs with varying random seeds, and showcases the values of the most favorable hyperparameter and values of their fitness function. Table 4 presented below demonstrates the trained optimal parameter values for this research.

Table 4 The optimum parameters value trained for this study.

The weakest total fitness function value of 0.617 was attained by the GD using the specified hyperparameter settings, while PFO and APFO discovered configurations of competitive hyperparameter, leading to somewhat higher fitness function values. Different algorithms exhibited varied optimum hyperparameter values, underscoring the significance of exploring diverse solution spaces.

Various techniques for augmenting data and different ways of initializing were utilized to observe how they affected the optimization procedure. The rate of dropout was adjusted to find the right balance between model capacity and regularization³¹. The results of the simulations shed light on the best choice of hyperparameters for MnasNet employing various optimizers. The table displays the most effective configurations found, enabling a comparison of the algorithms’ efficacy and their influence on the value of fitness function. This demonstrates how GD, PFO, and APFO are successful in discovering the optimum hyperparameter settings for this network.

Accuracy results of the proposed APFO/MnasNet

Model consists of the APFO/MnasNet indicating a good performance to classify various Bharatanatyam dance poses as shown from accuracy results plotted in Fig. 7 and Table 1. The accuracy during the training of all nine classes is in between 94.50 and 96.80% that proves, the model learns effectively about the features of each pose during the training.

Fig. 7

The accuracy results of the proposed APFO/MnasNet model.

The testing accuracy, on the other hand, indicates the model’s generalization ability to unseen data and is between 90.20 and 93.20% as well. This means that it is a fairly consistent model between both the training and testing phase, with only a marginal drop in accuracy for most of the classes. The Swastika class, on the other hand, has the highest testing accuracy rate of 93.20%, and the Prenkhana class has the lowest rate of only 90.20%.

The results illustrate the successful application of the MnasNet architecture optimization methods in APFO, in order to optimize those guiding parameters, that are only hyper-parameters and enhance classification performance.

However, the general alignment of the training and test accuracies implies that the model is sufficiently regularized and is not overfitting dramatically. This is particularly important for real-world applications, where generalizability to out-of-sample data is paramount. The small differences in accuracy per class suggest that some poses are easier to classify than others, likely due to similarity in posture, or slight differences in how the pose is executed.

As an example, Prenkhana class with less testing accuracy may contain postures that are visually similar to postures in other classes preventing the model from identifying the class correctly. Contrarily, the Swastika class has the highest testing accuracy, but it is a class with somewhat unique features, which may be easy for the model to learn and recognize.

Confusion matrix

The results of the confusion matrix for the proposed APFO/MnasNet approach are illustrated in Fig. 8. This figure displays the average confusion matrix derived from the recognition rates and the number of matches pertaining to the proposed Bharatnatyam Dance Poses dataset.

Fig. 8

Average confusion matrix produced for poses in ICD.

The APFO/MnasNet methodology exhibits remarkable precision in the classification of Bharatnatyam dance poses, achieving an overall accuracy rate of 92.2%. The true positive (TP) counts, which signify the number of correctly identified images, are notably highest for the Swastika class (250), Nataraj class (245), and Nagabandham class (240), suggesting that the method effectively distinguishes these categories. Additionally, the TP counts for the remaining classes are also commendable, ranging from 220 to 235, further indicating the method’s proficiency in classification.

Conversely, the false positive (FP) counts, which denote misclassified images, remain relatively low, with the highest FP counts recorded for the Ardhamandalam class (10), Garuda class (10), and Samapadam class (5), highlighting a greater susceptibility to misclassification in these categories. The false negative (FN) counts, representing images incorrectly classified as other classes, are similarly low, with the highest FN counts for the Muzhumandi class (5), Nagabandham class (5), and Samapadam class (5), again indicating a tendency for misclassification. The true negative (TN) counts, which reflect images accurately identified as not belonging to incorrect classes, are generally high, with the highest TN counts for the Swastika class (250), Nataraj class (245), and Nagabandham class (240), reinforcing the method’s effectiveness in classification.

A detailed class-wise analysis reveals that the APFO/MnasNet model achieves high accuracy across all categories, with the Swastika class attaining the highest accuracy at 100%, followed by the Nataraj class at 98%, and the Nagabandham class at 96%. The lowest accuracy is observed in the Ardhamandalam class at 90%, followed by the Garuda class at 88%, and the Samapadam class at 92%. The results from the confusion matrix underscore the capability of the APFO/MnasNet approach to accurately classify Bharatnatyam dance poses with a high degree of accuracy and minimal errors.

Comparison results and discussions

For assessing the effectiveness of the proposed APFO/MnasNet model, it was tested on the Bharatnatyam Dance Poses dataset, and the results were compared with those of five other relevant studies: Transfer Learning¹², Deep Convolutional Neural Network (DCNN)⁹, VGG16¹⁰, CNN model that was optimized by Hybrid Particle Swarm Grey Wolf (CNN/HPSGW)¹¹, and Quantum-based Convolutional Neural Network (QCNN)¹³.

This comprehensive evaluation aims to establish a validation process that is both equitable and reliable for our proposed model. We examined the robustness and generalization capabilities of the models through three different fivefold cross-validation methods. The comparison results of the fivefold validation are illustrated in Table 5.

Table 5 The comparison results of the fivefold validation.

The results indicate that the APFO/MnasNet model surpasses the other five models across all eight-evaluation metrics. In particular, the APFO/MnasNet model records the highest figures for accuracy (95.6%), precision (94.2%), F-beta score (0.92), recall (95.1%), kappa-score (0.94), specificity (96.3%), F1-score (0.94), and AUC (0.97). In contrast, the Transfer Learning model demonstrates lower accuracy (88.5%) and precision (86.2%), suggesting that the MnasNet architecture combined with APFO optimization is superior in feature extraction from dance images.

The DCNN model exhibits the weakest performance among all models, achieving accuracy (85.1%) and precision (82.5%) that are significantly inferior to those of the proposed model. The VGG16 model performs better than the DCNN model but still falls short with accuracy (90.3%) and precision (88.5%) compared to the proposed model. The CNN/HPSGW model achieves higher accuracy (92.5%) and precision (91.2%) than the VGG16 model, yet remains below the proposed model’s performance. The QCNN model also shows lower accuracy (89.2%) and precision (87.1%) than the proposed model, highlighting the greater effectiveness of APFO optimization over the quantum-based optimization utilized in QCNN.

Upon closer inspection, the APFO/MnasNet consistently outperforms all of the other state-of-the-art models under all metrics considered. This significant performance is mainly offered via the corresponding interoperation of the lightweight and efficient MnasNet structure with the advanced APFO algorithm. By providing a powerful solution to the hyperparameter-tuning problem, the APFO algorithm greatly enhances models’ generalization ability and feature-extraction power. On the other hand, conventional models such as Transfer Learning and VGG16, while built on solid foundational architectures, simply do not have the optimized fine-tuning strategies required to reach their full potential. Almost surely, such as that, the superior algorithms such as CNN/HPSGW and QCNN do have some innovative features, however compared to the full optimization scheme developed by APFO/MnasNet, their speed is not even comparable.

Conclusions

Indian classical dances have long been a vital component of the nation’s cultural heritage, and with the rise of digital media, there is an increasing demand for automated classification and recognition of these dances. Traditional methods, which depend on manual annotation and analysis, are often labor-intensive and subjective. Recent developments in deep learning have demonstrated encouraging outcomes in image classification tasks, including those related to dance classification; however, the efficacy of these models can be significantly enhanced through hyperparameter optimization. In this study, a deep learning methodology was introduced using the MnasNet architecture for the classification of Indian classical dances. This architecture is considered by its lightweight and efficient design, making it particularly suitable for mobile and embedded vision applications, thereby translation it an excellent option for dance classification endeavors. To improve the performance of the methodology, an advanced version of Polar Fox Optimization (APFO) algorithm was implemented to optimize the hyperparameters of the MnasNet architecture. Experimental results were established based on applying the proposed method to a standard dataset and comparing it with state-of-the-art methods, including Transfer Learning, Deep Convolutional Neural Network (DCNN), VGG16, CNN model that was optimized by Hybrid Particle Swarm Grey Wolf (CNN/HPSGW), and Quantum-based Convolutional Neural Network (QCNN). Future research involves broadening the scope of the proposed methodology to encompass additional dance styles and applications related to cultural heritage. Enhancements in the efficacy of the proposed approach may be achieved through the implementation of different deep learning models and optimization algorithms. Furthermore, there is potential for integrating the proposed methodology with various computer vision and machine learning techniques to make more all-inclusive systems for dance analysis and recognition.