Bipolar fuzzy outerplanar graphs approach in image shrinking

Abstract

Bipolar fuzzy outerplanar graphs are interesting and significant subclasses within the broader field of fuzzy graph theory. In this paper, bipolar fuzzy outerplanar graphs, and its properties are introduced. The subgraphs of bipolar fuzzy outerplanar graphs are identified by removing few vertices or edges from the bipolar fuzzy graphs. Additionally, both maximum and maximal bipolar fuzzy outerplanar subgraphs are explored with respect to vertex and edge deletion, using examples for illustration. Several relationships among the discussed concepts are expressed as theorems and conclusions. Further, bipolar fuzzy dual graph which is closely related to bipolar fuzzy outerplanar graphs is also described with interesting properties. These properties and characteristics help in understanding and utilizing bipolar fuzzy outerplanar graphs in various applications and research areas. In conclusion, we presented the use of bipolar fuzzy outerplanar graphs for the purpose of image shrinking.

Introduction

Fuzzy set theory is a mathematical framework for dealing with uncertainty and imprecision, developed by Lotfi A. Zadeh¹ in 1965. It extends classical set theory by allowing elements to have varying degrees of membership in a set, rather than just belonging or not belonging. Researchers like Azriel Rosenfeld² in 1975 developed the application of fuzzy set theory to image analysis and pattern recognition, laying the groundwork for further theoretical advancements. Subsequent studies have developed various algorithms for fuzzy graph operations, such as fuzzy shortest path, fuzzy clustering, and fuzzy graph isomorphism. These algorithms enable the practical application of fuzzy graph theory in diverse areas such as social network analysis, where relationships can be uncertain or varying, and decision-making processes that require handling imprecise information. More recent interdisciplinary research has explored the integration of fuzzy graph theory with artificial intelligence techniques, including neural networks and genetic algorithms, enhancing the capabilities of these systems in knowledge representation and reasoning. Overall, the field of fuzzy graph theory continues to evolve, with ongoing research focusing on refining theoretical models and expanding practical applications across different domains. Abdul-Jabber et al.³ initially introduced the idea of a fuzzy planar graph by combining fuzzy graphs with planar graphs. This fusion inspired many researchers to explore the importance of fuzzy graphs in the context of planarity. Fuzzy combinatorial dual graphs are described as fuzzy cycles where one fuzzy graph forms a cut set within another. Examples show that every combinatorial dual graph is planar.

Harary⁴ and Wilson⁵ highlighted notable characteristics of planar, non-planar, and dual graphs. Berthold et al.⁶ Kuratowski established a key property of planar graphs, stating that a graph is non-planar if it contains subdivisions of ${K}_{5}$ or ${K}_{\text{3,3}}$ and presented an efficient and easy-to-use algorithm to construct fuzzy graphs from example data, where the resulting fuzzy graphs are based on locally independent fuzzy rules operating on selected important attributes. Additionally, Maciej Sysło⁷ presented multiple characterizations of outerplanar graphs, offering efficient methods for testing, coding, and counting these graphs and also extends the results to k-outerplanar graphs, contributing to the understanding of their structural properties.

Further insights into outerplanar graphs were discussed. Chartrand et al.⁸ discussed a concept called “permutation graphs”, which are constructed by taking two identical copies of a labelled graph G and joining them according to a permutation α on the vertices of G and focuses on determining when such permutation graphs are planar and permutation graphs and provides a criterion for determining when they are planar, Petersen graph is given as an example of a non-planar permutation graph.

Fleischner et al.⁹ focused solely on establishing a criterion for determining the planarity of permutation graphs, without delving into the properties of outerplanar graphs or their weak duals. Hedetniemi et al.¹⁰ characterized interior graphs of maximal outerplane graphs (mops), providing necessary and sufficient conditions for a graph to represent such interiors and introduced the concepts like caterpillars and discussed their relationships with mops, including the conditions for 2-connected components, outline algorithms for determining feasible edge requirements, essential for classifying graphs as interiors of mops. Kulli¹¹ investigated minimally nonouterplanar graphs, focusing on their properties and characteristics and this provides insights into their structure and the implications of these properties in graph theory. Lu et al.¹² Established the sufficient conditions for a vertex-deleted subgraph of a 2r-regular, 2m-edge-connected graph of odd order to contain a k-factor for all vertices and generalizes existing theorems on k-factors, highlighting the impact of the parity of k and the relationship between k, m, and r. Mitchell¹³ presented the linear algorithms for recognizing maximal outerplanar and outerplanar graphs, simplifying existing methods by utilizing properties of biconnected graphs and 2-vertices and proposed algorithms operate in linear time, enhancing efficiency in graph theoretic computing. Maciej Sysło¹⁴ provided the characterizations, testing methods, coding techniques, and counting strategies for outerplanar graphs. It aims to enhance the understanding and application of outerplanar graph properties in combinatorial and computational contexts.

Pramanik et al.¹⁵ defined interval-valued fuzzy planar graphs, with related concepts like degree of planarity and interval-valued fuzzy faces, and studies the properties of IVFPGs and their interval-valued fuzzy dual graphs. Samanta et al.¹⁶ introduced the concepts of fuzzy multigraphs, fuzzy planar graphs, and fuzzy dual graphs, and defines properties and relationships between these graph types, as well as introducing the notion of fuzzy planarity value and strong fuzzy planar graphs. Ghorai et al.¹⁷ introduced m-polar fuzzy multi-sets and uses them to define m-polar fuzzy multi-graphs, m-polar fuzzy planar graphs, and m-polar fuzzy strong edges. Further, properties of m-polar fuzzy planar graphs, including the planarity value, the number of intersection points between strong edges, and the number of intersection points between considerable edges are studied. Mahapatra et al.¹⁸ was developed interval-valued m-polar fuzzy (IVmPF) graphs, which generalize m-polar fuzzy graphs by allowing the membership values of vertices and edges to be intervals rather than fixed numbers. The key contributions of the paper include defining concepts related to IVmPF graphs, such as complete IVmPF graphs, strong IVmPF graphs, and the faces and dual graphs of IVmPF planar graphs, as well as presenting a real-world application of IVmPF planar graphs. Mondal et al.¹⁹ derived by generalized m-polar fuzzy planar graphs (GmPFPGs), explores their properties, establishes a relationship between dual GmPFGs and GmPFGs, and presents a practical application in analyzing the activity of a social group based on various attributes.

Akram²⁰ defined bipolar fuzzy planar graphs, where the crossing of edges is allowed, unlike traditional fuzzy planar graphs. It introduces the notion of "bipolar fuzzy planarity value" to measure the degree of planarity in these graphs. Akram²¹ explored the decision-making methods using bipolar fuzzy graphical models, addressing bipolar information mathematical challenges and it examined properties and applications of bipolar fuzzy graphs in various fields, making it valuable for researchers and professionals in multiple disciplines. Akram²² presented the concept of bipolar fuzzy sets and extends it to multigraphs and planar graphs, introducing terms such as bipolar fuzzy multigraphs, bipolar fuzzy planar graphs, and bipolar fuzzy dual graphs. Akram²³ studied various concepts related to bipolar fuzzy graphs and discussed their properties and introduced bipolar fuzzy digraphs and the bipolar fuzzy influence graph of a social group. Akram²⁴ introduced the concepts of regular and totally regular bipolar fuzzy graphs and proves necessary and sufficient conditions for when they are equivalent, and it also introduces bipolar fuzzy line graphs and provides a necessary and sufficient condition for a bipolar fuzzy graph to be isomorphic to its corresponding bipolar fuzzy line graph. Akram et al.²⁵ introduced the bipolar fuzzy sets and applies it to multigraphs and planar graphs, defining notions like bipolar fuzzy multigraphs, bipolar fuzzy planar graphs, and bipolar fuzzy dual graphs. Akram et al.²⁶ investigated bipolar fuzzy graphs, describing their construction and properties, including isomorphisms and strong bipolar fuzzy graphs and discusses self-complementary and self-weak complementary strong bipolar fuzzy graphs. Alshehri²⁷ proved that intuitionistic fuzzy planar graphs as a generalization of fuzzy graphs to handle uncertainty and vagueness, defined the intuitionistic fuzzy multigraphs, intuitionistic fuzzy planar graphs, and intuitionistic fuzzy dual graphs, and analyses their properties. Balaraman²⁸ calculated the strong domination integrity for various families of graphs and fuzzy graphs, and bounds.

Ghorai et al.²⁹ explored the product bipolar fuzzy graphs, introduced concepts of regular and totally regular graphs and establishing conditions for their equivalence. And also discussed the product bipolar fuzzy line graphs and their properties, including isomorphism criteria. Various examples illustrate the characteristics and relationships of these graphs in the context of fuzzy set theory. Shriram et al.³⁰ presented a fuzzy planar subgraph formation model for partitioning large-scale integration networks, focusing on vertex-deletion and edge-deletion operations to derive fuzzy planar subgraph and introduced a novel Planar Partition subgraph approach for improving efficiency in identifying these subgraphs and discusses the concept of thickness value in fuzzy graphs. The findings are illustrated with examples and applied to partition networks in VLSI design. Mahapatra et al.³¹ introduced the concept of Generalized Neutrosophic Planar Graphs (GNPG), addressing limitations in existing definitions by redefining planarity scores based on true, indeterminate, and falsity values and also demonstrates practical applications of GNPG in urban traffic management.

Muhiuddin et al.³² introduced the cubic planar graphs, highlighting their effectiveness in representing membership degrees and handling uncertainties compared to traditional fuzzy graphs and explores their applications in road networks, emphasizing how these graphs can mitigate traffic issues and optimize planning by analyzing edge intersections and congestion. Naz et al.³³ modified the definition of product bipolar fuzzy graphs (PBFGs) and introduces new concepts such as product bipolar fuzzy multigraphs and planar graphs, exploring their properties and applications and establishes a product bipolar fuzzy planarity value, relating the planarity of these graphs to intersections and their strengths. Pramanik et al.³⁴ address the attributes and uses of bipolar fuzzy planar graphs, including image segmentation and city planning. Furthermore, they focus on related concepts including degree of planarity, strong edges, bipolar fuzzy faces, and bipolar fuzzy dual graphs. Poulik et al.³⁵ examined the connectivity index of bipolar fuzzy graphs (BFG) and introduces the average connectivity index, along with various types of nodes and their properties and discusses applications, including enhancing the popularity of women’s football in India and optimizing college placement in towns.

Ghorai et al.³⁶ developed m-polar fuzzy multi-graphs to deal with edge crossing in planar graphs. As they believed that edge crossings can be a problem in some application domains, they have developed some necessary definitions such as m-polar fuzzy multi-sets, planar graphs, and strong edges and studied their properties. This study is important because it shows how uncertainties of graph structures can be modeled for real-world applications. Samanta et al.³⁷ introduced the ideas of fuzzy planar graphs and fuzzy dual graphs, providing definitions and examples as well as some preliminary findings about their features and relationships. Samanta et al.³⁸ various features and conclusions for fuzzy planar graphs and their fuzzy duals, which have potential applications in circuit design, subway planning, and image representation, two types of edges in fuzzy graphs: effective edges (representing congested pathways) and substantial edges (indicating less congested routes) and also examines permitting crossovers between effective and significant edges in fuzzy planar graphs. Shriram et al.³⁹ Fuzzy combinatorial duals involve fuzzy cycles where one fuzzy graph creates a cut set within another. Examples show that all combinatorial dual graphs are planar. Various captivating research studies on fuzzy planar graphs are discussed. Yang et al.⁴⁰ identified and corrects flaws in definitions and propositions related to bipolar fuzzy graphs from a previous study, providing clearer formulations and introduced a generalized bipolar fuzzy graph, enhancing the theoretical framework for this area of study. Ramya and Lavanya⁴¹ introduced the concept of edge contraction in fuzzy graphs, along with examples to illustrate it. They presented theorems detailing how edge contraction affects the number of vertices and edges in these graphs. Additionally, Ramya and Lavanya⁴² explored edge contraction within the context of bipolar fuzzy graphs. They described the edge contraction operation, its application to various types of bipolar fuzzy graphs, and its impact on the domination number.

Poulik et al.⁴³ introduced the Wiener index and Wiener absolute index for bipolar fuzzy graphs, highlighting their properties and applications in assessing connectivity in networks and demonstrated these concepts through examples, including their relevance to journey planning between cities. Poulik et al. ⁴⁴ introduced the complexity function of fuzzy graphs and explores its applications in identifying the most affected cycles and busiest network routes, particularly in the context of COVID-19 transmission and internet routing and established various properties and boundaries of this complexity function to enhance network analysis in uncertain environments. Poulik et al. ⁴⁵ introduced and examined perfectly regular bipolar fuzzy graphs, focusing on their applications in international relations and communication systems and its highlights the importance of neighborhood degrees in understanding the relationships between nodes and edges within these graphs. Poulik et al. ⁴⁶ explored the application of the Randic index in fuzzy graphs to assess connectivity in Indonesia’s tourism sector, specifically analyzing routes between key locations and introduced algorithms and properties of fuzzy graphs to evaluate important crossroads and stoppages effectively.

Rama Kishore et al.⁴⁷ discussed the generalization of bipolar fuzzy sets to introduce m-Bipolar Fuzzy Planar Graphs, examining their properties and applications in graph theory, particularly in real-life scenarios like traffic and power line management and explored the concepts such as isomorphism and the degree of planarity in these graphs. Mondal et al.⁴⁸ introduced the concept of Inverse fuzzy mixed planar graphs, extending the theory of fuzzy mixed graphs by incorporating planarity through intersecting values and explored the properties of IFMGs and presents applications, including cost reduction in travel tours. Fujita et al. ⁴⁹ discussed advancements in uncertain combinatorics through methods like graphization, hyperization, and uncertainization, focusing on fuzzy, neutrosophic, soft, and rough set theories and reviewed various graph classes and their applications in modeling uncertainty in both mathematical and real-world contexts.

Bipolar fuzzy outerplanar graphs are an interesting and significant subclass within the broader field of fuzzy graph theory. This paper introduces bipolar fuzzy outerplanar graphs and explores their various properties. The subgraphs of bipolar fuzzy outerplanar graphs are identified by removing a few vertices or edges from the original bipolar fuzzy graphs. The paper examines both maximum and maximal bipolar fuzzy outerplanar subgraphs, with respect to vertex and edge deletion, using examples for illustration. Several relationships among the discussed concepts are expressed as theorems and conclusions. The paper also describes bipolar fuzzy dual graphs, which are closely related to bipolar fuzzy outerplanar graphs. Some important properties of bipolar fuzzy dual graphs are studied. Finally, an application discussed image shrinking using these concepts. These properties and characteristics help in understanding and utilizing bipolar fuzzy outerplanar graphs in various applications and research areas.

Motivation of the paper

In graph theory, a planar graph is one that can be embedded in a plane without any of its edges crossing. In contrast to how things typically work in the real world, every vertex and edge in a crisp graph has the same meaning. Fuzzy set theory, a mathematical framework designed to address uncertainty and imprecision, was developed by Zadeh¹ in 1965. In 1975, researchers such as Rosenfeld² applied fuzzy set theory to the fields of image analysis and pattern recognition, establishing a foundation for subsequent theoretical developments. Abdul-Jabber et al.³ was the first to propose the concept of a fuzzy planar graph by merging fuzzy graphs with planar graphs. This integration motivated numerous researchers to investigate the significance of fuzzy graphs in relation to planarity. Fuzzy combinatorial dual graphs are characterized as fuzzy cycles, where one fuzzy graph acts as a cut set within another. Examples demonstrate that every combinatorial dual graph is planar. Bipolar outerplanar graphs are planar graphs that have the property that there are no interior nodes. These special types of graphs help us understand the structure of networks, such as traffic networks. Deivanai et al.⁵⁰ explored fuzzy outerplanar graphs, a type of fuzzy graph where vertices lie on the exterior boundary, and examines their properties, applications, and the concepts of maximum and maximal fuzzy outerplanar subgraphs and highlights their potential use in modeling uncertain relationships in various fields, including transportation networks. In this paper, we attempt to explore the outerplanarity property of bipolar fuzzy graphs. Bipolar fuzzy graphs extend the concept of fuzzy graphs by incorporating a bipolarity aspect, where each edge and vertex can have both positive and negative degrees of membership. This allows for a more nuanced representation of real-world scenarios, capturing the complexities and variations in relationships. For example, in a social network, the relationship between two individuals may not be strictly positive or negative but could have varying degrees of both. Bipolar fuzzy graphs provide a framework to model such intricate relationships. Finally, we introduced the application of bipolar fuzzy outerplanar in image shrinking.

Throughout this paper, the following mathematical symbols are used and shown in the Table 1.

Table 1 Meanings of the symbols used in this article.

Preliminaries

This section explains the fundamental concepts related to bipolar fuzzy graphs.

Definition 1

Zhang⁵¹ Let ${\mathbb{X}}$ be a nonempty set. A bipolar fuzzy set $\mathcal{B}$ in ${\mathbb{X}}$ is defined as:

$$\mathcal{B}=\left\{(\mathcalligra{x},{\mu }_{\mathcal{B}}^{\mathcal{P}}(\mathcalligra{x}),{\mu }_{\mathcal{B}}^{\mathcal{N}}(\mathcalligra{x}))|\mathcalligra{x}\in {\mathbb{X}}\right\}$$

Here, ${\mu }_{\mathcal{B}}^{\mathcal{P}}:{\mathbb{X}} \to [0,1]$ and $\mu _{{\mathcal{B}}}^{{\mathcal{N}}} :{\mathbb{X}} \to [ - 1,0]$ are mappings. The positive membership degree ${\mu }_{\mathcal{B}}^{\mathcal{P}}(\mathcalligra{x})$ represents the degree to which an element $\mathcalligra{x}$ satisfies the property associated with the bipolar fuzzy set $\mathcal{B}$. Conversely, the negative membership degree ${\mu }_{\mathcal{B}}^{\mathcal{N}}(\mathcalligra{x})$ represents the degree to which an element $\mathcalligra{x}$ satisfies some implicit counter-property associated with $\mathcal{B}.$

If ${\mu }_{\mathcal{B}}^{\mathcal{P}}(\mathcalligra{x})\ne 0$ and ${\mu }_{\mathcal{B}}^{\mathcal{N}}(\mathcalligra{x})=0,$ it means $\mathcalligra{x}$ only positively satisfies the property of $\mathcal{B}.$

If ${\mu }_{\mathcal{B}}^{\mathcal{P}}(\mathcalligra{x})=0$ and ${\mu }_{\mathcal{B}}^{\mathcal{N}}(\mathcalligra{x})\ne 0$, $\mathcalligra{x}$ does not satisfy the property of $\mathcal{B}$ but somewhat satisfies the counter-property of $\mathcal{B}.$

It is also possible for $\mathcalligra{x}$ to have both ${\mu }_{\mathcal{B}}^{\mathcal{P}}(\mathcalligra{x})\ne 0$ and ${\mu }_{\mathcal{B}}^{\mathcal{N}}(\mathcalligra{x})\ne 0$ the membership functions of the property and its counter-property overlap in some region of ${\mathbb{X}}.$

For simplicity, the symbol $\mathcal{B}=({\mu }_{\mathcal{B}}^{\mathcal{P}},{\mu }_{\mathcal{B}}^{\mathcal{N}})$ will be used to denote the bipolar fuzzy set:

$$\mathcal{B}=\left\{(\mathcalligra{x}, {\mu }_{\mathcal{B}}^{\mathcal{P}}(\mathcalligra{x}),{\mu }_{\mathcal{B}}^{\mathcal{N}}(\mathcalligra{x}))|\mathcalligra{x}\in {\mathbb{X}}\right\}$$

Definition 2

Akram²⁶ A bipolar fuzzy graph $\psi =({\mathbb{V}},{\mathring{\rm A}}, \mathcal{B})$ consists of a non-empty set ${\mathbb{V}}$ along with a pair of functions ${\mathring{\rm A}}={(\mu }_{\mathcal{B}}^{\mathcal{P}}, {\mu }_{\mathcal{B}}^{\mathcal{N}}):{\mathbb{V}}\to [0,1]\times [-1, 0]$ and $\mathcal{B}=({\mu }_{\mathcal{B}}^{\mathcal{P}}, {\mu }_{\mathcal{B}}^{\mathcal{N}}):{\mathbb{V}}\times {\mathbb{V}}\to [0, 1]\times [0, 1]$.$\forall \mathcalligra{x},\mathcalligra{y}\in {\mathbb{V}},$ the conditions are given by;

$${\mu }_{\mathcal{B}}^{\mathcal{P}}(\mathcalligra{x}, \mathcalligra{y})=\min\left({\mu }_{{\mathring{\rm A}}}^{\mathcal{P}}(\mathcalligra{x}), { \mu }_{{\mathring{\rm A}}}^{\mathcal{P}}(\mathcalligra{y})\right)$$

$${\mu }_{\mathcal{B}}^{\mathcal{N}}(\mathcalligra{x},\mathcalligra{y})=\max\left({\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}(\mathcalligra{x}), {\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}(\mathcalligra{y})\right)$$

$\forall (\mathcalligra{x},\mathcalligra{y})\in {\mathbb{E}}.$ Here, ${\mathring{\rm A}}$ is the bipolar fuzzy vertex set of ${\mathbb{V}}$, and $\mathcal{B}$ is the bipolar fuzzy edge set of ${\mathbb{X}}.$ Additionally:

$${\mu }_{\mathcal{B}}^{\mathcal{P}}\left(\mathcalligra{x},\mathcalligra{y}\right)>0\text{ and }{\mu }_{\mathcal{B}}^{\mathcal{N}}\left(\mathcalligra{x},\mathcalligra{y}\right)<0\text{ for }(\mathcalligra{x},\mathcalligra{y})\in {\mathbb{V}}\times {\mathbb{V}}$$

$${\mu }_{\mathcal{B}}^{\mathcal{P}}\left(\mathcalligra{x},\mathcalligra{y}\right)= {\mu }_{\mathcal{B}}^{\mathcal{N}}\left(\mathcalligra{x},\mathcalligra{y}\right)=0\text{ for }(\mathcalligra{x},\mathcalligra{y})\notin {\mathbb{V}}\times {\mathbb{V}}$$

Furthermore, $\mathcal{B}$ is a symmetric bipolar fuzzy relation on ${\mathring{\rm A}}.$

Definition 3

Akram²⁶ Let $\psi =(V,A,B)$ be a bipolar fuzzy graph for a certain geometric representation, the graph has only one crossing between two bipolar fuzzy edges $\left[[{\mu }_{{\mathring{\rm A}}}^{\mathcal{P}}\left(\mathcal{w}\right),{\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}\left(\mathcal{w}\right)\right],\;$ $\left[{\mu }_{{\mathring{\rm A}}}^{\mathcal{P}}\left(\mathcalligra{x}\right),{\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}\left(\mathcalligra{x}\right)\right],\;$ $[{\mu }_{\mathcal{B}}^{\mathcal{P}}\left(\mathcal{w}\mathcalligra{x}\right)\;,$ ${\mu }_{\mathcal{B}}^{\mathcal{N}}(\mathcal{w}\mathcalligra{x})]]\;\text{and}\;$ $\left[[{\mu }_{{\mathring{\rm A}}}^{\mathcal{P}}\left(\mathcalligra{y}\right),{\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}\left(\mathcalligra{y}\right)\right],\;$$\left[{\mu }_{{\mathring{\rm A}}}^{\mathcal{P}}\left(\mathcal{z}\right),{\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}\left(\mathcal{z}\right)\right],\;$ $[{\mu }_{\mathcal{B}}^{\mathcal{P}}\left(\mathcalligra{y}\mathcal{z}\right),{\mu }_{\mathcal{B}}^{\mathcal{N}}(\mathcalligra{y}\mathcal{z})]]=(-\text{1,1})\; \text{and}\;$$\left[{\mu }_{\mathcal{B}}^{\mathcal{P}}\left(\mathcalligra{y}\mathcal{z}\right),{\mu }_{\mathcal{B}}^{\mathcal{N}}\left(\mathcalligra{y}\mathcal{z}\right)\right]=(\text{0,0}),$ then that the bipolar fuzzy graph has no crossing. Similarly, if $[{\mu }_{\mathcal{B}}^{\mathcal{P}}\left(\mathcal{w}\mathcalligra{x}\right),{\mu }_{\mathcal{B}}^{\mathcal{N}}(\mathcal{w}\mathcalligra{x})]$ has value near to $(-\text{1,1})$ and $(\text{0,0}),$ the crossing will not be important for the planarity. If $[{\mu }_{\mathcal{B}}^{\mathcal{P}}\left(\mathcal{w}\mathcalligra{x}\right),{\mu }_{\mathcal{B}}^{\mathcal{N}}(\mathcal{w}\mathcalligra{x})]$ has value near to $(-\text{1,1})$ and $\left[{\mu }_{\mathcal{B}}^{\mathcal{P}}\left(\mathcal{w}\mathcalligra{x}\right),{\mu }_{\mathcal{B}}^{\mathcal{N}}\left(\mathcal{w}\mathcalligra{x}\right)\right]$ has value near to $\left(-\text{1,1}\right),$ then the crossing very important for the planarity.

Let $\psi$ be a bipolar fuzzy planar graph, and let $\mathcal{B}$ be a set defined as $\left\{ {(\mathcalligra{x}\mathcalligra{y},\mu _{{\mathcal{B}}}^{{\mathcal{P}}} (\mathcalligra{x}\mathcalligra{y})i,\mu _{{\mathcal{B}}}^{{\mathcal{P}}} (\mathcalligra{x}\mathcalligra{y})i)|} \right.$ ${i \ge {\text{1,2}}, \ldots ,m,xy \in {\mathbb{V}} \times {\mathbb{V}}}$. A bipolar fuzzy face of ψ is a region bounded by a set of bipolar fuzzy edges ${\mathbb{E}}^{\prime}\subseteq {\mathbb{E}}$ in a geometric representation of $\psi$. The positive and negative membership values of the bipolar fuzzy face given by:

$$\min\left\{\frac{{\mu }_{\mathcal{B}}^{\mathcal{P}}(\mathcalligra{x}\mathcalligra{y})i}{\{{\mu }_{{\mathring{\rm A}}}^{\mathcal{P}}(\mathcalligra{x})\wedge {\mu }_{{\mathring{\rm A}}}^{\mathcal{P}}(\mathcalligra{y})},i\ge \text{1,2},\ldots,m|\mathcalligra{x}\mathcalligra{y}\in {\mathbb{E}}^{\prime}\right\}$$

$$\max\left\{\frac{{\mu }_{\mathcal{B}}^{\mathcal{N}}(\mathcalligra{x}\mathcalligra{y})i}{\{{\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}(\mathcalligra{x})\vee {\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}(\mathcalligra{y})},i\ge \text{1,2},\ldots,m|\mathcalligra{x}\mathcalligra{y}\in {\mathbb{E}}^{\prime}\right\}$$

Definition 4

Akram²⁶ The strength of the bipolar fuzzy edge $\mathfrak{a}\mathfrak{b}$ can be measured by the value ${I}_{\mathfrak{a}\mathfrak{b}}$, defined as:

$${I}_{\mathfrak{a}\mathfrak{b}}=({M}_{\mathfrak{a}\mathfrak{b}},{N}_{\mathfrak{a}\mathfrak{b}})=\left(\frac{{\mu}_{\mathcal{B}}^{\mathcal{P}}(\mathfrak{a}\mathfrak{b})i}{\left({\mu }_{{\mathring{\rm A}}}^{\mathcal{P}}(\mathfrak{a})\wedge {\mu }_{{\mathring{\rm A}}}^{\mathcal{P}}(\mathfrak{b})\right)},\frac{{\mu }_{\mathcal{B}}^{\mathcal{N}}(\mathfrak{a}\mathfrak{b})i}{\left({\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}(\mathfrak{a})\vee {\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}(\mathfrak{b})\right)}\right)$$

Definition 5

Samanta and Pal⁵² Let $\psi =({\mathring{\rm A}},\mathcal{B})$ represent a bipolar fuzzy graph, where ${\mathring{\rm A}}=({m}_{1}^{+},{m}_{1}^{-})$ and $\mathcal{B}=({m}_{2}^{+},{m}_{2}^{-})$ be two bipolar fuzzy sets defined over a non-empty finite set ${\mathbb{V}}$ and a subset  ${\mathbb{E}}\subseteq {\mathbb{V}}\times {\mathbb{V}}$ representing the edges. The order of the graph $\psi$ is denoted as $O( \psi )$ and is defined by the interval: $O\left( \psi \right)=({O}^{-}\left( \psi \right),{O}^{+}\left( \psi \right))$ Where the lower bound of the order ${O}^{-}\left( \psi \right)$ is calculated as:

$${O}^{-}\left(\psi \right)=\sum_{u\in {\mathbb{V}}}{m}_{1}^{-}\left(u\right)$$

The upper bound of the order ${O}^{+}\left( \psi \right)$ is given by:

$${O}^{+}\left(\psi \right)=\sum_{u\in {\mathbb{V}}}{m}_{1}^{+}\left(u\right)$$

Definition 6

Samanta and Pal⁵² Let $\psi =({\mathring{\rm A}},\mathcal{B})$  represent a bipolar fuzzy graph, where ${\mathring{\rm A}}=({m}_{1}^{+},{m}_{1}^{-})$ and $\mathcal{B}=({m}_{2}^{+},{m}_{2}^{-})$  are two bipolar fuzzy sets defined over a non-empty finite set ${\mathbb{V}}$ and a subset  ${\mathbb{E}}\subseteq {\mathbb{V}}\times {\mathbb{V}}$ representing the edges.The size of the graph $\psi$ is denoted as $S(\psi )$  and is defined by the interval: $S\left(\psi \right)=({S}^{-}\left(\psi \right), {S}^{+}\left(\psi \right))$

Where the lower bound of the size ${S}^{-}\left( \psi \right)$ is calculated as:

$${S}^{-}\left(\psi \right)=\sum_{u\in {\mathbb{V}}}{m}_{1}^{-}\left(u\right).$$

The upper bound of the size ${S}^{+}\left( \psi \right)$ is given by:

$${S}^{+}\left(\psi \right)=\sum_{u\in {\mathbb{V}}}{m}_{1}^{+}(u)$$

Definition 7

Akram et al.²⁵ Let $\psi =({\mathring{\rm A}},\mathcal{B},{\mathbb{V}},{\mathbb{E}})$ be a Bipolar fuzzy planar graph with degree of planarity 1 where, ${\mathring{\rm A}}=({\mathbb{V}},({\mu }_{{\mathring{\rm A}}}^{\mathcal{P}},{\mu }_{{\mathring{\rm A}}}^{\mathcal{N}})$ and $\mathcal{B}=({\mathbb{V}}\times {\mathbb{V}},({\mu }_{{\mathring{\rm A}}}^{\mathcal{P}},{\mu }_{{\mathring{\rm A}}}^{\mathcal{N}})$. Again, let ${\mathfrak{f}}_{1},{\mathfrak{f}}_{2},\dots ,{\mathfrak{f}}_{k}$ be the strong faces of $\psi$. The bipolar fuzzy dual graph of $\psi$ is a Bipolar fuzzy planar graph ${\psi }^{\prime}=({{\mathring{\rm A}}}^{\prime},{\mathcal{B}}^{\prime})$, where ${{\mathring{\rm A}}}^{\prime}$ is a Bipolar fuzzy set on ${\mathbb{V}}^{\prime}=\left\{{\mathcalligra{x}}_{i},i=\text{1,2},\dots ,k\right\}, {\mathcalligra{x}}_{i}$ is considered for the face ${\mathfrak{f}}_{i}$ of $\psi$ and ${\mathcal{B}}^{\prime}$ is a BFS on ${\mathbb{V}}^{\prime}\times {\mathbb{V}}^{\prime}.$

Definition 8

Akram et al.²⁵ The positive membership values of vertices are given by the mapping $\mu _{{\mathring{\rm A}}}^{{\prime {\mathcal{P}}}} = {\mathbb{V}}^{\prime } \; \to \;[0,\;1]$ such that ${\mu }_{{\mathring{\rm A}}}^{\mathcal{P}}$, $\left({\mathcalligra{x}}_{i}\right)=\text{max}\{{\mu }_{\mathcal{B}}^{\mathcal{P}}\left(u,v\right):\left(u,v\right)$ is an edge of the boundary of the face ${\mathfrak{f}}_{i}\}$. The negative membership values of vertices are given by the mapping ${\mu }_{\mathring{\rm A}}^{{\prime}{\mathcal{N}}}={\mathbb{V}}^{\prime}\to [-\text{1,0}]$ such that ${\mu }_{\mathring{\rm A}}^{\mathcal{N}}$, $\left({\mathcalligra{x}}_{i}\right)=\text{max}\{{\mu }_{\mathcal{B}}^{\mathcal{N}}\left(u,v\right):\left(u,v\right)$ is an edge of the boundary of the face ${\mathfrak{f}}_{i}\}$.

Between two faces ${\mathfrak{f}}_{i}$ and ${\mathfrak{f}}_{j}$ of $\psi$, there may exist more than one common edge. Thus, between two vertices ${\mathcalligra{x}}_{i}$ and ${\mathcalligra{x}}_{j}$ in bipolar fuzzy dual graph ${\psi }^{\prime},$ there may be more than one edge. We denote ${\mu }_{\mathcal{B}}^{l\left(\mathcal{P}\right)}\left({\mathcalligra{x}}_{i},{\mathcalligra{x}}_{j}\right)$ be the positive membership value of the $l$-th edge between ${\mathcalligra{x}}_{i}$ and ${\mathcalligra{x}}_{j}$. The membership values of the edges of the bipolar fuzzy dual graph are given by ${\mu }_{\mathcal{B}}^{l\left(\mathcal{P}\right)}\left({\mathcalligra{x}}_{i},{\mathcalligra{x}}_{j}\right)$ =${\mu }_{\mathcal{B}}^{l\left(\mathcal{P}\right)}{(u,v)}^{l}$ where ${(u,v)}^{l}$ is an edge adjacent to each of the two faces ${\mathfrak{f}}_{i}$ and ${\mathfrak{f}}_{j}$ (i.e. the number of edges between ${\mathcalligra{x}}_{i}$ and ${\mathcalligra{x}}_{j})$. Similarly, we denote ${\mu }_{\mathcal{B}}^{l\left(\mathcal{N}\right)}\left({\mathcalligra{x}}_{i},{\mathcalligra{x}}_{j}\right)$ be the negative membership value of the $l$-th edge connecting ${\mathcalligra{x}}_{i}$ and ${\mathcalligra{x}}_{j}$. The negative membership values of the edges of the bipolar fuzzy dual graph are given by ${\mu }_{\mathcal{B}}^{l\left(\mathcal{N}\right)}\left({\mathcalligra{x}}_{i},{\mathcalligra{x}}_{j}\right)={\mu }_{\mathcal{B}}^{l\left(\mathcal{N}\right)}{(u,v)}^{l}$ where ${(u,v)}^{l}$ is an edge adjacent to each of the two faces ${\mathfrak{f}}_{i}$ and ${\mathfrak{f}}_{j}$ and $l=\text{1,2},\dots ,s,$ where $s$ is the number of common edges adjacent to each of the faces ${\mathfrak{f}}_{i}$ and ${\mathfrak{f}}_{j}$. (i.e. the number of edges between ${\mathcalligra{x}}_{i}$ and ${\mathcalligra{x}}_{j})$.

Definition 10

Shriram et al.³⁰ Let $\psi$ be a fuzzy graph, and ${\mathbb{W}}$ be a subset of the vertex set ${\mathbb{V}}$, denoted by ${\mathbb{W}}\subseteq {\mathbb{V}}$. The fuzzy subgraph formed by removing the set ${\mathbb{W}}$ from $\psi$ is denoted as $\psi -{\mathbb{W}}$.

$\psi -{\mathbb{W}}=\left\{v\epsilon {\mathbb{V}}\backslash {\mathbb{W}}|\delta (\mathcalligra{x},\mathcalligra{y})\ne 0,\forall \mathcalligra{x},\mathcalligra{y}\in {\mathbb{V}}\backslash {\mathbb{W}}\right\}$.

The fuzzy graph $\psi -W$ is known as the Vertex Deletion fuzzy subgraph of graph $\psi$.

Definition 11

Shriram et al.³⁰ Let $\psi$ be a fuzzy graph and ${\mathbb{E}}\subseteq {\mathbb{U}}$. The fuzzy subgraph formed by removing the set ${\mathbb{W}}$ from $\psi$ is denoted by $\psi -{\mathbb{U}}$.

$$\psi -{\mathbb{U}}=\left\{\delta (\mathcalligra{x},\mathcalligra{y})\in {\mathbb{E}}\backslash {\mathbb{U}}|\delta (\mathcalligra{x},\mathcalligra{y})\ne 0,\forall \mathcalligra{x},\mathcalligra{y}\in {\mathbb{V}}\right\}$$

$\psi -{\mathbb{U}}$ is the edge deletion fuzzy subgraph of $\psi$.

Definition 12

Ramya and Lavanya⁴¹ Let $\psi =({\mathbb{V}},{\mathbb{E}})$ be a bipolar fuzzy graph. Let $uv$ be an edge of $\psi$, then the edge contracted Bipolar fuzzy graph of $\psi$ with respect to the edge $uv$ is denoted by $\psi /uv$ and is defined as a graph vertex set.

${\mathbb{V}}^{\prime}=\left\{\frac{\mathbb{V}}{\left\{\text{u},\text{v}\right\}}\cup \left\{\text{w}\right\}\right],$ where $\left({\mu }_{{\mathring{\rm A}}}^{\mathcal{P}},{\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}\right)\left(\frac{\psi }{uv}\right)=\left({\mu }_{{\mathring{\rm A}}}^{\mathcal{P}},{\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}\right)(\psi )$ for all vertices $x\in {\mathbb{V}}$, and

$${\mu }_{{\mathring{\rm A}}}^{\mathcal{P}}\left(w\right)=\min\{{\mu }_{{\mathring{\rm A}}}^{\mathcal{P}}\left(u\right),{\mu }_{{\mathring{\rm A}}}^{\mathcal{P}}\left(v\right)\}$$

$${\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}\left(w\right)=\max\{{\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}\left(u\right),{\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}\left(v\right)\}$$

and two vertices x and y are adjacent in $\psi /uv$ if any one of the following conditions hold.

• (i) If $\mathcalligra{x},\mathcalligra{y}\in {\mathbb{V}}$ & $\mathcalligra{x},\mathcalligra{y}$ are adjacent in $\psi$, then ${\left({\mu }_{\mathcal{B}}^{\mathcal{P}},{\mu }_{\mathcal{B}}^{\mathcal{N}}\right)}_{\frac{\psi }{uv}}\left(\mathcalligra{x}\mathcalligra{y}\right)={\left({\mu }_{\mathcal{B}}^{\mathcal{P}},{\mu }_{\mathcal{B}}^{\mathcal{N}}\right)}_{ \psi }\left(\mathcalligra{x}\mathcalligra{y}\right)$

• (ii) If $\mathcalligra{x}\in {\mathbb{V}}$ & $\mathcalligra{y}=w,$ then $\mathcalligra{x}$ and $\mathcalligra{y}$ are adjacent in $\frac{\psi }{uv}$ if either $\mathcalligra{x}$ is adjacent to $u$ or $v$ and

  $${\left({\mu }_{\mathcal{B}}^{\mathcal{P}}\right)}_{\frac{\psi }{uv}}\left(\mathcalligra{x}\mathcalligra{y}\right)=\min\left\{{\mu }_{{\mathring{\rm A}}}^{\mathcal{P}}(\mathcalligra{x}),\left.{\mu }_{{\mathring{\rm A}}}^{\mathcal{P}}(w)\right)\right\}$$
  $${\left({\mu }_{\mathcal{B}}^{\mathcal{N}}\right)}_{\frac{\psi }{uv}}\left(\mathcalligra{x}\mathcalligra{y}\right)=\max\left\{{\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}(\mathcalligra{x}),\left.{\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}(w)\right)\right\}$$

• (iii) If $\mathcalligra{x}\in {\mathbb{V}}$ & $\mathcalligra{y}=w,$ then $\mathcalligra{x}$ and $\mathcalligra{y}$ are adjacent in $\frac{\psi }{uv}$ if $\mathcalligra{x}$ is adjacent to both $u$ or $v$ in $\psi$ and

  $${\left({\mu }_{\mathcal{B}}^{\mathcal{P}}\right)}_{\frac{\psi }{uv}}\left(\mathcalligra{x}\mathcalligra{y}\right)=\text{min}\{{{\mu }_{\mathcal{B}}^{\mathcal{P}}}_{\psi }(\mathcalligra{x}u),{{\mu }_{\mathcal{B}}^{\mathcal{P}}}_{\psi }(\mathcalligra{x}v))\}$$
  $${\left({\mu }_{\mathcal{B}}^{\mathcal{N}}\right)}_{\frac{\psi }{uv}}\left(\mathcalligra{x}\mathcalligra{y}\right)=\text{max}\{{{\mu }_{\mathcal{B}}^{\mathcal{N}}}_{\psi }(\mathcalligra{x}u),{{\mu }_{\mathcal{B}}^{\mathcal{N}}}_{\psi }(\mathcalligra{x}v))\}$$

Bipolar fuzzy outerplanar graph

In this section, introduced the concept of bipolar fuzzy outerplanar graphs, which extend the classical notion of outerplanarity to graphs with bipolar fuzzy values. The focus is on defining the graph structure and understanding its properties in the context of bipolar fuzziness.

Definition 12.

A bipolar fuzzy graph $\psi$ qualifies as a bipolar fuzzy outerplanar graph when $\psi$ is embedded in the plane such that every vertex lies on the exterior boundary of the region.

Let $i\left(\psi \right)$ represent the number of vertices in a planar embedding that do not depend on the boundary of the outer region. Therefore, $\left(\psi \right)=0$ for a bipolar fuzzy outerplanar graph.

The graphs given in Figs. 1 and 2 are examples of bipolar fuzzy outerplanar graphs.

Fig. 1

Bipolar fuzzy outerplanar graph with cycle.

Fig. 2

Bipolar fuzzy outerplanar graph without cycle.

Definition 13.

A bipolar fuzzy graph that cannot be embedded in the plane so that each vertex lies on the exterior region’s boundary is known as a bipolar fuzzy non-outerplanar graph.

In other words, it’s a bipolar fuzzy graph that does not satisfy the property of being bipolar fuzzy outerplanar, where some vertices are in located the interior of the drawing rather than exclusively on the outer boundary.

If $i(\psi )\ne 0$, then a bipolar fuzzy planar graph is not a bipolar fuzzy outerplanar graph.

The graphs given in Figs. 3 and 4 are examples of bipolar fuzzy non outerplanar graphs.

Fig. 3

Bipolar fuzzy graph ${K}_{4}$.

Fig. 4

Bipolar Fuzzy planar embedding of ${K}_{4}$.

Characterization of bipolar fuzzy outerplanar graph

In this section, we explore the defining theorems and example criteria that characterize bipolar fuzzy outerplanar graphs.

Theorem 1.

A bipolar fuzzy graph $\psi$ is bipolar fuzzy outer planar if and only if it contains no bipolar fuzzy subgraph homomorphic from ${K}_{4}$ or ${K}_{\text{2,3}}$.

Proof.

It is known that ${K}_{4}$ or ${K}_{\text{2,3 }}$ are not bipolar fuzzy outerplanar. Thus, no bipolar fuzzy graph having a bipolar fuzzy subgraph homomorphic from ${K}_{4}$ or ${K}_{\text{2,3}}$ is bipolar fuzzy outerplanar graphs shown in the Figs. 5 and 6.

Fig. 5

Bipolar fuzzy graph ${K}_{4}$.

Fig. 6

Bipolar fuzzy graph ${K}_{\text{2,3}}$

Conversely, suppose $\psi$ is a bipolar fuzzy graph containing no bipolar fuzzy subgraph homomorphic from ${K}_{4}$ or ${K}_{2,3}$. By kuratowski’s theorem, $\psi$ is planar. Assume G is not bipolar fuzzy outer planar graph. Thus, without loss of generality, we assume that $\psi$ is a cyclic block which is not bipolar fuzzy outerplanar graph. Further we assume that $\psi$ is so embedded in the fuzzy plane that the exterior region contains maximum number of vertices.

The exterior region is bounded by a cycle C. Since not all vertices of $\psi$, lie on C, there are one or more vertices lying interior to C.

If there exist a vertex ${\mathfrak{v}}_{3}$ interior on C and three mutually disjoint paths between ${\mathfrak{v}}_{3}$ and three distinct vertices of C, then $\psi$ contains fuzzy subgraph homomorphic from ${K}_{4}.$

Otherwise, since $\psi$ is a cyclic block, there must exists a vertex ${\mathfrak{v}}_{3}$ and two disjoint paths between ${\mathfrak{v}}_{3}$ and two disjoint vertices ${\mathfrak{v}}_{1}$ and ${\mathfrak{v}}_{5}$ on C.

Moreover, from the above choice of C, the edge ${\mathfrak{v}}_{1}{\mathfrak{v}}_{5}$ does not belong to C. This implies $\psi$ contains a bipolar fuzzy subgraph homomorphic from ${K}_{\text{2,3}}$. This is a contradiction. Therefore, Fig. 7$\psi$ is a bipolar fuzzy outerplanar graph. This completes the proof.

Fig. 7

Bipolar fuzzy outerplanar graphs.

Theorem 2.

If $\psi$ is a connected bipolar fuzzy outerplanar graph, then it has a fuzzy dual ${\psi }^{*}$ there exist a vertex $\mathfrak{v}$ such that ${\psi }^{*}-\mathfrak{v}$ contains no fuzzy cycle.

Proof.

Let $\psi =({\mathbb{V}},\tau ,\delta )$ be a connected fuzzy outerplanar graph and there are no intersections of edges ${E}^{\prime}\subset E$ within the graph, we can divide the fuzzy graph into a finite number of regions. Each of these regions corresponds to a ${\mathfrak{f}}_{1},{\mathfrak{f}}_{2},{\mathfrak{f}}_{3},\dots {\mathfrak{f}}_{k}$ be the fuzzy faces and the positive and negative membership value for each face is determined by,

$$\min\left\{\frac{{\mu }_{\mathcal{B}}^{\mathcal{P}}(\mathcalligra{x}\mathcalligra{y})i}{\{{\mu }_{{\mathring{\rm A}}}^{\mathcal{P}}(\mathcalligra{x})\wedge {\mu }_{{\mathring{\rm A}}}^{\mathcal{P}}(\mathcalligra{y})},i\ge \text{1,2},\ldots,m|\mathcalligra{x}\mathcalligra{y}\in {\mathbb{E}}^{\prime}\right\}$$

$$\max\left\{\frac{{\mu }_{\mathcal{B}}^{\mathcal{N}}(\mathcalligra{x}\mathcalligra{y})i}{\{{\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}(\mathcalligra{x})\vee {\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}(\mathcalligra{y})},i\ge \text{1,2},\ldots,m|\mathcalligra{x}\mathcalligra{y}\in {\mathbb{E}}^{\prime}\right\}$$

When the bipolar fuzzy graph divided into regions with bipolar fuzzy face and values, it becomes very easy to bipolar fuzzy dual graph ${\psi }^{*}$ such that each face of $\psi$ corresponds to a vertex and each edge of $\psi$ corresponds to edge in ${\psi }^{*}=\left({\mathbb{V}}^{\prime},{\tau }^{\prime},{\delta }^{\prime}\right)$ . Consequently, the bipolar fuzzy dual graph ${\psi }^{*}$ exists for the bipolar fuzzy outerplanar graph.

Since $\psi$ is bipolar fuzzy outerplanar graph can be seen in Fig. 8a. It is outer face is a bipolar fuzzy cycle. Therefore, the graph ${\psi }^{*}-\mathfrak{v}$ that results from removing the vertex $\mathfrak{v}$ from ${\psi }^{*}$ shown in Fig. 8b, the resulting graph ${\psi }^{*}-\mathfrak{v}$ contains no bipolar fuzzy cycle is shown in Fig. 8c.

Fig. 8

(a) Connected bipolar fuzzy outerplanar graph $\psi$. (b) Bipolar fuzzy dual graph has bipolar fuzzy outerplanar graph ${\psi }^{*}$. (c) Vertex deletion bipolar fuzzy outerplanar graph ${\psi }^{*}-v$. (a)–(c) Example for bipolar fuzzy outerplanar graph $\psi$ has bipolar fuzzy dual graph ${\psi }^{*}$ then there exist $\mathfrak{v}$ such that ${\psi }^{*}-\mathfrak{v}$ contains no bipolar fuzzy cycle.

Example 1.

Consider the bipolar fuzzy outerplanar graph $\psi =({\mathbb{V}},\tau ,\delta )$ illustrated in the Fig. 8a. If the dotted lines in Fig. 8b are superimposed bipolar fuzzy dual graph of ${\psi }^{*}$ and separated diagram. The positive membership value and negative membership value is given in the Table 2. Then the bipolar fuzzy faces ${\mathfrak{f}}_{1}=\left(0.4,-0.6\right),{\mathfrak{f}}_{2}={\mathfrak{f}}_{4}=\left(0.375,-0.875\right),{\mathfrak{f}}_{3}=\left(0.6,-0.875\right).$ Each bipolar face of $\psi$ corresponds to a vertex and each edge of $\psi$ corresponds to edge in ${\psi }^{*}=\left({\mathbb{V}}^{\prime},{\tau }^{\prime},{\delta }^{\prime}\right)$ Then $\mathfrak{v}$ exists in such a way that ${\psi }^{*}-\mathfrak{v}$ contains no bipolar fuzzy cycle.

Table 2 Calculation of bipolar fuzzy faces.

Definition 14.

If an edge cannot be added to a bipolar fuzzy outerplanar graph $\psi$ without sacrificing its outer planarity property, then the graph is bipolar maximal fuzzy outerplanar graph.

The graphs given in Figs. 9 and 10 are examples of bipolar maximal fuzzy outerplanar graphs.

Fig. 9

Bipolar maximal fuzzy outerplanar graph.

Fig. 10

Bipolar maximal fuzzy outerplanar graph.

Definition 15.

A bipolar fuzzy planar graph $\psi$ is considered minimally bipolar fuzzy non-outerplanar if $i\left(\psi \right)\ne 0$ with atmost one vertex $\mathfrak{v}\in \psi \text{ such that }\tau (\mathcalligra{x})>0$ in the interior region.

The graphs given in Figs. 11 and 12 are examples of minimally bipolar fuzzy non- outerplanar graphs.

Fig. 11

Bipolar fuzzy graph ${K}_{4}$.

Fig. 12

Bipolar fuzzy graph ${K}_{\text{2,3}}$

Vertex deletion bipolar fuzzy outerplanar subgraph

In this section, the subgraph formed by removing specific vertices from the bipolar fuzzy graph, while also defining bipolar fuzzy outerplanar graphs and offering relevant illustrations.

Definition 16.

Assume $\psi$ is a bipolar fuzzy planar graph. If ${\psi }^{\prime}$ is the Vertex Deleted bipolar fuzzy subgraph possessing outerplanarity property, then it is called Vertex Deleted bipolar fuzzy outerplanar subgraph of $\psi$.

Example 2.

Let’s look at the bipolar fuzzy graph $\psi =({\mathbb{V}},\tau ,\delta )$ shown in Fig. 13a. The set of vertices in $\psi$ is ${\mathbb{V}}=\left\{{\mathfrak{v}}_{1},{\mathfrak{v}}_{2},{\mathfrak{v}}_{3},{\mathfrak{v}}_{4},{\mathfrak{v}}_{5},{\mathfrak{v}}_{6}\right\}$ and their membership values of these are as follows: ${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{1}\right)=0.6,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{1}\right)=-0.5,\;$${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{2}\right)=0.85,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{2}\right)=-0.9,\;$${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{3}\right)=0.4,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{3}\right)=-0.5,\;$${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{4}\right)=0.4,\; {\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{3}\right)=0.4,\;$${\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{3}\right)=-0.5,\;{\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{4}\right)=0.4,\;$${\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{4}\right)=-0.1,\;{\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{5}\right)=0.7,\;$${\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{5}\right)=-0.8,\;{\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{6}\right)=0.6,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{6}\right)=-0.7\;$ and the edges ${\mathbb{B}}$ is ${\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{1},\;{\mathfrak{v}}_{2}\right)=0.65,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{1},{\mathfrak{v}}_{2}\right)=-0.1,\;{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{1},{\mathfrak{v}}_{3}\right)=0.35,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{1},{\mathfrak{v}}_{3}\right)=-0.4,\;{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{2},{\mathfrak{v}}_{3}\right)=0.25,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{2},{\mathfrak{v}}_{3}\right)=-0.3,\;{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{2},{\mathfrak{v}}_{5}\right)=0.6,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{2},{\mathfrak{v}}_{5}\right)=-0.7,\;{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{3},{\mathfrak{v}}_{6}\right)=0.35,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{3},{\mathfrak{v}}_{6}\right)=-0.4,\;{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{5},{\mathfrak{v}}_{6}\right)=0.55,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{5},{\mathfrak{v}}_{6}\right)=-0.6,\;{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{6},{\mathfrak{v}}_{5}\right)=0.4,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{6},{\mathfrak{v}}_{5}\right)=-0.2,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{2},{\mathfrak{v}}_{4}\right)=0.4,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{2},{\mathfrak{v}}_{4}\right)=-0.4,\;{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{3},{\mathfrak{v}}_{4}\right)=0.4,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{3},{\mathfrak{v}}_{4}\right)=-0.2,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{4},{\mathfrak{v}}_{5}\right)=0.3,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{4},{\mathfrak{v}}_{5}\right)=-0.5,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{4},{\mathfrak{v}}_{6}\right)=0.4,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{4},{\mathfrak{v}}_{6}\right)=-0.2.$

Fig. 13

(a) Bipolar fuzzy graph $\psi$. (b) Vertex Deleted bipolar fuzzy subgraph ${\psi }_{1}$. (c) Vertex Deletion bipolar fuzzy outerplanar subgraph ${\psi }_{2}$.

The edges intersect between the sets $\delta ({\mathfrak{v}}_{2},{\mathfrak{v}}_{6})$ and $\delta ({\mathfrak{v}}_{4},{\mathfrak{v}}_{5})$ within bipolar fuzzy graph $\psi$. Let us define subsets ${\mathbb{X}}$ and ${\mathbb{Y}}$ in ${\mathbb{V}}$, where ${\mathbb{X}}=$ $\left\{({\mathfrak{v}}_{1}(0.6,-0.5)\right\}$ and ${\mathbb{Y}}=\left\{{\mathfrak{v}}_{4}(0.4,-0.1)\right\}$ in the bipolar fuzzy graph $\psi$.

The bipolar fuzzy subgraphs $\psi -{\mathbb{X}},$ represented as ${\psi }_{1}$ can be seen in Fig. 13b. Similarly, the bipolar fuzzy subgraph $\psi -{\mathbb{Y}}$ represented as ${\psi }_{2}$ is shown in Fig. 13c. It can be noted that, bipolar subgraph ${\psi }_{1}$ is categorized as a Vertex Deletion bipolar fuzzy subgraph, while ${\psi }_{2}$ is classified as a Vertex Deleted bipolar fuzzy outerplanar subgraph of ${\psi }$.

Note 1.

It is not necessary for the Vertex Deletion bipolar fuzzy subgraph of ${\psi }$ to be the Vertex Deletion bipolar fuzzy outerplanar subgraph of $\psi$. The bipolar graphs in Fig. 13b and c allow for the observation of this.

Theorem 3.

A bipolar fuzzy outerplanar graph $\psi$ always has a vertex deleted bipolar fuzzy outerplanar subgraph that is also a vertex deleted bipolar fuzzy subgraph of $\psi$.

Proof.

Let the bipolar fuzzy outerplanar graph be ψ. and ${\mathbb{H}}$ be the vertex deleted bipolar fuzzy subgraph of ${\psi }$. The vertices of the bipolar fuzzy graph $\psi$ will all be in the outer region since it is outerplanar. As a result, the bipolar subgraph that was created by deleting vertices still has outerplanarity. Any vertex deleted bipolar subgraph in $\psi$ is therefore a vertex deletion bipolar fuzzy outerplanar subgraph of $\psi$.

Theorem 4.

Let $\psi$ be a bipolar fuzzy outerplanar graph which is connected and let ${\mathbb{W}}$ be a subset of its vertices, such that ${\mathbb{W}}\subseteq {\mathbb{V}}$. The bipolar fuzzy outerplanar subgraph of $\psi$ with a vertex deleted is ${{\psi }}^{\prime}={\psi }\backslash {\mathbb{W}}$. Its bipolar fuzzy dual graph is $\psi^{\prime\prime}$.

Proof.

Let us consider a connected bipolar fuzzy outerplanar subgraph $\psi$ shown in Fig. 14a and ${\mathbb{W}}\subseteq {\mathbb{V}}$. let $\psi -{\mathbb{W}}$ form a Vertex deleted bipolar fuzzy outerplanar subgraph denoted ${\psi }^{\prime}$ $.$ Since there is no intersection of bipolar fuzzy edges in the subgraph ${\psi }^{\prime}$, we can divide the bipolar fuzzy graph into a finite number of regions. Each of these regions corresponds to a bipolar fuzzy face, and the positive and negative membership values for each face is determined by.

Fig. 14

(a) Connected bipolar fuzzy outerplanar graph. (b) Bipolar fuzzy dual graph has bipolar fuzzy outerplanar graph. (a), (b) Example for Vertex Deletion bipolar fuzzy outerplanar subgraph and its bipolar fuzzy dual graph.

$${\mathfrak{f}}^{\mathcal{P}}=\min\left\{\frac{{\mu }_{\mathcal{B}}^{\mathcal{P}}(\mathcalligra{x}\mathcalligra{y})i}{\{{\mu }_{{\mathring{\rm A}}}^{\mathcal{P}}(\mathcalligra{x})\wedge {\mu }_{{\mathring{\rm A}}}^{\mathcal{P}}(\mathcalligra{y})},i\ge \text{1,2},\ldots,m|\mathcalligra{x}\mathcalligra{y}\in {\mathbb{E}}^{\prime}\right\}$$

$${\mathfrak{f}}^{\mathcal{N}}=\max\left\{\frac{{\mu }_{\mathcal{B}}^{\mathcal{N}}\left(\mathcalligra{x}\mathcalligra{y}\right)i}{\{{\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}(\mathcalligra{x})\vee {\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}(\mathcalligra{y})},i\ge \text{1,2},\dots ,m|\mathcalligra{x}\mathcalligra{y}\in {\mathbb{E}}^{\prime}\right\}$$

Using the fact that each bipolar fuzzy graph with planarity value as 1 has bipolar fuzzy dual graph, $\psi -{\mathbb{W}}$ has a bipolar fuzzy dual graph ${\psi }^{\prime\prime}$ is shown in Fig. 14b. Consequently, the bipolar fuzzy dual graph exists for the Vertex Deleted bipolar fuzzy outerplanar subgraph of $\psi .$

Example 3.

From Example, it is evident that the bipolar subgraph ${\psi }^{\prime\prime}$ is the Vertex Deletion bipolar fuzzy outerplanar subgraph of $\psi$. The dotted lines represent the superimposed bipolar fuzzy dual graph of ${\psi }^{\prime\prime}$ in Fig. 14b. The bipolar fuzzy dual graph is associated with bipolar fuzzy face values, with all bipolar fuzzy faces having positive and negative membership values is given in the Table 3. Then the bipolar fuzzy faces (${{\mathfrak{f}}_{1}}^{\mathcal{P}},{{\mathfrak{f}}_{1}}^{\mathcal{N}})=\left(0.625,-0.8\right),\text{(}{{\mathfrak{f}}_{2}}^{\mathcal{P}},{{\mathfrak{f}}_{2}}^{\mathcal{N}})=\left(0.625,-0.777\right)$, (${{\mathfrak{f}}_{3}}^{\mathcal{P}},{{\mathfrak{f}}_{3}}^{\mathcal{N}})=\left(0.666,-0.75\right)$ and (${{\mathfrak{f}}_{4}}^{\mathcal{P}},{{\mathfrak{f}}_{4}}^{\mathcal{N}})=\left(0.666,-0.8\right).$ Therefore, the Vertex Deletion bipolar fuzzy outerplanar subgraph ${\psi }^{\prime\prime}$ indeed possesses a bipolar fuzzy dual graph.

Table 3 Calculation of bipolar fuzzy faces.

Example 4.

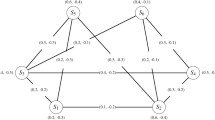
Let’s look at the bipolar fuzzy graph $\psi =({\mathbb{V}},\tau ,\delta )$ shown in Fig. 15a. The set of vertices in $\psi$ is ${\mathbb{V}}=\left\{{\mathfrak{v}}_{1},{\mathfrak{v}}_{2},{\mathfrak{v}}_{3},{\mathfrak{v}}_{4},{\mathfrak{v}}_{5},{\mathfrak{v}}_{6}\right\}$ and their membership values of these are as follows: ${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{1}\right)=0.6,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{1}\right)=-0.4,\;$${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{2}\right)=0.3,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{2}\right)=-0.2,$${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{3}\right)=0.7,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{3}\right)=-0.5,\;$${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{4}\right)=0.2,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{4}\right)=-0.4,$${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{5}\right)=0.7,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{5}\right)=-0.6,$${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{6}\right)=0.5,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{6}\right)=-0.7,\;$${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{7}\right)=0.8,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{7}\right)=-0.5,\;$${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{8}\right)=0.6,\;{\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{9}\right)=0.4,\;$${\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{9}\right)=-0.5,\;{\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{10}\right)=0.5,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{10}\right)=-0.5$ and the edges ${\mathbb{B}}$ is ${\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{1},{\mathfrak{v}}_{2}\right)=0.9,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{1},{\mathfrak{v}}_{2}\right)=-0.2,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{2},{\mathfrak{v}}_{3}\right)=0.8,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{2},{\mathfrak{v}}_{3}\right)=-0.3,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{3},{\mathfrak{v}}_{4}\right)=0.7,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{3},{\mathfrak{v}}_{4}\right)=-0.4,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{4},{\mathfrak{v}}_{5}\right)=0.6,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{4},{\mathfrak{v}}_{5}\right)=-0.3,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{5},{\mathfrak{v}}_{6}\right)=0.5,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{5},{\mathfrak{v}}_{6}\right)=-0.6,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{6},{\mathfrak{v}}_{7}\right)=0.4,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{6},{\mathfrak{v}}_{7}\right)=-0.3,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{7},{\mathfrak{v}}_{8}\right)=0.5,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{7},{\mathfrak{v}}_{8}\right)=-0.6,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{8},{\mathfrak{v}}_{1}\right)=0.2,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{8},{\mathfrak{v}}_{1}\right)=-0.4,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{1},{\mathfrak{v}}_{9}\right)=0.2,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{1},{\mathfrak{v}}_{9}\right)=-0.1,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{2},{\mathfrak{v}}_{9}\right)=0.4,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{2},{\mathfrak{v}}_{9}\right)=-0.2,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{2},{\mathfrak{v}}_{10}\right)=0.6,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{2},{\mathfrak{v}}_{10}\right)=-0.3,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{3},{\mathfrak{v}}_{10}\right)=0.8,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{3},{\mathfrak{v}}_{10}\right)=-0.4,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{8},{\mathfrak{v}}_{9}\right)=0.5,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{8},{\mathfrak{v}}_{9}\right)=-0.2,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{9},{\mathfrak{v}}_{10}\right)=0.2,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{9},{\mathfrak{v}}_{10}\right)=-0.3,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{10},{\mathfrak{v}}_{4}\right)=0.2,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{10},{\mathfrak{v}}_{4}\right)=-0.4,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{7},{\mathfrak{v}}_{9}\right)=0.7,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{7},{\mathfrak{v}}_{9}\right)=-0.1,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{6},{\mathfrak{v}}_{9}\right)=0.9,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{6},{\mathfrak{v}}_{9}\right)=-0.2 ,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{6},{\mathfrak{v}}_{10}\right)=0.3,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{6},{\mathfrak{v}}_{10}\right)=-0.3,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{5},{\mathfrak{v}}_{10}\right)=0.4,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{5},{\mathfrak{v}}_{10}\right)=-0.4.$

Fig. 15

(a) Bipolar fuzzy graph. (b) Bipolar fuzzy edge contraction. (c) Vertex deleted bipolar fuzzy outerplanar graph.

Let $\psi$ be the bipolar fuzzy graph. then the edge contracted bipolar fuzzy graph, denoted as $\psi \backslash {\mathfrak{v}}_{9}{\mathfrak{v}}_{10}$ derived from the Bipolar fuzzy graph $\psi =(\tau ,\delta )$ by contracting the edge ${\mathfrak{v}}_{9}{\mathfrak{v}}_{10}$. In this Fig. 15b the vertex set ${\mathbb{V}}^{\prime}=\left\{\frac{\mathbb{V}}{\left\{{\mathfrak{v}}_{9},{\mathfrak{v}}_{10}\right\}}\cup \left\{\mathfrak{w}\right\}\right],$ where $\left({\mu }_{{\mathring{\rm A}}}^{\mathcal{P}},{\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}\right)\left(\frac{\psi }{{\mathfrak{v}}_{9}{\mathfrak{v}}_{10}}\right)=\left({\mu }_{{\mathring{\rm A}}}^{\mathcal{P}},{\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}\right)(\psi )$ for all vertices $x\in {\mathbb{V}}.$ The membership value $\tau$ of $\psi /{\mathfrak{v}}_{9}{\mathfrak{v}}_{10}$ remains the same as $\tau$ in $\psi$ for all vertices $\mathcalligra{x}\in {\mathbb{V}},$ and the membership value of $\mathfrak{w}$ is calculated by ${\left({\mu }_{\mathcal{B}}^{\mathcal{P}}\right)}_{\frac{\psi }{{\mathfrak{v}}_{9}{\mathfrak{v}}_{10}}}\left(\mathcalligra{x}\mathcalligra{y}\right)=\min\left\{{\mu }_{{\mathring{\rm A}}}^{\mathcal{P}}(\mathcalligra{x}),\left.{\mu }_{{\mathring{\rm A}}}^{\mathcal{P}}(w)\right)\right\}, \left(\mathcalligra{x}\mathcalligra{y}\right)=\max\left\{{\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}(\mathcalligra{x}),\left.{\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}(w)\right)\right\}.$ The adjacency between two vertices $\mathcalligra{x}$ and $\mathcalligra{y}$ in $\psi /{\mathfrak{v}}_{9}{\mathfrak{v}}_{10}$ is determined by Definition (11) conditions.

The edge contracted bipolar fuzzy graph $\psi \backslash {\mathfrak{v}}_{9}{\mathfrak{v}}_{10}$, represented as ${\psi }_{1}$ can be seen in Fig. 15b. Similarly, the Bipolar fuzzy graph ${\psi }_{1 }-\text{V}$ represented as ${\psi }_{2}$ is shown in Fig. 15c. It can be noted that, is categorized as a Vertex Deletion Bipolar fuzzy outerplanar graph.

Maximum and maximal vertex deletion bipolar fuzzy outerplanar subgraph

In this section, defined the concepts of maximum and maximal vertex deletion bipolar fuzzy outerplanar subgraphs and explores the relationship between these two notions with appropriate examples.

Definition 17.

If ${\psi }^{\prime}=\left({\mathbb{V}}^{\prime},{\tau }^{\prime},{\delta }^{\prime}\right)$ is the Vertex Deletion bipolar fuzzy outerplanar subgraph of $\psi$ such that there is no other Vertex deleted bipolar fuzzy outerplanar subgraph of $\psi$ with maximum order and size compared to the bipolar subgraph ${\psi }^{\prime}$, then ${\psi }^{\prime}$ is said to be the maximum Vertex deleted bipolar fuzzy outerplanar subgraph of $\psi .$

Note 2.

Let positive and negative order ${a}^{\prime}=\left({a}_{\mathcal{P}}^{\prime},{a}_{\mathcal{N}}^{\prime}\right),{a}^{\prime\prime}=({a}_{\mathcal{P}}^{\prime\prime},{a}_{\mathcal{N}}^{\prime\prime})$ and positive and negative size ${b}^{\prime}=\left({b}_{\mathcal{P}}^{\prime},{b}_{\mathcal{N}}^{\prime}\right),{b}^{\prime\prime}=({b}_{\mathcal{P}}^{\prime\prime},{b}_{\mathcal{N}}^{\prime\prime})$ of the Vertex deleted bipolar fuzzy outerplanar subgraphs ${\psi }^{\prime}$ and ${\psi }^{\prime\prime}$ of $\psi$ be ${a}_{\mathcal{P}}^{\prime}>{a}_{\mathcal{P}}^{\prime\prime}$ then $\left|{a}_{\mathcal{N}}^{\prime}\right|>\left|{a}_{\mathcal{N}}^{\prime\prime}\right|$ and ${b}_{\mathcal{P}}^{\prime}>{b}_{\mathcal{P}}^{\prime\prime}$ then $\left|{b}_{\mathcal{N}}^{\prime}\right|>\left|{b}_{\mathcal{N}}^{prime\prime}\right|$ respectively. The bipolar subgraph ${\psi }^{\prime}$ is said to be maximum Vertex deleted bipolar fuzzy outerplanar subgraph of $\psi$ if $({a}_{\mathcal{P}}^{\prime}$,${b}_{\mathcal{P}}^{\prime}$)$>({a}_{\mathcal{P}}^{\prime\prime}$,${b}_{\mathcal{P}}^{\prime\prime}$) and $({a}_{\mathcal{N}}^{\prime}$,${b}_{\mathcal{N}}^{\prime}$)$>({a}_{\mathcal{N}}^{\prime\prime}$,${b}_{\mathcal{N}}^{\prime\prime}$). Suppose two Vertex deleted bipolar fuzzy outerplanar subgraphs ${\psi }_{1}$ and ${\psi }_{2}$ are obtained in the bipolar fuzzy graph $\psi$. If ${\psi }_{1}{\ne \psi }_{2}$ but the order and size of two bipolar subgraphs are equal (i.e.),$({a}_{\mathcal{P}}^{\prime}$,${b}_{\mathcal{P}}^{\prime}$)$=({a}_{\mathcal{P}}^{\prime\prime}$,${b}_{\mathcal{P}}^{\prime\prime}$) and $({a}_{\mathcal{N}}^{\prime}$,${b}_{\mathcal{N}}^{\prime}$)$=({a}_{\mathcal{N}}^{\prime\prime}$,${b}_{\mathcal{N}}^{\prime\prime}$), then the two bipolar subgraphs are maximum Vertex deleted bipolar fuzzy outerplanar subgraph of $\psi$.

Example 5.

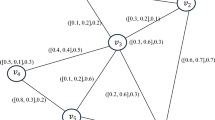
Let’s look at the bipolar fuzzy graph $\psi =({\mathbb{V}},\tau ,\delta )$ shown in Fig. 16. The set of vertices in $\psi$ is ${\mathbb{V}}=\left\{{\mathfrak{v}}_{1},{\mathfrak{v}}_{2},{\mathfrak{v}}_{3},{\mathfrak{v}}_{4},{\mathfrak{v}}_{5},{\mathfrak{v}}_{6}\right\}$ and their membership values of these are as follows: ${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{1}\right)=0.25,{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{1}\right)=-0.3,\;$${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{2}\right)=0.35,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{2}\right)=-0.7,{\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{3}\right)=0.4,{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{3}\right)=-0.5,\;$${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{3}\right)=0.4,{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{3}\right)=-0.5,\;$${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{4}\right)=0.7,{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{4}\right)=-0.8,\;$${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{5}\right)=0.15,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{5}\right)=-0.1,\;$${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{6}\right)=0.45,{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{6}\right)=-0.5\;$ and the edges ${\mathbb{B}}$ is ${\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{1},{\mathfrak{v}}_{2}\right)=0.5,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{1},{\mathfrak{v}}_{2}\right)=-0.6,\;{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{1},{\mathfrak{v}}_{6}\right)=0.1,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{1},{\mathfrak{v}}_{6}\right)=-0.2,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{2},{\mathfrak{v}}_{6}\right)=0.2,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{2},{\mathfrak{v}}_{6}\right)=-0.3,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{4},{\mathfrak{v}}_{6}\right)=0.3,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{4},{\mathfrak{v}}_{6}\right)=-0.6,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{5},{\mathfrak{v}}_{6}\right)=0.7,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{5},{\mathfrak{v}}_{6}\right)=-0.8,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{1},{\mathfrak{v}}_{5}\right)=0.25,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{1},{\mathfrak{v}}_{5}\right)=-0.35,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{2},{\mathfrak{v}}_{3}\right)=0.5,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{2},{\mathfrak{v}}_{3}\right)=-0.6,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{3},{\mathfrak{v}}_{4}\right)=0.4,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{3},{\mathfrak{v}}_{4}\right)=-0.5,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{4},{\mathfrak{v}}_{5}\right)=0.7,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{4},{\mathfrak{v}}_{5}\right)=-0.8.$

Fig. 16

Bipolar fuzzy graph $\psi$.

The vertex deleted of bipolar fuzzy outerplanar subgraphs of $\psi$ are shown in Fig. 17a–f. From the Table 4 note that Fig. 17e is the maximum vertex deleted bipolar fuzzy outerplanar subgraph of $\psi .$

Fig. 17

(a)–(f) Maximum Vertex Deletion bipolar fuzzy outerplanar subgraph.

Table 4 Calculation of order and size of these vertex deletion bipolar fuzzy outerplanar subgraphs.

Theorem 5.

The bipolar fuzzy outerplanar subgraph of Maximum Vertex Deletion has a bipolar fuzzy dual graph, but the converse need not be true.

Proof.

We can easily conclude that maximum Vertex Deletion bipolar fuzzy outerplanar subgraph has a bipolar fuzzy dual and that the converse need not be true based on the proof of Theorem 4.

Definition 18.

The maximal Vertex Deletion bipolar fuzzy outerplanar subgraph of ${\psi }^{\prime}$ is . This is because if a Vertex Deletion bipolar fuzzy outerplanar subgraph ${\psi }^{\prime}=({\mathbb{V}}^{\prime},{\tau }^{\prime},{\delta }^{\prime})$ induced on $\psi$ and all other bipolar subgraphs of $\psi$ induced by the vertex set ${\mathbb{V}}^{\prime\prime}={\mathbb{V}}^{\prime}\cup \left\{\mathfrak{v}\right\}$ (where $\mathfrak{v}\in {\mathbb{V}}\backslash {\mathbb{V}}^{\prime})$ does not satisfy the outerplanarity property.

Theorem 6.

The bipolar fuzzy outerplanar subgraph of each maximum vertex deletion is the maximal vertex deletion bipolar fuzzy outerplanar subgraph of $\psi$.

Proof.

Let ${\psi }^{\prime}$ denote the maximum bipolar fuzzy outerplanar subgraph of $\psi$ resulting from Vertex Deletion. A subset ${\mathbb{W}}\ne \mathbb{\varnothing }\subseteq {\mathbb{V}}$ exists, in which some of the $\psi$ vertices have been deleted. Choose a vertex u in ${\mathbb{W}}$, and consider ${\psi }^{\prime\prime}={\psi }^{\prime}\cup \left\{\mathfrak{u}\right\}$ where ${\psi }^{\prime\prime}=\left\{\mathcalligra{x}\in {\mathbb{V}}^{\prime}\cup \frac{\left\{\mathfrak{u}\right\}}{\mu \left(\mathcalligra{x},\mathcalligra{y}\right)}\ne \mathcal{\varnothing },\mathcalligra{x},\mathcalligra{y}\in {\mathbb{V}}\backslash {\mathbb{W}}\cup \left\{\mathfrak{u}\right\}\right\}$. Since ${\psi }^{\prime}$ is a maximum induced bipolar outerplanar subgraph, adding any of the vertex’s results u in ${f}_{\psi }\ne 1$. Hence, ${\psi }^{\prime}$ is the maximal induced vertex elimination bipolar fuzzy outerplanar subgraph of $\psi$. Therefore, every maximum induced vertex deleted bipolar fuzzy outerplanar graph is a maximal induced vertex deleted bipolar fuzzy outerplanar subgraph of $\psi$.

Theorem 7.

The answer to Theorem 6 is not necessarily true.

Proof.

Let $\psi$ be the bipolar fuzzy graph with ${\mathfrak{f}}_{\psi }\ne 1$ and, ${\psi }^{\prime}$ and ${\psi }^{\prime\prime}$ are the Vertex Deletion bipolar fuzzy outerplanar subgraphs of $\psi$. Let ${\mathbb{W}}_{1}$,${\mathbb{W}}_{2}$ be the subsets of vertex set ${\mathbb{V}}$ in $\psi . {\mathbb{W}}_{1}$ and ${\mathbb{W}}_{2}$ contains the deleted vertices from $\psi$ respectively. Then ${\psi }^{\prime}$ and ${\psi }^{\prime\prime}$ are said to be maximal bipolar fuzzy outerplanar subgraph if ${\psi }^{\prime}\cup \left\{\mathfrak{u}\right\}$ where $\mathfrak{u}\in {\mathbb{W}}_{1}$ and ${\psi }^{\prime\prime}\cup \left\{\mathfrak{v}\right\}$ where $\mathfrak{v}\in {\mathbb{W}}_{2}$ are bipolar fuzzy non outerplanar.

Consequently, these bipolar subgraphs are considered bipolar fuzzy outerplanar subgraphs with maximal vertex deletion of $\psi$. However, since fuzzy bipolar subgraphs can vary in order and size, a vertex deletion bipolar fuzzy outerplanar subgraph is defined as a maximal vertex deletion bipolar fuzzy outer subgraph that has the highest order and size. Thus, either ${\psi }^{\prime}$ or ${\psi }^{\prime\prime}$ qualifies as a maximal vertex deletion bipolar fuzzy outerplanar subgraph, but both bipolar fuzzy graphs are maximal. As a result, the bipolar fuzzy outerplanar subgraph of any maximal vertex deletion does not necessarily have to be a maximum vertex deletion bipolar fuzzy outerplanar subgraph.

Note 3.

Only when both bipolar subgraphs are maximum vertex Deletion bipolar fuzzy outerplanar subgraphs as defined by Note 2 are two Vertex Deletion bipolar fuzzy outerplanar subgraphs maximal.

Example 6.

Let’s look at the bipolar fuzzy graph $\psi =({\mathbb{V}},\tau ,\delta )$ shown in Fig. 18. The set of vertices in $\psi$ is ${\mathbb{V}}=\left\{{\mathfrak{v}}_{1},{\mathfrak{v}}_{2},{\mathfrak{v}}_{3},{\mathfrak{v}}_{4},{\mathfrak{v}}_{5},{\mathfrak{v}}_{6}\right\}$ and their membership values of these are as follows: ${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{1}\right)=0.35,,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{1}\right)=-0.7,$${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{2}\right)=0.45,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{2}\right)=-0.9,\;$${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{3}\right)=0.5,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{3}\right)=-0.6,\;$${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{4}\right)=0.7,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{4}\right)=-0.8,\;$${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{5}\right)=0.15,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{5}\right)=-0.2\;$ and the edges ${\mathbb{B}}$ is ${\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{1},{\mathfrak{v}}_{5}\right)=0.15,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{1},{\mathfrak{v}}_{5}\right)=-0.25,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{2},{\mathfrak{v}}_{5}\right)=0.7,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{2},{\mathfrak{v}}_{5}\right)=-0.8,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{3},{\mathfrak{v}}_{5}\right)=0.17,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{3},{\mathfrak{v}}_{5}\right)=-0.18,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{4},{\mathfrak{v}}_{5}\right)=0.6,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{4},{\mathfrak{v}}_{5}\right)=-0.7,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{1},{\mathfrak{v}}_{2}\right)=0.1,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{1},{\mathfrak{v}}_{2}\right)=-0.2,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{2},{\mathfrak{v}}_{3}\right)=0.2,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{2},{\mathfrak{v}}_{3}\right)=-0.3,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{3},{\mathfrak{v}}_{4}\right)=0.3,\;$ ${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{3},{\mathfrak{v}}_{4}\right)=-0.2,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{4},{\mathfrak{v}}_{1}\right)=0.2,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{4},{\mathfrak{v}}_{1}\right)=-0.3.$

Fig. 18

Bipolar fuzzy graph $\psi$.

All the graphs in Fig. 19a–e are maximal bipolar fuzzy outerplanar subgraph of $\psi$. But Fig. 19a is the maximum bipolar fuzzy outerplanar subgraph of $\psi$ in the Table 5. Then it can be observed that maximal bipolar fuzzy outerplanar subgraph need not be maximum bipolar fuzzy outerplanar subgraph of $\psi$.

Fig. 19

(a)–(e) Maximal vertex deletion bipolar fuzzy outerplanar subgraphs.

Table 5 Calculation of order and size of these vertex deletion bipolar fuzzy outerplanar subgraphs.

Edge deletion bipolar fuzzy outerplanar subgraphs

In this section, discussed the subgraph created by deleting specific edges from the bipolar fuzzy graph, while also defining bipolar fuzzy outerplanar graphs and providing relevant illustrations.

Definition 19.

If $\psi$ is a bipolar fuzzy planar graph and ${\psi }^{\prime}$ is its Edge Deletion bipolar fuzzy subgraph, then ${\psi }^{\prime}$ is the Edge Deletion bipolar fuzzy outerplanar subgraph of $\psi$ if and only if it preserves a bipolar fuzzy outerplanar.

Note 4.

There is no need for an edge deletion bipolar fuzzy outerplanar subgraph of $\psi$ to be an edge deletion bipolar fuzzy subgraph of $\psi$.

Theorem 8.

In a bipolar fuzzy outerplanar graph $\psi$, every Edge Deletion bipolar fuzzy subgraph is always an Edge Deletion bipolar fuzzy outerplanar subgraph of $\psi$.

Proof.

Let $\psi$ be a bipolar fuzzy outerplanar graph and let ${\mathbb{H}}$ be an edge deletion bipolar fuzzy subgraph of $\psi$. Since a bipolar fuzzy graph $\psi$ is outerplanar, all its vertices will be in the outer region. Thus, the subgraph obtained by edge deletion still possess outerplanarity property. Therefore, any edge-deleted bipolar fuzzy subgraphs in $\psi$ are edge-deleted bipolar fuzzy outerplanar subgraphs of $\psi$.

Theorem 9.

Let ${\mathbb{W}}$ be the subset of edges of a connected bipolar fuzzy outerplanar graph such that ${\mathbb{W}}\subseteq {\mathbb{E}}$. If ${\psi }^{\prime}$ is an edge deletion bipolar fuzzy outerplanar subgraph of $\psi$ if the resulting graph connects ${\psi }^{\prime}$ to the bipolar fuzzy dual graph.

Proof.

By using the same proof as Theorem 5 and which is obviously true for the case of edges.

Example 7.

Let’s look at the bipolar fuzzy graph $\psi =({\mathbb{V}},\tau ,\delta )$ shown in Fig. 20a. The set of vertices in $\psi$ is ${\mathbb{V}}=\left\{{\mathfrak{v}}_{1},{\mathfrak{v}}_{2},{\mathfrak{v}}_{3},{\mathfrak{v}}_{4},{\mathfrak{v}}_{5},{\mathfrak{v}}_{6},{\mathfrak{v}}_{7},{\mathfrak{v}}_{8},{\mathfrak{v}}_{9}\right\}$ and their membership values of these are as follows: ${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{1}\right)=0.2,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{1}\right)=-0.1,\;$${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{2}\right)=0.3,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{2}\right)=-0.2,\;$${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{3}\right)=0.4,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{3}\right)=-0.3,\;$${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{4}\right)=0.5,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{4}\right)=-0.4,$${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{5}\right)=0.6,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{5}\right)=-0.5,\;$ ${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{6}\right)=0.9\;,{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{6}\right)=-0.8,\;$ ${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{7}\right)=0.3\;,{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{7}\right)=-0.6,\;$ ${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{8}\right)=0.5,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{8}\right)=-0.4,\;$ ${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{9}\right)=0.8,{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{9}\right)=-0.9\;$ and the edges ${\mathbb{B}}$ is ${\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{1},{\mathfrak{v}}_{2}\right)=0.1,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{1},{\mathfrak{v}}_{2}\right)=-0.1,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{1},{\mathfrak{v}}_{4}\right)=0.6,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{1},{\mathfrak{v}}_{4}\right)=-0.3,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{1},{\mathfrak{v}}_{5}\right)=0.3,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{1},{\mathfrak{v}}_{5}\right)=-0.6,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{2},{\mathfrak{v}}_{3}\right)=0.2,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{2},{\mathfrak{v}}_{3}\right)=-0.3,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{3},{\mathfrak{v}}_{4}\right)=0.4,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{3},{\mathfrak{v}}_{4}\right)=-0.6,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{4},{\mathfrak{v}}_{5}\right)=0.4,\;$ ${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{4},{\mathfrak{v}}_{5}\right)=-0.5,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{2},{\mathfrak{v}}_{5}\right)=0.7,\;$;${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{2},{\mathfrak{v}}_{5}\right)=-0.4,{\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{5},{\mathfrak{v}}_{7}\right)=0.1,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{5},{\mathfrak{v}}_{7}\right)=-0.1,\;$ ${\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{6},{\mathfrak{v}}_{7}\right)=0.3,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{6},{\mathfrak{v}}_{7}\right)=-0.5,\;$${\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{7},{\mathfrak{v}}_{8}\right)=0.2,\;$ ${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{7},{\mathfrak{v}}_{8}\right)=-0.4,\;$ ${\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{6},{\mathfrak{v}}_{9}\right)=0.3,\;$ ${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{6},{\mathfrak{v}}_{9}\right)=-0.6,\;$${\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{7},{\mathfrak{v}}_{9}\right)=0.4,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{7},{\mathfrak{v}}_{9}\right)=-0.5,\;$${\delta }^{\mathcal{P}}\left({\mathfrak{v}}_{8},{\mathfrak{v}}_{9}\right)=0.6,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{v}}_{8},{\mathfrak{v}}_{9}\right)=-0.3,\;$

Fig. 20

(a) Bipolar fuzzy graph. (b) Bipolar fuzzy edge contraction. (c) Edge deleted bipolar fuzzy outerplanar graph.

Let $\psi$ be the bipolar fuzzy graph. then the edge contracted bipolar fuzzy graph, denoted as $\psi \backslash {\mathfrak{v}}_{5}{\mathfrak{v}}_{7}$ derived from the bipolar fuzzy graph $\psi =(\tau ,\delta )$ by contracting the edge ${\mathfrak{v}}_{5}{\mathfrak{v}}_{7}$. In this Fig. 20b the vertex set ${\mathbb{V}}^{\prime}=\left\{\frac{\mathbb{V}}{\left\{{\mathfrak{v}}_{5},{\mathfrak{v}}_{7}\right\}}\cup \left\{\mathfrak{w}\right\}\right],$ where $\left({\mu }_{{\mathring{\rm A}}}^{\mathcal{P}},{\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}\right)\left(\frac{\psi }{{\mathfrak{v}}_{5}{\mathfrak{v}}_{7}}\right)=\left({\mu }_{{\mathring{\rm A}}}^{\mathcal{P}},{\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}\right)(\psi )$ for all vertices $\mathcalligra{x}\in {\mathbb{V}}.$ The membership value $\tau$ of $\psi /{\mathfrak{v}}_{5}{\mathfrak{v}}_{7}$ remains the same as $\tau$ in $\psi$ for all vertices $\mathcalligra{x}\in {\mathbb{V}},$ and the membership value of $\mathfrak{w}$ is calculated by ${\left({\mu }_{\mathcal{B}}^{\mathcal{P}}\right)}_{\frac{\psi }{{\mathfrak{v}}_{5}{\mathfrak{v}}_{7}}}\left(\mathcalligra{x}\mathcalligra{y}\right)=\text{min}\{{\mu }_{{\mathring{\rm A}}}^{\mathcal{P}}(\mathcalligra{x}),{\mu }_{{\mathring{\rm A}}}^{\mathcal{P}}(w))\}, \left(\mathcalligra{x}\mathcalligra{y}\right)=\text{max}\{{\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}(\mathcalligra{x}),{\mu }_{{\mathring{\rm A}}}^{\mathcal{N}}(w))\}.$ The adjacency between two vertices $\mathcalligra{x}$ and $\mathcalligra{y}$ in $\psi /{\mathfrak{v}}_{5}{\mathfrak{v}}_{7}$ is determined by Definition (11) conditions.

The edge contracted bipolar fuzzy graph $\psi \backslash {\mathfrak{v}}_{5}{\mathfrak{v}}_{7}$ $,$ represented as ${\psi }_{1}$ can be seen in Fig. 20b. Similarly, the bipolar fuzzy graph ${\psi }_{1 }-\text{V}$ represented as ${\psi }_{2}$ is shown in Fig. 20c. It can be noted that, is categorized as a Vertex Deletion bipolar fuzzy outerplanar graph.

Maximum and maximal edge deletion bipolar fuzzy outerplanar subgraph

In this section, outlined the concepts of maximum and maximal edge deletion bipolar fuzzy outerplanar subgraphs and investigates the relationship between these two concepts, illustrated with suitable examples.

Definition 20.

Maximum ED- bipolar fuzzy outerplanar subgraph.

If ${\psi }^{\prime}=({\mathbb{V}}^{\prime},{\tau }^{\prime},{\delta }^{\prime})$ with positive and negative size ${b}^{\prime}=\left({b}_{\mathcal{P}}^{\prime},{b}_{\mathcal{N}}^{\prime}\right)$ is the Edge Deletion bipolar fuzzy outerplanar subgraph of non-outerplanar bipolar fuzzy graph $\psi =({\mathbb{V}},\tau ,\delta )$ such that there is no other Edge Deletion bipolar fuzzy outerplanar subgraph ${\psi }^{\prime\prime}$ of size $,{b}^{\prime\prime}=\left({b}_{\mathcal{P}}^{\prime\prime},{b}_{\mathcal{N}}^{\prime\prime}\right)$ of $\psi$ such that ${\dot{b}}^{\prime\prime}>{\dot{b}}^{\prime}$, then ${\psi }^{\prime}$ is the maximum bipolar fuzzy outerplanar subgraph of $\psi .$

Note 5

Suppose two Edge Deletion bipolar fuzzy outerplanar subgraphs ${\psi }_{1}$ and ${\psi }_{2}$ is obtained from the bipolar fuzzy graph $\psi$.If the sizes of the two bipolar subgraphs are equal but ${\psi }_{1}{\ne \psi }_{2}$. (i.e.)${\dot{b}}^{\prime}={\dot{b}}^{\prime\prime}$, then the two bipolar subgraphs are maximum Edge Deletion bipolar fuzzy outerplanar subgraphs of $\psi .$ This means that there is no unique maximum edge deletion bipolar fuzzy outerplanar subgraph of $\psi$.

Example 8

Let’s look at the bipolar fuzzy graph $\psi =({\mathbb{V}},\tau ,\delta )$ shown in Fig. 21a. The set of vertices in $\psi$ is ${\mathbb{V}}=\left\{{\mathfrak{v}}_{1},{\mathfrak{v}}_{2},{\mathfrak{v}}_{3},{\mathfrak{v}}_{4},{\mathfrak{v}}_{5},{\mathfrak{v}}_{6}\right\}$ and their membership values of these are as follows: ${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{1}\right)=0.33,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{1}\right)=-0.1,$ ${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{2}\right)=0.15,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{2}\right)=-0.1,$ ${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{3}\right)=0.25,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{3}\right)=-0.2,\;$ ${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{4}\right)=0.6,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{4}\right)=-0.1,\;$${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{5}\right)=0.5,\;{\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{5}\right)=-0.1,\;$${\tau }^{\mathcal{P}}\left({\mathfrak{v}}_{6}\right)=0.7,{\;\tau }^{\mathcal{N}}\left({\mathfrak{v}}_{6}\right)=-0.1\;$ and the edges ${\mathbb{B}}$ is ${\delta }^{\mathcal{P}}\left({\mathfrak{e}}_{1}\right)=0.15,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{e}}_{1}\right)=-0.1,\;$${\delta }^{\mathcal{P}}\left({\mathfrak{e}}_{2}\right)=0.35,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{e}}_{2}\right)=-0.2,\;$${\delta }^{\mathcal{P}}\left({\mathfrak{e}}_{3}\right)=0.55,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{e}}_{3}\right)=-0.3,\;$${\delta }^{\mathcal{P}}\left({\mathfrak{e}}_{4}\right)=0.25,\;$${\delta }^{\mathcal{N}}\left({\mathfrak{e}}_{4}\right)=-0.1,\;$${\delta }^{\mathcal{P}}\left({\mathfrak{e}}_{5}\right)=0.55.\;$${\delta }^{\mathcal{N}}\left({\mathfrak{e}}_{5}\right)=-0.2,{\delta }^{\mathcal{P}}\left({\mathfrak{e}}_{6}\right)=0.3.\;$${\delta }^{\mathcal{N}}\left({\mathfrak{e}}_{6}\right)=-0.1,{\delta }^{\mathcal{P}}\left({\mathfrak{e}}_{7}\right)=0.8.\;$${\delta }^{\mathcal{N}}\left({\mathfrak{e}}_{7}\right)=-0.3,{\delta }^{\mathcal{P}}\left({\mathfrak{e}}_{8}\right)=0.5.\;$${\delta }^{\mathcal{N}}\left({\mathfrak{e}}_{8}\right)=-0.1,{\delta }^{\mathcal{P}}\left({\mathfrak{e}}_{9}\right)=0.5.\;$${\delta }^{\mathcal{N}}\left({\mathfrak{e}}_{9}\right)=-0.1,{\delta }^{\mathcal{P}}\left({\mathfrak{e}}_{10}\right)=0.65.\;$${\delta }^{\mathcal{N}}\left({\mathfrak{e}}_{10}\right)=-0.2,{\delta }^{\mathcal{P}}\left({\mathfrak{e}}_{11}\right)=0.2.\;$${\delta }^{\mathcal{N}}\left({\mathfrak{e}}_{11}\right)=-0.1.$

Fig. 21

(a). Bipolar fuzzy graphs $\psi$. (b). Maximum and maximal Edge Deletion from a bipolar fuzzy subgraph of $\psi .$

In Fig. 21b, the maximal Edge deleted bipolar fuzzy outerplanar subgraph are shown. Thus, a result, $\psi -{\mathbb{U}}$ is the greatest Edge Deleted bipolar fuzzy outerplanar subgraph of $\psi$, and bipolar fuzzy subgraph is maximal.

The following section an application of bipolar fuzzy outerplanar graphs in image shrinking is demonstrated.

Application of bipolar fuzzy outerplanar graph in image shrinking

Image segmentation plays a vital role in dividing digital images into distinct parts or segments, which is essential for recognizing objects within those images. This process is particularly useful in areas such as computer vision and remote sensing. The primary objective of image segmentation is to extract specific objects of interest from the background, allowing for more focused analysis. Different methods can be employed for segmenting images. One such approach involves using Bipolar Fuzzy Outerplanar Graphs to facilitate image shrinking by segmenting various regions of an image. In this context, an image is composed of pixels, which can be grouped into homogeneous sections. Each pixel can be represented as a vertex in a graph, where its membership value either positive or negative is determined by its intensity. Overall, image segmentation serves as a foundational technique in digital image processing, enabling the identification and isolation of relevant features within an image through various methodologies.

Two adjacent pixels (vertices) are connected by edges. The positive membership value (or negative membership value) of an edge is determined by the dissimilarity (or similarity) value of the corresponding pixels (vertices). There are several methods to measure the dissimilarity or similarity between two pixels, and one of these methods is used to determine the edge membership values. Consequently, the entire image (see Fig. 22 as an example) is transformed into a Bipolar fuzzy graph (see Fig. 23), where each coloured vertex represents a corresponding segmented coloured section of the image from Fig. 22. The edge membership values for the graph shown in Fig. 23 are listed in Table 6. Clearly, this graph is a Bipolar fuzzy non outerplanar graph. Moreover, A bipolar fuzzy graph that cannot be embedded in the plane so that each vertex lies on the exterior region’s boundary. The Bipolar fuzzy dual graph of this Bipolar fuzzy outerplanar graph can be drawn using the method described (see Fig. 24). The face and edge membership values of the Bipolar fuzzy dual graphs shown in Fig. 24 are provided in Table 7. Now, we define related terms such as edge shrinking and kernel shrinking.

Fig. 22

An example of colour image for image shrinking.

Fig. 23

Bipolar fuzzy non-outerplanar graph corresponding to the image.

Table 6 The edge membership values associated with the edges in the graph shown in Fig. 22b.

Fig. 24

Corresponding Bipolar fuzzy dual graph of the Bipolar fuzzy non outerplanar graph.

Table 7 Faces and edge membership values in the bipolar fuzzy dual graph shown in Fig. 24.

Let $\psi =({\mathring{\rm A}},\mathcal{B})$ represent a bipolar fuzzy graph and consider an edge $(\mathfrak{a},\mathfrak{b})$. When this edge is shrunk, a new vertex, denoted as $\mathfrak{c}$, is created. This new vertex $\mathfrak{c}$ will have all the edges that were previously connected to vertices $\mathfrak{a}$ and $\mathfrak{b}$ now connected to it, while the edge $(\mathfrak{a},\mathfrak{b})$ is removed from the graph. The positive membership value for vertex $\mathfrak{c}$ is defined as ${\tau }^{\mathcal{P}}\left(\mathfrak{c}\right)=$ max $\{{\tau }^{\mathcal{P}}\left(\mathfrak{a}\right)$, ${\tau }^{\mathcal{P}}\left(\mathfrak{b}\right)\}$. Similarly, the negative membership value for vertex $\mathfrak{c}$ is given by ${\tau }^{\mathcal{N}}\left(\mathfrak{c}\right)=$ max $\{{\tau }^{\mathcal{N}}\left(\mathfrak{a}\right)$, ${\tau }^{\mathcal{N}}\left(\mathfrak{b}\right)\}$.

When multiple vertices are shrunk simultaneously, an extended shrinking technique known as kernel shrinking is applied. For instance, if the edges (${\mathfrak{v}}_{2},{\mathfrak{v}}_{6}),({\mathfrak{v}}_{4},{\mathfrak{v}}_{6})$ are to be shrunk at the same time, we denote the vertices involved as ${\mathfrak{v}}_{2},{\mathfrak{v}}_{4}$ and ${\mathfrak{v}}_{6}$ with their respective membership values defined as ${\tau }^{\mathcal{P}}\left(\mathfrak{i}\right)={\mathfrak{m}}_{\mathfrak{i}}, {\tau }^{\mathcal{N}}\left(\mathfrak{i}\right)={\mathfrak{n}}_{\mathfrak{i}}$. In this case, all these edges are merged into a single vertex, referred to as $\mathfrak{h}$. The positive membership value of vertex $\mathfrak{h}$ is determined max $\{{\mathfrak{m}}_{\mathfrak{i}},\mathfrak{i}={\mathfrak{v}}_{2},{\mathfrak{v}}_{4}\}$, while the negative membership value is given by max $\{{\mathfrak{n}}_{\mathfrak{i}},\mathfrak{i}={\mathfrak{v}}_{2},{\mathfrak{v}}_{4}\}$. It is important to note that the vertices ${\mathfrak{v}}_{2}$ and ${\mathfrak{v}}_{4}$ are combined into the new vertex $\mathfrak{h}$.

A collection of homogeneous pixels constitutes a homogeneous section. Two pixels or two homogeneous sections are considered nearly homogeneous if the difference in their membership values is less than a specified positive threshold. These nearly homogeneous sections undergo a process of shrinking at various levels, with each level derived from the previous one. As illustrated in Fig. 23, an image is segmented into distinct regions, each defined by boundaries. In the context of Bipolar fuzzy dual graphs, these edges represent the boundaries of the images.

Consider a bipolar fuzzy non outerplanar graph $\psi =({\mathbb{V}},{\mathring{\rm A}},\mathcal{B})$ as shown in Fig. 24 where ${\mathbb{V}}=\{{\mathfrak{v}}_{1},{\mathfrak{v}}_{2},{\mathfrak{v}}_{3},{\mathfrak{v}}_{4},{\mathfrak{v}}_{5},{\mathfrak{v}}_{6}\}$, ${\mathring{\rm A}}=\{({\mathfrak{v}}_{1}$, (0.3, −0.5)), (${\mathfrak{v}}_{2}$, (0.4, −0.6)), $({\mathfrak{v}}_{3}$, (0.6, −0.7)), $({\mathfrak{v}}_{4}$, (0.5, −0.8)), ${(\mathfrak{v}}_{5}$, (0.7, −0.9)), $({\mathfrak{v}}_{6}$, (0.5, −0.7))}, and $\mathcal{B}=\{(\left({\mathfrak{v}}_{1},{\mathfrak{v}}_{2}\right),\left(0.2,-0.2\right))$, ((${\mathfrak{v}}_{2},{\mathfrak{v}}_{3}),\left(0.3,-0.3\right)$,(( ${\mathfrak{v}}_{3},{\mathfrak{v}}_{4}),(0.1,-0.1)$), ((${\mathfrak{v}}_{4},{\mathfrak{v}}_{5})),\left(0.4,-0.4\right)$, ((${\mathfrak{v}}_{2},{\mathfrak{v}}_{5}),\left(0.3,-0.4\right))$, ((${\mathfrak{v}}_{2},{\mathfrak{v}}_{6}),\left(0.2,-0.3\right))$, ((${\mathfrak{v}}_{4},{\mathfrak{v}}_{6}),\left(0.4,-0.5\right)$ . The bipolar fuzzy non outerplanar graph has the following faces:

• (i) Bipolar fuzzy face ${\mathfrak{f}}_{1}$ is bounded by ((${\mathfrak{v}}_{2},{\mathfrak{v}}_{6}),\left(0.2,-0.3\right))$, ((${\mathfrak{v}}_{4},{\mathfrak{v}}_{6}),\left(0.4,-0.5\right)$, ((${\mathfrak{v}}_{2},{\mathfrak{v}}_{5}),\left(0.3,-0.4\right))$, ((${\mathfrak{v}}_{4},{\mathfrak{v}}_{5})),\left(0.4,-0.4\right),$

• (ii) Bipolar fuzzy face ${\mathfrak{f}}_{2}$ is bounded by ((${\mathfrak{v}}_{2},{\mathfrak{v}}_{6}),\left(0.2,-0.3\right))$, ((${\mathfrak{v}}_{4},{\mathfrak{v}}_{6}),\left(0.4,-0.5\right)$, ((${\mathfrak{v}}_{2},{\mathfrak{v}}_{3}),\left(0.3,-0.3\right)$,(( ${\mathfrak{v}}_{3},{\mathfrak{v}}_{4}),(0.1,-0.1)$),

• (iii) The outer bipolar fuzzy face ${\mathfrak{f}}_{3}$ is surrounded by ((${\mathfrak{v}}_{2},{\mathfrak{v}}_{5}),\left(0.3,-0.4\right))$, ((${\mathfrak{v}}_{4},{\mathfrak{v}}_{5})),\left(0.4,-0.4\right)$, ((${\mathfrak{v}}_{2},{\mathfrak{v}}_{3}),\left(0.3,-0.3\right)$,(( ${\mathfrak{v}}_{3},{\mathfrak{v}}_{4}),(0.1,-0.1)$), $(\left({\mathfrak{v}}_{1},{\mathfrak{v}}_{2}\right),\left(0.2,-0.2\right))$.

The bipolar fuzzy faces ${\mathfrak{f}}_{1}$, ${\mathfrak{f}}_{2}$ and ${\mathfrak{f}}_{3}$ are ($0.5,-0.5)$, ($0.2,-0.14)$ and ($0.2,-0.14).$ Then bipolar fuzzy faces as shown in the Fig. 25. Now it’s a Bipolar fuzzy outerplanar graph.

Fig. 25

Bipolar fuzzy faces but bipolar fuzzy outerplanar graph.

In stage 1 of the image pyramid shown in the Fig. 26, each pixel is treated as a vertex. Two adjacent pixels or regions that are homogeneous or nearly homogeneous are combined into a single section. This is achieved through edge or kernel shrinking on the Bipolar Fuzzy graph. As part of this process, the corresponding edges in the dual graph are also removed. The resulting shrunk image appears at the top stage of the pyramid.

Fig. 26

Image Shrinking of the image into image pyramid.

Bipolar fuzzy outerplanar graphs can be effectively utilized in image shrinking processes. By transforming a bipolar fuzzy non-outerplanar graph into a bipolar fuzzy dual graph, it becomes a bipolar fuzzy outerplanar graph. This transformation enables the use of the unique properties of bipolar fuzzy outerplanar graphs to reduce the image size efficiently. This approach maintains essential image features and structures while minimizing storage requirements. The bipolar fuzzy attributes provide a nuanced handling of image data, accounting for various levels of uncertainty and bipolarity in pixel values, resulting in high-quality, compressed images suitable for efficient storage and transmission.

Conclusion

In this paper, we introduced the concept of bipolar fuzzy outerplanar graphs and explored their various properties and characteristics. We demonstrated how subgraphs of bipolar fuzzy outerplanar graphs can be identified by the strategic removal of vertices or edges. Our analysis included a detailed examination of both maximum and maximal bipolar fuzzy outerplanar subgraphs, considered vertex and edge deletions, and provided illustrative examples to support our findings. Additionally, we delved into the properties of bipolar fuzzy dual graphs, which are closely related to bipolar fuzzy outerplanar graphs, and provided insights into their significance. By expanding the theoretical knowledge and practical utility of bipolar fuzzy outerplanar graphs, this research sets a foundation for continued exploration and innovation in the broader field of fuzzy graph theory. To conclude, we showcased the application of bipolar fuzzy outerplanar graphs in the process of image shrinking. These theories have the potential to enhance algorithms across various domains, including computer vision and image segmentation. The concept can also be expanded to other types of fuzzy graphs, such as interval-valued fuzzy outerplanar graphs and m-polar fuzzy outerplanar graphs. Currently, our focus is on developing interval-valued fuzzy outerplanar graphs.