Introduction

Yarn serves as a fundamental component in the production of most textile products. Spun yarns are created by grouping individual fibres into a continuous strand, typically held together through twisting. The term “staple yarn manufacturing” refers to the processes involved in producing this type of yarn. All natural fibres, including cotton, wool, and waste silk (excluding continuous filament silk), exist in the form of staple fibres. Similarly, most synthetic fibres, such as polyester, acrylic, and viscose, are also produced as staple fibres1. The quality of yarn is largely determined during the stages preceding the final production step, including blow room, carding, drawing, and speed frame. Collectively referred to as the spinning preparation process, these stages are critical to ensuring overall yarn quality. The quality of the roving and sliver produced during these processes is pivotal for achieving a high-quality final yarn2. Numerous variables, known as spinning preparation variables, influence yarn quality before the final production stage. These variables play a critical role in determining the quality of the resulting yarn. Due to the large number and varying levels of these variables, traditional trial-and-error methods for optimization are often time-consuming and costly. Consequently, researchers in recent years have increasingly adopted systematic approaches for modeling and optimization to enhance efficiency and accuracy.

In systematic research methodology, the Design of Experiments (DOE) provides a structured and rigorous approach to conducting experiments. It allows researchers to establish statistical and computational relationships between process input variables and the corresponding output responses, facilitating more efficient and precise analysis3. This technique encompasses various subsets and experimental designs, including full factorial design, Taguchi design, and the Response Surface Method (RSM)4. In the field of modeling and optimization of process variables, research has been conducted not only on systems related to the final stages of yarn production, such as ring, rotor, and jet-ring spinning, but also on the spinning preparation stages, utilizing Design of Experiments (DOE)5,6,7. For instance, Das et al.. conducted a study to optimize fiber friction as a material variable, along with front top roller pressure and gauge roller as machine variables, in the drawing frame, speed frame, and ring frame using the RSM8. RSM is a statistical and mathematical approach used to improve, adjust, and optimize processes, including yarn spinning9. In another study, Ishtiaque et al.. investigated the effect of high-speed drawing frame variables and their preparation on the packing density and quality properties of ring-spun yarns using the Box-Behnken design (BBD), a subset of RSM. The variables they examined included the breaker drawing frame delivery speed, coiler diameter of the card, and the card draft10,11. Similarly, Abdul Jabbar et al.. examined the effect of carding cylinder speed, carding production rate, and the number of drawing frame doublings on cotton yarn quality using the BBD12. In another study, Karthik and Murugan optimized the variables of the speed frame and ring frame using the BBD to improve the quality of blended cotton-milkweed yarn13. Singh et al.. also employed the BBD to investigate the effect of spring stiffness, delivery rate, and sliver coil position in the finisher drawing frame on cotton yarn quality14. Additionally, Al-Khateeb studied the effect of blow room machine process parameters on the openness degree of cotton fibres using the RSM and BBD15. Khurshid et al.. further applied the RSM and BBD to investigate the systematic effect of carding machine parameters on fiber orientation, fiber length, and sliver cohesion force16. Mebrat took a different approach, using a factorial optimization design to investigate the effect of carding machine parameters on the properties of cotton yarn17. Salhotra, Ishtiaque, and Kumar analyzed various spinning process variables, including lap hank, card draft, and draft/doubling, to evaluate their impact on the structural and physical properties of ring, rotor, and air-jet yarns using the Taguchi method18,19,20. The Taguchi method employed in these studies utilizes the signal-to-noise ratio (S/N) to measure the magnitude of changes in a product, reflecting the sensitivity of the product’s quality characteristics to external, uncontrollable factors in the manufacturing process21. More recently, Goyal et al.. investigated the effect of drafting zone variables in the speed frame on the strength and elongation of cotton yarn using the Taguchi design22. Although the Taguchi method allows optimization with a minimal number of experiments, it is limited to single-objective optimization and is not suitable for multi-objective optimization problems23.

In recent years, artificial intelligence (AI) and soft computing methods have been widely applied in systematic engineering studies, particularly in yarn spinning. Despite their computational complexity, these methods offer high capability in modeling and optimization. Artificial Neural Networks (ANNs) are computational models inspired by the human brain’s interconnected neurons. They excel at predicting complex, nonlinear patterns, making them useful for real-world problems. ANNs can also generalize, allowing them to provide accurate results even for unseen data24. In the spinning process, particularly in the preparation stages, researchers have explored the use of ANNs to optimize and predict key outcomes. In this regard, Farooq and Cherif modelled the quality characteristics of sliver output from the drawing frame and ring-spun yarn using ANN, with drawing machine parameters as inputs. Their results highlighted the robust performance of ANN in predicting the quality of silver and yarn. They also used ANN to identify correlations between key variables and optimal settings in the drawing frame25,26,27. Abd-ellatif applied ANN to predict the optimal Leveling Action Point (LAP) under various production conditions, comparing its performance to a regression model. The study demonstrated that ANN significantly outperformed the regression model in optimizing auto-leveling parameters28. Similarly, Erbil et al.. employed ANN and regression models to predict the tensile properties of polyester, viscose, and acrylic blended yarns, using blending methods and the number of drawing passages as input variables. ANN outperformed the regression model, particularly in predicting yarn elongation29. Jiang et al. developed a deep neural network model, the Broad Multilayer Neural Network (BMNN), to predict yarn unevenness using parameters from the carding stage to ring spinning30. Zhang et al.. further advanced prediction techniques by using an expert-weighted neural network optimized with a particle swarm optimization (PSO) algorithm to predict yarn strength31. Despite its relatively low contribution to the overall cost of yarn (less than 3%), the drawing frame significantly impacts yarn quality, especially in terms of unevenness and imperfections32. Yarn unevenness refers to variations in yarn thickness or weight per unit length, while the imperfection index measures thin places, thick places, and neps. These imperfections affect the visual and physical quality of textiles, such as fabrics and garments33,34,35. The drawing frame is a critical compensation point in the spinning mill sequence, where errors can be corrected before they propagate through subsequent stages, including the speed frame and ring frame. Errors in drafting at this stage are amplified in later stages, making the proper adjustment of drawing frame parameters crucial. High-performance drawing frames, capable of producing over 400 kg of sliver per hour, underscore the need for robust, systematic approaches to parameter optimization, as even minor defects can result in significant quantities of defective sliver36. The primary focus in the drawing frame is often on fine-tuning the drafting system to enhance quality, with adjustments tailored to the type of fiber being processed37. This systematic and reliable optimization ensures that yarn quality meets the desired standards, minimizing imperfections and improving overall production efficiency.

Most previous efforts to optimize spinning preparation variables and model yarn properties have focused primarily on predicting the quality of cotton yarns and blends with other fibres, such as polyester or viscose. Consequently, there has been less emphasis on analyzing yarns produced from 100% polyester. Polyester, a widely used synthetic fiber, is valued for its durability and versatility in various textile applications. Additionally, studies in this field, particularly those employing soft computing and AI techniques, have predominantly concentrated on predicting the properties of produced sliver and yarn, with fewer investigations addressing the precise optimization of the process due to the complexity of setting variables. While some studies have utilized ANN to identify optimal settings, it is important to recognize that ANN is primarily a predictive tool. For optimization tasks, other AI and soft computing methods, such as genetic algorithm (GA), are more appropriate. GA is a popular optimization method that finds the best solution by creating and evolving possible solutions, called chromosomes, through processes like crossover and mutation38,39. This study addresses a multi-objective optimization problem in a drawing frame used in a polyester spun yarn production line. The aim is to minimize the unevenness percentage (CVm%) and imperfection index (IPI) using a hybrid model. The drafting zone settings are the heart of the drawing frame, as the variables in this zone play a more crucial role than other factors such as the number of doublings, delivery rate, and similar parameters31. Since systematic studies aimed at improving process performance prioritize the most influential parameters, this study specifically focused on the variables within the drafting zone, including break draft, total draft, back roller gauge, and front roller gauge. A systematic and structured approach was employed, involving experimental trials designed using RSM. The resulting dataset was used to develop two RSM models based on second-order polynomial regression and two ANN models. The performance of each model will be evaluated to identify the most effective one for coupling with the GA during the optimization stage, ensuring the achievement of optimal results.

Data collection

Experimental design

A structured investigation was carried out to examine the influence of multiple independent variables on various dependent outcomes. In many engineering contexts, analyzing all possible combinations of independent variables, known as a full factorial design, can be impractical or challenging, particularly when numerous variables and levels are involved. To address this, the RSM is employed to minimize the number of experiments needed40. In this study, a quadratic single-block I-optimal RSM design was utilized, supplemented with 10 additional points generated through Design-Expert Software Version 13. The study aimed to evaluate the effects of break draft (X1), total draft (X2), back roller gauge (X3), and front roller gauge (X4) on two key response variables: unevenness percentage (Y1) and imperfection index (Y2) of polyester spun yarn. A comprehensive summary of the independent variables and their levels is provided in Table 1.

Table 1 Process independent variables.
Full size table

Implementing the RSM significantly reduced the total number of experimental combinations, cutting them down from 81 to 25. The combination of selected variables from the RSM subset designs is purposefully chosen to encompass all variations in the input space for accurate mapping to the output space. This is a key advantage of systematic approaches like RSM, as it enables reliable results with a smaller dataset. This reduction streamlined the experimental design, enabling a more focused and efficient investigation. The samples generated through the RSM design, outlined in Table 2, were utilized for further in-depth analysis in the subsequent stages of the study.

Table 2 Design of experiment for drawing process.
Full size table

Material and characterization methodologies

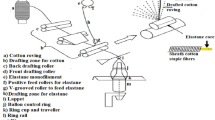
A batch of polyester fibres, measuring 44 mm in length and 1.6 dtex in fineness, was processed through a finisher drawing frame (Trützschler HSR 1000) following the blowroom, carding, and breaker drawing frame stages. According to the experimental design, slivers with a linear density of 4.75 ktex were produced under various combinations of the specified independent variables. These slivers were subsequently fed into a speed frame to create rovings with a linear density of 650 tex and a twist density of 25 TPM. The rovings were then processed on a Zinser RM350 ring frame to produce yarn samples with a count of 20 tex and a twist density of 715 TPM. Yarn quality parameters, including the coefficient of variation in mass (CVm%) and the imperfection index (IPI) calculated as the sum of thin places (sensitivity threshold of − 50%), thick places (sensitivity threshold of +50%), and neps (sensitivity threshold of +200%) were assessed using Uster Tester-3 equipment. These evaluations were conducted under experimental conditions at a speed of 400 m/min with a test duration of 2.5 min.

Data pre-processing

In general, variables with larger amplitudes tend to exert a more significant influence compared to those with smaller amplitudes41,42. To mitigate this quantitative bias, all data were normalized using Eq. (1), ensuring values fell within the range of 0.1 to 0.9. This normalization process preserves the core information of the data while enhancing the reliability of the modelling and optimization outcomes.

$$\:{X}_{n}=\left(b-a\right)\frac{X-min\left(X\right)}{max\left(X\right)-min\left(X\right)}+a$$
(1)

where a and b represent the lower (0.1) and upper (0.9) limits of the normalization domain. Generally, experimental data used for modelling is divided into two categories: training data and testing data. The training dataset is utilized to determine the unknown parameters of the models, such as the coefficients in the RSM model and the weight and bias values in the ANN. Conversely, the testing dataset is used to assess the performance and accuracy of the models43,44. In this study, the data were divided into training and testing sets at a ratio of 22:3. Table 2 provides an overview of the training and testing data.

Modeling and optimization steps

When presenting a model, it is crucial to assess its performance using an appropriate metric. One of the most effective metrics is the total goodness function (TGF), which evaluates the model’s overall performance during both the training and testing phases. TGF incorporates the effects of the coefficient of determination (R²) and the mean squared error (MSE). Previous studies45,46,47 have confirmed the validity of this metric, and we applied it to evaluate the performance of the models developed for CVm% and IPI. The ideal TGF value is 2, indicating perfect model accuracy. The calculation of TGF is provided in Eq. (2).

$$\:TGF=\frac{1}{N}\sum\:_{i=1}^{2}{n}_{i}({{R}^{2}}_{i}+{e}^{-{MSE}_{i}})$$
(2)

In which

$$\:{R}^{2}=1-\frac{\sum\:_{1}^{n}{(a-p)}^{2}}{\sum\:_{1}^{n}{(a-\stackrel{-}{a})}^{2}}$$
(3)
$$\:MSE=\frac{\sum\:_{1}^{n}{(a-p)}^{2}}{n}$$
(4)

where \(\:a\), \(\:p\), and \(\:\stackrel{-}{s}\) represent the actual value, the predicted value, and the mean of the actual values, respectively. Additionally, n and N denote the number of relevant data instances in either the training or testing phase, and the total number of data instances, respectively.

Response surface methodology

In this study, an RSM model, as shown in Eq. (5), was employed to map the independent variables (\(\:{X}_{1},\dots\:,{X}_{4}\)) to the dependent variables (\(\:{Y}_{1},{Y}_{2}\))48. In this model, X₁ to X₄ ​ correspond to the break draft, total draft, back roller gauge, and front roller gauge in the drawing frame, respectively. The term \(\:{a}_{0}\)​ represents the intercept, \(\:{a}_{i}\) denotes the linear effects, \(\:{a}_{ii}\)​ signifies the nonlinear effects, and \(\:{a}_{ij}\)​ accounts for the interaction (linear-linear) effects between the input parameters. All coefficients were determined using the Generalized Reduced Gradient (GRG) nonlinear solver in Microsoft Excel Software Version 2016.

$$\:\widehat{f}\left({X}_{1}.\dots\:.{X}_{4}\right)={a}_{0}+\sum\:_{1}^{4}{a}_{i}{X}_{i}+\sum\:_{1}^{4}{a}_{ii}{{X}_{i}}^{2}+\sum\:_{1}^{4}\sum\:_{1}^{4}{a}_{ij}{X}_{i}{X}_{j}$$
(5)

The results of the ANOVA analysis conducted using Design-Expert Software Version 13, along with the coefficients of the proposed models for both responses, are presented in Table 3. The analysis indicates that both models are significant at the 95% confidence level. However, although some terms were found to be statistically insignificant, they were retained in the model as the primary objective was to evaluate the overall performance of the RSM model, irrespective of the statistical significance of individual terms.

Table 3 ANOVA analysis of different terms of RSM-based models.
Full size table

Artificial neural network

The feedforward backpropagation neural network is a basic yet powerful type of neural network that learns by adjusting its connections based on errors. It is highly effective in modeling complex nonlinear relationships between independent and dependent variables, making it useful for predicting patterns in data. This network architecture includes several unknown hyperparameters, such as the number of hidden layers, the number of neurons per hidden layer, the activation functions for the hidden and output layers, the learning rate, the momentum value, the number of epochs, and the training function49. Previous studies50,51,52 have shown that a feedforward backpropagation ANN with a single hidden layer can successfully predict various engineering problems, similar to the one addressed in this study. The number of neurons in the hidden layer, the learning rate, and the momentum value were determined through a trial-and-error method, based on the network’s performance under different configurations. Figure 1a presents the neural network architecture used in this study to predict the CVm% and IPI of polyester spun yarn. Activation functions, including the sigmoid tangent function (Eq. (6)) and the pure linear function (Eq. (7)), were selected based on insights from prior research.

$$\:tansig\left(y\right)=\frac{2}{\left(1+{e}^{-2y}\right)}-1$$
(6)
$$\:purelin\left(y\right)=y$$
(7)

Table 4 summarizes the hyperparameter settings used in the ANN models, as optimized using MATLAB Software Version R2024a for the spinning process.

Table 4 Hyperparameter settings of the ANN models.
Full size table

The weights and biases of the trained neural networks used to predict CVm% and IPI are provided in Tables 5 and 6. These values allow for the precise replication of the neural network models for the two quality responses associated with polyester spun yarn, ensuring consistency and reproducibility in predictions.

Table 5 Weight and bias value of ANN model of CVm%.
Full size table
Table 6 Weight and bias value of ANN model of IPI.
Full size table

To assess the contribution of each input variable to the output of the ANN models, a sensitivity analysis was performed using Eq. (8). This analysis helps quantify the relative importance of each input variable within the network, enabling the identification of the most influential factors affecting the response53,54.

$$\:{\:R}_{i}\left(\%\right)=\frac{\sum\:_{j=1}^{{n}_{H}}\left[\frac{\left|{W}_{ij}\right|\left|{V}_{j}\right|}{\sum\:_{l=1}^{{n}_{I}}\left|{W}_{lj}\right|}\right]}{\sum\:_{i=1}^{{n}_{I}}\left[\sum\:_{j=1}^{{n}_{H}}\left[\frac{\left|{W}_{ij}\right|\left|{V}_{j}\right|}{\sum\:_{l=1}^{{n}_{I}}\left|{W}_{lj}\right|}\right]\right]}\times\:100$$
(8)

The results of the sensitivity analysis for the models predicting CVm% and IPI are illustrated in Fig. 1b. The analysis revealed that the break draft had the greatest impact on both responses, contributing 35.58% to the prediction of CVm% and 28.72% to the prediction of IPI for polyester spun yarn.

Fig. 1
figure 1

(a) Architecture of developed ANN models, (b) the relative importance of input variables.

Full size image

Genetic algorithm

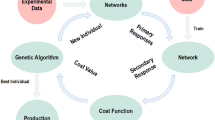
Traditional optimization methods often fall short in solving complex engineering problems. To address these limitations, soft computing techniques like GA, which mimics natural selection in evolution, can be combined with ANN. GA searches for the best possible input values by continuously improving solutions, while ANN learns patterns and relationships in data. Together, they optimize processes by minimizing errors and enhancing accuracy, making this approach highly effective for achieving desired outcomes in various applications38,40. In this study, a multi-objective optimization strategy is adopted to minimize the CVm% and IPI of polyester spun yarn by fine-tuning the drawing frame variables. The optimization workflow for the hybrid model developed in this study is depicted in Fig. 2. The cost function used for this optimization is defined in Eq. (9).

$$\:Minimize:\:f\left(\overrightarrow{x}\right)=\sqrt{{\left({{Y}_{1}}_{n}\right(\overrightarrow{x})-0\bullet\:1)}^{2}+{\left({{Y}_{2}}_{n}\right(\overrightarrow{x})-0\bullet\:01)}^{2}}$$
(9)

Subjected to

$$\:\overrightarrow{x}=\left\{{X}_{1},{X}_{2},{X}_{3},{X}_{4}\right\}$$
(10)

where \(\:\overrightarrow{x}\) represents a vector comprising the independent variables or inputs used during the optimization process.

Fig. 2
figure 2

Optimization diagram of the proposed hybrid model for adjusting drawing frame variables.

Full size image

The integration of the ANN and GA was implemented in MATLAB Software Version R2024a, with the hyperparameters of the GA determined through a trial-and-error approach to optimize results while minimizing computational time. The hyperparameter settings for the GA are summarized in Table 7. The optimization process utilized a double vector representation with a population size of 30 and a maximum of 30 generations. A uniform creation function was employed, and ranking was performed using a scaling function based on the Roulette method, with an elite count of 1. An adaptive feasible mutation function was applied, featuring a mutation rate of 0.50. Crossover was conducted using a two-point function with a crossover rate of 0.70. Additionally, a forward migration strategy was adopted, involving 10% of the population, with a migration rate of 0.3.

Table 7 Hyperparameter settings of GA.
Full size table

Results and discussions

Model selection

Figure 3 illustrates the performance of the developed RSM and ANN models in predicting CVm% and IPI of polyester spun yarn by comparing experimental and predicted results. The performance of the RSM model is suboptimal, particularly for the training dataset, with R² values of 0.7882 for CVm% and 0.8705 for IPI. The scattered distribution of most data points around the fitted line (red line) indicates a lack of precise alignment. Consequently, relying on this model in combination with a GA may not produce reliable optimization results. Unlike the RSM models, the ANN-based models exhibit high accuracy, with R² values approaching 1. The TGF values obtained from the ANN model for CVm% and IPI are 1.9996 and 1.9995, respectively, compared to 1.8035 and 1.8747 for the RSM model. This comparison confirms the superior predictive overall performance of the ANN model. These findings indicate that the ANN models effectively explain the nonlinear relationships between independent and dependent variables. Therefore, the ANN models were integrated with a GA to optimize the plotting frame variables for predicting CVm% and IPI.

Fig. 3
figure 3

Performance of the RSM and ANN models in predicting CVm% and IPI of polyester spun yarn for the training (a,e RSM and b,f ANN) and testing (c,g RSM and d,h ANN) datasets, respectively.

Full size image

Optimization of results

The optimization results are presented in Fig. 4. As shown in Fig. 4a, the optimization process converged after approximately 30 generations, demonstrating a significant improvement in the process. The cost was reduced from 0.2756 to approximately 0.0987. Figure 4b illustrates the changes in the drawing frame settings resulting from the optimization outcomes. A comparison between the initial optimal settings (based on experimental trends) and the optimized settings (derived from the proposed algorithm) shows notable adjustments: the break draft value decreased from 1.36 to 1.33, and the back roller gauge decreased from 61 to 60.5. Conversely, the total draft value increased from 6.5 to 7, and the front roller gauge increased from 47 to 47.5. As a result of these changes, the CVm% value improved, decreasing from 12.31 to 11.91, while the IPI value was reduced from 25 to 22.82. These findings highlight that the proposed algorithm effectively enhances the quality of the final product by identifying the optimal combination of system settings. This demonstrates the potential of optimization algorithms to improve the performance and efficiency of complex systems and processes.

Fig. 4
figure 4

(a) Performance of GA during optimization of drawing frame variables and (b) comparison between variables of optimized and optimum sample.

Full size image

Interpretation of results

Figures 5 and 6 illustrate the impact of drawing frame variables on the CVm% and IPI of polyester spun yarn. The influence of each variable on the responses was evaluated using the outputs of the developed ANN models, while holding the other variables constant at their identified optimal values. This approach helps reduce the black box nature of neural networks, making them a powerful tool for interpreting the impact of spinning process variables on the response55. Figure 5a shows that both extremely high and low levels of break draft, particularly low levels, significantly increase the CVm% of the sliver and the final yarn. At low break draft levels, insufficient friction reduction prevents the fiber strand from being adequately stabilized and prepared before entering the main drafting zone. Conversely, excessively high break draft levels make the drawing process less smooth, introducing more distortion and negatively affecting the CVm% of the final yarn. Figure 5b highlights the positive effect of high and intermediate total draft levels on yarn quality. Within the studied range, higher and intermediate total draft values effectively mitigate fiber friction in the sliver, resulting in improved CVm% in the final yarn. For the back roller gauge, Fig. 5c demonstrates that lower levels significantly increase the CVm% of the final yarn. This is attributed to the overlap of friction fields from the front and back rollers when the roller gauge is set too low, leading to disruptions in the drafting zone. In contrast, Fig. 5d reveals that higher levels of the front roller gauge increase the CVm% of the final yarn. Excessive front roller gauge distances increase the separation between friction fields, reducing control over floating fibers and adversely affecting yarn quality32.

Fig. 5
figure 5

Effect of drawing frame variables on the CVm% value of polyester spun yarn by ANN: (a) break draft (B.D), (b) total draft (T.D), (c) back roller gauge (B.R.G), and (d) front roller gauge (F.R.G).

Full size image

Figure 6a, b illustrate the significant negative impact of high levels of break draft and total draft on the IPI value of the final yarn. This can be attributed to the increased likelihood of individual fiber breakage at higher draft levels compared to lower levels. Fiber breakage during the drawing process can lead to entanglement and overlapping in subsequent stages, resulting in the formation of thick places and neps, which ultimately raise the IPI value of the final yarn. Figure 6c and d show a similar trend to that observed for CVm% in terms of the effects of the back and front roller gauges on the IPI, respectively. Specifically, higher back roller gauge levels and lower front roller gauge levels positively influence the quality of the final yarn produced. This effect can be explained by the same underlying mechanisms that govern the relationship between the roller gauges and fiber control during the drawing process. The findings in this section highlight the distinct effects of drawing frame variables on each yarn quality response, underscoring the complexity of the optimization problem addressed in this study.

Fig. 6
figure 6

Effect of drawing frame variables on the IPI value of polyester spun yarn by ANN: (a) break draft (B.D), (b) total draft (T.D), (c) back roller gauge (B.R.G), and (d) front roller gauge (F.R.G).

Full size image

As demonstrated earlier, the GA, as a soft computing-based optimization method, effectively minimized CVm% and IPI values, leading to improved yarn quality and increased efficiency in the spinning process. This optimization directly contributes to the production of higher-quality fabric with better uniformity, fewer defects, and enhanced aesthetic appeal. For textile manufacturers, refining these parameters ensures superior fabric performance, resulting in garments and textiles with a more polished appearance, improved durability, and greater market competitiveness.

Conclusion

In this study, multi-objective optimization of drawing frame variables was conducted to minimize CVm% and improve IPI in polyester spun yarns. The investigated variables included break draft, total draft, back roller gauge, and front roller gauge. RSM was used for experimental design, and both RSM and ANN models were developed. The ANN model demonstrated superior accuracy (R² ≈ 1) and was coupled with GA for hybrid optimization of drawing frame parameters. The main findings of this study are summarized as follows:

  1. 1.

    The ANN-GA approach successfully optimized drawing frame settings, improving CVm% from 12.31 to 11.91% and IPI from 25.00 to 22.81.

  2. 2.

    Sensitivity analysis indicated break draft had the most significant impact, contributing 35.58% to CVm% and 28.72% to IPI.

  3. 3.

    The ANN-GA hybrid model proved effective in optimizing yarn properties. Future research can extend this approach by using deep learning to analyze key variables across the entire spinning line, rather than a single machine. Integrating deep learning with optimization algorithms can further enhance yarn quality and production efficiency, offering valuable insights for textile manufacturers to optimize process parameters and reduce variability.

Future research can extend AI-driven optimization across the entire spinning process, integrating real-time adaptive control with IoT to enhance yarn quality. Hybrid AI models and deep learning can refine accuracy, while optimizing recycled fibers and reducing waste can support sustainable manufacturing. Digital twins and predictive maintenance in Industry 4.0 can further improve efficiency and automation in textile production.