Mechanical response characteristics of large-span double-arch tunnel construction and eccentric loading effect on the partition wall

Abstract

The frequent and complex stress variation of surrounding rock and load transfer of the lining structure during the construction of large-span double-arch tunnels pose certain challenges to subsequent construction control. This study employs a combination of physical model and numerical simulation to investigate the mechanical response of large-span double-arch tunnels during construction, and develops relevant model testing equipment and monitoring systems to provide references for similar tunnel mechanical response studies. The results show that: (1) The displacement and deformation of tunnel structures during construction experience three stages: " Slow deformation → Rapid deformation → Convergence deformation," with the settlement deformation on the same side accounting for over 80% due to construction in the same direction. (2) During excavation, the stress variation of surrounding rock and lining structures undergoes three processes: "Stress concentration → Stress release → Stress stabilization." The horizontal load transferred by the initial support causes abrupt changes in the horizontal thrust of the partition wall, while the vertical load induces an eccentric loading effect on the partition wall towards the leading side. This eccentric loading effect reaches its maximum when the leading side’s bench III is excavated to the left tunnel and decreases to a minimum and stabilizes when the excavation of the right tunnel’s monitoring face is completed. (3) The influence on tunnel crown settlement is in the order of Step I> Step II > Step III, while the influence length on surrounding rock stress is in the order of Step II > Step III > Step I. Therefore, these construction steps should be closely monitored initially. (4) Due to asymmetric construction, the partition wall of the double-arch tunnel is subjected to eccentric loading from the initial support load and the overlying surrounding rock load on the leading side. This effect improves as the trailing side is excavated, but the section bending moment still exhibits a "W" shape with flatter ends. The eccentric loading effect persists, increasing the risk of lateral displacement, bending-torsion, and shear failure of the partition wall.

Introduction

In recent years, with the rapid development of tunnel construction, the number of mega-span tunnels in China has been increasing. Especially in the deepening process of transportation infrastructure construction to the west, a number of extra-long oversize cross-section tunnels are being built and operated, are under construction and are being planned and designed¹. Continuous-arch tunnels are widely used as a form of tunnel structure with the advantages of large-span continuous-arch tunnels, smooth lines and high space utilization. However, due to the cumbersome construction process of continuous-arch tunnels, Its surrounding rock stress changes and lining structure load conversion frequent and complex, construction deformation prediction and control is more difficult, Therefore, it is of great importance to further develop the research on the mechanical response of the tunnel construction process.

Through numerical simulation and in situ monitoring: Luo et al². focused on the mechanical response of tunnel construction in the construction of large-span triple-arch tunnels, and analyzed the deformation characteristics of surrounding rocks through numerical simulation, Field monitoring was used to analyze the rock load evolution process and the mechanical behavior of the lining; Xu et al³. analyzed the mechanical evolution law and bias mechanism of the curved center wall of a composite continuous arch tunnel in the construction stage based on ABAQUS, Through the analysis of in situ monitoring, the stress ratio of each stage and the numerical model are basically close to each other, which verifies the reliability of the numerical model calculation results; Wang et al⁴. used numerical simulation and in situ monitoring methods to analyze the surrounding rock deformation and structural stress under the “whether symmetrical” two types of excavation schemes, taking into account the surrounding rock stability, structural safety and construction period and other factors, and ultimately determined the excavation scheme of the double-arch tunnel; Bai et al⁵. used Midas-GTS-NX to establish a three-dimensional double-connected-arch tunnel model to study the optimal longitudinal spacing between the leading and trailing caverns of a guided-arch tunnel without a center guide, and verified the credibility of the model through in situ monitoring; Zhao et al⁶.investigated the mechanical response of mega section tunnels constructed under soft and fractured surrounding rock by means of in situ testing and monitoring; Xu et al⁷. used numerical simulation for the stability study of the construction of a continuous arch tunnel using the mid-borehole method to analyze the indicators of surrounding rock deformation and structural forces, optimize the construction parameters, and illustrate the effectiveness of the model through in situ monitoring; Yang et al⁸. used numerical simulation to study a new construction method of continuous arch tunnel- “single tunnel without center wall” and compared it with the traditional construction method to optimize the construction scheme, and verified the feasibility of the new scheme through on-site monitoring and measurement; Yin et al⁹. established a two-dimensional stratigraphic model by FLAC3D to comparatively study the surrounding rock deformation and structural force characteristics of two centerless guideway construction schemes; Hu et al¹⁰. used ABAQUS to establish a model, combined with in situ monitoring to study the reasonable longitudinal dislocation spacing of the palm face, the excavation length of the superelevation arch, the excavation footage, and other parameters of the continuous arch tunnel when it is constructed by the micro-step method under the soft surrounding rock to ensure the construction is carried out safely and efficiently; Liu et al¹¹. used FLAC3D to establish a three-dimensional model of a continuous arch tunnel to study the regularity of four parameters, namely, main tunnel stagger, step length, diaphragm wall thickness and second lining application time, on the structural forces and deformation of a continuous arch tunnel constructed by the expanded excavation method without a middle guide tunnel; Liu¹²used FLAC3D to establish a large-span continuous-arch tunnel model and simulated tube-shed grouting by studying the surrounding rock displacement, stress and tube-shed support change characteristics, and then verified by numerical simulation;. For the study of model tests: Li et al¹³. established a model test system for the study of mechanical effects of construction of mega-span variable section tunnels, and simulated the construction of tunnels with multiple arch sections turning to large-span variable sections, exploring the mechanical effects of the construction of mega-span and variable section highway tunnels; Liu et al¹⁴. developed a large-scale assembled geomechanical model test system, carried out a mechanical model test of the construction process of oversized section tunnel in complex strata, and thoroughly studied the displacement and deformation of surrounding rock and stress release law during the construction process of oversized section tunnel; Sun et al¹⁵. developed a large-scale collocatable geomechanical model test system to study the mechanical response law of large-span and small-clearance tunnels during construction; Liu et al¹⁶. used an indoor model test to study the stability of surrounding rock in the construction of a continuous arch tunnel under bias conditions, and compared the results with numerical simulation to analyze and study; He et al¹⁷. utilized a self-developed large-scale model test rig and formulated similar materials for surrounding rocks of sand and pebble strata according to the similarity ratio to carry out the model test, and investigated the force and deformation characteristics of the lining structure of an asymmetric continuous arch tunnel; Chungsik Yoo et al¹⁸. used similarity ratio simplified indoor modeling tests to investigate the effect of underpassing of continuous arch tunnel construction on existing bridge piles; Jia et al¹⁹. investigated the force characteristics of the diaphragm wall during the construction of an existing tunnel expanded into a double continuous arch tunnel by a combination of model tests and numerical simulation.

In summary, previous scholars used different finite element analysis software for numerical modeling of large-span continuous-arch tunnels, mainly to study and analyze the deformation of surrounding rock, lining structure force, excavation plan selection, and the force characteristics of the diaphragm wall during the construction of large-span continuous-arch tunnels, and combined with the on-site monitoring and measurement to verify the reasonableness of the numerical model. For the research of modeling test, most scholars have developed modeling test box to study the surrounding rock deformation and stress release law during the construction of single tunnel, Rarely studied the biasing effect and load variation rule of lining structure and diaphragm wall during the staggered construction of continuous arch tunnel, And due to the cumbersome construction process of continuous-arch tunnel, its surrounding rock stress changes and lining structure load conversion frequent and complex, construction deformation prediction and control is difficult, the field test is difficult and costly, so further modeling tests to study the mechanical response of the construction process of large-span continuous-arch tunnel is of great engineering significance.

In order to study the spatial and temporal evolution of the mechanical response to the construction of large-span continuous-arch tunnels, we have independently developed a variety of pressurized loading geomechanical model test chambers, static stress–strain collection systems and tunnel arch settlement monitoring systems. Through this model test system, the changes of surrounding rock stresses and lining structure loads in the construction of large-span continuous-arch tunnels were collected to analyze the mechanical response of the construction to the deformation of the tunnel structure as well as the surrounding rock stresses. On top of that, Midas-GTS-NX is utilized to build a 3D double-connected arch tunnel model for simulation. Through the comparative study of model test and numerical simulation, the evolution law of surrounding rock stress and lining structure load during the construction of large-span continuous-arch tunnel is investigated, which reveals the interaction between the left and right tunnels in the construction of continuous-arch tunnel, as well as the mechanical response to the stability influence of the biasing effect of the diaphragm wall, which is conducive to the mastery of the change of surrounding rock stress and the deformation of the tunnel structure in the on-site construction. Based on the analysis of the mechanical response law during tunnel construction, the failure mechanism of the biasing effect of the diaphragm wall is revealed, and some suggestions are made for the construction and engineering control of large-span continuous-arch tunnels, and the results of the study can provide design basis and construction guidance for similar projects.

Project overview

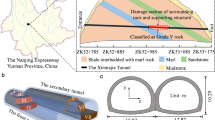
The Maling Canyon Tunnel is located in Xingyi City, Guizhou Province, and is a two-way six-lane continuous arch tunnel with a maximum depth of 114.5 m and a maximum span of 35.88 m. The tunnel plan location and the starting and ending pile numbers are shown in Fig. 1.

Fig. 1

Geographic location of the tunnel.

The geological conditions of the Maling Canyon Tunnel are as follows: the uppermost layer is red clay with an average thickness of 3.5 m, followed by dolomite, and the tunnel mainly passes through medium weathered dolomite. The longitudinal section of the tunnel at K10 + 075 ~ K10 + 175 and the cross-section design are shown in Fig. 2.

Fig. 2

Geological longitudinal and cross-sectional design of the tunnel.

Model test study

Tunnel structure and similar materials in surrounding rock

Similar materials for tunnel structures

Reference to similar material in existing studies^20,21, The similarity constant C = 50 was determined in conjunction with the requirements of the similarity modeling test. In this paper, gypsum, barite powder and water were selected as the raw materials for the lining structure, where 1/10 th of the mass of gypsum was added as barite powder to control the gravity of the similar materials. A total of 7 groups of standard specimens with water-paste ratios from 1:1.2 to 1:1.8 were made, with a total of 3 specimens in each group, and uniaxial compressive strength tests were conducted after the specimens were cured for 7 days as shown in Fig. 3.

Fig. 3

Measurement of mechanical parameters of paste materials.

The modulus of elasticity and compressive strength of the specimens were calculated from the output stress–strain curves. The water-paste ratio of 1:1.4 was finally selected, which best satisfies the similarity triple theorem, and the physical and mechanical parameters are shown in Table 1.

Table. 1 Lining materials and prototype mechanical parameters.

Similar materials in surrounding rock

As for the surrounding rock material configuration, scholars at home and abroad have made comparative analyses²², Barite powder (800 mesh), quartz sand (60 mesh) and petroleum jelly were selected as raw materials with reference to modeling tests and mechanical properties of surrounding rocks from existing literature. In accordance with the standard specimen shown in Fig. 4, WAW-100 micro-controlled electronic universal testing machine was used to carry out uniaxial compression test and straight shear instrument model ZJ strain-controlled straight shear instrument (quadruple shear) to carry out straight shear test to determine the mechanical parameters of surrounding rock materials. The mechanical parameter determination test of similar materials is shown in Fig. 4. By analyzing the results of the mechanical parameters of the formulated materials, it was finally determined that barite powder: quartz sand: petroleum jelly was used to make the similar materials for surrounding rock in the mass ratio of 7.2:5:1.

Fig. 4

Determination of similar material mechanical parameters of surrounding rock.

The density of the surrounding rock similar material under this ratio is 2.6 g/cm³ (direct weighing), and the calculated mechanical parameters of the surrounding rock prototype and the model similar material are shown in Table 2, which basically satisfy the similarity constants of the model test.

Table. 2 Mechanical parameters of surrounding rock materials.

Modeling of initial support

A common PVC sheet was chosen as the basic material and was analyzed by the similarity constant C = 50²³, To cut the molds for the initial support and diaphragm walls with a CNC machine and fix the assembly in layers, (It can be assembled according to the thickness of the material and the design height of the model as required). It is convenient to cast the lining structure of the continuous arch tunnel in one piece, which not only ensures the integrity of the tunnel structure, but also prevents the stress concentration in some areas due to the uneven thickness. The structural effect and model of the mold are shown in Fig. 5.

Fig. 5

Pouring mold and pouring model (a) Initial support fabrication, (b) diaphragm wall fabrication.

Large-span continuous-arch tunnel test system

In order to realistically simulate the construction process of large-span double-arch tunnels, further research on the deformation and stress-release evolution laws of the tunnel structure and surrounding rock during the construction process of double-arch tunnels is carried out. Self-developed and designed the double-arch tunnel lining casting mold and three-dimensional assembled large-scale geomechanical model test box (can be three-way pressurization), a stress–strain system based on static strain collection and a monitoring system for the lining structure designed on the basis of indicators have been constructed, forming a model test system for the mechanical response of the construction process of a large-span double-arch tunnel.

Model test box

The main part of the model test box is mainly made of I20a I-beam steel, steel plate and high-strength endurance plate into a closed box-type space, and the geometric dimensions of the internal space of the model box are 200 cm × 80 cm × 180 cm (length × width × height). In order to ensure sufficient visualization space, a size of 85 cm x 85 cm is reserved in the central position for the installation of the cut acrylic panels of the contour of the continuous arch tunnel, and this part can be freely replaced to meet the different shapes and sizes of the tunnel sections. The model test chamber can meet the scientific research requirements of many kinds of pressurized loading geomechanical model tests, and become the best choice for simulating various tunnel construction model tests¹⁴ the model test box is shown in Fig. 6.

Fig. 6

Schematic diagram of the model test box.

Stress- strain acquisition system

The acquisition instruments and components are shown in Fig. 7 (a). The data acquisition equipment is uT7160 static strain gauge, strain gauge model 120-20 AA, using 1/4 bridge + compensation wiring to connect the strain gauge, used to monitor the simulation of tunnel excavation process in the initial support force changes; The earth pressure box model is LY-350, the collection range is 0 ~ 200 kPa, and the full bridge wiring is used to connect the strain gauge, which is used to collect the surrounding rock stress changes during the excavation process;

Fig. 7

Stress–strain acquisition and tunnel structural deformation monitoring Arch settlement monitoring.

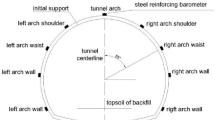
Tunnel structure deformation monitoring system

This trial uses an independently designed device to measure the deformation of the tunnel structure, the main components and their roles are: supporting the magnetic base, the whole set of testing devices will be magnetically attracted to the top of the model box for easy reading; The indicator, with an accuracy of 0.01 mm, is able to accurately read the changes in the structure; plastic tubes, twine and wire mesh, bonded to the surface of the structure, are able to directly measure the deformation of the structure caused by the excavation. The device is schematically shown in Fig. 7 (b). The specific operation is: Burying the poured and well-dried tunnel lining in similar material to the surrounding rock, cleaning the surface of the lining, then tying fine twine to the wire mesh and bonding them together on the left and right vaults and on the surface of the curved center wall. To prevent relative friction between the surrounding rock material and the fine twine, it is threaded through the plastic tube so that it is vertically centered in the tube and has no elastic contraction, and then the other end of the twine is tied to the measuring rod of the indicator and straightened. The plastic pipe was not attached to the surface of the initial support, which would not limit the deformation of the lining structure and would not affect the measurement results. The indicator was fixed on the sleeve of the indicator with the clip of the matching magnetic base, and then attached to the top of the model box together, which was used to measure the settlement of the lining structure during the tunnel excavation process.

Test program and construction simulation

Test preparation

In this paper, the study selects K10 + 075 ~ K10 + 175 section with burial depth of 19 ~ 25 m, and the tunnel burial depth is set to 50 cm, which corresponds to the actual burial depth of 25 m according to the similarity theorem. The distance from the bottom of the arch to the bottom of the model box was 28 cm, and the monitoring section was selected at the middle position of the model box (about 40 cm away). In this experiment, a method of pre-embedding followed by excavation was adopted to obtain the changes in the lining structure during construction and to assess the impact of each construction step on the lining structure. The sequence of the experimental phase is as follows: (1) The surrounding rock material was layered and filled to the bottom of the acrylic tunnel plate to a height of approximately 28 cm, and then the pre-compacted lining was sequentially placed into the middle of the model box to a depth of 40 cm, as shown in Fig. 8 (b). (2) Bury the earth pressure box at the bottom 5 cm and 10 cm of the diaphragm wall of this lining, and then put in the monitoring section shown in Fig. 8, and finally put the rest of the lining structure into the model box in order neatly as shown in Fig. 9(b); (3) Fill in the tunnel surrounding rock material again, and then bury the earth pressure box at 5 cm and 10 cm away from the left and right arch waist, the arch shoulder, and the top of the arch as shown in Fig. 8 (b); (4) Erect a vault settlement monitoring device, as shown in Fig. 8 (c); (5) The surrounding rock material was layered and compacted to the preset height, followed by rebalancing the experimental equipment to mitigate the adverse effects of additional loads during the backfilling process. The model was then left undisturbed for a certain period to ensure that the initial stress state conformed to the principles of similarity, thereby obtaining the initial vertical and horizontal stresses of the surrounding rock. The instrumentation and monitoring system were calibrated, completing the preparation for the experimental simulation of construction, as shown in Fig. 8 (d). The overall preparation process for the experiment is illustrated in Fig. 8.

Fig. 8

Overall schematic diagram of the model test.

Fig. 9

Test excavation process.

Construction phase simulation

In order to realistically simulate the actual construction of the dependent project, the test setup excavation scheme also follows the model similarity constants for construction simulation. The selected construction method is the benching method, which is the most widely applicable method within the New Austrian Tunneling Method (NATM). It features a large construction space, with each bench capable of advancing in parallel, thereby effectively improving construction efficiency. Additionally, this method can reduce project costs by minimizing the use of temporary supports. The disturbance to the surrounding rock is minimal, allowing the full utilization of the rock mass’s load-bearing capacity. The excavation and support of each bench are coordinated, enabling timely closure of the support ring and effective control of surrounding rock deformation. The construction process is divided into four main stages from b → i: (1) Construction and pouring of the center guide tunnel (2) Excavation of the left tunnel; (3) Removal of the initial support of the center guide tunnel; (4) Excavation of the right tunnel. Among them, 1–22 is the construction of the center guide tunnel, 23–32 is the casting of the diaphragm wall, 33–56 is the excavation of the left tunnel, and 48–71 is the excavation of the right tunnel. The two steps of excavation of the center guide hole and casting of the diaphragm wall still need to be carried out before the excavation of the main hole of the left and right lines can be carried out. While the tunnel was being excavated, the initial support for the center guideway exposed by the excavation was removed. The left and right main holes are excavated at 4 cm each time, and the left and right main holes are constructed at a staggered position of 60 cm (simulating the actual construction of the first row side for 30 m before the construction of the back row side). At the same time, the removal of the initial support of the center guide hole was carried out during the excavation of the left and right main holes. The excavation process of the model test is shown in Fig. 9.

Analysis of results

Analysis of vault settlement

In the process of the model test, through the real-time monitoring of the monitoring section of the initial tunnel support, the change rule of the settlement of vault with the number of excavation steps was obtained as shown in Fig. 10. After the casting of the middle guide and middle wall, the settlement of vault in the middle guide was 0.11 mm, but the settlement of vault in the left and right main caves remained almost unchanged. The settlement of vault in the left and right tunnels can be divided into three stages: ‘Slow deformation → Rapid deformation → Convergence deformation’. Before the palm face is excavated to the monitoring section, a small amount of slow deformation will occur in the settlement of vault in the monitoring section due to the disturbance of surrounding rock in front of the palm face by the excavation process; As the excavation proceeded to the monitoring section of the left tunnel, the rapid deformation of the left tunnel’s vault produced a displacement of 1.07 mm, while the right tunnel and the middle pilot tunnel had a settlement of vault of 0.17 mm and 0.26 mm due to the disturbance of the left tunnel excavation. When the monitoring section of the right tunnel was excavated, the displacement change of the vault was similar to that of the left tunnel, and the vault of the right tunnel sank rapidly, producing a rapid deformation of 1.41 mm. When the left and right tunnels are excavated at the same time, the excavation of the right tunnel will also have some impact on the settlement of vault of the left tunnel. When the right tunnel (the backward tunnel) was penetrated, the settlement of vaults in the middle pilot tunnel, left tunnel and right tunnel were also in convergent deformation, with final settlement values of 0.52 mm, 1.73 mm and 1.91 mm respectively. The largest final settlement of vault at the top of the arch occurs at the top of the right tunnel vault, which also indicates that the settlement of vault in the backward cave is slightly larger than that in the forward cave. The settlement of vault on the left side during the construction stage of the left tunnel accounted for about 83.2% of its final settlement value, and the settlement of vault on the right side during the construction stage of the right tunnel accounted for about 86.4% of its final settlement value. This indicates that the influence of the main tunnel excavation on the surrounding rock at the vault is mainly concentrated in the region of this side tunnel.

Fig. 10

Time course curve of settlement of vault.

Stress analysis of surrounding rock

As shown in Fig. 11(a), the vertical stresses in the vault have gone through the change stage of ‘Stress concentration → Stress release → Stress stabilisation’. Taking measurement point A3 as an example, when the first side of excavation I was excavated to the left monitoring section, the stress of surrounding rock of the arch began to be released, and the vertical stress decreased rapidly from −6.1kPa to −3.6kPa, and the stress release rate was 36.2%; When the first side of Excavation II was excavated to the left monitoring section, the vertical stress decreased rapidly from 3.6kPa to 1.3kPa, with a stress release rate of 33.3%; When the first side of excavation for Step III was excavated to the left monitoring section, the circumferential stress at the arch shoulder was reduced by 0.6 kPa, with a stress release rate of 8.7%. It can be seen that when using the step method to simulate the excavation, the excavation of the upper step has the greatest effect on the vertical stresses in the vault, the excavation of the middle step is the second largest, and the excavation of the lower step is the smallest. As the working face advances, the range of surrounding rock loosening in the left tunnel expands again, and the vertical stress in the vault increases and slowly tends to stabilise around −1.4kPa. The change rule of vertical stress in the right tunnel is similar to that of the left tunnel.

Fig. 11

Stresses in surrounding rock in left and right tunnels.

As shown in Fig. 11 (b), the change rule of horizontal stress at the arch waist of the left and right tunnels is similar to that of the vertical stress at the arch top, and only the arch waist measurement point A1 of the left tunnel is taken as an example. When the left tunnel step I was excavated to the monitoring section, the horizontal stress of the side wall began to be released, and the horizontal stress of the arch waist was reduced by 0.6kPa. Especially, when the first side of excavation I was excavated to the left monitoring section, the rate of stress release reached the maximum, and at this time, the horizontal stress of the arch waist was suddenly reduced by 1.4kPa; When the excavation of the left monitoring section was finished, the horizontal stress was reduced to a minimum, with a minimum value of 0.6kPa; as the left tunnel working face advanced forward, the horizontal stress at the arch waist began to rise slowly, and finally tended to stabilise at 1.4kPa.

As shown in Fig. 11 (c), the pattern of change of annular stress at the outer arch shoulder of the left and right tunnels shows a tendency of decreasing sharply at first and then increasing slowly. Taking measurement point A2 as an example to be analysed, when the first side of excavation of step I was excavated to the left side of the monitoring section, the circumferential stress of the arch shoulder was reduced by 1.8kPa. After the first side of excavation of Step II to the left monitoring section, the arch shoulder stress decreased by 1.2kPa. When the first side of excavation III was excavated to the left monitoring section, the stress at the arch shoulder decreased by 0.5 kPa. As the excavation moved forward, the stress at the arch shoulder slowly increased and stabilised at about −3.4 kPa.

As shown in Fig. 11 (d), the change rule of the circumferential stress at the inner shoulder of the left and right tunnels shows a trend of decreasing rapidly at first, then increasing rapidly and finally stabilising, and the stress at the inner shoulder of the left and right tunnels shows a trend of decreasing rapidly at first and then increasing rapidly at last. Taking measurement point A5 as an example for analysis, when the left tunnel step I was excavated to the monitoring section, the circumferential stress of the arch shoulder decreased by 0.6kPa. When the left tunnel step II was excavated to the monitoring section, the annular stress at the arch shoulder decreased by 1.2kPa. When the left tunnel step III was excavated to the monitoring section, the circumferential stress at the arch shoulder decreased by 0.9kPa, at which time the circumferential stress at the arch shoulder basically reached the minimum value. This indicates that the excavation of the left tunnel step II has the greatest influence on the change of the circumferential stress at the inner arch shoulder.. As the excavation of the working face advances, the circumferential stress at the arch shoulder starts to increase rapidly, which is due to the construction bias generated by the staggered construction of the left and right tunnels. When the right tunnel is excavated to the monitoring section, the bias situation is improved, and the circumferential stress at the inner arch shoulder tends to be stabilised at this time.

Analysis of internal forces in the initial support

Reference to relevant literature^24,25, Calculate the value of axial force N and bending moment M at each position according to Eqs. (2–1) and (2–2). Convert the axial forces and bending moments at each position of the original structure based on the similarity constant C = 50.

$$N=\frac{1}{2}\times E\times \left({\varepsilon }_{in}+{\varepsilon }_{out}\right)\times b\times h$$

(2-1)

$$M=\frac{1}{12}\times E\times \left({\varepsilon }_{in}-{\varepsilon }_{out}\right)\times b\times {h}^{2}$$

(2-2)

Style:E–– Modulus of elasticity; ε_in–– Strain on the inside of the initial support; ε_out–– Strain on the outside of the initial support; b–– Width of initial support; h–– Thickness of initial support;

From the axial force diagram of the initial support in Fig. 12, it can be seen that the initial support of the continuous arch tunnel during excavation are shown as a state of pressure, showing a ‘small top and big bottom’ distribution. The forces on the right side of the tunnel are less than those on the left side, with the minimum and maximum forces on the left and right sides of the tunnel located at the top of the arch and the foot of the arch. 362kN and 488kN on the left side, 356kN and 445kN on the right side, respectively. Due to the excavation of the first side of excavation (left tunnel), the surrounding rock stresses were redistributed and the initial support loads and the loads on the top surrounding rock acted on the left side of the middle wall, generating a bias in favour of the left side, so the support structure of the left tunnel was subjected to greater forces than that of the right tunnel. Due to the excavation on the later side of excavation (right tunnel), the forces on the middle wall are gradually subjected to the initial support loads on the left and right sides as well as the surrounding rock loads, and the distribution pattern is basically symmetrical, but the biasing effect still exists.

Fig. 12

Axial force diagram for monitoring section (kN).

From the bending moment diagram of the initial support in Fig. 13, it is clear that the values of bending moments at various locations on the first side of excavation are greater than those on the later side, for reasons similar to the differences in axial forces. For the biasing effect produced by the staggered construction of the left and right sides, the maximum bending moments of both the left and right sides appeared at the foot of the arch, which were −0.71kN-m and −0.68kN-m, respectively. The support structure of the arch and the bottom of the arch on the inside of the tensile state, for the structure of the most unfavourable position, because the ultimate compressive strength of the concrete structure is much greater than the tensile strength. Therefore, in terms of tunnel structure design, the most unfavourable position should be designed based on the arch top section to prevent the tunnel structure from tensile deformation cracking or even destruction.

Fig. 13

Monitoring section bending moment diagram (kN·m).

Stress analysis of surrounding rock at the base of the middle wall

Figure 14 shows that the surrounding rock stress at the bottom of the middle wall increases in a ‘Z’ shape with each step of excavation. When the first side of excavation reached the monitoring section, the left surrounding rock stress was redistributed, the stress was released and transmitted to the top of the middle wall through the lining structure, so that the bias load to the first side of the middle wall increased the stress on the left side, and as a result, the stress on the left side of the surrounding rock increased rapidly from 7.1kPa to 12.9kPa. And with the excavation of the backrow hole, the middle wall was subjected to the initial support loads on both the left and right sides at the same time, which made the biasing effect weakened and made the magnitude of the change slower than that on the left side (the stress in the surrounding rock on the right side increased from 7.1kPa to 11.6kPa). When the right tunnel excavation passes through the monitoring surface, the surrounding rock pressure at the bottom of the middle wall gradually tends to stabilise, and the difference in surrounding rock pressure between the two sides at the bottom of the middle wall narrows down from 7.7 kPa to 0.8 kPa at the end, which indicates that the biasing effect of the middle wall has been improved, but the biasing of the middle wall still exists and is biased in favour of the side of the pilot cavern.

Fig. 14

Surrounding rock pressure at the base of the middle wall.

Numerical simulation analysis

Material structure and mechanical parameters

Based on the geological data of the tunnel, the surrounding rock in the numerical model is represented by solid elements, which conform to the Drucker-Prager criterion. The Drucker-Prager criterion is adopted as the failure criterion for the numerical model primarily because it can more comprehensively account for the influence of the intermediate principal stress. This makes it suitable for complex stress states and enables it to accurately simulate the mechanical behavior during tunnel construction. The initial support and the intermediate wall are modeled using plate elements and solid elements that satisfy elastic constitutive laws, respectively, to better simulate actual engineering conditions. Based on the mechanism of action of overtopping in the surrounding rock support system, in this study, the ground surrounding rock reinforcement zone is modelled by enhancing the angle of internal friction (φ) and cohesion (c) of the rock surrounding the tunnel. The material physical and mechanical parameters are shown in Table 3.

Table. 3 Material physical and mechanical parameters.

Modelling and construction simulation

Considering the boundary effects in the computational process, a three-dimensional numerical model of a multi-arch tunnel was established using Midas GTS-NX. The model dimensions were 180 m × 60 m × 60 m (X × Y × Z), comprising approximately 140,000 finite elements. The model primarily considered self-weight stress, with stress and displacement boundaries defined as follows: the top surface was a free boundary subjected to the overburden weight of the overlying rock mass; the bottom surface had no vertical or horizontal displacements; the left and right surfaces had no horizontal displacements; and the front and back surfaces had no longitudinal displacements. During the numerical simulation, the same construction method used in the model tests was employed. Given the constraints of site size, economy, and safety in physical model tests, the model was scaled down by a similarity constant =50 to simulate the actual engineering scenario. In contrast, the numerical simulation closely approximated the actual construction process, with construction parameters set according to real-world conditions. Specifically, each excavation cycle advanced by 2 m. The simulation steps were as follows: Step 1 balanced the initial in situ stress and reset displacements to zero; Steps 2–33 simulated the construction of the middle pilot tunnel; Steps 34–63 represented the pouring of the central partition wall; Steps 64–100 involved excavation of the leading tunnel; and Steps 80–116 involved excavation of the trailing tunnel, totaling 117 steps. The excavation simulation was performed using the built-in"construction stage—stress"function in Midas GTS-NX. The term“activation data”referred to the inclusion of elements in the computation, commonly used to simulate support installation, while“deactivation data”referred to the exclusion of elements from the computation, used to simulate excavation. The initial support was installed one step behind the excavation front. The leading tunnel face was excavated for 30 m before the trailing tunnel face was initiated, resulting in a 30-m offset between the two tunnels. The model building and construction simulation is shown in Fig. 15. (Midas GTS-NX Software Version: midas GTS NX version 2022, URL: https://product.midasit.cn/index/products-GTS.asp).

Fig. 15

Numerical model and construction simulation.

Analysis of results

Analysis of changes in surface settlement

The settlement profile of the surface of the monitoring section during the construction phase is shown in Fig. 16. The settlement values at each point of the ground surface at the end of the construction of the middle pilot tunnel and the casting of the middle wall were all symmetrical around the axis of symmetry at the ground surface of the top of the middle wall, and the settlement values at each point accounted for about 15.1% and 23.3% of the final settlement value, respectively; When the left tunnel monitoring section was excavated, the settlement values of the surface points were analysed with the surface of the top of the middle wall as the axis of symmetry, and on the same axis of symmetry, the settlement values of the left side were greater than the settlement values of the right side; During the construction of the monitoring surface of the right tunnel, the left and right tunnels were constructed with the surface of the top of the middle wall as the axis of symmetry, and the difference in the settlement values at the same point of symmetry was slowly decreasing, but still the left side was slightly larger than the right side; When the tunnel passes through the two sides of the surface settlement value to the top of the middle wall surface as the axis of symmetry, the left and right sides of the same symmetry point settlement value is basically equal. In the case of the characteristic point of surface settlement at the top of the middle wall, for example, the construction-generated settlement value at the monitoring face of the left tunnel accounted for approximately 44.1 per cent of the total surface settlement value; The settlement values generated during construction to the monitoring face of the right tunnel account for approximately 32.7% of the total surface settlement values. Overall, the maximum values of settlement of the ground surface appeared at the top of the middle wall and at the top of the left tunnel pilot tunnel vault as the construction phase progressed, and then finally left–right symmetrically with the top of the middle wall as the axis of symmetry. The maximum value is −3.92mm.

Fig. 16

Time-course curve of surface settlement.

Analysis of settlement of vault variations

The temporal profile of vault settlement is shown in Fig. 17. After the casting of the middle pilot tunnel and the middle wall, the displacement change of the left and right tunnels’ vaults was very limited, only producing a displacement of −1.06mm, while the vault displacement of the middle pilot tunnel was 1.50 mm, which indicated that the excavation of the middle pilot tunnel had a small impact on the left and right tunnels. With the excavation of the first side of excavation, at about 0.7D from the monitoring section, the excavation disturbance was transferred to the monitoring section, and the settlement of vault on the left side of the tunnel started to deform over the top, with a change of 0.99 mm, which accounted for 18.3% of the total settlement of vault value. When the first side of excavation I excavation to the left tunnel monitoring section, the settlement rapidly deformed and increased by 1.01 mm, the first side of excavation I excavation caused by the settlement of vault accounted for 18.7% of the total settlement, is the largest step affecting the settlement of vault on the left side of the tunnel. After both the first side of steps II and III passed through the monitoring section, the settlement of vault on the left side gradually stabilised with the excavation; When the later side of excavation of Step I reached the monitoring section, the settlement of vault of the left tunnel started to converge and deform, and the final settlement value was around 5.40 mm. The settlement of vault pattern of the right tunnel is basically the same as that of the left tunnel. It is worth noting that there is still a slight increase in the displacement of the left tunnel vault when the monitoring surface of the right tunnel is under construction, which indicates that the excavation of the later side of excavation not only affects the tunnel of the present side, but also affects the first side of excavation to a certain extent. Therefore, after the completion of the construction of the pilot hole, monitoring should also be strengthened and appropriate measures should be taken to prevent sudden deformation of the surrounding rock.

Fig. 17

Time course curve of settlement of vault.

Stress analysis of surrounding rock

The vertical and horizontal stresses of the surrounding rock in the numerical model were extracted. Load decomposition can simplify complex loading conditions into more manageable components, facilitating the analysis of surrounding rock stresses. Therefore, directly from the finite element analysis software Midas GTS-NX, the vertical and horizontal stress data were extracted from the result files calculated by the finite element software, in accordance with the direction specified in our numerical modeling.

Vertical stress analysis

The evolution of vertical stresses in the surrounding rock reinforcement zone and the working face during the simulated excavation under actual working conditions in a continuous arch tunnel is shown in Fig. 18. Due to the staggered construction of the continuous arch tunnel, the surrounding rock stresses on the first side of excavation are released first, resulting in a complex vertical stress transition between the surrounding rock reinforcement area and the excavation face. This requires careful monitoring and analysis of stress changes during construction to ensure structural stability and construction safety. When the tunnel passes through, the vertical stress distribution is basically in symmetrical distribution, and the maximum vertical stress is −2.58MPa.

Fig. 18

Vertical stress evolution in surrounding rock reinforcement area and working face (kN/m²).

The changes in vertical stresses at the monitoring points on both sides of the vault and the top of the middle wall during construction are shown in Fig. 19. With the excavation of the first side of excavation, at a distance of about 0.7D from the monitoring section, the disturbance generated by the excavation increased the vertical stress in the surrounding rock, and with the excavation of Step I to the monitoring section of the left tunnel, the vertical stress at the monitoring point of the arch was rapidly reduced to a minimum. The vertical stresses in the vault stabilised during subsequent construction. The change rule of vertical stress at the monitoring point of the right vault is similar and will not be detailed here. The maximum vertical stress at the monitoring point of the left tunnel vault is 0.80 MPa, and the minimum is 0.01 MPa. The maximum vertical stress at the monitoring point of the right tunnel vault was 0.82 MPa and the minimum was 0.01 MPa.

Fig. 19

Vertical stresses in vault and middle wall.

The change rule of vertical stress on both sides of the top of the middle wall is similar. In general, it has experienced three stages of ‘stress concentration → stress release → stress stabilisation’. As an example, the vertical stress at the left side of the top of the middle wall increased rapidly with the excavation of the monitoring surface of the left tunnel at the monitoring point on the left side of the top of the middle wall. The rate of increase in vertical stress on the left side of the top of the middle wall slows down as the tunnel construction moves forward. Until the end of the construction of the monitoring surface of the right tunnel, the vertical stresses on the left side of the top of the middle wall slowly stabilised. The maximum values of vertical stresses on the left and right sides of the top of the middle wall were 3.58 MPa and 3.12 MPa, respectively. From the above analysis, it can be seen that the vertical stresses at the top of the middle wall produced extremely complex changes with the construction of the main hole, so the force deformation of the middle wall will be further analysed after this section.

Horizontal stress analysis

The horizontal stresses in the surrounding rock reinforcement area and the working face are shown in Fig. 20. Due to the staggered construction of the continuous arch tunnel, the surrounding rock stresses on the first side of excavation are released first, resulting in a complicated horizontal stress transition between the surrounding rock reinforcement area and the excavation surface. Particularly in the vicinity of the middle pilot tunnel, the changes in horizontal stresses manifested themselves in a particularly complex manner, which required careful monitoring and analysis of the stress changes during the construction process to ensure the stability of the structure and construction safety. After the tunnel passes through, the horizontal stress of the tunnel basically shows a symmetrical distribution, and the maximum horizontal stress is −1.17MPa, which is located at the top position of the middle wall.

Fig. 20

Evolution of horizontal stresses in the surrounding rock reinforcement and excavation areas (kN/m²).

Analysis of force deformation of middle wall

Displacement analysis of the middle wall

From the vertical displacement of the middle wall in Fig. 21 (a), it can be seen that the vertical displacement varies upwards as ‘up’ and the horizontal displacement varies upwards as offset to the right, respectively. As the first side of excavation, Step I, was excavated to the left tunnel monitoring section, the changing condition of the upper part of the middle wall was falling on the left and rising on the right. The lower part of the middle wall is rising on the left side, while the right side is basically unchanged. This is due to the transfer of initial support loads and surrounding rock stresses on the first side of excavation to the top and bottom of the middle wall. When the later side of excavation I is excavated to the right tunnel monitoring section, the changing condition of the upper part of the middle wall is rising on the left side and falling on the right side. The lower part of the middle wall is essentially stable on the left and rising on the right. With the later side of excavation of step III to the right side of the tunnel monitoring section, the vertical displacement deformation of the middle wall slowly converge, the lower part of the middle wall is basically at the same level, the upper part of the left and right deformation value slightly a little difference, this is due to the existence of the biasing effect, is the structure occurs to the first side of the deflection. The vertical displacements at the upper, middle and lower measurement points on the left side of the middle wall ended up being 1.73 mm, 0.54 mm and −1.06mm respectively; From the horizontal displacement of the middle wall in Fig. 21 (b), it can be seen that the horizontal displacement of the middle wall was continuously shifted to the right when the first side of excavation I reached the monitoring section; The horizontal displacement of the middle wall was continuously shifted to the left when the later side of excavation I was excavated to the monitoring section on the right side of the tunnel, and as the later side of excavation III was excavated to the monitoring section, the tendency of shifting to the left was slowed down and gradually converged. From the above analysis, it can be concluded that throughout the construction process the middle wall continued to deflect downwards and to the right as the construction process progressed.

Fig. 21

Displacement time course curves on both sides of the middle wall.

Horizontal load on middle wall

From the horizontal displacement change rule of the middle wall, it can be seen that the first side of excavation I to the left tunnel monitoring section, the top of the middle wall by the first side of initial support load as well as the top surrounding rock load. Taking the left and right sides of the upper part of the middle wall as the measurement points, the change of horizontal thrust transmitted to the middle wall by the initial support load and the top surrounding rock load is analysed, and the change rule is shown in Fig. 22. As the main cavern was constructed, the horizontal thrusts on either side of the top of the middle wall changed in complex ways. Horizontal thrust undergoes the process of ‘stress concentration → stress release → stress stabilisation’ and eventually becomes stable. Horizontal thrusts were all maximised when the same side step I was excavated to the tunnel monitoring section, with maximum values of 822kN and −738kN for the left and right horizontal thrusts respectively. During the excavation of Step II on the same side, the horizontal thrusts on the left and right sides decrease abruptly to 439kN and 379kN, respectively, at this time, both the left and right sides of the horizontal thrust are very close to the minimum value, it can be considered that the monitoring surface of the horizontal thrust release has been completed at this time. As the later side of excavation of Step III reached the right tunnel monitoring section, the horizontal thrusts on both sides gradually stabilised and converged.

Fig. 22

Variation curve of horizontal thrust at the top of the middle wall.

Stress analysis on both sides of the middle wall

As can be seen from Fig. 23 (a), the vertical stress in the middle wall undergoes three phases of ‘slow increase’, ‘rapid increase phase’ and ‘deceleration and stabilisation phase’ during the tunnel construction. During the excavation of the first side of excavation from Step II to Step III, the right side of the middle wall was strained in the middle and lower positions. With the excavation of the left side tunnel, the vertical stress reaches a maximum value of 6.10 MPa. The tensile stress on the right side of the middle wall also reaches a maximum value of 0.75 MPa. In the course of the monitoring section to which the later side of excavation was carried out, the compressive stresses on the left side of the middle wall gradually stabilised and converged, while the right side was gradually transformed from the original tensile state to the compressive state, the magnitude of change reaches its maximum in the later side of excavation of Step III to the monitoring section, and the vertical stresses gradually decelerate and stabilise after the excavation passes the monitoring section. From Fig. 23 (b), it can be seen that the horizontal stress increases with the excavation, and the horizontal stress increases the fastest in the excavation of the same side, and the increase accounts for 56.9% of the total horizontal stress. The horizontal stress on the left side of the same position is obviously larger than that on the right side. Their maximum values are 2.58 MPa and 1.15 MPa, respectively. From the above analysis, it can be seen that the horizontal load transmitted by the initial support will make the middle wall generate a large horizontal thrust. At the same time, the vertical load transmitted by the initial support will cause the middle wall to generate a biasing effect, which reaches its maximum during the construction of Step III of the left tunnel monitoring surface of the middle wall, and then decreases to a minimum and tends to stabilise at the end of the construction of the monitoring surface of the right tunnel.

Fig. 23

Vertical stress variation curves on both sides of the middle wall.

Analysis of biasing effect

The lower middle part of the middle wall is the vertical stress concentration area, and the vertical stress difference between the left and right sides of this position is the largest, which is the most unfavourable position, and this is used as a representative for the analysis of the biasing effect of the middle wall. The A-A section in Fig. 24 is selected for biasing effect analysis, and the biasing effect of the middle wall is shown in Fig. 24, where I is the surrounding rock load above the middle wall, II is the initial support load on the left side, and III is the initial support load on the right side.

Fig. 24

Schematic representation of the biasing effect of the middle wall.

The cross sectional moment M is introduced from Fig. 24 to describe the biasing effect of the middle wall and the calculation of the cross sectional moment is carried out in references^3,26,27. $\sigma_{l} ,\sigma_{m} ,\sigma_{r}$ Vertical stress values on the left, middle and right side of the middle wall, respectively., H is the thickness of the middle wall, The bending moment M of the analysed section per unit longitudinal length can be obtained from Eqs. (3–1) and (3–2).

$${M}_{A}={M}_{l}-{M}_{r}=\left\{\begin{array}{c}{M}_{l}={\sigma }_{m}\frac{{H}^{2}}{8}+({\sigma }_{l}-{\sigma }_{m})\frac{{H}^{2}}{12}\\ {M}_{r}=-{\sigma }_{r}\frac{(x+H)(H-2x)}{12}+{\sigma }_{m}\frac{{x}^{2}}{6}\end{array}\right.$$

(3-1)

$${M}_{R}={M}_{l}-{M}_{r}=\left\{\begin{array}{c}{M}_{l}={\sigma }_{m}\frac{{H}^{2}}{8}+({\sigma }_{l}-{\sigma }_{m})\frac{{H}^{2}}{12}\\ {M}_{r}={\sigma }_{r}\frac{{H}^{2}}{8}+({\sigma }_{m}-{\sigma }_{r})\frac{{H}^{2}}{24}\end{array}\right.$$

(3-2)

where: M is positive in counterclockwise direction;${M}_{A}, {M}_{R}$ re the bending moments of A-A section during the construction of the first and second rows of holes, respectively; ${M}_{l}$, ${M}_{r}$ re the bending moments of the Y-axis of the left and right side stresses, respectively.

The cross-section with the highest vertical stress in the middle wall is the lower part of the middle wall. Taking the lower part of the middle wall as the analysed cross-section, the bias moment curve of the middle wall during the construction stage of the main cavern is calculated as shown in Fig. 25.

Fig. 25

Bias bending moment curve of middle wall.

After the excavation of step I of the monitoring face of the left tunnel (advance hole), the bias bending moment increased sharply, and the middle wall was biased towards the direction of the advance hole under the action of the bias bending moment. During the excavation of step III on the monitoring surface of the left tunnel, the value of bending moment slowly increases to the maximum, and the maximum value is 2046 kN·m. And with the excavation of the monitoring surface step of the right tunnel (backward hole), the bending moment value decreases sharply, at this time, the biasing effect of the middle wall is weakened, and the value of the bending moment of the middle wall is slowly stabilised at 308 kN·m after the construction is completed. However, the bending moment value after stabilisation was significantly larger than that before the construction of the main tunnel and the biasing moment curve showed asymmetric changes, indicating that the biasing effect of the middle wall caused by the misaligned construction of the left and right tunnels always existed. Therefore, special attention should be paid to the asymmetric construction of the continuous arch tunnel, the middle wall may be due to the vertical surrounding rock stress transmitted to the initial support so that its structural deflection or bias torsion damage, in the construction process should be strengthened on the tunnel surrounding rock and the monitoring of the middle wall, to ensure that the construction of the safety. Therefore, special attention should be paid to the possibility of structural deflection or bias torsion failure of the middle wall during asymmetric construction of continuous arch tunnels due to the transmission of vertical surrounding rock stresses to the initial support. The monitoring of the surrounding rock and the middle wall of the tunnel should be strengthened in the construction process to ensure the safety of the construction.

Comparison and analysis of model tests and numerical simulations

Settlement of vault

During the model tests and numerical simulations, the effect of each construction step on the settlement of vault was obtained by real-time monitoring of the monitoring section and data extraction from the simulations, the model test is designed according to certain similar conditions, in the final settlement of vault results will have some differences with the numerical simulation, but the change rule as well as the corresponding key construction steps have certain similarity and reliability. When the three-step method is used to construct a large-span double-connected arch tunnel, different excavation sections of the tunnel section will have different effects on the settlement of vault. By calculating and analysing the deformation time-course curves of settlement of vault with construction steps in Fig. 10 and Fig. 17, the percentage of settlement of vault caused by different excavation sections was obtained, as shown in Fig. 26. Compared to the other excavation sections of the tunnel, Step I excavation caused the largest percentage of settlement of vault. Among them, (1) logarithmic model test: the settlement of vault produced by the excavation of the left tunnel step I is 0.7 mm, compared with the final settlement of vault of 1.73 mm accounting for 40.5%; The settlement of vault produced by the excavation of Step I of the right tunnel was 0.9 mm, which accounted for 47.1% compared to the final settlement of vault of 1.91 mm; (2) Numerical simulation results: the settlement of vault produced by the excavation of the left tunnel step I is 2.47 mm, which accounts for 45.0% compared to the final settlement of vault of 5.40 mm; The settlement of vault produced by the excavation of Step I of the right tunnel was 2.26 mm, which accounted for 41.2% compared to the final settlement of vault of 5.49 mm. Similarly, for the other excavation sections of the continuous arch tunnel, the degree of influence on the settlement of vault is in the order of step I > step II > step III. Therefore, in the construction of continuous arch tunnel, special attention should be paid to the settlement of vault deformation caused by the excavation of step I, the initial support should be carried out as soon as possible and the monitoring and measurement of the tunnel lining should be strengthened to ensure that the construction is carried out safely.

Fig. 26

Percentage settlement of vault due to different excavation sections.

Vertical surrounding rock stresses at the arch top

In the model tests and numerical simulations, the stress release pattern of vertical surrounding rock stress with excavation step is shown in Fig. 11 and Fig. 19, As an example, the surrounding rock stresses collected from the A3 and B3 measurement points at the left and right tunnel vaults. By calculating and analysing the vertical surrounding rock stresses, the percentage release of surrounding rock stresses by excavation in each construction section was obtained, as shown in Fig. 27. Step II contributed the largest percentage to the vertical surrounding rock stress relief compared to the other excavation sections. Among them, (1) for the model test: the stress change of surrounding rock in the excavation of the left tunnel step II is 2.4kPa, which is 40.0% compared to the final surrounding rock stress change of 6.0kPa; The change in surrounding rock stress from the right tunnel Step II excavation is 1.6kPa, which is 34.1% compared to the final surrounding rock stress change of 4.7kPa; (2) Numerical simulation results: The stress change of surrounding rock in the excavation of the left tunnel step II is 1.18MPa, compared with the final stress change of surrounding rock of 3.33MPa accounting for 35.4%; The change in surrounding rock stress from the right tunnel Step II excavation is 1.17 MPa, which is 37.5% compared to the final surrounding rock stress change of 3.12 MPa. Comprehensive model test and numerical simulation results analysis, step II excavation caused by the average value of vertical surrounding rock stress changes in the vault is 36.8%, for the other excavation sections of the continuous arch tunnel on the settlement of vault in the order of the degree of influence of step II > step III > step I.

Fig. 27

Percentage of surrounding rock stresses in the vault caused by different excavation sections.

Discussion

Analysis of failure of the middle wall

The damage mechanism for the construction of a large-span double-connected-arch tunnel is shown in Fig. 25 and Eqs. (3–1) and (3–2). As the construction of the middle pilot tunnel and the casting of the middle wall were carried out first, the construction of the subsequent tunnels was disturbed to varying degrees. During the construction of the first side of excavation the middle wall is subjected to a large biasing effect and a sharp increase in the biasing moment, which reaches its maximum value during the excavation of step III of the first hole. The biasing effect of the middle wall was gradually weakened and stabilised by subsequent excavation. However, the value of the bending moment after stabilisation is larger than that before the construction of the first hole, and the bias bending moment curve shows asymmetric changes, and the time course curve of the bias bending moment shows a ‘W’ shape with flat ends, and the bias bending moment curve shows a ‘W’ shape with flat ends. However, the eventual biasing effect was always present and it was not possible to harmonise the deformation of the left and right sides of the middle wall. In addition, the staggered construction of the left and right tunnels will result in the completion of the construction with the middle wall slightly offset to the side of the pilot cavern, this will cause the diaphragm wall structure to deform and squeeze against the secondary lining sidewalls, resulting in greater deformation of the initial support, which will lead to a significant increase in the risk of bending, torsion and shear failure of the tunnel structure and the middle wall.

Construction recommendations

By analysing the mechanical response response of model tests and numerical simulations for the construction of a large span continuous arch tunnel and the damage of the middle wall. Based on the research results, the following construction recommendations can be given:

• (1) During tunnel construction, due to the surrounding rock stress, the initial support structure load change frequently and complex, should be applied as early as possible spray anchor support and as soon as possible to complete the closure of the initial support into a ring. Monitoring and measurement should be strengthened during construction, especially for the construction step with high impact on construction, timely and accurately grasp the dynamic changes of surrounding rock and supporting structure during construction. Prevent the surrounding rock and lining structure from being stressed too quickly, and take relevant measures in time to ensure the safety and smooth progress of the construction.

• (2) Due to the asymmetric construction of the continuous arch tunnel, the middle wall will generate significant biasing effect, and its large biasing moment may cause bending and torsion failure and shear failure of the middle wall and even the supporting structure, it can pose a threat to the safety of the construction. Therefore, it is crucial to take stratum reinforcement measures to control surrounding rock deformation, and pre-grouting can be taken to reinforce the stratum, small conduit or pipe shed before excavation. The casting of the middle wall and the closing time of the secondary lining must be completed as soon as possible after the excavation is completed.

Limitations

• (1) Compared to actual field conditions, the model tests are still somewhat simplified. The surrounding rock stresses in real sites are influenced by various complex factors, such as the heterogeneity of the surrounding rock and the degree of construction disturbance. These factors may lead to deviations in the distribution and release rate of surrounding rock stresses from the actual conditions.

• (2) The research presented in this paper primarily focuses on model tests and numerical simulations, aiming to reduce the time and economic costs associated with on-site monitoring by conducting analyses under identical working conditions. However, the study lacks validation through field data comparison. Therefore, in the“Future Work”section of this paper, we actively supplement measured results to further improve our research.

Conclusions

Based on the K10 + 075 ~ K10 + 175 section of the Maling Canyon Tunnel of the North Ring Road in Xingyi City, Guizhou Province, which is a two-way six-lane continuous arch tunnel. Model tests and numerical simulations of the mechanical response to the construction of a large-span continuous arch tunnel were carried out. The displacement and deformation of surrounding rock and lining structure during the construction of large-span continuous arch tunnel, the study of stress release law and the study of bias failure mechanism of middle wall have been thoroughly investigated, and the following conclusions were drawn:

• (1) After the completion of the pilot tunnel and the central wall pouring, no significant changes were observed in the crown settlement of the left and right tunnels. This indicates that the construction of the pilot tunnel and the central wall has a relatively minor impact on the crown settlement of the tunnels, with similar settlement patterns observed in both tunnels. Regarding surface settlement, at the end of the pilot tunnel construction and central wall pouring, the settlement values at various surface points were symmetric about the central wall. As the left and right tunnels were excavated, the settlement trough of the surface settlement curve shifted towards the right tunnel and eventually became symmetric about the central wall. Therefore, it is essential to enhance the monitoring and measurement of twin tunnels during construction and promptly implement effective control measures to ensure safe construction

• (2) During tunnel construction, the structural deformation of the tunnel undergoes three distinct phases: “pre-excavation deformation → rapid deformation → convergent deformation.” Prior to the excavation face reaching the monitoring section, the disturbance caused by the excavation process ahead of the face induces minor pre-excavation deformation in the monitoring section, accounting for approximately 25% of the total settlement. As the excavation face reaches the monitoring section, the crown settlement changes rapidly, with the settlement caused by the excavation process accounting for approximately 70% of the total settlement. When both the left and right tunnels are excavated simultaneously, the excavation of the right tunnel also affects the crown settlement of the left tunnel. After the right tunnel (the trailing tunnel) is completed, the displacements of the pilot tunnel, left tunnel, and right tunnel all enter the convergent deformation phase, which accounts for approximately 5% of the total settlement. The influence of different excavation stages on crown settlement is in the order of Step I > Step II > Step III. Therefore, during the construction of twin tunnels, it is essential to promptly implement initial support and enhance the monitoring of tunnel lining to ensure safe construction.

• (3) During the excavation process, the stress variations in the surrounding rock and the lining structure experienced three stages: Stress concentration → stress release → stress stabilization. The impact of different excavation steps on the surrounding rock stress was in the order of Step II > Step III > Step I. The horizontal loads transferred by the initial support induced significant horizontal thrust in the central wall. Additionally, due to the asymmetric excavation of the twin tunnels, the vertical loads transferred by the initial support caused an eccentric loading effect on the central wall. This eccentric loading effect reached its maximum during the construction of Step III on the left tunnel side and gradually decreased and stabilized after the excavation of the right tunnel was completed. The eccentric loading moment curve exhibited a “W” shape with flatter ends.