Introduction

Typical individuals tend to bisect a horizontal line with a 1–2% error to the left of its true centre1,2,3. This bias, so-called “pseudoneglect”, is a robust behavioural observation that has been repeatedly demonstrated in numerous visuospatial tasks4,5. The underlying mechanism has perplexed researchers for decades, with theories pointing to asymmetrical attention circuits6,7 and interhemispheric imbalances in neurotransmitters8. However, both left and right biases have been found in different tasks depending on a number of task-specific factors and participants’ typical direction of scanning5. These findings indicate that the direction of human visuospatial biases is not consistent across tasks or individuals, and uncover a gap in explaining visuospatial biases from a unified computational theory.

Over the past two decades the Bayesian decision theory9,10 has gained prominence as a theoretical framework for understanding both human behaviour and brain’s processes, from perception to action, including explaining attentional asymmetries observed in stroke patients with unilateral neglect11,12. Could this framework also explain the computational mechanisms underlying biases in spatial perception?

According to the Bayesian framework, perception is an active process. Rather than passively registering information from the environment, the brain makes inferences about the most likely causes of incoming sensory data, given prior knowledge, or top-down predictions. A key assumption of this theory is that individuals’ weigh their decisions toward the more reliable source of information, be that from our senses or from prior knowledge13. In other words, when sensory information is deemed reliable, it will be taken into consideration in the inference process more so than when it is deemed unreliable, and similarly for the prior knowledge. Bayesian models have been very successful in explaining various cognitive processes14, from language acquisition to sensorimotor control, visual perception, and reward-based learning15.

The Bayesian approach has also been put forward to understand hemineglect11, a clinical condition typically following right hemisphere damage, and characterised by a substantial attentional bias towards the right (ipsilesional) side of space16,17. Patients with unilateral neglect fail to orient or react to stimuli on the contralesional side of space in daily life as well as in neuropsychological testing. Specifically, they tend to bisect lines to the right of the true midline (that is, the opposite of the previously described pseudoneglect). According to Garrido and Deouell11, the core deficit in neglect may arise from a precision asymmetry on the prior expectation about objects in the left and right space, with a reduced precision weighting of left side inputs, compared to the right.

This proposed mechanism may also be useful for understanding pseudoneglect. As their names suggest, pseudoneglect and unilateral neglect are considered two intrinsically linked phenomena18. Many studies have found that the two phenomena present with similar susceptibilities to a variety of modulating factors5. Varnava and coauthors19 showed that neurotypical individuals with a pre-existing left pseudoneglect (i.e., rightward bias) were more prone to exhibiting typical neglect-like behaviours when receiving inhibitory brain stimulation in the posterior parietal regions, suggesting shared neural mechanisms underlying pseudoneglect and neglect. Therefore, we hypothesise that pseudoneglect may also arise from an asymmetry in the brain’s encoding of prior expectations of objects in space.

To test our hypothesis of a Bayesian account of spatial biases, we used the ‘Coin Task’, a visual decision-making paradigm that captures human behaviour that is consistent with the Bayesian decision framework20,21. In essence, participants estimate the location of a hidden coin which falls into a pond, using both visual information about the splashes it makes (i.e., sensory evidence or likelihood), and prior expectations about where the coin is more likely to fall, which is learnt over the course of the experiment. The variance of prior expectations and sensory evidence are orthogonally manipulated.

We have conducted multiple versions of the Coin Task in our lab22,23,24,25. These studies have repeatedly shown that people flexibly adjust reliance on prior and likelihood information in accordance with their relative reliability. An exploratory analysis conducted on some of those data initially revealed a significant rightward shift in participant’s prior representation of the coin’s location in space, relative to its true location. In contrast with the prevailing literature, this finding suggested an overall rightward, rather than leftward, attentional bias.

To investigate the robustness of this surprising finding, Study 1 examines the meta-analytic evidence for a rightward bias across seven experiments and N = 1750 individuals using variations of the Coin Task.

Given that this rightward bias is consistent with the core syndrome of clinical spatial neglect, in Study 2 we developed a novel behavioural training protocol aimed at correcting this bias in N = 83 neurotypical individuals. We hypothesised that across all experiments participants would show an overall rightward bias in the prior expectations of objects in space, but that this bias would shift after our training intervention. To examine whether the effects of the training intervention generalise beyond the context of the Coin Task, it is essential to employ a well established measure of spatial attention biases. For this purpose, we selected the Line Bisection Task—a commonly used visuospatial paradigm for assessing pseudoneglect. Although the Coin Task and Line Bisection Task have discrepancies in task settings, with the former related more to probabilistic inference and the latter to perceptual judgement, both require estimating a location relative to a reference point through an action. Additionally, they are both sensitive to lateralised attentional biases in horizontal space. We therefore hypothesised a similar shifting pattern in the Line Bisection Task.

Methods

Participants

All experiments were conducted online and were approved by the University of Melbourne research ethics committee (research ethics 20592). All participants provided written informed consent prior to data collection. The research was performed in accordance with the Declaration of Helsinki. Participants were recruited using the University of Melbourne psychology research participation pool and online survey platform (Prolific; www.prolific.com). All participants completed a self-reported questionnaire to confirm that they had normal or corrected-to-normal visual acuity, and no history of neurological, psychiatric disorders or substance use (via Qualtrics online survey platform (www.qualtrics.com). Participants were compensated with course credits or £5 per hour for their time. All questionnaire and behavioural data were collected in an anonymised way to protect data privacy.

Study 1 comprises seven experiments and Study 2 is also referred to as experiment 8. Participant details of study 1 and 2 are summarised in Table 1 below. We note that there is variability in sample sizes across experiments. Experiment-specific sample sizes were determined as appropriate to address the questions of interest for each individual study listed. These research questions were mostly unrelated to each other and indeed unrelated to the current study. Whilst describing the rationale for each experiment and their sample size choice is beyond the scope of this paper, the full details can be found in the relevant cited papers22,23,25.

Table 1 Demographic table for Study 1 and 2.
Full size table

Power

For Experiment 8, since a shift in prior mean at baseline could be reliably detected in Experiment 1–4 with a minimum sample size of 80, we adopted this sample size to ensure a robust chance of observing a similar shift in prior mean at baseline.

Stimuli and apparatus

The experiments were built using the programming software PsychoPy 3 version 2020 (Experiments 1–7) and version 2022 (for Experiment 8)26. The minimum requirement for screen resolution was 1172 × 553 pixels. It was expected that all participants completed the experiment on a full-screen desktop or personal computer and sat at a comfortable distance away from the screen. All stimuli were set against a grey background and scaled as per the width unit defined in PsychoPy 3. All experiments took about 1.5 h to complete.

The Coin Task

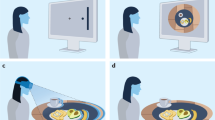
The procedure of each experiment has been described in detail previously. Here we explain the Coin Task because we conducted our meta-analysis using data from this specific task. In brief, the Coin Task21 (see Fig. 1) is a spatial inferential task used to model how participants use uncertain prior and likelihood information in decision-making. Participants were told that a coin (1.6% screen width in diameter) was thrown into a pond and were instructed to guess the location where the coin landed. To create a prior expectation, the participants were told that the person who threw the coin (illustrated at the beginning of the experiment, Fig. 1A) aimed at the centre of the screen (i.e., the prior mean). However, their throw was imperfect, meaning that the accuracy of the thrower (how often the coin fell close to the centre) varied across experiments and blocks and was sampled from Gaussian distributions with a given variance (i.e., high or low prior variance, see Fig. 1B). While the coin itself was hidden “underwater” during the moment of estimation, its “splashes” were visible through five dots of equal size (1.6% screen width in diameter). These splashes provided the sensory information (or likelihood) for the coin’s location. The horizontal positions of these five dots were drawn from a Gaussian distribution with a mean of the horizontal coin position in that trial and an assigned variance (i.e. high or low likelihood variance, see Fig. 1A).

Fig. 1
figure 1

Coin Task paradigm for experiment 2. The image depicts an example configuration from Experiment 2. Note the individual configurations for remaining experiments in Table 1, which use alternative levels of likelihood and prior variance. (A) Participants are shown an image of the thrower aiming at the centre of the screen at the beginning of the experiment, and they implicitly learn the prior’s mean and variance over the course of the trials. (B) The design for Experiment 2 is depicted graphically as varying levels of likelihood variance, manipulated as the distribution of splashes on each trial (Ln = narrow likelihood; Lw = wide likelihood) and varying levels of prior variance, manipulated through the accuracy of the coin thrower which is encoded by varying levels of variation of the coin’s location on each block (Pn = narrow prior; Pw = wide prior). (C) A single trial is shown with the time course: five blue dots are shown to represent the ‘splash’ the coin creates when it is thrown into the pond (upper panel). Participants are asked to move a blue “net” to the location where they believe the coin has landed (middle panel). Once a response is made, the coin’s true location is revealed (yellow dot, lower panel).

Full size image

Participants indicated their estimation of the coin’s location (i.e., the posterior) by moving a vertical blue bar (3.2% of screen width) across the screen. Only the x-axis location was relevant for the task because the blue bar covered the span of the screen vertically. After making a response with the spacebar, the true position of the coin was revealed as a yellow dot and a point was given if the blue bar captured the hidden coin (see Fig. 1C). Feedback (i.e., “Correct!” on screen) was also provided when correct responses were made. Prior studies21,22,23,24,25 have repeatedly shown that people respond in a Bayesian near-optimal manner in the Coin Task.

The true position of the coin was randomly drawn from a Gaussian distribution and centred at the middle of the screen with different levels of variance. The splash was represented by five identically sized dots varying in spread. The spread of the “splash” dots, also based on a Gaussian distribution, represented sensory information’s uncertainty. Low likelihood uncertainty trials had dots closer together, offering a more reliable coin location indicator, while high uncertainty resulted in wider spreads, making it a less reliable guide. Variations in the specific standard deviations for prior expectations for each experiment are detailed in Supplementary Table 3.

While previous reports focused on the weighting of prior and likelihood, here we focused on the mean of inferred prior locations of each experiment.

Procedure

Study 1

Experiments 2, 3, 4 and 6 followed a 2 × 2 design configuration for prior and likelihood variance (low, high). Experiments 1, 5 and 7 had a third likelihood condition (for the purposes of the individual research goals). This resulted in a 2 prior × 3 likelihood configuration, or 1 × 3. All trials were included in the main analysis as the prior mean remained consistent despite differing levels of prior variance and likelihood. Details of these configurations are noted in Table 1.

Study 2 (Experiment 8)

To investigate whether the rightward bias observed in Experiments 1–7 could be recalibrated, we introduced a training protocol and incorporated it with a modified version of the Coin Task (see Fig. 2 for detailed study flow). Since the primary aim was to shift participants’ mean prior expectations regarding the coin’s location, we adopt a 1 prior × 1 likelihood configuration (σprior = 0.085, σlikelihood = 0.15).

Fig. 2
figure 2

Study flow for experiment 8. Each phase of the coin estimation task has 3 blocks; each block has 40 trials followed by a 30-s break. For simplicity, it is stated as “3 blocks = 120 trials” in the figure. LBT refers to Line Bisection Task.

Full size image

Procedure for bias recalibration task

Participants completed a three-phase Coin Task aimed at recalibrating a bias in the expectation of objects in space. Each phase had three blocks of 40 trials, separated by 30-s breaks to reduce fatigue. The entire experiment spanned a 2-h window without specific time constraints for blocks or trials. Participants were asked to estimate the coin’s location across all phases, but the instructions changed slightly between phases as detailed below.

Phase 1: Pre-training phase. Participants were informed that an imperfect coin thrower aimed at the screen’s centre, with five blue dots serving as reference points (likelihood information) for estimating the coin’s location. The actual location, indicated by a yellow dot, was revealed for 1.2 s at the end of each trial, along with a "Correct!" message if participants successfully captured the hidden coin on the net. This phase aimed to establish a baseline for the participants’ initial expectations about the coin’s location (i.e., prior mean).

Phase 2: Training phase. We induced a leftward shift in participants’ prior mean by shifting the distribution of the true coin position by 8% of the screen width towards the left (see Fig. 3). The exact extent of this shift was not disclosed but was described to participants as being caused by a strong right-to-left wind causing the coin to deviate slightly to the left of the pond centre. Similar to phase 1, the shifted coin location was revealed at the end of each trial to facilitate learning and feedback was also provided.

Fig. 3
figure 3

Illustration of training manipulation on prior mean in probability density distribution. The red dotted distribution represents the shifted prior distribution induced by the manipulation (i.e., in phase 2), the black solid distribution represents the original prior distribution in phase 1 and 3. The x-axis is the horizontal location of the screen. The arrow refers to the leftward direction of the manipulation.

Full size image

Phase 3: Post-training phase. In this final phase, the manipulation regarding the true location of the coin was removed. Participants were also informed that the true coin location would not be revealed post-trial, and the “Correct!” sign feedback was replaced by an accumulative number of correct responses every 10 trials. This phase aimed to examine whether the induced left shift in the previous phase would persist.

Line bisection task

We used the Line Bisection Task to examine whether the induced shift in the prior mean induced in the recalibration version of the Coin Task is generalisable. This task is a common measure for unilateral neglect and pseudoneglect which essentially assess participants’ deviation from the true midpoint in their subjective perception of a horizontal line’s centre5.

Participants were first introduced to 2 practice trials before entering the main experiment. Following each phase of the Coin Task, participants were instructed to complete 30 trials of the Line Bisection Task where participants marked the centre of horizontal lines with different sizes and locations on the screen (Fig. 4). Participants were allowed to make multiple adjustments by re-clicking or sliding the indicator and were instructed to press the “Continue” button once they were ready for the next trial.

Fig. 4
figure 4

Line Bisection Task setup. The Line Bisection Task consists of three phases, each followed by the coin estimation task. each phase comprises 6 blocks, with each block containing 5 trials that represent 5 variations of horizontal lines. Only one line is shown on each trial. The three panels in the figure each represent a different set of variations specific to that phase. The line position and length were designed differently in three phases to avoid practice effects. Participants were asked to indicate the midpoint of each horizontal line.

Full size image

Data processing

Data processing was performed using R studio27 (Version 2023.03.0 + 386).

Data exclusion

Outlier detection was based on a median absolute deviation (MAD) method28 that excluded extreme posterior responses in trials. Within each study included in the meta-analysis, we removed prior mean responses which exceeded + /− 3SDs and + /− 0.3 of the screen’s centre, as this indicated non-compliance on the task. In total, 44 participants were excluded across Experiments 1–7. In Experiment 8, seven participants who reported taking therapeutic or illicit drugs were initially excluded due to potential impairments in sensory processing. Further, by applying the MAD criterion on each participant’s sensory weight (slope), six participants with an outlier slope in any of the three phases were excluded. Additionally, seven participants were further excluded for making extreme responses corresponding to a sensory weight > 1 or < 0, as these responses indicate non-compliance.

General analysis

We modelled the participants’ estimation of the coin location as a weighted sum of the sensory information (likelihood) and prior knowledge.

Estimating individual participants’ sensory weights

We adopted a least squares procedure to regress each participant’s estimated coin location against the likelihood mean27 (lm in stats). Since the slope of the best-fitted regression line quantifies how much weight participants rely on sensory data over prior knowledge, we call the slope sensory weight sw in this paper. A slope of 1 represents complete reliance on sensory information, while a slope of 0 indicates exclusive dependence on prior information. All values in between correspond to a given relative weighting of both sensory and prior information. We also calculated the intercept (\({\beta }_{0}\)) using the same procedure.

To test the assumption that participants respond in a manner consistent with Bayesian expectations, we conducted linear mixed modelling or mixed ANOVA on the sensory weighting parameters. Detailed methodologies for these analyses can be found in the supplementary material.

Estimating individual participant’s subjective prior mean to evaluate pseudoneglect

Based on the Bayesian rule, in the Coin Task participants estimate coin locations by combining prior and likelihood information according to their relative precision (i.e. inverse of variances \(\frac{1}{{\sigma_{{}}^{2} }}\)). The above relationship can be expressed using Eq. (1)21,29.

$$X_{est} = \frac{{1/\sigma_{p}^{2} }}{{1/\sigma_{p}^{2} + 1/\sigma_{L}^{2} }} \mu_{p} + \frac{{1/\sigma_{L}^{2} }}{{1/\sigma_{p}^{2} + 1/\sigma_{L}^{2} }} \mu_{L} = \frac{{\sigma_{L}^{2} }}{{\sigma_{L}^{2} + \sigma_{P}^{2} }} \mu_{p} + \frac{{\sigma_{P}^{2} }}{{\sigma_{L}^{2} + \sigma_{P}^{2} }} \mu_{L}$$
(1)

\(X_{est}\) is the estimated coin location. σL2 is the likelihood variance; σp2 is the prior variance. \(\mu_{L}\) and \(\mu_{P}\) are the means of likelihood and prior distributions, respectively.

As described in the last section, for each prior and likelihood combination, we linearly regressed between \(X_{est}\) and \(\mu_{L}\), expressing as Eq. (2).

$$X_{est} = \beta_{0} + \beta_{1} \mu_{L}$$
(2)

A comparison of Eq. (1) with (2) shows that, for an ideal Bayesian observer, the slope of the regression line (\(\beta_{1}\)), i.e., sw, equals to (\(\sigma_{P}^{2} /\sigma_{P}^{2} + \sigma_{L}^{2} )\). The comparison also reveals that for an ideal Bayesian observer \(\beta_{0}\) equals to \(\left( {1 - sw} \right)*\mu_{P}\), meaning each participant’s subjective prior mean can be estimated using Eq. (3):

$$\mu_{P} = \frac{{\beta_{0} }}{{\left( {1 - sw} \right)}}$$
(3)

To test the hypothesis that participants would show a rightward spatial bias when encoding information about the prior’s location in space, we compared participant’s represented prior mean acquired using Eq. (3) against the true prior mean. One-sample t-tests were used with effect size d to compare means.

Study 1-specific analysis: meta analytic process

We evaluated existing behavioural data across seven experiments from the Cognitive Neuroscience and Computational Psychiatry Laboratory at the University of Melbourne collected between 2021 and 2022. Pre-registration details can be found at https://osf.io/atyus. At the time of analysis, each experiment remained unpublished, except for one experiment published in a preprint repository23. Given this, an individual participant data (IPD) or retrospective pooled analysis was selected as the most appropriate meta-analytic method30,31.

An IPD meta-analysis uses individual participant data from published and unpublished studies to generate a pooled summary estimate31,32,33. In this case, the summary estimate was the horizontal screen coordinate of the participant’s represented prior mean. For the clearest interpretation of the magnitude of the bias with respect to on-screen measurement, a meta-analysis of means27 (metamean in meta) was deemed the most appropriate method of analysis34,35,36,37. A two-step approach using the inverse variance method with fixed-effects was also selected to achieve greater sensitivity given the expected similarity between studies, and to visualise trends across individual studies before calculating the pooled estimate34.

First, individual study estimates of each participant’s prior mean were recalculated using the equations above. Since the objective prior mean remained at 0.0, all trials were included in the generation of an overall summary statistic. Finally, for our meta-analysis of means, individual study estimates were weighted and pooled using the fixed-effect inverse-variance method, given the assumption that all samples were measuring the same underlying true effect34. The summary estimate was calculated as a weighted mean of the individual study estimates, meaning that smaller studies, with greater expected variance, were weighted less, and larger studies were weighted more34. Finally, sources of heterogeneity were assessed using Chi-squared tests and I236. The model for the fixed effect meta-analytic approach was as follows.

$$Summary\;\hat{\beta } = \frac{{\Sigma_{{s = 1 W_{s} \beta_{s} }}^{s} }}{{\Sigma_{{s = 1 W_{s} }}^{s} }},W_{s}^{{}} = \left[ {Var(\hat{\beta }_{s}) + \sigma_{\beta }^{2} )} \right]^{ - 1}$$
$$SE\;Summary\;\hat{\beta } = \sqrt {{\text{var}} iance} = \sqrt {\left[ {\Sigma_{s = 1}^{s} W_{s} } \right]}^{ - 1}$$

wheres = β + εs, s = 1 to S studies, β = true common effect estimate (e.g., pooled prior mean), εs = within-study variance, s = estimated effect estimates in study s.

Study 2-specific analyses

Statistical analysis Coin Task

We first examined whether participants had a rightward bias before training. We excluded the data from the first 50 trials of the pre-training phase while participants were still learning the task. A Wilcoxon signed-rank test was performed to compare prior means in pre-training phase to zero (screen centre). We used a Kruskal–Wallis rank-sum test to compare prior means across experimental phases. For post-hoc comparisons, pairwise Wilcoxon tests were used with Bonferroni’s correction.

Generalisability of training effect to the Line Bisection Tasks

We performed a one-way ANOVA to compare subjective midpoints on the Line Bisection Tasks across experimental phases. Pairwise t-tests with Bonferroni’s correction were used for post-hoc comparisons.

Significance statement

Our meta-analysis across seven experiments in 1750 neurotypical individuals shows that the spatial attentional bias known as pseudoneglect, despite typically manifesting as a leftward bias behaviourally, is caused by a rightward, not leftward, internal bias in the expectations of objects in space. Moreover, we show that this bias is malleable with a simple behavioural intervention that manipulates prior expectations. By successfully recalibrating a spatial bias, our research highlights the potential for cognitive adjustments in addressing spatial cognition challenges such as those in unilateral spatial neglect after stroke.

Results

Evidence for a rightward spatial bias?

All studies showed a significant rightward bias in the location of the prior mean. Positive numbers indicated placement to the right of centre, while negative numbers indicated the left of centre.

Given that our samples were unbalanced for sex, we tested whether this could introduce a demographic bias. A comparison between male and female participants in Experiment 7 (the experiment with the largest sample size) revealed no significant difference in prior mean (male: 0.0213; female: 0.0156), Z = 0.0208, p = 0.9834.

Meta-analytical evidence for an effect across samples

The pooled estimate of participant’s prior mean fell to the right of the true mean M = 0.0160, 95% CI [0.0135; 0.0185]. The model showed low to moderate heterogeneity between studies τ2 < 0.0001, χ2 = 10.34, df = 6, p = 0.11, I2 = 42%. Figure 5 shows the meta-analysis of means results with study weightings. A random effects model was also conducted to account for potential high heterogeneity (assessed only on post-hoc evaluation), however this produced identical results. For additional interpretation, meta-analysis using effect size d was also significant, and can be found in Supplementary Table 1.

Fig. 5
figure 5

Meta-analysis results. Meta-analysis results show each experiment’s prior mean, standard deviations SD, sample size n, and weightings using the inverse variance method. The size of each square represents its weight within the analysis. Horizontal lines surrounding the box indicate the prediction intervals for each study. The black diamond denotes the overall estimate, and the red bar shows the overall prediction interval for the model. The red dotted line denotes the true prior, screen coordinate 0.0.***p < .05.

Full size image

The fixed effect model showed an overall rightward bias of 0.0160 of a screen unit from the true centre. The overall model was significant, suggesting that the participant’s encoding of the prior mean was shifted 1.6% of the total screen width to the right of its actual location.

Participant’s posterior responses show a leftward shift with respect to priors

We next asked whether the rightwards shift of the prior mean was consistent with a motoric bias in the participant’s response, i.e., their decisional output, or posteriors. To answer this question, we calculated the overall location of the participant’s posterior across the task. Since the position of the target was presented at random to form a normal distribution around the X axis of the target coin (0.0), any deviations of the posterior from 0.0 gave us a measure of whether the participant favoured the left or right side of space in their motoric output, i.e., where they guessed the position of the target on any given trial. The overall effect across studies showed a significant overall shift of 0.24% to the right of the target coin, as shown in Fig. 6. This finding was significant at a meta-analytic level and within each study, except for Study 1. Furthermore, a paired samples t-test revealed that the participant’s overall posterior (M = 0.0024) was significantly leftward to their representation of the prior (M = 0.0160), t(1748) = − 11.22, p =  < 0.0001, d = − 0.27, with a mean difference of − 0.014 (see also Supplementary Table 2 for further details).

Fig. 6
figure 6

Overall prior mean shift (A). Shows participant’s encoded prior mean by experiment. Each coloured violin plot represents a single experiment. The black dot represents each study’s subjective prior mean. The X axis shows the location of the encoded prior mean as it appears on screen (note that the full screen width ranged from − 0.5 on the leftmost edge of the screen, 0.0 in the centre of the screen, to + 0.5 on the rightmost edge of the screen). Only the X-axis was measured in this task due to the net design (see Methods), therefore the Y axis here illustrates individual participant data points across the seven studies. The individual Y position within the experiment is arbitrary, used to reduce overlap between data points. The true prior mean is indicated by the black line at 0.0, while the solid red line shows the pooled estimate of the subjective prior mean across studies, which appears to the right of the true centre. All studies showed that the participants’ subjective representation of the true centre was, on average, to the right-hand side of its actual location on screen. Rightward bias in posterior responses across experiments (B). The vertical reference line x = 0 (as shown in black line) indicates the centre of the screen. Each coloured violin plot represents a single experiment. The black dots represent the mean of the posterior responses for that study. The red line indicates the common effect across studies for the average posterior response. A rightward bias was found across experiments. Note the discrepancy in the magnitude of the rightward bias between the participant’s prior mean and their posterior response.

Full size image

Recalibration protocol reduces rightward bias in the Coin Task

Figure 7 shows participants’ prior means across the 3 phases of the modified Coin Task in Study 2 with the recalibration training. Firstly, we show that in agreement with the meta-analysis results, there was a rightward shift in the prior mean for the pre-training phase (Mdn = 0.026, MAD = 0.073, Z = − 4.54, p =  < 0.001). We found a significant main effect of experimental phase on prior mean (Kruskal–Wallis, χ2(2) = 69.7, p < 0.001) and post-hoc comparisons indicated that participants’ prior means in the post-training phase significantly shifted to the left (Mdn = 0.003, MAD = 0.046) as compared to baseline (Mdn = 0.027, MAD = 0.078; p = 0.0089; Fig. 7). The large effect size η2 = 0.267 suggests that a substantial training effect was induced in our recalibration protocol. Importantly, the reduction of the original rightward bias in the prior was retained in the post-training phase, demonstrating a lasting effect after removal of the manipulation.

Fig. 7
figure 7

Prior means are recalibrated across experimental phases in the Coin Tasks. The vertical reference line x = 0 (as shown by the grey line) can be viewed as the centre of the screen when participants undertook the experiment on a laptop or computer. Datapoints on the right side of the line indicate a rightward deviation from the centre and data points on the left side of the line indicate a leftward deviation from the centre. The dotted line (x = − 0.08) represents our experimental manipulation in the training phase, which was an 8% horizontal shift of the prior (i.e., true coin location) to the left of the midline. The green dots represent the participants’ estimated prior mean across the 3 phases of training (pre, during, and post). The boxes indicated the range in which 50% of the data lies and the whiskers extend to the max/min data point within 1.5 of the interquartile range. The middle lines in the boxes correspond to the median in the distributions. The figure illustrates that participants’ prior means were initially shifted to the left with respect to the centre by the manipulation. Although there was a partial reversion towards the baseline after removal of manipulation, the prior means in the Post-Training Phase remained to be left of the baseline, suggesting the shift was retained in the Coin Estimation Task. **p < .01.

Full size image

Rightward bias mitigation with training does not generalise to the Line Bisection Task

Generalisability of the training effect was tested by examining whether the same effect could be found in a task commonly used to assess neglect such as the Line Bisection Task. A one-way ANOVA test did not show a significant effect of recalibration (experimental phase) on participants’ subjective prior means, F(2,246) = 0.644, p = 0.526. This suggested that the observed training effect of the Coin Task failed to generalise to the Line Bisection Task.

Figure 8 illustrates participants’ performance in bisecting horizontal lines. Despite the non-significant change across phases, participants’ subjective midpoints in both the pre-training (M = − 0.004, SD = 0.010) and the training phase (M = − 0.004, SD = 0.012) significantly deviated from the centre to the left (Z = − 3.53, p < 0.001; t(82) =  − 3.02, p = 0.003). These are consistent with the leftward bisection errors that have been predominantly found in previous studies5,18. However, the magnitude of errors in the current study (0.4%) is notably smaller than the commonly reported 1–2% deviation1,2.

Fig. 8
figure 8

Subjective midpoints in the Line Bisection Task unaffected by the recalibration protocol. The vertical reference line x = 0 (as shown in grey line) indicates the centre of the screen. The shaded area indicates the commonly reported 1–2% deviation. The green dots represent the participants’ responses across the 3 phases of training (pre, during, and post). The boxes indicated the range in which 50% of the data lies and the whiskers extend to the max/min data point within 1.5 of the interquartile range. The middle lines in the boxes correspond to the median in the distributions.

Full size image

Discussion

The current study demonstrates meta-analytical evidence for a robust rightward bias in the expectation about objects in space. We show this in data from N = 1750 individuals in seven experiments using slight variations of the Coin Task (Study 1, Experiments 1–7). This study, together with previous works in pseudoneglect5, challenges the conventional belief that humans manifest a leftward attentional bias, thereby paving a new path for understanding the internal mechanisms of spatial attention through Bayesian computation. We then developed and tested a novel behavioural training protocol (Study 2) to examine the potential for recalibrating participants’ spatial bias. While our training intervention resulted in the hypothesised bias shift in the Coin Task, it failed to generalise to the Line Bisection Task, one of the standard tasks for assessing pseudoneglect and unilateral neglect in stroke patients.

Variable nature of spatial biases

Since its introduction by Bowers and Heilman in 19804, pseudoneglect has consistently been depicted as a leftward bias. However, a meta-analysis by Jewell and McCourt5 challenged this notion, revealing that the direction and magnitude of biases in spatial perception can vary due to multiple factors. Recent studies also demonstrated that different spatial tasks tap into distinct aspects of spatial representation38,39. Our finding of a rightward bias further underscores this variability and reinforces the idea that different tasks reveal different facets of spatial representation. Jewell and McCourt5 showed that factors such as age, cueing, kinesthetic influences, and reading direction have been shown to influence pseudoneglect outcomes with a rightward, rather than the typical left, bias. Below we discuss these factors in turn arguing that none of these factors can explain our highly robust effect, further implying mechanisms other than those underlying pseudoneglect are at play in the bias we observed.

Age

Based on the meta-analysis of Jewell and McCourt5, younger adults tend to show a leftward bias on the line bisection, and older adults a rightward bias. Speculative explanations include age-related changes in the right hemisphere’s spatial attention40, however research has been inconclusive. Despite a predominantly young-adult sample, our results showed a rightwards bias instead, which is in contrast to the reported associations between younger age and leftward pseudoneglect.

Cueing

Cueing was considered a significant factor in determining spatial bias in Jewell & McCourt’s meta-analysis5 and findings from Ochando and Zago41. Cueing refers to the use of visual signals or prompts that can subtly direct participants’ attention or expectations towards a specific area of the visual field, thereby affecting their responses. While our task attempted to minimise overt cueing by drawing stimuli from a random distribution around the centre of the screen, our paradigm depicts a man who is positioned facing slightly to the right, using his right hand to throw the coin towards the centre. This may have unintentionally biased participants to position themselves ‘as if’ they are mimicking the position of the person on screen. Perceiving the body positioning of the thrower may produce a slight rightward tilt of the body and eyes, consistent with a rightward shift in the person’s spatial ego centre41. However, an earlier study by Sato and Körding42 which employed the Coin Task, also reported a small rightward bias in the prior mean, despite the absence of any cueing related to a right-handed thrower. Instead, the prior distribution in this earlier study—with a mean at the centre—was presented explicitly on the screen throughout. That finding suggests that the rightward bias we observed in our meta-analysis is not solely attributable to the visual cue.

Kinesthetic influences

Jewell and McCourt5 reported notable rightward biases in kinesthetic tasks, where participants use touch or proprioception, rather than visual cues, to locate the midpoint of a line or object. The Coin Task used in our experiment is primarily a visual task where participants’ movements were restricted to pressing buttons on a keyboard to move stimuli on a computer screen. As a result, their responses rely heavily on cognitive processes such as probability estimation and inference. Such a task clearly diverges away from the reliance on physical movement or spatial-body awareness, yet our results surprisingly revealed a rightward bias, implying factors other than kinesthetic feedback at play.

Reading direction

According to Jewell and McCourt5, habitual visual scanning direction, as influenced by reading direction (i.e., typically right to left in western readers), was reported as a significant factor in modulating error in the Line Bisection Tasks. Specifically, individuals who scan the horizontal line from left to right tend to err significantly to the left of the midpoint. Although participants’ scanning direction was not explicitly measured and controlled for in the meta-analysis, all participants were required to speak and read English fluently, and we recorded their other languages (mostly Mandarin) via a questionnaire. Interestingly, even though almost all participants spoke languages which elicit a left-to-right scanning pattern, our task results still showed an unexpected rightward bias.

It should also be noted that while scanning direction has often been cited as a key driver of spatial bias, animal studies suggest a more nuanced picture. Spatial biases are not unique to humans and have been documented in several non-human species. For example, birds such as domestic chicks and Clark’s nutcrackers show a leftward attentional bias when identifying ordinal positions in spatial arrays43,44,45. Evidence from non-human primates is more mixed46, though rhesus monkeys exhibit a magnitude-dependent shift in spatial attention: a leftward bias for smaller numerosities and a rightward bias for larger ones47. These effects occur in the absence of language or cultural exposure, suggesting that spatial-numerical associations and lateralised attention may have a biological basis rather than originating solely from cultural practices such as reading and writing direction. Nevertheless, evidence also indicates that functionally similar behaviours across species may arise from distinct neural mechanisms48. We also note, however, that these tasks related to numerosity and ordinality are not directly comparable to the processes underpinning both the line bisection and the Coin Tasks employed here. Taken together with our Coin Task findings, these results support the view that anatomical and functional brain asymmetries emerge from a complex interplay of genetic predispositions and environmental influences49,50.

Sex

Overall, our data have a greater proportion of females than males, which could have influenced our results. The meta-analysis on the Line Bisection Task5 showed only a modest sex difference with males having a slightly greater leftward error than females. However, for both males and females these errors were leftward, not rightward as observed in our meta-analytic effects. Moreover, our comparison between male and female participants also revealed no significant difference. Hence, an unbalanced sample for sex is unlikely to explain our finding of a rightward expectation bias.

So what could be the reasons behind this unexpected finding of rightward bias in the current study? We propose the following potential explanations:

Perception depends on expectation

Dietz et al.51 showed that there are spatial asymmetries when forming probabilistic expectations. This functional asymmetry in the brain’s coding of space is consistent with the right-hemisphere dominance model, where the left parietal lobe monitors the right side of space and the right parietal lobe monitors both sides6. Consequently, the right side of space is arguably given more attentional resources, which could explain the bias to the right. Our findings suggest that the brain inherently possesses a rightward bias, and the leftward bias (behavioural output) found in some Line Bisection Tasks may be a result of over-correction. Note that in our data, the posterior response (behavioural output) was also seen to the left of the prior mean, which is consistent with this idea. However, it was still ever so slightly to the right of the midline. In the case of unilateral neglect, the inherent rightward bias is much more pronounced than in pseudoneglect, potentially leading to a persistent rightward bias even after over-correction. This aligns with the prevalence of rightward bias in neglect cases, supporting the notion that the brain’s internal processing favours the right side of space.

The Coin Task addresses how the brain learns to perceive the environment as participants build probabilistic expectations, or priors, through dynamic updating over a series of trials21,24,42. In contrast to traditional tasks (e.g., line bisection), the target object (the coin) is invisible. Rather than discerning on a static object or explicit recall52 (Brooks et al.) like in the Line Bisection Task, in the Coin Task, participants update their internal representational model indirectly through feedback and statistical inference over time.

Unlike previous studies that primarily measured participants’ final outputs in tasks such as Line Bisection, our novel methodology taps into internal biases on the expectations about objects in space. We propose that the leftward bias observed in previous pseudoneglect studies reflects the final behavioural output rather than the underlying cognitive process. The fact that with our methodology we can tap into people’s internal representations is a unique strength relative to previous tasks. Moreover, it aligns more closely with current models of perception, which propose that perception is an active process that depends both on input (stimulus) and on our expectations about said input. Indeed, we are constantly making predictions about the environment based on levels of uncertainty, change, and feedback13. In this regard, our task may better tap into core elements of spatial neglect, because without a percept, we move away from object-based (stimulus driven) orienting, and toward egocentric (internally driven) orienting of attention53.

Cognitive load induces rightward spatial bias

Cognitive load might also play a role in the observed rightward bias. Cognitive load can be conceptualised as the mental effort exerted during task performance54. In our study, the Line Bisection Task involves relatively simple perceptual judgments based on the straightforward presentation of horizontal lines, whereas the Coin Task requires participants to determine a hidden target location based on dispersed sensory cues, which introduces additional cognitive load during the decision-making process. Studies have suggested that such high cognitive load could lead to an asymmetrical bias in spatial processing, predominantly favouring the right visual field55,56.

Takio et al.55 demonstrated this effect across various age groups by manipulating cognitive load through unilateral (low load) versus bilateral (high load) target presentations. Under the cognitively more demanding bilateral condition, a consistent rightward spatial bias was observed in all age groups. The finding is further supported by another study56 which examined the direct impact of cognitive load on spatial processing. It was found that the processing of visual stimuli on the left visual field was more adversely affected than the right as working memory load increased, resulting in a rightward bias.

As discussed, we have considered the possibility that this increased cognitive load may contribute to the observed rightward bias in the Coin Task. The result of our meta-analysis is in line with the rightward bias commonly observed in tasks requiring high cognitive demands. Future studies will have to determine whether the spatial bias described here is a general cognitive phenomenon or a phenomenon specific to probabilistic inference tasks.

Despite differences in complexity between the Coin Task and Line Bisection Task, the latter remains valuable for assessing generalisability. As noted in the Introduction, the two paradigms share key features. Including the Line Bisection Task as a complementary measure allows us to examine whether training-induced changes in the Coin Task extend to a more established and perceptually grounded paradigm.

Spatial bias can be recalibrated with training

We have previously suggested that the bias in unilateral spatial neglect after stroke might be caused by a rightward shift in the prior expectation about objects in space11. By demonstrating a rightward spatial bias in neurotypical individuals that can be adjusted by altering prior expectations with training, our findings provide the empirical evidence underscoring the explanatory power of the Bayesian framework in explaining spatial biases. The current study distinguishes itself by being the first to observe and recalibrate internal representational spatial biases.

Existing literature on recalibrating attentional bias has primarily centred on prism adaptation, a technique extensively employed in both clinical settings such as unilateral neglect and non-clinical instances of pseudoneglect57. It involves daily visuo-motor training sessions in which people are asked to wear either right- or left-shifting goggles that directly shift their visual field to the neglected areas58. Although the initial effectiveness of prism adaptation is well-documented, the long-term efficacy of this technique remains a topic of debate. A recent meta-analysis indicated that the therapeutic effect of prism adaptation for post-stroke unilateral neglect failed to last in the long term59. Further investigation into prism adaptation for pseudoneglect recalibration implies that the transient nature of this technique may not be exclusive to treating unilateral neglect but might be a broader characteristic of how sensorimotor adaptation affects spatial cognition. Michel et al.60 noted that the aftereffects of sensorimotor adaptation in pseudoneglect recalibration typically persist only for the duration of exposure, with the system quickly returning to its baseline state once normal visual inputs resume. By successfully recalibrating a spatial bias through cognitive adjustments in prior expectations, our research highlights the potential for cognitive adjustments in addressing spatial cognition challenges such as those in unilateral spatial neglect after stroke.

Presentation modality (paper vs. computer)

Previous research done by Luh61 suggested that stimulus presentation methods, especially differences in the motor aspects, can influence the magnitude of pseudoneglect. It was found that the Line Bisection Tasks administered using paper-and-pencil tend to elicit stronger leftward biases compared to computer-based versions, indicating a possible motor contribution to the performance asymmetries on visuospatial tasks. As our study employed computerised versions of both the Coin Task and the Line Bisection Task, we acknowledge that the observed spatial biases may, in part, be influenced by the mode of presentation. However, we note that our computerised version of the Line Bisection Task still presented the same leftward bias seen in the paper-based version. To further examine this effect, future studies could implement a paper-based version of the Coin Task experiment to assess the generalisability of training outcomes across different modalities.

Recalibration was specific to the trained task—Why no generalisability?

Although participants’ rightward bias was successfully shifted towards the centre by training in the Coin Task, this effect was not observed in the Line Bisection Task. This limited generalisability suggests that either the training was not enough, or that its effectiveness is task-specific.

For an effect observed in one task to be generalised to another, the tasks should be sufficiently similar. The results from the current study imply that the Coin Task and the Line Bisection Tasks may not be that comparable as initially hypothesised. In other words, the observed spatial bias in these two tasks may be fundamentally different. A key factor that may contribute to this difference is the source of uncertainty in each task. In the Coin Task, uncertainty originated from the dispersion of sensory cues on the hidden target. In contrast, Line Bisection Tasks only involve straightforward presentation of horizontal lines. Hence the uncertainty was much lower and primarily came from participants’ internal perceptual noise (e.g., participants’ inherent abilities to accurately perceive the length and position of the line). Further, the uncertainty in the Coin Task is also present around the hidden target (coin position) and in the setup of participants’ expectations about objects in space (the prior for where the coin typically falls). It is also worth noting that the Line Bisection bias may be more closely related to the motor bias of right-handed participants62, whereas the prior mean in the Coin Task relates to internal representations of space. The fact that training effects did not generalise to the Line Bisection Task implies that the observed rightward bias may not represent a universal or task-invariant feature of spatial attention. Rather, it may be shaped by task-specific features, aligning with recent evidence suggesting that recent evidence indicating that spatial biases emerge from the interplay of various cognitive and perceptual processes across different context38,39. Thus, while perception is increasingly being understood as a form of probabilistic inference, the context-specific framing embedded in our task may also help explain the lack of generalisation observed.

It is worth mentioning that even conceptually comparable tasks do not guarantee similar effects or identifiable generalisation. For instance, Learmonth et al.38 found four sub-types of left–right spatial biases across different visual pseudoneglect tasks, and Mitchell et al.39 reported low consistency between similar tasks within the same participant. All these studies have suggested that pseudoneglect is likely a multi-faceted phenomenon38. Therefore, it may be unrealistic to expect a single training approach that can recalibrate all facets of spatial attention. Instead, damages to different aspects of the attentional network may lead to different patterns of spatial bias38.

Limitations and future directions

In the current study, we chose the Line Bisection Task to test the generalisability of the rightward bias effect. The Line Bisection Task was chosen due to its prevalent use in research and clinical settings. The task was also selected due to its similarity to the Coin Task, since they both probe actions as a means of evaluating visuospatial perception. However, our results, in conjunction with previous studies, raise concerns about the reliability of this task. Mitchell et al.39 demonstrated that the Line Bisection Task exhibits little reliability across sessions with respect to response bias (Chronbach’s α =  − 0.11 across sessions). It is thus also possible that an absence of generalisation in our study was due to the inherent instability of Line Bisection Tasks. The bisection task also has several variations39. Future studies should consider variations that produce a more reliable response bias, such as the landmark task39 (α = 0.80).

Musical expertise has been associated with a reduced leftward bias in the Line Bisection Task63,64. Our participants were overwhelmingly university psychology students, and while we did not ask them about their musical training, it is unlikely that a substantial proportion met the criteria for high musical proficiency, which typically involves intensive training over about seven years on average63. Nonetheless, future research should investigate whether musical expertise is related to the rightward bias observed here.

Another limitation of the meta-analysis is that it included only coin-task studies conducted within the same laboratory, which constrains the robustness and broader generalisability of our findings. Future research should aim to include replications by independent groups and employ alternative paradigms to determine the strength and reach of our observations. Finally, the robust rightward spatial bias found in our studies, its dissociation from the Line Bisection Task, and the multitude of divergent effects discussed above merit a reconsideration of the usefulness of the term ‘pseudoneglect’ as representing a unitary tendency related to the clinical syndrome. Rather, they highlight the (a)symmetry of spatial representation as a flexible, task-dependent phenomenon.

Conclusion

Our meta-analysis across seven experiments in 1750 neurotypical individuals robustly demonstrates a rightward internal bias in the expectations of objects in space. Moreover, we show that this bias is malleable, with a simple behavioural intervention that manipulates prior expectations. By successfully recalibrating a spatial bias, our research highlights the potential for cognitive adjustments in addressing spatial cognition challenges such as those in unilateral spatial neglect after stroke.

Data statement

Figures 5 and 6 plot parameters estimated from raw data which were previously used for different purposes and published in https://pubmed.ncbi.nlm.nih.gov/37988398/ (Experiment 4 and 6) and https://pubmed.ncbi.nlm.nih.gov/38190413/ (Experiments 1–3, and 7). Note however, that these parameters were not published elsewhere as those two prior publications addressed different questions. Data from Experiment 5 has not been published elsewhere.