Updated probabilistic seismic hazard assessment using M_wg (Das magnitude scale) to address moment magnitude (M) scale inaccuracies below 7.5: a case study from Northeast India

Abstract

This study uses the Das magnitude scale (M_wg) to improve probabilistic seismic hazard assessment (PSHA) in Northeast India, where traditional M scales introduce inaccuracies for events below M 7.5. The M scale is mathematically flawed in this range, being based on an equation derived for Ms ≲ 7.0—an inconsistency evident in the observed data. Using a unified earthquake catalog of 9,968 events, calibrated to M_wg, in conjunction with region-specific seismogenic zones and observed-data-validated ground motion models, hazard spectra were derived for 475- and 2475-year return periods. The resulting PSHA indicates maximum peak ground accelerations (PGA) of 0.908 g and 1.5405 g for 10% and 2% exceedance probabilities over 50 years, respectively. Comparative analysis revealed significant discrepancies between M and M_wg, with M overestimating ground motion by up to 40% for the 475-year return period and 20% for The 2475-year return period, particularly in regions prone to medium-range earthquakes. This overestimation of the M scale (mainly for smaller and medium earthquakes) was previously reported by Choy and Boatwright in 1995 using the Gutenberg–Richter energy equation. This issue can be effectively addressed by adopting the M_wg scale, which provides a more accurate representation of seismic energy. Furthermore, M scale underestimated PGA by up to 10% for very large magnitude events. These discrepancies, particularly overestimation in smaller and medium earthquake ranges, have critical implications for structural design. The adoption of M_wg provides a more accurate seismic hazard representation, necessitating a reevaluation of current building codes and emergency response protocols in Northeast India.

Introduction

The northeastern part of India, situated near the Himalayan mountains, is considered one of the country’s most seismic-prone areas based on the Indian building code. Over the centuries, this territory has faced numerous devastating earthquakes, that have significantly affected its landscape and history. The most well-documented historical earthquakes in this area include the earthquake on June 12, 1897 (M_wg = 8.7) and the one that occurred in Assam on August 15, 1950 (M_wg= 8.1), which partially destroyed several cities in Northeast India. These two earthquakes rank among the most powerful globally to have shaken the area within the past 128 years. The high seismicity of Northeast India is primarily driven by the tectonic interactions of the Indian Plate, which collides with the Tibetan Plate to the north and the Burmese landmass to the east. Early seismic research (e.g.¹,) identified a seismic void located between the epicenters of the earthquakes from 1897 and 1950, referred to as the "Assam Gap," signaling an elevated risk of future destructive earthquakes. The region is also home to several critical national projects involving multi-billion-dollar investments, making a comprehensive seismic hazard assessment essential to mitigate risks using advanced scientific methods.

Seismic hazard maps are widely regarded as fundamental tools in shaping public policies related to emergency preparedness, insurance policies, construction guidelines, and land-use management (e.g.²,). A significant part of these assessments utilizes the PSHA approach, which has been applied in various regions around the world. However, there remain ongoing challenges in refining PSHA methodologies (e.g.³,). In addition, some researchers have explored alternative approaches, such as deterministic or neo deterministic strategies, to measure seismic hazards (e.g⁴.). Numerous seismic hazard assessment studies focusing on Northeast India have been performed by several investigators^5,6,7,8,9. These studies provide important foundational insights into the region’s seismic risks. However, there remains significant scope for improvement, particularly in incorporating more advanced datasets, modern methodologies, and validated ground motion models, which could further enhance the accuracy and reliability of seismic hazard assessments in this region.

PSHA typically relies on earthquake catalogs (e.g., seismic size), earthquake source models, and ground motion models (GMMs). Nevertheless, many existing seismic hazard maps for Northeast India have given limited attention to the creation of seismic event listings and the uncertainties related with them. Numerous studies (e.g.^10,11,) have shown that seismic activity metrics derived from improperly treated earthquake catalogs can introduce significant biases. Recent research (e.g.^12,13,14,15,) has indicated that the M scale may not be appropriate for smaller and medium magnitudes earthquakes globally, suggesting the need for alternative magnitude scales like the Das Magnitude scale (M_wg)^13,15,16. Das et al.¹⁶ derived the M_wg scale, which closely aligns with the observed m_b scale for earthquakes with magnitudes below 7.0¹⁷ and with the M_s scale for magnitudes between 5.0 and 8.0, providing a better representation of seismic radiated energy for smaller, medium, large and very large earthquakes.

This research aims to enhance the accuracy of seismic hazard assessments by incorporating the M_wg magnitude scale into PSHA. This integration is intended to reduce the significant discrepancies between observed energy and estimated energy using Gutenberg and Richter¹⁸. The reduction of the discrepancy is important because use of M scale leads to biased in seismic hazard evaluations and other seismological investigations.

The structure of this paper is presented as follows: “Preparation for unified earthquake catalog” section begins by examining magnitude scale considerations for earthquake size analysis, proceeds to describe the statistical methods utilized in the creation of a homogenous earthquake catalog calibrated to M_wg, and concludes with a detailed account of the declustering and completeness assessment performed on the catalog. “Derivation seismicity parameters and seismic source zonation” section delineates the seismicity parameter estimation and seismic source zonation. “Strong ground-motion-model” section focuses on strong ground motion models. “Seismic hazard assessment for northeast India” section presents the results of the PSHA, while “Summary and conclusion” section provides a comprehensive Summary and Conclusions.

Preparation for unified earthquake catalog

Seismic catalogs, vital for earthquake activity records, often suffer from inconsistencies in earthquake size assignments due to magnitude scale variations. As earthquake magnitude is critical for accurate seismic hazard assessment, these discrepancies hinder the understanding of earthquake energy and regional hazard evaluation. To enhance catalog reliability, a comprehensive understanding of magnitude scales is essential. Therefore, this study critically examines the scientific background of the M and M_wg magnitude scales to provide a clearer understanding of this issue.

Magnitude issue

Recent investigations have unequivocally highlighted the limitations of M scales and provided compelling evidence in support of adopting the M_wg scale^{12,13,14,15,16,19,20,21,22}. Below, we briefly outline some of the limitations of M scale.

Limitations of the M Scale below 7.5: When scientists had fewer instruments and less data, Kanamori²³ introduced the M_w scale, a significant advancement that resolved the issue of magnitude ‘saturation’ (where very large earthquakes appear to have the same magnitude). However, the methods used to extend the M_w scale, designated as the M scale¹⁷, to lower and medium magnitudes (specifically, below magnitude 7.5) contain mathematical flaws^{12,15,19,20,21}. In the abstract of Hanks and Kanamori¹⁷, it is explicitly stated that the M scale was defined for magnitudes greater than 3.0, considering the close coincidence of three equations: (1) log M₀ = 1.6M_w + 16.1, (2) Eq. (1) of Purcaru and Berckhemer²⁴, and (3) the equation log M₀ = 1.6M_L + 16.1 presented by Thatcher and Hanks²⁵. However, Purcaru and Berckhemer²⁴ clearly defined the applicability of their equation, Log M₀ = 1.5 Ms + 16.1, to magnitudes strictly below Ms ≲ 7.0, specifically within the interval 5.0 ≤ M_s ≲ 7.0. Conversely, Hanks and Kanamori¹⁷ erroneously attributed a broader range of 5.0 ≤ M_s ≤ 7.5 to this equation (as evidenced on Page 2348 of Hanks and Kanamori¹⁷, where they state, “Which is remarkably coincident with the M0-Ms relationship empirically defined by Purcaru and Berckhemer²⁴ for 5 ≲ M_s ≲ 7.5: LogM₀ = 1.5 Ms + 16.1 (± 0.1)”). This misrepresentation underscores the inherent limitations of the M scale for earthquakes below magnitude 7.5, a fact demonstrably supported by observational data (refer to Figures S2 and 3 of Das et al.¹⁶, published in BSSA, and Figure S5 of Das et al.¹⁵). In contrast to the M scale, which exhibits these mathematical deficiencies at magnitudes below 7.5, the M_wg scale removes the mathematical flaw of M scale using below 7.5. The foundation of M_wgscale is given in many literatures (e.g.^15,16,).

Regional validation of M scale: While the M_w scale for magnitudes greater than 7.5 was globally validated (see Tables S1, 2 of Kanamori²³), the M scale introduced by Hanks and Kanamori¹⁷ was only validated for the Southern California region. This lack of global validation is also evident in various datasets, where significant deviations between the Log Mo, and Ms or m_b (Figures S1, S2 and S3 of Das et al.¹⁶).

Use of constant values in Gutenberg energy equation: M scale was derived using constant values in Gutenberg energy equation, note that this constant value is applicable for shallow earthquakes. The inclusion of a constant term (5 × 10⁻⁵) in the Gutenberg energy equation makes the M_w or M scale highly selective, as this constant can vary significantly. Bormann and Di Giacomo (2010) reported that the constant term can range (− 7 θ_k − 3), whereas Kanamori adopted a value of θ_k = − 4.3. Consequently, the M_w and M scales face significant limitations due to the assumption of a fixed Es/Mo value of 5 × 10⁻⁵.

Overestimation of energy: Choy and Boatwright²⁶ demonstrated that the Gutenberg-Richter energy equation tends to overestimate energy, primarily due to its reliance on M scale below 7.5 (see Figure S4 of Choy and Boatwright²⁶). Similar conclusions were reached by Das and colleagues using global datasets (Figure S4 of Das et al.^13,16, and Figure S4 of Das and Das¹⁵).

Issue with surface wave-based magnitude scale: Gutenberg and Richter¹⁸ recommended developing a magnitude scale based on body waves rather than surface waves, as surface waves do not accurately represent the seismic source. This limitation arises because surface waves are influenced by regional geological conditions and propagation effects, making them less reliable for characterizing the true energy release of an earthquake.

Addressing misconceptions of Gasperini and Lolli²⁷ about the M_wg scale

Recent critiques of the M_wg scale, such as those by Gasperini and Lolli²⁷, rely on inaccurate and misleading claims, a point thoroughly refuted in existing literature and further addressed in the forthcoming work by Das and Das¹⁵. A key issue with these critiques is their misrepresentation of the original M formulation by Purcaru and Berckhemer²⁴, where Gasperini and Lolli²⁷ incorrectly advocate for extending the applicability of Eq. (1) given by Purcaru and Berckhemer²⁴ beyond its originally intended limit of Ms ≲7.0. Furthermore, it is noteworthy that these same authors have a history of offering inappropriate commentary on all of our methodological approaches¹³, including our adoption of Corrected General Orthogonal Regression (GOR1)—despite our documented justifications in Geophysical Journal International, the Bulletin of the Seismological Society of America (BSSA), and Seismological Research Letters (SRL) since 2012, and more recently, their 2024 commentary on our 2019 Das Magnitude Scale publication in BSSA. Specifically regarding GOR (General Orthogonal Regression), they asserted it was the best method considering the error variance ratio $\eta = \frac{{\sigma_{y} }}{{\sigma_{x} }}$, a statement that contradicts established statistical literature by overlooking equation error in estimation of $\eta$²⁸.

Following The 2024 publication of their critique of our 2019 work, we address the critical inaccuracies of their arguments within Das et al.²⁰. The following section addresses several critical inaccuracies found within these critiques.

No evidence for advocating adequacy of the M scale: Gasperini and Lolli²⁷ assert the adequacy of the M scale; however, this claim lacks scientific substantiation. While the M scale demonstrates reliability for earthquakes with magnitudes of M ≥ 7.5, its validation is geographically restricted to Southern California, also acknowledged by Gasperini and Lolli²⁷ themselves. This limited validation highlights a critical need for a globally applicable magnitude scale, such as M_wg. Furthermore, the M scale’s complete reliance on surface waves (e.g., Log Es = 1.5 Ms + 11.8, Log Mo = 1.5 Ms + 16.1) not only limits its ability to accurately characterize earthquake sources but also renders it ineffective for measuring earthquakes at intermediate and deeper depths. Recognizing surface wave limitations, Gutenberg and Richter¹⁸ advocated for the development of a magnitude scale based on body waves rather than surface waves¹⁵.

Misrepresentation of Eq. (1) of Purcaru and Berckhemer²⁴ to support adequacy of M scale below 7.5: Gasperini and Lolli²⁷ made a demonstrably false claim regarding the scope of Purcaru and Berckhemer’s²⁴ work. They attributed a magnitude range of 5 ≤ Ms ≤ 7.5 to Purcaru and Berckhemer’s Eq. (1), stating, “whereas Purcaru and Berckhemer²⁴ from earthquakes with 5 ≤ Ms ≤ 7.5 recorded all over the world obtained log10 M0 = 1.5Ms + 16.1.” However, this is a direct misquotation and misrepresentation. Purcaru and Berckhemer²⁴ explicitly defined their equation’s applicability to moderate to large earthquakes considering ranges of M_s and M_o (Ms ≲7, M₀ ≲10²⁷ dyn.cm), further specifying, “In the range of moderate to large earthquakes (Ms ≲7, M₀ ≲10²⁷ dyn.cm), where M_s is a reliable measure, the relation between Log M₀ and M_s is linear and average relation see Fig. 4:

Log M₀ = (16.1 ± 0.1) + 1.5Ms—(1) is established to give the best fit with the observed data”, Purcaru and Berckhemer²⁴, p. 189). Consequently, Gasperini and Lolli’s²⁷ assertion of M_s ≤ 7.5 significantly and unjustifiably expands the magnitude range (Ms ≲ 7) delineated by Purcaru and Berckhemer²⁴.

Based on the preceding discussion, the assertion by Gasperini and Lolli²⁷ that the M scale is sufficient and requires no further refinement is incorrect.

Justifications on linear relations for magnitude scale development: The development of magnitude scales, including M_w, M, M_e, and M_wg, commonly employ linear relationships between Log Mo and magnitude. For instance, the M scale’s development utilized the linear relationship Log M_o = 1.5 M_L + 16.1²⁵, based on Mo and M_L. Hanks and Kanamori¹⁷ recommended using M_L and m_b for magnitudes below 7.0 due to their 1-s wave basis, leading to a linear Log M_o vs. m_b relationship in that range. Das and Das¹⁵ further substantiate the theoretical basis for these linear relationships, aligning with the principles outlined by Kanamori and Anderson²⁹. However, Das et al.¹⁶ in page 1545 clarified that their aim was not to get the best fitting linear relationship between Log M_o and m_b within a specific range, but rather to develop an unsaturated magnitude M_wg that consistently aligns with observed body and surface wave magnitudes across low, medium, and high magnitude ranges, thereby providing a suitable scale for all magnitude ranges.

Justifications against Infinite Scaling (Gasperini and Lolli 2024): Gasperini and Lolli²⁷ argument about infinite number of magnitude scales based on calculated average differences and standard deviations between seismic energy and arbitrarily generated ‘dummy magnitudes’. However, this proposition lacks scientific foundation. The ‘dummy magnitudes’ employed are not derived from established seismological methodologies and exhibit significant deviations from scales like M or M_w above magnitude 7.5, thus violating the fundamental properties of these established scales. Specifically, the M scale is designed for accuracy above 7.5, a criterion the ‘dummy magnitudes’ fail to meet (see Figure S4 of Das and Das¹⁵). Moreover, Gasperini and Lolli's²⁷ methodology relies solely on minimizing average differences and standard deviations, disregarding established standards and norms used in developing robust magnitude scales. Unlike Das et al.¹⁶, who utilized rigorous statistical tests, Gasperini and Lolli²⁷ did not provide statistically significant validation for their proposed approach. Conversely, the development of M_wg, is justified by the documented limitations of the M and Mw scales, particularly below magnitude 7.5, and for global scales and earthquakes at intermediate and deep depths. M_wg addresses these limitations by providing a more accurate representation of seismic energy and is validated by rigorous statistical tests. Furthermore, the development of improved moment magnitude scale (M_wg) utilizing body waves aligns with the recommendations of Gutenberg and Richter¹⁸ and addresses the limitations of surface-wave based scales.

In their 2024 critique, Gasperini and Lolli raised the concern of a potentially infinite magnitude scale specifically regarding the M_wg scale. However, this concern is not only applicable to M_wg but also relevant to M, M_w, and M_e, as documented in Das and Das¹⁵. Furthermore, the argument of an infinite magnitude scale is not pertinent when considering scale improvements and corrections. Unlike the M scale, M_wg exhibits no inherent mathematical flaws or constancy issues. M_wg has also been validated worldwide and offers a simpler methodology. Furthermore, M_wg scale improves seismic energy estimation though Gutenberg-Richter equation.

In their critique on the Das scale, Gasperini and Lolli²⁷ employed incorrect mathematics, misused citations, and misrepresented quotations, significantly undermining the validity of their arguments. Below, we highlight these critical errors so that these errors cannot propagate further.

• 1. Incorrect Mathematics: Gasperini and Lolli²⁷ incorrectly used the value − 4.7 in their calculations, whereas the correct term is − 4.8. This mathematical error has a direct impact on their results and conclusions, rendering their analysis flawed and unreliable. Such inaccuracies raise serious concerns about the rigor of their critique¹⁵.

• 2. Misuse of Citations: Gasperini and Lolli²⁷ inaccurately cited Kanamori and Anderson²⁹, claiming that they recommended using m_b < 5. However, a thorough review of Kanamori and Anderson²⁹ work reveals that they did not make any such statement regarding m_b. This misrepresentation of prior research undermines the credibility of Gasperini and Lolli’s critique.

• 3. Misquotation of Purcaru and Berckhemer²⁴: Gasperini and Lolli²⁷ asserted that Purcaru and Berckhemer²⁴ developed their equation for the magnitude range 5 ≤ Ms ≤ 7.5 on a global scale. However, upon re-examination, it is evident that Purcaru and Berckhemer explicitly stated that their equation (Eq. 1) was primarily valid for magnitudes below 7.0 (Ms ≲ 7.0). This is because events below 7.0 M_s are considered more reliable for their formulation. Gasperini and Lolli’s overestimation of the applicable range misrepresents the original work and introduces inaccuracies into their critique.

These errors in mathematics, citations, and quotations demonstrate a lack of attention to detail and rigor in Gasperini and Lolli’s²⁷ critique. Readers are urged to approach their critique with caution and to refer to the original works, such as¹⁵, for a more accurate and reliable understanding of the M_wg scale.

Scientific benefits of adopting the M_wg scale over M¹⁵

In Das and Das¹⁵, we provided a comprehensive analysis highlighting the advantages of the M_wg scale over the M scale. For the convenience of readers, we briefly summarize these benefits below to facilitate a clearer understanding of the M_wg scale’s superiority in accurately estimating radiated seismic energy.

Mathematical consistency: Unlike the M scale, M_wg is free from inherent mathematical flaws and exhibits consistent applicability across all magnitude ranges, eliminating the discontinuity (7–7.4) observed in M. In PSHA, using a scientifically accurate magnitude scale as input is crucial—correct inputs lead to correct outputs. The adoption of the M_wg scale ensures more reliable and accurate seismic hazard estimates, improving the overall integrity of PSHA results.

Direct seismic moment consideration: M_wg is developed through the direct consideration of seismic moment values, avoiding the assumption of a constant stress drop (Es/M₀) inherent in the M scale (2/3Log Mo-10.7) derivation. The M scale’s sensitivity to constant values (e.g., Kanamori²³, used θk = − 4.3) introduces variability based on the chosen constants, a problem absents in M_wg.

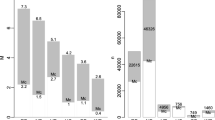
Enhanced Energy Quantification: M_wg provides an improved understanding of earthquake energy compared to the M_w scale as shown in Fig. 1. (see Figure S4 of Choy and Boatright 1995, Figure S4 and Tables S1, 2 and 3 of Das et al.¹⁶, Figure S1 of Das et al.¹³, and Figure S4 of Das and Das¹⁵). Our analysis reveals that 76% of the observed radiated energy of global data values align more closely with estimates from the M_wg scale, while only 24% align with those from the M_w scale. This statistically significant difference suggests that the M_wg scale provides a more accurate representation of radiated energy across diverse seismic events. These findings highlight the limitations of the M_w scale and support the adoption of the M_wg scale for improved energy estimation.

Fig. 1

Comparison of Seismic Energy Estimates Between M_w and M_wg Scales. The figure demonstrates that the M_w or M scales tends to overestimate seismic energy in the lower and medium magnitude ranges, as reported by Choy and Boatwright²⁶. Our datasets also show similar results. However, for large magnitude events, both the M_w and M_wg scales provide comparable energy estimates. The overestimation observed with the M_w scale (Green solid line) can be mitigated by using the M_wg scale (Blue solid line).

Improved Global Alignment: M_wg shows closer alignment with m_b and Ms globally compared to M, ensuring consistent energy distribution and improving the accuracy of Gutenberg-Richter parameters, deformation analyses, and related seismological studies (Figures S1, S2, and S3 and Table S1 of Das et al.¹⁶, Figure S5 of Das and Das¹⁵). The average difference between observed and estimated values is − 0.32 ± 0.31 (m_b–M) and 0.007 ± 0.30 (m_b–Mwg), while for Ms, it is − 0.44 ± 0.28 (Ms–M) and − 0.11 ± 0.21 (Ms–M_wg). This alignment is crucial for maintaining energy consistency in seismic analysis (Fig. 2).

Fig. 2

The above figure clearly illustrates the comparison between the M scale (Red Solid Line) and the M_wg scale. The M_wg scale (Blue solid line) shows a closer alignment with observed m_b in its applicable range (up to 7.0) and M_s in its applicable range (5.0–8.3). In contrast, the M scale demonstrates a significant deviation from both m_b and M_s, particularly within their respective applicable ranges. This deviation is statistically significant and leads to inconsistencies in energy quantification, resulting in biased seismic hazard assessments¹⁵.

Spectral analysis and high-frequency estimation: Due to the reliance of the M scale on long-period surface wave magnitudes, it is inadequate for accurately estimating high-frequency or strong-motion amplitude data, which are essential for evaluating the potential destructive effects of real-world earthquakes. Conversely, M_wg is derived from the analysis of both low- and high-frequency spectral components of seismic signals and correlates better with seismic damage potential.

Global validation: M_wg has been validated globally, whereas the M scale’s validation is primarily limited to Southern California.

Depth independence: M_wg is not constrained by surface wave limitations, enabling accurate magnitude determination for intermediate and deeper earthquakes, a limitation presents in the M scale.

In summary, the M_wg scale corrects the inherent errors of the M scale, offering improved consistency, global applicability, and improved energy quantification. Its use in PSHA ensures more precise inputs, leading to statistically robust and scientifically reliable seismic hazard assessments compared to the traditional M scale.

Regression relations

When creating a uniform earthquake catalog for an area with high seismic activity, the regression equations used to convert various magnitude types into a preferred magnitude scale are critical. Any bias introduced during this conversion can propagate errors in the Gutenberg-Richter frequency-magnitude distribution and ultimately affect the estimates of seismic hazard.

Standard linear regression (SLR)

Standard Linear Regression (SLR) is a widely utilized technique for developing a standardized earthquake catalog when one variable is assumed to be error-free or has a negligible error compared to the error in the other variable. However, using SLR is not suitable for converting earthquake magnitudes since both variables are subject to errors. Instead, the General Orthogonal Regression (GOR) approach is recommended, as it considers errors present in both the independent and dependent variables^10,28,30. Unfortunately, the GOR technique has been misapplied in seismic research^10,11,28. A corrected GOR method, GOR1 (Das et al.¹⁰) has been introduced in seismic studies to address the overestimation issue associated with conventional GOR (GOR2). The GOR1 procedure adopted in this study is explained in Das et al.¹⁰, so we will not repeat it here.

Following the methodology described in Das et al.¹⁰, GOR1 relationships were established with η = 0.2 to transform m_b,ISC to M_wg,GCMT for magnitudes between 4.5 and 6.9, and for m_b,NEIC to M_wg,GCMT for magnitudes from 4.4 to 6.9. These relationships were developed using datasets that included 290 and 239 events, respectively, covering the timeframe from 1976 to 2021. Furthermore, we derived regression equations for M_s,ISC and M_wg,GCMT, as well as for M_s,NEIC and M_w,GCMT, utilizing the newly introduced GOR method from Das et al.¹⁰ which involved 110 events in the range of 3.6 ≤ M_s,ISC ≤ 7.2 and 33 events in the range of 4.6 ≤ M_s,NEIC ≤ 7.2 (Fig. 3).

Fig. 3

Regression Relationship Plots illustrate the correlations among different magnitude scales and M_wg for (a) m_{b, ISC} into M_wg; (b) m_{b, NEIC} into M_wg; (c) M_{S, ISC} into M_wg; (d) M_S,NEIC into M_wg; and (e) M_L into M_wg, featuring GOR1 (solid blue line), GOR2 (dashed red line), and SLR (black dashed line).

Table 1 provides the magnitude conversion parameters for the respective regression relationships. Figure 4 illustrates a seismicity map for the northeastern region of India, showing earthquakes with a magnitude of M_wg ≥ 4.

Table 1 Regression relations developed for Northeast India region are presented in the table.

Fig. 4

Geographic information system (GIS) platform-based seismotectonic map, illustrating the epicenters of earthquakes and the tectonic characteristics within the Northeast India region. The map provides seismicity data for earthquakes with a magnitude equal to or greater than 4.0 (M_wg ≥ 4.0).

A procedure for homogenization of regional magnitudes into das magnitudes M_wg

A proposed methodology describes how different types of magnitude can be transformed into a single moment magnitude, referred to as M_wg.

• 1. The magnitudes in Bapat et al.’s (1983)³¹ catalog that have not been assigned are classified as M_s (Das and Meneses 2021).

• 2. Magnitudes from the catalog by Gupta et al.³² that do not have specific designations are regarded as Ms, following the approach of Das and Meneses (2021)

• 3. For events where magnitude types such as m_b and M_s are available, preference is given to the magnitude type derived from data collected from a greater number of stations.

• 4. If the body wave magnitude scale is insufficient for regional relationships, we rely on the corresponding global correlation¹³.

• 5. In cases where only MMI intensity data is available for an event, the intensity can be applied to the M_w,GCMT relationship, as outlined in Pallavi et al.²¹.

Declustering

The Poissonian distribution serves as the fundamental assumption for the Cornell-McGuire approach in PSHA. Foreshocks and aftershocks must be removed from the homogenized earthquake catalog to ensure data consistency. Multiple seismic events take place within a short period, typically linked to the main earthquake. The seismic events connected to the main event are referred to as aftershocks. Similarly, earthquake events that precede a major earthquake are generally called foreshocks. The delustering procedure, aimed at filtering out foreshocks and aftershocks, was implemented through a time–space window approach (Fig. 5). The choice of reference Uhrhammer³³ was based on its simplicity and widespread use. The initial earthquake count stood at 9968, but after the removal of foreshocks and aftershocks, it was reduced to 7,745.

Fig. 5

Foreshocks and aftershocks events based on magnitude dependent space and time windows. The asterisks which are just below the window lines are considered to be dependent events.

Completeness analysis of the catalog

To ensure the catalog’s completeness, we meticulously followed the methodology outlined in Stepp³⁴. According to this approach, the average earthquake rate in the catalog demonstrates an inverse relationship with the quantity of observed data within the catalog. To derive a precise estimate of the sample mean variance, the earthquake sequence was modeled using a Poisson distribution.

Let’s consider X₁, X₂, …, X_n to indicate the count of seismic occurrences within a specific time frame. Therefore, the average estimate of earthquakes for each time segment can be represented as:

$$\lambda = \frac{1}{n}\sum\nolimits_{i = 1}^{n} {X_{i} }$$

(1)

where ‘n’ represents the total count of time intervals. Assuming the Poisson process to be stationary, the standard deviation within the subinterval of the $\frac{1}{\sqrt T }$.

Our observations indicate that the completeness periods for various magnitude ranges are as follows: for magnitudes between 3.1 and 3.5, the completeness period is thirty years; for magnitudes ranging from 3.6 to 4.0, it is forty years; for magnitudes between 4.1 and 4.5, the completeness period extends to fifty years; for magnitudes from 4.6 to 5.0, it is sixty years; for magnitudes ranging from 5.1 to 5.5, the completeness period is sixty-five years; for magnitudes between 5.6 and 6.0, it extends to one hundred years; and for magnitudes ≥ 6.0, the completeness period is one hundred thirty years (Fig. 6). Notably, for lower earthquake magnitude intervals, the completeness period is shorter, reflecting the limited instrumentation available during those times. Consequently, we estimated seismicity parameters utilizing the complete portion of the catalog.

Fig. 6

Illustrates how the standard deviation of the mean estimate changes concerning both sample length and magnitude of annual events.

Estimation of M_max

A crucial variable in evaluating seismic hazards is the maximum magnitude (M_max). It reflects the largest potential earthquake a fault or thrust can unleash, exceeding the limitations of historical and instrumental records. M_max denotes the maximum possible earthquake size within a particular area and serves as a clear boundary, beyond which no larger earthquakes are anticipated. The current approaches for estimation are grouped into two primary types: deterministic and probabilistic. In the deterministic approach, M_max typically relies on observed relationships linking earthquake magnitude to fault characteristics. Various efforts have been made to explore these relationships, as reported by Wells and Coppersmith³⁵. Kijko³⁶ offers a robust and flexible approach for estimating M_max. It allows for various statistical distribution models and accommodates different levels of available seismicity data.Tested with synthetic and real earthquake catalogs, the method has proven its applicability and reliability in estimating M_max, particularly evident in results from Southern California. Notably, the non-parametric nature of this approach enhances the M_max estimate’s reliability by avoiding assumptions about the specific magnitude distribution. Following the generic equation provided by Kijko³⁶, the maximum magnitude (M_max) is calculated for every seismic zone.

Derivation seismicity parameters and seismic source zonation

Seismic source zones and seismicty parameters

Seismic events in Northeast India predominantly stem from the collision of the Indian Plate with the Eurasian Plate. This seismicity is intricately linked to the Himalayan seismic belt, occurring within the zones of the Main Boundary Thrust (MBT) and the Main Central Thrust (MCT). Shallow seismic events are common along the MCT and MBT, stretching from Sikkim to Arunachal Pradesh. In contrast, seismic occurrences beneath the Indo-Burma ranges are generally at greater depths.

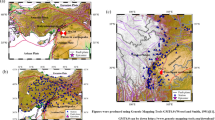
To carry out seismic hazard evaluations, identifying specific sources of seismicity is crucial. Despite differences in methodology, numerous researchers have focused on this area because of its notable seismic events. Based on local geological features, tectonic activity, and seismic patterns, the four main zones initially identified by Dutta³⁷ were expanded to include nine distinct seismic zones (e.g., Das et al. 2016), as illustrated in Fig. 7. In this study we used unified catalog data in terms of M_wg scale, faults and focal plane solution, and define the following nine seismic source zones.

Fig. 7

Illustration of the Seismic Source Regions Included in the Analysis for Northeast India. The red solid line indicates lineaments, “Neotec_Fault” denotes neotectonic faults, and “MFT” represents the Main Frontal Thrust. The figure also shows the distribution of normal, reverse, and strike-slip faults.

Zone 1. Covers parts of Assam, the entire Mizoram, and parts of Manipur. The highest recorded magnitude of an earthquake in this area was 6.8 and it took place on August 16, 1938. The structural feature in this area is marked by prominent anticlinal ridges and synclinal valleys formed by Surmas and Tipams from the Miocene epoch, alongside significant north–south oriented strike faults. The mean depths of earthquakes in this region is approximately 76 km, and the primary fault type identified here is mainly a reverse fault³⁸.

Zone 2. The seismic activity in this region predominantly exhibits a thrust faulting mechanism, with the thrusts oriented towards the southeast. This area is located within the northern Indo-Burma fold belt. The most recent significant earthquake in this region registered a magnitude of 7.1 on August 6, 1988. The longest interval between large earthquakes (M_wg ≥ 7.0) has been recorded as 31 years. Since 1988, a period of low seismic activity has been observed, continuing to the present. The structural orientation of the orogenic belt in this zone primarily trends NE–SW, beginning in Arunachal Pradesh and gradually shifting to NNE–SSW. The average depth of seismic events in this zone is estimated to be around 70 km.

Zone 3. This region includes Myanmar and is defined by the prominent north–south trending Saging fault system. The latest notable earthquake in this area registered a magnitude of 7.8 and took place on May 23, 1912. The estimated average focal depth of seismic events in this zone is around 66 km.

Zone 4. The area in question is known as the Mishmi Massif, a geological feature that trends from northwest to southeast. The highest magnitude earthquake recorded in this region was M_wg 8.5, which occurred on August 15, 1950. Seismic activity here is linked to various geological formations, including the Mishmi thrust, Lohit thrust, Tiding suture, Pochu Fault, and multiple lineaments. These structures are crucial in influencing the seismic behavior of the area. The average depth of earthquakes in this region is approximately 42 km.

Zone 5. The area in question pertains to the Tibetan Plateau. The average focal depth for earthquakes in this region is estimated to be about 37 km. This indicates that seismic events in the Tibetan Plateau typically occur at an average depth of roughly 37 km below the Earth’s surface. It is essential to recognize that this information is derived from existing data and research. Ongoing studies and continuous monitoring are vital for enhancing our understanding of seismic activity and the related hazards in the Tibetan Plateau.

Zone 6. This area corresponds to the Himalayan Mountain Belt. It includes the eastern segment of the Main Central Thrust (MCT). The highest recorded magnitude in this region is M_wg 6.4. The primary seismogenic structures here are the Main Boundary Thrust (MBT) and MCT. The average depth of seismic events in this zone is around 39 km.

Zone 7. This region is known as the Shillong Plateau. The highest magnitude earthquake recorded here was M_wg 8.6, which struck on June 26, 1897. The Dauki Fault, a significant geological feature extending approximately 450 km, is considered the probable cause of the major earthquake in 1897. The average depth of seismic activity in this area is estimated to be around 37 km.

Zone 8. Situated in the Bengal Basin, encompasses Tripura and certain areas of Bangladesh. It is characterized by the presence of an important tectonic feature known as the Sylhet fault. Within this zone, the highest reported earthquake reached a magnitude of M_wg 7.4 and occurred on July 8, 1918. The average focal depth of seismic events in this zone is estimated to be approximately 35 km.

Zone 9. The specified region is situated in the Himalayan Mountain belt and displays features that trend from northeast to southwest. The highest recorded earthquake magnitude in this area was M_wg 7.5, which took place on July 29, 1947. The average depth for seismic events in this region is estimated to be about 44 km, suggesting that seismic activity generally occurs at this average depth beneath the Earth’s surface.

A homogeneous declustered catalog has been compiled for each seismogenic zone, with an estimated magnitude of completeness (M_c) assigned to each zone. This comprehensive catalog allows for the accurate estimation of seismicity parameters. The maximum magnitude (M_max) for all zones is determined using the generic equation provided by Kijko³⁶. The seismicity of the region can be characterized by the frequency-magnitude recurrence law proposed by Gutenberg and Richter³⁹, expressed as log10 λ(m) = a–bm. Here, λ(m) represents the cumulative number of events with a magnitude greater than or equal to m, while ‘a’ and ‘b’ denote the seismicity parameters of the region. Seismicity parameters, such as ‘b’ and ‘a’, essential for PSHA, are derived using the maximum likelihood estimation technique as described by Aki⁴⁰ and Weichert⁴¹. The parameter ‘a’ is specifically calculated using Eq. (10) from Weichert⁴¹ with the assistance of the method outlined by Step (1972). These parameters (‘b’, ‘a’) capture the overall seismicity and the distribution of magnitude sizes within the seismic region. Figures 8 and 9 illustrates the Gutenberg-Richter relationship for the nine seismic source zones in the Northeast India region. Additionally, the figure presents a comparison between the Gutenberg-Richter relationship and the observed seismicity for each zone.

Fig. 8

Frequency relationships based on the Gutenberg–Richter law for nine seismic source regions in Northeast India.

Fig. 9

Das Magnitude Scale (_Mwg) versus moment magnitude (M_w) relationship (Anbazhagan · Harish Thakur⁴²).

The seismicity parameters, which include ‘a’, ‘b’, M_c, M_max, and the average focal depth (D), play a vital role in estimating seismic hazard assessment and are presented in Table 2. To facilitate comparisons of seismicity parameters (M_c, ‘b’, ‘a’) for the homogenized Northeast India catalog, we have compiled Table 3, which details values using both M_w and M_wg magnitude scales.

Table 2 Parameters related to the Gutenberg-Richter relationship and other associated factors for seismic sources in the Northeast India area.

Table 3 Comparisons of Seismicity parameters (e.g., M_c, ‘b’, ‘a’) for the homogenized catalog of Northeast India.

Strong ground-motion-model

The selection and application of strong ground motion models (GMMs) are pivotal in seismic hazard assessments, influencing the accuracy and reliability of predicted ground shaking intensities. In this study, five GMMs were carefully chosen to mitigate uncertainties inherent in prediction models. The use of GMMs based on observed data plays a critical role in understanding ground motion^43,44,45. While other GMMs are primarily based on synthetic simulations, we chose not to use them because our focus is on GMMs derived from observed data and expressed in Spectral Acceleration (SA), which we believe provide a more reliable basis for our assessment. The spectral attenuation relationships developed specifically for the study region, along with those calibrated for comparable tectonic settings elsewhere, were analyzed using a logic tree approach. This methodological framework allows for the systematic integration of multiple GMMs, each contributing with varying weights based on their performance metrics and the specific seismic scenarios considered.

GMMs are primarily developed using the M scale. Since both M and M_wg are derived from the Mo, GMMs expressed in terms of M can also be applied to M_wg (See Appendix). The key difference between these scales lies in the coefficients used in their respective formulations: the M scale is defined by the equation M = 2/3logM₀ − 10.7¹⁷, while the M_wg scale is given by M_wg = Log Mo/1.36–12.68¹⁶. As a result, only the magnitude values need to be adjusted when applying GMMs to the M_wg scale (see Fig. , 9 and Table 4). One can use equation M_wg = 1.10 M − 0.88 for converting M to M_wg. For instance, if a ground motion equation is calibrated for a magnitude M of 6.0, a corresponding magnitude of approximately 5.7 on the M_wg scale should be used to obtain comparable results (see Table 4 below). We provided detailed explanations of using M_wg scale in existing GMM (see Appendix).

Table 4 Comparison of M_wg and M scales for use with GMM models.

The GMMs utilized in this study include:

• Abrahamson et al.⁴⁶

• Zhao et al.⁴⁷

• Boore et al.⁴⁸

• Sharma et al.⁴⁹

• Gupta⁵⁰

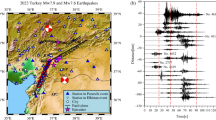
Each of these models was evaluated against observed strong ground motion data to assess their reliability and suitability for the study’s objectives. As there is no available observed earthquake data for large earthquakes of the study region, therefore, we used recent Turkey earthquake which has earthquake magnitude 7.8 M_wg of 18 km focal depths and available observed data (Fig. 10). While there are differences in specific tectonic settings between Northeast India and Turkey, both regions share fundamental characteristics of active tectonics, complex fault systems, and significant seismic activity with shallow focal depths. These similarities justify the comparative use of seismic data from Turkey to validate the ground motion model to enhance understanding and assessment of seismic hazards in Northeast India. When the used of global GMMs for a comprehensive assessment of seismic hazard in any local region is the standard practice then use of easily available observed ground motion data from Turkey earthquake may not be unreasonable to validate the GMM applicable for Northeast India. Validating these models with observed seismic data, such as that from Turkey, strengthens their applicability and reliability for regions where direct empirical data may be limited or unavailable. Furthermore, given the presence of a subduction zone in our study region, we incorporated observed earthquake subduction data, particularly from studies like Batias and Montalva (2016) (Fig. 10). This ensured a robust selection and application of attenuation relationships in our analysis.

Fig. 10

Comparison of Ground Motion Equations by Abrahamson et al. (2016), Boore et al.⁴⁸, Sharma et al.⁴⁹ and Gupta⁵⁰ for Magnitude 7.8 Turkey earthquake events (Fig. 9a) and Spectral Accelerations (SA) at 0.2 s (Fig. 9b) and 1 s (Fig. 9c) for the Mauli earthquake.

However, making decisions about which GMM is better across the entire range of magnitudes (from 5.0 to 9.0) is challenging because most existing GMMs for the study region are primarily based on small to medium-sized earthquakes. It is also important to note that a GMM effective for representing smaller and medium earthquakes may not be suitable for large earthquakes, and vice versa. This remains a global challenge, highlighting the need for further improvements. Notably, while Sharma et al.⁴⁹ and Gupta⁵⁰ validated their models using regional observed data during development, their validation did not extend to large earthquakes. In contrast, we have validated our model with large earthquakes.

Justification of GMM Selection Criteria: (a) Seismotectonic and Geological Compatibility: The selected GMMs were chosen based on their alignment with the seismotectonic and geological characteristics of the study area, which includes considerations of regional fault structures, tectonic activity, and geological formations. (b) Database of Natural Ground Motion Records: Preference was given to models developed using extensive databases of natural ground motion records, which provide empirical support and validation for their predictive capabilities. (c) Suitability for Engineering Applications: The structural period range covered by each GMM ensures their relevance for engineering applications, facilitating accurate assessments of seismic hazard and potential impacts on infrastructure.

In a logic tree formulation, the weights assigned to various GMPEs represent the degree to which each equation is deemed to be the best predictor of earthquake ground motions in that specific area⁵¹. Figure 11 illustrates the branching structure of the logic tree along with the assigned weights for each model.

Fig. 11

The logic tree framework for probabilistic seismic hazard assessment; the assigned weights are leveled in each arrow pointed towards ground motion equations.

When examining the available recordings for rupture distances less than 101 km, it was found that Abrahamson⁴⁶, Zhao et al.⁴⁷, and Gupta⁵⁰ correlate closely with the observed ground motion (Fig. 10). To evaluate the performance of different GMMs, we analyzed both the Average Absolute Deviation (AAD) and the Standard Deviation (STD) for each equation. Abrahamson et al.⁴⁶ demonstrated an AAD of 0.09 and an STD of 0.11. Similarly, Zhao et al.⁴⁷ exhibited an AAD of 0.08 and an STD of 0.108. Additionally, Boore et al.⁴⁸ reported an AAD of 0.25 and an STD of 0.30. Sharma et al.⁴⁹ recorded an AAD of 0.31 with an associated STD of 0.30. Moreover, Gupta⁵⁰ observed an AAD of 0.14 along with an STD of 0.12. These values provide insights into the performance and variability of each GMM.

Abrahamson et al.⁴⁶ is allocated a weight of 0.25 due to its AAD of 0.09 and STD of 0.11, indicating relatively low average differences and moderate variability. These metrics suggest that Abrahamson et al.⁴⁶ study provides reasonably accurate and consistent attenuation relationships, justifying its significant influence in the weighted scheme. Boore et al.⁴⁸ with an AAD of 0.25 and STD of 0.30, receives a weight of 0.15. These higher values in AAD and STD suggest more variability and potentially lower precision in its predictions compared to other studies. Thus, a lower weight is assigned to Boore et al.⁴⁸'s study to reflect its comparatively lesser reliability in providing precise attenuation estimates. Zhao et al.⁴⁷merits a weight of 0.25 due to its AAD of 0.08 and STD of 0.108, indicating both low average differences and low variability. This suggests high accuracy and precision in Zhao et al’s⁴⁷. attenuation relationships, warranting a significant influence in the weighted average. Gupta⁵⁰, with an AAD of 0.14 and STD of 0.12, receives a weight of 0.20. These metrics reflect moderate average differences and variability, suggesting Gupta’s⁵⁰ study offers reliable but slightly less precise attenuation relationships compared to others, hence its weight is appropriately set to balance its influence. Sharma’s⁴⁹ study, with an AAD of 0.31 and STD of 0.30, is assigned a weight of 0.15. These higher AAD and STD values indicate greater variability and potentially lower reliability in Sharma’s⁴⁹ predictions. Consequently, a lower weight is assigned to Sharma’s study to reflect its lower precision relative to the other studies considered. In conclusion, the weights assigned to each study are justified based on their AAD and STD values, ensuring that the weighted scheme appropriately reflects the accuracy, precision, and reliability of each attenuation relationship. This approach enables a balanced integration of diverse studies while emphasizing those with more consistent and precise seismic attenuation predictions in the overall analysis.

Previous research conducted in Northeast India has predominantly focused on evaluating seismic site conditions with an emphasis on soil behavior associated with different rock types. The National Earthquake Hazards Reduction Program (NEHRP) employs a metric known as Vs30, which indicates the shear wave velocity within the upper 30 m of the soil column⁵². In our study, we adopted the soil classification system outlined by NEHRP, as described in Table 5.

Table 5 Vs30 thresholds established by the United States Geological Survey (USGS) for assessing properties of seismic sites².

Seismic hazard assessment for northeast India

PSHA maps for Northeast India and its surrounding region were computed with a grid interval of 0.1° × 0.1° at the surface level. The analysis utilized a ground motion equation specific to the study area and incorporated a logic tree framework to encompass various GMMs. PSHA maps were created to illustrate key ground motion parameters, including PGA and SA at 0.2- and 1.0-s spectral time periods. These maps represent both a 10% and 2% probability of experiencing these ground motion levels within a 50-year timeframe (Figs. 12, 13). For scenarios with a 10% probability of exceedance over 50 years, surface-level PGA values were observed to range from 0.05 to 0.91 g (Fig. 12). Specific estimates for cities such as Guwahati, Imphal, Agartala, Shillong, Kohima, Gangtok, Itanagar, Tezpur, and Aizawl showed PGA values ranging from 0.5694 to 0.908 g for this probability level. The Table 6 provides a comparison of PGA values at various cities for a 10% probability of exceedance over a 50-year period, drawing from different studies, including the present one. The highest ground motion value recorded is 0.908 g, and it is situated around Dibang world life century, Arunachal Pradesh, India. This location experienced the most intense ground motion. The second-highest ground motion value, 0.8931 g, occurred at Shillong, indicating another area of significant ground motion. In Guwahati, the present study also reveals significantly higher PGA values of 0.8112 g compared to most other studies, indicating a relatively heightened seismic hazard. Imphal, Agartala, and Kohima exhibit a moderate seismic hazard with PGA values of 0.6825 g, 0.6084 g, and 0.6786 g, respectively. Itanagar also exhibits a moderate seismic hazard, with a present study PGA value of 0.70 g aligns with values reported in Nath et al.⁵⁵ study. Aizwal, in contrast, appears to have a lower seismic hazard with a PGA value 0.5694 g.

Fig. 12

Hazard maps showing (a) PGA, (b) Sa at 0.2 s, and (c) Sa at 1.0 s for a 10% likelihood of exceedance over 50 years.

Fig. 13

Hazard maps showing (a) PGA, (b) Sa at 0.2 s, and (c) Sa at 1.0 s for a 2% likelihood of exceedance over 50 years.

Table 6 An analysis of calculated peak ground acceleration (PGA) alongside findings from other research for a 10% likelihood of exceedance in selected cities over a 50-year period.

The results for a 2% exceedance probability over 50 years, expressed as PGA values, provide significant insights into the seismic hazard assessments for several cities in Northeast India. Among these cities, Shillong and Guwahati exhibit a relatively high seismic hazard with PGA values of 1.4547 g and 1.4235 g, respectively, indicating a notable risk of experiencing ground motion events at these levels. Itanagar, Kohima, and Tezpur are found to have seismic hazard values of 1.0686 g, 1.0569 g, and 1.3377 g, respectively. Gangtok exhibits a relatively lower seismic hazard with a PGA value of 0.897 g, and Agartala follows suit with a PGA of 0.9672 g, indicating lower seismic hazards compared to the aforementioned cities.

Crucially, the underlying geological and soil conditions play an important role in influencing those above ground motion levels and associated engineering responses. Guwahati and Tezpur, situated on alluvial deposits of the Brahmaputra Basin, are prone to amplified shaking and potential liquefaction, necessitating deep foundations and active groundwater control. In contrast, Shillong, located on hard Precambrian bedrock near active fault zones, is exposed to high-frequency shaking, requiring design strategies that focus on structural rigidity rather than soil amplification. Imphal and Agartala, underlain by lacustrine and alluvial sediments, are vulnerable to basin effects, and benefit from flexible structures and detailed micro zonation. The moderate-to-high hazard observed in Kohima and Itanagar is also consistent with their underlying geology of weathered sedimentary rocks and colluvial slopes, suggesting a combined risk from ground shaking and earthquake-induced landslides. Although Gangtok and Aizawl rest on bedrock, their steep topography within metamorphic and sedimentary terrains makes them susceptible to landslides, warranting the use of lightweight structures and slope reinforcement measures.

During The 2011 Japan earthquake, peak ground acceleration (PGA) exceeded 1 g at 20 sites, with the highest observed PGA reaching 2.9 g at the K-Net Tsukidate station. In our PSHA model, such extreme accelerations (≥ 2.9 g) correspond to return periods exceeding 10,000 years, far rarer than The 2011 event, reflecting the unique rupture dynamics of subduction zones that are not directly comparable to continental Himalayan seismicity. The 2010 Maule earthquake (M_wg 8.8) experienced a maximum acceleration of 0.93 g, which aligns closely with our modeled PGA of 0.908 g for a 10% exceedance probability in 50 years (return period ~ 475 years). The 2008 Nevada earthquake (Mwg 4.7), with a focal depth of 3.1 km, produced a PGA of 1.19 g at the MOGL station (< 1 km from the epicenter). This PGA corresponds to a return period of ~ 1100 years in our model, highlighting the localized impact of shallow, near-source earthquakes. This significant PGA due to very low focal depth indicates that intense shaking can occur near the epicenter of shallow-focus earthquakes in the eastern to western Himalayan region of India, where earthquakes predominantly have shallow focal depths. The 1897 Assam earthquake reportedly generated a PGA of 1 g⁵⁷. In our model, 1 g PGA corresponds to a 10% exceedance probability in 50 years (return period ~ 475 years), suggesting such events recur ~ 1–2 times per millennium. However, paleoseismic evidence indicates large Himalayan earthquakes (M_wg > 8) recur every ~ 500–1000 years, implying our model may underestimate the recurrence of extreme shallow-focus events due to limited historical catalogs.

The differences between our study and earlier ones may be attributed to several methodological advancements. Our analysis incorporated updated data and region-specific ground motion models that were validated against observed data, providing a more accurate representation of seismic conditions. Furthermore, the adoption of the M_wg scale enabled a more precise quantification of seismic energy release, leading to improved estimates of ground shaking (Fig. 1).

Design response spectra for buildings have been developed for nine important cities of Northeast India considering PGA and Spectral acceleration obtained in PSHA results (Fig. 14). The design spectra are determined by estimating the period T₂ that symbols the starting of the stable velocity range as the proportion of the pseudo spectral acceleration at 1.0 s and 0.2 s as

Fig. 14

Seismic hazard curves for selected cities in Northeast India. Each subplot (a–i) corresponds to a specific city as follows: (a) Guwahati, (b) Imphal, (c) Agartala, (d) Shillong, (e) Kohima, (f) Gangtok, (g) Itanagar, (h) Tezpur, and (i) Aizwal. The curves are computed assuming a 5% damping ratio and represent hazard levels for two probabilities of exceedance over a 50-year period: 10% (brown) and 2% (blue).

$T_{2} = \frac{{S_{pa} (1.0s)}}{{S_{pa} (0.2s)}}ls.$ The period T₁ that represents the starting of constant acceleration range has been calculated as a fraction of T₂ depending on the local characteristics (soil condition) as $T_{1} = \left( {\frac{1}{2}t_{0} - \frac{1}{5}} \right)T_{2}$ with a factor of 1/5 taken in the present case (for hard rock), as per the guidelines⁵⁸.

Sensitivity analysis on seismicity parameters and ground motion models

A sensitivity analysis was performed to quantify the impact of key seismicity parameters and GMMs on the outcomes of PSHA. The seismicity parameters considered include the Gutenberg–Richter a-value and b-value, Mc, and M_max. Additionally, the influence of the selected GMMs was investigated to assess model-induced epistemic uncertainty.

Monte Carlo simulations were employed to propagate the uncertainties associated with these parameters across all spatial grid points. A total of 200 synthetic earthquake catalogs were generated as used in earlier study of Das (2013). Each synthetic dataset was constructed by perturbing the seismicity parameters—specifically Mc and M_max within their plausible ranges (as outlined in Table 1)—while holding the GMM constant to isolate the effects of seismicity inputs.

The results indicate that the Mc exhibits the most pronounced influence on seismic hazard, particularly at shorter return periods (e.g., 100 years). Variations in Mc resulted in changes of approximately 20–40% in PGA estimates. This strong sensitivity arises from Mc’s direct control over the rate of small- to moderate-magnitude earthquakes, which dominate ground motion exceedance probabilities at shorter return intervals.

The a-value and b-value, which govern the frequency-magnitude distribution of seismicity, showed a moderate impact, inducing 10–30% variation in PGA levels, with a more prominent effect at short to intermediate return periods. These parameters influence the total seismicity rate and the relative proportion of large versus small events.

In contrast, the maximum magnitude (M_max) demonstrated a relatively limited influence on PGA estimates at short and intermediate return periods (10–15% variation). However, its contribution becomes more substantial at longer return periods, where the hazard is increasingly dominated by rare, high-magnitude events.

This analysis highlights the importance of accurate estimation and uncertainty quantification of Mc, a-value, b-value, and M_max in seismic hazard modeling, particularly when evaluating hazard for critical infrastructure with varying design life spans.

In a separate set of 200 simulations, the influence of GMMs was assessed by varying the GMMs while keeping the seismicity parameters—a-value, b-value, Mc, and Mmax—fixed across all realizations. This approach allowed for an isolated evaluation of the epistemic uncertainty introduced by the selection of GMMs in PSHA. The results revealed that the choice of GMMs constitutes the most significant source of epistemic uncertainty in the hazard estimates, with the PGA varying by approximately 20% to 120% across various models. This underscores the necessity of comparing GMM predictions with observed data and demonstrates that such variability can be effectively addressed through the implementation of logic trees. The observed variability originates from differences in functional forms, regression coefficients, regional calibration datasets, and foundational assumptions embedded within each GMM. Additionally, the aleatory variability captured by the standard deviation (σ) inherent to each GMM contributes significantly to hazard estimates, especially at longer return periods.

Summary and conclusion

The PSHA maps presented in this study are crucial for various stakeholders, including government agencies, city planners, insurance companies, community disaster management organizations, and initiatives aimed at reducing risk, particularly in the context of building codes (e.g., ICC 2009⁵⁹). Our research examined three fundamental aspects: the seismic catalog, seismic source zones, and GMMs. Through a comprehensive analysis, we developed a cohesive earthquake catalog using an advanced moment magnitude scale known as the Das Magnitude Scale (M_wg).

The creation of a cohesive earthquake catalog that includes 9,968 events in this study serves as a valuable resource for a broad range of seismological research, such as seismic hazard assessment, the development of GMMs, seismicity analysis, seismotectonics, and earthquake prediction in the study area. The established empirical correlations among various magnitude scales (i.e., m_b to M_wg, M_S to M_wg, M_L to M_wg) will enhance the understanding of local site influences on seismicity parameters.

The entire region of Northeast India has been divided into nine seismic source zones. This classification of seismic source zones, mainly determined by local differences in tectonic features, focal mechanisms, and geological conditions, has provided us with valuable insights. Each of these zones is characterized by specific seismicity parameters and distinct geological features, contributing to a comprehensive understanding of seismic hazards in the region (Table 2).

To assess the impact of different magnitude scales on seismic hazard estimates, we compared results obtained using the M_wg scale with those derived from the M_w scale. Initially, we prepared declustered catalogs based on both magnitude scales. For the M_wg catalog, we used the method described by Urhammer (1986), which led to the removal of 2223 events from an original dataset of 9968, representing approximately 22.29% of the total events. In contrast, the M_w catalog saw 3512 events declustered, accounting for about 35.22% of the total events. These underscore the M_wg scale’s effectiveness in identifying and removing clustered seismic events. Subsequently, we investigated how the choice of magnitude scale affects seismicity parameters by estimating parameters such as Mc, ‘a’ value, and ‘b’ value using both the maximum magnitude and entire magnitude range methods. Our analysis revealed significant variations based on the magnitude scale used: M_c was underestimated by 14%, 'b' values varied by 13%, and 'a' value changed by 7% (Table 3).

PSHA maps depicting surface-level ground motion were generated using the M_wg scale. The assessment was performed with grid spacing of 0.10 × 0.10 across the study area, utilizing a logic tree approach. Hazard curves for each grid location were calculated by averaging the various scenarios based on their assigned weights. Figure 11 shows the logic tree configuration for a particular site. The PGA values at the surface ranged from 0.01 to 0.91 g for the scenario with a 10% exceedance likelihood over a 50-year period. The estimated PGA values for 10% exceedance probability in 50 years at the surface for Guwahati, Imphal, Aagartala, Shillong, Kohima, Gangtok, Itanagar, Tezpur, and Aizwal are 0.81 g, 0.68 g, 0.61 g, 0.82 g, 0.68 g, 0.59 g, 0.66 g, 0.76 g, 0.57, 0.57 g, respectively. The estimated PGA values for 2% exceedance probability in 50 years at the surface for Guwahati, Imphal, Agartala, Shillong, Kohima, Gangtok, Itanagar, Tezpur, Aizwal 1.42 g, 1.07 g, 0.97 g, 1.45 g, 1.06 g, 0.89 g, 1.08 g, 1.34 g, 1.34 g, 0.87 g, respectively. The maximum Peak Ground Acceleration value associated with a 2% exceedance probability over a 50-year period was determined to be 1.54. Our investigation obtained relatively lower values along Himalaya plate boundary in the segment between 1987 and 1950 earthquake epicenters compared to other Himalayan Palte boundary areas of Northeast India. We attribute the discrepancy in ground motion estimation to the segment’s lack of significant earthquakes during the period in question, compounded by the limitations of the PSHA methodology. A PGA of roughly 1 g in this segment would not be surprising, as our PSHA estimation is constrained by a limited data window. The substantial acceleration experienced in Northeast India during The 1950 earthquake, approximately reaching 1 g, can be attributed to the relatively shallow focal depth characteristic of the Himalayan plate boundary.

Design spectra tailored to nine major cities in Northeast India were developed, offering valuable insights for the construction of earthquake-resistant infrastructure based on 475 and 2475 return periods (Fig. 14).

Importantly, we demonstrate that existing GMMs developed using the M scale can be directly applied to the M_wg scale, as both are fundamentally derived from seismic moment (Mo). A mathematically derived linear relationship (M_wg = 1.10 M–0.88) allows for consistent conversion, enabling seamless integration of M_wg into existing PSHA frameworks without recalibrating the GMM formulations. However, as the M scale tends to overestimate seismic energy for small to moderate earthquakes (Fig. 1), the development of new GMMs directly in terms of M_wg is recommended. Such models would more accurately reflect ground motion behavior across all magnitude ranges and improve the robustness of seismic hazard assessments.

The difference in the final PSHA results between the M_wg and M scales was calculated and found to be significant. In particular, the assessment based on the M scale results in an overestimation of ground motion up to 40% for a 475-year period and by 20% for a 2475-year duration, especially in regions where medium range earthquakes are possible (zones 1, 5, 6, and 8). This overestimation is attributed to the M scale’s tendency to overestimate earthquake energy in the lower and medium magnitude ranges (Fig. 1). Several studies already suggested that the M scale overestimates seismic radiated energy, as noted by Choy and Boatwright²⁶, Das et al.^13,15,16,60. However, the M_w scale underestimates the PGA by up to 10% when the maximum observed difference is 0.1 magnitude units for maximum magnitude earthquakes (with the maximum magnitude observed in the M_wg scale being 8.9, compared to 8.8 in the M scale at zone 4).

The key distinctions between this study and earlier research conducted in the Northeast India region are: (1) Comprehensive analysis of the earthquake catalog; (2) Earlier studies relied on the M scale and had a more localized focus; (3) GMMs applied in this research are weighted according to the best fitting observed data.

PSHA studies have inherent limitations due to their reliance on historical and instrumental earthquake data, which typically span only a few hundred years. This limited seismic record introduces challenges in assessing long-term seismic hazard (475 years and 2475 years), particularly in regions with sparse historical data. To address these limitations, integrating Global Navigation Satellite System (GNSS) data is recommended. GNSS provides continuous and precise measurements of ground deformation, offering critical insights into stress accumulation and release over extended time scales. By incorporating GNSS data, PSHA models can be refined to better predict long term seismic hazard²⁰.

Another limitation of this study is the use of the Poisson model for earthquake occurrences and the Cornell–McGuire approach, which assumes time-independent seismicity based on the Gutenberg-Richter recurrence law. While this is a widely accepted approach, future studies could explore alternative models, such as Gamma, Weibull, Markov, or Gumbel distributions, which consider different statistical properties of earthquake recurrence. Furthermore, this study did not incorporate fault-specific analysis or time-dependent seismicity models. Future probabilistic seismic hazard assessments should investigate the influence of different seismogenic source zones on hazard estimates. Additionally, conducting a detailed sensitivity analysis would help identify key model parameters and branches that significantly contribute to seismic hazard outcomes, enhancing the robustness of hazard assessments.

In summary, this study lays the groundwork for understanding seismic hazard in Northeast India, but there is room for further refinement and exploration of alternative models and methodologies to enhance the accuracy of seismic risk assessments in the region.