RCSAN residual enhanced channel spatial attention network for stock price forecasting

Abstract

This study proposes a stock price prediction model based on the Residual-enhanced Channel-Spatial Attention Network (R-CSAN), which integrates channel-spatial adaptive attention mechanisms with residual connections to effectively capture the multidimensional complex patterns in financial time series. The R-CSAN adopts an encoder-decoder architecture, where the encoder extracts feature correlations from historical data through multiple layers of channel-spatial attention modules, and the decoder incorporates a masking mechanism to prevent future information leakage and introduces a cross-attention mechanism to model inter-market correlations. Experiments conducted on four cross-market stock datasets, including Amazon, Maotai, Ping An, and Vanke, demonstrate that R-CSAN significantly outperforms not only traditional baseline models such as ARIMA, LSTM, and CNN-LSTM, but also recent Transformer-based approaches like Informer, Autoformer, and iTransformer on metrics including RMSE, MAE, MAPE, $R^2$, and return on investment. The model reduces RMSE by 17.3–49.3% compared to traditional methods and 6.2–11.6% compared to Transformer variants, with the highest $R^2$ reaching 93.17% and an increase in return on investment to 482.64%. Ablation experiments confirm the critical contributions of each component, with the temporal module removal causing an average increase of 38.6% in RMSE and channel-spatial attention removal resulting in a 21.3% increase. Moreover, the model provides an interpretative analysis of features and temporal dimensions through attention weight visualization, offering insights into both indicator importance and critical time periods for prediction. In practical applications, R-CSAN’s outputs can be integrated into quantitative trading strategies including breakout trading, moving average crossover signals, and portfolio allocation optimization, providing a new paradigm for robust prediction in highly volatile markets.

Introduction

Stock market prediction has long been a critical and challenging research topic in financial engineering and data science¹. Accurate stock forecasting is of immense practical importance to investors, financial institutions, and regulators. However, stock prices are influenced by a multitude of dynamic, nonlinear factors such as macroeconomic indicators², company fundamentals³, investor sentiment⁴, and geopolitical events⁵, making their behavior difficult to model with traditional statistical tools.

Classical forecasting approaches like ARIMA⁶ and GARCH⁷ assume linear stationarity, which severely limits their capacity to generalize in volatile markets. Traditional machine learning methods, such as SVM⁸ and Random Forests⁹, though capable of capturing nonlinearities, still require manual feature engineering and lack sequential modeling capabilities.

In response, recent research has turned to deep learning techniques for financial time series forecasting. Models like Long Short-Term Memory (LSTM)¹⁰ networks have demonstrated promising results in capturing temporal dependencies due to their specialized gating mechanisms that preserve long-term information while filtering irrelevant details. Convolutional Neural Networks (CNN)¹¹ excel at extracting local spatial patterns and hierarchical features, making them effective for identifying technical patterns in financial data.

Among deep learning approaches, hybrid models have gained increasing attention for their ability to leverage complementary strengths of multiple neural architectures. CNN-LSTM¹² combines CNN’s feature extraction capabilities with LSTM’s sequential modeling to better capture both spatial and temporal aspects of financial data. Graph Neural Networks (GNNs)¹³ model relationships between different stocks or market sectors, capturing cross-asset dependencies. Attention-based approaches like Transformers¹⁴ have revolutionized time series modeling by dynamically focusing on relevant historical periods through self-attention mechanisms. Recent variants such as Informer¹⁵, Autoformer¹⁶, and iTransformer¹⁷ have been specifically designed for long-sequence time series forecasting with enhanced efficiency.

Temporal fusion transformer (TFT)¹⁸ further advances this direction by integrating static covariates, attention mechanisms, and gating structures within a single framework. This architecture allows TFT to process both temporal features and static metadata, making it particularly suitable for complex financial data with diverse input sources. Similarly, LSTM-based ensembles with attention¹⁹ have shown improvements in stock prediction by focusing on the most relevant historical time steps.

However, despite these advances, existing methods still suffer from key limitations: they typically focus on either temporal dependencies or feature-wise interactions, but rarely model both simultaneously in a unified framework. CNN-LSTM models, while combining spatial and temporal aspects, often treat these dependencies in a pipelined rather than interactive manner, limiting their ability to capture complex interdependencies. Traditional attention mechanisms primarily focus on temporal relationships (identifying which past time points are most relevant) but may overlook the varying importance of different financial indicators. Even sophisticated Transformer-based models like Informer and Autoformer, while powerful for temporal modeling, may fail to capture the nuanced importance across heterogeneous financial indicators (e.g., technical indicators, volume, volatility) and their evolving relationships over time.

This limitation undermines model generalizability in complex financial environments where cross-indicator correlations are critical and constantly evolving. For instance, volume indicators may have higher predictive power during market rallies, while volatility metrics become more crucial during market corrections–a dynamic that requires simultaneous attention to both the feature dimension (which indicators matter) and the temporal dimension (when they matter).

To address these challenges, this paper proposes a novel Residual-Enhanced Channel-Spatial Attention Network (R-CSAN), which bridges the gap by jointly modeling temporal dynamics and cross-indicator relationships through a hybrid attention mechanism. The model introduces a dual-dimensional adaptive attention mechanism—channel attention for feature-level importance and spatial attention for time-step relevance—fused with residual connections²⁰ and normalization layers²¹ to enhance learning stability. This approach enables the model to dynamically adjust its focus across both financial indicators and time periods simultaneously, capturing complex patterns that are inaccessible to traditional single-focus attention mechanisms.

The main contributions of this paper are summarized as follows:

• We propose R-CSAN, a hybrid attention architecture that simultaneously captures temporal and feature-wise interactions, addressing a major limitation of existing hybrid models and attention-based forecasting approaches.

• We design channel-spatial adaptive attention blocks that enhance interpretability and allow dynamic focus on key indicators and time points in stock movement prediction, with the capability to adapt to different market regimes.

• We integrate residual connections and normalization strategies to alleviate gradient vanishing and improve deep network training efficiency in volatile financial data, enabling the construction of deeper networks with enhanced learning capacity.

• We conduct extensive experiments on both U.S. and Chinese stock datasets, demonstrating the superiority and cross-market robustness of R-CSAN in terms of predictive accuracy and return compared to both traditional forecasting methods and state-of-the-art Transformer-based approaches.

The remainder of this paper is organized as follows: “Related work” reviews related work in traditional and deep learning-based financial forecasting, with particular focus on hybrid models and attention mechanisms. “Methods” details the architectural design of R-CSAN, including data preprocessing, overall architecture, channel-spatial attention modules, cross-attention mechanism, and training process. “Experiment” presents experimental results on multiple datasets, comparing R-CSAN with both traditional models and modern Transformer-based approaches. “Discussion” discusses the interpretability, generalization capabilities, and potential real-world applications in quantitative trading strategies. “Conclusion” concludes the paper with a summary of findings, limitations of the current approach, and directions for future research.

Related work

Traditional methods for financial time series prediction

Traditional financial time series prediction methods primarily include statistical models²² and classic machine learning algorithms. In terms of statistical models, AutoRegressive Integrated Moving Average (ARIMA) and Generalized AutoRegressive Conditional Heteroskedasticity (GARCH) models are widely used in financial data analysis. These models construct linear or nonlinear relationships based on historical data, attempting to predict future financial indicators through past observations. The ARIMA model, by integrating AutoRegression (AR)²³, Integration (I)²⁴, and Moving Average (MA) techniques²⁵, can capture trends and seasonal variations within time series. However, these statistical models show significant limitations when dealing with high-dimensional, non-stationary, and complex financial data, particularly in rapidly changing market environments, where their predictive capability often fails to remain stable.

In the realm of machine learning, algorithms such as Support Vector Machines (SVM)²⁶, Random Forests²⁷, and Gradient Boosting Trees²⁸ are extensively used for stock price prediction. These methods can handle nonlinear relationships and extract latent patterns from data through complex decision boundaries or ensemble learning techniques. Support Vector Machines classify and regress by constructing optimal hyperplanes; Random Forests enhance prediction accuracy through the ensemble of multiple decision trees; Gradient Boosting Trees build powerful predictive models iteratively. Although these algorithms perform well in specific scenarios, they typically face two main challenges: firstly, they require extensive feature engineering, relying on domain experts’ prior knowledge; secondly, they struggle to autonomously capture the inherent long-term dependencies and complex spatiotemporal patterns present in financial time series data.

The limitations of traditional methods highlight the urgent need for more intelligent and flexible prediction techniques. With the rapid advancement of deep learning technologies, researchers have begun to explore more advanced methods to address the complexities of financial time series prediction. These new approaches can not only automatically learn features but also better capture the nonlinear relationships and time dependencies within the data.

Applications of deep learning in financial forecasting

In recent years, deep learning techniques have been extensively applied in financial forecasting, bringing revolutionary changes to traditional financial analysis methods^29,30,31. Long Short-Term Memory networks (LSTMs)³², originally proposed by Hochreiter and Schmidhuber, have rapidly become mainstream for time series forecasting due to their unique gating mechanisms and exceptional ability to handle long-term dependencies. Fischer and Krauss³³ demonstrated that LSTMs significantly outperform traditional methods in stock market prediction by addressing vanishing gradient problems through forget, input, and output gates. Subsequent studies by Nelson et al.³⁴ and Baek and Kim¹⁰ further validated LSTM’s effectiveness in capturing and memorizing crucial information over extended financial time series, making them particularly prominent for processing complex data such as stock prices and trading volumes. The hybrid architecture combining Convolutional Neural Networks (CNNs) and LSTMs has further enhanced financial forecasting performance. LeCun et al.³⁵ introduced CNNs for spatial feature extraction, which Sezer and Ozbayoglu³⁶ successfully adapted for financial time series by treating price movements as image-like patterns. The CNN-LSTM model¹² proposed by Lu et al. cleverly combines these strengths: CNNs excel in extracting local spatial features and capturing short-term patterns in financial indicators, while LSTMs model long-term temporal dependencies and overall trends. This complementary architecture has been further developed by Hoseinzade and Haratizadeh¹¹, who demonstrated significant improvements in prediction accuracy and stability. However, these hybrid models typically process spatial and temporal information sequentially rather than jointly, limiting their ability to capture complex interdependencies. The introduction of attention mechanisms^18,37 has opened new avenues for performance enhancement in deep learning models. Vaswani et al.³⁷ proposed the Transformer architecture with self-attention mechanisms, which Qin et al.³⁸ adapted for time series prediction through dual-stage attention mechanisms. Recent Transformer variants have shown particular promise: Zhou et al.¹⁵ developed Informer for efficient long-sequence forecasting, Wu et al.¹⁶ proposed Autoformer with decomposition-based attention, and Liu et al.¹⁷ introduced iTransformer for improved time series modeling. Li et al.³⁹ and Chen et al.⁴⁰ further demonstrated that attention mechanisms can dynamically allocate varying weights to different parts of input sequences, enabling models to focus on critical information. However, existing attention mechanisms often limit their focus to the temporal dimension, overlooking complex interrelationships among financial indicators, as noted in comprehensive surveys by Lim and Zohren⁴¹ and Torres et al.⁴². Recent comprehensive reviews have highlighted both the potential and limitations of deep learning in finance. Heaton et al.⁴³ demonstrated deep learning’s effectiveness in portfolio management, while Ozbayoglu et al.⁴⁴ provided extensive analysis of deep learning applications across various financial tasks. Gu et al.⁴⁵ conducted large-scale empirical studies showing that machine learning methods can improve asset pricing, though they noted challenges in model interpretability and stability. Despite considerable potential, numerous challenges remain, particularly in designing architectures that simultaneously consider temporal evolution and indicator correlations–a critical issue identified by Zhang et al.³¹ as driving the development of financial artificial intelligence.

Application of attention mechanisms in time series analysis

Attention mechanisms initially achieved significant success in the field of natural language processing and quickly extended to multiple research domains, including time series analysis. In the context of financial time series forecasting, attention mechanisms provide a dynamic and flexible method for feature selection and weight distribution, allowing the model to adaptively focus on historical data points and features most relevant to the prediction targets. This selective attention mechanism greatly enhances the model’s ability to capture complex latent patterns in time series. However, existing attention mechanisms have significant limitations: most methods tend to focus on a single dimension, either concentrating on temporal progression or analyzing feature importance, with few capable of addressing both dimensions simultaneously. This unidimensional focus makes it challenging for models to fully comprehend the multidimensional complexity of financial data. Particularly in finance, stock prices are influenced by multiple factors from time series and various financial indicators, making traditional single-dimension attention mechanisms inadequate.

The Residual-enhanced Channel-Spatial Attention Network (R-CSAN) proposed in this paper is designed to bridge this critical gap. The model innovatively introduces a channel-spatial adaptive attention mechanism that simultaneously focuses on both time and feature dimensions. In the channel dimension, the model focuses on the intrinsic relationships between different financial indicators; in the spatial dimension, it captures key patterns within the time series. This multidimensional, multilevel attention mechanism enables the model to understand the complex dynamics of financial data more comprehensively and deeply. To further enhance the model’s learning capability, this paper introduces residual connections. Residual connections establish direct information transfer channels within deep networks, effectively mitigating the common problem of gradient vanishing in deep learning. This design allows the model to handle information flow within deep networks more efficiently, continuously learning and extracting more abstract and discriminative feature representations while retaining original features. Through this innovative architectural design, R-CSAN not only breaks through the limitations of traditional attention mechanisms but also provides a more intelligent and flexible technical path for financial time series forecasting. The core value of the model lies in its ability to capture the complex patterns of financial data more comprehensively and deeply, offering investors and researchers more accurate and insightful predictive tools.

Methods

Data preprocessing

The raw encoder input $X_{\textrm{en}}$ and decoder input $X_{\textrm{de}}$ undergo a normalization process before being fed into the model, as outlined below:

To standardize the price-based features (such as Open, Close, High, Low, Volume), the Min-Max scaling technique is applied, which transforms the data into the $[0,1]$ range using the formula:

$$\begin{aligned} {X^{(i)}_{\text {norm}} = \frac{X^{(i)} - \displaystyle \min _{j}(X^{(j)})}{\displaystyle \max _{j}(X^{(j)}) - \displaystyle \min _{j}(X^{(j)})}, \quad i = 1, \dots , N} \end{aligned}$$

(1)

Here, $X^{(i)}$ is the original value of feature $i$, and the denominator ensures that all features are rescaled to a common range, improving convergence in neural networks.

For technical indicators such as RSI, MACD, and Bollinger Bands, Z-score normalization is used to standardize features into a distribution with a mean of 0 and standard deviation of 1:

$$\begin{aligned} {X^{(i)}_{\text {norm}} = \frac{X^{(i)} - \mu _i}{\sigma _i}, \quad i = 1, \dots , N} \end{aligned}$$

(2)

where $\mu _i$ is the mean and $\sigma _i$ is the standard deviation of feature $i$. This process helps maintain consistent input scales across features with varying ranges or units.

Additionally, forward filling is used to impute missing values in a time-consistent manner. Masking is applied to distinguish imputed values during training. Outliers and extreme price fluctuations are further managed via a robust scaling strategy using a moving window to mitigate their influence.

These preprocessing steps ensure numerical stability, reduce the risk of model overfitting, and enhance the overall training effectiveness for complex financial time series data.

Overall architecture

This study introduces the R-CSAN (Residual-Enhanced Channel-Spatial Attention Network) model, a deep learning framework with a hybrid attention mechanism, specifically designed for stock market prediction. This architecture integrates channel-spatial adaptive attention mechanisms with residual connections to effectively capture the temporal dependencies and cross-sectional relationships within financial time series data.

The model consists of two main branches, each handling different aspects of the input data:

• 1. Encoder branch: Processes the raw financial features through multiple layers of channel-spatial adaptive attention blocks. Each attention block includes residual connections that allow information to flow directly from shallow to deeper layers, effectively mitigating the vanishing gradient problem common in deep networks.

• 2. Decoder branch: Handles the combination of token embeddings and initial state representations, using masked channel-spatial adaptive attention to prevent information leakage from future time steps. Similarly, each decoder block also includes residual connections, enhancing the learning of long-term dependencies.

Both branches are stacked N times and are combined with residual connections and normalization layers to facilitate gradient flow and stabilize the training process. The introduction of residual connections is one of the core innovations of the R-CSAN model, allowing raw information to flow directly to deeper layers, significantly enhancing the learning capacity of deep networks, especially for capturing long-term temporal dependencies.

Additionally, normalization layers within the model further stabilize the training process, enabling the model to effectively handle the high volatility common in financial data. The final output layer consists of a fully connected network, generating stock prediction targets, including price forecasts and trend classifications.

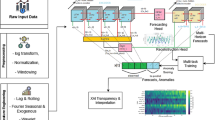
Figure 1 shows the overall architecture of the R-CSAN model. From the diagram, it is evident that the encoder and decoder branches of the model work together to capture complex patterns in financial time series data. The encoder focuses on processing historical features, while the decoder is responsible for merging historical information and generating future predictions. The interaction between the two branches through the cross-attention mechanism further enhances the model’s ability to capture long-term dependencies.

The architectural design of the R-CSAN model makes it particularly suitable for handling the characteristics of financial time series data, including nonlinear relationships, long-term dependencies, and cross-market correlations. The application of residual connections allows the model to build deeper network structures without being affected by the gradient vanishing problem, thus enabling it to learn more complex patterns in financial data.

Fig. 1

The overall architecture of the R-CSAN model (modified).

Channel-spatial adaptive attention module

The Channel-Spatial Adaptive Attention Module is a core innovation of the R-CSAN model, designed to simultaneously capture feature-wise importance and temporal relevance in financial time series. This dual-dimension attention mechanism consists of two sequential components that work in tandem: the Channel Attention Module followed by the Spatial Attention Module.

The Channel-Spatial attention flow follows a hierarchical pattern:

• 1. First, the input feature map $F \in {\mathbb {R}}^{C \times H \times W}$ is processed by the Channel Attention Module, which generates channel attention weights $M_c \in {\mathbb {R}}^{C \times 1 \times 1}$ through a combination of different pooling operations and shared MLP layers.

• 2. The channel-refined features $F' = M_c \odot F$ are then fed into the Spatial Attention Module, which creates a spatial attention map $M_s \in {\mathbb {R}}^{1 \times H \times W}$ focusing on important temporal patterns.

• 3. Finally, the module outputs the refined feature representation $F'' = M_s \odot F'$, which emphasizes both important financial indicators and critical time points.

This integrated approach differs from conventional attention mechanisms that typically address either feature dimensions or temporal aspects independently. By cascading channel and spatial attentions, our module creates a comprehensive feature refinement process that enhances the network’s ability to focus on the most informative aspects of financial data across both dimensions. The module is further strengthened by residual connections, allowing the original information to flow alongside the attended features, which is crucial for preserving primary financial patterns while highlighting significant signals.

Channel attention module

In the R-CSAN model, the channel attention module is a key component of the residual-enhanced channel-spatial adaptive attention mechanism. This module is specifically designed to capture the complex relationships between various financial indicators, such as price, volume, and technical indicators, which is crucial in financial time series prediction due to the rich predictive information contained in the interactions between different indicators.

The computation process of the channel attention module is as follows:

• 1. Multi-feature extraction: The module first extracts information from input features through three different pooling operations-max pooling, median pooling, and average pooling. Each type of pooling captures different aspects of feature statistics:

  • Max pooling focuses on the most significant values, aiding in the capture of exceptional market fluctuations.

  • Median pooling offers robustness against outliers, reducing the impact of market noise.

  • Average pooling calculates the overall trend, reflecting the general market state.

• 2. Shared MLP processing: The pooling results are processed through a shared Multi-Layer Perceptron (MLP) for nonlinear transformation, enhancing feature expressiveness. This reduces parameter count and facilitates interaction between different pooling results.

• 3. Application of channel-level attention: Channel attention weights are generated and applied to the original features to emphasize financial factors critical for the prediction task.

The mathematical expression for channel attention is given by:

$$\begin{aligned} M_c= & \sigma \left( \text {MLP}\left( \text {AvgPool}(F)\right) + \text {MLP}\left( \text {MaxPool}(F)\right) + \text {MLP}\left( \text {MedianPool}(F)\right) \right) \end{aligned}$$

(3)

$$\begin{aligned} F'= & M_c \odot F \end{aligned}$$

(4)

where $\sigma$ is the sigmoid activation function, normalizing the attention weights to between 0 and 1, and $\odot$ represents element-wise multiplication. This design allows the model to dynamically adjust the emphasis on different financial indicators based on their relevance to the predictive task, thereby enhancing or suppressing specific features adaptively.

The output $F'$ from the channel attention is used to refine the subsequent processing stages, strengthening the network’s ability to focus on crucial features for prediction. This process ensures that the attention mechanism does not ignore subtle but potentially critical patterns in the financial time series, enhancing the model’s predictive accuracy by focusing on the most relevant features.

Spatial attention module

In the R-CSAN architecture, the spatial attention module is a vital complement to the channel attention module, specifically designed to capture temporal dimension patterns within financial time series data. While channel attention focuses on the relationships between different financial indicators, spatial attention concentrates on key moments and important patterns in the time series, which is particularly important for predicting market turning points and trend changes.

The computation process of the spatial attention module is as follows:

• 1. Multi-scale convolution processing: The module applies a 5 $\times$ 5 convolution kernel to the feature maps, enabling the capture of a wider temporal context. This larger convolution kernel facilitates attention across several trading days, aiding in the identification of medium-term market trends.

• 2. Multi-depth convolution implementation: By executing convolution operations at multiple depths, the module effectively captures various time-scale patterns. This capability allows the R-CSAN to manage short-term fluctuations, medium-term trends, and long-term cycles, significantly boosting the model’s comprehension of complex market structures.

• 3. Temporal dimension attention application: Spatial attention weights are generated from average and max pooling results and applied to the feature maps, emphasizing the most significant periods within the time series. This focus helps the model prioritize days with pivotal signals, like market reversals, periods of high volatility, or major economic events.

The spatial attention is mathematically represented as follows:

$$\begin{aligned} M_s= & \sigma \left( \text {Conv}_{5 \times 5}\left( [\text {AvgPool}(F'); \text {MaxPool}(F')]\right) \right) \end{aligned}$$

(5)

$$\begin{aligned} F''= & M_s \odot F' \end{aligned}$$

(6)

where $\sigma$ denotes the sigmoid activation function, compressing the attention values between 0 and 1, $\text {Conv}_{5 \times 5}$ indicates a 5x5 convolution operation, brackets [] denote feature concatenation, and $\odot$ represents element-wise multiplication. This computation crafts a temporal attention mask that highlights the most predictive time points.

The output from the spatial attention module, $F''$, is an enhanced feature representation, formulated by processing the channel attention module’s output, $F'$. This layered design ensures that the model initially concentrates on significant financial indicators before identifying crucial temporal patterns. It exemplifies a progressive attention strategy that evolves from “features” to “time.”

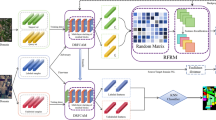
Figure 2 illustrates the complete Channel-Spatial Adaptive Attention Mechanism structure. The left side shows the Channel Attention Module, which employs three parallel pooling operations (max, average, and median pooling) followed by shared MLP layers to generate channel attention weights. The right side depicts the Spatial Attention Module, which utilizes convolutional operations on pooled feature maps to create a spatial attention mask. The figure demonstrates how these two components are sequentially connected, with channel attention output serving as the input to spatial attention, forming an integrated dual-dimension attention mechanism. This structure enables the model to first highlight important financial indicators and then focus on critical temporal patterns within those indicators, creating a progressive refinement process essential for capturing complex financial time series dynamics.

Fig. 2

Detailed structure of the channel-spatial adaptive attention mechanism.

Cross-attention mechanism

In the R-CSAN model, the cross-attention mechanism is a crucial component that overcomes the limitations of the channel-spatial adaptive attention, allowing the model to establish complex networks of relationships between different market sectors, stocks, or macroeconomic factors. This mechanism is essential for a comprehensive understanding of systemic risks and interdependencies in financial markets, especially in how specific stocks are influenced by overall market trends, industry dynamics, or economic indicators.

The cross-attention mechanism is implemented based on the Transformer architecture’s classical query-key-value (Q, K, V) paradigm. In R-CSAN, this mechanism operates as follows:

• 1. Relationship modeling: The module uses one feature sequence (e.g., a stock’s features) as the query (Q), and another feature sequence (e.g., industry indexes or related stocks) as the key (K) and value (V), establishing cross-sequence dependencies by calculating their correlations.

• 2. Multi-head design: Cross-attention employs a multi-head design, allowing the model to simultaneously learn relationships from different representational subspaces and capture richer patterns of interdependencies.

• 3. Scale normalization: Attention scores are normalized by dividing by the square root of the dimension of the key vectors, ensuring stability of gradients during back-propagation.

The computation formula for cross-attention is:

$$\begin{aligned} \text {Attention}(Q, K, V) = \text {softmax}\left( \frac{QK^T}{\sqrt{d_k}}\right) V \end{aligned}$$

(7)

Where $Q$ is the query matrix, representing the currently needed enhanced features. $K$ is the key matrix, used to compute correlations with the query. $V$ is the value matrix, providing the actual information content. $\sqrt{d_k}$ is the dimension of the key vectors, used for scale normalization. softmax function converts attention scores into a probability distribution.

In the implementation within R-CSAN, the cross-attention sits between the encoder and decoder branches, acting as an information bridge. The encoder’s processed historical financial features serve as keys and values, while the decoder’s output serves as the query, allowing the model to selectively focus on the historical information most relevant to the current prediction task.

This design makes the R-CSAN model particularly suitable for dealing with the “contagion effects”⁴⁶ and “spillover effects”⁴⁷ frequently seen in financial markets, such as how fluctuations in one sector or region can impact others. For example, the model can learn how energy price fluctuations affect airline stocks, or how the performance of tech giants can drive the entire technology sector.

By incorporating cross-attention, R-CSAN not only captures patterns within a single time series but also understands complex interactions between different financial entities, thus considering a broader market environment when predicting individual stock trends, offering more comprehensive and accurate forecasts.

Implementation details of cross-attention

For the specific implementation in stock price forecasting, we utilize market-level and sector-level indices as complementary information sources for the Cross-Attention mechanism. The structured data processing and alignment work as follows:

• 1. Data sources and dimensionality:

  • Primary stock sequence: For each target stock (e.g., Amazon), we utilize its processed feature representation from the encoder branch as the query (Q).

  • Market index data: For U.S. stocks, we incorporate S&P 500 and NASDAQ indices. For Chinese stocks, we use CSI 300 and industry-specific indices. Each index contributes 5 features (Open, High, Low, Close, Volume).

  • Sector peer stocks: For each target stock, we select 3-5 peer companies from the same industry sector. For example, for Amazon, we include Microsoft, Google, Apple, and Facebook.

• 2. Temporal alignment: All complementary data (indices and peer stocks) are aligned with the primary stock using the same trading dates. Non-trading days are handled using forward-fill imputation to ensure consistent sequence lengths.

• 3. Feature transformation: Before serving as keys and values in the cross-attention mechanism, the complementary data undergoes the same preprocessing steps as the primary stock data.

The implementation of the cross-attention mechanism can be formalized as follows:

Algorithm 1

Cross-attention mechanism for financial data.

This implementation enables the model to effectively incorporate broader market context and related stock information when predicting the target stock’s price movements. The keys and values derived from market indices and peer stocks provide contextual information about wider market trends and sector-specific movements, allowing the model to better understand how the target stock’s price movements correlate with broader financial patterns.

The multi-head implementation further enhances this capability by allowing the model to attend to different aspects of the complementary data simultaneously, capturing various relationships between the target stock and market conditions.

Residual connections and normalization

One of the core innovations of the R-CSAN model is the organic integration of residual connections and layer normalization techniques into the channel-spatial attention network, forming a “Residual-Enhanced” architecture. This design is particularly effective in processing financial time series data, especially given the high volatility and complex nonlinear relationships in financial markets.

In the R-CSAN architecture, each attention submodule (including channel attention, spatial attention, and cross-attention modules) is equipped with residual connections and layer normalization components. This design offers the following three key advantages:

• 1. Effective mitigation of the vanishing gradient problem: In deep neural networks, gradients can decay rapidly as network depth increases, making it difficult for shallow layers to update. Residual connections provide a shortcut for gradients, allowing information and gradients to flow directly across multiple layers, significantly alleviating the vanishing gradient problem. This is particularly important for financial forecasting, where capturing long-term dependencies often requires deeper network structures.

• 2. Support for deeper network structures: With residual connections, R-CSAN can stack more attention layers without significantly increasing training difficulty. This enhances the model’s expressive power, enabling it to learn more complex patterns in financial data, especially those involving multiple time scales.

• 3. Stabilization of the financial data learning process: Financial time series often exhibit high volatility and non-stationary characteristics. Layer normalization, by standardizing the output of each layer, helps control the variability of feature distributions and reduces internal covariate shift, making the learning process more stable. This is particularly valuable in dealing with extreme financial scenarios like market crashes and sudden events.

The residual connections in R-CSAN can be represented as:

$$\begin{aligned} X_{i+1} = \text {LayerNorm}(X_i + F(X_i)) \end{aligned}$$

(8)

Where $X_i$ is the input feature of layer $i$. $F(X)$ is the layer’s nonlinear transformation function (which could be channel attention, spatial attention, or cross-attention). $\text {LayerNorm}$ is the layer normalization operation, which standardizes the feature distribution for each sample.

This mechanism ensures that the original input information can be preserved and directly transmitted to the next layer, while the current layer’s transformation acts as an enhancement or correction. If a layer’s transformation does not benefit prediction, the optimization process can push the transformation’s weights towards zero, making the residual path the main information channel.

Moreover, R-CSAN’s residual connections are adaptive, able to adjust the information flow based on different market conditions. In stable markets, the model may rely more on historical patterns, with residual connections ensuring the effective transmission of this information; in volatile market conditions, the attention modules may generate stronger transformations, which merge with the original information through residual connections to form an adaptive response to market changes.

This “Residual-Enhanced” design makes R-CSAN a powerful predictive framework capable of deeply mining potential patterns in financial data while robustly handling market fluctuations.

Temporal module

The Temporal Module in R-CSAN is designed to explicitly model time-dependent patterns in financial sequences. This module implements a bidirectional LSTM (BiLSTM) architecture, which processes the input sequence in both forward and backward directions to capture comprehensive temporal dependencies.

The structure of the Temporal Module is as follows:

• 1. Input sequence processing: Feature maps processed by the Channel-Spatial Attention mechanism are fed into the Temporal Module, preserving both the enhanced feature representation and temporal ordering.

• 2. Bidirectional LSTM architecture: The module employs a two-layer BiLSTM with hidden dimension of 256 units, facilitating the capture of both short-term fluctuations and long-term trends in financial time series:

  $$\begin{aligned} \overrightarrow{h}_t= & \text {LSTM}_{\text {forward}}(x_t, \overrightarrow{h}_{t-1}) \end{aligned}$$

  (9)
  $$\begin{aligned} \overleftarrow{h}_t= & \text {LSTM}_{\text {backward}}(x_t, \overleftarrow{h}_{t+1}) \end{aligned}$$

  (10)
  $$\begin{aligned} h_t= & [\overrightarrow{h}_t, \overleftarrow{h}_t] \end{aligned}$$

  (11)

  where $\overrightarrow{h}_t$ and $\overleftarrow{h}_t$ represent the forward and backward hidden states at time step t, respectively.

• 3. Temporal integration: The bidirectional outputs are concatenated and processed through a projection layer to maintain dimensionality consistency with the overall network architecture.

The Temporal Module plays a crucial role in the overall performance of R-CSAN, as confirmed by our ablation experiments where its removal led to an average RMSE increase of 38.6%. This significant performance degradation underscores the module’s effectiveness in capturing complex temporal dynamics in financial markets that cannot be fully addressed by attention mechanisms alone.

By integrating this module with the Channel-Spatial Attention mechanism, R-CSAN achieves a comprehensive modeling approach that captures both feature-wise importance and temporal progression simultaneously, which is essential for accurate stock price forecasting.

Training process

The R-CSAN model employs an end-to-end training approach, optimizing network parameters through the backpropagation algorithm. Given the specificity of stock market prediction tasks, the training process integrates various optimization techniques to ensure model stability, generalizability, and predictive accuracy.

The R-CSAN uses a composite loss function to simultaneously optimize price prediction (a regression task) and trend prediction (a classification task), with the formula:

$$\begin{aligned} L = \alpha \times \text {MSE}(y_{\text {pred}}, y_{\text {true}}) + (1 - \alpha ) \times \text {CrossEntropy}(c_{\text {pred}}, c_{\text {true}}) \end{aligned}$$

(12)

Where $\alpha$ is a balance parameter that adjusts the relative importance of the two loss components. This multi-objective learning strategy enables the model to concurrently focus on the precise values of prices and the direction of market trends, providing a more comprehensive set of predictive insights. Practice shows that this composite loss significantly enhances the practicality of the model, especially in supporting trading decisions.

For optimizer selection, R-CSAN utilizes the Adam optimizer⁴⁸with learning rate scheduling to update parameters. The Adam optimizer, which combines the advantages of momentum methods and adaptive learning rates, is particularly suited for handling the sparse gradients and non-stationary features commonly found in financial time series. The learning rate scheduling strategy includes a warm-up phase, step-wise decay, and an early stopping mechanism based on validation loss, which helps the model find optimal solutions in complex parameter spaces while avoiding overfitting.

Considering the inherent noise and limited nature of financial data, R-CSAN implements multiple regularization strategies. Dropout technology⁴⁹ is applied after the attention layers and fully connected layers, randomly deactivating a certain percentage of neurons to prevent the model from overly depending on specific features and enhancing its robustness against market noise. L2 regularization adds a penalty for the L2 norm of the parameters to the loss function, limiting weight growth and favoring simpler explanations, thereby enhancing generalization. The combination of these regularization techniques enables the model to perform well on test sets and in real applications, even in the face of unseen market conditions. To further stabilize the training process and accelerate convergence, batch normalization is applied after each major component. Batch normalization reduces internal covariate shift, making the training of deep networks more stable, especially when dealing with highly volatile financial data. Combined with gradient clipping and mini-batch training techniques, R-CSAN can effectively handle exceptional samples (such as market crash days) and optimization difficulties encountered during training.

This comprehensive training methodology allows the R-CSAN model to fully exploit the potential of its “Residual-Enhanced” channel-spatial attention architecture, effectively learning complex patterns in financial time series while maintaining adaptability to market changes and robustness to noise. Experiments show that this carefully designed training process is one of the key factors maintaining high predictive performance of the R-CSAN model under various market conditions.

Experiment

Datasets

This study employs the historical trading data of four different stocks to evaluate the performance of the proposed R-CSAN model, including one American stock (Amazon) and three Chinese stocks (Moutai, Ping An, and Vanke). The specific details of these datasets are as follows:

• 1. Amazon dataset: Contains 6155 records covering the historical trading data of Amazon stock from May 15, 1997 to October 27, 2021. Each record includes seven basic features: date, opening price, highest price, lowest price, closing price, adjusted closing price, and trading volume. This dataset spans a long historical period, enabling a comprehensive reflection of the trends of American tech stocks across multiple economic cycles.

• 2. Moutai dataset: Contains 1723 records documenting the historical trading data of Guizhou Moutai stock from September 2, 2015 to September 30, 2022. This dataset includes 8 features; in addition to the basic price and trading volume information, it also includes the Open Interest (OpenInt) feature. As the leading stock in the Chinese baijiu market, Moutai exhibits high volatility and serves as an industry representative.

• 3. Ping an dataset: Contains 1723 records covering the historical trading data of Ping An from September 2, 2015 to September 30, 2022, also including 8 features. As a representative stock in the financial and insurance sector, Ping An’s price trends are significantly influenced by macroeconomic conditions and industry policies.

• 4. Vanke dataset: Contains 1588 records documenting the historical trading data of Vanke stock from September 2, 2015 to September 30, 2022, including the same 8 features as the other Chinese stocks. As a leading enterprise in the real estate industry, Vanke’s stock price movements reflect the overall condition of the Chinese real estate market.

These four datasets encompass representative stocks from different countries and industries, including technology, baijiu, financial insurance, and real estate. They provide a solid basis for comprehensively evaluating the model’s predictive capabilities under different market environments and time periods. The data collection period covers both normal market conditions and special periods such as financial crises and the COVID-19 pandemic, which is beneficial for testing the model’s performance under extreme market conditions.

Experimental setup

Data splitting and preprocessing

In this experiment, a rigorous time-series splitting strategy is adopted, whereby all datasets are divided in chronological order into training (70%), validation (10%), and testing (20%) sets. This division ensures that no “future data leakage” occurs during the model training process and conforms to the predictive requirements of real-world applications. For the Amazon dataset, approximately 4308 records are used for training, 616 for validation, and 1231 for testing; for the Chinese stock datasets, approximately 1206 records are used for training, 173 for validation, and 344 for testing.

Data preprocessing follows the normalization process described in “Data preprocessing”, specifically including:

• Applying min-max normalization to price-related features to map the values to the [0, 1] range.

• Applying Z-score standardization to technical indicators, converting them to a distribution with a mean of 0 and a standard deviation of 1.

• Using a forward-fill strategy to handle missing values and employing masking techniques to mark the filled positions.

• Utilizing moving-window robust scaling to handle outliers and extreme market fluctuations.

Evaluation metrics

To comprehensively evaluate the performance of the model, this study employs multiple complementary evaluation metrics:

• Root mean square error (RMSE):

  $$\begin{aligned} \text {RMSE} = \sqrt{\frac{1}{n}\sum _{i=1}^{n}(y_i-{\hat{y}}_i)^2} \end{aligned}$$

  (13)

  where $y_i$ represents the actual value and ${\hat{y}}_i$ the predicted value. RMSE is more sensitive to large errors, making it suitable for assessing the model’s ability to predict abnormal market fluctuations.

• Mean absolute error (MAE):

  $$\begin{aligned} \text {MAE} = \frac{1}{n}\sum _{i=1}^{n}|y_i-{\hat{y}}_i| \end{aligned}$$

  (14)

  which provides the average absolute magnitude of prediction errors. It is relatively insensitive to outliers and reflects the overall stability of the model.

• Mean absolute percentage error (MAPE):

  $$\begin{aligned} \text {MAPE} = \frac{100\%}{n}\sum _{i=1}^{n}\left| \frac{y_i-{\hat{y}}_i}{y_i}\right| \end{aligned}$$

  (15)

  expressing the error as a percentage, which facilitates comparisons across stocks with different price ranges.

• Coefficient of determination ($R^2$):

  $$\begin{aligned} R^2 = 1 - \frac{\sum _{i=1}^{n}(y_i-{\hat{y}}_i)^2}{\sum _{i=1}^{n}(y_i-{\bar{y}})^2} \end{aligned}$$

  (16)

  where ${\bar{y}}$ is the mean of the actual values. The closer $R^2$ is to 1, the stronger the model’s explanatory power.

• Return on investment (ROI):

  $$\begin{aligned} \text {ROI} = \frac{\text {Final Assets} - \text {Initial Assets}}{\text {Initial Assets}} \times 100\% \end{aligned}$$

  (17)

  which directly reflects the practical economic value of the model’s predictions.

Baseline model comparison

To validate the effectiveness of the R-CSAN model, five representative baseline models are selected for comparison:

• 1. ARIMA⁵⁰: The AutoRegressive Integrated Moving Average model represents traditional statistical models. In this experiment, the optimal $(p,d,q)$ parameter combination is determined through grid search, where $p$ and $q$ range from 0 to 5 and $d$ ranges from 0 to 2.

• 2. LSTM⁵¹: The Long Short-Term Memory network serves as a basic deep learning time series model. The experiment employs a 2-layer LSTM architecture with a hidden dimension of 128, using the Adam optimizer with a learning rate of 0.001 and a batch size of 64.

• 3. CNN-LSTM¹²: This hybrid architecture combines Convolutional Neural Networks with LSTM. The convolutional layer uses three convolutional kernels of size $(3,1)$ to extract local features, and the LSTM layer is configured identically to that of the basic LSTM model.

• 4. Random forest⁵²: An ensemble learning method that trains 500 decision trees with a maximum depth of 10 and a feature sampling ratio of 0.7, using Mean Squared Error as the splitting criterion.

• 5. LLM-augmented linear transformer-CNN⁵³: A complex model representing the latest research advancements. It integrates a linear Transformer augmented by a large language model with a CNN architecture, with 8 attention heads, a feed-forward network dimension of 512, and employs a Cosine learning rate scheduler.

• 6. Informer¹⁵: A sparse self-attention based Transformer³⁷ designed for long-sequence time series forecasting. It utilizes ProbSparse attention to enhance efficiency and adopts an encoder–decoder structure for multistep prediction.

• 7. Autoformer¹⁶: A decomposition-based Transformer that models seasonal-trend components separately via a progressive decomposition architecture, achieving high performance in time series with trend shifts.

• 8. iTransformer¹⁷: A lightweight and efficient Transformer variant that exploits inter-series and intra-series dependencies with dual-resolution temporal processing. We adopt the official PyTorch implementation and follow the standard multistep forecasting setup.

All experiments were conducted under the same hardware environment (NVIDIA Tesla V100 GPU, 32GB RAM) and software environment (Python 3.8, PyTorch 1.10) to ensure fairness in performance comparisons. Each model was optimized using the same cross-validation strategy for hyperparameter tuning and employed an identical early stopping strategy (halting if validation performance did not improve for 10 consecutive epochs) to prevent overfitting.

Visualization analysis of prediction results

In order to visually evaluate the predictive performance of the model, this study conducted a visualization analysis of the prediction results of the R-CSAN model on four different stock datasets. Figure 3 shows the prediction fitting performance of the model on the Amazon, Moutai, Ping An, and Vanke stock datasets. By comparing the trends of the model’s predicted values (green line) with the actual stock prices (blue line), the prediction accuracy and robustness of the model are thoroughly validated.

The visualization results reveal the following key observations:

• 1. Prediction accuracy: In all four datasets, the model’s prediction curve closely aligns with the actual price trends, indicating that the R-CSAN model can effectively capture the complex patterns of stock price fluctuations. This high consistency demonstrates the outstanding performance of the channel-spatial adaptive attention mechanism proposed in this paper for financial time series forecasting.

• 2. Market adaptability: Under different market environments and industry characteristics, the model exhibits remarkable predictive capabilities. For instance, for the highly volatile Moutai stock and the relatively stable Amazon stock, the model accurately tracks the trend of price changes, highlighting its cross-market generalization ability.

• 3. Volatility capture: The model is sensitive to both the micro fluctuations and the overall trend of stock prices. This performance is especially evident in the Vanke and Ping An datasets, where the model not only accurately captures the general trend but also precisely reproduces the subtle features of local price fluctuations.

Fig. 3

Prediction fitting performance of the R-CSAN model on different stock datasets.

It can be observed from Fig. 3 that, although there are differences in the amplitude and frequency of price fluctuations among the datasets, the R-CSAN model consistently maintains a high level of prediction consistency. This stability further validates the effectiveness of the hybrid attention mechanism and residual enhancement architecture proposed in this paper. Particularly in highly volatile stock datasets such as Moutai, the model still maintains relatively accurate predictions, which fully demonstrates its potential in handling complex financial time series.

The visualization results not only intuitively display the model’s predictive performance but also provide strong evidence for its application in real-world financial forecasting scenarios. By precisely capturing the price fluctuation patterns of stocks in different markets and industries, the R-CSAN model offers a promising technological pathway for investment decision support systems.

Comparison of experimental results

Table 1 presents the performance comparison of different models on four stock datasets. It is evident that the proposed R-CSAN model outperforms all baseline models across every evaluation metric. In terms of predictive accuracy, R-CSAN consistently achieves the lowest RMSE, MAE, and MAPE values while attaining the highest R² scores, indicating smaller deviations from actual stock prices and stronger explanatory power for price variance. On the Amazon dataset, the RMSE of R-CSAN is 18.73, which is 47.2% lower than ARIMA (35.48), 27.2% lower than LSTM (25.74), and 1.6% lower than LLM-Aug LT-CNN (19.03). Compared to Transformer-based models, R-CSAN also outperforms Informer (20.84), Autoformer (21.27), and iTransformer (19.92). On the Maotai dataset, which is more volatile, R-CSAN still achieves an RMSE of 32.16, 52.2% lower than ARIMA (67.32) and 7.1% lower than iTransformer (33.28). For Pingan, R-CSAN achieves an RMSE of 21.58 and R² of 91.62%, outperforming all other models including iTransformer (22.68), and on the Wanke dataset, R-CSAN delivers the strongest results, with an RMSE of 15.32, R² of 93.17%, and return of 482.64%.

Table 1 Performance comparison of different models on four stock datasets.

Although some Transformer-based baselines (e.g., iTransformer and Informer) exhibit competitive performance in specific scenarios, R-CSAN consistently maintains a clear advantage in both accuracy and investment returns across all datasets. These results validate the effectiveness of integrating residual connections with spatial-channel attention mechanisms to capture both temporal dynamics and feature interactions in financial time series. Furthermore, the strong cross-market generalization observed in both U.S. and Chinese stock data demonstrates the practical value of R-CSAN in real-world financial forecasting.

Fig. 4

Performance comparison of the R-CSAN model and baseline models on different evaluation metrics.

Figure 4 presents a comprehensive visual comparison of the R-CSAN model and eight baseline models across five key evaluation metrics: RMSE, MAE, MAPE, R², and Return (%). The figure highlights performance across four representative stock datasets: Amazon, Maotai, Pingan, and Wanke.

The R-CSAN model consistently outperforms all baselines, achieving the lowest RMSE and MAE values, and the highest R² and return values. In particular, R-CSAN demonstrates substantial advantages over Transformer-based baselines (marked in red), including Informer, Autoformer, and iTransformer. Although iTransformer shows competitive performance in some datasets (e.g., Wanke), R-CSAN maintains superiority across all scenarios, confirming the robustness of its spatial-channel attention design.

From an inter-model comparison perspective, the predictive performance of R-CSAN is significantly better than that of the traditional statistical model ARIMA, reducing RMSE by approximately 49.3% on average. Compared to the basic deep learning model LSTM, R-CSAN lowers RMSE by an average of 30.6%. Against the hybrid architecture CNN-LSTM, it reduces RMSE by an average of 17.3%. Relative to Random Forest, it achieves an average RMSE reduction of 37.3%.

Compared with the state-of-the-art Transformer-based models, R-CSAN surpasses Informer (average RMSE gap of 9.8%), Autoformer (average gap of 11.6%), and iTransformer (average gap of 6.2%) across all datasets. These comparisons highlight the superiority of the residual-enhanced spatial-channel attention mechanism over pure temporal attention architectures in modeling complex financial time series.

These results validate that the design principle of combining the channel-spatial adaptive attention mechanism with residual connections can more effectively capture both temporal dependencies and cross-sectional relationships in financial data.

Experimental results also indicate that R-CSAN performs well on both U.S. and Chinese market stocks, demonstrating excellent cross-market generalization capability. The prediction results for different industries reflect the impact of sector characteristics on prediction difficulty—for example, the relatively high RMSE for Maotai (32.16) may be attributed to its high volatility, while Wanke achieves the lowest RMSE (15.32), possibly due to the more stable and cyclical nature of the real estate industry.

In terms of investment application, R-CSAN delivers significantly higher returns than all baseline models across all datasets, reaching a maximum of 482.64%. This suggests not only strong academic performance but also considerable potential for practical investment decision support.

In summary, the comparison experiments validate the effectiveness of the R-CSAN model not only against conventional and hybrid baselines but also against recently proposed Transformer-based forecasting architectures. This confirms the model’s competitiveness and provides an interpretable and high-performing solution for real-world stock prediction tasks.

Ablation experiment

In order to thoroughly verify the effectiveness of each component in the R-CSAN model, we designed a systematic ablation experiment. By selectively removing key modules from the model, we aim to quantitatively evaluate the contribution of each component to the overall performance of the model. As shown in Table 2 and Fig. 5, the experimental results reveal the importance of each module in the model architecture.

Table 2 Performance comparison of R-CSAN model components in ablation experiments.

• 1. First, on all datasets, removing any key component led to a significant decrease in model performance. Among them, removing the temporal module had the most pronounced impact on the model’s predictive ability. For example, on the Amazon dataset, the RMSE rose sharply from 18.73 to 25.17; on the Moutai dataset, the RMSE increased from 32.16 to 46.58, an upsurge of 44.9%. This result highlights the crucial role of capturing temporal dependencies in financial time series prediction.

• 2. Attention mechanism and data augmentation module removal also caused a noticeable decline in performance metrics. After removing the attention mechanism, the average RMSE of the four datasets increased by 21.3%, while removing data augmentation increased RMSE by an average of 16.7%. This finding indicates that the channel-spatial adaptive attention mechanism and data augmentation techniques play critical roles in extracting effective features and reducing model overfitting.

• 3. Changes in the ${\bf {R^2}}$ metric and return on investment further support the above analysis. The full model achieves ${\bf {R^2}}$ values above 90% on all four datasets, whereas removing key modules leads to a significant drop, with the lowest ${\bf {R^2}}$ falling to 75.68%. The return on investment follows a similar trend, decreasing from a maximum of 482.64% with the Full Model to 387.63% in the basic structure model.

Fig. 5

Performance trend after removing various components of the R-CSAN model.

Figure 5 visually presents these performance changes. Whether for RMSE or ${\bf {R^2}}$ metrics, the difference between the ablation models and the Full Model is striking. This visual presentation not only reinforces the quantitative analysis but also offers readers a more intuitive understanding. It is worth noting that the degree of impact varies slightly across different datasets, potentially due to inherent differences in stock types, market environments, and volatility characteristics. For instance, the Moutai dataset, representing a highly volatile stock, shows a relatively more pronounced decline in performance.

The results of the ablation experiment provide empirical support for the architectural design of the R-CSAN model. The channel-spatial adaptive attention mechanism, feature fusion, temporal module, and data augmentation strategy collectively form the key mechanisms by which the model captures the complex patterns in financial time series. This multi-level, multi-dimensional feature extraction and learning paradigm enables the model to maintain outstanding predictive performance across different market environments.

Discussion

Model performance analysis

The deep learning model based on the hybrid attention mechanism proposed in this study demonstrates remarkable performance advantages in the task of stock forecasting, which can be explained from multiple perspectives:

• 1. The channel-spatial adaptive attention mechanism is the core driving force behind the model’s performance improvement. This innovative design can simultaneously focus on the intrinsic relationships among financial indicators and the key patterns within the time series. Stock prices are influenced by complex, multidimensional factors, exhibiting not only temporal dependencies but also interactions among different indicators. Traditional models often struggle to capture these multi-layered associations at the same time, while the dual-attention mechanism proposed in this paper precisely fills this gap.

• 2. The cross-attention mechanism further enhances the model’s ability to understand systemic market risks. By establishing connections among different market sectors, individual stocks, and even macroeconomic factors, the model can more comprehensively analyze how overall market trends affect the performance of individual stocks. Capturing these cross-dimensional correlations is crucial for accurate stock price prediction.

• 3. The introduction of residual connections and normalization layers fundamentally improves the learning mechanism of deep networks. These techniques effectively mitigate the common vanishing gradient problem in deep learning, enabling the model to better learn the long-term dependencies in financial time series. Ablation experiments clearly demonstrate the significant contribution of these components to the model’s performance: once removed, the model’s predictive ability declines markedly.

Overall, by ingeniously integrating channel-spatial attention, cross-attention, and residual connections, the model proposed in this paper achieves a more comprehensive and in-depth understanding of financial time series, providing a more intelligent and efficient approach for stock price forecasting.

Generalization ability across different markets

The experiments in this study span two distinct financial markets, the United States and China, covering four representative stocks: Amazon, Moutai, Ping An, and Vanke. The results provide strong evidence for the model’s cross-market adaptability and demonstrate its outstanding generalization capabilities.

Stability under different market environments is a key indicator for evaluating the performance of machine learning models. Although there are significant differences between the U.S. and Chinese stock markets in terms of market mechanisms, investor behavior, and economic conditions, our proposed R-CSAN model, through its flexible hybrid attention mechanism, can adaptively capture the unique characteristics of each market. This adaptability stems from the model’s ability to dynamically adjust its focus on different financial indicators and temporal patterns, rather than relying on predetermined fixed rules. Notably, the model’s performance exhibits subtle yet profound variations across different markets. In the relatively stable U.S. tech stock market (Amazon), the model shows highly accurate predictive capabilities; in the more volatile Chinese market (e.g., Moutai), the prediction accuracy is slightly lower. This difference does not indicate a limitation of the model but rather reflects its sensitivity to market complexity. Even in highly volatile markets, the R-CSAN model still significantly outperforms traditional forecasting methods, fully demonstrating its unique advantages in handling complex financial time series.

This cross-market stability suggests that the hybrid attention architecture we propose has potential universality. It can handle stocks from different countries and industries while adapting to varying levels of market volatility, offering a promising technological pathway for financial forecasting research.

Model interpretability

Deep learning models have long been regarded as “black box’ due to their complex internal decision-making mechanisms, which are often difficult to comprehend. The R-CSAN model proposed in this paper offers a unique solution to this dilemma through its innovative hybrid attention mechanism, achieving a significant breakthrough in model interpretability.

The channel attention mechanism reveals the key feature weights in financial forecasting. By analyzing the attention weights of various financial indicators, we can precisely identify which indicators have the greatest influence on stock price prediction. For instance, in certain market conditions, trading volume may reflect stock trends more effectively than the opening price; in other scenarios, technical indicators such as the Relative Strength Index (RSI) or moving averages may play a more critical role. This fine-grained feature importance analysis provides investors with deep insights that extend beyond a single predictive output.

The spatial attention mechanism, on the other hand, focuses on the critical time points within the time series. By visualizing spatial attention weights, we can pinpoint the moments where stock price changes are most pronounced or represent turning points. These key moments often coincide with major market events, quarterly earnings releases, or adjustments in macroeconomic policies. Understanding these pivotal time points not only helps elucidate the model’s predictive logic but also assists investors in better grasping market trends.

More importantly, this interpretability approach bridges the gap between “prediction” and “understanding.” While traditional forecasting models merely provide numerical outputs, our model offers context and rationale for each prediction. Investors are no longer forced to blindly trust a “black box” algorithm; instead, they can gain insight into the model’s reasoning process, thereby significantly enhancing its credibility and practical utility.

Looking ahead, there is considerable scope for further research on model interpretability. We envision enhancing model transparency through the following approaches:

• 1. Attention weight visualization: Developing interactive charts that intuitively display the importance of different features and time points.

• 2. Natural language explanation generation: Utilizing large language models to convert complex mathematical weights into human-readable explanations.

• 3. Scenario-based explanations: Providing personalized predictive interpretations and risk warnings tailored to different market environments.

This study not only advances the interpretability of stock forecasting models from a technical perspective but also contributes significantly to the reliability of financial artificial intelligence. By opening the “black box” of deep learning models, we transform the technology from being remote and inaccessible into an intelligent tool that investors can truly use and understand.

Real-world application scenarios

In practical financial applications, the outputs of the R-CSAN model can be directly integrated into quantitative trading strategies to support investment decision-making. Specifically, the model’s trend prediction and price forecasting capabilities provide a foundation for rule-based strategy formulation. For example, the predicted price breakout levels can be used to trigger “breakout trading” strategies, where a long (buy) position is initiated once the predicted price exceeds a recent resistance level. Conversely, if the model indicates a downward trend below the support level, a short (sell) position can be considered.

Moreover, the predicted price trajectory can be combined with moving average signals to construct “moving average crossover” strategies. For instance, when the predicted price consistently surpasses a dynamically calculated moving average (e.g., 10-day MA), it indicates a bullish signal that can guide position accumulation. In contrast, a drop below the moving average may serve as a signal to reduce or exit positions.

Additionally, for institutional investors, the model’s multi-day forecast outputs can be used to adjust portfolio allocations over time. For example, in a multi-asset portfolio, the model can identify stocks with upward momentum and high return-to-risk ratios, thereby guiding capital reallocation towards these favorable assets while reducing exposure to declining assets.

These applications demonstrate the model’s potential not only as a predictive tool but also as an intelligent decision-support system. By integrating R-CSAN into real-world trading environments, investors can enhance return performance while managing risk with greater precision and transparency.

Conclusion

This study proposes a Residual-Enhanced Channel-Spatial Attention Network (R-CSAN) for stock price forecasting, which integrates channel-spatial adaptive attention mechanisms with residual connections to efficiently model complex, multidimensional patterns in financial time series. This dual-dimensional attention approach–focusing on both financial indicators through channel attention and temporal patterns through spatial attention–addresses a critical limitation of existing models that typically handle either temporal dependencies or feature interactions separately, rarely combining them in a unified framework. Experiments on four cross-market stock datasets (Amazon, Maotai, Ping An, and Vanke) demonstrate that R-CSAN significantly outperforms both traditional models (ARIMA, LSTM, CNN-LSTM) and recent Transformer-based approaches (Informer, Autoformer, iTransformer). The model reduces RMSE by 17.3–49.3% compared to traditional methods and 6.2–11.6% compared to Transformer variants, while achieving the highest $R^2$ of 93.17% and ROI of 482.64%. This confirms R-CSAN’s superior capability in capturing nonlinear relationships, long-term dependencies, and market correlations. Ablation experiments verify the critical contributions of each component, with the temporal module removal causing a 38.6% average RMSE increase and channel-spatial attention removal resulting in a 21.3% increase. The model achieves interpretability through attention weight visualization, offering insights into both feature importance and critical time periods for prediction.

In practical applications, R-CSAN’s outputs can be integrated into trading strategies including breakout trading, moving average crossover signals, and portfolio allocation optimization. For institutional investors, the model’s multi-day forecasts can guide capital reallocation toward assets with favorable risk-return profiles. Despite these strengths, R-CSAN has limitations: (1) it is not optimized for high-frequency trading requiring millisecond-level latency; (2) its sensitivity to unexpected macroeconomic shocks or black swan events remains limited; and (3) as a supervised learning approach, it requires substantial historical data for training. Future research should explore: (1) incorporating Graph Neural Networks to model explicit stock relationships and sector dependencies; (2) integrating sentiment analysis from financial news to enhance responsiveness to exogenous events; and (3) developing reinforcement learning frameworks to create adaptive trading systems based on R-CSAN’s predictions.