Enhanced EfficientNet-Extended Multimodal Parkinson’s disease classification with Hybrid Particle Swarm and Grey Wolf Optimizer

Abstract

Parkinson’s disease (PD) is a chronic neurodegenerative disorder characterized by progressive loss of dopaminergic neurons in substantia nigra, resulting in both motor impairments and cognitive decline. Traditional PD classification methods are expert-dependent and time-intensive, while existing deep learning (DL) models often suffer from inconsistent accuracy, limited interpretability, and inability to fully capture PD’s clinical heterogeneity. This study proposes a novel framework Enhanced EfficientNet-Extended Multimodal PD Classification with Hybrid Particle Swarm and Grey Wolf Optimizer (EEFN-XM-PDC-HybPS-GWO) to overcome these challenges. The model integrates T1-weighted MRI, DaTscan images, and gait scores from NTUA and PhysioNet repository respectively. Denoising is achieved via Multiscale Attention Variational Autoencoders (MSA-VAE), and critical regions are segmented using Semantic Invariant Multi-View Clustering (SIMVC). The Enhanced EfficientNet-Extended Multimodal (EEFN-XM) model extracts and fuses image and gait features, while HybPS-GWO optimizes classification weights. The system classifies subjects into early-stage PD, advanced-stage PD, and healthy controls (HCs). Ablation analysis confirms the hybrid optimizer’s contribution to performance gains. The proposed model achieved 99.2% accuracy with stratified 5-fold cross-validation, outperforming DMFEN-PDC, MMT-CA-PDC, and LSTM-PDD-GS by 7.3%, 15.97%, and 10.43%, respectively, and reduced execution time by 33.33%. EEFN-XM-PDC-HybPS-GWO demonstrates superior accuracy, computational efficiency, and clinical relevance, particularly in early-stage diagnosis and PD classification.

Introduction

Neurodegenerative disorders are progressive diseases involving the deterioration of nerve cells in the brain and spinal cord, causing cognitive, motor, and behavioral impairments¹. While more common in older adults, they can also affect younger individuals due to genetic, environmental, or pathological factors². PD results from the gradual loss of dopamine-producing neurons in the substantia nigra, a midbrain region crucial for motor control^3,4. This leads to reduced dopamine levels, especially in the putamen, disrupting motor pathway communication. The deficiency causes key PD symptoms such as tremors, rigidity, and slowed movement⁵. Early and accurate diagnosis is vital for effective treatment, including medication, therapy, and deep brain stimulation, to improve quality of life.

PD progresses from early to advanced stages, each characterized by distinct neurological and clinical changes⁶. Early-stage PD presents with mild, typically one-sided symptoms like tremors, stiffness, and slowed movements due to dopamine loss from neuronal degeneration in the substantia nigra^1,7. T1-weighted MRI detects early structural changes using radiomics features such as volume, intensity, and texture^8,9,10. As PD advances, symptoms become bilateral with neurodegeneration spreading to the striatum, especially the putamen. Advanced stages involve severe motor impairments, including balance problems and higher fall risk, often requiring daily assistance. DaTscan imaging measures reduced dopamine transporter uptake in the putamen via uptake values and binding ratios, serving as critical biomarkers for staging^11,12. Combining MRI, DaTscan, and gait scores reflecting motor function impairments like reduced stride length and gait variability improves classification accuracy^13,14. Since traditional diagnosis relies on late-appearing motor symptoms and subjective evaluation, objective, biomarker-based, and technology-driven methods are essential for earlier and more accurate PD diagnosis and staging¹⁵.

DL offers potential for accurate PD diagnosis and classification but faces challenges such as small, imbalanced datasets, poor generalization, limited interpretability, and reliance on single-modal data focused mainly on advanced PD¹⁶. Inconsistent data standards and lack of external validation also limit clinical use. Addressing these issues requires explainable models with multimodal data integration¹⁷. EEFN-XM, integrates T1-weighted MRI, DaTscan images, and gait scores to differentiate early-stage PD, advanced stage PD, and HCs. By combining structural, functional, and behavioral data, it improves accuracy, especially for early diagnosis. The framework uses MSA-VAE to denoise images, enhancing data quality for feature extraction^18,19,20. SIMVC segments key regions substantia nigra and putamen enabling precise assessment of structural and dopaminergic changes, crucial PD biomarkers²¹. To optimize model performance, a HybPS-GWO balances global and local search for efficient parameter tuning, speeding convergence and reducing overfitting^22,23. This multimodal^24,25,26, denoising, and segmentation-driven approach improves classification accuracy, interpretability, and addresses key limitations of traditional PD methods, offering a robust, clinically relevant solution for accurate staging and early stage diagnosis^27,28.

EEFN-XM for PD classification enhances the baseline EfficientNet-B1 by integrating segmented neuroimaging data and gait pattern scores, creating a comprehensive framework to capture diverse PD features. While EfficientNet models excel in single-modal image classification with scalable architecture, EEFN-XM extends this to fuse multi-source inputs including segmented regions of interest (ROIs) from MRI and DaTscan images (substantia nigra and putamen) along with quantitative gait scores²⁹. Incorporating gait data allows detection of motor dysfunctions often present early in PD but not visible on imaging alone. The segmentation step improves feature quality by focusing on disease-relevant areas and reducing background noise. Evaluated against methods like DMFEN-PDC, MMT-CA-PDC, and LSTM-PDD-GS, EEFN-XM emphasizes key brain regions and motor patterns, improving early-stage diagnosis. Its multimodal design enhances accuracy, generalization, and interpretability. Hybrid optimization³⁰ and attention mechanisms refine feature extraction across modalities³¹, significantly boosting classification accuracy, sensitivity, and specificity. This integrative approach enables precise differentiation between healthy controls, early, and advanced PD, improved earlier stage diagnosis and supports clinical decision-making.

Research contribution

The key contributions of the proposed work are summarized below:

• (1) Developed a novel EEFN-XM method integrated with HybPS_GWO optimization for classifying PD into advanced-stage, early-stage and HCs using multimodal data including T1-weighted MRI, DaTscan images, and gait scores sourced from NTUA and PhysioNet repository respectively.

• (2) This work strengthens the proposed classification framework by integrating MSA-VAE for image denoising and SIMVC for precise segmentation of the substantia nigra and putamen, targeting structural changes and dopaminergic activity, respectively. Integration of Sparse Group Lasso enhanced the suitable radiomics feature extraction, while the HybPS-GWO optimization algorithm fine-tunes model parameters to improve convergence speed and overall classification performance.

• (3) An ablation study demonstrates the individual and combined impact of EEFN-XM and HybPS-GWO optimization on model performance. The proposed method exhibits high computational efficiency, with reduced training time and memory usage, making it suitable for large-scale and clinical applications.

The structure of the paper is organized as follows: “Literature survey” provides a review of recent research related to PD diagnosis and classification. “Proposed methodology” details the proposed methodology. “Results and discussion” presents the experimental results and discussion, including a comparative analysis with existing approaches. “Conclusion” concludes the study by summarizing the key findings, while “Limitations and future work” discusses the study’s limitations and suggests directions for future work.

Literature survey

Recent advances in DL have significantly improved PD classification and early-stage diagnosis using various data types, including MRI, gait analysis, genetic data, and sensor-based features. This literature review examines major methods, datasets, performance metrics, and model architectures, providing a clear overview of current trends, challenges, and research gaps in PD classification.

Most of the PD detection research focuses on neuroimaging, particularly MRI and DaTscan images, utilizing convolutional neural network (CNN)-based architectures., Sangeetha et al.³² introduced a Deep Maxout Fuzzy EfficientNet framework incorporating multi-view MRI images, achieving 92.6% accuracy one of the highest in PD classification. Shastry et al.³³ employed a multi-stage EfficientNet CNN with transfer learning for MRI-based PD classification, achieving high accuracy, particularly with the EfficientNet B6 variant. Similarly, Yang et al.³⁴ proposed an interpretable 3D ResNet model with 3D Grad-CAM and UPDRS scoring to detect PD from whole-brain MRIs, reporting 96.1% cross-validation accuracy and emphasizing the significance of the frontal lobe beyond the traditionally studied substantia nigra. Complementing these studies, Pechetti and Rao³⁵ integrated MobileNetV3 with IDMO and PCFAN, achieving 99.34% accuracy on the PPMI and NTUA datasets. For SPECT imaging, Keles et al.³⁶ introduced PARNet, a retrained COVID-19 ResNet architecture adapted for PD detection, attaining 95.43% accuracy, thereby demonstrating the potential of model transfer across medical domains. Further enhancing segmentation, Tassew et al.³⁷ developed PDDS software utilizing YOLOv7x for detection and an ensemble of UNETs for segmentation of PD-relevant brain regions.

Given that motor abnormalities are hallmark symptoms of PD, gait analysis through wearables has emerged as a reliable diagnostic tool. Naimi et al.³⁸ proposed a hybrid ConvNet-Transformer architecture to analyze gait signals, achieving 88% classification accuracy. Torghabeh et al.³⁹ used LSTM models optimized with Bayesian techniques for gait signal classification, attaining an exceptional 99.19% detection accuracy. Reshma et al.⁴⁰ combined ICNN and MBi-LSTM with Enhanced Sunflower Optimization (ESO) for gait analysis, reporting 99.5% accuracy. Aşuroğlu et al.³ also demonstrated the utility of CNN combined with Locally Weighted Random Forest for gait data, achieving 99.5% accuracy.

Multimodal data integration has been shown to enhance diagnostic reliability. Studies shown that developed Parkinson’s Integrative Diagnostic Gated Network (PIDGN) that fused SNP and sMRI data, achieving an accuracy of 85.8% and AUROC of 89.7%, while identifying significant genetic markers and brain regions using SHAP and Grad-CAM. Similarly, Huang et al.⁴¹ proposed an adaptive sparse learning model based on manifold learning for multimodal PD detection, achieving up to 95.35% accuracy with 12-month data, outperforming traditional models through effective feature integration. Sensor-based neurocognitive analysis provides an alternative, non-invasive approach for PD assessment. Templeton et al.⁴² used decision tree models on tablet-based neurocognitive assessments and functional movement data, achieving 92.6% accuracy in differentiating PD from controls and 73.7% accuracy in staging PD (early vs. advanced). Their study emphasized the gap between perceived and actual sensor-based functional performance, suggesting the value of objective measurements in PD diagnostics. Al-Tam et al.⁴³ explored a variety of classifiers, including Random Forest, SVM, Gradient Boosting, and Stacking Ensembles, across two benchmark datasets. Their Stacking Ensemble classifier combining SVM, Gradient Boosting, and Logistic Regression achieved up to 96.18% accuracy with an AUC of 96.27%.

These studies highlight the impact of deep learning, multimodal data fusion, and advanced ML models in improving early-stage PD diagnosis⁴⁴. Combining MRI, gait data, and techniques like EfficientNet and hybrid models enhances accuracy and supports non-invasive, and early-stage detection of PD^45,46. This progress paves the way for better diagnostic tools and treatment strategies for PD. Despite progress in PD detection using deep learning and multimodal approaches, key research gaps remain. Most models rely on limited datasets, reducing generalizability to diverse, real-world settings. Many focus on either early detection or isolated symptoms, lacking comprehensive stage-wise diagnostics that integrate motor and non-motor features. Additionally, high computational demands limit clinical use, especially in low-resource environments. Few studies combine multiple modalities with real-time adaptability for personalized care. Developing scalable, efficient, and holistic models is essential to improve PD diagnosis and management.

Proposed methodology

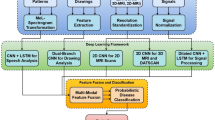
This section introduces the proposed EEFN-XM-PDC-HybPS-GWO method for PD classification, highlighting its core components and the overall computational pipeline. This approach integrates denoising, segmentation, and optimization techniques within an enhanced EfficientNet-extended multimodal deep learning framework to improve the accuracy and robustness of PD classification. T1-Weighted MRI, DaTscan images, and gait pattern scores were used in this study to classify PD as advanced stage PD, early stage PD, and HCs. Image augmentation is applied to increase dataset size and mitigate overfitting. Pre-processing strategies are employed to enhance classification performance by reducing noise and preserving essential information, thereby improving the effectiveness of high-level learning tasks. It employs MSA-VAE for denoising input images, SIMVC for segmenting ROI from denoised MRI and DaTscan images, which is essential for assessing structural changes and dopaminergic activity respectively and EEFN-XM method to extract and measure radiomics features from ROI and classification of PD based on the scores from extracted radiomics features and gait parameters. The following subsections provide a detailed explanation of each stage, including data acquisition, denoising, image augmentation, segmentation, feature extraction and classification with hybrid optimization. Figure 1 illustrates the block diagram of the EEFN-XM-PDC-HybPS-GWO framework for PD classification.

Fig. 1

Block diagram of EEFN-XM-PDC-HybPS-GWO.

Data acquisition

The dataset utilized to train and test the proposed EEFN-XM-PDC-HybPS-GWO method is sourced from National Technical University of Athens (NTUA)⁴⁷ and PhysioNet repository⁴⁸. Data from NTUA includes T1-weighted MRI images (350), and DaTscan images (370) from individuals at different stages of PD, including early and advanced stages, as well as HCs. The PhysioNet gait data includes stride interval, step interval, stride length, gait speed, stance time, swing time, step time variability, double support time, and cadence for PD classification. This diverse dataset provides a solid foundation for training and testing, improving the model’s capacity to accurately classify Parkinson’s disease at various stages. Through demanding pre-processing, variations in data distribution and scale are minimized, enabling the model to effectively learn discriminative features for accurate disease classification. The integration of diverse data modalities and meticulous pre-processing enhances the robustness and generalization capabilities of the EEFN-XM-PDC-HybPS-GWO model, facilitating precise and reliable classification of PD across different stages and patient populations.

Image denoising using MSA-VAE

This section focuses on image denoising, which involves eliminating unwanted noise from an image while preserving its essential features and details. In medical imaging, noise can be introduced by factors such as scanning errors or environmental influences. The goal of denoising is to enhance image quality, making it clearer and more reliable for analysis and classification. In this study, MSA-VAE are used to improve the signal-to-noise ratio by reconstructing the image from noisy inputs, ensuring that key features are maintained without introducing any artifact. Effective denoising enhances the accuracy of analysis and ensures clear visualization of critical structures, which is particularly important in MRI and DaTscan images used for PD classification.

The MSA-VAE method integrates Multiscale feature extraction, attention mechanisms, and variational learning, providing a robust framework for improving image quality prior to model training. The Multiscale component of MSA-VAE enables the processing of images at multiple spatial resolutions, effectively capturing both local fine-grained details and global structural information. This multilevel analysis ensures that different noise patterns and structural features across scales are adequately handled. The incorporated attention mechanism further enhances denoising performance by selectively focusing on the most relevant regions of the images, particularly those affected by noise, while preserving the integrity of important anatomical areas. In the variational autoencoders structure, input images are encoded into a lower-dimensional latent space, characterized by a probabilistic distribution defined by its mean and variance parameters. This variational framework not only facilitates effective reconstruction of clean images but also accommodates data uncertainty and variability, enhancing the model’s resilience to noise. By leveraging these combined strengths, the proposed MSA-VAE approach ensures robust denoising of MRI and DaTscan images, thereby improving the quality of input data and supporting precise and reliable PD diagnosis. By evolving weight values over generations, MSA-VAE achieves superior convergence and robustness, effectively preserving crucial image features while eliminating noise, thus improving denoising performance for medical image analysis are calculated in Eq. (1)

$$\:{\tau\:}_{elb{o}_{x}}={F}_{{a}_{s}\approx\:{q}_{a}}\left[{F}_{{p}_{\theta\:}\left({k}_{x}\times\:{A}_{s}\right)}\left[\text{l}\text{o}\text{g}{Q}_{\theta\:}\left({A}_{s}\times\:{k}_{s}\right)\right]-{\delta\:}_{0}{Z}_{hg}\left({p}_{\phi\:}\left({k}_{s}\times\:{A}_{s}\right)*Q\left(p\right)\right)\right].$$

(1)

where $\:{\tau\:}_{elb{o}_{x}}$ denotes the convergence of image fitting collectively with the regularization $\:S$, $\:{F}_{{a}_{s}\approx\:{q}_{a}}$ represent the tuning external hyper parameters within the VAE, $\:{A}_{s}\:$is the time taken in images, $\:{k}_{s}$is the time taken in parameter value of image, $\:{Q}_{\theta\:}\:$is the posterior of image, $\:{F}_{{p}_{\theta\:}\left({k}_{x}\times\:{A}_{s}\right)}\:$is the hyper parameters and time taken from image, $\:{\delta\:}_{0}\:$is the initial weight value of image, $\:{Z}_{hg}\:$is the improved parameter from image, $\:{p}_{\phi\:}$is the probabilistic encoding of corrupted image, $\:Q$ is the quality of image. This iterative processing of weights and latent variables results in high fidelity reconstructions and effective noise removal, preserving crucial image features. Then the generative process of $\:{q}_{\theta\:}$ estimates the posterior calculation is given in Eq. (2).

$$\:{q}_{\theta\:}(a\times\:q)={\prod\:}_{s}\:{q}_{\theta\:}\left(\left({a}_{s}\times\:{q}_{s}\right)\right..$$

(2)

where $\:{q}_{\theta\:}$ represent the generative process in image, $\:a$ represent the process of image, $\:q$ is the encoder of image, $\:{\prod\:}_{s}\:$is the iteration training of image, $\:{a}_{s}\times\:{q}_{s}\:$is the calculation of iteration in process and encoder images. The MSA-VAE facilitates inner outer joint training of images by simultaneously processing the inner Variational parameters and outer generative model parameters. Then the inner outer joint training of image is calculated in Eq. (3).

$$\:\{\delta\:,e\}=\left(\left({\delta\:}_{1},{e}_{1}\right),\dots\:\left({\delta\:}_{N},{e}_{N}\right)\right).$$

(3)

where $\:\{\delta\:,e\}$ represent the inner outer joint training of image, $\:\left({\delta\:}_{1},{e}_{1}\right)\:$is the first order inner outer joint training of image, $\:\left({\delta\:}_{N},{e}_{N}\right)\:$is the number of inner outer joint training of image. This iterative processing of weights and latent variables fosters variation and adaptability, enabling MSA-VAE to more effectively capture intricate image distributions. Then improve their diversity and evolutionary capacity in image is calculated in Eq. (4).

$$\:W:{\delta\:}_{s+1}={\delta\:}_{s+1}+{\zeta\:}_{w}.$$

(4)

where $\:W$ represent diversify of image taken, $\:{\delta\:}_{s+1}$is the inherited from the current moment of image, $\:{\zeta\:}_{w}\:$is the random variable sampled from the image. Leveraging its evolutionary capacity, MSA-VAE efficiently addresses noise artifact, culminating in superior quality denoised images. Then, removing noise from the images is calculating the Eq. (5).

$$q_{w} = \frac{1}{\pi }\left( {\frac{1}{{1 + \delta _{{s + 1}}^{2} }}} \right)$$

(5)

where $\:{q}_{w}$ represent the Cauchy distribution diversify of image, $\:\frac{1}{\pi\:}\:$is the probability value, $\:{\delta\:}_{s+1}^{2}$is the calculation of inherited from the current moment of image. Consequently, the MSA-VAE module enhances image quality by effectively removing noise while preserving essential structural information, ensuring more reliable feature extraction for subsequent classification.

Image augmentation

Image augmentation is employed to expand the training dataset by generating synthetic samples from existing medical images through controlled geometric transformations. This approach enhances data diversity, improves the model’s generalization ability, and helps mitigate overfitting, especially when working with limited datasets. The proposed method applies augmentation techniques such as rotation, translation, scaling, and shearing to introduce spatial variability while preserving the anatomical integrity of MRI and DaTscan images. Rotation involves rotating the image by a fixed angle, typically ± 15°, to simulate variations in patient positioning and improve the model’s robustness to orientation changes. Translation shifts the image along the x or y axis to mimic slight patient movements or misalignments. Scaling adjusts the image size up or down to account for differences in anatomical size or imaging zoom, while maintaining proportions. Shearing applies a shear transformation with a typical value of ± 0.2 to slant the image axes, simulating minor distortions during acquisition. After the augmentation process, unwanted images with excessive distortions or outliers are removed to maintain the quality and relevance of the dataset. As a result of these augmentations, the total number of MRI images increases to 1155, consisting of 380 for Advanced stage PD, 385 for Early stage PD, and 390 for HCs. Similarly, the DaTscan image dataset expands to 1170, with 385 for Advanced stage PD, 395 for Early stage PD, and 390 for HCs.

Image segmentation using SIMVC

In this section, SIMVC method is discussed for accurately segmenting key brain regions from MRI and DaTscan images. Denoised images are fed into segmentation phase for segmenting ROIs, which helps to assess structural changes in substantia nigra (MRI) and dopaminergic activity in posterior putamen region (DaTscan). The process begins with extracting modality-specific features: MRI provides intensity profiles, texture descriptors, and gradient information for anatomical delineation, while DaTscan contributes dopamine transporter binding potential and regional intensity distributions for functional characterization. These features undergo semantic learning to create invariant representations where corresponding regions across modalities share similar embeddings. The multi-view clustering algorithm then minimizes both within-cluster variance and between-view disagreement through an objective function that optimizes clustering assignment matrices while respecting anatomical constraints. For substantia nigra, the algorithm leverages its distinct hypo intensity in MRI and relative location to surrounding structures, while posterior putamen segmentation relies primarily on DaTscan signal intensity supplemented by MRI-derived anatomical boundaries. A weighted consensus formation combines results from both modalities based on confidence scores, followed by post-processing steps including morphological operations and anatomical constraint application. This approach yields superior accuracy by harnessing the structural precision of MRI with the functional specificity of DaTscan, particularly valuable for these small deep brain structures that are challenging to segment using single-modality techniques. SIMVC thus offers a comprehensive framework for precise segmentation and quantitative dopamine assessment, pivotal for elucidating PD pathology and disease progression. This ensures robust substantia nigra identification, and putamen region, which is crucial for PD research. Then, enhancing semantic discrimination is calculated given in Eq. (6).

$$\:\mathfrak{I}={\gamma\:}_{eft}{\mathfrak{I}}_{eft}+{\mathfrak{I}}_{kbv}$$

(6)

where $\:\mathfrak{I}$ denotes the Fixed trade-off hyper parameter,$\:\:{\gamma\:}_{eft}$ is the semantic invariance learning loss, $\:{\mathfrak{I}}_{eft}\:$is the samples assigned to the cluster, $\:{\mathfrak{I}}_{kbv}\:$is the clusters to be compact. Then, the semantic invariance learning loss is calculated given in Eq. (7).

$$\:{\mathfrak{S}}_{eft}=-g(q\times\:y/u)\text{*}-g(q\times\:y)+g(q\times\:u)$$

(7)

where, $\:-g$ is the encoder of image, $\:q$ is the quality of image, $\:y/u$ is to enhance semantic discrimination, $\:q\times\:y$ is the multiple calculation in image discriminative quality, $\:q\times\:u$ is the multiple calculation in image encoder quality. Semantic invariance learning loss enhances the stability of semantic invariance in an image by ensuring consistent representation of the same concept across different views. Then enhance the stability of semantic invariance of an image are calculated in Eq. (8).

$$\:{I_{wsq}} = S{\left\| {y - \mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftharpoonup$}} \over i} (g(y))} \right\|^2}$$

(8)

where $\:{\mathfrak{I}}_{wsq}$ represent hyper-parameter that regulates how well semantic discrimination is balanced $\:S$ is the Variational distribution, ${\mathord{\buildrel{\lower3pt\hbox{$\scriptscriptstyle\leftharpoonup$}} \over i} }$is the sigmoid representation, $\:g\left(y\right)\:$is the maps a latent representation. SIMVC utilizes multi-modal MRI brain images to segment the substantia nigra, essential for assessing structural changes and putamen region for dopaminergic activity. By integrating different imaging modalities, SIMVC captures comprehensive information, enhancing segmentation accuracy. Then, segmenting the substantia nigra region, essential for assessing neuromelanin (NM) concentration is calculated in Eq. (9).

$$\:{\mathfrak{I}}_{kbw}=S\Vert\:y-f\left(g\left(y\right){\Vert\:}^{2}\right.$$

(9)

where $\:{\mathfrak{I}}_{kbw}$ represent the hyper-parameter that controls the balance between denotes a shared encoder, $\:S$ is the variational distribution, $\:g\left(y\right)$is the maps a latent representation. Finally, the segmentation of the substantia nigra is crucial for assessing structural changes and putamen region for dopaminergic activity within the image. Precise segmentation advances our knowledge of PD and facilitates research and diagnosis. Finally, the Semantic Invariant Multi-view Clustering identified the region of interest for measuring the structural changes in substantia nigra from MRI and dopaminergic activity in putamen region from DaTscan images.

Feature extraction and classification using EEFN-XM method

This section presents the EEFN-XM method for effective feature extraction and classification of PD from the segmented outputs. Proposed EEFN-XM is an enhanced version of the EfficientNet-B1 baseline, specifically tailored to handle multimodal inputs, including MRI scans, DaTscan images, and gait scores, for more accurate and robust PD classification. EfficientNet is a highly effective convolutional neural network architecture that achieves superior accuracy with significantly fewer parameters and computational costs. Its key innovation is a compound scaling method that uniformly scales the network’s depth, width, and input resolution, enabling better performance across various resource constraints. EEFN-XM extends these advantages by incorporating architectural modifications that better capture PD-specific features from heterogeneous data sources and by employing a HybPS-GWO optimization algorithm to fine-tune model parameters. EEFN-XM is optimized for handling both image (MRI, and DaTscan) and numerical data (gait scores), offering superior feature representation, improved convergence, and enhanced classification performance tailored to the nuances of PD diagnosis. Figure 2 illustrates the architectural overview of the EEFN-XM.

Fig. 2

Overview of EEFN-XM architecture.

EEFN-XM architecture comprises several specialized layers, systematically organized into distinct stages, each dedicated to specific tasks in the feature extraction and classification of PD using multimodal data. It begins with an input layer that receives both image data (MRI and DaTscan) and numerical gait scores. The stem layer performs initial feature extraction and spatial down sampling using convolutional filters, followed by batch normalization to stabilize and accelerate training and the Swish activation function, a self-gated non-linearity that enhances model expressiveness and smooth gradient flow. A series of MBConv layers then extract deep hierarchical features using depthwise separable convolutions for efficiency, combined with Squeeze-and-Excitation (SE) modules to recalibrate channel importance and emphasize disease-relevant patterns. To handle multimodal integration, attention mechanisms including cross-modal attention layers are used to align and highlight relevant information between imaging and gait data. A feature fusion layer uses concatenation and attention-based fusion to integrate extracted image features and a gait embedding module, which converts numerical gait scores into compatible high-level representations. These are fed into a fully connected dense layer that combines the multimodal embeddings to form a comprehensive, discriminative feature vector.

Additionally, the Sparse Group Lasso regularization is applied during feature fusion to promote sparsity by selecting the most relevant features while preserving important feature groups, thereby improving generalization and reducing overfitting. The architecture includes Global Average Pooling to condense spatial information and reduce overfitting, with dropout and additional batch normalization layers throughout the network to further enhance robustness and training stability. At the final stage, a SoftMax-activated output layer performs multi-class classification, distinguishing between healthy controls, early-stage, and advanced PD. The HybPS-GWO is employed to optimize classification-level parameters and fusion weights in the classification layer, ensuring fine-tuned decision boundaries and improved convergence. Collectively, these layers and components enable EEFN-XM to effectively extract, fuse, and classify multimodal medical data with high accuracy and efficiency.

Segmented outputs of MRI and DaTscan images are fed to the stem layer for feature extraction through input layer. EEFN-XM employs a hierarchical architecture with multiple layers of convolutional and pooling operations to extract features from input images at different levels of abstraction. Pooling layers preserve important information while reducing the feature maps from convolutional layers in terms of height and width. As the network progresses, it gradually learns to analyze grayscale features in its deeper layers. By scaling the network, EEFN-XM achieves superior accuracy compared to traditional CNN architectures while being more computationally efficient.

Let $\:{X}_{MRI\:}\in\:{I}^{H\times\:W\times\:C}$ and $\:{X}_{DaT}\:\in\:{I}^{H\times\:W\times\:C}$denotes the segmented outputs of MRI and DaTscan images, and $\:{F}_{gait}\in\:{I}^{g}$denotes the gait scores. The heterogeneous inputs are processed in parallel to enable modality feature extraction. The stem layer is the first convolutional layer, essential for extracting features from given input followed by batch normalization. The Swish activation function enhances gradient flow is given by the Eq. (10),

$$\:{S}_{stem}=\delta\:\left(BN\right({W}^{\left(0\right)}*X+{b}^{\left(0\right)}))$$

(10)

where, $\:BN$ is batch normalization, $\:\delta\:\:$is swish activation function, $\:{W}^{\left(0\right)}$ weight kernel, $\:*$ 2D convolution. This reduces spatial dimensions and enhances discriminative features for subsequent layers.

A depthwise convolution followed by a pointwise convolution to reduce computation while preserving spatial information. MBConv blocks performs squeeze-to-excitation to channel wise recalibration by weighting features based on their importance. Multiple convolutional layers are stacked sequentially, with each layer learning increasingly complex features. The inverted bottleneck structure first expands the number of channels to a higher-dimensional space, processes them using efficient depthwise convolutions, and then projects them back to a lower-dimensional space. This design preserves essential features while significantly reducing parameter count and computational load, making it well-suited for medical imaging tasks where model efficiency and accuracy are critical. The depthwise convolutions apply to separate filter to each input channel is represented by (11),

$$\:{Y}^{\left(dw\right)}=\sum\:_{m,n}{S}_{i+m,j+n,k}\cdot\:{\text{{\rm\:K}}}_{m,n,k}$$

(11)

where, $\:{Y}^{\left(dw\right)}$represents the depthwise convolution, $\:\sum\:_{m,n}\:$ denotes the summation over the spatial of the filter (kernel), typically the height and width. $\:{S}_{i+m,j+n,k}$ The value from the input feature map at location$\:(i+m,j+n)$, and channel$\:K$, where a local region being convolved.$\:\:{\text{{\rm\:K}}}_{m,n,k}$ represents depthwise kernel (filter) applied at spatial location $\:(m,n)$ for channel$\:K$. Depthwise convolutions inside MBConv blocks improve efficiency, and preserve spatial features within each channel.

The channel wise features are recalibrated by SE module, explicitly depend between feature channels, enabling the network to focus on the most informative representations relevant to PD disease stages. The squeeze step aggregates global spatial information into a compact descriptor through global average pooling, and is defined by the expression (12),

$$\:{Z}_{c}=\frac{1}{H\times\:W}\sum\:_{i=1}^{H}\sum\:_{j=1}^{W}{Y}_{i,j,c}^{\left(dw\right)}$$

(12)

This computes the average activation for each channel c, creating a descriptor vector $\:Z$. From the above equation, $\:H$ denotes the height of the feature map $\:{Y}^{\left(dw\right)}$, $\:W$ denotes the width of the feature map $\:{Y}^{\left(dw\right)}$, $\:{Y}_{i,j,c}^{\left(dw\right)}$ represents the activation at location $\:(i,\:j)$ in channel $\:c$ after depthwise convolution. To assign important weights to each channel, a lightweight gating excitation step is used and this channel-wise attention mechanism improves representational capacity by amplifying meaningful features and suppressing irrelevant ones. The channel wise importance weights from the squeezed descriptors is formulated as (13),

$$\:{e}_{fc}=\:\sigma\:({W}_{2}\cdot\:ReLU\left({W}_{1}\cdot\:{Z}_{c}\right))$$

(13)

where, $\:\sigma\:(\cdot\:)$Sigmoid activation function; maps output to range $\:\left[\text{0,1}\right]$, $\:{W}_{1},\:{W}_{2}$ are the weight matrix of the first and second fully connected layer. The channel wise feature map is recalibrated by its corresponding learned weight and the rescaled equation is given by (14),

$$\:{\stackrel{\sim}{Y}}^{c}=\:\:{e}_{fc}\:\cdot\:{Y}_{\colon\colon\:,\:c}^{\left(dw\right)}$$

(14)

where, $\:{Y}_{\colon\colon\:,\:c}^{\left(dw\right)}$ denotes the output feature map from depthwise convolution, at channel$\:\:c$, $\:{e}_{fc}$ Represents the channel-wise importance weight for channel $\:c$ learned during the excitation step. After extracting high-level feature representations from MRI and DaTscan modalities, the Global Average Pooling (GAP) operation is applied to reduce the spatial dimensions of each feature map into compact, channel-wise descriptors, effectively summarizing the spatial information while retaining essential discriminative features. Compact feature vector with preserved depth produced by GAP operation applied to MRI for converting 2D spatial representation to 1D feature vectors is given by the formula (15),

$$\:{Y}_{MRI}^{GAP}=\:\frac{1}{H\cdot\:W}\sum\:_{i=1}^{H}\sum\:_{j=1}^{W}{Y}_{MRI}^{\left(out\right)}[i,j,:]$$

(15)

where, $\:{Y}_{MRI}^{\left(out\right)}[i,j,:]$ is the output feature map for MRI at position $\:(i,j)$ across all channels. GAP operation applied on DaTscan feature maps to convert them from 2D spatial representations into 1D feature vectors is given by the following Eq. (16),

$$\:{Y}_{DaT}^{GAP}=\:\frac{1}{H\cdot\:W}\sum\:_{i=1}^{H}\sum\:_{j=1}^{W}{Y}_{DaT}^{\left(out\right)}[i,j,:],$$

(16)

where, $\:{Y}_{DaT}^{\left(out\right)}[i,j,:]$ is the output feature map for DaTscan at position $\:(i,j)$ across all channels. This significantly reduces the number of parameters and avoid overfitting. The gait score vector $\:{F}_{gait}\in\:{I}^{g}$is passed through a gait embedding layer to transform it into a compatible embedding and given by(17),

$$\:{Y}_{gait}=ReLU({W}_{gait}{F}_{gait}+{b}_{gait}).$$

(17)

An effective integration of heterogeneous features extracted from segmented MRI, DaTscan, and gait scores is done by feature fusion layer. It performs a concatenation operation and attention mechanism to form a unified representation suitable for downstream classification and integrate features of the MRI, DaTscan and gait scores. A unified representation by combining semantic information from both imaging modalities and clinical gait data is given by (18),

$$\:{Y}_{concat}=Concat({Y}_{MRI}^{GAP},\:{Y}_{DaT}^{\left(out\right)},{Y}_{gait}),$$

(18)

where, $\:{Y}_{MRI}^{GAP}$ : Feature vector obtained from Global Average Pooling of the MRI modality. $\:{Y}_{DaT}^{\left(out\right)}:$Feature vector obtained from Global Average Pooling of the DaTscan modality. $\:{Y}_{gait}\::\:$The gait score embedding, which is a transformed vector representation of numerical gait scores using a learnable embedding layer. This fused vector serves as a comprehensive multimodal descriptor, which is then passed to downstream attention, and classification layers for improved PD classification. Let $\:{F}_{i}$ be the feature representation extracted from each modality, then the final fused feature representation, weighted sum of the individual features computed as (19),

$$\:{Y}_{fused}=\sum\:_{i=1}^{3}{\aleph\:}_{i}\cdot\:\:{F}_{i},\:\:$$

(19)

where, $\:{\aleph\:}_{i},\:\:is\:the\:$attention weight applied and this learns modality relevance dynamically during training.

To select the most discriminative and relevant features Sparse Group Lasso Regularization is applied after the fusion layer, which promotes sparsity across individual features and reduces overfitting and improves interpretability of which features contribute to classification. To encourage group-wise sparsity and reduce redundancy, the formulation is given by (20),

$$\:{L}_{SGL}=\:{\xi\:}_{1}\sum\:_{l=1}^{L}{\parallel\:{w}_{l}\parallel\:}_{2}+\:{\xi\:}_{2}{\parallel\:{w}_{l}\parallel\:}_{1}$$

(20)

where, $\:{w}_{l}$ weights of the group, $\:{\xi\:}_{1},\:{\xi\:}_{2}$ are the hyper parameters. Image based features from the convolutional layers and gait score features are fused in feature fusion layer, the resulting multimodal feature vector, passed through a fully connected dense layer with dropout and batch normalization, to integrate and transform the high-dimensional concatenated features into a compact, discriminative representation for classification. This layer learns complex nonlinear relationships between features from MRI, DaTscan, and gait scores and dropout applied to enhance generalization and prevent overfitting by randomly deactivating a fraction of neurons, is given by (21),

$$\:{Y}_{drop}=Dropout({Y}_{dense},p)$$

(21)

where, $\:Dropout$ randomly sets a fraction $\:p$ of the activation in $\:{Y}_{dense}$ to zero during training. $\:p$ is denoted as dropout probability. Also batch normalization incorporated before or after activation functions to stabilize learning, accelerate convergence, and reduce internal covariate shift is given by (22),

$$\:{Y}_{dense}=ReLU\left(BN\left({W}_{d}{Y}_{fused}+{b}_{d}\right)\right).$$

(22)

The dense layer takes the high-level features and learns complex, non-linear combinations and act as a bridge between the extracted features and the output classification. This helps the network understand global patterns across all features. The final dense layer contains a single neuron with a SoftMax activation function, generating a probability score. Classification layer map the learned, high level feature vector into distinct output classes corresponding to different stages of PD as advanced, early and HCs. The probability prediction of PD multiclass classification is given in Eq. (23),

$$\:\stackrel{\sim}{y}=Softmax({W}_{out}{Y}_{drop}+{b}_{out}).$$

(23)

With pre-trained weights streamlining the process, EEFN-XM guarantees robust and reliable multiclass classification outcomes. Utilizing EEFN-XM standardizes accuracy score preferences through its advanced architecture, ensuring consistent assessments across diverse datasets and tasks. Then normalize the preference of accuracy score is calculated in Eq. (24),

$$\:\eta\:\left(a\right)=\frac{1}{1+{a}^{a}},$$

(24)

where $\:\eta\:\left(a\right)$ represent sigmoid function of classifying image, $\:{a}^{a}$is the arrangement of pictures. The PD method classification into early and the advanced stages relies on distinct clinical markers and progression patterns. Early stage PD features mild motor symptoms with minimal functional impairment, while advance stage PD exhibits severe motor complications and significant disability. The loss function for classification of PD as early stage of PD, advance stage of PD is given by (25),

$$\:\text{L}\text{o}\text{s}\text{s}=(1-b)\frac{1}{2}{\left({C}_{\varpi\:}\right)}^{2}+\left(B\right)\frac{1}{2}{\left(\text{m}\text{a}\text{x}\left(0,m,-{C}_{a}\right)\right\}}^{2}$$

(25)

where $\:{\left({C}_{\varpi\:}\right)}^{2}$ represent the square of difference among predicted value and actual label, $\:\:\frac{1}{2}$ represent normalize the loss. Distinguishing among PD patients, healthy controls involve analyzing range of clinical markers and symptoms. Finally, EEFN-XM‘s weight and bias parameters are adjusted using HybPS-GWO. Accurate classification relies on diagnostic criteria such as imaging and neurological assessments. Early stage diagnosis and intervention are vital for managing PD progression and enhancing quality of life. HybPS-GWO is employed to optimize the trainable parameters of the classification layer in the proposed EEFN-XM model. HybPS-GWO is used to enhance convergence and improve classification performance, particularly for complex multimodal features.

Optimization using HybPS-GWO algorithm

To enhance the classification performance and prevent suboptimal convergence, a hybrid optimization approach (HybPS-GWO) is integrated with the final layer of the EfficientNet-XM classifier. Unlike traditional backpropagation-based optimizers like Adam or SGD, HybPS-GWO operates in a wrapper fashion post initial training. It refines the classification layer parameters using the search dynamics of PSO and the leadership hierarchy of GWO. This metaheuristic optimizer is employed to fine-tune the weights and biases of the dense layer, leveraging the global search capability of PSO and the leadership-based exploitation strength of GWO. This approach is particularly effective in optimizing the EEFN-XM architecture, which integrates multimodal data like MRI, DaTscan images and gait scores for PD classification. In PS phase, particles explore the global parameter space to identify regions with promising solutions and passes the global best solution (gBest) to GWO for local fine-tuning. In GWO phase, it refines the gBest solution from PS to further optimize the parameters. It applies bias correction to mitigate initialization bias and stabilizes the learning process using exponentially decaying moving averages of the past and squared gradients. By balancing global best solution-based methods and adaptive learning rates, algorithm achieves faster convergence and superior generalization performance, enhancing efficiency of the HybPS-GWO.

Stepwise process of HybPS-GWO

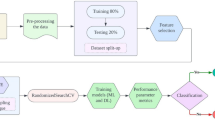
The optimal value of EEFN-XM is determined here by a stepwise approach that is dependent on HybPS-GWO. First, HybPS-GWO distributes the population equally to improve the EEFN-XM’s optimal parameter; this promotes the perfect solution, and a related flowchart is presented in Fig. 3.

Fig. 3

Flowchart of HybPS-GWO workflow.

Step 1: Initialization

Initial population of HybPS-GWO is initially generated by algorithm designed to optimize the performance of EEFN-XM, a crucial gene in neural signaling, through precise weight initialization. The HybPS-GWO optimizer was configured with a population size of 30 and a maximum of 100 iterations. PSO-specific parameters were set as inertia weight $\:\omega\:=0.7$ and acceleration coefficients$\:{c}_{1},\:{c}_{2}=1.5$. The GWO component followed its standard alpha, beta, and delta hierarchy with a linearly decreasing control parameter from 2 to 0. These settings ensured a balance between convergence speed and exploration capability. PS optimization initializes the particle swarm and each particle represents a candidate set of parameters. GWO initializes the wolf population with the same parameter space. In EEFN-XM training, the selection of optimization algorithms and weight initialization methods greatly influences both convergence speed and accuracy. The particles (PS) and wolves are initialized with random positions, velocities, and weights. Then, the population initialization of N particles is given in Eq. (26).

$$\:X=\left[\begin{array}{c}{X}_{1}\\\:{X}_{2}\\\:\cdot\:\\\:\cdot\:\\\:{X}_{N}\end{array}\right]\left[\begin{array}{ccccc}{X}_{\text{1,1}}&\:{X}_{\text{1,2}}&\:\cdot\:&\:\cdot\:&\:{X}_{1,d}\\\:{X}_{\text{2,1}}&\:{X}_{\text{2,2}}&\:\cdot\:&\:\cdot\:&\:{X}_{2,d}\\\:\cdot\:&\:\cdot\:&\:\cdot\:&\:\cdot\:&\:\cdot\:\\\:\cdot\:&\:\cdot\:&\:\cdot\:&\:\cdot\:&\:\cdot\:\\\:{X}_{N,1}&\:{X}_{N,2}&\:\cdot\:&\:\cdot\:&\:{X}_{N,d}\end{array}\right]$$

(26)

where, $\:{X}_{i,\text{j}}\:\:$represents the $\:{j}^{th}$dimension of the $\:{i}^{th}$solution.

Step 2: Random population generation

Randomly generate N particles (potential solutions) representing the hyper parameters of a neural network, initialize the positions and velocities of each particle and set the personal best position (pbest) of each particle as its current position. For each particle/wolf $\:{\:X}_{i}$, generate random positions is given by an Eq. (27),

$$\:{X}_{i,j}={X}_{\text{m}\text{i}\text{n},j}+r\cdot\:\left({X}_{\text{m}\text{a}\text{x},j}-{X}_{\text{m}\text{i}\text{n},j}\right)$$

(27)

where $\:r$ is a random number in [0, 1].

Step 3: Fitness evaluation.

For each candidate solution, the fitness function evaluates model performance using metrics like classification accuracy, balance of precision and recall for imbalanced classes and cross-entropy loss for the model. This fitness score guides the Hybrid PS-GWO algorithm in selecting the best solutions across iterations. By integrating both global and local search capabilities, the strategy enhances convergence toward optimal performance in the classification layer. To generate a random solution, the initialized assessments are employed .It is assessed using the parameter optimization value in order to optimize the classifier’s weight parameter, EEFN-XM. This is given in Eq. (28).

$$\:F\left(X\right)=\frac{1}{1+\text{L}\text{o}\text{s}\text{s}\left(x\right)}+\beta\:\cdot\:\frac{1}{\text{C}\text{o}\text{s}t\left(x\right)}$$

(28)

where, $\:\:\:F\left(X\right)$: is the fitness function, $\:\text{L}\text{o}\text{s}\text{s}\left(x\right)$: represents the classification loss of the proposed model for a candidate configuration, $\:\text{C}\text{o}\text{s}t\left(x\right)$: gives the computational cost,$\:\:\beta\:\:$: balances the trade-off between model performance and computational efficiency.

Step 4: Exploration phase

In exploration phase, update positions according to PS rules. The algorithm focuses on global exploration to cover the widest possible search area. Particles navigate the search space, adjusting their velocities and positions based on the Eqs. (29) and (30),

$$u_{i}^{{\left( {t + 1} \right)}} = w \cdot u_{i}^{{\left( t \right)}} + c_{1} \cdot r_{1} \cdot \left( {pB_{i} - z_{i}^{{\left( t \right)}} } \right) + c_{2} \cdot r_{2} \cdot \left( {gB - z_{i}^{{\left( t \right)}} } \right)$$

(29)

$${z}_{i}^{(t+1)}={z}_{i}^{\left(t\right)}+{u}_{i}^{(t+1)}$$

(30)

where, $\:{u}_{i}$: Velocity of particle I, $\:{z}_{i}$​: Position of particle I, $\:\omega\:$: Inertia weight (controls exploration vs. exploitation), $\:{c}_{1},\:{c}_{2}$ ​: Cognitive and social coefficients, $\:{r}_{1},\:{r}_{2}$​: Random numbers between 0 and 1,$\:\:p{B}_{1}$ ​: Personal best position of particle I,$\:\:gB$: Global best position across all particles. PS ensures the model explores diverse configurations in the parameter space by preventing premature convergence.

Step 5: Exploitation phase.

GWO refines the best solutions found by PS. The hierarchical wolf pack (alpha, beta, and delta) adjusts the positions and the equation is given by (31) and (32),

$$\:\begin{array}{ll}{D}_{\alpha\:}=\left|{C}_{1}\cdot\:{X}_{\alpha\:}-X\right|,&\:{X}_{1}={X}_{\alpha\:}-{A}_{1}\cdot\:{D}_{\alpha\:}\\\:{D}_{\beta\:}=\left|{C}_{2}\cdot\:{X}_{\beta\:}-X\right|,&\:{X}_{2}={X}_{\beta\:}-{A}_{2}\cdot\:{D}_{\beta\:}\\\:{D}_{\delta\:}=\left|{C}_{3}\cdot\:{X}_{\delta\:}-X\right|,&\:{X}_{3}={X}_{\delta\:}-{A}_{3}\cdot\:{D}_{\delta\:}\end{array}$$

(31)

$$\:X=\frac{{X}_{1}+{X}_{2}+{X}_{3}}{3}$$

(32)

where, $\:{X}_{\alpha\:},{X}_{\beta\:},{X}_{\delta\:}$: Positions of alpha, beta, and delta wolves, $\:X$: Current solution position, $\:A,\:C$: Adaptive coefficients controlling convergence. GWO fine-tunes the parameters in a focused region, improving local convergence.

Combine results from both PS and GWO techniques for an improved position equation is given by (33):

$$\:{X}_{\text{hybrid\:}}={w}_{1}\cdot\:{X}_{PS}+{w}_{2}\cdot\:{X}_{GWO}$$

(33)

where, $\:{w}_{1}$, $\:{w}_{2\:\:}$are weights balancing PS and GWO contributions.

Step 6: Termination condition.

The weight parameters value of $\:w,gB,X,{u}_{i}$ from EEFN-XM are optimized by utilizing HybPS-GWO, and the process continues through step 3 until the stopping criteria are met. The EEFN-XM-PDC-HybPS-GWO effectively evaluates and analyzes PD classification with higher accuracy.

Results and discussion

The results and performance analysis of EEFN-XM-PDC-HybPS-GWO for PD classification are presented and discussed in this section.

Experimental setup

The proposed EEFN-XM-PDC-HybPS-GWO model was developed in Python 3.8 using Tensorflow 2.9 and trained on an NVIDIA RTX 3080 Ti GPU with an Intel Core i7 CPU and 32 GB RAM. EEFN-XM, an enhanced EfficientNet-B1 variant, was modified to handle six-channel multimodal inputs (segmented MRI and DaTscan images) and integrated numerical gait scores through dense layers after global average pooling. The model used the Adam optimizer, with learning rate, batch size, and dropout rate tuned by the Hybrid Particle Swarm and Grey Wolf Optimizer (HybPS-GWO). Training ran for up to 200 epochs with early stopping and mixed-precision (FP16) for efficiency. Swish activation was used in hidden layers and Softmax in the output layer. A stratified 5-fold cross-validation ensured balanced class distribution and generalizability. Each fold included an internal 80:20 validation split to monitor performance, reduce prediction variance, prevent overfitting, and avoid arbitrary data partitioning. Table 1 provides a detailed overview of the training parameters used in the EEFN-XM-PDC-HybPS-GWO model, which is tailored for PD classification using multimodal data (image and gait).

Table 1 Training parameters of EEFN-XM-PDC-HybPS-GWO.

Performance measures

This study evaluates the performance of the proposed EEFN-XM-PDC-HybPS-GWO using various metrics: accuracy, sensitivity, specificity, and ROC for PD classification; DSC, Jaccard Index, precision, and recall for segmentation; and PSNR, SSIM, and MSE for denoising quality. The computational efficiency is assessed through time complexity, space complexity, resource utilization, and scalability. These metrics are employed to evaluate and compare the performance of the proposed method with that of existing approaches.

Performance analysis

This section presents the performance evaluation of EEFN-XM-PDC-HybPS-GWO using key metrics: accuracy, sensitivity, and specificity for classification; DSC and RI for segmentation; and PSNR, SSIM, and MSE for denoising. A comparative analysis with existing methods highlights the framework’s effectiveness. An ablation study assesses the contribution of individual components, while computational efficiency is evaluated through time complexity, memory usage, and resource utilization, demonstrating the model’s practicality and robustness for clinical application. Figures 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22 and 23; Tables 2, 3 and 4 present the experimental results of EEFN-XM-PDC-HybPS-GWO in comparison with existing methods, including DMFEN-PDC, MMT-CA-PDC, and LSTM-PDD-GS.

Comparative study of denoising performance

This section compares the denoising performance of the proposed method with existing techniques using MRI and DaTscan images. Evaluation is based on standard metrics PSNR, SSIM, and MSE to assess noise reduction and detail preservation, demonstrating the method’s effectiveness in maintaining anatomical and functional integrity. The denoising results are shown in Fig. 4 and the comparative analysis between the proposed method and existing techniques is illustrated in Figs. 5, 6 and 7.

Fig. 4

Output results of proposed denoising method.

Fig. 5

Comparative analysis of PSNR.

Figure 5 presents the PSNR comparison across noise levels (2.5–20%) for the proposed EEFN-XM-PDC-HybPS-GWO using MRI and DaTscan images, against DMFEN-PDC, MMT-CA-PDC, and LSTM-PDD-GS. The proposed method consistently achieves the highest PSNR, indicating strong denoising performance and robustness to noise. MRI-based results peak at 43.50 dB, while DaTscan reaches 41.80 dB. Competing methods show lower PSNR values across all noise levels, with LSTM-PDD-GS performing worst. These findings validate the superiority of the proposed hybrid-optimized model in maintaining image quality under varying noise conditions.

Fig. 6

Comparative analysis of SSIM.

Figure 6 compares SSIM values across noise levels (2.5–20%) for the proposed EEFN-XM-PDC-HybPS-GWO model (MRI and DaTscan) and existing methods. The proposed model with MRI input achieves the highest SSIM (0.99 to 0.90), followed closely by DaTscan (0.97 to 0.87), indicating strong structural preservation. DMFEN-PDC and MMT-CA-PDC show moderate performance, while LSTM-PDD-GS exhibits the lowest SSIM (0.90 to 0.76). These results highlight the proposed model’s robustness and superior ability to retain anatomical integrity under noise, outperforming other approaches across both imaging modalities.

Fig. 7

Comparative analysis of MSE.

Figure 7 shows MSE values across noise levels (2.5–20%) for the proposed EEFN-XM-PDC-HybPS-GWO model (MRI and DaTscan) and existing methods. The proposed model achieves the lowest MSE for MRI (0.005 to 0.050) and DaTscan (0.008 to 0.059), indicating high accuracy and noise robustness. DMFEN-PDC and MMT-CA-PDC show moderate error increases, while LSTM-PDD-GS has the highest MSE (0.043 to 0.110), reflecting poorer performance under noise. These results confirm the superior reconstruction accuracy of the hybrid PSO-GWO optimized model across both modalities, especially at higher noise levels.

Analysis of segmentation performance metrics

The segmentation performance of the proposed EEFN-XM-PDC-HybPS-GWO was evaluated using DSC, JI, Precision, and Recall on MRI and DaTscan images across Advanced PD, Early PD, and HCs. This analysis highlights the model’s strengths in identifying disease-specific patterns, providing valuable insights into its diagnostic utility for PD classification while also enhancing computational efficiency. Figures 8 and 9 illustrate the model’s ability to isolate relevant brain regions, enhancing classification accuracy and diagnostic reliability while maintaining computational efficiency.

Fig. 8

Analysis of segmentation performance metrics on MRI.

Figure 8 shows the proposed SIMVC segmentation method’s strong performance in delineating brain MRI regions across Advanced PD, Early PD, and HCs. The model achieved high DSC scores of 0.880, 0.900, and 0.910, with consistently high Precision and Recall, peaking at 0.920 in HCs. Although the Jaccard Index was slightly lower in Advanced PD (0.800), it remained acceptable given structural complexity. The increasing metrics from Advanced PD to HCs demonstrate the method’s robustness in handling anatomical variations, confirming its reliability and precision in ROI segmentation.

Fig. 9

Analysis of segmentation performance metrics on DaTscan images.

Figure 9 shows the proposed SIMVC segmentation method’s strong performance in DaTscan images across PD stages. It achieved DSC scores of 0.890 (Advanced PD), 0.880 (Early PD), and 0.900 (HCs), with corresponding JI, Precision, and Recall values reflecting accurate region detection despite subtle early-stage features and some false positives. The results demonstrate the method’s robustness in segmenting regions of interest across varying disease severities, confirming its effectiveness for DaTscan image analysis.

Comparative evaluation of classification performance metrics

This section evaluates the classification performance of the proposed EEFN-XM-PDC-HybPS-GWO model using accuracy, sensitivity, specificity, and ROC metrics across PD stages. As shown in Table 2; Figs. 10, 11, 12, 13, 14, 15, 16 and 17, the model outperforms existing methods due to its effective denoising and precise segmentation, enhancing region identification and reducing misclassification. These results underscore the model’s robustness and potential clinical utility for PD classification.

Table 2 Performance analysis of accuracy, sensitivity and specificity.

Fig. 10

Comparative evaluation of accuracy.

Figure 10 presents a comparative accuracy assessment of the proposed EEFN-XM-PDC-HybPS-GWO model against existing methods DMFEN-PDC, LSTM-PDD-GS, and MMT-CA-PDC across different stages of PD: Advanced Stage PD, Early Stage PD, and HCs. The proposed model outperforms existing approaches with 7.10%, 8.90%, and 15.00% higher accuracy for Advanced Stage PD; 7.90%, 11.80%, and 17.80% for Early Stage PD; and 6.90%, 10.60%, and 15.10% for HC, when compared to DMFEN-PDC, LSTM-PDD-GS, and MMT-CA-PDC, respectively. These results clearly demonstrate that the EEFN-XM-PDC-HybPS-GWO model significantly boosts classification accuracy by effectively integrating multimodal data from MRI, DaTscan images, and gait scores.

Fig. 11

Comparative evaluation of sensitivity.

Figure 11 presents a comparative sensitivity analysis of the proposed EEFN-XM-PDC-HybPS-GWO model against existing methods DMFEN-PDC, LSTM-PDD-GS, and MMT-CA-PDC across Advanced Stage PD, Early Stage PD, and HCs. Compared to existing models, the proposed method shows an increased sensitivity of 8.00%, 10.80%, and 16.50% for Advanced Stage PD; 7.80%, 10.00%, and 14.00% for Early Stage PD; and 9.00%, 8.60%, and 7.10% for Healthy Controls over DMFEN-PDC, LSTM-PDD-GS, and MMT-CA-PDC, respectively. These improvements highlight the superior true positive detection capability of the proposed model using multimodal data fusion.

Fig. 12

Comparative evaluation of specificity.

Figure 12 illustrates the specificity performance of the proposed EEFN-XM-PDC-HybPS-GWO model compared to DMFEN-PDC, MMT-CA-PDC, and LSTM-PDD-GS across advanced Stage PD, early Stage PD, and HCs. For Advanced Stage PD, the proposed model shows a specificity improvement of 8.20%, 14.90%, and 17.70% over DMFEN-PDC, MMT-CA-PDC, and LSTM-PDD-GS, respectively. In Early Stage PD, it outperforms the same models by 6.10%, 11.10%, and 13.00%, respectively. For Healthy Controls, it achieves gains of 7.60%, 9.30%, and 15.11%. These consistent improvements demonstrate the proposed model’s strong capability in reducing false positives and accurately identifying non-PD cases using multimodal input from MRI, DaTscan images, and gait scores.

Fig. 13

Comparative evaluation of ROC curves.

Figure 13 presents the ROC curve comparing the classification performance of proposed method and existing methods based on the balance between TPR and FPR. The proposed EEFEN-XM-PDC-HybPS-GWO model achieves the highest AUC of 0.996, clearly surpassing the performance of DMFEN-PDC (0.878), MMT-CA-PDC (0.822), and LSTM-PDD-GS (0.818). This demonstrates the proposed model’s outstanding ability to distinguish between PD stages and healthy controls with high accuracy.

Fig. 14

Confusion matrix on MRI-based classification.

Figure 14 shows the confusion matrix for MRI-based classification using EEFN-XM-PDC-HybPS-GWO. The model correctly classified 370/382 Advanced PD, 375/384 Early PD, and 380/389 HCs, with minimal misclassifications primarily occurring between PD stages and HCs. High diagonal values reflect strong classification accuracy, while low off-diagonal values (ranging from 3 to 7) indicate minimal confusion. These results confirm the model’s robust capability to differentiate between PD stages and healthy controls, demonstrating its reliability and effectiveness for MRI-based Parkinson’s disease classification.

Fig. 15

Confusion matrix on DaTscan-based classification.

Figure 15 presents the confusion matrix for DaTscan-based classification using EEFN-XM-PDC-HybPS-GWO. The model correctly identified 369/381 Advanced PD, 380/396 Early PD, and 378/393 HCs. Misclassifications were minimal, with errors ranging from 5 to 9, primarily involving Early PD overlapping with Advanced PD and HCs. High diagonal values (369, 380, 378) confirm the model’s strong classification capability, while low off-diagonal entries reflect minimal confusion, reinforcing the model’s effectiveness in distinguishing PD stages and healthy controls using DaTscan images.

Fig. 16

Training vs. validation accuracy of EEFN-XM-PDC-HybPS-GWO.

Figure 16 depicts the training and validation accuracy of a model across 175 epochs. The training accuracy (orange line) begins at approximately 35% and increases steadily, plateauing around 95% after epoch 100 and remaining consistent through epoch 175. The validation accuracy (blue line) starts near 30%, rises more sharply, surpasses the training accuracy by epoch 50, and reaches about 98% by epoch 100, maintaining this level thereafter. The close alignment of both accuracy curves indicates strong generalization performance with minimal overfitting, as the slightly higher validation accuracy suggests the model effectively captures relevant patterns and performs well on unseen data.

Fig. 17

Stratified five-fold cross-validation graph.

Figure 17 shows the stratified five-fold cross-validation results, demonstrating the model’s robust performance and generalization. Across all folds, training and validation loss decrease steadily and stabilize, indicating efficient learning with minimal overfitting. Training and validation accuracy consistently rise and converge between 98% and 100%, with only minor gaps. The consistent trends across folds, supported by stratified sampling, confirm the model’s stability, strong generalization, and high classification accuracy.

Hyperparameter sensitivity analysis

Table 4 highlights the robustness of the EEFN-XM-PDC-HybPS-GWO framework under varied training configurations. Despite changes in learning rate, batch size, and optimizer parameters, the model consistently achieved high accuracy, sensitivity, and specificity, demonstrating stability across different hyperparameter settings.

Table 3 Hyperparameter sensitivity analysis of classification performance.

The minimal variation observed across different settings indicates that the model’s performance is not overly dependent on specific hyperparameter choices. This reinforces the generalizability of the proposed framework and provides strong evidence that the observed results are not artifacts of overfitting or favorable parameter initialization, but rather reflect the inherent effectiveness of the model architecture and training strategy.

Statistical robustness analysis

Figure 18 illustrates the statistical robustness of the proposed model across different random seed initializations using a heatmap representation. This visualization highlights the consistency of performance metrics accuracy, sensitivity, and specificity under varying random seeds, thereby demonstrating the stability of the model’s predictions regardless of initial weight distributions.

Fig. 18

Statistical robustness sensitivity heatmap.

Multiple independent runs were conducted using different random seeds and key evaluation metrics were computed along with their Mean ± Standard Deviation (SD) and 95% Confidence Intervals (CI). The results Accuracy (99.20% ± 0.10%, CI [99.12%, 99.28%]), Sensitivity (99.10% ± 0.10%, CI [99.00%, 99.20%]), and Specificity (99.00% ± 0.12%, CI [98.88%, 99.12%]) exhibited minimal variation across different initializations. This high consistency demonstrates the stability of the model, alleviates concerns about overfitting or sensitivity to random initialization, and reinforces the generalizability and reproducibility of the proposed framework for real-world applications.

An ablation study on EEFN-XM-PDC-HybPS-GWO

An ablation study was performed to assess the individual contributions of key components within the proposed EEFN-XM-PDC-HybPS-GWO for PD classification. The study examined the impact of two main elements: the Enhanced EfficientNet-Extended Multimodal (EEFN-XM) module compared to the baseline EfficientNet-B1, and the Hybrid Particle Swarm-Grey Wolf Optimizer (HybPS-GWO) against the standard GWO. The analysis evaluates their influence on classification Accuracy, feature extraction quality, convergence behavior, Specificity, and Sensitivity. Table 4; Fig. 19 highlights the significance of each component in enhancing the overall performance of the framework on MRI, DaTscan images, and gait pattern data across Advanced Stage PD, Early Stage PD, and HCs.

Table 4 Ablation study on EEFN-XM-PDC-HybPS-GWO.

Fig. 19

Component-level impact analysis of EEFN-XM-PDC-HybPS-GWO.

Table 4; Fig. 19 present an ablation study evaluating key components of the EEFN-XM-PDC-HybPS-GWO framework using accuracy, sensitivity, and specificity. The baseline EfficientNet-B1 achieved 87.6% accuracy, showing limited multimodal handling. Integrating EEFN-XM and GWO improved performance to 90.9% accuracy, demonstrating the benefit of cross-modal features and segmentation. Proposed model, combining HybPS-GWO, advanced denoising, and segmentation, achieved the highest metrics 99.2% accuracy, 99.1% sensitivity, and 98.3% specificity highlighting the synergistic impact of multimodal learning, hybrid optimization, and preprocessing.

Comparative analysis of computational efficiency

This section presents a comparative computational efficiency analysis to evaluate the proposed EEFN-XM-PDC-HybPS-GWO against existing methods. The analysis focuses on critical aspects such as time complexity, space complexity, memory usage, CPU utilization, and scalability. These metrics provide insights into the model’s operational performance, resource consumption, and suitability for real-time clinical deployment. Figures 20, 21, 22 and 23 demonstrate that the proposed method surpasses existing approaches, exhibiting enhanced computational efficiency.

Fig. 20

Comparative analysis of time complexity.

Figure 20 compares CPU operations versus input size for PD classification methods. The proposed EEFN-XM-PDC-HybPS-GWO shows slower CPU growth, indicating superior scalability and lower time complexity. LSTM-PDD-GS has the steepest increase, while MMT-CA-PDC and DMFEN-PDC show moderate growth. The efficiency of the proposed model results from optimized denoising, segmentation, and hybrid optimization, reducing redundant computations and improving convergence. This confirms its enhanced computational efficiency and scalability compared to existing methods.

Fig. 21

Comparative analysis of space complexity.

Figure 21 compares memory usage against input size for four PD classification models. The proposed EEFN-XM-PDC-HybPS-GWO shows the lowest memory growth, demonstrating superior space efficiency. LSTM-PDD-GS and MMT-CA-PDC exhibit steep increases, exceeding 150 GB and 120 GB respectively, while DMFEN-PDC plateaus at high input sizes. The proposed model’s efficiency arises from its compact architecture, optimized denoising, lightweight segmentation, and hybrid optimization. This confirms its enhanced scalability and space efficiency for large-scale multimodal data.

Fig. 22

Comparative analysis of resource utilization.

Figure 22 compares CPU, memory, and GPU usage of four PD classification models. The proposed EEFN-XM-PDC-HybPS-GWO shows the lowest resource consumption at 115% (CPU 40%, memory 35%, GPU 40%), demonstrating superior efficiency. LSTM-PDD-GS uses the most resources at 165%, with high memory and GPU demands. DMFEN-PDC and MMT-CA-PDC show moderate-to-high usage, driven by elevated CPU and memory loads. The proposed model’s efficiency derives from lightweight preprocessing, effective multimodal feature extraction, and hybrid optimization, making it suitable for resource-limited clinical environments.

Fig. 23

Comparative analysis of scalability.

Figure 23 compares scalability of four PD classification models based on CPU use, memory, execution time, and error rate. The proposed EEFN-XM-PDC-HybPS-GWO achieves the highest scalability (~ 95%), outperforming LSTM-PDD-GS (80%), MMT-CA-PDC (85%), and DMFEN-PDC (90%). It reduces memory use by 36%, execution time by 33%, and error rate by 57% compared to LSTM-PDD-GS, while also lowering CPU utilization by 27%. These gains reflect its efficient multimodal design, MSA-VAE denoising, SIMVC segmentation, and hybrid HybPS-GWO optimizer.

EEFN-XM-PDC-HybPS-GWO framework demonstrates robust performance for Parkinson’s disease (PD) classification by integrating multimodal neuroimaging (T1-weighted MRI, DaTscan) and gait scores. Key components include MSA-VAE for denoising, SIMVC for segmentation, and EEFN-XM for multimodal feature extraction and classification, optimized via Hybrid PSO-GWO. The model achieved 99.2% classification accuracy, surpassing state-of-the-art methods such as DMFEN-PDC, MMT-CA-PDC, and LSTM-PDD-GS. Sensitivity and specificity reached 99.1% and 98.3%, respectively. For denoising, it maintained high PSNR (43.5–35.5 dB), SSIM (0.99–0.90), and low MSE (0.005–0.050) under varying noise levels. Segmentation results were consistently strong with Dice Similarity Coefficient (0.880–0.910) and Jaccard Index (0.800–0.880). ROC analysis showed an AUC of 0.996, and confusion matrices revealed minimal misclassification across PD stages and HCs. The integration of Sparse Group Lasso improved interpretability by selecting the most relevant features from the substantia nigra and putamen. The 5-fold stratified cross-validation ensured robustness and generalizability. Computational efficiency was demonstrated with reduced resource usage (40% CPU, 35% memory, 40% GPU), 33.3% faster execution, and 57.14% lower error rate. To ensure the generalizability of the proposed model, a comprehensive Hyperparameter Sensitivity Analysis was performed by varying critical parameters, including learning rate, batch size, and hybrid optimizer settings. The model consistently achieved high performance across all configurations, indicating low sensitivity to hyperparameter changes. Additionally, a Statistical Robustness Analysis was conducted using multiple independent runs with different random seeds (Seeds A–E). The results, summarized using Mean ± Standard Deviation (SD) and 95% Confidence Intervals (CI), showed minimal variation demonstrating stable accuracy, sensitivity, and specificity across runs. These findings confirm the model’s robustness to initialization and hyperparameter variation, enhancing its reliability and reducing concerns of overfitting or performance bias. Ablation studies confirmed the impact of each module, with the complete model outperforming reduced configurations. External validation on the PPMI dataset yielded 96.7% accuracy, confirming generalizability. Overall, this framework enables precise PD staging and early stage diagnosis by leveraging multimodal integration and hybrid optimization, offering a clinically viable, high-performance solution for real-world deployment.

Conclusion

The proposed Enhanced EfficientNet-Extended Multimodal framework with Hybrid Particle Swarm and Grey Wolf Optimizer (EEFN-XM-PDC-HybPS-GWO) was designed to classify Parkinson’s Disease (PD) stages early, advanced, and healthy controls using T1-weighted MRI, DaTscan images (NTUA dataset), and gait scores (PhysioNet). Leveraging MRI and DaTscan biomarkers of nigral degeneration and dopaminergic loss, the model integrates MSA-VAE for denoising, SIMVC for structural segmentation, and radiomics-driven multimodal feature extraction via EEFN-XM. Optimized with HybPS-GWO, it achieved 99.2% accuracy, outperforming existing models: DMFEN-PDC (by 7.30%), MMT-CA-PDC (15.97%), and LSTM-PDD-GS (10.43%). It also demonstrated strong sensitivity (99.1%) and specificity (98.3%). Ablation studies validated each module’s contribution, with EEFN-XM and HybPS-GWO significantly enhancing classification performance and convergence speed. Sparse Group Lasso further refined feature selection, while HybPS-GWO improved optimization efficiency. The model also exhibited reduced training time and memory usage, supporting its scalability for high-dimensional multimodal data. Comparative evaluations confirmed EEFN-XM-PDC-HybPS-GWO’s superiority in accuracy, computational efficiency, and robustness, making it a promising tool for reliable PD stage classification and potential clinical deployment.

Limitations and future work

The proposed model shows strong potential as a clinical decision-support tool for early-stage PD diagnosis, enabling timely intervention and improved patient outcomes. However, its current validation is limited to single-center datasets, which may impact generalizability. Future work will focus on multi-center validation using diverse populations to enhance robustness and clinical applicability. While experimental results are promising, real-world deployment, including integration into clinical workflows and support for real-time diagnosis, remains to be addressed. The model will also be extended to incorporate data from wearable devices for continuous PD monitoring. Although the EEFN-XM framework uses attention mechanisms during feature extraction and fusion, it lacks explicit interpretability tools, which may limit clinical trust. To address this, future enhancements will include Grad-CAM for visualizing spatial attention in MRI and DaTscan images and SHAP for explaining feature contributions such as gait scores and imaging biomarkers. These additions will improve model transparency and support clinical validation. Further developments will focus on adapting the framework for other neurodegenerative diseases like Alzheimer’s, refining classification precision with advanced deep learning methods, and creating personalized diagnostic models by integrating genetic and patient-specific data, thereby enhancing the model’s utility in precision medicine.