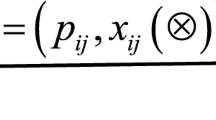Introduction

The communication satellite network constitutes a critical component of the national information infrastructure, holding significant economic and social implications. As pivotal elements within these networks, communication satellites exhibit high technical complexity, lengthy development cycles, challenging maintenance requirements, and substantial investment costs, necessitating rigorous reliability assessments. During operation, satellites endure wear and tear, failure mechanisms, and diverse operational environments, where subsystem component failures may degrade satellite performance levels. Conventional reliability theory, grounded in the “two-state assumption” of binary operational states (full functionality vs. complete failure), simplifies practical problem-solving but fails to address performance degradation-induced multistate system characteristics. The multistate system reliability theory offers a novel resolution to this challenge1,2.

Since its inception, multistate system reliability theory has yielded substantial research outcomes and found extensive applications across power systems, transportation networks, aerospace engineering, and related domains2,3,4,5. Among multistate reliability assessment methodologies, Monte Carlo simulations demand extensive data support, while decision diagrams (BDD), Bayesian networks, and Petri nets encounter state-space explosion in complex systems. The Universal Generating Function (UGF) method combines discrete random variables through polynomial representations, defines system-specific operators via logical relationships, and derives system-level performance polynomials through multilayer recursion, effectively capturing multistate characteristics. Originally proposed by Ushakov6 in 1986 and subsequently refined by Gregory7, UGF has gained prominence for its computational efficiency and low complexity in multistate system reliability analysis8. However, UGF focuses on steady-state performance and probabilities, overlooking temporal dynamics and limiting applicability to discrete variables with static probability distributions. To address this, scholars developed the Lz-transform—a specialized operator integrating stochastic processes with UGF, analogous to Lz-transform for discrete variables—which ensures uniqueness in dynamic reliability analysis9,10.

Multistate reliability analysis of communication satellites via UGF requires subsystem state performance data and corresponding probabilities. However, satellite structural complexity, low component failure rates, and information scarcity hinder precise determination of subsystem state transition rates and performance levels. Grey system theory, pioneered by Deng Julong for small-sample, information-deficient scenarios11, provides an effective analytical framework. The interval grey number—a fundamental grey system element—facilitates multi-attribute uncertainty decision-making12,13. While conventional interval grey numbers assume uniform value probabilities, practical applications often involve non-uniform distributions. Furthermore, complex system operations amplify uncertainty propagation in interval grey number computations, increasing decision errors. To mitigate these limitations, Luo14,15 introduced three-parameter interval grey numbers, which have enabled advancements in sustainable transport evaluation16, grey target decision-making17, and prospect theory-based group decisions18. Despite progress, existing methods exhibit shortcomings: geometric distance-based dominance metrics in16 disregard distribution characteristics, subjective weighting persists, and distance measures in19 inadequately reflect parameter distributions. This paper contributes through:

  1. (1)

    Defining system performance-demand relationships via three-parameter interval grey number possibility functions, overcoming geometric distance limitations in distribution characterization.

  2. (2)

    Implementing computational algorithms for satellite state probabilities and dynamic reliability, resolving the state-space explosion in complex multistate systems.

  3. (3)

    Establishing a theoretical framework integrating three-parameter interval grey numbers with possibility functions, grey Markov processes, and Lz-transform for transient multistate satellite reliability analysis.

Preliminarie

Definitions

Definition 1

In real-world systems, beyond binary operational states (perfect functionality and complete failure), there typically exist multiple degraded states. Such systems are formally defined as multi-state systems (MSS)20,21. When system performance rates and corresponding state probabilities are represented by grey numbers, the system is termed a grey multi-state system (GMSS).

Definition 2

Let \(\left\{ {{X_n},n \in T} \right\}\) denote a stochastic process. If for any integer n and states \({i_0},{i_1}, \cdots ,{i_{n + 1}} \in I\), the conditional probability satisfies: \(P(X_{n+1}=i_{n+1}|X_{0}=i_{0}, X_{1}=i_{1},\cdots , X_{n}=i_{n})=P(X_{n+1}=i_{n+1}|X_{n}=i_{n})\), then \(\left\{ {{X_n},n \in T} \right\}\) is known as a Markov chain. For any \(n \in T\) and state \(i,j \in I\),\({P_{ij}}\left( n \right) = P\left( {\left. {{X_{n + 1}} = j} \right| {X_n} = i} \right)\) is as the transition probability of the Markov chain. If the transition probability \({P_{ij}}\left( n \right)\) s grey element ,then \(\left\{ {{X_n},n \in T} \right\}\) is called a grey Markov chain22.

Definition 3

A grey number (denoted by \(\otimes\)) represents an uncertain quantity whose exact value is unknown but bounded within a specific interval or set23.

Definition 4

An interval grey number is defined as \(a\left( \otimes \right) = \left[ {{a^l},{a^u}} \right]\) where \({a^l} \le {a^u}\) and \({a^l},{a^u} \in \mathrm{{R}}\). If \({a^l} = {a^u}\), the interval grey number reduces to a real number23.

Definition 5

A three-parameter interval grey number extends the interval grey number by incorporating a central tendency parameter: \(a\left( \otimes \right) = \left[ {{a^l},{a^ * },{a^u}} \right]\), where \({a^ * }\) denotes the center of gravity (most probable value). When \({a^ * }\) is unspecified, the three-parameter form degenerates to a standard interval grey number14.

Definition 6

Let \(a(\otimes ) = [a^l, a^*, a^u]\) and \(b(\otimes ) = [b^l, b^*, b^u]\). The arithmetic operations are defined as24:

$$\begin{aligned} {\textbf {Addition:}}&\quad a(\otimes ) + b(\otimes ) = [a^l + b^l, a^* + b^*, a^u + b^u] \\ {\textbf {Subtraction:}}&\quad a(\otimes ) - b(\otimes ) = [a^l - b^u, a^* - b^*, a^u - b^l] \\ {\textbf {Multiplication:}}&\quad a(\otimes ) \times b(\otimes ) = \left[ \min \{a^l b^l, a^l b^u, a^u b^l, a^u b^u\},\ a^* b^*,\ \max \{a^l b^l, a^l b^u, a^u b^l, a^u b^u\}\right] \\ {\textbf {Minimum Operation:}}&\quad \min \{a(\otimes ), b(\otimes )\} = \left[ \min \{a^l, b^l\},\ \min \{a^*, b^*\},\ \min \{a^u, b^u\}\right] \\ {\textbf {Scalar Multiplication }} (k \ge 0):&\quad k \cdot a(\otimes ) = [k a^l, k a^*, k a^u] \\ {\textbf {Scalar Multiplication }} (k < 0):&\quad k \cdot a(\otimes ) = [k a^u, k a^*, k a^l] \\ {\textbf {Power Operation }} (k \ge 0):&\quad [a(\otimes )]^k = \left[ (a^l)^k, (a^*)^k, (a^u)^k\right] \end{aligned}$$

Acronym and notation

To ensure methodological consistency, all acronyms and mathematical notations adopted in this framework are systematically documented in Table 1.

Table 1 List of Acronyms and Notations.
Full size table

Dynamic reliability assessment model for grey multi-state communication satellites

Structure analysis

A communication satellite comprises five principal unit systems: power, communication, control, telemetry command, and antenna. The power unit system integrates solar cells and batteries in a parallel configuration. During sunlit periods, the batteries are charged, while during eclipses, they provide stable power to onboard equipment. The communication unit system consists of two key subsystems: transponders and antennas. Functioning as relay stations, transponders receive, process, and retransmit signals—essentially operating as broadband transceivers. The control unit system incorporates various electromechanical adjustment devices, including thrusters, actuators, thermal regulation units, and switching mechanisms, which maintain satellite attitude, orbital positioning, and antenna orientation under telemetry command. The telemetry command unit system collects operational parameters (voltage, current, frequency, temperature) and attitude data through sensors, transmitting them to ground stations while receiving control commands. The antenna unit system employs dedicated telemetry/command and communication antennas for directional signal transmission. Figure 1 illustrates the satellite’s structural configuration.

Fig. 1
figure 1

Block diagram of the reliability of the communication satellite system.

Full size image

In operational terms, the satellite serves as a wireless relay through the coordinated operation of these unit systems. Critical components employ redundancy strategies: transponder receivers and power amplifiers typically use cold standby configurations, while telemetry processors adopt hot redundancy. As any unit system failure would result in satellite failure, reliability analysis models the satellite as a series combination of five unit systems. When considering internal subsystem redundancy within each unit system as parallel configurations, the reliability structure appears as shown in Fig. 2.

Fig. 2
figure 2

Structural block diagram of a communications satellite.

Full size image

During the service life of a communication satellite system, the effects of radiation, alternating temperatures, and vacuum environments can cause random system failures in local subsystem components. These failures may occur when the system does not need to be completely taken offline and its output performance is in a derated operation mode. Let each subsystem have \({k_i} + 1\) performance levels, that is,\(0,1,2 \cdots ,{k_i}\). As can be seen from Fig.2, a communication satellite system composed of grey multi-state subsystems forms a multi-layer grey multi-state system. Let the performance levels of the power subsystem \({M_{11}}, \cdots ,{M_{1{n_1}}}\), communication subsystem \({M_{21}}, \cdots ,{M_{2{n_2}}}\), control subsystem \({M_{31}}, \cdots ,{M_{3{n_3}}}\), telemetry command subsystem \({M_{41}}, \cdots ,{M_{4{n_4}}}\) and antenna subsystem \({M_{51}}, \cdots ,{M_{5{n_5}}}\) at time t be represented by the random variables \(g_i^ \otimes \left( t \right) \in \left\{ {g_{i0}^ \otimes \left( t \right) ,g_{i1}^ \otimes \left( t \right) , \cdots ,g_{i{k_i}}^ \otimes \left( t \right) } \right\} ,i = 1,2, \cdots ,5\). The performance of the power supply system, communication system, control system, telemetry and command system, and antenna system, which are composed of the aforementioned subsystems, is denoted as \(G_j^ \otimes \left( t \right) ,j = 1,2, \cdots 5\), and the performance of the single communication satellite system is represented as \(G_s^ \otimes \left( t \right)\).

Lz-transform integration with UGF and Markov processes

For a discrete random variable G representing system performance levels with states \(G = \left\{ g_1, g_2, \cdots , g_N \right\}\) and corresponding probabilities \(P = \left\{ p_1, \cdots , p_N \right\}\),where \(p_i = \Pr \left\{ G = g_i \right\}\), the Universal Generating Function (UGF) is defined as25:

$$\begin{aligned} u(z) = \sum _{i=1}^N p_i \cdot z^{g_i}, \end{aligned}$$
(1)

where z is a formal algebraic operator with no numerical interpretation, serving solely to pair performance levels with their probabilities.

While UGF effectively models steady-state performance, it lacks temporal resolution for transient analysis. To address this limitation, the Lz-transform was subsequently developed by integrating stochastic processes with UGF.

Let \(G\left( t \right) = \left\{ {{g_1},{g_2}, \cdots ,{g_N}} \right\}\) denote a continuous-time Markov process with:

  • State transition rate matrix \(D = \left\| {{d_{ij}}\left( t \right) } \right\|\)

  • Time-dependent state probabilities \({p_i}\left( t \right) = {P_r}\left( {G\left( t \right) = {g_i}} \right)\)

  • Initial probability distribution:

    $$\begin{aligned} P_0 = \begin{bmatrix} p_1(0) = \Pr (G(0) = g_1),&p_2(0) = \Pr (G(0) = g_2),&\dots ,&p_N(0) = \Pr (G(0) = g_N) \end{bmatrix}. \end{aligned}$$
    (2)

The Markov process is formally expressed as:

$$\begin{aligned} G(t) = \langle g, D, P_0 \rangle . \end{aligned}$$
(3)

The Lz-transform of this process is given by:

$$\begin{aligned} Lz{G(t)} = u(z,t,P_0) = \sum _{i=1}^N p_i(t) \cdot z^{g_i}, \end{aligned}$$
(4)

where \({p_i}\left( t \right)\) represents the transient probability of state i at time \(t \ge 0\). The operator z retains its abstract algebraic role—it does not represent a numerical variable but rather a symbolic separator between performance levels and their associated probabilities. This formalism ensures a bijective mapping between the transform and the system’s stochastic behavior under given \({P_0}\).

G-Markov model for repairable subsystems

The reliability analysis of communication satellite systems relies on subsystem performance levels and their transient probabilities. However, the structural complexity and limited test samples make precise parameter determination challenging. When performance levels and associated parameters are expressed as three-parameter interval grey numbers, the corresponding Lz transformation is termed Three-Parameter Interval Grey Number Lz Transformation (T-PIGN-Lz).

A grey multi-state repairable subsystem must satisfy the following conditions:

  1. (1)

    Performance Space : Subsystem i has a discrete performance space \(\left\{ {0,1, \cdots ,{k_i}} \right\}\) where states are non-negative integers..

  2. (2)

    Grey Performance : The performance level \(g_i^ \otimes \left( t \right)\) is a three-parameter interval grey number.

  3. (3)

    Grey Transition Rates : State transition rates between performance levels are three-parameter interval grey numbers.

The performance level set \(g_i^ \otimes \left( t \right) = \left\{ {g_{i0}^ \otimes \left( t \right) ,g_{i1}^ \otimes \left( t \right) , \cdots ,g_{i{k_i}}^ \otimes \left( t \right) } \right\}\) s modeled through discrete Markov states, forming a G-Markov chain with grey transition probabilities, as shown in Fig.3. Here, \({k_i}\) denotes the optimal performance state while 0 represents complete failure.

Fig. 3
figure 3

G-Markov model for multi-state subsystem i performance states.

Full size image

Subsystem state probabilities are governed by the Kolmogorov differential equations:

$$\begin{aligned} \begin{aligned} \frac{d p_{ik_i}^\otimes (t)}{dt}&= \sum _{h=0}^{k_i-1} \mu _{i(h,k_i)}^\otimes p_{ih}^\otimes (t) - p_{ik_i}^\otimes (t) \sum _{h=0}^{k_i-1} \lambda _{i(k_i,h)}^\otimes , \\ \frac{d p_{ij}^\otimes (t)}{dt}&= \lambda _{i(k_i,j)}^\otimes p_{ik_i}^\otimes (t) - \mu _{i(j,k_i)}^\otimes p_{ij}^\otimes (t), \quad 0< j < k_i, \\ \frac{d p_{i0}^\otimes (t)}{dt}&= \lambda _{i(k_i,0)}^\otimes p_{ik_i}^\otimes (t) - \mu _{i(0,k_i)}^\otimes p_{i0}^\otimes (t). \end{aligned} \end{aligned}$$
(5)

Assuming the process initiates from the optimal state \({k_i}\) with performance level \(g_{i{k_i}}^ \otimes\) , the initial conditions are:

$$\begin{aligned} p_{ik_i}^\otimes (0) = 1, \quad p_{ij}^\otimes (0) = 0 \quad \text {for } j = 0, 1, \dots , k_i-1. \end{aligned}$$
(6)

Applying Laplace-Stieltjes transformation to (5) yields:

$$\begin{aligned} \begin{aligned} sp_{ik_i}^\otimes (s) - 1&= \sum _{h=0}^{k_i-1} \mu _{i(h,k_i)}^\otimes p_{ih}^\otimes (s) - p_{ik_i}^\otimes (s) \sum _{h=0}^{k_i-1} \lambda _{i(k_i,h)}^\otimes , \\ sp_{ij}^\otimes (s)&= \lambda _{i(k_i,j)}^\otimes p_{ik_i}^\otimes (s) - \mu _{i(j,k_i)}^\otimes p_{ij}^\otimes (s), \quad 0< j < k_i, \\ sp_{i0}^\otimes (s)&= \lambda _{i(k_i,0)}^\otimes p_{ik_i}^\otimes (s) - \mu _{i(0,k_i)}^\otimes p_{i0}^\otimes (s). \end{aligned} \end{aligned}$$
(7)

Here, \(L\left[ \cdot \right]\) denotes the Laplace-Stieltjes operator. Inverse transformation yields time-domain probabilities:

$$\begin{aligned} p_{ij}^\otimes (t) = L^{-1}\left[ p_{ij}^\otimes (s) \right] = f_{ij}\left( \lambda _i^\otimes , \mu _i^\otimes , t \right) , \end{aligned}$$
(8)

where \(\lambda _i^ \otimes = \Big \{ \lambda _{i({k_i},{k_i}-1)}^ \otimes , \cdots ,\lambda _{i(1,0)}^ \otimes \Big \}\) and \(\mu _i^ \otimes = \left\{ {\mu _{i\left( {{k_i} - 1,{k_i}} \right) }^ \otimes , \cdots ,\mu _{i\left( {0,{k_i}} \right) }^ \otimes } \right\}\) represent degradation and repair rate vectors, respectively.

T-PIGN-Lz transform for communication satellite system

T-PIGN-Lz transform for subsystems

The T-PIGN-Lz transform aggregates the performance levels and transient probabilities of a subsystem into a grey function. For subsystem i, this transform combines9,26:

  • \(k_i + 1\) discrete performance levels \(g_{ij_i}^\otimes\) (where \(j_i = 0, 1, \dots , k_i\))

  • Corresponding time-dependent probabilities \(p_{ij_i}^\otimes (t)\)

  • A placeholder variable z (with no numerical value) to separate performance terms

$$\begin{aligned} Lz\left\{ g_i^\otimes (t)\right\} = u_i^\otimes (z, t, P_{i0}^\otimes ) = \sum _{j_i=0}^{k_i} p_{ij_i}^\otimes (t) \cdot z^{g_{ij_i}^\otimes }, \end{aligned}$$
(9)

where \(g_{ij_i}^\otimes\) represents the performance level \(g_{ij_i}^\otimes\), weighted by its probability \(p_{ij_i}^\otimes (t)\).

Generic combinatorial operator \(\Omega _\varphi ^\otimes\)

This operator combines the T-PIGN-Lz transforms of subsystems or unit systems according to their structural relationships (e.g., series, parallel). The operator applies a structure function \(\varphi\) to map subsystem performances to the system-level performance.

For a unit system j composed of n subsystems:

$$\begin{aligned} Lz\left\{ G_j^\otimes (t)\right\} = \Omega _\varphi ^\otimes \left( Lz\left\{ g_1^\otimes (t)\right\} , \dots , Lz\left\{ g_n^\otimes (t)\right\} \right) , \end{aligned}$$
(10)

Expanded form:

$$\begin{aligned} \sum _{j_1=0}^{k_1} \cdots \sum _{j_n=0}^{k_n} \left( \prod _{i=1}^n p_{ij_i}^\otimes (t) \cdot z^{\varphi (g_{1j_1}^\otimes , \dots , g_{nj_n}^\otimes )} \right) . \end{aligned}$$
(11)

Structure functions

  • Series Systems (\(\varphi _s\)): The system performance equals the minimum subsystem performance27,28:

    $$\begin{aligned} \varphi _s\left( g_1^\otimes , \dots , g_n^\otimes \right) = \min \left( g_1^\otimes , \dots , g_n^\otimes \right) . \end{aligned}$$
    (12)

  • Parallel Systems (\(\varphi _p\)): The system performance equals the sum of subsystem performances27,28:

    $$\begin{aligned} \varphi _p\left( g_1^\otimes , \dots , g_n^\otimes \right) = \sum _{i=1}^n g_i^\otimes . \end{aligned}$$
    (13)

System-level T-PIGN-Lz transform

For a communication satellite system composed of N unit systems:

$$\begin{aligned} Lz\left\{ G_s^\otimes (t)\right\} = \Omega _\varphi ^\otimes \left( Lz\left\{ G_1^\otimes (t)\right\} , \dots , Lz\left\{ G_N^\otimes (t)\right\} \right) , \end{aligned}$$
(14)

Expanded form:

$$\begin{aligned} \sum _{i_1=0}^{K_1} \cdots \sum _{i_N=0}^{K_N} \left( \prod _{j=1}^N p_{ji_j}^\otimes (t) \cdot z^{\varphi (g_{1i_1}^\otimes , \dots , g_{Ni_N}^\otimes )} \right) , \end{aligned}$$
(15)

where \(K_j\) is the number of states for unit system j.

State space mapping

The system’s performance levels arise from the Cartesian product of unit system states25:

$$\begin{aligned} \left\{ g_{10}, \dots , g_{1K_1}\right\} \times \cdots \times \left\{ g_{N0}, \dots , g_{NK_N}\right\} \rightarrow \left\{ g_1, \dots , g_{K_s}\right\} , \end{aligned}$$
(16)

where \(K_s = \prod _{j=1}^N K_j\) represents the total system states.

Dynamic reliability calculation

The system reliability \(D(W_\otimes , t)\) computes the probability that the system meets mission requirements \(W_\otimes\)29,30:

$$\begin{aligned} D(W_\otimes , t) = \sum _{s=1}^{K_s} p_s^\otimes (t) \cdot p\left( G_s^\otimes \ge W_\otimes \right) . \end{aligned}$$
(17)

The term \(p\left( G_s^\otimes \ge W_\otimes \right)\) is evaluated using the possibility function f(x):

$$\begin{aligned} f(x) = {\left\{ \begin{array}{ll} 0 & x \notin [a^l, a^u], \\ \frac{x - a^l}{a^* - a^l} & x \in [a^l, a^*), \\ 1 & x = a^*, \\ \frac{a^u - x}{a^u - a^*}, & x \in (a^*, a^u]. \end{array}\right. } \end{aligned}$$
(18)
Fig. 4
figure 4

Relationship between system performance levels and task demand performance.

Full size image

Usually, the possibility of taking the value of \(a(\otimes )=\left[ a^{l},a^{*},a^{u} \right]\) decreases from the center of gravity point \(a^{*}\) to the upper bound \(a^{u}\) and the lower bound \(a^{l}\). From Fig.4 it can be seen that when the system performance demand is \({W_{1 \otimes }}\), the system is unreliable, that is \(p\left( {G_s^ \otimes \ge {W_{1 \otimes }}} \right) = 0\); when the system performance demand is \({W_{2 \otimes }}\), the system is reliable, that is \(p\left( {G_s^ \otimes \ge {W_{2 \otimes }}} \right) = 1\); when the user demand is \({W_{3 \otimes }}\) or \({W_{4 \otimes }}\), there is uncertainty as to whether the system is reliable or not, that is \(0< p\left( {G_s^ \otimes \ge {W_{3\left( 4 \right) \otimes }}} \right) < 1\). Therefore, it is necessary to analyze which performance state satisfies the task demand.

Let \(r_s^ \otimes = g_s^ \otimes - {W_ \otimes }\), \(p\left( {G_s^ \otimes \ge {W_ \otimes }} \right)\) denote the probability that \(G_s^ \otimes \ge {W_ \otimes }\) and \(f\left( {r_{_s}^ \otimes } \right)\) be the possibility function for \({r_s}\). The probability of \(G_s^ \otimes \ge {W_ \otimes }\) is defined as

$$\begin{aligned} p\left( {r_s^ \otimes \ge 0} \right) = \frac{{\int \limits _{r_s^ \otimes \ge 0} {f\left( {r_s^ \otimes } \right) dr_s^ \otimes } }}{{\int \limits _\Omega {f\left( {r_s^ \otimes } \right) dr_s^ \otimes } }}. \end{aligned}$$
(19)

An illustrative example

Consider a multi-state communication satellite system comprising five unit systems and six performance degradation subsystems, whose structure is illustrated in Fig. 5. Unit system 1 contains the power system (subsystem 1). Unit system 2 incorporates two homogeneous and isomorphic communication systems (subsystems 2 and 3). Unit system 3 encompasses the control system (subsystem 4). Unit system 4 includes the telemetry command system (subsystem 5), while unit system 5 comprises the antenna system (subsystem 6). The communication system primarily facilitates control command transmission, establishes space-ground links, and ensures reliable inter-satellite connectivity, which critically determines the operational success of the satellite communication system. Redundancy strategies such as cold standby configurations for receivers and high-power amplifiers in satellite transponders are implemented to maintain operational stability. Parallel structures represent the component redundancy. Each subsystem’s performance levels and state transition rates are defined as three-parameter interval grey numbers, as detailed in Table 2. Subsystem 2 exhibits identical state transition rates and performance characteristics to Subsystem 3. Given the mission-required performance threshold of the communication satellite system \({W_ \otimes } = \left( {0.4,0.5,0.6} \right)\), evaluate the system reliability at \(t=1\) year.

Fig. 5
figure 5

Architecture diagram of a communication satellite system.

Full size image
Table 2 Performance parameters of the subsystems.
Full size table

Solving for dynamic reliability of communication satellites

G-Markov state probability solution for each subsystem

The probabilities of subsystems 1 to 6 operating at each performance level can be derived from the established G-Markov model, as presented in Table 3.

Table 3 The probability that each subsystem is at each performance level.
Full size table

T-PIGN-Lz transformation functions for subsystems

The T-PIGN-Lz transformation for each subsystem at t=1 can be directly derived from the performance levels in Table 2 and their corresponding probability distributions in Table 3 using Equation (20).

$$\begin{aligned} \begin{array}{l} Lz\left\{ {g_1^ \otimes \left( 1 \right) } \right\} = \sum \limits _{j = 0}^2 {p_{1j}^ \otimes \left( 1 \right) {z^{g_{1j}^ \otimes }}} = \left( {0.0077,0.0117,0.0304} \right) \cdot {z^{\left( {0,0,0} \right) }} + \left( {0.0305,0.0442,0.0549} \right) \cdot {z^{\left( {0.5,0.55,0.7} \right) }}\\ \mathrm{ } + \left( {0.9147,0.9441,0.9618} \right) \cdot {z^{^{\left( {0.928,0.95,0.965} \right) }}},\\ Lz\left\{ {g_2^ \otimes \left( 1 \right) } \right\} = Lz\left\{ {g_3^ \otimes \left( 1 \right) } \right\} =\sum \limits _{j = 0}^3 {p_{2j}^ \otimes \left( 1 \right) {z^{g_{2j}^ \otimes }}} = \left( {0.0047,0.0171,0.0235} \right) \cdot {z^{\left( {0,0,0} \right) }}\\ + \left( {0.0237,0.0245,0.0308} \right) \cdot {z^{\left( {0.2792,0.3329,0.3821} \right) }} + \left( {0.0083,0.0132,0.0228} \right) \cdot {z^{\left( {0.1754,0.387,0.4234} \right) }}\\ + \left( {0.9229,0.9452,0.9633} \right) \cdot {z^{\left( {0.6996,0.8223,0.939} \right) }},\\ Lz\left\{ {g_4^ \otimes \left( 1 \right) } \right\} = \sum \limits _{j = 0}^3 {p_{4j}^ \otimes \left( 1 \right) {z^{g_{4j}^ \otimes }}} = \left( {0.0134,0.0149,0.0187} \right) \cdot {z^{\left( {0,0,0} \right) }} + \left( {0.0277,0.0309,0.0355} \right) \cdot {z^{\left( {0.396,0.4209,0.48} \right) }}\\ + \left( {0.0326,0.0349,0.0379} \right) \cdot {z^{\left( {0.5418,0.6209,0.665} \right) }} + \left( {0.9079,0.9193,0.9263} \right) \cdot {z^{\left( {0.7736,0.8836,0.9665} \right) }},\\ Lz\left\{ {g_5^ \otimes \left( 1 \right) } \right\} = \sum \limits _{j = 0}^2 {p_{5j}^ \otimes \left( 1 \right) {z^{g_{5j}^ \otimes }}} = \left( {0.0219,0.0243,0.0277} \right) \cdot {z^{\left( {0,0,0} \right) }} + \left( {0.0244,0.0276,0.0298} \right) \cdot {z^{\left( {0.452,0.523,0.597} \right) }}\\ + \left( {0.9425,0.9481,0.9537} \right) \cdot {z^{\left( {0.795,0.835,0.942} \right) }},\\ Lz\left\{ {g_6^ \otimes \left( 1 \right) } \right\} = \sum \limits _{j = 0}^2 {p_{6j}^ \otimes \left( 1 \right) {z^{g_{6j}^ \otimes }}} = \left( {0.004,0.0123,0.0215} \right) \cdot {z^{\left( {0,0,0} \right) }} \mathrm{ } + \left( {0.0289,0.0315,0.0316} \right) \cdot {z^{\left( {0.3736,0.441,0.565} \right) }}\mathrm{ }\\ + \left( {0.9469,0.9561,0.9672} \right) \cdot {z^{\left( {0.88,0.9,0.915} \right) }}. \end{array} \end{aligned}$$
(20)

T-PIGN-Lz transformation functions for unit systems

As shown in Fig.5, the performance level of subsystem 1 corresponds directly to unit system 1, expressed as \(G_1^ \otimes = g_1^ \otimes\). Similarly, the relationships hold: \(G_3^ \otimes = g_4^ \otimes ,G_4^ \otimes = g_5^ \otimes ,G_5^ \otimes = g_6^ \otimes\).

$$\begin{aligned} \begin{array}{l} Lz\left\{ {G_1^ \otimes \left( 1 \right) } \right\} = Lz\left\{ {g_1^ \otimes \left( 1 \right) } \right\} = \sum \limits _{j = 0}^2 {p_{1j}^ \otimes \left( 1 \right) {z^{g_{1j}^ \otimes }}},\\ Lz\left\{ {G_3^ \otimes \left( 1 \right) } \right\} = Lz\left\{ {g_4^ \otimes \left( 1 \right) } \right\} = \sum \limits _{j = 0}^3 {p_{4j}^ \otimes \left( 1 \right) {z^{g_{4j}^ \otimes }}}, \\ Lz\left\{ {G_4^ \otimes \left( 1 \right) } \right\} = Lz\left\{ {g_5^ \otimes \left( 1 \right) } \right\} \mathrm{ } = \sum \limits _{j = 0}^2 {p_{5j}^ \otimes \left( 1 \right) {z^{g_{5j}^ \otimes }}} \mathrm{ },\\ Lz\left\{ {G_5^ \otimes \left( 1 \right) } \right\} = Lz\left\{ {g_6^ \otimes \left( 1 \right) } \right\} = \sum \limits _{j = 0}^2 {p_{6j}^ \otimes \left( 1 \right) {z^{g_{6j}^ \otimes }}}. \end{array} \end{aligned}$$
(21)

Unit system 2 contains two parallel subsystems with identical performance characteristics, where \(G_2^ \otimes = {\varphi _p}\left( {g_2^ \otimes ,g_3^ \otimes } \right)\):

$$\begin{aligned} \begin{array}{l} Lz\left\{ {G_{{f_2}}^ \otimes \left( 1 \right) } \right\} = \Omega _\varphi ^ \otimes \left( {Lz\left( {g_2^ \otimes \left( 1 \right) } \right) ,Lz\left( {g_3^ \otimes \left( 1 \right) } \right) } \right) = \Omega _\varphi ^ \otimes \left( {\sum \limits _{j = 0}^3 {p_{2j}^ \otimes \left( 1 \right) {z^{g_{2j}^ \otimes }}},\sum \limits _{j = 0}^3 {p_{3j}^ \otimes \left( 1 \right) {z^{g_{3j}^ \otimes }}} } \right) = \sum \limits _{j = 0}^3 {\sum \limits _{j = 0}^3 {\left( {\prod \limits _{i = 2}^3 {p_{ij}^ \otimes \left( 1 \right) \cdot {z^{\sum {g_{ij}^ \otimes } }}} } \right) } } \\ = {\left( {p_{20}^ \otimes \left( \mathrm{{1}} \right) } \right) ^2} \cdot {z^{\left( {0,0,0} \right) }} + 2p_{20}^ \otimes \left( \mathrm{{1}} \right) p_{21}^ \otimes \left( \mathrm{{1}} \right) \cdot {z^{\left( {0.2792,0.3329,0.3821} \right) }} + 2p_{20}^ \otimes \left( \mathrm{{1}} \right) p_{22}^ \otimes \left( \mathrm{{1}} \right) \cdot {z^{\left( {0.1754,0.387,0.4234} \right) }} \\ +2p_{20}^ \otimes \left( \mathrm{{1}} \right) p_{23}^ \otimes \left( \mathrm{{1}} \right) \cdot {z^{\left( {0.6996,0.8223,0.939} \right) }} + {\left( {p_{21}^ \otimes \left( \mathrm{{1}} \right) } \right) ^2} \cdot {z^{\left( {0.5584,0.6658,0.7642} \right) }} + 2p_{21}^ \otimes \left( \mathrm{{1}} \right) p_{22}^ \otimes \left( \mathrm{{1}} \right) \cdot {z^{\left( {0.4546,0.7199,0.8055} \right) }}\\ + 2p_{21}^ \otimes \left( \mathrm{{1}} \right) p_{23}^ \otimes \left( \mathrm{{1}} \right) \cdot {z^{\left( {0.9788,1.1552,1.3211} \right) }} + {\left( {p_{22}^ \otimes \left( \mathrm{{1}} \right) } \right) ^2} \cdot {z^{\left( {0.3508,0.774,0.8468} \right) }} + 2p_{22}^ \otimes \left( \mathrm{{1}} \right) p_{23}^ \otimes \left( \mathrm{{1}} \right) \cdot {z^{\left( {0.875,1.2093,1.3624} \right) }}\\ + {\left( {p_{23}^ \otimes } \right) ^2} \cdot {z^{\left( {1.3992,1.6446,1.878} \right) }}. \end{array} \end{aligned}$$
(22)

Reliability analysis of communication satellite systems

The integrated communication satellite system consists of five serially connected unit systems, expressed as:

$$\begin{aligned} \begin{array}{l} Lz\left\{ {G_s^ \otimes \left( 1 \right) } \right\} = {\phi _s}\left( \begin{array}{l} Lz\left( {G_1^ \otimes \left( 1 \right) } \right) ,Lz\left( {G_2^ \otimes \left( 1 \right) } \right) , Lz\left( {G_3^ \otimes \left( 1 \right) } \right) ,Lz\left( {G_4^ \otimes \left( 1 \right) } \right) , Lz\left( {G_5^ \otimes \left( 1 \right) } \right) \end{array} \right) \\ = \phi _s\left( \begin{aligned} & \sum _{j=0}^2 p_{1j}^{\otimes }(1)z^{g_{1j}^{\otimes }}, \ & \phi _p\left( \sum _{j=0}^3 p_{2j}^{\otimes }(1)z^{g_{2j}^{\otimes }}, \sum _{j=0}^3 p_{3j}^{\otimes }(1)z^{g_{3j}^{\otimes }}\right) , \ & \sum _{j=0}^3 p_{4j}^{\otimes }(1)z^{g_{4j}^{\otimes }}, \sum _{j=0}^2 p_{5j}^{\otimes }(1)z^{g_{5j}^{\otimes }}, \ & \sum _{j=0}^2 p_{6j}^{\otimes }(1)z^{g_{6j}^{\otimes }} \end{aligned} \right) \\ = \sum \limits _{j = 0}^2 {\sum \limits _{j = 0}^9 {\sum \limits _{j = 0}^3 {\sum \limits _{j = 0}^2 {\sum \limits _{j = 0}^2 {\left( {\prod \limits _{i = 1}^5 {p_{ij}^ \otimes \left( 1 \right) } \cdot {z^{\min \left\{ {g_{ij}^ \otimes } \right\} }}} \right) } } } } }. \end{array} \end{aligned}$$
(23)

The system exhibits \(K_{s}\)=3\(\times\)10\(\times\)4\(\times\)3\(\times\)3=1080 distinct performance levels, with its T-PIGN-Lz transformation formulated as:

$$\begin{aligned} Lz\left\{ {G_s^ \otimes \left( t \right) } \right\} = \sum \limits _{s = 1}^{1080} {p_s^ \otimes \left( t \right) * \mathrm{ }} {z^{g_s^ \otimes }}. \end{aligned}$$
(24)

System reliability at \(t=1\) year given mission requirement \({W_ \otimes } = \left( {0.4,0.5,0.6} \right)\) is computed through comparative analysis of performance levels:

$$\begin{aligned} D(W_{\otimes },t) = \sum _{s=1}^{1080} p_s^{\otimes }(t) \cdot P(G_s^{\otimes } \ge W_{\otimes }) = (0.7467, 0.8736, 0.9991). \end{aligned}$$
(25)

Communications satellite system reliability analysis

Sensitivity analysis

Communication satellite systems require varying performance levels for different missions, necessitating reliability analysis under diverse performance requirements. As the system’s mission demands performance ranges from 0 to 0.9, the reliability of the communication satellite system decreases with increasing demand. Fig.6 demonstrates that when the mission demand performance is 0, the reliability of the system asymptotically approaches 1 at t = 1. For mission demand performance between 0.1 and 0.4, the impact on system reliability is minimal. However, when the demand increases to 0.5–0.9, the reliability declines sharply, eventually approaching zero. This indicates an inverse relationship between task demand performance and system reliability.

Fig. 6
figure 6

The impact of changes in mission requirement performance on system reliability.

Full size image

To analyze the combined effects of time and performance requirements on system reliability, a three-dimensional bar chart (Fig.7) illustrates the most probable reliability values across time (1–10 years) and task demand performance (0–0.9). Fig.7 reveals that system reliability decreases with higher demand, particularly when \({W_ \otimes } > 0.4\). Over time, reliability diminishes for fixed demand levels, with larger demands exacerbating this trend. At low task demand performance, reliability primarily depends on time; as demand increases, task performance requirements dominate reliability variations.

Fig. 7
figure 7

The impact of variations in task demand performance and time on system reliability.

Full size image
Fig. 8
figure 8

System reliability under normal operation versus unit failure conditions.

Full size image

Weakness analysis

The reliability-based vulnerability assessment evaluates the impact of individual unit system failures on overall system reliability. The critical vulnerability is identified as the component demonstrating the most substantial influence. Initial system reliability is calculated under nominal operating conditions. Subsequent fault simulations employ exhaustive traversal methodology, systematically evaluating each unit failure scenario (excluding T-PIGN-Lz transformations for failed units). Significant deviation from baseline reliability identifies vulnerable components. Fig. 8 demonstrates comparative reliability metrics for failures in Unit Systems 1–5, with nominal operation as reference. The analysis reveals Unit System 1 as the primary reliability bottleneck, followed by Unit System 2.

Further, Parametric sensitivity analysis examines \(\lambda _{1\left( {2,0} \right) }^ \otimes\) and \(\lambda _{1\left( {2,1} \right) }^ \otimes\) effects on system reliability within Unit System 1. Figures 9 and 10 quantify reliability variations when scaling these parameters under constant mission requirements. The results demonstrate greater sensitivity to \(\lambda _{1\left( {2,1} \right) }^ \otimes\) perturbations, identifying it as the critical vulnerability. Mitigation strategies include either enhancing \(\mu _{1\left( {1,2} \right) }^ \otimes\) or reducing \(\lambda _{1\left( {2,1} \right) }^ \otimes\).

Fig. 9
figure 9

Impact of \(\lambda _{1\left( {2,0} \right) }^ \otimes\) changes on system reliability.

Full size image
Fig. 10
figure 10

Impact of \(\lambda _{1\left( {2,1} \right) }^ \otimes\) changes on system reliability.

Full size image

Comparative analysis

Under the mission requirement \({W_ \otimes } = \left( {0.4,0.5,0.6} \right)\), Fig. 11 compares the reliability predictions between the proposed method and the traditional reliability assessment method. The results show high consistency between the two approaches, which empirically validates the accuracy of the proposed model to a certain extent. However, it is worth noting that traditional reliability assessment methods have limitations when evaluating systems with a large number of states. For instance, in the case study presented in this paper, the total number of system states reaches 1,080. Traditional methods struggle to effectively handle reliability evaluation at such a large scale of states, whereas the proposed method demonstrates the capability to rapidly assess reliability for systems with extensive state configurations (as exemplified by the 1,080-state system in this study). This highlights the significant advantage of the proposed method over traditional approaches in handling reliability assessment for complex systems.

Fig. 11
figure 11

Comparison of system reliability between traditional and proposed methods.

Full size image

As shown in Fig. 12, when the system state performance takes the most probable value, the proposed method exhibits strong agreement with the Monte Carlo simulation results, validating the mathematical rigor of our approach. Notably, by introducing a confidence interval prediction mechanism, the proposed method fully encapsulates all Monte Carlo simulation results within its prediction bounds, demonstrating superior capability in uncertainty quantification. In terms of computational efficiency, the Monte Carlo simulation requires 8,520 seconds to complete due to exhaustive state-space sampling, while the proposed method achieves equivalent accuracy in only 50 seconds through state-space dimensionality reduction—a 170× speedup. This highlights the synergistic optimization of accuracy and efficiency in the proposed method, making it particularly suitable for real-time reliability assessment of large-scale multi-state systems.

Fig. 12
figure 12

Comparison of system reliability between Monte Carlo and proposed methods.

Full size image

Conclusion

This paper applies the three-parameter interval grey number to characterize the performance of grey multi-state systems, establishing a novel framework for reliability assessment of communication satellites through the integration of Lz-transformation and grey Markov processes. Our methodology defines the performance-demand relationship using possibility functions of three-parameter interval grey numbers, effectively addressing interval expansion challenges in reliability computation. The proposed approach reduces computational complexity in determining state probabilities through algorithmic optimization and computer-assisted solutions, while demonstrating superior performance in handling transient states compared to traditional methods. Future research should focus on: (1) extending the framework to multi-satellite constellation reliability modeling with inter-satellite dependencies; (2) developing hybrid models combining T-PIGN-Lz with Bayesian networks for complex failure propagation analysis; and (3) investigating time-varying mission requirement patterns and their reliability implications.