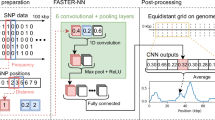
Abstract
Monitoring species’ presence in an ecosystem is crucial for conservation and understanding habitat diversity, but can be expensive and time consuming. As a result, ecologists have begun using the DNA that animals naturally leave behind in water or soil (called environmental DNA, or eDNA) to identify the species present in an environment. Recent work has shown that when used to identify species, convolutional neural networks (CNNs) can be as much as 150 times faster than ObiTools, a traditional method that does not use deep learning. However, CNNs are black boxes, meaning it is impossible to “fact check” why they predict that a given sequence belongs to a particular species. In this work, we introduce an interpretable, prototype-based CNN using the ProtoPNet framework that surpasses previous accuracy on a challenging eDNA dataset. The network is able to visualize the sequences of bases that are most distinctive for each species in the dataset, and introduces a novel skip connection that improves the interpretability of the original ProtoPNet. Our results show that reducing reliance on the convolutional output increases both interpretability and accuracy.
Similar content being viewed by others
Introduction
Species monitoring is vital to maintaining the health of our ecosystems. By observing and cataloging which species are present within a given area, we gain valuable insights into the biodiversity of that environment. This foundational knowledge is important for research and understanding, as well as conservation efforts focused on individual flora and fauna populations. Additionally, species monitoring allows us to detect the presence of invasive species, which is critical for preventing the spread of harmful non-native organisms and safeguarding the natural balance of ecosystems1. By monitoring multiple ecosystems, it also becomes possible to compare biodiversity spatially and track the movement of species over time. Monitoring biodiversity is increasingly relevant as the effects of climate change drive species away from their historic ranges. For example, this is seen in the Gulf of Maine where water is warming and affecting many fish, especially Atlantic herring, winter flounder, haddock, and alewife2.
Species monitoring has traditionally been conducted using physical observation, trail cameras, acoustic monitoring, and trawling. However, these methods can be costly and time-intensive (physical observation, trail cameras), invasive and damaging to ecosystems (trawling), and require skilled labor (acoustic monitoring). Environmental DNA (eDNA) metabarcoding provides an alternative approach to species monitoring that is more thorough and versatile while also being less invasive, time consuming, and expensive. Species monitoring using eDNA metabarcoding works by collecting environmental samples that contain genetic materials naturally shed by all species into their environment, whether that be through excrement, urine, skin, death, or by other means. Traces of DNA can then be extracted from water or sediment—in this work, we will focus on eDNA collected from water. By pumping collected water samples through a filtration capsule, it is possible to collect some of these DNA traces. Amplifying and sequencing the desired gene fragment produces a DNA sequence that can be used to identify the species. For a detailed description of eDNA metabarcoding, see Ruppert et al.3.
The last step in the eDNA metabarcoding process has traditionally involved comparing the collected sequences against a reference database. This reference database is created by taking a known species and sequencing its DNA, then repeating that process for multiple organisms in order to capture the natural variations in the species’ DNA. Doing this for multiple species creates a list which can be used to identify the species that produced a new, collected DNA sequence. Usually, comparison is done in large batches of collected sequences, given that eDNA can produce millions of reads. For example, the dataset used in Flück et al. has two million sequences4. Although determining all of the species present in a sample is the goal, the sheer scale of the number of sequences makes the process time-consuming. This comparison step is an ideal candidate for machine learning (ML). Once a model has been trained, using it to classify sequences can be rapid. In fact, Flück et al. created a model that was 150 times faster than the bioinformatics software ObiTools, while achieving similar accuracy4.
Although deep neural networks are fast, they are generally black boxes. This means that they perform manipulations of the input data in a complex formula, and it is impossible for a human to readily understand all of the reasons why a model makes a prediction. There are many ways to approach this problem. One category of explanations is post-hoc methods, which attempt to explain a model after it has been trained. Post-hoc approaches include SmoothGrad5, GradCam6, and Grad-CAM + +7 in the category of saliency visualization. The category of activation maximization includes multifaceted feature visualization8 and acceleration-based activity recognition9. Perturbation-based approaches include LIME10, SHAP11, and Fong et al.12, who used extremal perturbations and smooth masks. TCAV13 is a concept-based explanation. These methods can be beneficial because they can foster trust in the model’s predictions, help identify bias in a model or dataset, and possibly find the reason for incorrect predictions.
However, these post-hoc explainability methods have no guarantee of being faithful to the underlying black-box model. For this reason, post-hoc approaches can be unhelpful or misleading if one relies on these explanations to truthfully explain decisions. Interpretable ML models—models which are constrained to follow a transparent reasoning process—overcome this limitation. Interpretability has many benefits. First, if the actual decision-making process of a model is comprehensible to humans, it becomes easier to rely on its outputs. Second, humans can use information about the model’s reasoning to debug and manually make fixes to a network, based on instances where the model is making decisions using irrelevant features. Third, interpretability aids in assessing the model’s ability to generalize to new data. If we know how a model is making decisions, then we can infer how well the decision-making process would work in new environments. Fourth, interpretability can yield new insights about a domain, potentially uncovering correlations or pieces of knowledge in the data that are not obvious. For these reasons, the incorporation of interpretability into machine learning models is not a hindrance, but a desirable trait that has important benefits14.
In this work, we built an interpretable convolutional neural network (CNN)-based model for species classification. We used the same dataset as Flück et al., which contained fish sequences from South America4. We first built a non-interpretable CNN, which we called the base network. This model took a DNA sequence as an input, and gave a species prediction as an output. This model shared the same objective as Flück et al., which was to allow fast and accurate species identification4. After creating this base network, we removed the linear classification layer and added a prototype layer to the backbone, based off of the ProtoPNet from Chen et al.15. In addition to producing a species prediction, this final model learned prototypes, short subsequences of DNA, upon which decisions were made. The goal of this step was to add interpretability such that humans may understand the reasons behind a prediction by looking at which prototypes were most highly activated. This layer also provided insights via its prototypes, since the learned prototypes make it possible to view the DNA sequences that best distinguish each species. In addition to applying the ProtoPNet to the domain of DNA sequences instead of its original application of images, this work introduces a novel mechanism for connecting the input directly to prototypes learned by ProtoPNet, such that both the original sequence and the convolved input are used in decision making. In making use of the raw input, rather than fully relying on an incomprehensible convolved output, the decisions of this model are more interpretable to humans.
In this paper, we will first describe the dataset, data processing, the CNN, and the ProtoPNet in the Methods section. This section will explain the novel aspect of the raw input comparison (the skip connection), and the application of the ProtoPNet in the new domain of eDNA. In the Results section, we will convey our outcomes in terms of both quantitative metrics and visualizations. We will also show two key hyperparameters in our model, and how they affected performance. In the Discussion section, we will reflect on our results, compare this work to other work, and mention future possibilities of research.
Methods
In this section we describe the dataset and our preprocessing methods, and then show how we constructed a ProtoPNet for classifying eDNA sequences. We also briefly explain the ProtoPNet itself.
Dataset and preprocessing
The dataset used in this work was introduced by Flück et al.4. It consists of 12S ribosomal fish DNA samples from French Guiana in South America, collected from the Maroni and Oyapock rivers. This area holds 368 species of freshwater fish. The samples were collected from 200 different sites between 2014 and 2020. The sequences comprise an average of 64 bases. We mimicked the data preprocessing steps of Flück et al. in order to make our results directly comparable to theirs. We used data with the tag, primer, and their reverse complements removed. Additional details pertaining to the collection and processing of the dataset are presented in the paper from Flück et al.4.
Offline preprocessing occurred before any model was run. First, we removed any sequence whose species had less than two sequences in the dataset. This operation eliminated 212 species and 30% of all of the sequences in the dataset. This resulted in an average of 3.02 sequences per species (with a standard deviation of 4.36), making it easier to split the data into training and test sets.
We used the same training and test sets as Flück et al.4, who reserved 70% of the data for training and reserved 30% for testing, stratified based on species. For the ProtoPNet, we used a static validation set. For the base CNNs, we added fivefold cross validation to the training procedure. Because many species had fewer than 5 sequences in the training partition, there was no clear way to partition the training set into five folds. We addressed this by oversampling the entire dataset (except for the test set), before splitting it into folds, such that there was at least one instance of each class to allocate to each fold. To perform oversampling, we first found the class that had the most sequences—for example, in one fold, the class with the greatest number of sequences contained eight sequences. Then, for each species, we duplicated randomly chosen sequences from the species until that species had eight sequences in total. This made the training and validation datasets perfectly balanced for each class. To get genuine test results, we did not artificially add or remove any sequences to the test set like we did with the training set. As a result, the test set is not balanced. We report all results using performance on the test set.
We also performed online data augmentation during training. Upon loading each training sequence, 0–2 random nucleotide bases were inserted at random positions, and 0–2 random nucleotide bases were removed. There was also a 5% mutation rate, meaning that every base had a 5% chance of being switched to one of the other three base pairs. We also explored other training and testing noise levels, as discussed in the Metrics subsection of the Results section.
To provide consistent inputs to the network, each sequence was either truncated or padded to the same length. Considering the distribution of the number of bases in the sequences, we tried a variety of lengths ranging from 60 to 70. No value in this range showed superior performance, so we used a length of 70 throughout our experiments. Truncation was performed by removing bases from the end of the sequence, and padding was performed by adding ‘N’ characters.
Like the ‘N’ character, not every character in a sequence was a member of {A,T,G,C}. Errors naturally occur during the eDNA collection process, such that we may be unsure about what base is located at a particular position. Sometimes, for example, we may know that the base is either ‘A’ or ‘T’ (since we know it is not ‘G’ or ‘C’). These uncertainties are encoded as different characters. If we knew that the base at some position was either ‘A’ or ‘C’, then we would put an ‘M’ at that position. If the base could be any of the four bases, we would put an ‘N’. The full list of encodings is called the IUPAC ambiguity codes.
CNNs, which have been successful in working with images, were used in this situation by reframing the DNA sequences as one-dimensional “pictures” with four channels, as shown in Fig. 1. Each of the four channels corresponded to one of the four bases. Each base was turned into a four-dimensional one-hot vector, where the first channel (index 0) represented ‘A’, the second channel (index 1) ‘T’, the third channel (index 2) ‘C’, and the fourth channel (index 3) ‘G’. This turned each DNA sequence into an array of 4 channels and length 70. We encoded ambiguities as the average of the one-hot vectors for each possible nucleotide. For example, H (indicating the base is either ‘A’ or ‘C’ or ‘T’) would turn into [1/3, 1/3, 1/3, 0]. Taking these steps transformed the DNA sequence into an image-like input that was digestible by a CNN.
To summarize, after offline preprocessing is finished (removal of species with fewer than two sequences and oversampling), the training and evaluation begins. As each individual sequence is fetched, it is preprocessed with online augmentation (insertions, deletions, mutation, and encoding). Then, the array is fed to the CNN.
Developing the ProtoPNet
The Prototypical Part Network (ProtoPNet), introduced by Chen et al., is a deep learning architecture designed to make interpretable predictions with explanations that have true fidelity15. Unlike black-box models, a ProtoPNet learns and uses prototypes—representative examples of each class—to classify data. This approach provides interpretability by directly linking model decisions to recognizable features in the data, making it easier to understand why the model makes its predictions.
The ProtoPNet developed for this application consists of three primary components: a backbone \(f:{\mathbb{R}}^{4\times {l}_{input}}\to {\mathbb{R}}^{d\times l}\) that computes a latent representation of a given input sequence, a prototype layer \(g:{\mathbb{R}}^{d\times l}\to {\mathbb{R}}^{m}\) that compares a set of learned prototypes to this latent representation, and a final linear layer \(h:{\mathbb{R}}^{m}\to {\mathbb{R}}^{c}\) that maps from the similarity between the input and each prototype to a final classification. Here, 4 is the number of channels of an input eDNA sequence, \({l}_{input}\) the length of the input eDNA sequence, \(d\) the dimension of the latent representation extracted by the backbone, \(l\) the length of the latent representation, \(m\) the number of prototypes learned, and \(c\) the number of output classes. A prediction \(\widehat{y}\in {\mathbb{R}}^{c}\) is formed for each input sequence \(x\in {\mathbb{R}}^{4\times {l}_{input}}\) as \(\widehat{y}=h\circ g\circ f\left(x\right).\) We describe each of these components in the context of this application below. In our experiments, we used \({l}_{input}=70,d=512,l=35,m=468,\) and \(c=156.\)
Backbone
At the core of the ProtoPNet is a backbone network \(f\) that condenses input data into a compact latent space. Since our application involves sequential data, we selected a 1D convolutional neural network (CNN) with Leaky ReLU activations as the backbone, after evaluating nearly 25,000 hyperparameter and architecture combinations to find optimal performance in classifying species. The final selected architecture consisted of a single 1D convolutional layer with Leaky ReLU activations, followed by a max-pooling of size 2 and stride 2.
For a given input sequence \(x\in {\mathbb{R}}^{4\times {l}_{input}}\), let \({x}^{\left(a\right)}\in {\mathbb{R}}^{4}\) denote the input vector at position \(a\) (\(a=1, \dots , {l}_{input}\)). Let \(z=f\left(x\right)\) denote the latent representation of input \(x\) produced by \(f\), and let \({z}^{\left(a\right)}\in {\mathbb{R}}^{d}\) denotes the latent vector at position \(a\) of \(z\) (\(a=1, \dots , l\)). As a result of the max-pooling in the CNN backbone, every position \({z}^{\left(a\right)}\) in the latent representation produced by \(f\) corresponds to two input positions \({x}^{\left(2a-1\right)}\) and \({x}^{\left(2a\right)}\). Once trained, this CNN backbone served as the foundation for building the ProtoPNet architecture, providing a condensed representation of inputs that facilitated prototype comparison.
Prototype layer
The prototype layer \(g\) computes how “similar” each of the \(m\) learned prototypes is to a given input sequence. In particular, \(g\) contains a set of prototypes \(\mathcal{P}=\{{P}_{j}{\}}_{j=1}^{m},\) where each prototype \({P}_{j}\in {\mathbb{R}}^{d\times {l}_{proto}}\) is a learnable sequence of \({l}_{proto}\) vectors in the latent space of the CNN. We denote the \(a\)-th position of a prototype \({P}_{j}\) as \({p}_{j}^{\left(a\right)}\in {\mathbb{R}}^{d}\) (\(a=1, \dots , {l}_{proto}\)). Intuitively, we interpret each prototype to represent a prototypical DNA subsequence of \(2{l}_{proto}\) bases, since each latent position corresponds to two bases in the input DNA sequence. In our experiments, we use \({l}_{proto}=5,\) which means each prototype represents a subsequence of 10 bases in the original input space.
Let \({z}_{a}^{stack}=stack\left({z}^{\left(a\right)},{z}^{\left(a+1\right)},\dots {z}^{\left(a+{l}_{proto}-1\right)}\right)\), where “stack” denotes the operation of stacking multiple vectors into a single vector, and let \({p}_{j}^{stack}=stack\left({p}_{j}^{\left(1\right)},{p}_{j}^{\left(2\right)},\dots ,{p}_{j}^{\left({l}_{proto}\right)}\right)\). Using a 1D convolution, we can calculate the cosine similarity at a given position between each prototype \({P}_{j}\) and an input \(z\) as \({s}_{j}^{\left(a\right)}=\frac{\langle {p}_{j}^{stack},{z}_{a}^{stack}\rangle }{{\Vert {p}_{j}^{stack}\Vert }_{2}{\Vert {z}_{a}^{stack}\Vert }_{2}}\). Taken over all prototypes and positions, we can combine these similarities into a single activation map \(S\in {\left[-\text{1,1}\right]}^{m\times \left(l-{l}_{proto}+1\right)}\). This map represents how similar each of the \(m\) prototypes is to each subsection of the input sequence, offering an additional layer of interpretability by showing where and how each prototype activates. We compute the maximum similarity to a prototype across locations as \({s}_{j}^{max}=\underset{a\in \{\text{1,2},\dots ,l-{l}_{\mathit{proto}}+1\}}{\text{max}}{s}_{j}^{\left(a\right)},\) and the output of the prototype layer \(g\) is then computed as \(g\left(z\right)=stack\left({s}_{1}^{max},{s}_{2}^{max},\dots ,{s}_{m}^{max}\right).\) Each prototype is assigned to correspond to a particular class, and encouraged through training and network construction to contribute to reasoning for that class. In our experiments, we used 3 prototypes per class. Since there are 156 classes, the total number of prototypes used by our ProtoPNet model is 468. As in the original ProtoPNet, each prototype is also constrained to be the latent subsequence of a training sequence from the same class. This ensures that every prototype can be visualized using the corresponding subsequence of a training instance.
Although the ProtoPNet is interpretable in the fact that it uses prototypes directly to produce predictions, it is still a “black box” in one critical area: the backbone. The convolutions in the backbone are not interpretable, which is problematic because prototypes are compared to the latent representation extracted by the CNN backbone – not the input itself. The usage of a CNN backbone is the only aspect that is holding the ProtoPNet back from being completely interpretable.
To alleviate this issue, we introduce a novel extension to ProtoPNet: the skip connection. Rather than comparing prototypes exclusively to the CNN’s representation of the input, we added a skip connection that includes the raw input sequence in prototype comparison, bypassing the backbone entirely. Comparing prototypes to the raw input is completely interpretable and does not utilize the CNN backbone.
However, as discussed in the Results section, we observed two conflicting phenomena. First, when we compare prototypes only to the raw input sequence, the overall network performs poorly due to overfitting. In contrast, when we compare prototypes only to the CNN’s representation of the input sequence, we found that prototypes made unintuitive comparisons. As such, we compute the similarity between a prototype and an input sequence as a weighted average of these two comparisons, where the weight is a hyperparameter. In the CNN implemented for this work, each latent position corresponds to two raw input positions, where each raw input position is represented using a four-dimensional vector along the channel axis. As such, we add eight channels to each prototype, which are compared to the concatenation of the two four-dimensional vectors directly from the input sequence. In particular, we learn an additional input space component \({Q}_{j}\in {\mathbb{R}}^{8\times {l}_{proto}}\) for each prototype \(j\). We then compute the weighted similarity to the \(j\)-th prototype at position \(a\) as:
where \({q}_{j}^{stack}\) is defined analogously to \({p}_{j}^{stack}\), \({x}_{a}^{stack}=stack\left({x}^{\left(a\right)},{x}^{\left(a+1\right)},\dots {x}^{\left(a+2{l}_{proto}-1\right)}\right)\). With this skip connection, the output of prototype layer \(g\) is \(g\left(z\right)=stack\left({s}_{1}^{{\prime}max}{s}_{2}^{{\prime}max},\dots ,{s}_{m}^{{\prime}max}\right)\), where \({s}_{j}^{{\prime}max}=\underset{a\in \{\text{1,2},\dots ,l-{l}_{\mathit{proto}}+1\}}{\text{max}}{s}_{j}^{{\prime}\left(a\right)}\) is the maximum weighted similarity to the \(j\)-th prototype across all positions. We refer to \(\kappa\) as the latent weight. We experimented with different latent weights, ranging from completely using the latent comparison (\(\kappa =1\)) to using only the raw input comparison (\(\kappa =0\)). This is illustrated in Supplementary Figure S1. The use of the latent weight \(\kappa\) reduces reliance on the uninterpretable latent output from the CNN backbone. The ProtoPNet architecture that incorporates this skip connection is shown in Fig. 2.
How the model makes a prediction using the skip connection. The skip connection is separate from the feature extraction, and contributes to learning intuitive prototypes. The output of the convolution and the stacked raw input are concatenated. This array is then compared to every single prototype. Since a single prototype is only of length 5 and this array is of length 35 due to pooling, the comparison step produces a similarity score (using cosine similarity) at 31 different positions within the array. The maximum of these scores is taken as the overall score for a given prototype. Then, each prototype’s score is fed into a single fully-connected linear layer with no bias, which produces a confidence output for each of the 156 classes. The class with the highest confidence becomes the model’s prediction.
Final linear layer
Following Chen et al.15, the weights in the final linear layer \(h\), which map prototype activations to class scores, are initialized with values of \(1\) or \(-0.5\). Weights connecting a prototype to its assigned class are set to \(1\), encouraging these prototypes to contribute positively, while all other weights are set to \(-0.5\). We chose to use three prototypes per class. This initialization strategy, combined with an \({L}_{1}\) penalty to push weights between prototypes and classes other than their assigned class toward zero, promotes a classification approach based on positive associations with each class’s prototypes (“this looks like a prototype from class A, so I predict class A”) rather than negative associations (“this does not look like a prototype from class A, so I predict class Z”).
Training
We trained our ProtoPNet by minimizing cross entropy and two additional loss functions: cluster loss and separation loss, as defined by Chen et al.15 and as adapted to our setting. Formally, we define cluster and separation loss as:
\({l}_{clst}=-\frac{1}{n}{\sum }_{i=1}^{n}\underset{j\in \{\text{1,2},\dots ,m\}:\mathit{class}\left(j\right)={y}_{i}}{\text{max}}{g}_{j}\left(f\left({x}_{i}\right)\right)\) and \({l}_{sep}=\frac{1}{n}{\sum }_{i=1}^{n}\underset{j\in \{\text{1,2},\dots ,m\}:\mathit{class}\left(j\right)\ne {y}_{i}}{\text{max}}{g}_{j}\left(f\left({x}_{i}\right)\right)\),
respectively, where \({x}_{i}\) denotes the i-th eDNA sequence in the training dataset and \({y}_{i}\) the corresponding class label, \(class\left(j\right)\) is the class associated with the \(j\)-th prototype, \({g}_{j}\left(\cdot \right)\) denotes the \(j\)-th output of \(g\) (i.e., \({g}_{j}\left(f\left(x\right)\right)={s}_{j}^{{\prime}max}\) for an input \(x\)), and \(n\) is the number of samples in the training dataset. Cluster loss ensures that at least one prototype closely represents each input, encouraging each class’s prototypes to form distinct clusters. Separation loss encourages samples of one class to remain distant from prototypes of other classes, refining each prototype’s distinctiveness.
In keeping with Chen et al.15, our training involved three key steps:
-
1.
Prototype Training: We train only the prototypes using stochastic gradient descent, freezing other parameters.
-
2.
Projection Step: Each prototype is set equal to the nearest training subsequence of the same class in the latent space, ensuring that prototypes directly represent specific input features.
-
3.
Final Layer Optimization: We adjust the weights in only the last layer to account for the newly aligned prototypes. Weights in the CNN backbone and the prototypes are frozen.
We repeated these steps iteratively, with adjustments made to jointly train both the convolutional layers and prototypes in later iterations. Importantly, we ended training after the final layer optimization (not after the prototype training) to preserve the proximity between learned prototypes and input representations of the same class, and to ensure that each prototype is tied to a training subsequence and can therefore be visualized by humans.
This training framework enhanced both classification accuracy and prototype quality, creating a model where each prototype is not only representative but also contributes meaningfully to the final predictions. By visually associating each prototype with an actual training input, ProtoPNet clarifies its decision-making process, allowing users to trace predictions back to specific, meaningful data features. For further technical details, we refer readers to Chen et al.15, where the foundational principles of ProtoPNet are elaborated in depth.
Our model took the input, which was of length 70, and compressed it to a latent length of 35. For details about the hyperparameters we found for our model, refer to Supplementary Table S2. The hyperparameters were found by splitting the training dataset into a smaller training set and a validation set, training ProtoPNet models with various hyperparameter settings on the smaller training set, and evaluating the models on the validation set. The hyperparameters from the best performing model on the validation set are the hyperparameters we chose for training the final model on the entire training set. In particular, based on experiments conducted on a validation set, we set the number of prototypes per class to three. Keeping the number of prototypes low helped minimize the risk of overfitting.
Results
In this section we will compare the results of our CNN and ProtoPNet with each other, with a set of baselines, and with previous work. We will study the impact of latent weight and prototype length, and then visualize learned prototypes and their respective subsequences.
Metrics
To validate the use of deep learning for this application, we compared our results to a suite of baseline ML models. We evaluated k-nearest neighbors, naïve bayes, support vector machine, logistic regression, decision tree, random forest, XGBoost, and AdaBoost classifiers. The data fed to these models was the same data fed to the CNN models. Sequences were truncated or padded to 70 bases for consistency with the neural networks, and oversampling was performed to make the class distribution uniform. These baseline models were trained on a tabular dataset constructed with a k-mer representation. K-mer representations are the count of the number of times any sequence of length k occurs in a given sequence. For example, for k = 2, the possible k-mers are: [AA AT AC AG TA TT TC TG CA CT CC CG GA GT GC GG]. The frequency of each of these in a given sequence would form the input vector to the above classifiers—for example, the 2-mer representation of AAC (if we use the order from above) would be [1 0 1 0 0 … 0]. We used k-mers of length 3, 5, and 8, and trained and evaluated each baseline with all three of these datasets. We chose these lengths since k-mers shorter than 3 would not encode useful information, while k-mers greater than 8 would require more computational resources. Intermediate k-mer lengths (4, 6, and 7) were not included, because based on our preliminary investigation using logistic regression, using these k-mer lengths did not significantly contribute to improving the model’s performance relative to the selected lengths. Since including ambiguity codes as their own features made the number of features much higher and typically decreased accuracy, we randomly assigned the ambiguity codes to be one of the possible nucleotide bases. For example, ‘N’ was turned into a random pick from {A,T,C,G}. The results of the most accurate model from each model type are presented in Table 1. The best baseline test result, with no noise added to the test set, was achieved by logistic regression trained on k-mers of length 8. The full tables of results, which show all of the models and hyperparameters we evaluated, are available in the GitHub repository.
In the wild, a small number of errors naturally occur in the PCR amplification and sequencing process, resulting in extra variation between sequences within a species. Given that the reference databases already contain sequences obtained through this process, they inherently include these natural errors and variations. To further simulate challenging real-world conditions and ensure robustness, we tested different levels of added noise for the training and test sets. Discovering an appropriate amount of noise to add to the training set helped prevent overfitting, making the models better generalize to new data. Following Flück et al.4 and Busia et al.16, for training we used a 5% mutation rate, added between 0 and 2 bases, and removed between 0 and 2 bases for each sequence. For testing, we used a 2% mutation rate and a single insertion and deletion for each sequence. We refer to this as noise level 1. We also added noise level 2, which doubled the noise level 1 with a 10% mutation rate, between 0 and 4 insertions, and between 0 and 4 deletions for the training set. The test set noise was also doubled at this level, with a 4% mutation rate and 2 insertions and 2 deletions per sequence. We also included evaluations at noise level 0, where no mutations, insertions, or deletions were performed on any training or test sequences.
For the CNN, we saw that deeper models were not only less interpretable but less accurate, as shown in Fig. 3. For the skip connection, our validation data showed us that a latent weight of 0.7 performed almost equally as well as a latent weight of 1, and that weights between 0.7 and 1 actually performed better than a latent weight of 1. Given that lower latent weight is more interpretable (discussed more below), we chose a latent weight of 0.7. The optimal hyperparameters we found for the CNN and ProtoPNet are available in Supplementary Tables S1 and S2, respectively.
Test accuracies for our updated CNN models trained on noise level 1 and tested on noise level 0. This illustrates that a single-layer CNN achieved accuracy that was similar to CNNs with two, three, and four layers. Deeper CNNs required more computation and were less interpretable, which is why we chose a single-layer CNN. Error bars are standard deviation for n = 5 runs. The output dimension of every layer is 512.
We also tested transformer models with 1, 2, and 3 multi-headed self-attention layers to assess whether attention-based models could serve as a strong backbone. Specifically, we trained and evaluated these transformers using the same dataset as our CNN classifiers. As shown in Fig. 3, the transformers did not outperform the CNNs in terms of test accuracy, with deeper transformers performing much worse than the 1-layer transformer and the CNNs. This is likely due to the greater complexity of transformers, which tend to overfit more severely compared to CNNs. This may also reflect the nature of eDNA classification, where short- to medium-term context may be more useful for species identification, while long-term dependencies have less impact. CNNs are better suited for capturing these shorter-range patterns, making them more effective for this task compared to transformers, which excel at modeling long-range interactions but may not offer an advantage in this context. Therefore, in this work, we used a CNN backbone for creating our ProtoPNet.
While the baseline results are presented in Table 1, the neural network results are presented in Table 2. Our models improve upon the previous work from Flück et al.4, and we also present high baseline accuracies using k-mer lengths of 5 and 8. When trained with noise but tested without noise, our ProtoPNet, which was built on top of our CNN, not only adds interpretability but also improves on the base CNN’s performance. The fact that our ProtoPNet not only matched but even sometimes surpassed the accuracy of the black-box CNN on which it is based demonstrates that adding interpretability does not come at the expense of accuracy. We found that every one of the baseline models achieved higher accuracy when trained on data with no added noise than when trained on data with high added noise. In contrast to the simpler baseline models, the more complex CNN and ProtoPNet performed better when trained with noise, rather than when trained without noise. In conjunction with the findings from Fig. 3, this shows that complicated models can overfit and perform more poorly without adding noise to augment the data. For the CNN and ProtoPNet, adding noise aids in reducing this overfitting and improves performance, meaning that these models are reliable options for situations where sequencing errors are common.
Hyperparameter analysis
It is possible to change a single parameter in the ProtoPNet while freezing the rest and observing the change in results. This type of study was performed for all the hyperparameters, but this section shows two in particular: prototype length and latent weight. When we were first developing the ProtoPNet, we found that the optimal prototype length was close to the length of the latent representation. However, as we modified the other hyperparameters and achieved higher accuracies, we found that the optimal prototype length became much shorter. For the final set of hyperparameters based on validation data, the best prototype length was 5. Figure 4 shows that for the test data, the optimal prototype length was 3.
Test accuracies of ProtoPNet models with varying prototype lengths, at 0.7 latent weight. The best prototype lengths were short. The test results here show that the best prototype length would be 3, though we chose a prototype length of 5 based on the validation results. The ProtoPNet models here were trained on noise level 1 and tested on noise level 0. Note that the y-axis ranges from 84 to 98% accuracy for purposes of comparison. Error bars are standard deviation for n = 5 runs. The fact that the ideal length based on the validation and the test set were similar shows that the validation set had good generalizability.
A primary novel contribution of this work is comparing the prototypes not only to the latent representation, but also to the raw input. The combination of both aspects is useful because each position of the latent representation captures context around the two corresponding bases, while the raw input does not consider such context. A latent weight of 0 makes prototype comparisons completely comprehensible, as the prediction is only based on the comparison of the prototypes to the raw input. However, it sacrifices performance since this direct comparison cannot capture any context around a given subsequence. A latent weight of 1 makes it impossible for a layperson to readily understand why a decision is made. This is because a model with a latent weight of 1 compares the prototypes exclusively with the incomprehensible latent representation of the input produced by the CNN backbone. Unexpectedly, the best accuracies were not produced by models that used a latent weight of 1; the best latent weight was 0.7 on the validation set and 0.8 on the test set. A model using a latent weight as low as 0.5 achieved higher accuracy than a model using a latent weight of 1. As shown in Fig. 5, decreasing reliance on convolutional layers not only increases interpretability, but increases accuracy as long as the latent weight does not fall below 0.5.
Test accuracies from ProtoPNet models trained at different latent weights. These models used prototype length 5, and were trained on noise level 1 and tested on noise level 0. This shows that slightly lowering the reliance on the convolved output actually increases accuracy. For latent weights lower than 0.5, the higher the reliance on the convolved input, the better the test accuracy. However, for latent weights above 0.5, the test accuracies were within 1% of each other. Choosing a lower latent weight makes decisions more interpretable, so we wanted to choose the lowest latent weight without sacrificing significant accuracy. We selected a latent weight of 0.7 based on the validation data, but the test results here show that the latent weight could have been lowered to as low as 0.5 without a significant penalty to accuracy. Note that the y-axis spans from 88 to 97% accuracy for purposes of comparison. Error bars are standard deviation for n = 5 runs.
Visualizations
Visualizing the prototypes learned in the ProtoPNet is important, as it allows humans to extract meaningful insights from prototypes, identify unhelpful prototypes that are based on spurious correlations, and see why the model makes the predictions it does. We will first show how the prototypes are used to make a prediction in Fig. 6. Given a randomly selected sequence from our test set, Fig. 6 shows why the model predicts that the sequence belongs to the species Gymnotus anguillaris. Rows a—c show the three prototypes for Gymnotus anguillaris. Each of these prototypes is compared against the sequence (as well as the convolved sequence, as determined by the latent weight). This produces three comparison scores, each of which is multiplied by its respective weight in the classification layer. The results are summed for each class, and the class with the highest sum is chosen as the prediction. In rows d—f we can see the prototypes for the species Japigny kirschbaum. The sum of the comparison scores for its three prototypes multiplied by their last layer weights is lower than that for Gymnotus anguillaris, which is why Japigny kirschbaum is not the predicted class.
The reasoning process for a test sequence; how prototypes produce a comparison score and contribute to the weighted sum to create a score for each class. There are three prototypes per class. The prototypes in rows a-c are from the class Gymnotus anguillaris and contribute to the score for that class, and the three prototypes from rows d-f are from class Japigny kirschbaum and contribute to the score for that class. Since the score for Gymnotus anguillaris is the highest of any class, the model predicts that class as the species.
To better understand our prototypes, we can run a sequence through the model and look at all of the most activated prototypes, regardless of the class to which they contribute. In Fig. 7, we can see that the two most activated prototypes for a given sequence of Cyphocharax gouldingi have near maximal similarity values. These prototypes have exact matches in the original input sequence, as shown in the figure.Since the two most activated prototypes are from the correct class, they are well-formed and meaningful. Similarly, the matched subsequence of the third-ranked prototype, though from an incorrect class, appears visually identical to the prototype. However, it has an activation lower than the maximum possible value (which is 1) because the context around this subsequence is a poorer match for the prototype than the first two cases, and this comparison includes a non-zero latent weight. If the latent weight had been 0, all three maximum activations would have been 1.00. As we look at prototypes with lower maximum activations, the differences between the prototypes and the matched subsequences become larger.
The most activated prototypes from across all classes for a given test sequence. This example shows that the class has two well-formed prototypes, since they both activate nearly perfectly and are the most activated prototypes out of all of the prototypes. The third-most activated prototype is from a different class. Although it visually matches the raw subsequence perfectly, it achieves a slightly lower maximum activation than the other two since the unseen latent component reduces its activation.
Visualization is also useful for comparing the interpretability resulting from different latent weights. In Fig. 8, we examine the three test sequences on which a given prototype activates most highly. Note that the prototypes for different latent weights differ because the prototypes for each latent weight come from different models. Figure 8 shows that, with a latent weight of 0, each prototype matched perfectly to its target species, but also matched perfectly to several other species. This means that the model did a poor job of learning prototypes that were discriminative between classes, likely because the model could not consider the context around these subsequences. This explains the reason why models with lower latent weights achieve lower accuracies in Fig. 4. On the other hand, with a latent weight of 1, we see more base-pair mismatches between each prototype and its most similar test subsequences. This is because the model is not obligated to make any direct comparison between the input and prototype base pairs when the latent weight is 1. An intermediate latent weight generally provides better alignment between each prototype and its most similar test subsequences than a latent weight of 1.
The three closest test subsequences from any class to a given prototype sequence. X represents a base mismatch between the visualized prototype and the raw test sequence. As shown in the figure, at a latent weight of 0, each prototype matches perfectly with the closest test subsequences, but those test subsequences often belong to incorrect classes. On the other hand, at a higher latent weight, there are more base-pair mismatches between a prototype and its most similar test subsequences, but those test subsequences are more likely from the same class as the corresponding prototype. This also explains why higher latent weights produce higher accuracies, since they learn prototypes that better capture the most discriminative features of their assigned classes.
Discussion
In this section, we reflect on the differences between DNA and image classification and explain why the novel skip connection in this paper benefits interpretability. We discuss limitations of our model, compare our approach to previous work, and talk about challenges specific to our dataset. Finally, we mention areas of possible future work and summarize our results.
This work faced interesting challenges in terms of visualization and interpretability within the domain of DNA classification. In the original paper, ProtoPNet was used as an image classifier for birds. Prototypes were easily visualizable by any observer, as they often pictured an orange beak, a pair of skinny legs, or a distinctive wing pattern. In the domain of DNA, our prototypes can still be visualized, but their information cannot be assessed as easily. While it is easy for a layman to intuitively recognize distinctive parts of images of birds, that is not the case for DNA. Thus, by learning prototypes, our model actually generates a form of new knowledge in discovering the most distinctive parts of DNA. While these prototypes may be more difficult to understand than image-based prototypes, this information could be used for in-depth research on DNA in novel applications.
This work also introduces a novel mechanism to connect the raw input directly to latent prototypes, addressing the key reason why the ProtoPNet is not entirely interpretable. The benefit of using latent representations is that a CNN can learn to be invariant to variations that are common within a species. For example, if a mutation in the k-th base pair is common within a species, a CNN may learn that any nucleotide at that position is equally acceptable and should not impact the overall classification or prediction. Matching using raw input sequences alone does not have this capacity; it would produce a lower similarity score for individuals with some mutated base pairs, and would produce overly specific representations that fail to generalize across individuals within the same species. This leads to overfitting because the model learns to rely on exact sequence matches, including rare or insignificant variations, rather than capturing broader, biologically relevant patterns. The downside of using the latent representation is that any use of a multi-layer neural network poses a challenge to interpretability since it can perform complex non-linear transformations of an input. By providing a way of relying less on the latent representation of the input, we put humans in control of the balance between interpretability and accuracy. For our application, we found that the relationship was not linear; decreasing the latent weight by a small amount actually increased the accuracy. Based on evaluation on our validation data, we found that we could reduce the latent weight to as low as 0.7 and still achieve accuracy similar to results when using a latent weight of 1. Test data showed that we could have lowered this number even further. In another domain, it could be possible to bring the latent weight even lower while achieving the same accuracy. Adding this flexibility made it so that our framework is applicable to a variety of applications in which both model interpretability and accuracy can be maximized.
Using our model for species analysis has several limitations. While the eDNA metabarcoding process itself is a sensitive and efficient method for detecting and assessing biodiversity, it has limitations when used alone for quantifying absolute abundance. Environmental factors can affect eDNA degradation rates, and eDNA can be transported in different ways, making time and location information less reliable. Among other challenges, it also requires a reference database to exist (for comparison or for model training), which may have errors or be incomplete17. Another limitation is that our model cannot be used to detect the presence of species that are not already in the training set (i.e., the unseen species). Recent work has addressed this issue with various approaches. For example, Zito et al.18 used a non-parametric Bayesian approach to detecting new species at each taxonomic level from DNA barcodes. Impiö and Raitoharju19proposed a hybrid approach that integrates DNA barcoding and image-based monitoring to detect outlier species. Nanni et. al20. proposed an ensemble approach that integrates neural networks with support vector machines (SVM), which can assign known samples to specific species and grouping unknown ones at the genus level using both images and DNA barcodes. Using a similar technique, Nanni et al.21 developed a hybrid neural network-SVM model for identifying known insects while grouping unknown insects at the genus level. In future work, we plan to incorporate the ability to detect novel species into our model.
We used several sequences from the NCBI GenBank, a database distinct from our dataset, to further validate our learned prototypes. Since environmental factors can lead to degradation in eDNA readings, DNA drawn directly from the tissue of target species is considered the gold standard for confirming the biological validity of DNA classification models. We found that prototypes from our model produced strong Smith-Waterman alignment scores across three rare species with samples in the NCBI GenBank – Guianacara geayi (accession LC069581.1), Cichla ocellaris (accession LC069581.1), and Apteronotus albifrons (accession U33639.1). In particular, for each of these samples, at least one prototype of the correct class produced an alignment score greater than the average alignment of prototypes from other species. This validates that our model – trained using eDNA – has learned biologically valid prototypes that align well with the DNA drawn directly from individuals of the target species.
The success of our model for DNA classification came from a shallow architecture and small prototypes. Both our base model and the model developed by Flück et al.4 used a shallow depth of one or two convolutional layers. Unlike Flück et al., we used only one fully-connected layer, rather than two or three. These findings suggest that deep, complex models are not necessary for classifying DNA sequences. The idea of a small part of the DNA being able to classify the entire sequence has been explored before. Busia et al.16 experimented with different read lengths, meaning that they tried to classify smaller sections of sequences, instead of looking at the entire sequences. They found that classifying sequences of length 50 was just as effective as classifying sections of length 250. Their findings support the idea that small sections of the DNA hold the key to differentiating species.
In our experiments, we adjusted the prototype length to prevent both overfitting and underfitting. We found that a model with shorter prototypes tend to perform better, as shown in Fig. 5. This is because increasing the prototype length could lead to overfitting, as the model is compelled to capture more details from the specific training sequence the prototype is derived from, even if those details are biologically irrelevant. While longer prototypes may improve precision by incorporating more information, they also tend to reduce recall by becoming too specific and failing to generalize across variations. This tradeoff between precision and recall likely contributes to the observed reduction in test accuracy with longer prototypes. On the other hand, prototypes must still be long enough to effectively discriminate between classes and capture their unique characteristics.
One distinctive challenge we encountered was the small dataset we used to train the model—there were only 1.86 sequences per class on average, before processing. Although Dully et al.22 used a random forest instead of a neural network, they also experimented with datasets with few sequences per class. They found that their model achieved a similar performance when trained on the entire dataset (more than 12,500 sequences per species) as when trained on the challenging dataset (with only 50 sequences per species). They also found that accuracy did not change when the dataset was balanced or unbalanced. Similarly, they saw that the number of species being classified did not affect the accuracy. This is starkly different from most machine learning applications, where more classes, fewer data points, and an unbalanced dataset makes for a more difficult problem. Our work contributes to the theory that these supposedly difficult datasets are tractable for eDNA classification. To build a dataset, one could use synthetic gene fragments. Kronenberger et al.23 used solid-phase DNA synthesis and DNA assembly to create artificial DNA sequences, which improved accuracy. Using synthetic data could avoid throwing away much of a dataset when enforcing a minimum number of examples per class.
Hase et al.24 tackled the problem of predicting the taxonomy of images, in addition to predicting the class alone. Similarly, Busia et al.16 was able to directly predict the genus, family, and order, in addition to the species. Although Flück et al.4 found difficulty doing that with this dataset, there are many methods that could be used to achieve that goal other than extrapolating that information from the species, such as separating out each classification into its own model.
The paper to which we compare our results, Flück et al.4, included training and evaluation on uncleaned data—sequences with tags and primers (base pair sequences added during the sequencing process) still attached, and with reverse complements not added. Coming out of the sequencer, DNA sequences will have tags and primers, and may be forward or backward reads. In this work, the tag is 17 bases long, and the primer is 20 bases long. The format of raw sequences is < tag > < forward primer > < original sequence > < reverse complement of reverse primer > < reversed tag >. Because of the presence of these extra bases, we can preprocess eDNA data to remove everything but the actual relevant sequence. Flück et al. tried creating a model using raw data without preprocessing, with the idea that the model would learn to ignore all but the relevant bases in the sequence, and preprocessing would not be necessary. They achieved 2% lower accuracy for raw data than for preprocessed data. Although this accuracy drop is small, simple preprocessing (removing the tags and primers, and adding reverse complements) takes a negligible amount of time. For this reason, we trained and evaluated only on preprocessed data in order to achieve the highest possible accuracy. Additionally, Flück et al. focused on minimizing false positives, whereas our approach did not prioritize this aspect. In particular, they incorporated a 0.9 binarization threshold into their approach, where the model would refrain from making predictions for any sequence about which it was less than 90% confident. The choice to use or not use a binarization threshold would depend on whether a model is being used to search for rare and invasive species, or if it is being used to classify known species with high confidence and accuracy.
There are many variations of the ProtoPNet that could be used to extend this work. Wang et al.25 created the Transparent Embedding Space Network (TesNet), which has a standardized latent space in which prototypes are basis vectors that are close to orthogonal and exist within a hypersphere. Another avenue is to use the ideas of Nauta et al.26 and replace the fully-connected layer with a decision tree, where each node in the tree is associated with a particular prototype, and the classes are the leaf nodes. This change creates a global classifier that shows explanations for the model as a whole. Rymarczyk et al.27 allowed prototypes to be shared among multiple classes in ProtoPShare, and Rymarczyk et al.28 also integrated this sharing process into the training stage in ProtoPool. Prototype visualization could be improved with visual-attribute explanations as performed by Nauta et al.29, or by citing multiple training inputs as performed by Ma et al.30.
Very recently, advances in large language models (LLMs) have spurred interest in their application to DNA sequence classification. LLMs, typically used in natural language processing tasks, have been adapted for genomic sequences by treating DNA as a form of “language.” In particular, several models inspired by LLMs31,32,33 have been explored for DNA sequence classification tasks, although the application of LLMs or gLMs (genomic language models)34,35 remains limited. Many focus on synthetic sequence generations36,37,38, and are trained on entire genomes to infer biological functions39,40, instead of being trained on short metabarcoding sequences for taxonomic classification as was done in this study. While LLMs trained on DNA sequences show promise, their performance has been mixed, particularly when they are not fine-tuned for domain-specific applications32. Following the work by Mourad and Batut33, we fine-tuned a pre-trained genetic LLM by adding a linear classification head over its hidden states to adapt it for our species classification task. With this setup, we observed a maximum accuracy of 75.4% when both training and test data had no noise (level 0), with lower accuracies in all other noise settings. This result highlights the limitation of using LLMs for tasks with relatively small datasets, as is the case in our study, and suggests that LLMs require extensive fine-tuning on larger datasets in order to outperform traditional methods.
To summarize, we were first able to make a CNN that was 94.48% accurate on the test set, surpassing the accuracy of previous work. We then used this network to produce a latent space for a ProtoPNet, creating the first adaptation of the ProtoPNet to DNA sequence data. We introduced a novel method of incorporating the raw input in order to create more intuitive prototypes and predictions, rather than a traditional ProtoPNet which reasons only using latent representations. This interpretable model performed better than the non-interpretable models, achieving over 95% test accuracy when trained at noise level 1 and tested with no noise. This aids in dispelling the notion that interpretability comes at the price of accuracy. Unlike other work previously done on eDNA, this model explicitly learns prototypes, which represent short sequences of nucleotide bases that characterize each species. Prototypes can then be visualized to evaluate model performance and glean insights. Additionally, we performed this work on a small, challenging dataset of fish DNA sequences from a diverse ecosystem. In the big picture, our work is beneficial for conservation efforts through ecosystem monitoring, as well as furthering eDNA research by improving the speed and insights of species classification.
Data availability
The data used in this paper was obtained from Flück et al.4, who assembled the dataset based on sequences collected in other works42,43,44,45,46,47,48. Specifically, partial data used in this study can be downloaded from https://datadryad.org/downloads/file_stream/13860 and https://datadryad.org/downloads/file_stream/3695374. Complete data can be obtained by request from the corresponding authors of Flück et al.4, Benjamin Flück (benjamin.flueck@usys.ethz.ch) and Loic Pellissier (loic.pellissier@usys.ethz.ch). This data is covered under Creative Commons 4.0.
Code availability
The code produced in this study for model training, analysis, and visualization, as well as the logs of intermediate and final results, is available in our eDNA GitHub repository, https://github.com/SamWaggoner/eDNA.
References
Kress, W. J. & Erickson, D. L. DNA barcodes: Methods and protocols. Methods Mol. Biol. 858, 3–8 (2012).
Fernandez, I. J., Birkel, S., Schmitt, C. V., Simonson, J., Lyon, B., Pershing, A., Stancioff, E., Jacobson, G. L. & Mayewski, P. Maine’s Climate Future: Update. (2020).
Ruppert, K., Kline, R. & Rahman, M. S. Past, present, and future perspectives of environmental DNA (eDNA) metabarcoding: A systematic review in methods, monitoring, and applications of global eDNA. Glob. Ecol. Conserv. 17, e00547 (2019).
Flück, B. et al. Applying convolutional neural networks to speed up environmental DNA annotation in a highly diverse ecosystem. Sci. Rep. 12, 10247 (2022).
Smilkov, D., Thorat, N., Kim, B., Viégas, F. & Wattenberg, M. SmoothGrad: removing noise by adding noise. Preprint at http://arxiv.org/abs/1706.03825 (2017).
Selvaraju, R. R. et al. Grad-CAM: Visual Explanations from Deep Networks via Gradient-based Localization. Int. J. Comput. Vis. 128, 336–359 (2020).
Chattopadhay, A., Sarkar, A., Howlader, P. & Balasubramanian, V. N. Grad-CAM++: Generalized Gradient-Based Visual Explanations for Deep Convolutional Networks. in WACV 839–847. https://doi.org/10.1109/WACV.2018.00097 (2018).
Nguyen, A., Dosovitskiy, A., Yosinski, J., Brox, T. & Clune, J. Synthesizing the preferred inputs for neurons in neural networks via deep generator networks. in NeurIPS 3395–3403 (Curran Associates Inc., 2016).
Yoshimura, N., Maekawa, T. & Hara, T. Toward Understanding Acceleration-based Activity Recognition Neural Networks with Activation Maximization. in IJCNN 1–8 IEEE. https://doi.org/10.1109/IJCNN52387.2021.9533888, (2021).
Ribeiro, M. T., Singh, S. & Guestrin, C. ‘Why Should I Trust You?’: Explaining the Predictions of Any Classifier. in SIGKDD 1135–1144 (ACM). https://doi.org/10.1145/2939672.2939778 (2016).
Lundberg, S. M. & Lee, S.-I. A unified approach to interpreting model predictions. in NeurIPS 4768–4777 (Curran Associates Inc., 2017).
Fong, R., Patrick, M. & Vedaldi, A. Understanding Deep Networks via Extremal Perturbations and Smooth Masks. Preprint at http://arxiv.org/abs/1910.08485 (2019)
Kim, B., Wattenberg, M., Gilmer, J., Cai, C., Wexler, J. & Viegas, F. Interpretability Beyond Feature Attribution: Quantitative Testing with Concept Activation Vectors (TCAV). in ICML 2668–2677 (PMLR). at https://proceedings.mlr.press/v80/kim18d.html (2018)
Ali, S. et al. Explainable Artificial Intelligence (XAI): What we know and what is left to attain Trustworthy Artificial Intelligence. Inform. Fusion 99, 101805 (2023).
Chen, C. Li, O., Tao, C., Barnett, A. J., Su, J. & Rudin, C. This Looks Like That: Deep Learning for Interpretable Image Recognition. Advances in Neural Information Processing Systems, 32 (NeurIPS, 2019).
Busia, A., Dahl, G.E., Fannjiang, C., Alexander, D.H., Dorfman, E., Poplin, R., McLean, C.Y., Chang, P.C. & DePristo, M A deep learning approach to pattern recognition for short DNA sequences. 353474 Preprint at https://doi.org/10.1101/353474 (2019).
Beng, K. C. & Corlett, R. T. Applications of environmental DNA (eDNA) in ecology and conservation: Opportunities, challenges and prospects. Biodivers. Conserv. 29, 2089–2121 (2020).
Zito, A., Rigon, T. & Dunson, D. B. Inferring taxonomic placement from DNA barcoding aiding in discovery of new taxa. Methods Ecol. Evol. 14, 529–542 (2023).
Impiö, M. & Raitoharju, J. Improving Taxonomic Image-based Out-of-distribution Detection With DNA Barcodes. in 2024 EUSIPCO 1272–1276. https://doi.org/10.23919/EUSIPCO63174.2024.10715139. (2024).
Nanni, L., Gobbi, M. D., Junior, R. D. A. M. & Fusaro, D. Advancing Taxonomy with Machine Learning: A Hybrid Ensemble for Species and Genus Classification. Algorithms 18, 105 (2025).
Nanni, L. et al. Insect identification by combining different neural networks. Expert Syst. Appl. 273, 126935 (2025).
Dully, V., Wilding, T. A., Mühlhaus, T. & Stoeck, T. Identifying the minimum amplicon sequence depth to adequately predict classes in eDNA-based marine biomonitoring using supervised machine learning. Comput. Struct. Biotechnol. J. 19, 2256–2268 (2021).
Kronenberger, J. A. et al. eDNAssay: A machine learning tool that accurately predicts qPCR cross-amplification. Mol. Ecol. Resour. 22, 2994–3005 (2022).
Hase, P., Chen, C., Li, O. & Rudin, C. Interpretable Image Recognition with Hierarchical Prototypes. HCOMP 7, 32–40 (2019).
Wang, J., Liu, H., Wang, X. & Jing, L. Interpretable Image Recognition by Constructing Transparent Embedding Space. in ICCV 875–884 (IEEE). https://doi.org/10.1109/ICCV48922.2021.00093 (2021).
Nauta, M., Van Bree, R. & Seifert, C. Neural Prototype Trees for Interpretable Fine-grained Image Recognition. in CVPR 14928–14938 (IEEE, 2021). https://doi.org/10.1109/CVPR46437.2021.01469 (2021)
Rymarczyk, D., Struski, Ł., Tabor, J. & Zieliński, B. ProtoPShare: Prototypical Parts Sharing for Similarity Discovery in Interpretable Image Classification. in SIGKDD 1420–1430 (ACM, 2021). https://doi.org/10.1145/3447548.3467245 (2021).
Rymarczyk, D., Struski, Ł., Górszczak, M., Lewandowska, K., Tabor, J. & Zieliński, B. Interpretable Image Classification with Differentiable Prototypes Assignment. in ECCV 351–368 (Springer-Verlag, 2022). https://doi.org/10.1007/978-3-031-19775-8_21 (2021).
Nauta, M., Jutte, A., Provoost, J. & Seifert, C. This Looks Like That, Because... Explaining Prototypes for Interpretable Image Recognition. in ECML-PKDD 441–456 (Springer, Cham, 2021). https://doi.org/10.1007/978-3-030-93736-2_34 (2021).
Ma, C., Zhao, B., Chen, C. & Rudin, C. This Looks Like Those: Illuminating Prototypical Concepts Using Multiple Visualizations. Advances in Neural Information Processing Systems, 36 (NeurIPS). (2023).
Gunasekaran, H., Wilfred Blessing, N. R., Sathic, U. & Husain, M. S. Enhanced Viral Genome Classification Using Large Language Models. Algorithms 18(6), 302 (2025).
Lin, K. H. et al. Benchmarking large language models GPT-4o, llama 3.1, and qwen 2.5 for cancer genetic variant classification. npj Precis. Oncol. 9(1), 1–10 (2025).
Mourad, R. & Batut, B. Fine-tuning a LLM for DNA Sequence Classification. Online (2025); accessed June 6: https://training.galaxyproject.org/training-material/topics/statistics/tutorials/genomic-llm-pretraining/tutorial.html, (2025).
Benegas, G., Ye, C., Albors, C., Li, J. C. & Song, Y. S. Genomic language models: opportunities and challenges. Trends in Genetics (2025).
Consens, M. E. et al. Transformers and genome language models. Nature Mach. Intell. 7, 346–362 (2025).
Fishman, V. et al. GENA-LM: A family of open-source foundational DNA language models for long sequences. Nucleic Acids Res. 53(2), gkae1310 (2025).
Shao, B. & Yan, J. A long-context language model for deciphering and generating bacteriophage genomes. Nature Commun. 15(1), 9392 (2024).
Nguyen, E. et al. Sequence modeling and design from molecular to genome scale with Evo. Science 386(6723), eado9336 (2024).
Boshar, S., Trop, E., de Almeida, B. P., Copoiu, L. & Pierrot, T. Are genomic language models all you need? Exploring genomic language models on protein downstream tasks. Bioinformatics 40(9), btae529 (2024).
Hwang, Y., Cornman, A. L., Kellogg, E. H., Ovchinnikov, S. & Girguis, P. R. Genomic language model predicts protein co-regulation and function. Nature Commun. 15(1), 2880 (2024).
Waggoner, S. Creating Interpretable Deep Learning Models to Identify Species Using Environmental DNA Sequences. Honors Thesis, University of Maine (2024). https://digitalcommons.library.umaine.edu/honors/856
Cilleros, K. et al. Unlocking biodiversity and conservation studies in high-diversity environments using environmental DNA (eDNA): A test with Guianese freshwater fishes. Mol. Ecol. Resour. 19, 27–46 (2019).
Cilleros, K., Valentini, A., Allard, L., Dejean, T., Etienne, R., Grenouillet, G., Iribar, A., Taberlet, P., Vigouroux, R. & Brosse, S. Data from: Unlocking biodiversity and conservation studies in high‐diversity environments using environmental DNA (eDNA): a test with Guianese freshwater fishes. datadryad https://doi.org/10.5061/dryad.dc25730 (2018).
Coutant, O. et al. Environmental DNA reveals a mismatch between diversity facets of Amazonian fishes in response to contrasting geographical, environmental and anthropogenic effects. Glob. Change Biol. 29, 1741–1758 (2023).
Cantera, I. et al. Characterizing the spatial signal of environmental DNA in river systems using a community ecology approach. Mol. Ecol. Resour. 22(4), 1274–1283 (2022).
Cantera, I., Decotte, J.B., Dejean, T., Murienne, J., Vigouroux, R., Valentini, A. & Brosse, S. Data from: Characterizing the spatial signal of environmental DNA in river systems using a community ecology approach. datadryad https://doi.org/10.5061/dryad.pvmcvdnmr (2021).
Coutant, O. et al. Amazonian mammal monitoring using aquatic environmental DNA. Mol. Ecol. Resour. 21(6), 1875–1888 (2021).
Coutant, O., Richard‐Hansen, C., de Thoisy, B., Decotte, J.B., Valentini, A., Dejean, T., Vigouroux, R., Murienne, J. & Brosse, S. Data from: Amazonian mammal monitoring using aquatic environmental DNA. figshare https://doi.org/10.6084/m9.figshare.13739086.v7 (2021).
Acknowledgements
We are grateful to Kate Beard-Tisdale, Salimeh Yasaei Sekeh, and Roy M. Turner for their counsel. Our thanks also goes to Tristan Zippert who began related work. Sam Waggoner thanks the University of Maine Center for Undergraduate Research (CUGR) for funding on a thesis that contributed to this work41. This work was directly benefited by the GPU cluster, funded by NSF MRI # 1919478, at the Advanced Computing Group at the University of Maine. This project was supported by the National Science Foundation (NSF) grants #1849227 RII Track-1: Molecule to Ecosystem: Environmental DNA as a Nexus of Coastal Ecosystem Sustainability for Maine (Maine-eDNA) and # 2416915 Collaborative Research: E-RISE RII: Enhancing Maine Forest Economy, Sustainability, and Technology Ecosystem To Accelerate Innovation. This material is based upon work supported by the National Science Foundation Graduate Research Fellowship under Grant No. DGE 2139754. Figures were created by the authors using Microsoft PowerPoint, matplotlib 3.9 (https://matplotlib.org), seaborn 0.13 (https://seaborn.pydata.org), and draw.io (https://www.drawio.com). Much of the work on this project was performed as part of a thesis from the University of Maine41. This thesis is available on the UMaine Digital Commons, https://digitalcommons.library.umaine.edu/honors/856/.
Funding
National Science Foundation, 1919478, 1849227, 2416915, 2139754.
Author information
Authors and Affiliations
Contributions
C.C. conceptualized the ProtoPNet, L.J. interpreted data, and C.C. and L.J. provided counsel. J.D., R.G., and S.W. performed implementation, and S.W. and J.D. wrote the manuscript. All authors reviewed the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Waggoner, S., Donnelly, J., Gurung, R. et al. Creating interpretable deep learning models to identify species using environmental DNA sequences. Sci Rep 15, 27436 (2025). https://doi.org/10.1038/s41598-025-09846-7
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1038/s41598-025-09846-7