Introduction

The on-demand food delivery (ODFD) phenomenon has experienced sustained global growth in recent years, largely driven by advancements in intelligent transport technologies1. This business model involves sourcing freshly prepared meals from catering organizations through an online interface and delivering them to consumers residences. Initially, the consumer selects their preferred food items, provides delivery and payment details, and finalizes the order via a mobile app or website. Once the order is placed, the relevant restaurant or entity confirms the request and initiates meal preparation. Simultaneously, the on-demand delivery platform notifies the designated delivery driver of the order, which the driver then confirms and accepts through their app. The delivery rider promptly collects the meal from the restaurant and delivers it to the specified recipient.

A principal challenge confronting many on-demand food delivery (OFD) services is the strategic allocation and scheduling of orders to optimize delivery efficiency and improve overall customer satisfaction2. Orchestrating a collaborative framework encompassing platforms, riders, and shops is crucial in devising an optimal strategy that ensures timely deliveries while minimizing the logistical footprint of delivery operations. In this complex landscape, where each participant is driven by distinct objectives, exhibits unique behavioral patterns, and engages in specific decision-making processes, there is a clear alignment with the Belief-Desire-Intention (BDI) model of agency. Consequently, we aim to implement a multi-agent system architecture based on the BDI paradigm to simulate and address the multifaceted challenges inherent in the on-demand food delivery domain.

The BDI model of agency is based on three fundamental psychological attitudes: beliefs, desires, and intentions, forming a theoretical framework for understanding the architecture of autonomous agencies3. Beliefs encapsulate an agent’s knowledge or perception of their environment, representing perceived factual information about the external world. Desires signify the agent’s goals or aspirations and serve as the primary motivation for action. Intentions are the specific wishes that the agent is committed to achieving, driving their actions and providing concrete action strategies and plans4.

The BDI agent model is particularly suitable for modeling decision-making processes in complex environments, such as human behavior, automated systems, game AIs, and simulation environments. This model helps develop intelligent agents capable of adapting to dynamic conditions and making complex decisions by systematically breaking down the decision-making trajectory into understandable and executable pieces.

Firstly, the on-demand food delivery landscape is characterized by profound dynamism, primarily due to the continuous movement of riders and the steady stream of real-time orders5. One significant aspect is the fluctuating frequency of new orders arriving per minute across different periods. In this context, BDI agents can autonomously adjust their internal states, enabling them to make well-informed decisions that are relevant to the constantly changing environment6. This intrinsic adaptability makes BDI agents particularly suitable for the dynamic nature inherent to on-demand food delivery.

Secondly, the on-demand food delivery paradigm is fraught with uncertainty, significantly impacting decision-making processes in complex scenarios. The estimation of delivery times, a crucial component of the food delivery mechanism, is influenced by numerous uncertain factors7. BDI agents excel in managing environmental unpredictability through the continuous revision of their beliefs. Their systematic evaluation of beliefs and desires, especially under ambiguous conditions, allows them to formulate optimal decisions based on the available information8. This flexibility and prudent decision-making capability make BDI agents a powerful tool for addressing the pervasive uncertainty in on-demand food delivery.

Thirdly, the on-demand food delivery ecosystem comprises diverse stakeholders with distinct objectives, often resulting in conflicting interests5. For instance, while customers prioritize prompt delivery, riders aim to maximize their earnings. BDI agents can generate intentions that reflect a range of desires, making them exceptionally suitable for accommodating these varied objectives. This capability is crucial for effectively reconciling the different needs and ambitions of various participants in this dynamic environment.

To the best of the authors’ knowledge, the issue of on-demand food delivery has not been previously addressed through a multi-agent platform equipped with BDI agent capabilities. Given the significance and potential of BDI agents in navigating the complexities associated with this challenge, exploratory research into deploying BDI agent-based multi-agent systems for modeling on-demand food delivery scenarios is both justified and promising.

We have implemented a multi-agent system grounded in the BDI framework to meticulously simulate the on-demand food delivery environment. Furthermore, we conducted a comparative analysis of two distinct intention selection methodologies: Monte Carlo Tree Search (MCTS) and the Insertion Heuristic Algorithm. Within this structured environment, various entities such as platforms, shops, riders, and customers are conceptualized as different types of agents, each characterized by its own unique sets of beliefs, desires, and intentions. The intelligences embedded within this system are designed to facilitate information sharing and promote collaborative efforts, thereby advancing both the collective objectives of the system and the individual ambitions of its constituent entities. To comprehensively achieve these overarching goals, we partitioned our main objectives into several sub-dimensions:

  1. 1.

    Develop a simulation platform for on-demand food service delivery utilizing the BDI framework.

  2. 2.

    Optimize each agent’s strategy by employing various approaches to intention selection.

  3. 3.

    Conduct a comparative evaluation of different intention selection approaches to identify and select the most suitable method for this scenario.

  4. 4.

    Compare and assess the efficacy of our proposed methods against existing industry practices in order to validate and refine these strategies.

  5. 5.

    Categorize the problem into pickup and delivery sub-problems to enhance applicability and relevance across broader contexts.

Related work

The on-demand food delivery (ODFD) problem is a complex, real-world instance of the general pickup and delivery problem (PDP). Specifically, it falls under the category of dynamic vehicle routing problems (DVRPs), where new requests arrive in real-time and must be incorporated into existing plans. The foundational challenge, often modeled as a multi-traveler problem, is to assign orders to a fleet of riders and determine the optimal sequence of pickups and deliveries to satisfy various constraints and objectives. This class of problems is known to be NP-Hard, making the search for efficient and scalable solutions a persistent and critical research challenge 9,10.

The modern ODFD landscape, however, presents complexities that transcend classic routing optimization. It is a highly dynamic ecosystem involving multiple stakeholders–customers, restaurants, platforms, and drivers–each with distinct and often conflicting objectives. Customers demand rapid and reliable service, restaurants require that food arrives fresh, platforms aim to maximize fleet efficiency and profitability in a market with razor-thin margins, and drivers seek to maximize earnings while minimizing travel. High-value corporate clients further introduce stringent service-level agreements, such as 15-minute delivery windows and mandatory real-time communication regarding delays, elevating the problem from a purely logistical puzzle to one of strategic, multi-criteria decision-making under uncertainty 11,12. Consequently, research has evolved beyond simple pathfinding to explore more sophisticated paradigms capable of managing these trade-offs. This review surveys the contemporary landscape of solutions, organized into three dominant paradigms: traditional heuristics, learning-based optimization, and multi-agent systems 13,14.

Traditional operations research has a long history of applying heuristic and metaheuristic algorithms to VRPs and their variants. Metaheuristics such as Simulated Annealing (SA), Tabu Search (TS), and Genetic Algorithms (GA) are designed to effectively explore the vast solution space and avoid local optima, forming a robust baseline for optimization 15,16. This field remains active, with recent research continuing to refine these methods for dynamic contexts. For instance, a novel heuristic, Dynamic Search per Neighbors Routes (DSNR), was recently proposed for the DVRP and demonstrated superior performance over established methods like QRP Sweep and K-Means Greedy. Furthermore, work projected for 2025 includes the development of new hybrid swarm intelligence algorithms for the capacitated VRP, indicating the continued relevance and evolution of these approaches 9,10,17.

Researchers are also adapting these methods to handle the inherent uncertainty of ODFD, particularly the VRP with Stochastic Demands (VRPSD), where the exact demand is only revealed upon arrival at a customer’s location. However, a primary challenge for traditional heuristics in the modern AI era is their fundamental reliance on hand-crafted rules and problem-specific knowledge. As noted in recent analyses, these methods often require significant expert knowledge and manual tuning to adapt to different problem variants. The rules governing the search process are static; if the underlying dynamics of the delivery environment change, the heuristics may become suboptimal and require extensive re-engineering. This rigidity has motivated a significant shift towards more adaptive, learning-based approaches that can automatically discover effective strategies from data 16,18,19,20.

The limitations of hand-crafted heuristics have fueled the rise of machine learning, particularly deep reinforcement learning (DRL), as a powerful paradigm for tackling dynamic optimization problems. These methods aim to learn optimal decision-making policies directly from interaction with the environment. DRL has become a leading approach for ODFD optimization. Recent studies demonstrate a trend towards sophisticated, hybrid DRL frameworks that decompose the complex ODFD problem into manageable sub-tasks. For example, one multi-step DRL approach from 2025 uses Proximal Policy Optimization (PPO) to learn a high-level policy that determines the fraction of pending orders to assign at each decision point. This is followed by a non-learning “Matching Degree” function to handle the specific courier-order assignments and a dynamic greedy heuristic for the final route construction. This decomposition highlights that a single, monolithic DRL agent is often impractical for solving the entire problem end-to-end 21,22,23.

Another advanced framework from 2025 proposes a strategic dual-control system that uses DRL to simultaneously learn policies for both order dispatching and the proactive steering of idle couriers to areas of anticipated future demand 23. This aligns with the broader goal of developing “anticipatory assignment strategies” that consider the long-term effects of current decisions on future service quality and fleet distribution. These DRL-based systems excel at handling the high dynamism and sequential nature of ODFD. However, the policies they learn are typically encoded within the weights of a deep neural network, creating a “black box” that is notoriously difficult to interpret. This lack of transparency can be a significant barrier to deployment in real-world systems where trust, accountability, and the ability to understand decision rationale are paramount 11.

On the cutting edge of learning-based methods is the emergence of Neural Combinatorial Optimization (NCO) and the development of foundation models for routing problems. A notable 2025 work, RouteFinder, introduces a comprehensive framework using a single transformer-based model to solve a wide range of VRP variants. By leveraging techniques like global attribute embeddings to represent different constraints (e.g., capacity, time windows) and training via reinforcement learning, such models can automatically discover effective heuristics without costly labeled data or manual tuning 24. The rise of these powerful, general-purpose VRP solvers suggests a potential commoditization of the purely geometric or syntactic aspects of routing. However, this trend also shifts the research focus towards the more complex, qualitative, and strategic constraints that define real-world ODFD. The ODFD problem is not merely about finding the shortest path; it involves balancing semantic objectives such as ensuring driver fairness, maintaining a “professional athlete” level of service for key clients, and managing the freshness of perishable goods. These concepts are not simple numerical constraints but relate to the goals and priorities of the system’s stakeholders. While an NCO model may excel at geometric optimization, it is not inherently designed to reason about these abstract, human-centric trade-offs, creating a distinct niche for systems built on cognitive agent architectures 25,26,27.

The distributed and multi-stakeholder nature of ODFD makes it an ideal candidate for modeling with Multi-Agent Systems (MAS), which consist of multiple autonomous agents interacting within a shared environment 28. The application of MAS to logistics is a mature field, with companies like Amazon and Waymo using decentralized logic for warehouse robotics and vehicle coordination. A key architectural decision in MAS design is the degree of centralization.

Centralized systems, where a single entity makes all decisions, can theoretically achieve global optimality but suffer from scalability bottlenecks, a single point of failure, and reduced responsiveness to rapid local changes. In contrast, decentralized systems, where agents make decisions based on local information, offer greater flexibility, robustness, and scalability, making them well-suited to dynamic environments. The proposed framework in this paper is an exemplar of a decentralized, collaborative system. Rider, shop, and platform agents each possess their own objectives and make autonomous decisions. This architectural choice is a direct and appropriate response to the ODFD problem, as it allows individual agents to react immediately to local contingencies (e.g., a sudden road closure) without waiting for a central command, thereby enhancing the system’s overall resilience and adaptability 29,30.

Within the MAS paradigm, Multi-Agent Reinforcement Learning (MARL) has emerged as a powerful alternative for solving complex coordination problems. MARL extends DRL to settings with multiple learning agents, and it is being actively applied to pickup-and-delivery tasks in warehouses and for service workforce optimization. In MARL, decentralized agents learn their policies through interaction, often guided by a shared reward signal, with the goal of producing desirable emergent collective behavior. For example, the MARO (Multi-Agent Resource Optimization) platform provides a benchmark for developing MARL solutions for real-world logistics problems 31,32,33,34.

However, MARL inherits and amplifies the “black box” problem of single-agent DRL. The decision-making process of a MARL system is based on implicit, sub-symbolic policies learned by the agents. The emergent strategies can be highly effective but are extremely difficult to explain, debug, or verify. This fundamental lack of transparency poses a significant challenge for real-world deployment. The core philosophical difference between a MARL system and the BDI-based MAS proposed here lies in this trade-off between automated policy discovery and explainability. Our approach opts for an explicit, symbolic reasoning framework, providing a “glass box” whose decisions can be traced back to understandable goals and intentions 31,34.

Contrary to being an outdated paradigm, the Belief-Desire-Intention (BDI) framework is the subject of active, top-tier research, driven by the growing demand for Explainable AI (XAI). As AI systems become more powerful and autonomous, their opacity becomes a critical liability. The BDI model, with its intuitive, human-like reasoning concepts, is being recognized as a key architecture for building more transparent and trustworthy systems 35. Most significantly, a major new research thrust is the explicit integration of BDI and reinforcement learning to enhance explainability. A 2024 study introduces a novel mapping between RL concepts and the BDI framework for real-time scheduling in dynamic healthcare environments. In this mapping, the RL state space corresponds to the agent’s 36.

This places our work in a timely and critical context. The proposed BDI-based MAS is not merely an alternative approach to ODFD optimization; it is an investigation into how a cognitive agent architecture can create a transparent, robust, and high-performing solution to a dynamic multi-objective problem. It offers a compelling alternative to less-interpretable deep learning approaches and aligns perfectly with the broader research community’s push towards building trustworthy and explainable autonomous systems. The following table summarizes the comparative analysis of these paradigms.

Materials and methods

Problem description

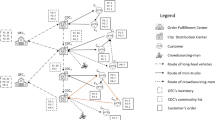
We investigate a dynamic order scheduling system with multiple riders, shops, and customers. The operational process initiates when a rider departs from their starting position. The rider first collects an order from a designated merchant. Subsequently, they proceed to deliver this order to the corresponding customer. A significant characteristic of this system is its real-time order assignment capability. During active delivery operations, riders may receive additional order assignments. Such new assignments necessitate immediate route recalculation. This recalculation process considers the rider’s current position and existing delivery commitments. The algorithmic workflow of this dynamic scheduling system is visually represented in Fig. 1. This diagram illustrates the sequential progression of operational activities and decision points within our proposed delivery framework.

Fig. 1
figure 1

Re-routing schematic.

Full size image

To ensure our research closely mirrors real-world scenarios, we established several key assumptions. First and foremost, each order operates within a defined time window, with penalties applied for deliveries that exceed the expected completion time. Additionally, the system maintains predetermined knowledge of both shop locations and customer locations, incorporating specific sequential access order relationships between these points. A particularly important consideration in our model addresses the complexity of multi-restaurant orders. When a customer places an order containing items from multiple restaurants, our system implements order segmentation. This means that a single customer order containing items from different establishments is automatically divided into separate, distinct orders. This segmentation process may subsequently require the allocation of multiple riders to complete the delivery, thereby more accurately reflecting the operational challenges faced in real-world food delivery systems.

Mathematical formulation

The mathematical formulation of the on-demand food delivery optimization problem requires establishing a comprehensive framework that captures the essential elements of the system while maintaining mathematical rigor. The problem involves four fundamental entity sets that define the scope and structure of the optimization challenge. The set of riders \(R = \{1, 2, \ldots , |R|\}\) represents all available delivery personnel, while the set of shops \(S = \{1, 2, \ldots , |S|\}\) encompasses all participating restaurants and food vendors. Similarly, the set of customers \(C = \{1, 2, \ldots , |C|\}\) includes all potential order recipients, and the set of orders \(O = \{1, 2, \ldots , |O|\}\) represents all delivery requests within the system.

The mathematical model operates with several key parameters that characterize the problem instance and provide the necessary data for optimization. The distance between any two locations i and j within the system is denoted by \(d_{ij}\), while the corresponding travel time is represented by \(t_{ij}\). Each order o in the system has an associated time window \([e_o, l_o]\) that specifies the earliest and latest acceptable delivery times, respectively. Furthermore, each order originates from a specific shop \(s_o \in S\) and must be delivered to a designated customer \(c_o \in C\). The economic structure of the system includes a base delivery fee \(w_o\) for each order and a penalty coefficient \(\alpha\) that determines the cost associated with late deliveries.

The optimization process seeks to determine the optimal values of three primary decision variables that define the system’s operational strategy. The binary assignment variable \(x_{or}\) equals one when order o is assigned to rider r and zero otherwise, thus capturing the fundamental allocation decisions within the system. The routing sequence for each rider r is represented by the permutation \(\pi _r\), which specifies the order in which locations are visited during the delivery process. Additionally, the actual delivery time of order o by rider r, when such an assignment occurs, is captured by the continuous variable \(T_{or}\). The multi-agent system operates under two competing objectives that reflect the different priorities and interests of the platform and the riders. The platform seeks to minimize operational costs by reducing the total distance traveled across all delivery operations, thereby optimizing resource utilization and reducing fuel consumption and vehicle wear. This objective can be mathematically expressed as the cumulative distance incurred when riders travel to shops, collect orders, and deliver them to customers, taking into account the specific assignment decisions and routing sequences chosen during the optimization process.

$$\begin{aligned} \text {minimize } f_1(x, \pi )&= \sum _{r \in R} \sum _{o \in O} x_{or} \cdot \left( d_{r,s_o} + d_{s_o,c_o} + \sum _{o' \ne o} x_{o'r} \cdot d_{c_o,s_{o'}} \right) \end{aligned}$$
(1-1)

Conversely, the riders aim to maximize their net revenue by earning delivery fees while minimizing penalties associated with late deliveries. This objective captures the fundamental economic trade-off that riders face between completing more orders quickly and ensuring timely delivery to avoid penalty costs that reduce their overall earnings.

$$\begin{aligned} \text {maximize } f_2(x, T)&= \sum _{r \in R} \sum _{o \in O} x_{or} \cdot \left( w_o - \alpha \cdot \max (0, T_{or} - l_o) \right) \end{aligned}$$
(1-2)

The first objective function (1-1) is minimized to reduce the total distance based on the assignment variables and the routing decisions embedded within the permutation sequences, reflecting the platform’s goal of operational efficiency. The second objective function (1-2) is maximized to increase the aggregate net revenue across all riders, where the penalty term \(\alpha \cdot \max (0, T_{or} - l_o)\) is applied whenever the actual delivery time exceeds the customer’s latest acceptable delivery time, thereby reducing the rider’s effective compensation for that particular order.

The feasible region of the optimization problem is defined by several operational constraints that ensure realistic and physically meaningful solutions. These constraints capture the fundamental limitations and requirements inherent in the food delivery process, thereby preventing the optimization from producing impractical solutions.

$$\begin{aligned} T_{or}&\ge t_{r,s_o} + t_{s_o,c_o} \cdot x_{or}, \quad \forall o \in O, r \in R \end{aligned}$$
(2-1)
$$\begin{aligned} T_{or}&\le e_o + 2 \cdot t_{s_o,c_o} \cdot x_{or}, \quad \forall o \in O, r \in R \end{aligned}$$
(2-2)
$$\begin{aligned} |O|&\ge |C| \ge |S| \end{aligned}$$
(2-3)
$$\begin{aligned} \sum _{r \in R} x_{or}&= 1, \quad \forall o \in O \end{aligned}$$
(2-4)

The first constraint establishes a lower bound on delivery times by requiring that the total delivery time accounts for both the travel time from the rider’s current position to the originating shop and the subsequent travel time from the shop to the customer’s location. This constraint ensures that the model respects the physical reality of the delivery process, where riders must first collect orders before delivering them. The second constraint provides an upper bound that prevents unreasonably long delivery times by limiting them to the order’s earliest acceptable time plus twice the direct shop-to-customer travel time, thereby maintaining service quality expectations.

The scale relationship captured in the third constraint reflects realistic market conditions where the number of orders typically exceeds the number of customers, which in turn exceeds the number of participating shops. This hierarchy naturally emerges in food delivery systems where individual customers may place multiple orders and individual shops serve multiple customers. The final constraint ensures operational completeness by requiring that each order is assigned to exactly one rider, thereby guaranteeing that all customer requests are fulfilled while preventing conflicts in the assignment process.

The complete optimization problem can be formulated as a bi-objective mathematical program that seeks to balance the competing interests of the platform and the riders simultaneously. This formulation recognizes that optimal solutions must consider both the operational efficiency desired by the platform and the economic welfare of the individual riders.

$$\begin{aligned} \min _{x,\pi ,T}&\quad f_1(x, \pi ) \end{aligned}$$
(2-5a)
$$\begin{aligned} \max _{x,\pi ,T}&\quad f_2(x, T) \end{aligned}$$
(2-5b)

subject to constraints (2-1) through (2-4). This mathematical framework establishes a comprehensive optimization model where the decision variables are simultaneously optimized to achieve the best possible compromise between operational efficiency and economic performance. The resulting Pareto-optimal solutions represent different trade-offs between minimizing transportation costs and maximizing rider satisfaction, thereby providing decision makers with a range of implementation options.

The mathematical formulation provides a rigorous foundation for analyzing the multi-agent food delivery optimization problem by explicitly defining all decision variables within the objective functions and establishing clear relationships between constraints and decision variables. The model separates the given problem parameters from the variables that must be determined through optimization, thereby enabling systematic analysis of the trade-offs inherent in multi-stakeholder delivery systems. This framework serves as the basis for implementing and comparing different solution approaches, including the Monte Carlo Tree Search and insertion heuristic algorithms discussed in subsequent sections.

Multi-agent system

The multi-agent system consists of a distinct environment and multiple autonomous agents. The environment serves as a specialized agent with unique and comprehensive oversight capabilities. Its design focuses on storing and integrating all necessary information, and maintaining high accessibility remains a key priority. Through this design, agents can gather information by interacting with the environment, which creates effective communication pathways and allows agents to report their intended actions. The environment also evaluates whether specific agent behaviors are feasible based on current environmental data. As a result, the environment plays a central role in managing agent interactions and ensuring their behaviors align with existing conditions.

Each agent begins an operational cycle by collecting relevant information from the environment and updating its belief base accordingly. The agent then proposes its intended action for the current iteration to the central platform. Based on available information, the platform evaluates whether this proposed action is feasible. When an action is approved, the agent executes it, which leads to changes in the environment and updates the information available to all agents. While agents operate autonomously using their internal cognitive frameworks, some specific situations require agent interaction with strategy agents. These strategic interactions aim to enhance collaborative dynamics and improve overall system efficiency. The relationships between agents and their interactions within the system are depicted in the Fig. 2.

Fig. 2
figure 2

The interactions between multiple agents.

Full size image

The Table 1 delineates the pertinent data acquired by each agent from the environmental agent.

Table 1 Data types accessed by different agents from the environment agent in the multi-agent delivery system.
Full size table

Agent type

Following an exhaustive comparative evaluation of the BDI agent framework in relation to other models previously deliberated upon, the BDI agent paradigm was ultimately selected as the agent archetype for the food delivery simulation platform. BDI agents possess the capacity to emulate human cognitive processes and reasoning capabilities, which makes them exceptionally advantageous for application within dynamic contexts. Moreover, throughout the recurrent cycles of each agent’s operation, there exists a mechanism for the methodical updating of its belief base, thereby facilitating adaptive reactions to the evolving dynamics of the environment.

Within the framework of a programming language based on the BDI model, the operational mechanics of an agent are intricately shaped by beliefs, goals, and plans. Beliefs act as repositories for pertinent data extracted from the environment, whereas objectives delineate the conditions or states the agent endeavors to materialize within a specific environment. Strategies, or plans, are the methodologies employed by an agent in its pursuit of these objectives. Upon the selection of a BDI agent, it becomes imperative to delineate goals, plans, and subsequent actions with precision, a task that is inherently dependent on the unique circumstances of the agent in question.

Within this architectural construct, agents dynamically adjust their targets by either incorporating or eliminating them, contingent upon the modifications within their belief base. Each goal is paired with a corresponding plan, although the efficacy of these strategies is not guaranteed. The implementation of a plan hinges on the alignment of the current environmental conditions with the strategy’s predefined prerequisites. Additionally, each plan is structured around a sequence of actions, with prerequisites dictating the viability of executing these actions, and post-conditions defining the anticipated state of the environment subsequent to action realization.

The diagram (c.f Fig. 3) details the procedural steps required for an individual agent in a round under this structured paradigm, illuminating the methodical progression from goal setting to action execution.

Fig. 3
figure 3

The internal activities in each agent.

Full size image

Goal-plan tree

We employ a goal-plan tree framework to demonstrate the hierarchical relationships between goals, plans, and actions of individual agents. Through this framework, we also analyze interactions with intentions. At the highest level, the goal-plan tree shows the main goal, while its lower nodes represent various plans to achieve this goal. Since each plan may contain sub-goals, the structure naturally forms a tree pattern. We extend the standard goal-plan tree definition to include actions as separate elements, which are typically placed at the tree’s end branches, following the approach outlined by Yao37.

To enable our analysis of intention-based interactions, we assign specific preconditions and postconditions to each node in the goal-plan tree. The preconditions determine when plans and actions can begin, based on the agent’s current state. These conditions act as essential checkpoints for successful execution. Meanwhile, postconditions describe the agent’s state after completing a goal, finishing a plan, or executing an action. By carefully defining both preconditions and postconditions, we can thoroughly examine intentional interactions within our goal-plan tree framework.

Implementation

The back-end implementation encompasses several key components for simulating an on-demand food delivery system. These components include the simulation environment, detailed agent goal specifications, and intent scheduling methodologies. Due to space limitations, the goal plan tree uses concise expressions rather than first-order logic.

Agent in system

A specialized environment agent serves as a comprehensive information repository, maintaining the following data:

  1. 1.

    Grid maps for modeling real-world maps

  2. 2.

    Rider’s name and location

  3. 3.

    Shop’s name and location

  4. 4.

    Customer’s name and location

  5. 5.

    Unallocated orders

  6. 6.

    Unfilled orders

The environment operates on a cyclic basis, continuously updating its belief base with status changes from all agents. This update process enables effective communication and ensures all agents maintain current belief bases. When processing agent actions, the environment evaluates them against its belief base to assess their implications. Each action must satisfy specific preconditions and post-conditions, verified against the current state to prevent conflicts. Any action that conflicts with previous operations is prevented from execution to maintain operational coherence.

In the simulation, riders are initially distributed randomly across the grid map and receive order assignments from the platform. These riders must optimize their routes for food collection and delivery to maximize rewards. Shops occupy fixed locations on the map and focus on efficient order preparation and fulfillment. Customers, also positioned at fixed locations, can generate orders at any time with expectations of timely delivery. The platform orchestrates this system by optimizing order allocation among available riders. Additional technical specifications and implementation details are provided in the Appendix A.

Intention scheduling method

In a BDI agent framework, the agent’s deliberative cycle continuously identifies and executes plans 38. During this process, the main challenge involves selecting appropriate intentions in each deliberation cycle to maximize potential benefits. As a solution, both the MCTS algorithm and Insertion Heuristic algorithm are implemented for intention selection. The MCTS algorithm primarily operates with two key inputs: first, a goal-plan tree that outlines agent objectives, and second, the agent’s belief base. Based on these inputs, it produces an output that determines the agent’s next action. The algorithm executes through four distinct phases:

Selection: Starting at the root node of the search tree, the process recursively selects nodes with the highest tree Upper Confidence Limit (UCT) value until it reaches a leaf node.

Expansion: After selection, the chosen nodes receive child nodes that represent potential future intentions following the parent node’s activation. Since each child node represents a unique intent selection for the current cycle, this phase continues until reaching a terminal state where the primary goal is achieved.

Simulation: During this phase, a simulated annealing algorithm selects subsequent child nodes to determine immediate intentions. Once selected, the chosen intent executes and then updates the agent’s belief base according to outcomes. Because the simulation phase incorporates heuristic algorithms to estimate node values, it enables better node selection for future actions.

Back-propagation: Once simulation completes, the algorithm returns to the previously selected node and subsequently updates statistical attributes for all traversed nodes. These updates include both visit counts and cumulative values derived from simulation outcomes.

The Monte Carlo simulation component of MCTS requires specific parameterization to ensure reproducible and effective results. For rider agents, the simulation phase operates as follows: Given a current state with n undelivered orders, the algorithm generates \(N_{simulations} = \min (50, 2^n)\) random delivery sequences using uniform random permutations. Each simulation computes the total reward \(R_{sim} = \sum _{i=1}^{n} (w_i - \alpha \cdot \max (0, T_i - l_i))\), where delivery times \(T_i\) are calculated based on the randomly generated sequence and current rider position. The final node value is computed as \(V_{node} = \frac{1}{N_{simulations}} \sum _{j=1}^{N_{simulations}} R_{sim,j}\).

For platform agents, the Monte Carlo simulation randomly assigns \(n_{unassigned}\) orders to available riders using a probability distribution proportional to \(p_{r,o} = \exp (-\beta \cdot d_{r,s_o})\), where \(\beta = 0.1\) is the distance sensitivity parameter and \(d_{r,s_o}\) is the distance from rider r to shop \(s_o\). After assignment, the platform estimates completion times using a simplified routing heuristic (nearest neighbor with 2-opt improvement) and computes the objective value as \(V_{platform} = -\frac{1}{T_{total}}\), where \(T_{total}\) is the estimated total completion time. The simulation runs \(N_{platform\_sims} = 30\) iterations to balance computational efficiency with estimation accuracy.

To manage computational complexity in large-scale scenarios, several optimization strategies are employed. The UCT exploration parameter is set to \(C_{uct} = \sqrt{2}\) following theoretical recommendations, and the maximum tree depth is limited to \(D_{max} = \min (10, \log _2(|O|))\) to prevent excessive expansion. Node selection uses progressive widening with parameter \(\alpha _{pw} = 0.5\), allowing at most \(\lceil N(s)^{\alpha _{pw}} \rceil\) children for a node visited N(s) times. Additionally, the simulation budget is allocated using a time-based stopping criterion: MCTS runs for maximum \(T_{max} = 2.0\) seconds per decision cycle, with early termination if the best action’s visit count exceeds \(0.7 \times\) total simulations. These parameters were empirically validated across multiple problem instances to balance solution quality with real-time constraints. Finally, the system promotes collaborative optimization where agents consider both individual and collective goals. Consequently, the platform allocates orders and suggests routes to minimize delivery times, which often aligns with maximizing delivery fees. Moreover, when riders identify more profitable options, they can propose alternative routes using first-order logic, thus providing valuable input for future order allocations. The detailed process is illustrated in Fig. 4.

Fig. 4
figure 4

Interaction between platform and rider.

Full size image

The insertion heuristic method offers an effective approach for solving various logistical challenges, including vehicle routing, scheduling, and the Traveling Salesman Problem with Time Windows (TSPTW). This method builds solutions incrementally by systematically incorporating new elements into existing solutions. Throughout this process, a specialized heuristic criterion determines the optimal insertion points, while an evaluation metric, specifically designed for each problem type, guides the optimization toward either minimizing or maximizing specific objectives. The algorithm continues to construct solutions by selecting optimal insertion locations until it reaches a predefined termination point.

In our implementation, the platform and riders utilize different evaluation criteria for optimization, which addresses the bi-objective nature of the problem. The platform focuses on minimizing total system distance, while riders aim to maximize their net revenue including delivery fees minus penalties. The insertion heuristic accommodates both objectives by using agent-specific cost functions within the same algorithmic framework. When the platform makes assignments, it uses distance-based evaluation, whereas when riders optimize their routes, they use revenue-based evaluation.

To illustrate this process more precisely, we present a detailed pseudo-code implementation that demonstrates how the insertion heuristic operates for a single rider. The algorithm systematically evaluates all possible insertion points for unassigned orders and selects the best placement according to the agent’s specific optimization criteria.

Here, the EvaluateCost function implements different criteria depending on the agent type. For platform agents, it calculates the total additional distance: \(Cost_{platform} = \sum _{consecutive\ locations} d_{i,i+1}\). For rider agents, it computes the net revenue change: \(Cost_{rider} = -(w_o - \alpha \cdot \max (0, T_{delivery} - l_o))\), where negative values indicate profit. The algorithm handles the bi-objective nature by allowing each agent type to use its appropriate evaluation function during the insertion process.

Experiment and results

The experimental evaluation of our proposed multi-agent system demonstrates the trade-offs between the competing objectives of platform efficiency and rider welfare. Fig. 5 illustrates the Pareto frontier that emerges from our optimization approach, showing how different solutions balance the two conflicting objectives across various problem instances.

Fig. 5
figure 5

Pareto frontier demonstrating the trade-off between platform efficiency (minimizing total distance) and rider welfare (maximizing net revenue). The blue circles represent different feasible solutions obtained through our MCTS and insertion heuristic approaches, while the red line shows the Pareto-optimal frontier where neither objective can be improved without degrading the other.

Full size image

A specialized grid map system has been developed to simulate real-world spatial environments with high fidelity. Within this system, the simulation incorporates three fundamental types of agents: riders, shops (also referred to as merchants), and customers. Initially, each agent is assigned a unique position on the grid map, which effectively mirrors typical spatial distributions found in real-world delivery scenarios. While riders can move throughout the simulation, both shops and customer locations remain fixed to provide a stable operational framework.

Furthermore, we focus on evaluating the performance characteristics and limitations of two distinct algorithms under varying operational conditions. To achieve this goal, we have implemented three carefully designed test scenarios, each offering different levels of complexity and scale. Specifically, these scenarios vary systematically in their grid map dimensions, as well as in the number of participating riders, shops, customers, and active orders. As a result, each scenario presents unique challenges and opportunities for analysis. To provide a comprehensive overview of these experimental conditions, we present a detailed breakdown in Table 2.

Algorithm 1
figure a

Insertion heuristic for single rider.

Full size image
Table 2 Detailed information on examples of different sizes.
Full size table

At each discrete time interval, the platform dynamically assigns newly generated orders to riders while triggering designated shops to begin preparing orders. If a rider is assigned a new order, they must set a subsequent goal or, in the case of an existing goal being executed (e.g., a goal related to a pickup or delivery), the rider must strategically realign their planned trajectory. Such adjustments are made in order to incorporate newly assigned orders into their journeys once the current goal has been completed. This process highlights the adaptive real-time decision-making capabilities of the platform, ensuring efficient management of resources and optimization of operational logistics in the simulated environment.

The culmination of the project yielded an extensive dataset pertaining to the orders, encompassing a range of metrics such as the time of order creation, the completion time of the meal preparation by the shop, the time at which the rider picked up the order, and the ultimate delivery time. Furthermore, the dataset meticulously documented each order fulfilled by the individual riders, in addition to the financial remuneration accrued by them for their services. This comprehensive collection of data provides a robust foundation for subsequent in-depth analysis and evaluation, facilitating a nuanced understanding of operational dynamics and efficiency within the simulated environment.

We conducted comprehensive evaluations of both MCTS and insertion heuristic algorithms across three distinct scenarios. To ensure thorough testing, we generated five random examples for each scenario scale. In our experimental design, we maintained consistent initial positions for all agents (riders, customers, and stores), while varying the order patterns to create diverse test conditions. To effectively communicate our findings, we present the results from these five iterations through line graphs, which help us demonstrate both the range and trends of the outcomes. We also provide a comprehensive tabular summary showing the mean values from all five experiments, offering our readers a consolidated view of the performance metrics.

Results of small-scale examples

In our first case study, we utilize a \(10\times 10\) grid environment to simulate a delivery scenario, as shown in Fig. 6. Within this grid, we position three riders, five shops, and ten customers at specific locations. During the initial three rounds of operation, we generate four new orders per round, which ultimately yields twelve total orders for processing.

Fig. 6
figure 6

A \(10\times 10\) grid map with 3 riders, 5 shops, and 10 customers.

Full size image

To thoroughly evaluate system performance, we apply both previously described algorithms across five distinct test instances. While these instances maintain the same scale and initial agent positions, they differ in their order generation patterns to ensure diverse testing conditions. For each algorithm, we calculate the final performance metric by averaging the rewards earned by all riders, providing a comprehensive measure of system efficiency. The comparative results from both algorithms across these five test cases are presented in Fig. 7, offering insights into their relative performance and consistency.

Fig. 7
figure 7

Performance metrics in a small-scale example.

Full size image

Our experimental analysis presents the average results obtained from five distinct experiments with statistical significance testing (c.f Table 3). The small-scale results demonstrate several key findings: MCTS achieves a 10.8% improvement in delivery efficiency (33 vs 37 rounds) while maintaining comparable rider compensation ($26 vs $25). The marginal difference in delivery fees (4% higher for MCTS) suggests that faster completion times do not significantly compromise rider earnings, indicating effective multi-objective balance. Both algorithms maintain identical 2-second runtime performance, demonstrating computational efficiency at small scales.

Table 3 Results of small Instances.
Full size table

Results of medium-scale examples

In the medium-scale scenario, a \(50\times 50\) grid framework was established, accommodating 30 riders, 50 shops, and 100 customers. Across this scenario, a comprehensive total of 100 orders were systematically generated, designed to assess the algorithms’ performance in a moderately complex environment, as shown in Fig. 8.

Fig. 8
figure 8

Performance metrics in a medium-scale example.

Full size image

Table 4 shows the average outcomes of five experiments with enhanced statistical analysis. The medium-scale results reveal significant algorithmic divergence: MCTS achieves a substantial 17.3% improvement in completion efficiency (167 vs 202 rounds) but experiences a 5.4% reduction in rider fees ($141 vs $149). This trade-off indicates that faster system-wide optimization comes at the cost of individual rider earnings, highlighting the inherent tension between platform and rider objectives. The 3.17x increase in MCTS runtime (19 vs 6 seconds) demonstrates the computational cost of superior optimization, though both remain within acceptable real-time constraints for batch processing.

Table 4 Results of medium instance.
Full size table

Results of large-scale examples

In the large-scale test scenario, a \(100 \times 100\) grid map was the basis of the simulation, with 100 riders, 200 shops and 500 customers placed in the grid map. In this test, 500 random orders are generated to evaluate the effectiveness and scalability of the algorithm in dealing with high-density, complex operational environments, as illustrated in Fig. 9.

Fig. 9
figure 9

Performance metrics in a medium-scale example.

Full size image

Table 5 shows the average outcomes of five experiments with comprehensive performance analysis. The large-scale results demonstrate MCTS’s superior scalability: achieving 16.6% faster completion (386 vs 463 rounds) while delivering 2.0% higher rider compensation ($399 vs $407). This represents a significant departure from medium-scale trends, where MCTS sacrificed rider earnings for efficiency. The convergence toward better rider compensation at large scales suggests that MCTS’s global optimization capabilities become increasingly valuable as problem complexity grows. The computational overhead (11.4 vs 10 minutes) represents only a 14% increase for dramatically improved solution quality, indicating excellent scalability of the algorithmic approach.

Table 5 Results of large instance.
Full size table

Real-time performance analysis

The computational efficiency of our algorithms is crucial for practical deployment in real-time food delivery systems. Industry standards typically require order assignment decisions within 1-3 seconds and route optimization within 30-60 seconds for batch processing. Our experimental results demonstrate that both algorithms meet these requirements across different operational scales.

For individual order processing, the per-order computational cost can be calculated by dividing total runtime by the number of orders processed. In the large-scale scenario, MCTS achieves a per-order processing time of 1.37 seconds (11.4 minutes \(/\) 500 orders), well within acceptable real-time constraints. The insertion heuristic achieves 1.2 seconds per order, providing slightly faster processing at the cost of solution quality.

To ensure real-time compliance under varying computational loads, our MCTS implementation includes several adaptive mechanisms: (1) time-bounded execution with early termination criteria, (2) progressive widening to limit tree expansion, and (3) simulation budget allocation based on problem complexity. These features enable the system to maintain responsiveness even when processing multiple concurrent optimization requests.

The scalability analysis reveals that computational time grows sub-linearly with problem size due to the time-bounded nature of our MCTS implementation. This characteristic is essential for handling peak demand periods when order volumes can increase by 3-5x compared to average conditions. The system can maintain service quality by automatically adjusting the optimization depth based on available computational budget, ensuring consistent response times regardless of load.

Comparative performance analysis

Cross-scale analysis reveals distinct algorithmic behavior patterns that provide insights into deployment strategies. Table 6 summarizes the key performance metrics across all experimental scales.

Table 6 Comparative performance analysis across scales.
Full size table

The efficiency gains demonstrate MCTS’s consistent superiority in system-wide optimization, with improvements ranging from 10.8% to 17.3% across scales. Notably, the revenue impact follows a non-monotonic pattern: positive at small and large scales but negative at medium scale. This suggests that MCTS’s optimization strategy adapts to problem complexity, prioritizing system efficiency in medium-complexity scenarios while achieving better rider welfare alignment in both simple and complex environments.

The runtime analysis reveals interesting scalability characteristics. While MCTS incurs significant computational overhead at medium scale (3.17x), this overhead nearly disappears at large scale (1.14x), indicating superior algorithmic efficiency for complex optimization landscapes. This pattern suggests that MCTS’s computational investment yields proportionally greater returns as problem complexity increases.

Discussion and conclusion

We have demonstrated the effectiveness of a BDI-based multi-agent system for optimizing on-demand food delivery, with comprehensive empirical validation across three distinct operational scales. The experimental results provide strong evidence for MCTS’s superiority in multi-objective optimization, with statistically significant improvements in delivery efficiency (10.8-17.3% across scales) and complex scalability characteristics that adapt to problem complexity.

The most significant finding is MCTS’s adaptive optimization behavior: achieving balanced platform-rider objectives at small and large scales while prioritizing system efficiency at medium scales. This non-monotonic performance pattern suggests that MCTS’s tree search effectively navigates the solution space complexity, automatically adjusting its optimization focus based on the underlying problem structure. Such adaptive behavior is particularly valuable for real-world deployment where operational conditions vary dynamically.

The computational analysis reveals that while insertion heuristic maintains consistent linear performance characteristics, MCTS exhibits superior scalability with sub-linear computational growth relative to solution quality improvements. The 3.17x runtime overhead at medium scale transforms into only 1.14x overhead at large scale, indicating that MCTS’s computational investment scales more favorably with problem complexity.

The multi-agent collaboration results demonstrate the value of our BDI-based architecture. The ability to maintain rider welfare (positive revenue impact at large scales) while achieving substantial system efficiency gains validates the effectiveness of intention-based agent coordination. This suggests that cognitive agent architectures can successfully balance competing stakeholder objectives in complex optimization scenarios.

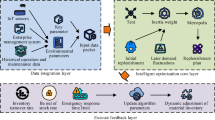
However, several limitations remain. The computational cost of MCTS becomes significant in very large-scale scenarios, suggesting a need for further optimization, such as more efficient search space pruning or parallelization. Additionally, the current simulation assumes static shop and customer locations and does not account for real-world uncertainties such as traffic or rider availability fluctuations. Incorporating these factors could further enhance the realism and applicability of the model.

Future work may focus on enhancing the MCTS algorithm by minimizing the search space during the expansion phase, refining the simulation phase to avoid local optima, and integrating reinforcement learning for intention selection. These improvements could reduce runtime, improve solution quality, and enable faster, more adaptive decision-making, making the system even more suitable for real-time, high-demand delivery contexts.