Introduction

The concept of global warming potential (GWP) serves as a comparative measure of the amount of heat a greenhouse gas traps in the atmosphere relative to the heat trapped by an equivalent mass of carbon dioxide. Consequently, the GWP factor of CO2 is set at 1. GWP is typically calculated over specific time horizons of 20, 100, or 500 years1. Climate is characterized by mean air temperature, relative humidity, wind patterns, precipitation, and frequency of extreme weather events, typically measured at least thirty years2. Climate change represents the most significant global threat humanity primarily driven by atmospheric carbon emission3. Climate change can occur naturally due to variation in the Sun's energy or through persistent human activities, such as the emission of greenhouse gases, sulfate aerosol or black carbon or changes in the land use4. Examples of climate change include global warming and the increase severity and frequency of floods and drought in various part of the world over recent decades5. Climate change includes both natural variability and anthropogenic changes6. According to the Sixth Assessment Report (AR6 2021) by the Intergovernmental Panel on Climate Change (IPCC), human activities have warmed the atmosphere, ocean, and land7. The United Nations is concerned primarily with anthropogenic climate change, both because it poses a threat to global security and because it can be altered by altering human and governmental behavior. For this reason, the United Nation Framework of Climate Change defines climate change as a change of climate which is attributed directly or indirectly to human activity that alters the composition of the global atmosphere and which is in addition to natural climate variability observed over comparable time periods8. The international agreements overseen by the United Nations Framework Convention on Climate Change (UNFCCC), including the 1992 Kyoto Protocol and 2015 Paris climate agreement sought to build global consensus on fighting climate change and set clear goals for emission reductions9. The climate conference in Kyoto, Japan, resulted in an argument by industrialized nations to reduce emissions of six key greenhouse gases (GHGs) to about 5% below 1990 emissions level by the year 201210. Reducing greenhouse gas emissions is one of the significant benefits of biomass. Biomass may function on a closed carbon cycle, in contrary to fossil fuels, which emit carbon dioxide stored for millions of years. This indicates that, when biomass is burned sustainably, the amount of carbon dioxide released during combustion is about equal to the amount absorbed by the plants during growth, leaving a net neutral effect on atmospheric CO2 levels11. Additionally, biomass contributes to energy security through dedicated energy crops and municipal solid waste conversion, while stimulating economic development in rural areas by creating jobs and revitalizing economies. The integration of biomass with other renewables like solar and wind, coupled with ongoing technological advancements, improves efficiency and competitiveness, making it essential for achieving net zero emissions (NZE) of IEA (International Energy Agency, France) targets and addressing climate change12.

Biomass serves as a key renewable bio-resource, offering a carbon–neutral alternatives that is widely available across the globe13. Defined broadly, biomass encompasses all organic materials derived from plants, including algae, trees, and crops. The materials results from the process of photosynthesis, where green plants convert sunlight into organic matter14. Biomass includes terrestrial and aquatic vegetation as well as organic waste materials. The composition of biomass primarily consists of three polymers: cellulose, hemicellulose, and lignin, with variations contingent upon the specific type of biomass15. For instance, hardwood and herbaceous biomass contain approximately 43–47% and 33–38% cellulose, 25–35% and 26–32% hemicellulose and 16–24% and 17–19% lignin, respectively16. Biomass can be evaluated for its energy potential by analyzing its higher heating values (HHV) and ultimate analysis, which provides information on its elemental composition, including the percentage of carbon (C), hydrogen (H), nitrogen(N), sulfur (S), and oxygen (O). The HHV, measured using bomb calorimeter, is a crucial indicator of biomass energy content. Biomass with higher C and H, and/or O and H contents, and lower N and S contents, is preferable for energy use as enhances the HHV17. Biomass is highly responsive to Near Infrared (NIR) radiation, particularly indicated by spectra shown in the range of 1100 nm to 2500 nm17. It primarily interacts with hydrogen bonds in biological materials like C-H, O-H, N-H and S-H and C=O too. This property makes biomass suitable for assessment using Near Infrared Spectroscopy (NIRS) which combined NIR spectral variables to chemometric algorithms to determine energy-related properties such as HHV and elemental composition18, where provide rapid, non-destructive analysis with minimal or no sample preparation and no chemical used leading to environment safe. In the present scenario, biomass is one potential source of renewable energy and the conversion of plant material into a suitable form of energy, usually electricity or as a fuel for an internal combustion engine, can be achieved using a number of different routes, each with specific pros and cons19. For carbondioxide (CO2) emission from biomass combustion though will be achieving net zero emissions (NZE) as explained, though, by GWP of CO2 calculated by IPCC can be used for estimation of how much heat can be absorbed by biomass plants. For methane (CH4) and nitrous oxide (N2O), using Global Warming Potential (GWP) indices higher than those specified by the Kyoto Protocol (100-year time horizon) would better reflect historical temperature trends. The GWP of CH4 aligns most accurately with historical temperature data when calculated over a 44-year time horizon. In contrast, the GWP of N2O does not closely match historical temperatures regardless of the time horizon used20. Hao and Ward21 reported about 85% of the total CH4, emitted in the tropical area, is mainly the result of shifting cultivation, fuelwood use, and deforestation and may have increased by at least 9% during the last decade because of increases in tropical deforestation and the use of fuelwood. There were some reports on N2O emissions by biomass burning e.g. from power geration using oil palm empty fruit branch was reported22 and using rice husk23.

A complex pattern of peaks and troughs of NIR spectrum can be analyzed using chemometric techniques to deduce the sample's chemical composition and physical properties. The advantage of NIRS lies in its ability to provide rapid, non-destructive analysis with minimal or no sample preparation and no chemical used leading to environment safe. This makes it particularly valuable in fields such as agriculture, pharmaceuticals, and food industries, where it is used for quality control and compositional analysis.

Fourier Transform Near Infrared (FT-NIR) spectrometer is a analytical instrument that utilizes the NIR region to analyze materials. FT-NIR spectroscopy is a powerful analytical technique used for identifying and quantifying gases due to its high sensitivity and accuracy24. This method involves measuring the absorption of NIR radiation by gases, allowing for precise determination of their concentrations in the atmosphere. By integrating GWP estimation with FT-NIR spectroscopy, by result at the end of this report, it becomes possible to enhance the accuracy of greenhouse gas inventories and improve the reliability of climate models, thereby supporting more effective climate action.

The principle behind the IPCC’s used the GWP calculation to quantify the impact of various green house gases (GHGs), mainly carbon dioxide (CO2), along with smaller amounts of methane (CH4) and nitrous oxide (N2O), on global warming relative to CO2 is depended on the HHV which is the total energy content in the biomass, including the energy contained in the water vapor produced during combustion. It is important for estimating the potential emissions per unit of biomass. IPCC’s GHG emissions estimation is calculated by using Emission Factor is a standard coefficient provided by IPCC guidelines, which estimates the amount of a specific greenhouse gas emitted per unit of energy produced by the biomass. The emission factors typically measure emissions in kilograms of CO2, CH4, or N2O per unit of energy (TJ) in the biomass, and they allow us to quantify the emission per unit of HHV. How much heat a gas traps in the atmosphere over a specific period, typically 20, 100 or 500 years, compared to CO2. This is based on the radiative efficiency of the gas (how effectively it absorbs heat per molecule) and its atmospheric lifetime (how long it remains in the atmosphere). CO2 is set as the baseline (GWP = 1) for comparison, as it is the most prevalent GHG emitted by human activities. Other gases are compared relative to CO2’s warming effect. GWP values depend on a chosen time horizon (e.g. GWP-20, GWP-100). Short lived gases, like CH4, have a higher GWP over a 20-year horizon due to their potent but shorter-lived impact, whereas the GWP-100 of CH4 is lower because it dissipates faster than CO2. GWP represents the cumulative impact of a pulse emission over the chosen time horizon. The calculation integrates the warming effects of the gas over time, taking into account both the immediate warming effect and gradual decay of the gas. This method provides a standardized way to compare the warming impacts of different GHGs and is instrumental for climate policy, as it allows policymakers to prioritize mitigation efforts based on the long term and short-term impacts of various gases.

The database report presents developed models tailored for different biological materials, for example, the evaluation of HHV sorghum samples25, using partial least squares regression (PLSR) and principal component regression (PCR), calibration models were constructed for both full and reduced wavenumber regions to predict HHV and the contents of carbon, hydrogen, nitrogen, sulfur, and oxygen. Particularly noteworthy was the exceptional accuracy demonstrated by the HHV and carbon content models, underscoring their reliability in prediction and with a rapid measurement time (from 100 to 1 min)25. Predicting Global Warming Potential (GWP) using FT-NIR spectroscopy represents a novel approach. To develop the prediction model, the reference two key papers that utilize PLSR. There were two reports of our research group contributed to the results of NIR prediction models for ultimate analysis parameters of the non-wood and wood samples, including Pitak, Sirisomboon, Saengprachatanarug, Wongpichet, and Posom26 who developed the PLSR using the spectra obtained by line-scan NIR hyperspectral imager in which the most effective model for the prediction of C, H and N content of 160 non-wood and wood biomass pellets The second report was contributed by Shrestha et al.17 using FT-NIR spectrometry, where the ground non-wood and wood samples spectra, which were 110 samples of agricultural residues and 90 samples of fast growing trees, were used to develop the PLSR models combined with multi-preprocessing methods for ultimate analysis.

The prediction model that is applicable for determining the GWP for different species and utilized the species as for GWP production is essential for the policy makers, energy companies, and researchers who can utilize these findings for proper identification, management, and the utilization of resources to save the planet. Therefore, the main objective of this research is to propose a novel estimation approach for GWP by combined the GWP calculation method obtained from IPCC11 which utilizing HHV of the biomass and FT-NIR spectra of biomass samples by formulating a PLSR prediction model which can drastically reduce the experiment period from 40 min for HHV measurement by bomb calorimeter include sample preparation time17 to a reduction to 3 min by only use the spectrum of the biomass chips.

Traditional methods are time-consuming (40 min), chemical unavoidable (e.g. tablets of benzoic acid and combustion polyethylene bag) cause non-environmental friendly, well trained technician is required, costly (15 USD per sample) and destructive whileFT-NIR offers a fast (3 min), chemical free cause environmental friendly, general worker can work, evaluation and operation cost per sample (< 1 USD) and non-destructive.

It is an AI approach to be an alternative instead of traditional method for estimating GWP from biomass, aiding sustainable biomass utilization and climate impact assessment. We believe readers will find this work insightful and valuable, as it introduces a rapid, non-destructive, and cost-effective approach for GWP assessment, addressing a critical gap in biomass analysis and climate change mitigation.

Materials and methods

In this manuscript, we introduce a novel approach for predicting Global Warming Potential (GWP) using a spectroscopy non-destructive and rapid method but by using diverse biomass sources including fast growing tree and agricultural residue collected in Shrestha et al.17. In Shrestha et al.17 only the higher heating value and ultimate analysis elements were predicted. To the best of our knowledge, no prior research has explored this specific application, making it a novel contribution to the field, especially in climate change environment sector.

This research is the longitudinal research and builds on the study referenced at Shrestha et al.17 https://doi.org/https://doi.org/10.3390/en16145351, where in previous paper traditional CHN/S elemental analyzer was used to determine elements such as C, N, O, and S, and bomb calorimeter was used for measuring HHV. Using of same sample spectrum set, we have developed a new model that offers an alternative approach to determining GWP and HHV data using PLSR. This streamlined model is designed to provide a faster and more accessible method for estimating GWP in biomass applications.

Figure 1 illustrates the comprehensive research methodology for assessing the HHV and GWP of ground biomass for energy applications, employing NIRS in conjunction with PLSR analysis.

Fig. 1
figure 1

Flow chart of the overall research methodology for the evaluation of the GWP by HHV using NIRS combined with PLSR.

Full size image

Biomass

Shrestha et al.17 gathered Nepal biomass samples focusing on five fast-growing tree species: Alnus nepalensis, Pinus roxburghii, Bambusa vulgaris, Bombax ceiba, and Eucalyptus and five types of agriculture residues: Zea mays (cob, shell, and stover), Oryza sativa (husk), and Saccharum officinarum (bagasse). There were 200 samples in total.

Outliers in the GWP calculated data were identified using z-score equation in Eq. (1), which is the Z score and when the Z score is ≥ 3, it means that the x value is outside the ± 3SD range where 99.7% of data is and the x value will be considered as outlier27. x is the reference value of GWP, \(\overline{\text{x} }\) is the average GWP, and SD is the standard deviation. There were 3 outliers found.

$$ \frac{{{\text{X}}_{{\text{i}}} - {\overline{\text{X}}}}}{{{\text{SD}}}} \ge |\pm 3| $$
(1)

The spectral outlier samples were determined by using the Mahalanobis distance limit, based on the distribution of all calibration spectra, where a normal distribution, a one-sided limit is defined that covers a probability of 99.999%28. However, there was no spectral outlier found. Hence, 197 samples for modeling.The investigation is significant as it addresses biomass sample from both tree species and agricultural residues, offering a board understanding of the potential energy yields from two critical categories of biomass resources. The study sheds light on renewable energy opportunities that can be derived from diverse plant species and residues, each with its distinct chemical and structural characteristics.

Spectroscopy scanning

Shrestha et al.17 scanned biomass samples using an FT-NIR spectroscopy (MPA, Bruker, Germany) in diffuse reflectance mode with a rotating sample holder. The use of diffuse reflectance mode and the rotating mode holder was instrumental in achieving uniform sample exposure to the spectrometer beam, which is critical in analyzing heterogeneous materials like biomass. The study highlights the importance of proper background calibration and careful sample handling in obtaining accurate FT-NIR spectra ensuring that environmental factors such as humidity and temperature for no skew the results29.

Wet-lab measurement

The complex nature of NIR absorbance data, it is essential to correlate it with reference values obtained from a standard laboratory method to ensure accuracy30. Accordingly, the reference data for the biomass samples, which included higher heating (HHV), were evaluated following the procedure outlined by Shrestha et al.17 after scanning with an FT-NIR spectrometer. Prior to HHV measurement, the grinding process is crucial for it ensures uniform particle size, which in turn improves the consistency of the combustion process and enhances the precision of the calorimetric analysis. The using Bomb calorimeter to find the HHV is widely recognized for its reliability in determining the calorific value of various type of fuel, including biomass. The use of an automatic bomb calorimeter ensures precise temperature control during combustion, allowing accurate measurement of the energy content released by the samples. This data is crucial for understanding the potential of biomass as a renewable energy source and optimizing its use in various applications.

Estimation of global warming potential and emission of greenhouse gas (GHG)

IPCC guidelines7,31 was used to obtain main emission factors for CO2, CH4, and N2O from stationary biomass combustion on the 100 years based reported in AR67. These emission factors are typically expressed in grams of gas per unit of fuel burned energy (e.g., CO2 kg TJ-1 of fuel). Calculate the emissions of CO2, CH4, and N2O from the biomass combustion using the following formula:where Emissions is the total amount of emissions produced (kg); Mass of sample is the total mass of a sample being burned (kg); High Heating Value is the Gross Calorific Value, measures the total amount of energy that can be obtained from a fuel sample when it is completely burned (TJ.kg-1); Emission Factor is based on energy consumption for wood/ woody residues: 112 kg CO2 TJ-1, 30 kg CH4 TJ-1, and 4 kg N2O TJ-17,31.

To determine the emission factor for biomass combustion, follow a systematic approach to ensure accuracy. Begin by identifying the type of biomass, such as fast-growing trees and agriculturalresidues, as each type has distinct emission factors. Reliable sources for these factors include the IPCC Guidelines. Next, measure the HHV of the biomass, often determined experimentally via bomb calorimetry and expressed in TJ kg-1. Select an appropriate emission factor based on the biomass type and combustion conditions; for example, wood combustion factors range from 1 to 150 kg CO2 TJ-1.

Determine the GWP of the emissions using the IPCC's GWP values for a specific time horizon (e.g. 100 years). The GWP are calculated by converting the emissions of CH4 and N2O into CO2-equivalents (CO2e) based on their relative warming potential.

$${\text{GWP}} = \frac{{\mathop \smallint \nolimits_{0}^{a} aicidt}}{{\mathop \smallint \nolimits_{0}^{a} a{\text{CO}}_{2} {\text{CCO}}_{2} dt}}$$
(2)

where ai is Absolute instantaneous concentration of the gas i at time t; ci is Radiative efficiency (or radiative forcing) of the gas i per unit mass; aco2 is Absolute instantaneous concentration of CO2 at time t; cco2 is Radiative efficiency (or radiative forcing) of CO2 per unit mass; a is Time horizon over which the GWP is calculated 100 years (typically 20 or 100 years); t is Time variable.

The total GWP calculated the combined impact of different greenhouse gases (GHGs) on global warming. Each GHG has a specific GWP value, which represents its warming effect relative to CO2 over a specific time horizon, typically 100 years. For calculation, the total GWP is determined by summing the products of the GWP values and the emission quantities for each gas. Specifically, it includes the GWP of CO2 multiplied by the amount of CO2 emissions, the GWP of methane (CH4) multiplied by the amount CH4 emissions, and the GWP of nitrous oxide (N2O) emissions multiplied by the amount N2O emissions. By accounting for the different contributions of these gases, the formula provides a comprehensive measure of the overall impact of multiple GHGs on climate change, allowing for a more accurate assessment of their collective influence on global warming.

For calculating GWP, use the formula:

$$ \begin{gathered} {\text{Step}}\;{1}:\left( {{\text{CO}}_{{2}} ,{\text{CH}}_{{4}} ,{\text{N}}_{{2}} {\text{O}}} \right){\text{emissions}}\left( {{\text{kg}}} \right) = {\text{Mass}}\;{\text{of}}\;{\text{Fuel}}\left( {{\text{kg}}} \right) \hfill \\ \quad \times {\text{Carbon}}\;{\text{emission}}\;{\text{factor}}\left( {{\text{kg}}\;{\text{TJ}}^{{ - {1}}} } \right) \times {\text{HHV}}\left( {{\text{kg}}\;{\text{TJ}}^{{ - {1}}} } \right) \hfill \\ \end{gathered} $$
$$ \begin{gathered} {\text{Step}}\;{2}:\;{\text{Total}}\;{\text{GWP}} = \left( {{\text{GWP}}\;{\text{of}}\;{\text{CO}}_{{2}} \times {\text{CO}}_{{2}} \;{\text{emissions}}} \right) \hfill \\ \quad + \left( {{\text{GWP}}\;{\text{of}}\;{\text{CH}}_{{4}} \times {\text{CH}}_{{4}} \;{\text{emissions}}} \right) + \left( {{\text{GWP}}\;{\text{of}}\;{\text{N}}_{{2}} {\text{O}} \times {\text{N}}_{{2}} {\text{O}}\;{\text{emissions}}} \right) \hfill \\ \end{gathered} $$

Table 1 shows example of emission gases by Alnus Nepalensis biomass combustion.

Table 1 Calculation example of emission gases by Alnus nepalensis biomass combustion.
Full size table

The Table 2 shows the compares the GWPs of three greenhouse gases i.e. CO2, CH4, and N2O—over two different time periods (100 years and 20 years) based on assessments from the IPCC's Assessment Reports (AR4 200732, AR5 201433, and AR6 20217). For CO2, the GWP remains consistent across all reports and time periods with a value of 1, indicating its role as the baseline for comparison. CH4 shows variations in GWP depending on its origin (fossil or non-fossil) and whether climate-carbon feedback is considered. The GWP for fossil-origin CH4 increases from 25 in AR4 to 34 in AR6 over a 100-year period, highlighting the growing recognition of its impact. For non-fossil-origin CH4, the GWP is slightly lower at 27.2 over 100 years in AR6. Over a 20-year period, CH4's GWP is significantly higher, emphasizing its short-term potency as a greenhouse gas. N2O also shows variations, with its GWP slightly decreasing from AR4 to AR5 but increasing again in AR6, both over 100-year and 20-year periods. The data reflects the evolving understanding of the greenhouse effects of these gases, with updates in each assessment report based on the latest scientific research.

Table 2 Global warming potential (GWP) of greenhouse gas emissions indicated in IPCC AR6 report7.
Full size table

Model development and validation

The PLSR method were used to develop the model. The samples were divided into calibration set (80%) and a prediction set (20%) by using Kennard-Stone method. Kennard-Stone data separation algorithm is based on an Euclidian distance calculation, where the sample with maximum distance to all other samples are selected, then the samples which are as far away as possible from the selected samples are selected, until the selected number of samples is reached34. This means that the samples are selected in such a way that they will uniformly cover the complete sample space, reducing the need for extrapolation of the remaining samples34. Initially, the model was developed using raw spectra, standard normal variate (SNV), 1st derivative and 2nd derivative transformations. The model was optimized by selecting wavenumbers through various variable selection methods, including the Correlation Method (CM), Variance Method (VM), Co-Variance Method (COVM), and Variable Importance Projection (VIP). The spectral data were pretreated using raw spectra, standard normal variate (SNV), as well as first derivative and second derivative transformations. The following spectra pretreatment methods: Standard Normal Variate (SNV) is for corrects scatter effects and baseline variations35, 1st and 2nd Derivative enhances spectral resolution by removing baseline shifts and emphasizing key spectral features, leading to better signal clarity35.

Feature selection methods: Correlation-based selection identifies the most relevant spectral variables by assessing their relationship with dependent variable which in our case is GWP and HHV; VIP prioritizes key spectral features that significantly contribute to the PLSR model, enhancing predictive accuracy, VM selects variables based on their variance, ensuring only features with significant variation are retained and COVM identifies variables with strong covariance relationships, helping in feature reduction while preserving important predictive information36.

MATLAB-R2020b (MathWorks, Natick, MA, USA) was used for both spectrum pretreatment and model development. The calibration model’s performance was assessed using the coefficient of determination (R2c) and root mean square error of calibration (RMSEC).

The obtained model wasvalidated using the prediction set, and their performance was evaluated based on coefficient of determination of prediction (R2p), root mean square error of prediction (RMSEP), bias and the ratio of prediction of deviation (RPD).

These parameters were calculated as follows, where y is the measured value, \(\hat{\text{y}}\) is the predicted value, i is subscript used to indicate the number of the sample, y is mean of the measured value, N is the number of samples in respective set, and SD is the standard deviation of the measured values of the prediction set:

$$ {\text{R}^{2}}_{{\text{c}}} ,\,{\text{R}^{2}}_{{\text{p}}} = 1 - \frac{\sum ({\text{y}}_{{\text{i}}} - {\hat{\text{y}}}_{{\text{i}}} )^{2}}{\sum {\text{(y}}_{{\text{i}}} - {\overline{\text{y}}}_{{\text{i}}} )^{2}}$$
(3)
$$ {\text{RMSEC}},{\text{ RMSEP}} = \sqrt {\frac{{\mathop \sum \nolimits_{{\text{i=1}}}^{{\text{N}}} \left( {{\text{yi}} - {\hat{\text{y}}\text{i}}} \right)^2}}{{\text{N}}}} $$
(4)
$$ {\text{RPD}} = \frac{{{\text{SD}}}}{{{\text{RMSEP}}}} $$
(5)
$$ {\text{Bias}} = {\frac{{\mathop \sum \nolimits_{{\text{i=1}}}^{{\text{N}}} \left( {{\text{yi}} - {\hat{\text{y}}}} \right)}}{{\text{N}}}} $$
(6)

The better model was selected based on the tradeoff value between the highest R2C, R2P and RPD and lowest RMSEC, RMSEP, and bias. In this study, the performance result, namely the R2 and RPD value were interpreted based on the recommendations of Williams et al.37.

Result

Spectral data processing

In data of 200 biomass samples for GWP PLSR modeling, 3 outliers were identified and removed, resulting in a final dataset of 197 samples. The removal of outliers ensured the genuine performance of the model, allowing for more accurate predictions.

Figure 2a illustrates the raw spectra of log (1/R) versus wavenumber in the range of 3600–12500 cm−1, showing high absorption peak such as 6711, 5076 and 4636 cm−1 for both fast growing tree and agriculture residues sample. It shows the significant absorption features corresponding to various molecular vibrations in the biomass. The peak at 6711 cm−1 (1490 nm) of the broad band can be the shifted peak of 1471 nm is the first overtone of N-H stretching of CONHR typically found in amides or proteins and or 1450 nm attributed to 1st overtone of O–H vibration including of water and starch38,39. The combustion of starch is a significant process, as it releases carbon dioxide (CO2), a major greenhouse gas that contributes to global warming40,41,42 for example in biomass combustion, though, it is carbon neutral fuel.

Fig. 2
figure 2figure 2

Spectra of biomass chips of fast-growing trees and agricultural residue: raw (a) and pretreated spectra by SNV (b), 1st derivative (c) and 2nd derivative (d) where (a) raw spectra showing unprocessed near-infrared (NIR) data with baseline variations and scattering effects. (b) Standard Normal Variate (SNV) corrected spectra, reducing baseline shifts and scattering effects. (c) 1st derivative corrected spectra, to obtain common spectra baseline. (d) 2nd derivative corrected spectra, to obtain common spectra baseline and reveal overlapping peaks.

Full size image

The peak at 5076 cm−1 (1970 nm) is the shifted peak of 1940 nm is linked to O–H combination of fundamental of O-H stretching and bending vibrations38. The peak of 4636 cm−1 (2157 nm) corresponds to C-H aromatic C-H38. The wavenumber increases beyond 6000 cm−1 shows the flat spectral lines without dominant peaks, suggesting in the biomass a very less bond vibration in the wavenumber range due to NIR absorption.

Posom et al.43 indicated the similar peaks for milled bamboo which is solely one specie of biomass where the main peaks were 6823 cm−1 (1466 nm), 5192 cm−1 (1926 nm), 4752 cm−1 (2104 nm) and 3992 cm−1 (2505 nm). These indicate the influence of different kinds of biomass species on average spectrum.

Figure 2b shows the absorbance spectra pretreated using SNV transformation. A similar peak structure of raw spectrum is maintained in SNV spectrum. However, SNV preprocessing effectively mitigates baseline shifts, enhancing spectral comparability. Although both sample types exhibit similar spectral characteristics, but the main peaks after 12,500–6000 cm−1 the absorption of agricultural residue exhibit higher, including the range between 4397 cm−1 (2274 nm, lignin vibration) and 4011 cm−1 (2493 nm, lignin and cellulose vibration)44 and near to 4755 cm−1 (2103 nm) is the band for α-d- glucose, and 4000 cm−1 (2500 nm) is the band corresponding to C-H stretching + C-C stretching of starch39. But the vibration of between 6000–5600 cm−1 which is broad weak band of lignin and cellulose where the peak 5951 cm−1 (1680 nm) is the peak of pure lignin43, the band of both species is very close absorption. Though, beyond 6000 cm−1 the absorption is lower obviously.

Figure 2c shows the plot of the 1st derivative of log (1/R) versus wavenumber that reveals distinct spectral features. Significant peaks were observed in the 4000 to 7000 cm−1 range, with the most prominent peaks around 7050, 5245, 4775, 4428, 4381 and 4057 cm−1. Specifically, the peak at 7050 cm−1 is related to C–H combination bands found in hydrocarbons or aromatic38. The peak at 5245 cm−1 relates with P–OH groups in phosphate38. The peak of 4775 cm−1 corresponds to the O-H deformation band, which is present in alcohol or water38. The peak at 4428 cm−1 represents lignin38. The peak at 4381 cm−1 corresponds to C-H stretching and CH2 deformation bending in polysaccharides38. The peak 4057 cm−1 corresponds to the CONH2 groups commonly present in proteins38. These peaks indicate the rapid change absorption points in raw spectra at these wavenumbers. Beyond 7000 cm-1, the data trend stabilizes, showing minimal variations up to 12500 cm−1. This stabilization suggests very low and consistent absorption characteristics in the higher wavenumber range. The zero absorption in 1st derivative spectrum is the peak absorption in raw spectrum.

Figure 2d shows the 2nd derivative plot of log (1/R) versus wavenumber providing insights to reveal the overlapping peaks in the raw absorption spectra and due to the gap of derivative, the shifted peaks of 6711 cm−1 (1490 nm), 5951 cm−1 (1680 nm), 5076 cm−1 (1970 nm), near to 4755 cm−1 (2103 nm), 4636 cm-1 (2157 nm), 4397 cm−1 (2274 nm), 4011 cm−1 (2493 nm), and 4000 cm−1 (2500 nm) in raw and SNV spectra are shown.

Statistic values of GWP and HHV

The provided data in Table 3 comprehensively details the statistical analysis used in the development of a PLSR model. It shows that the GWP parameter in calibration set includes 148 samples. The values range from a maximum of 0.0390 to a minimum of 0.0330, with a mean of 0.0330 and an SD of 0.0012. The SD is approximately 36.4 times less than the mean (0.0330/0.0012), suggesting that the data points are closely clustered around the mean value. The prediction set of 50 samples is designed to test the accuracy and precision of the model developed using the calibration data set. For the GWP parameter, the prediction set samples have a slightly lower maximum, minimum and mean value and a higher SD of 0.0030 shows greater variability in the prediction set data compared to the calibration set.

Table 3 Statistic values of GWP and HHV for modeling.
Full size table

The HHV (J g-1) statistics in the prediction set has slightly lower variation than the calibration set with SD of 836 J g-1 compared to 848 J g-1 indicating the same distribution of data.

Predicting performance of biomass GWP using PLSR

GWP is a critical metric for assessing the environmental impact of various biomass. Accurate prediction of GWP can inform sustainable practices and policy decision. In this study, the PLSR method is utilized to model and predict the GWP of different biomass samples including fast growing trees and agricultural residue.

Table 4 shows the results for predicting GWP of various biomass developed from raw spectra and different spectra pre-treatment and different number of wavenumbers from the respective feature variable selection method, demonstrating by the number of latent factors, R2C, RMSEC, R2P, RMSEP, RPD and Bias. The prediction results depended on the development methods, spectral pre-treatment, and the number of wavenumbers. The models with different variable selection methods gave the same performance, but the number of wavenumbers differed. The model developed with CM (reduction of 1150 wavenumber of full range to 325 wavenumber) of 1st derivative spectra, gave best performance with R2P was 0.87 (Table 4).

Table 4 Prediction of GWP of biomass of fast-growing tree and agriculture residue by PLSR.
Full size table

In the context of predicting GWP of biomass using FT-NIR spectroscopy, the following Williams et al.37 indicated R2 showed the proportion of the variance of the NIRS predicted data, i.e. GWP can be explained by the spectral variables or log 1/R and shows the degree of which the predicted data can be change, for a given change in the spectral data which higher values of R2 indicating better predictive accuracy.

Figure 3 illustrates the scatter plot of the GWP of biomass calculated using IPCC method and predicted by NIRS using the 1st derivative of the 325 wavenumbers obtained by COVM which outperformed the other predictive model's performance of GWP. The COVM variable reduction method helps identify and retain the most relevant wavenumber, enhancing the model's efficiency and accuracy. The R2C and R2P of featured wavenumber selection model was 0.92 and 0.85, respectively, indicating a linear relationship between the predicted and calculated values during both the calibration and prediction. From Table 4 the RMSEC is 0.00053, and RMSEP is 0.00063 show low prediction errors. The bias, which measures the systematic error, is -0.00014, showing minimal deviation from zero and thus negligible bias in the predictions. The RPD value of 2.6 signifies a fair predictive capability of the model for functional parameter including GWP, as values 2.5–2.9 were considered for screening applications37. This method effectively enhances average the model's performance by focusing on the most informative wavenumber prediction and reducing dimensionality, leading to more accurate and reliable predictions. These high R2P values (0.85) in predicting the GWP indicate the model usable with caution for most application including research which the threshold of R2 indicated by Willams guidelines is between 0.83–0.9037.

Fig. 3
figure 3

IPCC calculated GWP versus NIRS predicted GWP in calibration and prediction sets. This PLSR modeling based on the first derivative spectra of 325 selected wavenumbers by covariance method, which demonstrated superior predictive performance compared to other models (R2C = 0.92, R2P = 0.85).

Full size image

Prediction result of HHV using PLSR

Table 5 displays the optimal result of PLSR-based models using the full wavenumber range (3600–12,500 cm-1) to evaluate the HHV of the chip biomass from the fast-growing trees and agricultural residues. Shrestha et al.17 has described the HHV of the grounded biomass measured using the isoperibol method with an automatic bomb calorimeter (IKA C 200, Staufen, Baden-Württemberg, Germany). The data presents the performance of various pre-processing techniques—Raw Spectra, SNV, First Derivative, and Second Derivative—across calibration and prediction sets. Key metrics such as the number of latent factors, R2C and R2p, RMSEP, bias, and RPD were provided. Among these techniques, SNV demonstrates the highest R2C and R2p, though the value were low i.e. R2C (0.5879) and R2p (0.4972) values, indicating that while SNV provides some improvement in model performance compared to other preprocessing methods, the overall predictive capability of the model remains limited26. Additionally, SNV exhibits the lowest SEP (1.44 J g-1) and RMSEP (2.88 J g-1) values, suggesting more precise and accurate predictions compared to other techniques, though the R2P is very low making the model is not recommended to be used.

Table 5 Result of HHV prediction by PLSR using different preprocessing spectra and different variable selected methods.
Full size table

Figure 4 shows the best model for predicting the HHV of biomass was developed using the 2nd derivative spectra and variable selection by the COVM method. This approach reduced the number of variables from 1150 to 365 wavenumbers, significantly enhancing the model's performance (R2C of 0.98 and R2P of 0.87) indicating the model usable with caution for most application including research in predicting the HHV, and RPD value of 2.7 signifies a fair predictive capability of the model for functional parameter including GWP, as values 2.5–2.9 were considered for screening applications37.

Fig. 4
figure 4

HHV measured by bomb calorimeter versus predicted value by NIR spectroscopy. The optimal model for predicting the HHV of biomass was developed using the 2nd derivative spectra combined with wavenumber selection via the correlation method. This approach reduced the number of variables from 1150 to 365 wavelengths, significantly improving model performance (R2C = 0.98, R2P = 0.86).

Full size image

Regression coefficient and x-loading of GWP model

Prominent peaks were identified and the bond vibration interpretation is shown in Table 7 and the vibration indicated by Workman and Weyer38 at the wavenumbers in bold were not found or not related to biomass.

Figure 5a presents the regression coefficient plot for the optimal PLS model predicting the GWP in biomass using the full-range wavenumber spectra. Prominent peaks were found at 4011 (Cellulose), 4196 [C-H (1ν) + C-H (1δ)], 4651 [C-H (1ν) + C-C (1ν)], 4744, 5214 (water), 5400, 6001, 6086, 6441 (water) and 7151 [CH3 (2ν) + CH3 (1δ)] cm−1. In comparison, the regression coefficient plot for the selected wavenumber model (Fig. 5b) revealed key peaks at 4142 [C-H (1ν) + C-H (1δ)], 4389 [C-H (1ν) + CH2 (1δ)], 4605 proteins, 4867 amides/proteins, 5338, 6017, 7097, 7189 [CH3 (2ν) + CH3 (1δ)] and 8686 cm−1.

Fig. 5
figure 5

Regression coefficient of GWP calibration model using 1st derivative spectra with full wavenumbers (a) and selected wavenumber (b). The peaks in the regression coefficient plot highlight molecular bond vibrations, where high positive and high negative peaks indicate the vibration of the wavenumber is significantly high influence theprediction values.

Full size image

Figure 6a shows the X-loading plot of the first latent variable (LV1) for the full-spectrum model, highlighting wavenumbers that contribute significantly to model performance. Notable peaks were observed at 4196, 4451, 4528 [N-H (3ν)], 5060 (water), 5292, 6791, and 7050 cm−1, where the X-loading of 1st latent variable Selected wavenumber-loading plot for the selected wavenumber model (Fig. 6b) shows influential peaks at 4065 [CH3 (3δ)], 4304 [C-H (1ν) + CH2 (1δ)], 4397 (glucose), 4682, 5230 (phosphate), 5307, 6970, 7436, and 8647 cm−1.

Fig. 6
figure 6

X-loading plot of latent variable 1 of GWP model developed using 1st derivative spectra with full wavenumber range (a) and selected wavenumber (b). The peaks in the X-loading plot highlight molecular bond vibrations, where high positive and high negative peaks indicate the vibration of the wavenumber is significantly high influence the latent variable score values.

Full size image

The vibration of most molecular bonds which had strong contribution in prediction of GWP, were in hydrocarbons including cellulose; glucose; water; and protein, even GWP is a functional properties not a constituent in the biomass.

Regression coefficient and x-loading of HHV model

Prominent peaks were identified and the bond vibration interpretation is shown in Table 7 and the vibration indicated by Workman and Weyer38 at the wavenumbers in bold were not found or not related to biomass.

For the HHV prediction model, the regression coefficient plots are presented in Fig. 7. In the full-spectrum model (Fig. 7a), prominent peaks were observed at 4397 (glucose), 4960 [C-H (1ν) + O-H (1δ)], 5168 (water), 5330, 5947 [C-H (2ν)], 6672, and 7506 cm−1. In contrast, the selected wavenumber model (Fig. 7b) exhibited dominant peaks at 4111 [C-H (1ν) + C-H (1δ)], 4520 [N-H (3ν)], 4644 [C-H (1ν) + C-C (1ν)], 5307, 5369, 5978 [C-H (1ν) + C-H (1ν)], 6063, 7020, and 7220 cm−1.

Fig. 7
figure 7

Regression coefficient of HHV calibration model using 1st derivative spectra with full wavenumbers (a) and selected wavenumber (b). The peaks in the regression coefficient plot highlight molecular bond vibrations, where high positive and high negative peaks indicate the vibration of the wavenumber is significantly high influence the prediction values.

Full size image

The LV1 of X-loading plots, shown in Fig. 8, highlights the critical wavenumbers contributing to the model’s performance. In the full-spectrum model (Fig. 8a), significant peaks were found at 4165 [C-H (1ν) + C-H (1δ)], 4435, 4520, 5037, 5292, 6595, and 7112 [O-H (2ν)] cm−1. The selected wavenumber model (Fig. 8b) revealed key peaks at 4034, 4134 [C-H (1ν) + C-H (1δ)], 4443, 4983, 5230 (phosphate), 5361, 5963 [C-H (2ν)], 7081 and 7274 cm−1.

Fig. 8
figure 8

X-loading plot of HHV model developed by using 2nd derivative spectra with full wavenumbers (a) and selected wavenumber (b). The peaks in the regression coefficient plot highlight molecular bond vibrations, where high positive and high negative peaks indicate the vibration of the wavenumber is significantly high influence the prediction values.

Full size image

The similar bond vibration contributed to prediction of both HHV and GWP including 5230 (phosphate), (5168 and 5214 nm, respectively) water, (4651, 4644 nm, respectively) [C-H (1ν) + C-C (1ν)], (4520, 4528 nm, respectively) [N-H (3ν)], 4397 (glucose), and (4134, 4142 nm, respectively) [C-H (1ν) + C-H (1δ)], obviously.

Averaging reference value of GWP and HHV parameter of biomass

GWP and HHV are essential for optimizing biomass as a renewable energy source and mitigating its environmental impact. The environmental sustainability of biomass is primarily assessed using the GWP measured in CO2 equivalents over a 100-year period.

Table 6 illustrates the average reference value of GWP and HHV (J g-1) of fast-growing trees and agricultural residues. It shows that the fast-growing trees possess variability in their values reflect slight variations in their chemical composition and energy content, influencing the different biomass applications. They underline the variability within agricultural residues, impacting their efficiency and environmental impact when used as bioenergy sources. It shows that fast-growing trees generally possess higher heating values and carbon content, making them more efficient as biomass fuels. However, the GWP values indicate varying degrees of environmental impact, whichis crucial for sustainable energy production. Most of agricultural residues, while slightly lower in energy content, offer a viable alternative due to their abundance and ease of collection with their lower GWP values necessitate careful consideration in their use to mitigate climate impact. These insights into the chemical and energy profiles of various biomass resources provide a foundation for selecting optimal materials for bioenergy, balancing efficiency, and environmental sustainability (Table 7).

Table 6 Average of reference value of GWP and HHV (J g-1) of fast-growing trees and agricultural residues.
Full size table
Table 7 The function groups corresponding to wavenumber shown in regression coefficient plot and x-loading plot of models for GWP and HHV.
Full size table

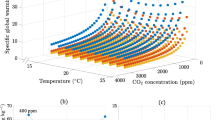
The scatter plot illustrates the correlation between GWP and HHV across three distinct sample groups: fast-growing trees (Fig. 9a), agricultural residues (Fig. 9b), and a mixture of fast-growing trees and agricultural residues (Fig. 9c). The results indicate a strong linear relationship between GWP and HHV, with a coefficient of determination (R2) equal to 1, demonstrating perfect fit. The equation governing the calculation of GWP from HHV is consistent across all sample types and is expressed as GWP or GWP total = 2098.0 × HHV in TJ kg-1 = 0.000002098 × HHV in kJ kg-1 = 0.000002098 × HHV in Jg-1.

Fig. 9
figure 9figure 9

Scatter plots of GWP value with different HHV of every sample of fast-growing trees (a), every sample of agriculture residues (b) and every sample of fast-growing trees and agriculture residue (c). The scatter plot with a trend line, illustrating the relationship between Higher Heating Value (HHV) and Global Warming Potential (GWP) for fast-growing trees and agricultural residue biomass. The plot shows a positive correlation, indicating that biomass with higher HHV tends to contribute more to GWP. Data points are color-coded by biomass type and mostly fall within the mid-range of HHV (15,800–18,000 J g⁻1) and GWP (0.0320–0.0380). This suggests that higher energy content in biomass is associated with greater environmental impact due to increased emissions.

Full size image

However, the HHV directly measurement is destructive, time consuming and chemical is necessary, therefore, it is not environmentally friendly. But our NIRS proposed method in this report is non-destructive, fast and no chemical is necessary, therefore, environmentally friendly.

It can be perfect fit based on the IPCC guideline recommendation, the GHG emission in our calculation is for 1 kg biomass sample (It can be perfect fit even if the different number is used but it have to be fixed throughtout the calculation).

The calculation for proving the perfect fit between GWP and HHV is shown in following

$$ \begin{gathered} {\text{GHG}}\;\left( {{\text{e}}.{\text{g}}.{\text{ CO}}_{{2}} ,\;{\text{or}}\;{\text{CH}}_{{4}} ,\;{\text{or}}\;{\text{N}}_{{2}} {\text{O}}} \right){\text{Emissions }}\left( {{\text{kg}}} \right) \hfill \\ \quad = {\text{Mass}}\;{\text{of}}\;{\text{biomass}}\;{\text{sample}}\;\left( {{\text{kg}}} \right) \times {\text{HHV}}\;{\text{of}}\;{\text{biomass}}\;{\text{sample}}\left( {{\text{TJ}}\;{\text{kg}}^{{ - {1}}} } \right) \hfill \\ \quad \times {\text{Emission}}\;{\text{Factor}}\;\left( {{\text{EF}}} \right)\;{\text{of}}\;{\text{corresponding}}\;{\text{GHG}}\;\left( {{\text{kg}}\;{\text{TJ}}^{{ - {1}}} } \right) \hfill \\ \end{gathered} $$
(7)

GHG Emissions (kg) represents the total amount of emissions produced. Mass of biomass samples (kg) refers to the total mass of the biomass sample burnt. High heating value (HHV) (TJ kg-1) is the total amount of energy in TJ obtained by 1 kg of biomass completely burnt in bomb calorimeter. According to the IPCC 2021 Guidelines, default greenhouse gas emission factors (in kg TJ-1) for wood and woody biomass combustion are 112 kg CO2/TJ (non-biogenic CO2 only), 30 kg CH4/TJ, and 4 kgN2O/TJ, expressed based on energy content of the fuel burned7.

Substitute the constant numbers and solely the HHV is variable which multiplied with constant number provided simple linear equation and the constant number is slope of the equation

GHG (e.g. CO2, or CH4, or N2O) Emissions (kg) = 1 (kg) × HHV of biomass sample (TJ kg-1) × 112 kg CO2/TJ (non-biogenic CO2 only) or 30 kg CH4/TJ, or 4 kg N2O/TJ, respectively, used for Emission Factor (EF) of corresponding GHG (kg TJ-1)

CO2, or CH4, or N2O Emissions (kg) = 112 × HHV, 30 × HHV and 4 × HHV for CO2, or CH4, or N2O) Emissions, respectively

Using the Global Warming Potential (GWP) values recommended by IPCC (2021) 6th Assessment Reports (AR6)7, 1 by CO2, 29.8 by CH4, and 273 by N2O, the total GWP was computed for 100 year based as:

Substitute the constant numbers and solely the HHV is variable which multiplied with constant number provided simple linear equation and the constant number is slope of the equation

$$ \begin{gathered} {\text{GWP}}\;{\text{for}}\;{\text{CO}}_{{2}} ,\;{\text{or}}\;{\text{CH}}_{{4}} ,\;{\text{or}}\;{\text{N}}_{{2}} {\text{O}}\;{\text{Emissions}} = ({1} \times {\text{CO}}_{{2}} \;{\text{Emission}}) \hfill \\ \quad {\text{or}}\;({29}.{8} \times {\text{CH}}_{{4}} \;{\text{Emission}})\;{\text{or}}\;({273} \times {\text{N}}_{{2}} {\text{O}}\;{\text{Emission}}) \hfill \\ \quad = ({1} \times {112}\;{\text{HHV}})\;{\text{for}}\;{\text{CO}}_{{2}} {\text{Emissionor}}({29}.{8} \times {3}0\;{\text{HHV}}) \hfill \\ \quad {\text{for}}\;{\text{CH}}_{{4}} \;{\text{Emissionor}}({273} \times {4}\;{\text{HHV}})\;{\text{for}}\;{\text{N}}_{{2}} {\text{O}}\;{\text{Emission}} \hfill \\ \quad = {112}.0 \times {\text{HHV}}\;{\text{for}}\;{\text{CO}}_{{2}} \;{\text{Emissionor}}\;{894}.0 \times {\text{HHV}} \hfill \\ \quad {\text{for}}\;{\text{CH}}_{{4}} \;{\text{Emissionor}} \;{1}0{92}.0 \times {\text{HHV}}\;{\text{for}}\;{\text{N}}_{{2}} {\text{O}}\;{\text{Emission}} \hfill \\ \quad {\text{and}}\;{\text{GWP}}\;{\text{total}} = {2}0{98}.0\left( {{\text{HHV}},\;{\text{TJ}}\,{\text{kg}}^{{ - {1}}} } \right) \hfill \\ \quad = 0.00000{2}0{98}\,{\text{kJ}}\,{\text{kg}}^{{ - {1}}} = 0.00000{2}0{98}\,{\text{Jg}}^{{ - {1}}} \hfill \\ \end{gathered} $$
(8)

Discussion

The prediction of GWP of biomass using FT-NIR spectroscopy presents an innovative approach to evaluating the environmental impact of biomass energy sources. Biomass is increasingly considered a vital renewable energy resource, but its sustainability is contingent upon a comprehensive understanding of its environmental implications, particularly its GWP, which reflects its contribution to climate change.

Correlation between HHV and GWP

The results exhibit a correlation between the chemical composition of biomass within its FT-NIR spectrum, and its GWP. The FT-NIR technique scanned the vibrational signatures of molecular bonds in the biomass, which reveal its composition, particularly in terms of cellulose, hemicellulose, lignin, and moisture content45. These compositional factors directly influence the biomass's HHV and, consequently, its GWP. The positive correlation examined in the study between HHV and GWP suggests that biomass with a higher energy content tends to have a higher GWP, likely due to the increased carbon content, which results in greater CO2 emissions upon combustion. NIR spectroscopy can be used to assess biomass's carbon content, which is directly connected to the amount of CO2 it emits when burned46. Building on this, our work incorporates emissions of CH4 and N2O in addition to CO2 and establishes a direct correlation between GWP and the NIR spectral data.

Prediction model and its accuracy

The predictive models shown in Fig. 3 used FT-NIR data and modeling technique of PLSR exhibit for the acceptable accuracy in estimating the GWP of various biomass types. The R2P values of 0.85 indicated optimized 325 wavenumber found by COVM with 1st derivative spectra in our study provided the model with a substantial proportion of the variance in GWP can be explained by the spectral data, affirming the effectiveness of FT-NIR as a non-destructive, rapid, and cost-effective method for GWP estimation. The prediction of GWP in real-time can substantially enhance the decision-making process in biomass selection for energy production, ensuring sustainability goals. This is the innovative and unique model to find out the GWP using FT-NIR spectroscopy. The model performance of HHV is shown in Fig. 4, where the R2P values is 0.86 by 2nd derivative spectra of optimized 365 wavenumbers found by COVM.

Williams et al.37 have developed a guideline for model performance interpretation based on R2P value and RPD value, where, our case, R2P of 0.85 for GWP and 0.86 for HHV is in the range of 0.83–0.90 is usable with caution for most applications including research and RPD of 2.6 for GWP and 2.7 for HHV are in the range of 2.5–2.9 for functionality parameter such as GWP and HHV indicating the models are fair and can be used for screening. We therefore, interpret our GWP and HHV optimized models can be usable with caution for most applications including research based on its R2P.

The developed PLSR model is built on a mixture of five fast-growing tree species and five types of agricultural residues, which is same biomass data set as Shrestha et al.18 who reported the effect of diffent species to model performance for prediction of C, H, N, and O content in biomass. The result shows for C model to be better the pine and corn stover should not be include in modeling, for N model, pine, and bagasse should not be included, for H, pine, Alnus, corn shell, and bagasse should not be included; and for O, pine should not be included for better performance of the models18. This indicated pine was not be included in any model of these groups of biomass with the rational by Williams principle37 to be explained.

Williams et al.37 explained that the rate of change of Y (measured value) is a function of the rate of change of X (NIR predicted value) can be indicated by slope of the trend line ploted between Y and X18,37, when the R approached 1 and the slope approached 1 and the intercept approached zero, the model approached excellence37. This is the dictation principal to remove or keep the species which have negative and positive effect, respectively, on the model performance. The combined different species of biomass, for example, in our case, the fast-growing trees and agricultural residue, Shrestha et al.18 indicated the inclusion of different species in a model, the species have to be not only in the different values of the constituents to make a wider range for a robust model, but every specie also must provide the characteristic of the same rate of change of NIR predicted values with the measured values (same slope and slope should approach 1, and intercept is same (no gap) and approached zero), for high performance of prediction. Some species whose characteristics were similar, the trends were common supported the each other but might positively or negatively to the prediction performace of the model18. By scatter plot (trend line) analysis, which of the species affecting the model negatively were identified and dictated how to improve the model performance18.

The H content contributed more on HHV compared to C content47,48. Higher concentrations of O and moisture (H2O), in turn, lower the HHV, resulting in incomplete combustion48. High C and H but low in N, S, and H2O is the besttype of biomass maximizing the amount of energy i.e. HHV48. These element in biomass highly related to GHG emissions48, therefore, GWP. The further study and investigation of these relations can bring some conclusions of Global warming management effectively.

Analysis of traditional method and FT-NIR spectroscopy

The traditional methods of GWP estimation, which often involve complex chemical analyses and life cycle assessment (LCA) models whereas FT-NIR spectroscopy approaches a more streamlined. Traditional methods, while comprehensive, can be time-consuming and resource intensive. FT-NIR, by contrast, provides rapid results, making it an attractive tool for routine analysis and large-scale biomass screening39.

Though, FT-NIR offers rapid, non-destructive, and cost-effective GWP prediction, it has certain limitations. For instance, the developed model's accuracy will be affected by other variability in biomass composition, such as differences in moisture content, lignin, or cellulose levels, if were not included in the model. The updating model can be optimized by include more varieties and species of biomass to obtain more robust prediction performance. However, it is essential to note that while FT-NIR can predict GWP based on biomass composition, it does not account for the entire lifecycle emissions, such as those from cultivation, harvesting, transportation or processing. While FT-NIR is highly effective for rapid screening, it should be used in conjunction with other LCA tools for a holistic assessment.

Sustainable approach to implications for biomass energy sector

The ability to predict GWP using FT-NIR spectroscopy has significant implications for the biomass energy sector. By enabling more precise selection of biomass feedstocks with lower GWP, this approach supports the development of more sustainable bioenergy systems. This could lead to a reduction in the overall carbon footprint of bioenergy production, making it a more competitive alternative to fossil fuels in the context of global climate change mitigation49.

Future research and way forward

Future research should focus on expanding the database of biomass types analyzed using FT-NIR to improve the robustness and generalizability of the predictive models. Additionally, integrating FT-NIR data with thermogravimetric analysis (TGA) where the simulation of different type thermal conversion of biomass degrading in which the different emission gases are generated and with gas chromatography-mass spectrometry (GC–MS) for evaluation of concentration of the generated emission gases could further refine GWP predictions by providing more comprehensive insights and exact content of emission gases effect global warming to support the IPCC. Moreover, exploring the use of FT-NIR in conjunction with different machine learning algorithms could enhance the predictive power of the models, allowing for more accurate GWP estimation across a broader range of biomass types.

Conclusion

In this research, PLSR-based model developed and compared using FT-NIR spectroscopy to analyze the global warming potential (GWP) of fast-growing trees and agricultural residue biomass. All chip biomass samples were scanned within 3600–12,500 cm-1 on the diffuse reflectance with macro sphere sample rotating mode, with a particular emphasis on their suitability for energy applications. The prediction model was developed using the full standard normal variate (SNV) or featured wavenumbers obtained by Correlation Matrix (CM), Variance Matrix (VM), Covariance Matrix (COVM) and Variable Importance of Projection (VIP) coupled with four pretreatment methods including raw spectra, 1st Derivative, 2nd Derivative, and standard normal variate (SNV). The model with the optimum performance was selected based on trade-off parameters of R2C, RMSEC, R2P, RMSEP, RPD and bias.

This research lays a foundation in NIRS, showing that preprocessing on the full wavenumber range spectra with various techniques can enhance model accuracy. The recommended PLSR models for rapid assessing GWP by biomass combustion developed by 1st derivative pretreated spectra with selected wavenumber obtained by COVM can serve as a reliable and nondestructive alternative method without of using the measured higher heating value (HHV) value when employing NIRS which only the NIR spectrum of the biomass is needed. It is nondestructive protocol developed for the first time for climate change which usable with caution for most applications including research interpreted followed Williams Guidelines37. Therefore, it is necessary to expand sample size from various samples to enhance the model robustness and validate it with unknown samples for proving. We employed the GWP calculation method indicated by IPCC combined with PLSR (Partial Least Squares Regression) modeling achieving a prediction model performance with R2C = 0.92 and R2P = 0.85 which demonstrates an optimized model could be used with caution for most application including research. In upcoming paper modeling, we plan to further enhance the model performance by other machine learning techniques such as Random Forest and Support Vector Regression and deep learning such as CNN which may or may not be more accurate in GWP predictions than PLSR in this manuscript.

GWP varies significantly with changes in both HHV and the Emission Factor. This analysis indicates that while both parameters directly influence GWP, the magnitude of their impact can differ depending on specific conditions. For instance, a 10% increase in the Emission Factor could result in a significant rise in GWP, whereas a similar 10% increase in HHV might have a less impact on GWP. This explains that focusing on reducing emissions (e.g. through cleaner combustion technologies or better fuel treatment) could be more effective in reducing overall GWP than merely increasing fuel efficiency.

Furthermore, the research finding could assist academic and research institutions, policymaking think tanks, and energy companies in effective planning, managing, and utilization of bio-resources to meet future energy demands and mitigating the global warming. Additionally, this research outcomes open opportunities for NIR-based research to implement similar approaches.