Path-based evaluation of deep learning models for solving inverse kinematics in a revolute-prismatic robot

Abstract

This study investigates the generalization performance of deep learning (DL) models for solving the inverse kinematics (IK) problem in a 2-degrees of freedom (DOF) revolute-prismatic (RP) robotic manipulator. The goal is to evaluate how effectively different neural architectures predict joint configurations from end-effector positions across diverse workspace regions. Two training strategies were used: quadrant-based and full workspace training. To improve robustness, k-fold cross-validation (CV) was applied to the deep feedforward neural network (DFNN). The models evaluated include DFNN with k-fold CV using 2-input 1-output and 2-input 2-output formulations and without k-fold CV, long short-term memory (LSTM), and gated recurrent unit (GRU). Performance was tested on predefined Square and Circle paths within each quadrant and the full workspace. The DFNN with k-fold CV (2-input, 1-output) consistently achieved the lowest Cartesian deviation errors- for instance, 0.289 mm in Q1, 0.410 mm in Q2, 0.508 mm in Q3, and 0.715 mm in Q4 on Square path. Similar trends were observed on the Circle path, with errors of 0.312 mm, 0.366 mm, 0.438 mm and 0.662 mm in Q1 to Q4 respectively. In full workspace testing, it maintained strong performance with 1.594 mm (Square) and 2.084 mm (Circle) errors. In contrast, DFNN with k-fold CV (2-input, 2-output), without k-fold CV, LSTM and GRU exhibited significantly higher errors. These findings demonstrate that the k-fold CV-based DFNN with single-output formulation, achieves high accuracy and generalization and also capable of handling singularities and ambiguity in joint solutions.

Introduction

Inverse kinematics (IK) is a fundamental problem in robotics, where the goal is to determine the joint parameters of a robotic manipulator for a given end-effector position. Traditional analytical and numerical methods, though widely used, often struggle with real-time constraints and workspace singularities. This makes machine learning (ML)-based approaches, particularly neural networks (NNs), a promising alternative for efficiently solving the IK problem. Recent studies have demonstrated the ability of NNs to approximate non-linear mappings and generalize across various workspaces using random points in the workspace, but few explore how these models generalize to continuous trajectories.

Several studies have leveraged artificial neural networks (ANNs) and deep learning (DL) to improve IK computation accuracy and efficiency. Adar¹ proposed a real-time IK solution for a 5-degrees of freedom (DOF) manipulator using a multi-layer perceptron (MLP) combined with a proportional-integral (PI) control system, achieving root mean square error (RMSE) < 0.85. Wagaa et al.² compared analytical and DL methods, including ANN, convolutional neural network (CNN), long short-term memory (LSTM), gated recurrent unit (GRU), and bidirectional long short-term memory (BiLSTM), for solving IK and trajectory tracking of a 6-DOF robotic arm, achieving RMSE between 0.0042 and 0.0149 with a position error < 1 mm. Vu et al.³ developed a ML-based framework for real-time IK computation of a 7-DOF redundant manipulator, achieving RMSE < 0.05 for the KUKA LBR iiwa 14 R820. Ma et al.⁴ applied a backpropagation neural network (BPNN) for soft actuators, reducing average IK errors to 2.46%.

Other works have focused on enhancing convergence speed and generalization. Sharkawy⁵ utilized a multilayer feedforward neural network (MLFNN) for forward kinematic (FK) and IK of a 2-DOF manipulator, achieving zero approximation error. Pang et al.⁶ introduced an improved BPNN for solving IK in a 7-DOF rehabilitation robot, achieving position errors < 1 mm and posture errors < 0.1 mm. Wang & Deng⁷ applied deep reinforcement learning (DRL) for multi-robot coordination in dynamic environments, ensuring robust task completion but lacking real-world validation. Gao⁸ optimized BPNN for 6-DOF robots, improving convergence and accuracy but limiting validation to simulations. Semwal & Gupta⁹ compared NNs with analytical methods for 3-DOF manipulators, finding limitations in sparsely trained regions but highlighting potential scalability to higher-DOF robots.

Several hybrid approaches have been introduced to enhance performance. Shareef¹⁰ implemented a deep artificial neural network (DANN) with 10 hidden layers for solving IK on the 6-DOF PUMA 260, achieving a maximum error of 1.579% and R² ≈ 0.99981, though limited to a single robot model. Shastri et al.¹¹ hybridized ANN with particle swarm optimization (PSO), simplified particle swarm optimization (SPSO), and modified simplified particle swarm optimization (MSPSO) for a 3-DOF robot, improving convergence speed and accuracy but at high computational cost. Aggogeri et al.¹² optimized a 3-DOF ANN with genetic algorithms (GAs), reducing trajectory error by 97%. Tammishetty et al.¹³ developed a multimodal input ANN for a 3-DOF manipulator, achieving 99% accuracy but with high computational overhead. Jiménez-López et al.¹⁴ combined quaternion algebra with ANN for a 3-DOF robot, achieving < 1 mm position error but focusing only on planar configurations.

Toquica et al.¹⁵ compared analytical IK with MLP, LSTM, and GRU models for a 3-DOF IRB360 robot, finding GRU to be the most stable and MLP to converge fastest. Gholami et al.¹⁶ applied an MLP with online retraining for real-time IK control of a 3-DOF Delta robot, improving tracking precision but requiring retraining for dynamic tasks. Zhu et al.¹⁷ introduced a hybrid artificial bee colony (ABC)-based BPNN and quaternion-multilayer Newton (QMn-M) algorithm for FK of a 6-DOF Gough–Stewart platform, improving accuracy near singular configurations. Tagliani et al.¹⁸ developed a GA-optimized sequential ANN for 6-DOF IK, reducing errors by 42.7–56.7% compared to global methods.

Recent work has further improved accuracy and speed. Lu et al.¹⁹ proposed an MLP-based IK solution for 6-DOF robots using joint space segmentation, classification models, and Newton–Raphson refinement, achieving position errors < 0.001 mm and orientation errors < 0.01°. Wang et al.²⁰ proposed a Gaussian-damped least squares (GDLS) IK solver for 7-DOF redundant robots, integrating ANNs with optimization principles. Their approach achieved RMSE < 0.01 mm and a convergence accuracy of 96.23%. Wu et al.²¹ introduced OTDPP-Net, a deep neural network (DNN)-based path planner using CNNs for value iteration. Sharkawy & Khairullah²² proposed an MLFFNN-based approach using the Levenberg–Marquardt (LM) algorithm for solve FK and IK of a 3-DOF manipulator. Their model achieved high accuracy, with mean squared error (MSE) values of $\:4.59\times\:{10}^{-8}$ for FK, $\:9.07\times\:{10}^{-7}$ for IK, ensuring minimal error and fast computation. Gadringer et al.²³ proposed a hybrid robot calibration approach that combines a kinematic model with an ANN and geometric calibration using a laser tracker, achieving a maximum position error of 0.605 mm and a maximum orientation error of 3.753mrad, ultimately reducing positioning and orientation errors by 93% and 92%, respectively, compared to the uncalibrated model. Shah et al.²⁴ developed and experimentally validated a DANN model for a 5-DOF manipulator. Their network trained for 500 epochs with the LM algorithm, demonstrated an MSE of $\:8.926\times\:{10}^{-7}$ and positional deviations within $\:\pm\:0.05$mm.

Hamarsheh et al.²⁵ developed an ANN approach to solve the IK of a 6-DOF KUKA industrial manipulator using a Non-Linear Autoregressive NN with Exogenous Inputs and an Adaptive Feedforward NN, trained on FK data using MATLAB, achieving the best MSE of 0.005 with Bayesian Regularization and 250 neurons. Dalmedico et al.²⁶ proposed an ANN approach to solve the IK of a 4-DOF robotic arm in 3D using a MLP trained on FK data with the LM algorithm, achieving Euclidean errors of 0.112 cm in simulation 1 and 0.219 cm in simulation 2. Yang et al.²⁷ developed a novel IK algorithm for a 7-DOF manipulator with offset, combining analytical and numerical methods while incorporating joint and position constraints to enhance accuracy, generating multiple solutions using the gradient method. Guo et al.²⁸ developed an analytical IK computation method for a 7-DOF manipulator with an S-R-S configuration, utilizing FK based on the Denavit-Hartenberg (DH) modelling approach and decoupling redundancy through arm angle parameterization, with the method verified using robotics toolbox and ROS simulation. Shaar and Ghaeb²⁹. developed a Recurrent Neural Network (RNN) model to solve the IK of a 6-DOF industrial manipulator, training it on 100,000 FK -generated samples with a single hidden layer of 12 neurons, achieving a MSE of 0.0013 and a regression factor (RF) of 0.99. Bouzid et al.³⁰ analysed the performance of ANNs in solving IK for a 2-DOF robotic arm with varying arm lengths, training the model on FK data using three dataset types (fixed step, random step, and sinusoidal) and evaluating three optimization algorithms (LM, Bayesian regularization, and scaled conjugate gradient), achieving the best MSE of 2.1573 using the random step dataset with the LM algorithm. Joshi et al.³¹ applied DFNNs, CNNs, RNNs, and LSTMs with Bayesian optimization and SHAP analysis for 6-DOF anthropomorphic robots, achieving real-time IK prediction with MSE of $\:1.934-3.522\times\:{10}^{3}$ and latency of ~ 1.25 ms/sample. Zhao et al.³² proposed MAPPO-IK, a reinforcement learning-based algorithm using Gaussian and cosine distance rewards for real-time, unique IK solutions. It demonstrated superior generalization, computational efficiency, and dynamic adaptability. Palliwar et al.³³ integrated GANs with computer vision to replicate human hand motions via robotic joints, achieving high motion accuracy and efficiency. Khaleel et al.³⁴ applied NNGA and PSO to solve IK of a 3-DOF redundant arm, with PSO outperforming NNGA in trajectory accuracy. Bouzid et al.³⁵ utilized ANN for 4-DOF SCARA robots using LM, BR, and SCG training algorithms on diverse datasets.

This study focuses on a prismatic and revolute joint system, which is commonly used in industrial and medical robots. The main contributions of this work include a novel quadrant-based and full workspace learning and testing approach for IK, a comparative analysis of deep feed-forward neural network (DFNN), LSTM, and GRU architectures in continuous paths, the introduction of path-based validation for real-world applicability, improved generalization testing across different workspace regions, and a data-efficient, computationally viable methodology that enhances real-time feasibility without constant retraining or excessive computational resources.

Proposed methodology

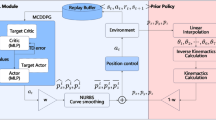
We consider a robot with a prismatic joint and a rotational joint as shown in the Fig. 1 designed specifically for evaluating IK performance using NNs. The goal is to generate the workspace for different values of prismatic joint extension (d) and rotation angle (θ) and then derive the IK to find the required joint parameters for a given end-effector position. To evaluate the accuracy and generalization of NN-based IK models, we employed a structured dataset division and K-fold cross-validation technique. Two training formats were used: Quadrant-Based Training and Full Workspace Training. To ensure robust evaluation and prevent overfitting, K-fold cross-validation was applied, allowing the model to be trained and validated on different subsets of data. Additionally, we compared standard DFNN with recurrent models such as LSTM and GRU to determine their effectiveness in learning IK relationships, particularly for continuous motion prediction. This comprehensive methodology ensures a thorough comparison between analytical and DL-based IK solutions, providing a detailed assessment of model robustness and accuracy.

Fig. 1

Kinematic structure of revolute-prismatic joint robot.

Forward kinematics

FK establishes the relationship between joint parameters (d, θ) and the Cartesian coordinates (x, y) of the end-effector. The robot consists of:

• (1) A prismatic joint that allows linear motion along a fixed direction.

• (2) A rotational joint providing angular rotation around the z-axis.

Using trigonometry, the position of the end-effector is given by Eqs. (1) and (2):

$$\:x=d\text{cos}\theta\:$$

(1)

$$\:y=d\text{sin}\theta\:$$

(2)

where d represents the prismatic extension and θ the rotational angle. The workspace is formed by varying d and θ. For each $\:d\in\:\left[\text{200,400}\right]$mm and $\:\theta\:\in\:[0^\circ\:,360^\circ\:]$, the end-effector traces circular paths of increasing radii, creating a ring-shaped workspace as shown in Fig. 2. These equations are validated across the full range of prismatic joint extensions, from the inner radius (200 mm) to the outer radius (400 mm), ensuring consistent applicability across the entire reachable workspace.

Inverse kinematics

IK determines the joint parameters ($\:\theta\:,\:d$) from a given end-effector position (x, y). The rotation angle $\:\theta\:$ is calculated by Eq. (3), while the prismatic extension $\:d$ is obtained using the Euclidean distance formula, as shown in Eq. (4). This provides the radial distance from the origin, corresponding to the prismatic joint extension.

$$\:\theta\:={\text{tan}}^{-1}\left(\frac{y}{x}\right)$$

(3)

$$\:d=\sqrt{{x}^{2}+{y}^{2}}$$

(4)

Although FK and IK are conceptually inverse processes, they are not directly reversible. IK is more complex due to issues such as non-uniqueness, singularities and the possibility of infeasible solutions. Therefore, learning-based methods and optimization techniques are essential for achieving stable and accurate inverse solutions across the manipulator’s workspace. As mentioned earlier, two strategies were employed,

Fig. 2

Visual representation of the robot’s reachable workspace.

• (1) Quadrant-Based Training

The dataset was divided into four quadrants. For each quadrant, training was performed using respective quadrant’s data, while testing involved evaluating the model on square and circular paths within each quadrant. Error analysis focused on the deviations between predicted and actual paths, and performance was assessed by comparing the path errors between the desired trajectories and those generated by the DL models. The dataset generation process involved systematically computing the robot’s workspace coordinates (x, y) for a given range of prismatic joint values d (200–400 mm, in increments of 0.15 mm) and rotational joint angles θ (0–90°, in increments of 0.15°). This forms the datasets for the first quadrant. To generate datasets for the remaining three quadrants, coordinate transformations were applied by swapping and negating x and/or y, and adjusting θ by $\:90^\circ\:$, $\:180^\circ\:$, $\:270^\circ\:$, respectively. Given 1,334 prismatic joint values and 601 rotational angle values, the total dataset size per quadrant is 801,734 data points. The step size of 0.15 mm (linear) and 0.15° (angular) was selected based on resolution sensitivity experiments to ensure smooth trajectories and accurate model learning without introducing unnecessary redundancy. Although these angular and linear increments share the same numerical value, they are not spatially equivalent. A change in angle $\:\theta\:$ results in a Cartesian displacement that depends on the current radius d, whereas the linear increment from the prismatic joint translates directly along a fixed axis. Nonetheless, this balanced sampling strategy in polar coordinates results in a uniformly distributed Cartesian workspace, thereby improving learning consistency across all quadrants without assuming equivalence between angular and linear units. Figure 3 illustrates the quadrant-based workspace, and Table 1 summarizes the transformations used for generating each quadrant.

Table 1 Quadrant-based coordinate and angle transformations.

Fig. 3

Quadrant-based partitioning of the robot workspace for individual training.

• (2) Full Workspace Training

In this approach, the model was trained on the entire dataset and tested on continuous paths (square and circle) spanning the full workspace. Error analysis examined the deviations between predicted and actual paths, while performance was assessed by comparing path errors between the desired trajectories and those generated by the DL models. To generate the workspace, the joint parameters are varied as follows:

• (i) “Prismatic Joint Extension (d)”: 200 mm to 400 mm in increments of 0.25 mm.

• (ii) “Rotation Angle (θ)”: 0° to 360° in increments of 0.25°. The number of discrete values for each parameter is.

  for $\:d:\:\frac{400-200}{0.25}+1=801$

  for $\:\theta\::\:\frac{360-0}{0.25}+1=1441$

Since each (d, θ) pair corresponds to a unique (x, y) coordinate, the total number of workspace data points is 801 × 1441 = 1,153,041. Thus, the dataset contains over 1.15 million points, covering the entire reachable workspace of the robot’s end-effector as shown in Fig. 2.

Deep learning models and results

This section presents an in-depth evaluation of DL models trained using both quadrant-wise and full workspace strategies for solving the IK problem of a revolute-prismatic (RP) robot. The primary objective is to identify the most effective model in terms of generalization, precision and adaptability to spatial and geometric variations. Challenges such as ambiguity in joint configurations, singularities, and the presence of multiple feasible solutions make data-driven IK solutions highly non-trivial. To address overfitting and enhance model stability, k-fold cross- validation (CV) with K = 5 was applied during the training of DFNN models. This technique reduces variance associated with specific train-test splits and ensures consistent learning across varying data distributions. Although validation loss, measured using MSE, provides insight into how well the model fits the training data, it is not sufficient on its own to evaluate real-world usability. For each path, predicted joint angles were used to compute the end-effector position via FK, as defined in Eqs. (1) and (2). A more practical and application-relevant metric is the deviation error, defined as the Euclidean distance between the predicted and actual end-effector positions, as shown in Eq. (5)

$$\:e=\sqrt{{({x}_{d}-{x}_{p})}^{2}+{({y}_{d}-{y}_{p})}^{2}}$$

(5)

where, $\:e$ is the error between the predicted and desired end-effector positions, $\:({x}_{d},{y}_{d})$ are the desired coordinates, and $\:({x}_{p},{y}_{p})$ are the predicted coordinates. This metric directly quantifies the spatial accuracy of the robotic arm and reflects how closely it tracks the desired paths. Model performance was evaluated using deviation error on both circular and square trajectories across different quadrants. These paths were chosen to represent different geometric complexities: square paths contain sharp turns, testing the model’s ability to generalize across discontinuities, while circular paths test smooth interpolation capability. All models DFNN, LSTM, and GRU demonstrated successful learning during training and achieved low MSE values. However, significant differences in performance emerged when tested on unseen paths, particularly in terms of deviation error. This highlights the fact that low validation loss does not guarantee strong spatial generalization or practical trajectory accuracy. The same models were used for both quadrant-wise and full workspace training, with appropriate hyperparameter tuning for each case. The architectures of the DL models are illustrated in Fig. 4.

Quadrant-wise training and evaluation

The workspace was divided into four quadrants (Q1, Q2, Q3, and Q4), and all models were trained separately for each quadrant. This allows localized evaluation and also reduces complexity by constraining the range of outputs, thereby improving learning stability. The DFNN models were trained with and without k-fold CV for both single-output ($\:\theta\:\:$or $\:d$) and dual-output ($\:\theta\:$, $\:d$) configurations.

• (1) First Quadrant (Q1)

The single-output DFNN consisted of four hidden layers, each with 128 neurons and ReLU activation. It was trained using 5-fold CV with L2 regularization a strength of 0.0005 is applied to prevent overfitting. The model was trained using the Adam optimizer and MSE loss for 150 epochs, with early stopping (patience = 10) to avoid unnecessary training. A batch size of 32 was used to ensure efficient learning. This model achieved an average CV loss of 0.0150 for $\:\theta\:$ and 0.0722 for $\:d$. The dual-output DFNN, with three hidden layers was also trained for 150 epochs and achieved a CV loss of 0.03742. The DFNN model without CV used 80% of the data for training and 20% for testing. It had five densely connected hidden layers, each containing 128 neurons with ReLU activation, and was trained for 500 epochs achieved a validation loss of 0.0427. The performance comparison of DFNN model with k-fold CV is shown in Table 2 and without k-fold CV is shown in Table 3. The LSTM model, comprising three stacked LSTM layers was trained for 1000 epochs, and achieved a validation loss of 0.0866. The GRU model, trained for 250 epochs, achieved validation loss of 0.00415. Table 4 summarizes the performance of both the LSTM and GRU models. However, the real differentiator was the deviation error, where the single output DFNN model with CV produced the lowest error of 0.289 mm on the square path and 0.312 mm on the circular path. The GRU model also performed competitively on the circular path (0.677 mm) but showed error on the square (0.957 mm). These results highlight that square paths are more sensitive to error accumulation, requiring the model to handle abrupt geometric changes effectively. The generalization performance of the models across different paths is summarised in Table 5. Figure 5 shows the comparison of (a) Square path and (b) circular path in the X- Y coordinate plane. The same strategy was applied to the other 3 quadrants with different hyperparameters tailored for each case.

Fig. 4

Proposed DL models architecture for (a) DFNN with k-fold cross validation (1 o/p), (b) 2 o/p, (c) DFNN without k-fold cross validation, (d) LSTM, and (e) GRU.

Table 2 DFNN model performance in Q1 with K-fold.

Table 3 DFNN model performance in Q1 without k-fold.

Table 4 LSTM and GRU model performance in Q1.

• (2) Second Quadrant (Q2)

Models reused Q1 architecture with slight modifications in training parameters. The single-output DFNN consisted of five hidden layers each with 128 neurons, ReLU activation. It was trained using 5-fold CV with a batch size of 64 for 150 epochs, achieving a CV loss of 0.0208 for $\:\theta\:$ and 0.3953 for $\:d$. The dual-output DFNN shares the same architecture as in Q1 and achieved an average CV loss of 0.00415. Similarly, the DFNN without CV reused the Q1 model and achieved a validation loss of 0.0018. Table 6 shows.

Table 5 Deviation errors on circular and square paths in Q1.

the performance of the DFNN models with k-fold CV and Table 7 shows the results for models without k-fold CV. The LSTM model using the same architecture as in Q1, was trained for 200 epochs and achieved a validation loss of 0.012, while the GRU model obtained a validation loss of 0.01146. Table 8 summarizes the performance of the LSTM and GRU models. On trajectory-based evaluation, the dual-output DFNN slightly outperformed the other models, achieving a deviation error of 0.378 mm on the square path, while the GRU and LSTM models shows comparable performance. These small differences underscore the importance of trajectory-based evaluation, where spatial performance differences become more evident beyond what MSE alone can capture. These generalization performance across different paths is summarised in Table 9. Figure 6 illustrates the comparison of (a) Square and (b) circular paths in the X-Y coordinates plane.

• (1) Third Quadrant (Q3)

For the single-output case, the same DFNN model architecture used in Q1 was employed, but with three hidden layers each containing 128 neurons and a batch size of 32. This model achieved an average CV loss of 0.067 for $\:\theta\:$ and 0.053 for $\:d$. For the dual-output case ($\:\theta\:,\:d$), the same model architecture as used in Q1 was applied, resulting in an average CV loss of 0.249. The DFNN without CV also sharing the same model as used in the previous 2 quadrants, achieved a validation loss of 0.0067. Table 10 presents the performance of the DFNN models with k-fold CV, and Table 11 summarizes the results for models without k-fold CV. The LSTM and GRU models used the same architectures as in Q2. The LSTM model achieved a validation loss of 0.00307, while the GRU model achieved 0.0137. Although GRU had a lower validation loss compared to LSTM, it underperformed in terms of deviation error (1.295 mm vs. 0.521 mm on square path). This highlights that learning temporal dependencies does not always ensure accurate joint- space projection unless spatial consistency is also effectively learned. Table 12 shows the performance of the LSTM and GRU models. Generalization performance was evaluated by testing the models on both circular and square paths as summarised in Table 13. Comparatively DFNN with CV (2 i/p and 1 o/p) outperform the other models, achieving the lowest deviation error of 0.508 mm on the square path and 0.438 mm on the circular path. Figure 7 shows the (a) Square and (b) circular path comparison in X–Y coordinates plane. The square and circle paths were intentionally sized differently to assess the model’s adaptability to varying geometries. Despite differences in path length and curvature, model accuracy remained consistent. Errors were measured relative to each shape using Cartesian deviation, ensuring fair and comparable evaluation across trajectories.

Table 6 DFNN model performance in Q2 with K-fold.

Table 7 DFNN model performance in Q2 without k-fold.

Table 8 LSTM and GRU model performance in Q2.

Table 9 Deviation errors on circular and square paths in Q2.

Table 10 DFNN model performance in Q3 with K-fold.

Table 11 DFNN model performance in Q3 without k-fold.

Table 12 LSTM and GRU model performance in Q3.

Fig. 5

Desired and predicted trajectory coordinates of proposed DL models on Q1 for (a) square path, (b) circle path.

Fig. 6

Desired and predicted trajectory coordinates of proposed DL models on Q2 for (a) square path, (b) circle path.

Fig. 7

Desired and predicted trajectory coordinates of proposed DL models on Q3 for (a) square path, (b) circle path.

Table 13 Deviation errors on circular and square paths in Q3.

• (1) Fourth Quadrant (Q4)

For the single-output case, the same DFNN model architecture used in Q3 was employed. It achieved a CV loss of 0.4792 for $\:\theta\:$ and 0.6102 for $\:d$. For the dual-output case ($\:\theta\:,\:d$), the model attained an average CV loss of 0.2877. The DFNN without CV yielded a validation loss of 0.0067. Table 14 shows the performance of DFNN models trained with k-fold CV, while Table 15 summarizes the results for the models trained without k-fold CV.

The LSTM and GRU models, sharing the same architecture used in previous quadrants, achieved validation losses of 0.0148and 0.0304 respectively. Table 16 shows the performance metrics for both.

Table 14 DFNN model performance in Q4 with K-fold.

Table 15 DFNN model performance in Q4 without k-fold.

models. The difference in the number of hidden layers between the LSTM (3 × 64) and GRU (4 × 64) was determined empirically through hyperparameter tuning. The GRU model required an additional layer to ensure stable convergence and maintain performance in Q4 without overfitting. Interestingly, although the GRU had a higher validation loss than LSTM, it exhibited better spatial generalization (0.689 mm on circular path compared to 1.103 mm for LSTM). This suggests that GRU’s gating mechanisms support stable convergence on smoother trajectories but may be less effective for abrupt geometric transitions. The generalization capability of all models was further evaluated on both circular and square trajectories, as detailed in Table 17. Figure 8 illustrates the predicted versus actual paths in X-Y coordinates for (a) square and (b) circular shapes. Comparatively, the DFNN with CV (2 i/p and 1 o/p) outperformed the other models, achieving the lowest deviation error of 0.715 mm for square path and 0.662 mm for the circular path. Across all quadrants, the DFNN models with k-fold CV and single-output architecture consistently delivered the lowest deviation errors. This reinforces the advantages of modular learning and validation-aware training over monolithic or untuned approaches.

Table 16 LSTM and GRU model performance in Q4.

Table 17 Deviation errors on circular and square paths in Q4.

Full workspace training

The same process and models used in the quadrant wise training were applied here to evaluate global generalization, with models trained on the entire workspace covering the full rotational range ($\:0^\circ\:-360^\circ\:$). The architecture consisted of two separate DFNNs for single output case ($\:\theta\:$ or $\:d$). Each model had an input layer with 2 neurons (for $\:x,\:y$), followed by 3 fully connected hidden layers, each containing 128 neurons with ReLU activation. L2 regularization (strength = 0.0005) was applied to prevent overfitting. Models were trained using the Adam optimizer and MSE loss for 150 epochs, employing early stopping (patience = 10) to avoid unnecessary training. A batch size of 32 was used. The output layer contained 1 neuron predicting either $\:\theta\:$ or $\:d$. This single-output DFNN model achieved an average CV loss of 2.1397 for $\:\theta\:$ and 0.09308 for $\:d$. It also yielded a deviation error of 1.594 mm on the square path, the lowest among all full-workspace models but had a slightly higher error of 2.084 mm on the circular path. For the dual-output case ($\:\theta\:$, $\:d$), the same architecture was used but with L2 regularization strength of 0.0001 and early stopping patience of 25. When trained for 150 epochs, this model achieved an average CV loss of 0.375, with deviation errors of 4.861 mm for the square path and 1.907 mm for the circular path. The performance of the DFNN models trained with k-fold for both single-dual-output configurations is summarised in Table 18.

Among the evaluated models, the DFNN trained without CV used 80% of the data for training and 20% for testing. Its architecture consisted of five fully connected hidden layers: the first four layers with 128 neurons each, followed by a fifth layer with 256 neurons, all using ReLU activation. The model was trained for 750 epochs with a batch size of 32 using the Adam optimizer and MSE loss. Despite achieving a validation loss of 0.4263, the deviation errors were significantly higher: 8.41 mm for the square path and 5.214 mm for the circular path. This result, detailed in Table 19, underscores that.

Fig. 8

Desired and predicted trajectory coordinates of proposed DL models on Q4 for (a) square path, (b) circle path.

trajectory deviation is a more meaningful metric than validation loss. To evaluate sequence models, various LSTM architectures with different depths (3 to 6 stacked layers) were tested for IK prediction. An initial baseline model with three stacked LSTM layers, each with 64 neurons and ReLU activation, followed by a dense output layer with two neurons, was trained for 300 epochs using an 80:20 train-test split. This model achieved a validation loss of 0.02603, but performed poorly on trajectory tracking, with deviation error of 25.088 mm on the square path and 1.911 mm on the circular path. To study the impact of depth, models with 4, 5, and 6 LSTM layers were evaluated. The 4-layer model performed best on the circular path with a deviation error of 0.873 mm, but failed to meet accuracy requirements on the square path (5.775 mm). Increasing depth further degraded performance:

• 5-layer model: 4.66 mm (square), 3.411 mm (circle).

• 6-layer model: 17.668 mm (square), 25.823 mm (circle).

These results suggest that increasing model depth may initially improve performance but can lead to overfitting or training instability, particularly for continuous trajectory tasks. Since the application requires high-precision predictions with deviation errors below 1 mm, only the 4-layer LSTM model met the criterion for the circular path, while, none satisfied it for the square path. The GRU model sharing the same architecture as the LSTM baseline, was trained for 1000 epochs and achieved a validation loss of 0.05792. Table 20 compares the performance of LSTM and GRU models. To assess global trajectory accuracy, all models were tested on continuous paths spanning the full workspace as shown in Fig. 9. The results confirmed that low training loss alone does not ensure functional usability, trajectory-based metrics are essential for reliable evaluation. These findings highlight that model capacity, regularization, and architectural balance are crucial. Overly deep models may achieve low training loss but perform poorly under geometric constraints, whereas well-regularized, shallower DFNNs with k-fold CV provide robust and predictable performance. The generalization performance across different paths is presented in Table 21. Figure 10 illustrates the X-Y coordinate comparisons for (a) Square and (b) circular paths.

Table 18 DFNN model performance in full workspace with K-fold.

Table 19 DFNN model performance in full workspace without k-fold.

Table 20 LSTM and GRU model performance in full workspace.

Conclusion

This study evaluates the generalization capability of deep learning (DL) models—including DFNN (with and without k-fold CV), LSTM, and GRU—for solving IK using both quadrant-based and full workspace training strategies. Although all models achieved low MSE during training, their performance on predefined square and circular trajectories revealed notable differences in practical accuracy, highlighting the limitations of MSE as the sole evaluation metric.

Across all four quadrants (Q1–Q4), the DFNN with k-fold CV (single-output configuration) consistently outperformed others by achieving the lowest deviation errors, demonstrating strong generalization across both sharp (square) and smooth (circular) paths. The lowest deviation error observed was 0.289 mm on the square path in Q1, while the highest deviation error was 1.295 mm on the square path in Q3 by the GRU model. On circular paths, the same GRU model also performed poorly, with an error of 1.269 mm, reaffirming its limited stability in local generalization. In contrast, the DFNN with k-fold CV (single-output) model also performed well on circular paths, with a low error of 0.312 mm in Q1, confirming its consistency across path types and workspace zones.

In Q1, the best-performing model was DFNN with k-fold CV (single-output), achieving 0.289 mm on the square path and 0.312 mm on the circular path. The worst performance in Q1 was by DFNN without CV, with 1.301 mm on the square path and 1.785 mm on the circular path.

In Q2, DFNN with k-fold CV (dual-output) showed the best result with 0.378 mm (square) and on circle DFNN with k-fold CV (single-output) showed the best result with 0.366 mm, while DFNN without CV again recorded the worst errors with 0.511 mm (square) and on circle DFNN with k-fold CV (dual-output) showed the worst result with 0.708 mm.

In Q3, the DFNN with k-fold CV (single-output) remained the best with 0.508 mm (square) and 0.438 mm (circle), whereas the GRU model performed worst with 1.295 mm (square) and 1.269 mm (circle).

In Q4, the DFNN with k-fold CV (single-output) had the best performance with 0.715 mm (square) and 0.662 mm (circle), while DFNN without CV showed the poorest results with 1.076 mm (square) and 1.174 mm (circle), respectively.

Under full workspace training, which evaluates global generalization, the DFNN with k-fold CV (single-output) again delivered the best results, with 1.594 mm on the square path and 2.084 mm on the circular path. The GRU model exhibited the highest errors 24.13 mm on the square path and 4.076 mm on the circular path indicating significant instability when exposed to a wider spatial distribution.

The shape of the trajectory significantly influenced model performance. Square paths, due to their abrupt transitions, challenged models with insufficient depth or regularization, while circular paths allowed smoother and more stable tracking. The use of k-fold CV was found to enhance model robustness and generalization. Moreover, single-output DFNN architectures were more reliable across diverse trajectory types and spatial domains. Importantly, deviation error was shown to be a more meaningful performance metric than MSE in applications where spatial precision is essential. This trajectory-aware evaluation framework offers practical insights for the future design and deployment of DL-based IK systems, particularly in high-precision tasks such as robotic welding and painting, where accuracy and consistency are critical.

Fig. 9

Full robot workspace with (a) square path, (b) circle path visualization.

Table 21 Deviation errors on circular and square paths in full workspace.

Fig. 10

Desired and predicted trajectory coordinates of proposed DL models on full workspace for (a) square path, (b) circle path.