Introduction

It is known that the function of many biological systems (e.g., embryos, tumors) depends on the spatial organization of the cells1. This dependence motivates the field of spatial transcriptomics, in which gene expression and spatial information at the cellular or spot level are used to model biological systems. Advancements in sequencing technologies, such as STARmap, have enabled robust intact-tissue RNA sequencing capable of simultaneous measurement of over 1,000 genes while preserving spatial information2.

Interest in identifying sub-populations of cells based on gene expression and spatial location has motivated the development of statistical clustering methods for spatial transcriptomics data. Methods such as Giotto3 and Seurat4 are based on dimension reduction and nearest-neighbor clustering. The Python library stLearn makes use of graph-based community detection methods for clustering on normalized cellular spatial and gene expression data5. Although based on robust and well-understood methodology, these methods require specification of K, the total number of clusters, which may not be known a priori.

There are methods that can automatically select K, which tend to be Bayesian approaches. Such methods include BayesSpace6, which implements a Markov random field model for clustering. Using this method, K can either be specified beforehand or obtained from the elbow of the pseudo-log-likelihood. SPRUCE7 employs a Bayesian mixture model for clustering, either prespecifying K or using the widely applicable information criterion to determine K. DR-SC8 performs dimension reduction and spatial clustering jointly using a hidden Markov random field model. Similarly to SPRUCE, K is either fixed or selected using the modified Bayesian information criterion. These methods, although capable of identifying sub-populations without specification of K, do not incorporate information from multiple related spatial transcriptomics samples, which are becoming more and more available.

Allen et al.9 introduced MAPLE, a method which utilizes a spatial autoencoder, neighbor network, and finite Bayesian mixture model to jointly cluster observations using multiple spatial transcriptomics samples. However, it is often of interest to compare multiple groups of spatial transcriptomics data (e.g., healthy versus diseased tissue), and determine information common to each group and idiosyncratic within each group, which MAPLE is not capable of.

To address the aforementioned limitations of the existing methods, we propose a Bayesian nonparametric mixture model capable of performing spatial clustering on multiple spatial transcriptomics datasets with a data-driven determination of K, and can be used to identify information common to all experimental groups and idiosyncratic to each group. We also include a variable selection component, which can identify the genes most significant in the clustering process via a spike-and-slab prior. This joint clustering and variable selection approach bypasses the post-selection inference problem, which arises when one first identifies clusters and then, given the clusters, identifies significant differentially expressed genes across clusters. Simulation results show that our method outperforms other established methods such as DR-SC in terms of clustering accuracy. The simulations also show that our variable selection is accurate. We further demonstrate the proposed method with the motivating STARmap dataset2 and discuss the significance of our findings.

Methods

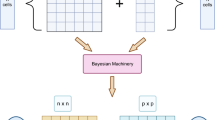
Let \({\textbf{Y}}_{j}\in {\mathbb {R}}^{n_j\times p}\) denote gene expression for \(n_j\) cells and p genes in group/donor \(j=1,\dots , J\) and let \({\textbf{X}}_j\in {\mathbb {R}}^{n_j\times 2}\) denote the matching spatial coordinates of the cells. Our goal is to cluster cells into unknown cell types from multiple spatial transcriptomic datasets \(({\textbf {Y}}_j,{\textbf {X}}_j)_{j=1}^J\) and, simultaneously, select genes that are differentially expressed across cell types. We call our method, Multiple Spatial Sparse Clustering (MSC). A schematic illustration of the proposed MSC is provided in Fig. 1, which depicts three key inferential goals: (i) cell types common to all groups, (ii) cell types idiosyncratic to each group, and (iii) differentially expressed genes.

Fig. 1
figure 1

Schematic illustration of the proposed MSC (created with BioRender).

Full size image

To achieve those goals, we introduce three sets of latent variables. First, let \(r_{ji}\in \{0,1\}\) be a binary variable such that \(r_{ji}=0\) if cell i in group j belongs to a cell type that is common to all groups (i.e., every donor has cells of this type) and \(r_{ji}=1\) if the cell type is idiosyncratic/unique to group j (i.e., only donor j has such cell type). Let \(n_0=\sum _{j=1}^J\sum _{i=1}^{n_j}I(r_{ji}=0)\) and \(n_j^*=\sum _{j=1}^J\sum _{i=1}^{n_j}I(r_{ji}=1)\) then be the number of cells from the common cell types and from the cell types idiosyncratic to group j, respectively. Second, let \(s_{ji}^0\in \{1,\dots ,q_{n_0}\}\) be a categorical variable such that \(s_{ji}^0=\ell\) if cell i in group j belongs to the common cell type \(\ell\). Similarly, let \(s_{ji}\in \{1,\dots ,q_{n_j^*}\}\) be a categorical variable such that \(s_{ji}=\ell\) if cell i belongs to cell type \(\ell\) idiosyncratic to group j. Note that both the number of common cell types \(q_{n_0}\) and the number of idiosyncratic cell types \(q_{n_j^*}\) are unknown and allowed to grow with \(n_0\) and \(n_j^*\), respectively. Lastly, let \(z_h\in \{0,1\}\) be a binary variable such that \(z_h=1\) if gene h is differentially expressed across cell types and \(z_h=0\) otherwise. We propose a new Bayesian nonparametric hierarchical model that allows us to make inferences on these latent variables.

Specifically, given \(z_h\), we assume the ith row \(\varvec{Y}_{ji}=(y_{ji1},\dots ,y_{jip})\) of \(\varvec{Y}_j\) follows,

$$\begin{aligned} \varvec{Y}_{ji}\sim \prod _{h=1}^p N(y_{jih}|\theta _{jih},\tau _{h})^{z_h}N(y_{jih}|\eta _{jih},\tau _h)^{1-z_h}. \end{aligned}$$

Since \(z_h=1\) means that gene h is differentially expressed across cell types, a sophisticated prior model will be used for \(\theta _{jih}\) to accommodate the heterogeneity whereas a simple prior model would suffice for \(\eta _{jih}\).

Let \(\varvec{\theta }_{ji}=\{\theta _{jih}|z_h=1\}\) and let \(\pi _{n_0}=\{S_1^0,\dots ,S_{q_{n_0}}^0\}\) be the partition of \(n_0\) cells from the common cell types where \(S_\ell ^0=\{(j,i)|s_{ji}^0=\ell \}\). Let \(\delta _a(\cdot )\) denote a point mass at a. We assume that conditional on \(r_{ji}=0\) (i.e., common cell types),

$$\begin{aligned} \varvec{\theta }_{ji}|r_{ji}=0\sim \sum _{\ell =1}^{q_{n_0}}I(s_{ji}^0=\ell )\delta _{\varvec{\phi }_\ell }(\cdot ), ~~~~\varvec{\phi }_\ell \sim G_0,~~~~\pi _{n_0}\sim p(\pi _{n_0}), \end{aligned}$$
(1)

where \(G_0\) is a base distribution and \(p(\pi _{n_0})\) is a random partition distribution, both to be specified later. In words, (1) implies that cells of the same type (say, \(\ell\)) share the same mean gene expression, i.e., \(\varvec{\theta }_{ji}=\varvec{\phi }_\ell\) for all (j, i) such that \(s_{ji}^0=\ell\).

Similarly, let \(\pi _{n_j^*}=\{S_1^j,\dots ,S_{q_{n_j^*}}^j\}\) be the partition of \(n_j^*\) cells from the cell types idiosyncratic to group j where \(S_\ell ^j=\{(j,i)|s_{ji}=\ell \}\). We assume that conditional on \(r_{ji}=1\) (i.e., idiosyncratic cell types),

$$\begin{aligned} \varvec{\theta }_{ji}|r_{ji}=1\sim \sum _{\ell =1}^{q_{n_j^*}}I(s_{ji}=\ell )\delta _{\varvec{\psi }_{j\ell }}(\cdot ), ~~~~\varvec{\psi }_{j\ell }\sim G_0,~~~~\pi _{n_j^*}\sim p(\pi _{n_j^*}). \end{aligned}$$

To incorporate the spatial information in partitioning the cells, we leverage the Ewens-Pitman attraction (EPA) distribution10. Specifically, let \(\lambda (\cdot ,\cdot )\) denote a similarity function such that \(\lambda (i,i')=1/d_{ii'}\) where \(d_{ii'}\) is the Euclidean distance between cells i and \(i'\). The EPA distribution sequentially allocates cells to clusters. The order in which cells are allocated is random, determined by a random permutation \(\varvec{\sigma } = (\sigma _1,\dots ,\sigma _n)\) of \(\{1,\dots ,n\}\), where the ith cell allocated is \(\sigma _i\). The EPA distribution for the common partition is then given by,

$$\begin{aligned} p(\pi _{n_0})=\prod _{j=1}^J\prod _{i:r_{ji}=0}p_{ji}(\alpha ,\delta ,\lambda ,\pi (\sigma _1,\dots ,\sigma _{n_{ji}})), \end{aligned}$$

where \(\delta\) is a discount parameter \(\delta \in [0,1)\), \(\alpha\) is a mass parameter \(\alpha >-\delta\), \(n_{ji}=\sum _{j'=1}^j\sum _{i'=1}^{i-1}I(r_{j'i'}=0)\), \(p_{ji}(\alpha ,\delta ,\lambda ,\pi (\sigma _1,\dots ,\sigma _{n_{ji}}))=1\) for (j, i) such that \(r_{ji}=n_{ji}=0\), and, for other (j, i) such that \(r_{ji}=0\) and \(n_{ji}>0\),

$$\begin{aligned} p_{ji}(\alpha ,\delta ,\lambda ,\pi (\sigma _1,\dots ,\sigma _{n_{ji}}))= \textsf{P}(\sigma _{n_{ji}+1} \in S\mid \alpha ,\delta ,\lambda ,\pi (\sigma _1,\dots ,\sigma _{n_{ji}})) \\ \quad = {\left\{ \begin{array}{ll} \frac{n_{ji} - \delta q_{n_{ji}}}{\alpha + n_{ji}} \times \frac{\sum _{\sigma _s \in S}\lambda (\sigma _{n_{ji}+1}, \sigma _s)}{\sum _{s = 1}^{n_{ji}} \lambda (\sigma _{n_{ji}+1}, \sigma _s)} & \text {for } S \in \pi (\sigma _1,\dots ,\sigma _{n_{ji}}) \\ \frac{\alpha + \delta q_{n_{ji}}}{\alpha + n_{ji}} & \text {otherwise} \end{array}\right. } \end{aligned}$$

Note that \(\frac{\sum _{\sigma _s \in S}\lambda (\sigma _{n_{ji}+1}, \sigma _s)}{\sum _{s = 1}^{n_{ji}} \lambda (\sigma _{n_{ji}+1}, \sigma _s)}\) encourages cell i in group j to be allocated to cluster S if it is spatially close to the cells that are already in cluster S. To make the inference of partition invariant to the order of allocations, Dahl et al. (2017)10 assumes a uniform prior on the permutation, \(\varvec{\sigma }_{0}=(\sigma _1,\dots ,\sigma _{n_0})\sim p(\varvec{\sigma }_{0})\propto 1\), which we follow.

Similarly, for \(j=1,\dots , J\), the EPA distribution for the partition idiosyncratic to group j is given by,

$$\begin{aligned} p(\pi _{n_j^*}) =\prod _{i:r_{ji}=1}p_{ji}^*(\alpha ,\delta ,\lambda ,\pi (\sigma _{j1}^*,\dots ,\sigma _{jn_{ji}^*}^*)), \end{aligned}$$

where \(n_{ji*}^*=\sum _{i'=1}^{i-1}I(r_{ji}=1)\), \(p_{ji}^*(\alpha ,\delta ,\lambda ,\pi (\sigma _{j1}^*,\dots ,\sigma _{jn_{ji}^*}^*))=1\) for i such that \(r_{ji}=1\) and \(n_{ji}^*=0\), and, for other i,

$$\begin{aligned} p_{ji}^*(\alpha ,\delta ,\lambda ,\pi (\sigma _{j1}^*,\dots ,\sigma _{jn_{ji}^*}^*))= \textsf{P}(\sigma _{n_{ji}^*+1}^* \in S\mid \alpha ,\delta ,\lambda ,\pi (\sigma _{j1}^*,\dots ,\sigma _{jn_{ji}^*}^*)) \\ \quad = {\left\{ \begin{array}{ll} \frac{n_{ji}^* - \delta q_{n_{ji}^*}}{\alpha + n_{ji}^*} \times \frac{\sum _{\sigma _s^* \in S}\lambda (\sigma _{jn_{ji}^*+1}^*, \sigma _s^*)}{\sum _{s = 1}^{n_{ji}^*} \lambda (\sigma _{jn_{ji}^*+1}^*, \sigma _s^*)} & \text {for } S \in \pi (\sigma _{j1}^*,\dots ,\sigma _{jn_{ji}^*}^*) \\ \frac{\alpha + \delta q_{n_{ji}^*}}{\alpha + n_{ji}^*} & \text {otherwise}, \end{array}\right. } \end{aligned}$$

and \(\varvec{\sigma }^*_j=(\sigma _{j1}^*,\dots ,\sigma _{jn_j^*})\sim p(\varvec{\sigma }^*_j)\propto 1\).

We complete the specification of MSC with conjugate priors for the remaining hyperparameters,

$$\begin{aligned}&\tau _h\sim IG(a_\tau ,b_\tau )\\&G_0=N(0,\tau _h / \kappa )\\&r_{ji}\sim \text {Bernoulli}(\varepsilon ),~~\varepsilon \sim \text {beta}(a_\varepsilon ,b_\varepsilon )\\&z_h\sim \text {Bernoulli}(\rho _z),~~\rho _z\sim \text {beta}(a_z,b_z) \end{aligned}$$

In all our implementation, we set \(\alpha , a_\tau , b_\tau , a_\varepsilon , b_\varepsilon , a_z\) and \(b_z\) equal to 1, \(\delta\) to 0, and \(\kappa\) to 0.008. We choose to non-informative hyperparameters rather than set hyperpriors on them to retain the conjugacy of our model, otherwise we introduce more computational complexity into our inference. \(\alpha = 1\) is a typical choice for Dirichlet process mixture models1112. The choice of \(\delta = 0\) in the EPA distribution implies that the distribution of subsets in our data partition is equivalent to a Dirichlet process mixture10. We choose a small value for \(\kappa\) to ensure a high variance in our likelihood, which provides a larger scope when searching for clusters across the sample space.

Posterior inference

We use the blocked Gibbs sampler to draw posterior inference. We choose to ’block’ (i.e., sample simultaneously) cluster and grouping labels for computational benefits and potential help with mixing and convergence13. For simplicity, we assume \(J=2\) as in our real data. The sampler iteratively samples parameters \((r_{ji}, s_{ji}), \varepsilon , z_h\), and \(\rho _z\) from their respective full conditional distributions, which is outlined below.

  1. 1.

    Sampling \((r_{ji}, s_{ji})\). For each observation \(Y_{ji}\), we consider four cluster assignment options: 1) assignment to an existing idiosyncratic cluster, 2) generation of a new idiosyncratic cluster, 3) assignment to an existing common cluster, and 4) generation of a new common cluster. Let \(\phi\) and \(\varphi\) denote the normal-inverse-gamma posterior predictive distribution and the marginal likelihood, respectively. Suppose we have \(K_j\) clusters in each idiosyncratic group and \(K_0\) clusters in the common group. Then the probability for each option is given by,

    $$\begin{aligned}&u_{jk} \propto (1 - \varepsilon )p(\pi _{n_j}\mid s_{ji} = k) \prod _{h=1}^p \phi (y_{jih} \mid \varvec{Y}_{-jih}), \\&u_{j}^* \propto (1 - \varepsilon )p(\pi _{n_j} \mid s_{ji} = K_j + 1)\prod _{h=1}^p\varphi (y_{jih}),\\&u_{0k} \propto \varepsilon \, p(\pi _{n_0} \mid s_{0i} = k)\prod _{h=1}^p \phi (y_{jih} \mid \varvec{Y}_{-jih}),\\&u_{0}^* \propto \varepsilon \, p(\pi _{n_0} \mid s_{0i} = K_0 + 1)\prod _{h=1}^p\varphi (y_{jih}), \end{aligned}$$

    where \(\varvec{Y}_{-jih}\) is the set of all the other observations of gene h in the same cluster to which i belongs. Using the above probabilities, we sample:

    $$\begin{aligned} (s_{ji}, r_{ji}) = {\left\{ \begin{array}{ll} (k, 1) & \text {with probability } u_{jk}, \text { for } k = 1, \dots , K_j, \\ (K_j + 1, 1) & \text {with probability } u_j^*, \\ (k, 0) & \text {with probability } u_{0k}, \text { for } k = 1, \dots , K_0, \\ (K_{0} + 1, 0), & \text {with probability } u_0^*. \end{array}\right. } \end{aligned}$$
  2. 2.

    Sampling \(\varepsilon\). We sample \(\varepsilon\) directly from \(\text {Beta}(a_\varepsilon + n_0, b_\varepsilon + \sum _jn_j^*).\)

  3. 3.

    Sampling \(z_h\). Let \(K=K_0 + K_1+ K_2\) be the total number of clusters across both experimental groups. For gene \(h=1,\dots ,p\), let \({\textbf{Y}}_{kh}\) be the cells in cluster \(k=1,\dots ,K\) and \({\textbf{Y}}_h\) be all the cells. We sample \(z_h\) from the following probabilities,

    $$\begin{aligned}&\textsf{P}(z_h = 1 \mid \rho _z, {\textbf{Y}}_h) \propto \rho _z \, \prod _{k = 1}^K \varphi ({\textbf{Y}}_{kh}),\\&\textsf{P}(z_h = 0 \mid \rho _z, {\textbf{Y}}_h) \propto (1 - \rho _z) \varphi ({\textbf{Y}}_h). \end{aligned}$$
  4. 4.

    Sampling \(\rho _z\). We sample \(\rho _z\) directly from \(\text {Beta}\left( a_z + \sum _{h=1}^p z_h, b_z + p - \sum _{h=1}^p z_h\right)\).

To improve mixing, we implement an additional split-merge update for cluster (\(s_{ji}\)) and group (\(r_{ji}\)) assignments.

We propose to split a common cluster into multiple idiosyncratic clusters, or merge multiple idiosyncratic clusters into one common cluster.

  • Split move. Sample \(k \in \{1,\dots , K_0\}\) uniformly. Let \(\varvec{r} = [\varvec{r}_1, \varvec{r}_2]\), and define \(\varvec{Y}\) similarly. Then the Metropolis-Hastings ratio of accepting the splitting of the common cluster k into two new idiosyncratic clusters is given by,

    $$\frac{(1/K_0)\prod _{l = 1}^2\left( \varphi ({\textbf{Y}}_l \mid {\textbf{s}}_l = k, {\textbf{r}}_l = 1) (1 - \varepsilon )^{n_l} p(\pi _{n_l} \mid {\textbf{s}}_l = k) \right) }{\prod _{l=1}^2(1 / K_l)\left( \varphi ({\textbf{Y}} \mid {\textbf{r}} = 0)\varepsilon ^{n_0} p(\pi _{n_0})\right) },$$

    If the splitting is accepted, we increase \(K_1\) and \(K_2\) by 1 and decrease \(K_0\) by 1.

  • Merge move. Sample \(k_1 \in \{1, \dots , K_{1}\}\) and \(k_2 \in \{1, \dots , K_{2}\}\) uniformly. Then the Metropolis-Hastings ratio of accepting the merge of idiosyncratic clusters \(k_1\) and \(k_2\) into one common cluster is given by

    $$\frac{(1 / K_{1})(1 / K_{2}) \varphi ({\textbf{Y}} \mid {\textbf{s}}_0 \in \{k_1, k_2\}, {\textbf{r}} = 0)\varepsilon ^{n_0}p(\pi _{n_0} \mid {\textbf{s}}_0 \in \{k_1, k_2\})}{(1 / K_0)\varphi ({\textbf{Y}}_{1} \mid {\textbf{r}}_{1} = 0) \varphi ({\textbf{Y}}_{2} \mid {\textbf{r}}_{2} = 0)(1 - \varepsilon )^{n_{1}n_{2}}p(\pi _{n_{1}})p(\pi _{n_{2}})}.$$

    If the merge is accepted, we decrease \(K_1\) and \(K_2\) by 1 and increase \(K_0\) by 1.

We give a pseudocode summary of the sampler below. Functions mentioned in the pseudocode are explained in more detail in the supplementary materials.

Sampler pseudocode

figure a
figure b

Real data

We demonstrate the proposed model on a publicly available real spatial transcriptomic dataset obtained from the work of Wang et al., taken from the visual cortices of a number of mice using the STARmap single-cell RNA sequencing technique2. The mice were placed under two experimental conditions: one given an hour of light exposure after 4 days kept in a dark environment, and the other kept in continual darkness. We randomly picked one mouse from the light exposure group \((n_1 = 837)\) and another from the continual darkness group \((n_2 = 927)\). We will refer to them as Mouse 1 and Mouse 2, respectively. We considered the same 17 spatially varying genes as in Chakrabarti et al. (2023)14. We also followed their preprocessing steps: we removed cells showing extreme expression of genes and log-normalized the data with a scaling factor equal to the median expression of total reads per cell. Genes were standardized and spatial distances were normalized to (0, 1). Our goal is to cluster cells based on gene expression and spatial location both within each experimental group and across the groups and to select differentially expressed genes across clusters. We ran a Markov chain for 5,000 iterations with a thinning factor of 1/25. No burn-in period was implemented.

Results

Of the 17 genes, we identified 12 significant differentially expressed genes: PLCXD2, RORB, Cux2, Pcp4, NRN1, Nectin3, ARX, OTOF, PROK2, Homer1, eRNA3, and SLC17A7.

We investigate the significance of the selected genes. PLCXD2 by itself has no known function in the brain, but together with another gene, GPR158, it is part of a signaling complex responsible for the development of the dendritic spine15. RORB, according to GeneCards16, is linked to circadian rhythms and plays a role in the development of epilepsy. Cux2, like PLCXD2, is involved with the development of the dendritic spine17. Pcp4 is expressed in bone marrow stem cells, in which it is associated with the deposition of calcium18. NRN1 is associated with neurodevelopment and synaptic plasticity and serves as a biomarker for schizophrenia19. Nectin3 regulates the creation of cellular adhesive molecules called nectins20. ARX plays a role in the development of the forebrain, pancreas, and testes21. Mutations in the OTOF gene have been shown to result in auditory neuropathy22. PROK2 is a biomarker for Kallmann syndrome, which is characterized by impaired sense of smell and delayed puberty23 due to the underdevelopment of neurons in the brain that signal the hypothalamus. Homer1, similarly to PLCXD2 and Cux2, is involved with the development of the dendritic spine24. eRNA3 is known to regulate gene expression, but its function remains debated25. SLC17A7 is a member of the SLC17 family of genes found in neuron-rich areas of the brain, responsible for glutamate transport26.

A gene set enrichment analysis was performed on the 12 selected genes using Enrichr27,28,29. Analysis was performed on the MGI Mammalian Phenotype Level 4 2024 ontology30.

Fig. 2
figure 2

Gene set enrichment results for the MGI Mammalian Phenotype Level 4 2024 ontology.

Full size image

As shown in Fig. 2, the phenotype term most strongly associated with our gene set is abnormal miniature excitatory postsynaptic currents, which is a “defect in the size or duration of spontaneous currents detected in postsynaptic cells that occur in the absence of an excitatory impulse”30. The associated genes were NRN1, Homer1, OTOF, and SLC17A7. This may suggest that the difference in light exposure between the mice could be related to the aforementioned defect. The second term, impaired contextual conditioning behavior, denotes impaired ability to associate an aversive experience with the neutral environment30. The associated genes are NRN1, Homer1, and ARX. As with the first term, our results may indicate that light exposure or lack thereof inhibits this conditioning.

Fig. 3
figure 3

Gene set enrichment results for the WikiPathway 2023 Human database. A star indicates that the p-value adjusted for multiple testing is also significant.

Full size image

To see how such genes are functionally relevant for humans, we also performed an enrichment analysis using the WikiPathway 2023 Human database31. As shown in Fig. 3, our selected gene set is most closely related to the circadian rhythm genes. The overlapping genes were Homer1, PROK2, and RORB. The significance of these enriched genes in Mouse 1 and Mouse 2 indicates that the relationship between the difference in light exposure and the expression of genes associated with circadian rhythm may be worth further investigation. Also, interestingly, a significant pathway in the WikiPathway enrichment results is related to the disruption of postsynaptic signaling by copy number variations, reinforcing the connection between the 12 selected genes and postsynaptic signaling as suggested in MGI enrichment results.

Fig. 4
figure 4

Protein-protein interaction graph obtained from the STRING database. 11 of the 12 selected genes are shown (eRNA3 was not available in the database).

Full size image

A graph of protein-protein interactions was obtained from the STRING database32 and is shown in Fig. 4. The graph shows coexpression for Slc17a7 between both Homer1 and RORB, reinforcing their connection to synaptic/circadian functions in our enrichment analysis. Interestingly, no connections among NRN1, Homer1, ARX, or OTOF are shown in the graph although they are associated in the mammalian phenotype enrichment analysis.

In terms of the clustering results, our algorithm assigned most cells to the 5 common cell types shared between the two mice (589 out of 837 cells for Mouse 1, and 610 out of 927 cells for Mouse 2). We found 26 idiosyncratic clusters for Mouse 1, and 16 idiosyncratic clusters for Mouse 2. The clustering results are visualized spatially in Fig. 5. To visualize these clusters, we applied UMAP33 to the gene expression to reduce the data to 2 dimensions, which shows the similarity of cells in gene expression in a 2-dimensional space.

Fig. 5
figure 5

Clustering results on the cellular measurement locations for each mouse. Colors represent cluster assignment, and the point type corresponds to group assignment (circles for the common model, triangles for idiosyncratic).

Full size image
Fig. 6
figure 6

UMAP embedding of cells assigned to the common clusters and idiosyncratic clusters in Groups 1 and 2 from left to right. Cluster assignments are indicated by colors.

Full size image

Fig. 6 displays the UMAP embeddings of cells assigned to the common clusters and idiosyncratic clusters in Groups 1 and 2. It reveals distinct clusters in the embedded space, especially for the common clusters. We also see that each idiosyncratic group covers a different region in the 2-dimensional space, which would be expected for information unique to each group. Compared to the common clusters, there are much more cell clusters in the idiosyncratic groups. There are a few potential explanations for this somewhat expected result. For example, mitochondrial content, which is known to affect gene expression34, was not measured in our data. The cell cycle stages of individual cells can also affect gene expression35 and hence the clustering. These would lead to higher cellular heterogeneity in terms of gene expression than the heterogeneity arising from cell types alone, which could partially explain why we found many more idiosyncratic clusters than the expected number of cell types in mouse brains.

Fig. 7
figure 7

Autocorrelation function for the model log-likelihood. Blue dashed lines are the boundaries of a 95% confidence interval.

Full size image

To assess convergence, the autocorrelation function was calculated for the model log-likelihood, and is plotted in Fig. 7. Rapid decay toward 0 indicates that the sampler has converged and produces independent draws from the posterior distribution. The Geweke diagnostic was calculated on our log-likelihood chain, resulting in a Z-score of \(-0.8591\) and a corresponding p-value of 0.3903, providing further evidence of convergence.

Inference was run on a personal computer using an AMD Ryzen 5 3600 processor and 16 GB of memory. Using this machine yielded a computing time of 13 days. Although our computing time is heavy compared to existing methods, our method allows for much richer inference including spatial clustering, variable selection, comparison between experimental groups, and uncertainty quantification. Most of our code was implemented in R, aside from the function for obtaining partition probabilities from the EPA distribution (section 1.2.4 in the supplementary materials), which was coded in C++. A full C++ implementation may improve computing time, and will be a subject of our future investigations.

Simulations

In addition to real data, we also conduct simulations to evaluate the proposed method. We consider 6 scenarios with varying dimensions \(p = 15, 20, 25, 30, 40, 50\). Under each scenario, we fix the number of signal variables to 5 (i.e., \(p-5\) variables are noises) and the number of samples per group to \(n_j = 100\) for group \(j = 1,2\). The five signal variables are generated together with the two-dimensional spatial coordinates from a mixture of seven-dimensional multivariate Gaussian distributions, with a proportion \(\varepsilon = 0.6\) of data in each group generated from a common model with three clusters, and the remaining generated from two idiosyncratic models with two clusters for each group. The mixture of Gaussian shares the same banded covariance matrix where the diagonal elements are equal to 0.15, the vth diagonals are 0.03/v for \(v = 1,2,3,4\), and the rest are 0. The mean for each cluster is sampled from a grid of seven equally spaced numbers ranging from 1 to 10. The \(p - 5\) noise variables are generated from independent standard normal distributions.

A Gibbs sampler was used to obtain cluster labels \(s_{ji}\), group assignment \(r_{ji}\), and variable selection \(z_h\) over 3000 iterations, discarding a burn-in period of 2000 iterations. Cluster labels \(s_{ji}\) were determined via the least-square criterion36, and variable selection \(z_h\) and the selection \(r_{ji}\) of common vs idiosyncratic model were determined by the mean probability model (i.e., using 0.5 as a cutoff to threshold their probabilities). For evaluation, we calculated the normalized mutual information (NMI) for cluster labels \(s_{ji}\), misclassification rate for \(r_{ji}\), and true positive & false discovery rates for variable selection \(z_h\). NMI was calculated on the two groups of labels concatenated to one vector, compared to the true labels (also concatenated to one vector). We compare the clustering performance of our method to the popular K-means model, the joint dimension reduction and spatial clustering (DR-SC8) method, and BayesSpace6. Both K-means and DR-SC were applied separately to each experimental group with the true number of clusters \(K = 5\) (3 common and 2 idiosyncratic clusters per experimental group), and NMI was calculated on the resulting group labels concatenated to a single vector, also compared to the true labels. BayesSpace was implemented for 5000 iterations, discarding a burn-in period of 2000 iterations.

For \(p = 15\) across 50 replicates, our method achieved a mean NMI 0.993, a mean misclassification rate for r 0.06, and a true positive rate of 1 and a false negative rate of 0 for z. In comparison, K-means obtained mean Group 1 and Group 2 NMI of 0.877, DR-SC returned NMI of 0.955, and BayesSpace returned an NMI of 0.895. Our method outperforms the others similarly in terms of clustering across the other scenarios of varying data dimension, as shown by Table 1. The true positive and false negative rate of z is 1 and 0 respectively across all scenarios. For \(p=\{20, 25, 30, 40, 50\}\), we obtain respective r misclassification rates of \(\{0.05, 0.06, 0.03, 0.06, 0.05\}\). We emphasize that the competing method cannot make inferences about variable selection or group assignment.

Table 1 Combined group NMI from our simulations. Standard errors are given in parentheses. There are 5 signal variables in each scenario, the others being noise.
Full size table

Conclusion

We have introduced a Bayesian nonparametric model for clustering observations from multiple datasets and grouping observations across datasets using information common across all datasets and idiosyncratic to each dataset in this paper. Clustering, grouping, variable selection, and K are all determined automatically in the proposed Bayesian model. Our simulations and real data application demonstrate the proposed method, with simulations showing the advantage of the method over existing clustering algorithms.

We designed our model as a synthesis of a nonparametric Bayesian method for combining inference across experiments, and a partition distribution prior indexed by pairwise information. We have shown how the model is implemented in a Gibbs sampler. Our model was applied to spatial transcriptomic data for two mice, showing its ability to cluster and group observations using gene expression and pairwise distances, and its capability for selecting significant genes. We have discussed the selected genes and their biological significance.

There remain many extensions and possible future work for this model. Here, we have applied our model to two groups of data, but theoretically, this model may be used for an arbitrary number of datasets. The limiting factor in scaling this method to include more datasets is runtime. A component for data preprocessing could also be added to the model, allowing all-in-one analysis of raw transcriptomic data. In future work, we will investigate ways to improve computing efficiency and including additional components to bolster the versatility of our model.