Short-term traffic flow prediction research based on ICEEMDAN-MPE-PSO-DELM model

Abstract

Based on historical data, a new short-term traffic flow prediction model (ICEEMDAN-MPE-PSO-DELM-ARIMA) for intersections is proposed. In order to improve prediction accuracy, ICEEMDAN decomposition algorithm is applied on traffic flow time series to obtain multiple Intrinsic Mode Function (IMF) components. Then PSO-MPE algorithm is introduced to obtain the multi-scale permutation entropy values of each IMF component, to judge the randomness. According to the randomness, different prediction models are established. Prediction models based on PSO-DELM algorithm are established for IMF components with big randomness. ARIMA prediction models are established for IMF components with small randomness. In order to obtain the final predicted traffic flow values, multiple prediction results are added together. Finally, two actual intersections are selected to verify the proposed model. Results show that compared with other models, the proposed model has the smallest prediction errors and the best fitting effect with the real values, which can effectively improve prediction accuracy.

Introduction

With the rapid development and update of computer technologies such as intelligent sensing technology, big data, cloud computing and artificial intelligence, Intelligent Transportation Systems (ITS) have been widely used in urban road traffic management.

As an important basis for ITS traffic management and guidance, traffic flow prediction can effectively reflect the operation status of urban road network through the analysis and prediction of acquired real-time, complete and all-condition road traffic information, and provide reliable data support and scientific decision-making basis for urban traffic management planning¹.

Traffic flow forecasting is to predict the state of traffic flow in the future period of time based on historical data. According to the prediction time scale, traffic flow prediction can be divided into short-term, medium-term and long-term prediction models. Short-term prediction models mainly focus on traffic predictions at the hour or minute level, such as traffic congestion prediction and parking space demand prediction. Medium-term forecasting models mainly focus on traffic forecasts at the weekly or monthly level, such as passenger flow forecasts and demand for public transportation routes. Long-term prediction models mainly focus on traffic predictions for different grades, such as the prediction of demand for transportation network expansion and the prediction of market demand scale.

Long-term prediction can help understand the travel patterns of the entire city in advance and is mainly used for traffic management and traffic planning. Short-term prediction can provide real-time information on the current road traffic conditions and is mainly used for traffic early warning and traffic guidance. Due to the complexity of the transportation network and the uncertainty of traffic data, real-time and accurate short-term traffic flow prediction is of great significance for improving road traffic efficiency and alleviating traffic congestion. Therefore, short-term traffic flow prediction is always an important research direction in the field of intelligent transportation systems.

Among various parameters of traffic flow, traffic volume can reflect the frequency of road use. Therefore, this paper mainly studies traffic volume prediction. By constructing a combined traffic flow prediction model, this paper can provide model support for the prediction and decision-making of ITS and theoretical basis for the operation decision-making of the transportation network.

Related works

For short-term traffic flow forecasting methods, domestic and foreign scholars have carried out a lot of theoretical researches.

The existing researches can be divided into three categories: parametric models, non-parametric models and combined prediction models.

Parameter prediction models are mainly used to forecast traffic flow through the construction of mathematical models, such as exponential smoothing algorithm², autoregressive comprehensive moving average (ARIMA) model³, Markov chain prediction model, Kalman filter prediction model⁴, etc. The disadvantage of this kind of model is that it has limitations in dealing with complex traffic environment.

Non-parametric prediction models⁵ are used to predict future traffic conditions by analyzing potential laws and relationships between historical data, such as support vector machine model (SVM)^6,7 and artificial neural network model (BP)⁸. It is suitable for processing small sample data, simple and efficient. However, there are some limitations when dealing with large sample data and complex nonlinear functions.

With the application and popularization of intelligent algorithms, combined prediction methods are proposed. The combination of deep learning algorithms and neural network is constantly applied to the deep structure model of short-term traffic flow prediction, which promotes the rapid development of models such as neural network and deep learning based on data-driven methods^9,10 and provides more accurate traffic flow prediction tools.

Using improved wavelet packet to carry out fine decomposition of the time series, Zhang et al.¹¹ constructed IWPA-LSTM model and input the reconstructed subsequence into the model for prediction, which has higher practicability in the case of small samples. Wei et al.¹² combined the principle of Empirical Mode Decomposition (EMD) and BP neural network, and verified the effectiveness of the method. Tan et al.¹³ firstly used wavelet transform to reduce the noise of the original traffic flow data center, and then built a prediction model based on de-noising data set and mixed traffic flow.

Yang et al.¹⁴ proposed a hybrid traffic flow multi-step prediction method based on EMD and superimposed automatic coding model, and confirmed the reliability of the prediction. Li et al.¹⁵ proposed a travel time prediction model integrating empirical mode decomposition and random vector function connected networks, which is superior to other models in a number of error measurement indicators. Wang et al.¹⁶ studied the deep learning theory and built the LSTM-RNN urban expressway traffic prediction model, and verified that the accuracy, practicability and expansibility of the prediction algorithm were improved. Polson et al.¹⁷ proposed a deep learning structure to predict traffic flow and proved that the deep learning structure can capture nonlinear space-time effects. Xing et al.¹⁸ proposed a predictive model for OD flows, which merged GCN and LSTM-Attention. The model effectively improved the accuracy of OD prediction in urban rail transit. Based on improved deep extreme learning machine algorithm, Tian et al.¹⁹ built a new traffic flow prediction method. Once again, the advantages of the hybrid prediction model in traffic flow prediction have been proved.

Among the existing prediction methods, chaos theory, neural network and support vector machine have obvious advantages in the analysis of complex nonlinear uncertain systems. Although the above algorithms have achieved good results in traffic flow prediction, there are still many aspects to be improved and perfected. For example, in traffic flow data decomposition, there are some disadvantages such as mode aliasing, poor adaptability and stability. Moreover, the traditional neural network usually adopts gradient descent method, which is easy to fall into local optimization and slow learning speed.

In the field of traffic prediction, compared with traditional models, deep learning can effectively conduct dependent modeling of traffic data, extract relevant features, and carry out traffic uncertainty prediction. The uncertainty of the model is quantified through the obtained prediction interval, effectively improving the reliability and credibility of traffic prediction. Therefore, this paper introduces the Deep Extreme Learning Machine algorithm and selects the PSO algorithm to optimize it, constructing a combined traffic flow prediction model, expecting to further improve the operational efficiency and prediction accuracy.

The contributions and innovations of this article are as follows:

• (1) PSO-DELM algorithm as a relatively novel algorithm is firstly used to predict traffic volume, which can effectively improve the prediction accuracy.

• (2) MPE algorithm is used to quantitatively analyze the randomness characteristics of IMF components.

• (3) According to different random properties, different prediction models are built. The IMF components with big randomness are input into the PSO-DELM prediction models. The IMF components with small randomness are input into the ARIMA prediction models.

• (4) Different types of prediction models are constructed to comparatively analyze and evaluate the validity of the model proposed in this paper. And actual data verification is carried out.

Proposed system model

System overview

In order to obtain more stable traffic flow decomposition data, reduce the interference of the original traffic flow data to the prediction results, and obtain the best model parameter values, this paper optimizes the short-time traffic flow combination algorithm.

Deep extreme learning machine (DELM), proposed by Huang et al.²⁰ in 2011, is one of the important prediction technologies in artificial neural networks. The idea of DELM algorithm is to minimize the reconstruction error so that the output can be infinitely close to the original input, and through the training of each layer, the advanced features of the original data can be learned.

Compared with the traditional Extreme learning machine (ELM)²¹, DELM algorithm can more fully capture the mapping relationship between the data, so as to improve the ability of nonlinear fitting and forecast performance. And DELM has no reverse fine-tuning process, which can greatly shorten the network training time.

Since the number of neurons in each hidden layer in DELM algorithm needs to be manually set, and generally the setting is large to improve the accuracy. Therefore, a large number of data and simulation experiments are needed to verify the values. However, with the increase of the neurons number in the hidden layer, the neurons number in each experiment fluctuates greatly. And the experimental process is too complicated, leading to an increase in the uncertainty of the model. Compared with other optimization algorithms, Particle Swarm Optimization (PSO) algorithm has the characteristics of fast convergence speed, high efficiency and simplicity. Therefore, PSO algorithm is used to select the number of hidden layers and find the optimal neurons number in each hidden layer through optimization.

The randomness and nonlinear characteristics of traffic flow data directly affect the training and prediction accuracy of the observed data. Therefore, part of the research introduces the signal decomposition algorithm to decompose the traffic flow data and then conduct model training and prediction.

In feature extraction methods, traditional finite element methods such as fast fourier transform (FFT), wavelet packet transform (WPT), and lifted Wavelet transform are mostly based on basis expansions. The explicit basis is only constructed from the prior information of the signal, and these expansions are subject to orthogonality constraints, and their performance is greatly limited. Based on the above limitations, adaptive mode decomposition (AMD) technology is introduced due to its ability to analyze complex signals. Empirical mode decomposition (EMD) is the most widely used in AMD, but it has low sensitivity and lacks mathematical ideas. Local mean decomposition (LMD) has the advantage of adaptation, but it has the same endpoint effect as EMD decomposition. Both ensemble empirical mode decomposition (EEMD) and variational mode decomposition (VMD) can avoid the problem of mode aliasing. However, the decomposition efficiency of EEMD is relatively low, and the decomposition effect of VMD is limited by the number of decomposition layers and the penalty factor. However, the complete ensemble empirical mode decomposition with adaptive noise (CEEMDAN)²² eliminates the errors caused by EMD through adaptive noise addition. This reduces the influence of mode aliasing on information extraction to a certain extent, achieves higher-precision decomposition, and can handle the nonlinear and unstable signals very well. There are still noise and pseudo-components in the components decomposed by CEEMDAN algorithm. As an improved algorithm, Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise (ICEEMDAN)²³ can effectively improve the problem of noise residue. Therefore, ICEEMDAN algorithm is selected to conduct prior analysis on the original traffic flow data in this paper.

Autoregressive integrated moving average (ARIMA) model is a commonly used time series prediction model. The basic principle is based on the autocorrelation of time series. By analyzing historical data, the inherent laws of the data are captured. It is supported by relatively mature theories, and the prediction results have certain reliability and stability. Furthermore, without the need for a large number of external explanatory variables, modeling and prediction can be carried out mainly relying on the historical data of the time series itself, which is relatively simple in terms of data collection and processing. It can fit the changing trend of short-term time series well and often achieve relatively accurate results for short-term predictions.

ARIMA requires that the time series must be stationary or can be transformed into stationary series through methods such as difference. If the data shows obvious trends or seasonality, it needs to be processed first to stabilize it. Otherwise, it will affect the estimation and prediction effect of the model. It is applicable to time series with linear relationships, that is, the relationships between variables can be approximately described by linear equations. For data with strong nonlinear relationships, the ARIMA model may not be able to accurately capture their patterns. ARIMA is more suitable for short-term prediction. As the prediction period extends, the prediction error will gradually increase.

The long-short term memory (LSTM) model is a special recurrent neural network (RNN), mainly used for processing sequential data. The model structure is complex, and the training and inference processes require a large amount of computing resources and time. There are many model parameters. If the amount of training data is insufficient or the data features are not rich enough, overfitting is likely to occur, resulting in poor generalization ability on the test set or new data. The quality and format requirements for the input data are relatively strict. Operations such as preprocessing and normalization of the data are needed. Otherwise, it may affect the performance of the model.

Based on the above analysis, the ARIMA model has accurate prediction results for low-frequency stationary time series, while the LSTM neural network can achieve better prediction accuracy for high-frequency non-stationary time series. Therefore, in this paper, the ARIMA model is taken as the basic prediction model for low randomness sequences.

Based on the existing research results, considering the combined forecasting method in the advantage of short-term traffic flow prediction, this paper puts forward an ICEEMDAN-MPE-PSO-DELM-ARIMA combined prediction method. The new proposed model process is shown in (Fig. 1).

Firstly, correlation analysis is carried out on historical traffic data, and Pearson Correlation Coefficient²⁴ is adopted in this paper.

Pearson Correlation Coefficient, also known as Pearson Product-Moment Correlation Coefficient (PPMCC), is proposed by Karl Pearson in the 1880s. It is widely used to measure the degree of correlation between two variables, whose values are between (−1) and 1, and its formula is as follows:

$$r=\frac{{\sum\limits_{{i=1}}^{n} {\left( {{X_i} - \overline {X} } \right)\left( {{Y_i} - \overline {Y} } \right)} }}{{\sqrt {\sum\limits_{{i=1}}^{n} {{{\left( {{X_i} - \overline {X} } \right)}^2}} } \sqrt {\sum\limits_{{i=1}}^{n} {{{\left( {{Y_i} - \overline {Y} } \right)}^2}} } }}$$

(1)

Where r is the correlation coefficient between variable $X=\left\{ {{X_i}} \right\}\left( {1 \leqslant i \leqslant n} \right)$ and variable $Y=\left\{ {{Y_i}} \right\}\left( {1 \leqslant i \leqslant n} \right)$. When r > 0, it means that the variables X and Y are positively correlated, r < 0 means that they are negatively correlated, and r = 0 means that they are not correlated. ${X_i}$ is the measurement of the variable X at position i, and $\overline {X}$ is the mean of the variable X. ${Y_i}$ is the measurement of the variable Y at position i, and $\overline {Y}$ is the mean of the variable Y. n is the number of samples of the variable X or Y. The greater the absolute value of r, the stronger the correlation will be.

Fig. 1

Intersection traffic flow prediction process based on ICEEMDAN-MPE-PSO-DELM-ARIMA model.

Then, ICEEMDAN method is used to decompose the traffic flow time series, and multiple IMF components are obtained. The multi-scale arrangement entropy of IMF component is calculated by PSO-MPE algorithm. According to the size of the standardized MPE values, the randomness of each decomposition sequence is obtained.

In order to improve the forecasting accuracy, the IMF component sequences of each traffic decomposition are normalized before establishing the forecasting model:

$$X'\left( i \right){\text{=}}\frac{{\left( {X\left( i \right) - \hbox{min} \left\{ {X\left( i \right)} \right\}} \right)}}{{\left( {\hbox{max} \left\{ {X\left( i \right)} \right\} - \hbox{min} \left\{ {X\left( i \right)} \right\}} \right)}}$$

(2)

Where, $X'\left( i \right)$ is the normalized traffic data and $X\left( i \right)$ is the IMF data of the traffic sequence component.

The IMF sequence with big randomness after normalization is input into the PSO-DELM forecasting model, and the IMF component with small randomness is input into the ARIMA forecasting model. Then multiple forecasting result sequences are obtained.

The sequence of each prediction result is reverse-normalized:

$$X\left( i \right)=X'\left( i \right) \cdot \left( {\hbox{max} \left\{ {X\left( i \right)} \right\} - \hbox{min} \left\{ {X\left( i \right)} \right\}} \right)+\hbox{min} \left\{ {X\left( i \right)} \right\}$$

(3)

Finally, multiple prediction sequences are added to obtain the final prediction results of the model. In order to verify the validity of this model, two actual intersections are selected for traffic prediction.

ICEEMDAN

The original traffic flow time series is denoted by $s\left( n \right)$. The standard normally distributed white noise sequence added at the $i\left( {1,2,...,I} \right)$ time is ${v^i}\left( n \right)$, and $M\left( \cdot \right)$ is the local mean of the signal. The symbol $\left\langle \cdot \right\rangle$ represents the average operation during decomposition. Then the traffic flow sequence of the i th decomposition can be expressed as ${s^i}\left( n \right)=s\left( n \right)+{v^i}\left( n \right)$. ${E_k}\left( \cdot \right)$ and $\widetilde {{IM{F_k}}}$ are defined as the kth modal components produced by EMD and ICEEMDAN, respectively.

The steps of ICEEMDAN algorithm²³ are as follows:

Step 1 Similar to EMD algorithm²², the first flow margin series is obtained by calculating the local mean ${s^i}\left( n \right){\text{=}}s\left( n \right)+{\beta _0}{E_1}\left( {{v^i}\left( n \right)} \right)$ of the ith decomposition results of the traffic flow time series, as formula (4).

$${r_1}\left( n \right)=\left\langle {M\left( {s{{\left( n \right)}^{\left( i \right)}}} \right)} \right\rangle$$

(4)

Step 2 When $k=1$, calculate the first modal component, as formula (5).

$$\widetilde {{IM{F_1}}}\left( n \right)=s\left( n \right) - {r_1}\left( n \right)$$

(5)

Step 3 The second flow margin sequence is calculated as the local mean of the flow sequence ${r_1}\left( n \right)+{\beta _1}{E_2}\left( {{v^i}\left( n \right)} \right)$. Then, the second modal component is obtained as formula (6).

$$\widetilde {{IM{F_2}}}\left( n \right)={r_1}\left( n \right) - {r_2}\left( n \right)={r_1}\left( n \right) - \left\langle {M\left( {{r_1}\left( n \right)+{\beta _1}{E_2}\left( {{v^i}\left( n \right)} \right)} \right)} \right\rangle$$

(6)

Step 4 Similarly, calculate the K $\left( {3,...,K} \right)$ flow margin sequence for the other stages.

$${r_k}\left( n \right)=\left\langle {M\left( {{r_{k - 1}}\left( n \right)+{\beta _{k - 1}}{E_k}\left( {{v^i}\left( n \right)} \right)} \right)} \right\rangle$$

(7)

Step 5 Calculate the kth mode component.

$$\widetilde {{IM{F_k}}}\left( n \right)={r_{k - 1}}\left( n \right) - {r_k}\left( n \right)$$

(8)

Step 6 Return to Step 4. The algorithm ends when the resulting margin sequence cannot be decomposed further.

From the above steps, it can be seen that ICEEMDAN’s decomposition process is complete and can achieve accurate recombination of the original traffic flow time series.

PSO-MPE

Permutation entropy (PE) algorithm is a new algorithm proposed by Bandt et al.²⁵ in 2002, which can be used to characterize the randomness of time series and has been widely used in various time series analysis. Permutation entropy can only detect the complexity and randomness of time series on a single scale. Generally, the output time series of complex systems contain feature information on multiple scales, so PE algorithm cannot study the multi-scale complexity change of time series.

Multi-scale Permutation Entropy (MPE)²⁶ is an effective feature extraction method based on the PE²⁵ algorithm, which can describe the complexity of time series on a multi-scale. Firstly, multi-scale coarse-grained time series is established. Secondly, the arrangement entropy of coarse-grained sequences of different scales is calculated to achieve multi-dimensional description.

As we all know, intersection traffic flow time series is a typical non-stationary random sequence, so in order to reduce the scale of calculation, MPE algorithm can be used to analyze the random characteristics of traffic flow decomposition sequences.

The basic steps of MPE algorithm are as follows:

Step 1 Assuming that the original traffic flow time series is $X = \left\{ {x_{i} ,i = 1,2,3 \ldots ,n} \right\}$, the multi-scale time series can be obtained after coarse-grained processing as formula (9).

(9)

Where S is the scale factor.

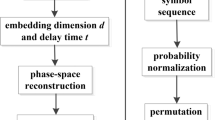
Step 2 Phase space reconstruction operation is performed on $Y_{j}^{{(s)}}$

(10)

Where, m is the embedding dimension and τ is the time delay. l represents the lth reconstruction component. Besides, formula $1 \le l \le n - \left( {m - 1} \right)\tau$ exists.

Step 3 The components of the reconstructed sequence are arranged in ascending order to obtain any permutation ${N_r}$, and the occurrence probability of any permutation is denoted as ${P_r},r=1,2, \cdots ,R\left( {R \leqslant m!} \right)$.

Step 4 The multi-scale arrangement entropy of the coarse-grained sequence is calculated and normalized.

$${H_p}= - \sum\limits_{{r=1}}^{{m!}} {{P_r}\ln {P_r}/\ln \left( {m!} \right)}$$

(11)

The MPE algorithm flow is shown in (Fig. 2).

Fig. 2

MPE algorithm flow.

The selection of scale factor s is particularly important in the coarse-grained process. If the value of s is too small, the characteristic information of the signal cannot be extracted to the maximum extent. If the value of s is too large, the complexity difference between signals may be erased. In addition, in the calculation process of MPE algorithm, if the embedding dimension m is too small, the mutation detection performance of the algorithm will be reduced. If the value of m is too large, it will not be able to reflect subtle changes in the time series. Time scale N and delay time t also have different effects on MPE value. To sum up, the parameter selection of MPE algorithm is very important, and it is necessary to optimize the parameter selection.

In this paper, PSO algorithm²⁷ is used to optimize the parameters of MPE algorithm.

PSO is a heuristic global optimization search algorithm. The basic principle is that initialize a group of random particles (random solutions), and then find the optimal solution through iteration. In each iteration, the particle is updated by tracking two “extreme values” (P_best, G_best).

In summary, the steps of PSO algorithm are as follows:

Step 1. Particle swarm initialization. Set population size m, initial location and speed. For any i and s, uniformly distributed ${x_{is}}$ is generated in the interval $\left[ { - {x_{\hbox{max} }},{x_{\hbox{max} }}} \right]$, and uniformly distributed ${v_{is}}$ is generated in the interval $\left[ { - {v_{\hbox{max} }},{v_{\hbox{max} }}} \right]$. For any i, set ${y_i}={x_i}$.

Step 2. Calculate the fitness value of each particle.

Step 3. The ${p_{is}}$ fitness value of the local best position is compared with the fitness value of the current particle. If the current particle fitness value is better than the ${p_{is}}$ fitness value, it is used as the local best location.

Step 4. The global best position ${p_{gs}}$ fitness value is compared with the fitness value of the current particle. If the current particle fitness value is better than the ${p_{gs}}$ fitness value, it is regarded as the global best position.

Step 5. Update the particle position and velocity.

Step 6. Calculate the particle fitness value. Update local and global extreme values.

Step 7. The termination condition of the algorithm is judged. If it is satisfied, the solution is output and the algorithm ends. Otherwise, Step 2 is returned and the algorithm continues to execute.

The PSO algorithm flow is shown in (Fig. 3).

Fig. 3

PSO algorithm flow.

When analyzing the overall trend of the data, the central trend of the data can be observed by finding average value. However, the mean value cannot completely represent the overall situation of the data, so the skewness of the data can be calculated. Therefore, this paper selects the average function of MPE skewness as the fitness function of PSO algorithm to find its minimum value.

Skewness is used to characterize the degree to which a random sequence with a non-normal probability density deviates from the normal distribution. The value is zero, indicating a symmetric distribution. The value greater than zero indicates that the distribution of the asymmetric part tends to be more positive. The value less than zero indicates that the asymmetric part of the distribution tends to be more negative.

The permutation entropy of traffic flow time series $X=\left\{ {{x_i},i=1,2, \cdots ,N} \right\}$ at all scales is denoted as${H_p}\left( X \right)=\left\{ {{H_p}\left( 1 \right),{H_p}\left( 2 \right), \cdots ,{H_p}\left( s \right)} \right\}$, and skewness $Ske$ is calculated, as shown in formula (12).

$$Ske=E{\left[ {{H_p}\left( X \right) - H_{p}^{m}\left( X \right)} \right]^3}/{\left[ {H_{p}^{d}\left( X \right)} \right]^3}$$

(12)

Where, $H_{p}^{m}\left( X \right)$ is the mean value of the sequence ${H_p}\left( X \right)$. $H_{p}^{d}\left( X \right)$ is the standard deviation of the sequence ${H_p}\left( X \right)$. $E\left( \cdot \right)$ is the expectation of the sequence.

The PSO process for optimizing MPE is as follows:

Step 1. Input original traffic flow time series, set the parameters of optimization algorithm, and initialize MPE parameters.

Step 2. Fitness function is calculated. MPE parameters are optimized by PSO algorithm, and optimization parameters are output.

Step 3. Calculate MPE value and output.

Through the above steps, the MPE value of each IMF component can be calculated. Then the randomness of each decomposition sequence is obtained, which provides the basis for the prediction model establishment.

PSO-DELM

According to the random characteristics of each IMF component obtained by the PSO-MPE algorithm, the component with big randomness is input into the PSO-DELM prediction model, and the component with small randomness is input into the ARIMA model. And multiple traffic prediction results obtained are added together to obtain the final forecasted traffic flow.

DELM algorithm

ELM algorithm is a machine learning algorithm based on single hidden layer feedforward neural network. It generates the weights and thresholds of the hidden layer randomly, and then obtains the optimal solution through simple calculation, which has good learning efficiency and fitting ability.

Autoencoders are a common unsupervised learning algorithm that can be trained to copy input information to output data. It is introduced into ELM algorithm to form the extreme learning machine-automatic encoder (ELM-AE) to achieve more effective feature information extraction. ELM-AM consists of input layer, hidden layer and output layer. The number of nodes in the input layer and the output layer is both m, and the number of nodes in the hidden layer is n. If m = n, ELM-AE implements equidimensional feature mapping. If m > n, dimensionality reduction feature mapping is realized. If m < n, high-dimensional feature mapping is implemented.

DELM algorithm is a deep network system which is cascaded by several ELM-AEs. Similar to traditional deep learning algorithms, DELM algorithm trains the network using a layer-by-layer greedy training method, and the input weights of each hidden layer are initialized using ELM-AE to perform hierarchical unsupervised training.

In the DELM training process, the original input sample data is used as the target output matrix of the first ELM-AE, and the output weight matrix is obtained, which is orthonormalized as the input weight matrix of the first hidden layer of DELM. Then the output of the first hidden layer of DELM is used as the input matrix of the next ELM-AE, and so on, and the output weight matrix of the last layer is finally obtained, thus completing the DELM training process.

There are Q sets of training data $\left\{ {\left. {\left( {{x_i},{y_i}} \right)} \right|i=1,2, \cdots ,Q} \right\}$ and M hidden layers, and the training data sample is input to obtain the first weight matrix ${{\mathbf{\beta }}^1}$ according to the ELM-AE theory, and then the hidden layer feature vector ${{\mathbf{H}}^1}$,…, is obtained. By analogy, the input layer weight matrix ${{\mathbf{\beta }}^M}$ and the hidden layer feature vector ${{\mathbf{H}}^M}$ of layer M can be obtained, then the mathematical model expression of DELM algorithm is as formula (13).

$${y_i}=\sum\limits_{{j=1}}^{L} {\sum\limits_{{k=0}}^{Z} {\beta _{j}^{k}{g_{jk}}} } \left( {\sum\limits_{{p=1}}^{n} {w_{j}^{{ih}}{x_i}+{b_j}} } \right),j=1,2, \cdots ,Q$$

(13)

Where L is the number of neurons in the hidden layer, Z is the number of derived neurons corresponding to neurons in the hidden layer, $\beta _{j}^{k}$ is the weight vector between the kth derived neurons corresponding to neurons in the jth hidden layer and the output layer. ${g_{jk}}$ is the k-order derivative function of the activation function of neurons in the jth hidden layer, and n is the number of neurons in the input layer. $w_{j}^{{ih}}$ is the weight vector between the input layer and the jth hidden layer neurons, and ${b_j}$ is the bias of the jth hidden layer node.

PSO-DELM algorithm

PSO-DELM algorithm is an improvement of DELM algorithm.

The steps of the PSO-DELM algorithm are as follows:

• Step 1. The traffic flow time series is divided into training set and prediction set.

• Step 2. Initialize PSO parameters, including inertia factor w, learning factor c1 and c2.

• Step 3. Determine the DELM topology and set related parameters.

• Step 4. The mean square error obtained by DELM training is used as the fitness value of PSO.

• Step 5. The initial optimal solution is updated (Pbest, Gbest), by moving the population (updating the particle position and velocity), calculating the new fitness value, and updating the current optimal solution to see whether the fitness value is satisfied. If not, iterate again.

• Step 6. The optimal node number of each hidden layer obtained by PSO is substituted into DELM.

• Step 7. Training test.

• Step 8. Output prediction result.

The PSO-DELM algorithm flow is shown in (Fig. 4).

Fig. 4

Flow chart of PSO-DELM algorithm.

ARIMA

Time series analysis is an effective parametric time-domain analysis method for dealing with dynamic data. In the 1970s, G.E. Box and G. M. Jenkins²⁸ proposed the Autoregressive Integrated Moving Average (ARIMA) model for analyzing time series. Compared with stationary time series and periodic time series models, this method is more mathematically perfect and has higher prediction accuracy.

The general expression of the ARIMA model is as formula (14).

$${x_t}={\varphi _1}{x_{t - 1}}+{\varphi _2}{x_{t - 2}}+ \ldots +{\varphi _p}{x_{t - p}}+{\varepsilon _t} - {\theta _1}{\varepsilon _{t - 1}} - {\theta _2}{\varepsilon _{t - 2}} - \ldots - {\theta _q}{\varepsilon _{t - q}}$$

(14)

In the formula, ${\varphi _1},{\varphi _2}, \ldots ,{\varphi _p}$ is the autoregressive coefficient and p is the autoregressive order. ${\theta _1},{\theta _2}, \ldots ,{\theta _q}$ is the moving average coefficient, and q is the order of the moving average. $\left\{ {{\varepsilon _t}} \right\}$ is a sequence of white noise. If the difference order is represented by d, the model is often denoted as ARIMA (p, d, q).

Experiment setup

In order to verify the effectiveness of the combined prediction method, two actual intersections are selected to verify the short-term traffic flow prediction. The two intersections are denoted as intersections 1 and 2, respectively.

The traffic flow at the west entrance of intersection 1 is analyzed. The traffic flow of straight traffic and right turn traffic at the south entrance of intersection 2 is analyzed. The data comes from the SCATS signal control system, which collects 5 min flow data for 5 consecutive working days.

The experimental settings of this paper are as follows: the processor CPU is 13th Gen Intel(R) Core (TM) i7-1360P (2.20 GHz), and the machine RAM is 32.0 GB. The computer software operating system is Windows 11. The training and testing stages of the model are all carried out in the MATLAB 2022b environment.

Firstly, the original traffic flow time series of the intersection is preprocessed. The threshold method is used to detect and eliminate abnormal data, and then the missing data is repaired based on historical data.

After pre-processing, two sets of traffic flow time series can be obtained, each containing 1440 data points. The flow distribution sequence at intersection 1 is shown in (Fig. 5). The flow distribution sequence at intersection 2 is shown in (Fig. 6).

Fig. 5

Traffic flow distribution of intersection 1.

Fig. 6

Traffic flow distribution of intersection 2.

The Pearson correlation coefficient of formula (1) is used to conduct correlation analysis on the 5-day traffic data of two intersections, and the correlation between the traffic data is obtained, as shown in (Tables 1 and 2). Sequences X₁₁ to X₁₅ are the 5 min flow data of intersection 1 from Monday to Friday, respectively. Sequences X₂₁ to X₂₅ are the 5 min flow data of intersection 2 from Monday to Friday, respectively.

Table 1 Correlation degree r of 5-day traffic flow of intersection 1.

Table 2 Correlation degree r of 5-day traffic flow of intersection 2.

As can be seen from Table 1, the correlation value of the 5-day traffic data in the direct direction of the west entrance of intersection 1 is greater than 0.8, indicating a strong correlation, and the historical traffic can be used to predict the future traffic. As can be seen from Table 2, the correlation value of the traffic data of the south entrance of intersection 2 for 5 days is greater than 0.85, indicating a strong correlation, and the historical traffic can be used to predict the future traffic.

Therefore, 1152 data points in the first 4 working days of the two intersections are used for forecasting model training, and the data in the fifth working day are used for model prediction effect verification.

Traffic flow sequence decomposition

Through MATLAB software programming, ICEEMDAN decomposition is performed on the original intersection flow time series of intersections 1 and 2. I = 500 groups of white noise signals are added during decomposition, and the noise standard deviation is 0.2. The ICEEMDAN algorithm running time for the two intersections is both about 8s. The calculation time can meet the requirement of traffic flow prediction time.

The decomposition results of traffic data at intersection 1 are shown in (Fig. 7). Figure 8 shows ICEEMDAN decomposition percentage error of traffic flow sequence at intersection 1. Figure 9 shows the box diagram of iterations of each IMF component at the intersection.

As can be seen from Fig. 7, the original time series of traffic flow at intersection 1 can be decomposed into 10 IMF components. As can be seen from Fig. 8, the decomposition error of this flow time series is very small, and the percentage error reaches the 10^–14 level. As can be seen from Fig. 9, with the process of decomposition, the number of iterations of each IMF component gradually decreases until it reaches zero. According to Figs. 8 and 9, the traffic sequence at intersection 1 is completely decomposed, which proves the effectiveness of this method.

Fig. 7

Traffic flow data decomposition results by ICEEMDAN algorithm of intersection 1.

Fig. 8

Relative percentage error of improved ICEEMDAN for intersection 1.

Fig. 9

Iterations boxplot of each IMF component for intersection 1.

The decomposition results of traffic data at intersection 2 are shown in (Fig. 10). Figure 11 is the ICEEMDAN decomposition percentage error diagram of traffic flow sequence at Intersection 2. Figure 12 shows the box diagram of iterations of each IMF component at the intersection.

As can be seen from Fig. 10, the original time series of traffic flow at intersection 2 can be decomposed into 9 IMF components. As can be seen from Fig. 11, the decomposition error of this flow time series is very small, and the percentage error reaches the 10^–14 level. As can be seen from Fig. 12, with the decomposition process, the number of iterations of each IMF component gradually decreases until it reaches zero. By synthesizing Figs. 11 and 12, it can be seen that the traffic sequence of intersection 2 is completely decomposed, which proves the effectiveness of this method.

Fig. 10

Traffic flow data decomposition results by ICEEMDAN algorithm of intersection 2.

Fig. 11

Relative percentage error of improved ICEEMDAN for intersection 2.

Fig. 12

Iterations boxplot of each IMF component for intersection 2.

Analysis of random

PSO-MPE algorithm is used to calculate the multi-scale arrangement entropy of each IMF component obtained from the decomposition of two intersections’ traffic data. Firstly, the PSO algorithm is used to optimize MPE parameters. The population size is set as follows: P_number = 10, acceleration constant C1 = 2, C2 = 2, inertia weight W = 1, MaxNum = 20. The signal length is set to 1440, the embedding dimension m is set to (3,8), the delay time t is set to (1,5), and the scale factor s is set to (1,16). The maximum speed is V_max = 25 and the minimum speed is set to V_min=-V_max.

The convergence curve of the PSO-MPE algorithm at intersection 1 is shown in (Fig. 13). The convergence curve of the PSO-MPE algorithm at intersection 2 is shown in (Fig. 14).

Fig. 13

PSO-MPE algorithm convergence curve of intersection 1.

Fig. 14

PSO-MPE algorithm convergence curve of intersection 2.

Through optimization, the embedded dimension m of traffic sequence at intersection 1 is 4.88, and the scale factor s is 12.99. The delay time t is 5. In order to facilitate calculation, m and s are rounded, that is, m = 5, s = 13. Then, the MPE values of each IMF component are obtained, as shown in (Fig. 15).

Through optimization, the embedded dimension m of traffic flow sequence at intersection 2 is 3.09, the scale factor s is 16, and the delay time t is 1. In order to facilitate calculation, m is rounded, that is, m = 3. Then, the MPE values of each IMF component are obtained, as shown in (Fig. 16).

Fig. 15

MPE values of IMF components at intersection 1.

Fig. 16

MPE values of IMF components at intersection 2.

When s is 13, the MPE values of each IMF component at intersection 1 and the MPE differences of adjacent IMF components are shown in (Table 3). When s is 16, the MPE values of IMF components at intersection 2 and the MPE differences of adjacent IMF components are shown in (Table 4).

Table 3 The permutation entropy of each IMF component when s = 13 for intersection 1.

Table 4 The permutation entropy of each IMF component when s = 16 for intersection 2.

Taking ICEEMDAN decomposition results and MPE values into account, the random characteristics of IMF component sequences at intersections are analyzed and reorganized.

It can be seen from Table 3; Fig. 15 that the arrangement entropy of IMF1 component at intersection 1 is the largest, indicating that the randomness of IMF1 component is the largest and its influence on the prediction result is also the largest. With the increase of IMF sequence number, the permutation entropy decreases gradually until it decreases to 0. The permutation entropy of IMF1 to IMF6 components is large, indicating that the randomness of the sequence is large, and the MPE difference between adjacent components is small, both less than 0.1, so it is input into the PSO DELM model. The permutation entropy of IMF7, IMF8, IMF9 and IMF10 components is small, which is input into the ARIMA model. Then the prediction results of each model are added together to get the final prediction results.

Similarly, IMF1 to IMF6 of intersection 2 is input into the PSO-DELM prediction model, and IMF7-IMF9 is input into the ARIMA model, and then the results are added.

Prediction model construction

The rolling flow single-step forecasting method is adopted, that is, the historical traffic flow data is used to predict the traffic at the next moment. The model input is the traffic sequence two hours before the forecast point, and the model output is the predicted value sequence. Then 1128 sets of input-output data can be constructed from 1152 traffic data points in the first 4 days of the two intersections to form a training set of the model and predict the traffic flow on the 5th day.

In order to verify the effectiveness of the proposed method, ARIMA model, SVM model, LSTM model, DELM model and PSO-DELM model are constructed respectively. In addition, ICEEMDAN-DELM model, ICEEMDAN-PSO-DELM model and ICEEMDAN-MPE-PSO-DELM-ARIMA model are constructed to compare and analyze the prediction effect.

The ARIMA model, SVM model, LSTM model, DELM model and PSO-DELM prediction model are constructed using the original flow sequence. ICEEMDAN-DELM model, ICEEMDAN-PSO-DELM model, and ICEEMDAN-MPE-PSO-DELM-ARIMA model are constructed using ICEEMDAN decomposition sequences.

SPSS software is used to construct ARIMA algorithm. MATLAB software is used to build other algorithm models.

The activation function of DELM algorithm and PSO-DELM algorithm is set to Sig, the regularization parameter C is set to inf, and the hidden layer i set to 2 layers, with 2 and 3 nodes in each layer respectively. In the PSO algorithm, the population size is set to 20 and the maximum number of iterations is set to 50. The lower boundary of the weight is lb=-1, and the upper boundary is set to ub = 1. The maximum speed value is 1. The minimum speed value is -1.

After testing, the PSO-DELM algorithm calculation time is about 9s to 13s. The iterations number in this paper is set as 50 times. When the number of iterations decreases, the running time of the algorithm will be further reduced.

In summary, the calculation time of the new proposed algorithm in this paper under the operation of the hardware and software is less than 20s. In practical application, by improving the hardware and software environment, the algorithm running time can be further reduced. And then the algorithm running efficiency can be further improved.

Results and discussion

The prediction effect curves of each model at intersection 1 are shown in (Fig. 17), and the prediction effect curves of each model at intersection 2 are shown in (Fig. 18).

As can be seen from Fig. 17, compared with other prediction models, the predicted traffic value obtained by ICEEMDAN-MPE-PSO-DELM-ARIMA model proposed in this paper is the closest to the real value.

As can be seen from Fig. 18, the degree of fitting between ARIMA model and DELM model and the true value is low, and the degree of deviation from the true value is large. Compared with ICEEMDAN-PSO-DELM model after sequence decomposition and the model in this paper, the predicted value of PSO-DELM model is relatively better fitted to the real value, but the deviation from the real value is still large. By synthesizing Figs. 17 and 18, it can be seen that the predicted flow value of the model in this paper has the smallest deviation from the real value, and the highest degree of fitting.

Fig. 17

Prediction results of each model for intersection 1.

Fig. 18

Prediction results of each model for intersection 2.

In order to more directly reflect the prediction effect of each model, the mean absolute error (MAE), mean absolute percentage error (MAPE), mean square error (MSE) and equality coefficient (EC) are selected as the evaluation indexes of model prediction.

$${\text{MAE=}}\frac{1}{n}\sum\limits_{{i=1}}^{n} {\left| {{y_i} - \widehat {{{y_i}}}} \right|}$$

(15)

$${\text{MAPE=}}\frac{1}{n}\sum\limits_{{i=1}}^{n} {\left| {\frac{{{y_i} - \widehat {{{y_i}}}}}{{{y_i}}}} \right|}$$

(16)

$${\text{MSE}}=\frac{1}{n}\sum\limits_{{i=1}}^{n} {{{\left( {{y_i} - \widehat {{{y_i}}}} \right)}^2}}$$

(17)

$$EC=1 - \frac{{\sqrt {\sum\limits_{{i=1}}^{n} {{{\left( {{y_i} - \widehat {{{y_i}}}} \right)}^2}} } }}{{\sqrt {\sum\limits_{{i=1}}^{n} {{{\left( {{y_i}} \right)}^2}} } +\sqrt {\sum\limits_{{i=1}}^{n} {{{\left( {\widehat {{{y_i}}}} \right)}^2}} } }}$$

(18)

Where $\widehat {{{y_i}}}$ and ${y_i}$ represent the predicted and true values at the first moment, and n is the sample size. The smaller the MAE, MAPE and MSE values, the smaller the prediction error and the better the effect. The closer the EC value is to 1, the higher the fit between the predicted value and the true value, and the better the effect will be.

The prediction performance evaluation indexes of each model at intersection 1 are shown in (Table 5).

As can be seen from Table 5, for intersection 1, the MAE and MSE values of ICEEMDAN-MPE-PSO-DELM-ARIMA model are lower than those of other models, indicating the smallest prediction error and the highest prediction accuracy. In addition, the EC value of the new proposed model is 0.917, higher than that of the ARIMA model (0.883). Compared with other methods, the EC value is closest to 1, indicating that the predicted value has the smallest deviation from the true value, the best prediction effect and the best stability of the model.

The prediction performance evaluation indexes of each model at intersection 2 are shown in (Table 6). As can be seen from Table 6, for intersection 2, all the errors obtained by the proposed model are smaller than other comparison models, and the degree of fitting with the true value is the highest.

In conclusion, ICEEMDAN-MPE-PSO-DELM-ARIMA intersection combination prediction model constructed in this paper has good performance and can meet the prediction requirements.

Table 5 Prediction performance indexes comparisons of each prediction model for intersection 1.

Table 6 Prediction performance indexes comparisons of each prediction model for intersection 2.

The main error sources of the new proposed model in this paper are analyzed. The model in this paper decomposes the original traffic flow data first, and then builds combined traffic flow prediction model. As shown in Tables 5 and 6, the errors of the new proposed model are smaller than those of ICEEMDAN-PSO-DELM model. Take the traffic flow prediction of intersection 1 as an example, the sequences input of the two models are different. For the new proposed model, from IMF1 to IMF6 sequences are input into PSO-DELM prediction models, and from the IMF7 to IMF10 sequences are input into ARIMA prediction models. The input of the PSO-DELM model is the IMF1 to IMF10 sequences. The difference between the two models lies in the prediction of IMF7 to IMF10 sequence, leading to the errors difference between the two models. Therefore, it can be proved again that PSO-DELM model is more suitable for predicting sequences with big randomness. ARIMA model is more suitable for predicting sequences with small randomness. When sorting the prediction results, it can also be concluded that the prediction errors of IMF7 to IMF10 sequences by ARIMA models are very small. Similarly, the same conclusion can also be obtained for intersection 2.

The prediction errors of PSO-DELM model are smaller than those of DELM model, which proves that PSO optimization can improve the prediction accuracy effectively. The main error source of the new proposed model is the error after the superposition of individual predictions of multiple sequences. And ICEEMDAN decomposition can reduce the error to some extent.

To sum up, part of the errors of the model in this paper come from the PSO-DELM prediction model and the other part comes from the ARIMA prediction model. After analysis, the prediction errors of PSO-DELM model should be the main error source. Therefore, in the following researches, it is necessary to further optimize the parameters of PSO-DELM algorithm, which is expected to further improve the prediction accuracy.

In order to better compare the prediction effect of different prediction models, SPSS software is applied to carry out pairwise sample t-test on the predicted value of each model, and the confidence interval is 95%. The t-test results of intersection 1 are shown in (Table 7), and the t-test results of intersection 2 are shown in (Table 8).

Table 7 Results of paired t-test for intersection 1.

As can be seen from Table 7, for intersection 1, the p value of the predicted values between ARIMA and SVM models is 0.018, and the p of the predicted values between ARIMA and LSTM is 0.000. The p value between ARIMA and DELM is 0.005, and the p of the predicted values between ARIMA and ICEEMDAN-DELM is 0.000. The p value between DELM and ICEEMDAN-DELM is 0.006. Besides, the p value between ICEEMDAN-PSO-DELM and ICEEMDAN-MPE-PSO-DELM-ARIMA proposed in this paper is 0.000. The above six p values are all less than 0.05, indicating that there are significant differences in the predicted values among the models of each group.

Table 8 Results of paired t-test for intersection 2.

As can be seen from Table 8, for intersection 2, the p value of the predicted values between ARIMA and SVM models is 0.000, and the p of the predicted values between ARIMA and LSTM is 0.000. The p of the predicted values between ARIMA and ICEEMDAN-DELM is 0.000. The p value between DELM and ICEEMDAN-DELM is 0.000. Besides, the p value between ICEEMDAN-PSO-DELM and ICEEMDAN-MPE-PSO-DELM-ARIMA proposed in this paper is 0.000. The above five p values are all less than 0.05, indicating that there are significant differences in the predicted values among the models of each group.

Based on Tables 7 and 8, it can be concluded that compared with ARIMA model, the prediction error of ICEEMDAN-DELM model is reduced and the accuracy is improved. The results of ICEEMDAN decomposed prediction model are better than those of undecomposed prediction model. In addition, the prediction results of the model proposed in this paper are significantly different from those of ICEEMDAN-PSO-DELM model, which also proves the validity of the prediction results proposed in this paper.

By combining the results of Figs. 17 and 18; Tables 5, 6, 7 and 8, the conclusions can be drawn that the hybrid prediction model constructed in this paper has good performance and can meet the prediction requirements.

Conclusion and future work

Based on the historical traffic flow data of intersections, this paper proposes a combined intersections prediction model ICEEMDAN-MPE-PSO-DELM-ARIMA based on improved extreme learning machine algorithm.

Considering the nonlinear and stochastic characteristics of traffic flow, ICEEMDAN-PSO-MPE algorithm is used to analyze the sequence decomposition and randomness of traffic flow. According to the MPE value of each IMF component, its random characteristics are obtained. According to the different randomness, the PSO-DELM prediction model and ARIMA prediction model are constructed respectively, and the results of each prediction model are added together to get the final forecast flow. Finally, based on the traffic data of two different actual intersections for 5 consecutive working days, the traffic forecast is carried out, and the prediction effect is compared. The results show that, compared with other prediction models, the proposed model has the smallest errors and the best fitting effect with the actual values, indicating that the proposed model can effectively improve the prediction accuracy and prove the effectiveness of the proposed algorithm.

Due to the limitations of the experimental conditions and time, the amount of experimental data in this paper is limited. In the following researches, validation data will be added, and additional experiments will be conducted on larger and more diverse datasets to further verify the performance of the model.