Introduction

To accomplish an optimal performance of shunt compensator, proper reference current generation strategy is essential. Various algorithms are reported in literature for compensation of distorted system conditions1,2,3,4,5. Amongst all, instantaneous active and reactive power theory (IRP p-q) introduced by Akagi et al.6 is proved to be best solution for DSTATCOM applications. However, fundamental methodology of this algorithm works unsatisfactory when source is unbalanced and distorted.

Further, the IRP p-q Theory has no advantages with respect to the time interval needed for the identification of load properties over power theories. Unfortunately, there is a major ambiguity with respect to one of the most commonly used powers namely the apparent power, in three phase systems. This ambiguity exists even at sinusoidal voltages and currents3. Although the IRP p-q Theory is commonly used as a theoretical fundamental for the control algorithm of compensators for the power factor improvement, this theory does not provide an explicit relationship between and powers (or between active and reactive currents) and the power factor. Although the IRP p-q Theory is applied mainly for compensator control in the presence of harmonics, some deficiencies of this theory in compensation related issues seem to be visible even in systems with sinusoidal voltages and currents. The IRP p-q Theory handles the energy oscillation and required capability of the compensator for energy storage in terms of the mean and the oscillating component value of the active and reactive powers. Since the association of these powers with specific power phenomena in the circuit is ambiguous, also the issue of the relationship between the required capability of energy storage of the compensator and power properties of the load remains unclear25.

To resolve the limitations of basic IRP theory, different approaches of this theory in various situations and applications are proposed7,8,9,10,11,12,13,14,15,16,17. But, these concepts have certain restrictions like breakdown of current into orthogonal.

constituents in place of power components, limited or partial compensation for desired power factor requirement and limited options for different kind of compensations.

For unbalance conditions, synchronous detection method (SDM) and its extensions20,21 viz. equal power; equal current and equal impedance gives better solution. However, to generate reference compensator currents, these methods need synchronization of all phases (a, b and c) and are only able to regulate magnitude unbalance in source. All methods of synchronous detection algorithm are not able to regulate unbalance and distortion in supply voltages. A new approach given in22 proposed well-designed method for load compensation under distorted source condition but found to be computational extensive and unable to fix the desired power factor. Instantaneous symmetrical component theory (ISCT) based algorithm with fundamental positive sequence is recommended in23,24 for shunt load compensation under unbalanced supply voltages. However, symmetrical and inverse symmetrical component transformation increases computational complexities. Moreover, basic algorithm does not work under distorted source conditions and also shows slightly higher THD in compensated source currents.

Therefore, main aim of this paper is to suggest a new approach for reference current extraction based on broadly recognized instantaneous reactive power theory for load compensation. It uses the equal current approach of SDM by formulating algorithm with magnitude unbalance, phase unbalance and distortions in the source to extract fundamental source voltages. Further, these fundamental positive sequence source voltages are used to generate the reference compensator currents. This theory gives balanced and sinusoidal source currents with nearly zero neutral current and facilitates the compensator to set desired power factor. Proposed approach also prevails over the misconceptions of basic IRP theory [Section VII] without sacrificing its benefits and effectively works under any source unbalance and distortion conditions. Suggested approach is confirmed through detailed simulation and experimental studies.

Instantaneous reactive power theory: a basic approach

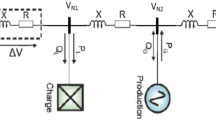
A stiff 3-ph 4-wire distribution system is shown in Fig. 1. In instantaneous reactive power theory, 3-ph voltages and currents on a-b-c coordinates are transformed into those 0-α-β.

Fig. 1
figure 1

AA 3-ph 4-wire distribution system.

Full size image

coordinates with standard Clarke transformation [Fig. 2].

The instantaneous active power p(t), and reactive power q(t) are as stated:

$$\begin{aligned} {p_{3\phi }}(t) & ={V_{sa}}\,{\kern 1pt} {i_a}+{V_{sb}}\,{\kern 1pt} {i_b}+{V_{sc}}\,{i_c}\, \\ & ={V_\alpha }\,{i_\alpha }+{V_\beta }\,{i_\beta }+{V_0}\,{i_0}={P_{\alpha \beta }}+{P_0} \\ \end{aligned}$$
(1)
$${\text{Where}}\;\;{p_{\alpha \beta }}={p_\alpha }+{p_\beta }={V_\alpha }\,{i_\alpha }+{V_\beta }\,{i_\beta };\;{\text{and}}\;{P_0}={V_0}\,{i_0}$$
(2)
$$\begin{aligned} q(t) & ={q_{\alpha \beta }}={V_\alpha }\,{i_\beta } - {V_\beta }\,{i_\alpha } \\ & = - \tfrac{1}{{\sqrt 3 }}\left[ {{V_{bc}}\,{i_a}+{V_{ca}}\,{i_b}+{V_{ab}}\,{i_c}} \right] \\ \end{aligned}$$
(3)

Referred to compensator, currents i0, iα and iβ can be expressed in terms P0, Pαβ and qαβ as below:

$$\left[ {\begin{array}{*{20}c} {i_{{f0}} } \\ {i_{{f\alpha }} } \\ {i_{{f\beta }} } \\ \end{array} } \right] = \frac{1}{{V_{0} \left( {\mathop V\nolimits_{\alpha }^{2} + \mathop V\nolimits_{\beta }^{2} } \right)}}\left[ {\begin{array}{*{20}c} {\mathop V\nolimits_{\alpha }^{2} + \mathop V\nolimits_{\beta }^{2} } & 0 & 0 \\ 0 & {V_{0} \,V_{\alpha } } & { - V_{0} \,V_{\beta } } \\ 0 & {V_{0} \,V_{\beta } } & {V_{0} \,V_{\alpha } } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\overline{{p_{{l0}} }} } \\ {\mathop {p_{l} }\limits^{\sim } - \overline{{\Delta p}} } \\ {q_{l} } \\ \end{array} } \right]$$
(4)

For satisfactory compensation, reactive power load must be same as compensator and equal zero sequence power should exchange between system and the compensator. Also, for real time compensation, switching and conduction losses should be met from source to maintain dc link voltages at their references. Therefore,

$$\begin{gathered} p_{{f0}} = p_{{l0}} \hfill \\ p_{{f\alpha \beta }} = \tilde{p}_{l} - \overline{{\Delta p}} = \tilde{p}_{l} + \overline{{P_{0} }} - \overline{P} _{{loss}} \hfill \\ q_{{f\alpha \beta }} = q_{l} \hfill \\ \end{gathered}$$

For real time implementation, retransformed compensator currents in a-b-c frame are.

$$\left[ {\begin{array}{*{20}c} {\mathop i\nolimits_{{fa}}^{*} } \\ {\mathop i\nolimits_{{fb}}^{*} } \\ {\mathop i\nolimits_{{fc}}^{*} } \\ \end{array} } \right] = \sqrt {\tfrac{2}{3}} \left[ {\begin{array}{*{20}c} {\tfrac{1}{{\sqrt 2 }}} & 1 & 0 \\ {\tfrac{1}{{\sqrt 2 }}} & { - \tfrac{1}{2}} & {\tfrac{{\sqrt 3 }}{2}} \\ {\tfrac{1}{{\sqrt 2 }}} & { - \tfrac{1}{2}} & { - \tfrac{{\sqrt 3 }}{2}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {i_{{f0}} } \\ {i_{{f\alpha }} } \\ {i_{{f\beta }} } \\ \end{array} } \right]$$
(5)

It is observed that when fundamental IRP p-q theory is applied under unbalanced and distorted source and load condition, source currents become unbalanced and heavily distorted, indicating non-attainment of desired target of compensation. This is perhaps; because control algorithm based on Clarke transformation directly utilizes instantaneous values of source voltages. Further, variation in angular speed of voltage phasor modifies compensator currents. Therefore, currents that result from IRP p-q theory are not the required reference compensator currents for complete load compensation under unbalanced and distorted source. Additionally, this theory exhibits some important misconception regarding consistency, existence and resolution of active and reactive component of current, Power Factor and apparent power as per the basic definitions of electrical engineering as follows.

  • Instantaneous active and reactive current in IRP algorithm do not have cohesion with conception of active and reactive currents used in basic electrical engineering.

  • In spite of absence of reactive load, reactive current found in load lines.

  • Even though nature of load is linear and free from harmonics, resolutions of active and reactive components of current based on p-q theory shows 3rd harmonic which contradicts the fundamental concept of active and reactive current introduced by Fryze29 in balanced 3-phase circuit.

  • IRP p-q theory is not clear to describe ambiguity in apparent power in unbalanced three-phase system. Therefore, it provides unclear impression about true value of power factor.

In order to justify above statements, when linear resistive load is considered with balanced source voltages, active and reactive powers using IRP p-q theory is obtained as

$$\left. \begin{gathered} P_{{\alpha \beta }} (t) = V_{\alpha } i_{\alpha } + V_{\beta } i_{\beta } = \sqrt 3 Vi\left[ {1 + \cos 2\left( {\omega t + 30^{ \circ } } \right)} \right] \hfill \\ q_{{\alpha \beta }} (t) = V_{\alpha } i_{\beta } + V_{\beta } i_{\alpha } = \sqrt 3 Vi\left[ {\sin \left( {\omega t + 30^{ \circ } } \right)} \right] \hfill \\ \end{gathered} \right\}$$
(6)

Also, the active and reactive component of currents in phase-a are given as

$$\left. \begin{gathered} {i_{\alpha p}}=\frac{i}{{\sqrt 6 }}\left[ {2\sin wt+\sin \left( {wt+{{60}^ \circ }} \right) - \sin \left( {3wt+{{60}^ \circ }} \right)} \right] \hfill \\ {i_{\beta p}}= - \frac{i}{{\sqrt 6 }}\left[ {\sin wt+2\sin \left( {wt+{{60}^ \circ }} \right) - \sin \left( {3wt+{{120}^ \circ }} \right)} \right] \hfill \\ {i_{\alpha q}}=\frac{i}{{\sqrt 6 }}\left[ {\sin \left( {wt+{{60}^ \circ }} \right)+\sin \left( {3wt+{{60}^ \circ }} \right)} \right] \hfill \\ {i_{\beta q}}=\frac{i}{{\sqrt 6 }}\left[ { - \sin wt - \cos \left( {3wt+{{30}^ \circ }} \right)} \right] \hfill \\ \end{gathered} \right\}$$
(7)

Thus, from (6) it is clear that the pair of values of instantaneous active and reactive powers does not draw any conclusion regarding the power properties of three-phase unbalanced load even under sinusoidal voltages. Since, the instantaneous active and reactive powers are the time varying quantities, using IRP p-q theory the power properties of such loads cannot be identified instantaneously.

Further, in (7), the names instantaneous active current and instantaneous reactive current given in IRP p-q theory do not have commonality with the notion of active and reactive currents used in electrical engineering. Also, the reactive current iq occurs in supply lines of load in spite of the absence of the reactive element in the load. Furthermore, the nature of load is linear (resistive) and harmonics are absent, still the resolution of active and reactive components of the current based on IRP p-q theory shows 3rd harmonics. Moreover, the active current ip that results from this theory is not the current that should remain in the supply lines after the load is compensated to unity power factor as defined by Fryze29. This contradicts the basic notion of the active current that was introduced to electrical engineering. Thus, it seems a major misconception of electrical phenomenon in three phase circuits with balanced sinusoidal voltages for linear load that do not have harmonics. Therefore, the above conceptions in IRP p-q theory strongly contradict the basic fundamental definitions.

Proposed approach for reference current generation

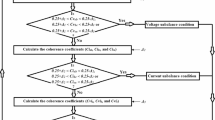
This section explains proposed approach based on IRP theory, in order to overcome the limitations of basic IRP p-q theory in terms of shunt compensation. Proposed idea for reference current extraction is depicted in Fig. 2.

Determination of compensator reference currents

Let the unbalanced and non-sinusoidal instantaneous source voltages are represented by

$$\left. \begin{gathered} V_{{sa}} = \sum\limits_{{n = 1}}^{k} {V_{{sman}} \sin \left( {n\theta } \right)} \hfill \\ V_{{sb}} = \sum\limits_{{n = 1}}^{k} {V_{{smbn}} \sin \left( {n\theta - {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {3 + \delta _{b} }}} \right. \kern-\nulldelimiterspace} {3 + \delta _{b} }}} \right)} \hfill \\ V_{{sc}} = \sum\limits_{{n = 1}}^{k} {V_{{smcn}} \sin \left( {n\theta + {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {3 + \delta _{c} }}} \right. \kern-\nulldelimiterspace} {3 + \delta _{c} }}} \right)} \hfill \\ \end{gathered} \right\}$$
(8)

Where n and k are order and upper harmonic number in the phase voltages, respectively. It is assumed that, equal harmonic order (distortion) is present in all three phase source voltages.

Based on equal current approach, we have

$$i_{{sam}} = i_{{sbm}} = i_{{scm}} = i_{{sm}} = \frac{{2\;P_{{lavg}} }}{{3\sum\limits_{{n = 1}}^{k} {V_{{smn}} \;cos\theta } \;}}$$
(9)

Using (9), (10) depicts average power.

$$P_{{lavg}} = \frac{3}{2}i_{{sm}} \sum\limits_{{n = 1}}^{k} {V_{{smn}} \;\cos \theta } \;$$
(10)

When there exists magnitude, phase unbalance and distortions in the source, the average power obtained will be,

$$\begin{aligned} P_{{lavg}} & = \frac{1}{2}i_{{sm}} \left\{ {\left( {\sum\limits_{{n = 1}}^{k} {V_{{samn}} \cos \,n\theta } } \right) + } \right.\left( {\sum\limits_{{n = 1}}^{k} {V_{{samn}} \,(\cos \,n\theta + \delta _{b} )} } \right) \\ & \;\;\;\left. { + \left( {\sum\limits_{{n = 1}}^{k} {V_{{scmn}} \,\cos \,(n\theta + \delta _{c} )} } \right)} \right\} \\ \end{aligned}$$
(11)

Equating (10) and (11), and by using summation convention (Tensor analysis) we get

$$V_{{sm}} = \frac{1}{3}\left( {V_{{sam}} + V_{{sbm}} \;\gamma _{b} + V_{{scm}} \;\gamma _{c} } \right)$$
(12)

Where,

$$\gamma _{b} = \frac{{\cos \left( {n\theta + \delta _{b} } \right)}}{{\cos \,n\theta }}\;{\text{and}}\;\gamma _{c} = \frac{{\cos \left( {n\theta + \delta _{c} } \right)}}{{\cos \,n\theta }}$$

Thus, balanced source voltages are derived as

$$\left. \begin{gathered} V_{{sa}} * = V_{{sm}} \;\sin \,\theta \hfill \\ V_{{sb}} * = V_{{sm}} \;\sin \,\left( {\theta - {{2\pi } \mathord{\left/ {\vphantom {{2\pi } 3}} \right. \kern-\nulldelimiterspace} 3}} \right) \hfill \\ V_{{sc}} * = V_{{sm}} \;\sin \,\left( {\theta + {{2\pi } \mathord{\left/ {\vphantom {{2\pi } 3}} \right. \kern-\nulldelimiterspace} 3}} \right) \hfill \\ \end{gathered} \right\}$$
(13)
Fig. 2
figure 2

Proposed IRP p-q theory based reference generation algorithm.

Full size image

Using (13), proposed algorithm can eliminate magnitude and phase unbalance from source currents but cannot assure them to be fully sinusoidal. In order to make source current purely sinusoidal, algorithm is further extended with computation of fundamental component from source voltages as given in (14);

$$\left. \begin{gathered} V_{{sa1}} = V_{{sm}} \,\sin \,\theta \hfill \\ V_{{sb1}} = V_{{sm}} \,\sin \,\left( {\theta - {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {3 + }}} \right. \kern-\nulldelimiterspace} {3 + }}\phi } \right) \hfill \\ V_{{sc1}} = V_{{sm}} \,\sin \,\left( {\theta + {{2\pi } \mathord{\left/ {\vphantom {{2\pi } {3 + }}} \right. \kern-\nulldelimiterspace} {3 + }}\phi } \right) \hfill \\ \end{gathered} \right\}$$
(14)

The fundamental components of source voltage obtained using (14) replaces instantaneous source voltages Vsa, Vsb, Vsc of IRP p-q theory. Since voltages obtained using (14) are free from magnitude, phase unbalance and distortion (harmonics), they represent balanced and sinusoidal source, forces basic theory of instantaneous reactive power to work satisfactorily under any unbalance and distortion in source and load. Furthermore, compensator reference currents are derived using (5), following steps given in Fig. 2.

Implementation under various source conditions

In case of balanced and sinusoidal source voltages with unbalanced and non-linear load, angles δb = δc = 0. As source is balanced, source voltage magnitudes are equal and thus fundamental positive sequence extraction is also not required.

Therefore, algorithm works similar to basic theory of IRP p-q and effectively nullifies the unbalance and distortions in source currents appearing due to load.

In case of only magnitude unbalance in supply voltages (with unbalanced and non-linear load), Vsm from unequal magnitudes Vsam, Vsbm, and Vscm needs to be determine using (12). Since, no phase unbalance exists in source voltages (δb = δc = 0), γb and γc becomes unity, without calculating the fundamental positive sequence components.

When there exists magnitude as well as phase unbalance in source voltages (load unbalanced and distorted) with or without source distortion, to nullify the magnitude unbalance, peak source voltage magnitudes is determined using equal current approach. To eliminate phase unbalance from supply, existing unbalance in phase-b and phase-c with respect to phase-a is measured and substituted in (12) [(δb = 10° and δc = -20°) for phase-b (-110°) and phase-c (100°), respectively)]. Further, by extracting the fundamental positive sequence component using (14), balanced and sinusoidal source voltages are determined. All the basic approaches viz. equal current approach, positive sequence extraction and improvement in terms of proposed modified instantaneous IRP p-q theory based approaches are indicated clearly in Fig. 2, which clearly shows the improvement and modifications incorporated in proposed algorithm.

Compensator structure and modulation control

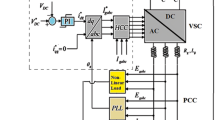
A 3-ph 4-wire distribution system under study is demonstrated in Fig. 3. Shunt compensator is realized using 3-leg 3-level Neutral-Point-Clamped (NPC) Voltage Source Inverter (VSI) connected in shunt PCC with the help of interface inductor (Lf) and resistance (Rf) [Rf indicates inverter switching losses in terms of real power exchanged with system]. Each leg of inverter uses 4-switches (S1a-S4a). Two clamping diodes (D+, D-) are used to hold the voltage level to null value. The Three achievable levels through this inverter are Vdc1, 0 and -Vdc2 (Vdc1= Vdc2). 4-wire system requires that n’ of split capacitors (Cdc1, Cdc2) be connected to neutral N-n of the system. The use of 3-level NPC VSI helps to reduce THD to certain extent, simultaneously adding the benefits of multilevel inverter26,27. An unbalanced and non-linear load is supplied by a balanced/unbalanced/distorted source. In order to achieve desired load compensation, extraction of reference currents using suggested theory are depicted in Fig. 2.

The sequence of firing pulses for 3-level NPC inverter are established using hysteresis current control due to its multiple benefits and shown in Fig. 3b4. For 3-level switching, it is important to apply zero voltage level at suitable instants. Dead band (δ) is added (less than h) so that it should not leads towards two-level switching. 3-level switching logic implemented for NPC inverter is evident by (15). Where, er represents error between reference and actual compensator current and us is the switching function. Parameters mentioned in Table 1 are utilized to carry out simulation and experimental studies.

Fig. 3
figure 3

(a) 3-ph 4-wire DSTATCOM compensated system (b) control scheme for the proposed compensator structure.

Full size image
$$\left. \begin{gathered} {\text{If}}\;\;{e_r}>{\text{ }}0, \hfill \\ \;\;\;\;\;\;\;\;\;{e_r}\,>\,+\,h,{u_s}={\text{ 1}} \hfill \\ \;\;\;\;\;\;\;\;\;{e_r}<{\text{ }}={\text{ }}+d,{u_s}={\text{ }}0 \hfill \\ {\text{Else if}}\;\;{e_r}<{\text{ }}0,{\text{ }} \hfill \\ \;\;\;\;\;\;\;\;\;{e_r}<{\text{ }}={\text{ }} - h,{u_s}={\text{ }} - {\text{1}} \hfill \\ \;\;\;\;\;\;\;\;\;{e_r}>{\text{ }}={\text{ }} - d,{u_{\text{s}}}={\text{ }}0 \hfill \\ \end{gathered} \right\}$$
(15)

Result and discussion

3-ph 4-wire (3p4w) compensated system presented in Fig. 3 is simulated using parameters in Table 1 with conventional IRP p-q theory and proposed control. The overall performance is evaluated under various source conditions for unbalanced and distorted loads as mentioned below.

Figure 4 shows the comparative compensator performance using both IRP p-q and proposed algorithm. Figure 4a, b shows balanced source voltages and unbalanced and distorted load currents, respectively. As observed, basic approach of IRP p-q theory works satisfactory under balanced source condition, providing balanced and sinusoidal source currents as shown in Fig. 4c and corresponding compensator currents are illustrated in Fig. 4e. When proposed algorithm is applied, compensated source currents with balanced and sinusoidal wave shape and injected currents (tracking performance for.

Table 1 System parameters.
Full size table

ph-a) are shown in Figs. 4d, f. It is seen that proposed algorithms shows comparable performance to IRP p-q theory, effectively compensating source currents.

Mainly, proposed algorithm is structured to compensate source currents under unbalanced (magnitude and phase) and distortion in supply voltage. The control performance is demonstrated for above conditions in source, separately. Figure 5 shows system working under magnitude unbalance in source. As discussed, ± 20% magnitude unbalanced with respect to ph-a voltage is considered resulting as Vsma = 325.269 V, Vsmb = 390.269 V and Vsmc = 260.269 V. This unbalance in magnitude of source voltages is depicted in Fig. 5(a), while load currents indicating corresponding source magnitude unbalance and load distortions is evident from Fig. 5(b). When basic IRP p-q algorithm is applied, it is observed from Fig. 5(c) that compensator is inefficient to mitigate magnitude unbalance from source and could not maintain the desired unity power factor (UPF). However, it is seen that IRP theory can completely settle neutral current. When proposed algorithm is implemented, compensator absolutely mitigate magnitude unbalance in source and all unbalance and distortions in load, providing exactly sinusoidal and balanced source currents with unity power factor, as depicted from Fig. 5(d). This theory is also capable to bring neutral current almost to zero. Supplied compensator currents are evident in Fig. 5(e) while phase-b and phase-c UPF are shown in Fig. 5(f).

To verify the compensator working under given conditions, + 20%, -20% magnitude unbalance and + 10°, -20° phase unbalance in phase-b and c is considered, respectively. The magnitude and phase unbalance conditions are displayed in Fig. 6a, b. Figure 6(c) evident that magnitude and phase unbalance in source voltage persist in source current indicating poor performance of compensator with IRP p-q theory. Rather compensation makes source currents more distorted but.

maintained the neutral current almost to zero. On contrary, when proposed algorithm is applied, source currents become balanced and sinusoidal; simultaneously compensating neutral current. In order to focus the effectiveness of algorithm, UPF operation for all the three phases are shown in Figs. 6(d) and Fig. 6(f), with the fundamental components of respective source voltages. Figure 6(e) indicates corresponding compensator currents. The results for compensated source currents (Fig. 6(d)) and UPF for phase-b, c (Fig. 6(f)) are shown intentionally for little longer period to demonstrate effectiveness of proposed algorithm.

Finally, system performance is evaluated for distorted source condition and depicted in Fig. 7. Distorted source voltages (2nd and 3rd harmonics) and corresponding source currents including unbalance and distortion in load are evident in Fig. 7(a) and Fig. 7(b). Further, it is seen from Fig. 7(c) that basic approach of IRP algorithm is unable to remove distortions from source currents. However, when proposed control is applied, compensator reflects balanced and sinusoidal source currents, nullifying neutral current which can be observed from Fig. 7(d). Required injected currents and UPF operation are shown in Fig. 7(e) and (f), respectively. For all the results showing compensated source currents and UPF, source voltages are scaled down by factor 30 to indicate clear phase relation between source current and voltage. In Fig. 7(d) and (f) small notches are observed in compensator currents, because of load rectifier operation and finite value of interface inductor. Under all the situations, neutral current is maintained almost zero since NPC topology is capable to provide return path for zero sequence current of load. From above analysis it is clear that proposed algorithm can provide satisfactory compensation under any source and load condition.Furthermore, proposed control needs synchronization of only one phase (phase-a) to realize positive sequence voltages for all three phases. It is seen that basic IRP p-q theory works well under balanced source condition. Therefore, proposed algorithm is similar to IRP theory when there exist no unbalance and distortion in supply, thus retaining all the major benefits of basic IRP theory.

Looking towards resolving misinterpretations of IRP p-q theory, the proposed algorithm is based on extraction of fundamental positive sequence components which are further utilized to derive instantaneous active and reactive power as well as reference compensator currents. Therefore, overall concept works in consistence with fundamental active and reactive currents. Also, based on proposed concept, suggested algorithm does not contain non-sinusoidal component in case of linear load; hence not generating harmonics in a system with balanced sinusoidal supply voltages. Thereafter, from wave shape of reference compensator currents generated using proposed control; nature and properties of load as well as source can be identified as these reference currents are generated in accordance with variation in source and load conditions. Lastly, proposed algorithm gives true value of power factor under balanced/unbalanced/distorted supply voltages thus enables to determine actual power rating of compensator needed to achieve UPF.

Fig. 4
figure 4

With balanced source condition (a) Source voltages (b) uncompensated source currents (c) Compensated source currents using IRP p-q theory (d) compensated source currents using proposed theory (e) Injected currents under IRP theory (f) Injected current tracking (Phase-a) proposed theory.

Full size image
Fig. 5
figure 5

Under source magnitude unbalanced (a) Source voltages (b) Uncompensated load/Source currents (c) Compensated source currents using IRP p-q theory (d) Compensated source currents using proposed theory (e) Injected currents under proposed theory (f) UPF for Phase-b, phase-c.

Full size image
Fig. 6
figure 6

Under source magnitude and phase unbalanced (a) Source voltages (b) Uncompensated load/Source currents (c) Compensated source currents using IRP p-q theory (d) Compensated source currents using proposed theory (e) Injected currents under proposed theory (f) UPF for Phase-b, phase-c.

Full size image
Fig. 7
figure 7

Under distorted source (a) Source voltages (b) Uncompensated load/Source currents (c) Compensated source currents using IRP p-q theory (d) Compensated source currents using proposed theory (e) Injected currents under proposed theory f) UPF for Phase-a wrt Vsa fund.

Full size image
Fig. 8
figure 8

(a) Schematic of experimental prototype of the proposed IRP (b) Experimental photograph.

Full size image

Experimental studies

The schematic of experimental prototype for proposed IRP based theory is shown in Fig. 8. DSP with Field-programmable gate array (FPGA) is used to realize of proposed control. Figure 8(a) shows the detailed experimental execution of the proposed work. DSP TMS320F2812 with 150 MHz frequency is used for hardware implementation. The Hall effect sensors LEM LV 25- P, LEM LA 55-P are used for processing phase power quantities suitable for DSP (± 5 V). Further it is reduced to 0–3 V range with the help of signal conditioning circuit (SCC), so that it should be compatible with analog channels of processor. For sampling 80 ns period is available which can provide the sampling frequency of around 12 MHz for maximum switching frequency of 21 kHz. The SCC circuits are provided proportionate with available ADC channels of DSP. The DSP also receives signal from the synchronizing circuit which is used for calculation of reference quantities28. The synchronizing circuit is required to synchronize the reference signal. DSP calculate reference compensator currents using proposed algorithm (using (5)). The reference values are to be compared with the actual measurements made using Hall Effect sensors and switching function is decided on the basis of Eq. (15) to generate the firing signals for NPC VSI. These firing signals have to be passed through the blanking circuit to include dead time. Blanking circuit is used for safety of compensator.

Fig. 9
figure 9

Experimental results for balanced source voltage (Timebase:4ms/div) (a) Source voltages (b) load currents (c) Compensated source currents using IRP p-q theory (d) Compensated source currents using proposed algorithm.

Full size image
Fig. 10
figure 10

Source magnitude unbalance (Timebase:4ms/div) (a) Source voltages (b) load currents (c) Compensated source currents using IRP p-q theory (d) Compensated source currents using proposed algorithm.

Full size image
Fig. 11
figure 11

Source magnitude and phase unbalance (Timebase:4ms/div) (a) Source voltages (b) load currents (c) Compensated source currents using IRP p-q theory (d) Compensated source currents using proposed algorithm.

Full size image
Fig. 12
figure 12

Distorted source (a) Source voltages (b) load currents (c) Compensated source currents using IRP p-q theory (d) Compensated source currents using proposed algorithm.

Full size image
Fig. 13
figure 13

Critical load unbalance (Phase-b disconnected) (Timebase:4ms/div) (a) Source voltages (b) load currents (c) Compensated source currents using IRP p-q theory (d) Compensated source currents using proposed algorithm.

Full size image
Fig. 14
figure 14

50% source magnitude unbalance ( in Phase-c) (Timebase:4ms/div) (a) Source voltages (b) load currents (c) Compensated source currents using IRP p-q theory (d) Compensated source currents using proposed algorithm.

Full size image
Fig. 15
figure 15

Simulation results under transient conditions (a) Source voltage (b) Load currents (c) Tracking performance phase (a) (d) Uncompensated Source currents using proposed algorithm.

Full size image

To validate the efficacy of the proposed theory, experimental results for 3p4w distribution compensated system with unbalanced, distorted source and load condition are depicted in Figs. 9, 10, 11 and 12.

By extracting the positive sequence voltages with implementation of actual algorithm, the reference currents are calculated by means of (5). The experimental values are same as those given in simulation analysis. It is seen from Figs. 9, 10, 11 and 12 that the hardware results validate the simulation studies as explained in Section V.

When system performance is assessed for balanced source voltages with unbalanced and distorted load [Fig. 9(a)-(b)], it is observed from experimental studies that both the algorithms (earlier PQ theory and proposed one) offer reasonable compensation with slightly lesser high switching frequency components in case of proposed algorithm as seen from Fig. 9(c)-(d). However, under source voltages magnitude unbalance, it is seen from Figs, 10(a)-(b) that this unbalance gets reflected in source voltages and currents. As apparent from the experimental results, the IRP theory shows weak compensation performance as shown in Fig. 10(c). Rather, an improved performance of proposed algorithm can be seen from Fig. 10(d). The similar effects can be observed in case of magnitude and phase unbalance condition. The superior effects using proposed approach are depicted from Fig. 11(c)-(d) as compared to IRP theory. Lastly, the system is tested under the distorted source voltages (2nd, 3rd harmonics). It is observed from Fig. 12(a)-(d) that, when source voltages are distorted, the basic IRP theory do not provide satisfactory compensation as evident in Fig. 12(c). On the other side, the proposed reference generation is able to remove all the harmonics from the system arising due to distorted source and load, providing exactly balanced and sinusoidal source currents with almost zero neutral current and UPF.

Fig. 16
figure 16

Experimental results under transient conditions (Timebase:4ms/div) (a) Source voltage (b) Load currents (c) Tracking performance (phase (a), current error, inverter voltage (d) Uncompensated Source currents using proposed algorithm.

Full size image

Further, the results are provided for critical unbalance, phase-b load disconnected with the same harmonic order and unbalance in source voltages. In this case only linear unbalanced load is taken into account. From Fig. 13(a)-(b), it is observed that the same harmonics are introduced in the load currents with ilb = 0. The better performance of the proposed algorithm can be seen from Fig. 13(c)-(d) on IRP p-q theory.

Moreover, the performance of both the algorithms is demonstrated in Fig. 14 under 50% source unbalance in phase-c, with simultaneously different harmonic order and load unbalanced and distorted. It can be again seen from the Fig. 14(a)-(b) that the source voltages are highly unbalanced and distorted showing the resulting effects in load currents. From Figs. 14(c)-(d), it is evident that the proposed algorithm can work efficiently under critical source unbalance and distorted conditions and can provide balanced and sinusoidal source currents with zero neutral current as compared to basic IRP p-q theory. The compensation of the source magnitude unbalance upto 50% using proposed algorithm satisfies the standard practical compensation criteria and proves the efficacy of the algorithm.

Furthermore, to justify the superiority and efficacy of the proposed algorithm, the comparison of the proposed modified instantaneous reactive power (IRP) theory is compared with the other existing control algorithms (PQ, SRF, EP, EC(SDM) etc.) in terms of power factor, compensation capabilities under various conditions and computational complexities (Table 2).

In order to show the robustness and faster dynamic response of the compensator with proposed control algorithm, the system is tested under the transient conditions by simulating under the fast changing unbalance and distorted loads. The system is simulated under the balanced source and unbalance and distorted load conditions. Initially, the load is unbalanced (as given in Table 1) and at instant t = 0.02 s, the non-linear load is switched in addition to unbalanced load. It is seen that the load currents are increased and changed from unbalanced to unbalanced and distorted (as seen in Fig. 15 (a)-(b). The compensator performance under this transient condition is tested and shown in Fig. 15 (c), observing that the compensator with proposed algorithm provides completely balanced and sinusoidal source current with response time less than half cycle as depicted in Fig. 15 (d). Also, the system performance under transient conditions are validated using experimental studies. It is observed that the proposed algorithm works efficiently to compensate the sudden fast changing load conditions, providing sinusoidal and balanced source currents. Also the zero current error indicates the exact tracking of reference currents as seen from Fig. 16 (c). The experimental results validating simulation results are shown in Fig. 16(a)-(d).

Fig. 17
figure 17

Simulation Results under composite disturbance (magnitude unbalance, harmonics, phase unbalance) (a) unbalanced and distorted Source voltages (b) ) unbalanced and distorted Source currents (c) Compensated source currents using IRP p-q theory (d) Compensated source currents using proposed theory.

Full size image

Furthermore, the compensator performance is tested under the composite conditions with magnitude unbalanced, harmonics with different harmonic order and phase unbalance in the source voltages. The distorted source voltages containing different harmonic order with phase-a containing 3rd harmonic, phase-b containing 5th harmonic and phase-c with 7th harmonic order with magnitude unbalanced (325.260 V, 390.260 V, and 260.269 V) and phase unbalance (+ 10° in phase b and − 20° in Phase c) as given in Table 1 and depicted in Fig. 17. The load are considered as unbalanced and distorted (as in Table 1). The corresponding source current as shown in Fig. 17(a) and the load currents are depicted in Fig. 17(b). From Fig. 17(c) – (d), it is observed that the proposed algorithm is quite capable to compensate the composite disturbance (magnitude unbalance + harmonics + phase shift) by providing balanced and sinusoidal source currents as compared with IRP p-q theory.

To prove the efficacy of the proposed algorithm with real time studies, the experimentation is carried out using existing IRP pq theory and proposed algorithm. It is seen from Fig. 18(a) – (d) that the experimental results are found to be exactly in consistent with the simulation studies (Fig. 17(a)-(d)) validating the efficacy of the proposed algorithm in comparison with the existing IRP p-q theory.

Also, the proposed algorithm is compared with the existing IRP p-q theories in Table 3 in terms of computation complexities, degree of freedom etc. which proved its efficacy.

Fig. 18
figure 18

Experimental Results under composite disturbance (magnitude unbalance, harmonics, phase unbalance) (Timebase:4ms/div) (a) unbalanced and distorted Source voltages (b) ) unbalanced and distorted Source currents (c) Compensated source currents using IRP p-q theory (d) Compensated source currents using proposed theory.

Full size image

Prevail over misinterpretations of IRP theory using proposed approach

As per the analysis carried out by Czarnecki in25, some issues in IRP theory contradicts the basic definitions of electrical engineering.

In order to justify these misconceptions (Section-II) in IRP p-q theory, the power invariance is ensured in αβ0 and abc frames. It is proved that the instantaneous power P(t) and q(t) remains same in both transformations. However, again the question is raised whether these instantaneous quantities can identify the power properties? Further, the reactive current iq in supply lines in absence of reactive load is because of instantaneous reactive power q due to load imbalance. But the problem occurs that how could this unbalance be identified using instantaneous reactive power? Moreover, non-zero current ip in the circuit in spite of zero active power of load is the supply current of the load that has the active power p. However, issue begins that why this current remains in the supply lines of load after the compensating all non-beneficial current components? In addition, these two currents ip, iq in the circuit with sinusoidal supply voltages can be non-sinusoidal even if there is no source of current distortion in the load.

To address these issues, the proposed algorithm works on the assumptions of classical load balancing. Hence, it always requires the positive sequence source voltages. As we need the compensated load to be unity power factor, the imaginary components of the positive sequence component of line currents (i.e. due to load susceptance) becomes zero (similar to CPC theory29), by cancelling the negative sequence current due to load conductance. Therefore, for purely resistive load, only active and unbalanced current will contribute to flow line current and for purely reactive unbalanced load, it is sum of reactive and unbalanced currents. Also, the extraction of fundamental positive sequence components over a period of at least one cycle in time domain can exactly identify the load unbalance and load properties.

Table 2 Comparison of various control algorithms.
Full size table
Table 3 Comparison of proposed theory with existing p-q based theories.
Full size table

As the proposed algorithm is based on extraction of fundamental positive sequence components, the overall concept works in consistence with the fundamental active and reactive currents. Also, due to fundamental positive sequence components, the suggested algorithm does not contain the non-sinusoidal component in case of linear load; hence not generating the harmonics in a system with balanced sinusoidal supply voltages. Thereafter, from the wave shape of reference compensator currents, the nature and properties of the load as well as source can be identified as these reference currents are generated in accordance with the source and load conditions. Lastly, the proposed algorithm gives true value of power factor under balanced/unbalanced/distorted supply voltages using positive sequence components thus enables to determine the under balanced/unbalanced/distorted supply voltages using positive sequence components thus enables to determine the actual power rating of the compensator.

Thus, the proposed approach avoids the ambiguities of IRP p-q theory in terms of presence of reactive/active current in the supply lines in absence of reactive/active loads, presence of harmonic components and identifying the load power properties with simultaneously retaining the major benefits of fundamental IRP p-q theory.

Conclusion

In this paper an attempt is made to propose modification in basic approach to IRP p-q theory for reference current generation in order to achieve an efficient performance of shunt compensator under unbalanced and distorted source voltages. The proposed algorithm alleviates the major limitations of basic IRP theory and provides exactly balanced and sinusoidal source currents even in presence of unbalance in magnitude and phase with distortions in the source under unbalanced and non-linear load. The system is also tested under the different degree of distortion in supply voltages. It is seen that the proposed algorithm works efficiently and satisfactorily provides balanced and sinusoidal source currents. Further, the resolutions of misinterpretations of basic IRP theory are also discussed. As the proposed algorithm works on extraction of fundamental positive sequence components, the overall concept works in consistence with the fundamental active and reactive currents.

Also, due to fundamental positive sequence components, the suggested algorithm does not contain the non-sinusoidal component in case of linear load; hence not generating the harmonics in a system with balanced sinusoidal supply voltages. The simulation and experimental studies establish the efficacy of the proposed algorithm over the basic IRP theory for shunt compensation.