Introduction

As of the end of the United States COVID-19 Public Health Emergency on May 11 2023, the COVID-19 global pandemic has resulted in over 1.18 million deaths and 104.7 million cases in the United States1. Of these, over 37.2 thousand deaths and 3.09 million cases occurred in the state of Georgia alone1. While the original public health emergency has waned, it is critical to reflect on the pandemic and understand where improvements can be made to the elements of the public health response, especially relating to dynamic data-based decision-making.

The severity and transmission of COVID-19 were largely unknown during the early stages of the pandemic and rapid and accurate detection of infection represented critical information for local prevention responses and staffing of healthcare systems. Measurement and surveillance of COVID-19 through diagnostic testing provided the main method to identify clusters of incident infections and to formulate local containment and healthcare staffing plans accordingly. Without reliable testing data, non-pharmaceutical interventions (NPIs) such as social distancing, school and workplace closures, and city-wide lockdowns were often implemented in an ad-hoc manner. With no unified national plan for disease surveillance, state and county level administrations were tasked with implementing their own (again, ad-hoc) testing plans, which in some cases resulted in health inequities in testing access2,3. In the sections below, we propose an integrated statistical and optimization framework providing an effective diagnostic test site allocation plan that balances three key system-wide objectives: (i) access to testing for the population of interest, (ii) precision in COVID-19 incidence estimates, and (iii) sociodemographic equity among those tested. Each of the three objectives have been considered separately, but to our knowledge, treating them jointly with a multi-objective optimization represents a novel contribution to improving the analytic infrastructure for public health surveillance and response.

An optimal COVID-19 testing plan for a given area boils down to a spatial problem: where are the best locations to place testing sites in order to achieve these objectives? This question of interest falls into a rich history of location-allocation problems wherein one seeks to optimize the location of certain assets. Such problems appear frequently within the operations research literature4,5,6,7. A common healthcare scenario involves allocating a small number of primary healthcare facilities (sites) among a larger number of potential site locations. The locations selected for the sites are those that optimally provide service under the objective function (or, in our case, functions), often evaluated at a series of demand points. Previous applications include allocation of healthcare facilities in Tehran, Iran8 and Hong Kong9 by minimizing the travel costs and distance for the populations they are meant to service. While some approaches are single-objective, e.g., only focusing on travel distance10, many other studies pursue multiple objectives at once, including land-use incompatibility, cost of building a new facility, and total cost borne by the healthcare system8,9,11. A variety of constraints are also considered in the literature. Due to the sheer combinatorial size of these location-allocation problems, most utilized optimization algorithms rely on heuristic approaches such as the genetic algorithm (GA).

Optimal design is a related field of study focusing on the optimal placement of observation sites in order to minimize local and overall prediction error within a spatial prediction framework. Such spatial prediction, treated in detail in the field of geostatistics, is often implemented through a process called kriging or Gaussian process regression12. A key input into any spatial prediction algorithm is the set of locations at which measurements are sampled. Optimal design identifies the best set of sample locations to minimize average prediction error and bias in spatial parameter estimation13,14,15,16,17, and is frequently employed in the monitoring of environmental contaminants18.

The unique features that place COVID-19 and other infectious disease surveillance beyond location-allocation and optimal design are the pandemic’s geographic spread and its evolution over time. Both location-allocation and optimal design, as commonly applied, are better suited for static allocation problems. While many of the inputs to the aforementioned allocation problems (demographics, building costs, and land use) are not expected to change drastically in a short period of time, COVID-19 hotspots and high-test-demand areas could appear and disappear in a region within a few months or even weeks19. These features necessitate an optimal testing site allocation strategy designed to adapt to the spread of the virus.

Building on this setting, we propose model-based geostatistics (MBG)20 as an attractive framework to capture the spatiotemporal nature of COVID-19 spread for optimal test site allocation, or, more generally, test site allocation for any infectious disease (including, e.g., influenza). Several spatiotemporal models have been published on the spread of COVID-1921. Because the local transmission and incidence of COVID-19 (or other infectious disease) is a process that evolves over time, standard site-allocation methods would be unable to adapt their results to the changing spread of the disease. An appropriate site allocation method for public health surveillance should be able to add testing sites according to the dynamic nature of infectious disease transmission.

Despite MBG’s ability to capture the spatiotemporal nature of the disease, additional methodological extensions are required to effectively use the information to allocate test sites. The disease surveillance literature has shown recent interest in geospatial model-based adaptive designs, especially related to neglected tropical disease (NTD) surveillance. Several NTDs are targets for elimination and require renewed focus on tracking approaches that conserve time and resources as their incidence approaches zero22,23. These new adaptive geostatistical designs (AGDs) optimize over some design criteria (e.g., prediction variance or precision, hotspot classification accuracy, entropy), while guarding against redundancy by incorporating a distance constraint to prevent sites from being located too close together24,25. Precision, the inverse variance of a statistical estimate (in this case of disease incidence), is especially important in pandemic scenarios. An area with a high precision estimate has low uncertainty regarding its disease incidence, whereas an area with low precision indicates highly uncertain incidence, and should be a target area for testing to improve monitoring of the pandemic. Precision has been used for adaptive optimization criteria in previous applications26,27 and is critical for decision-makers to grasp the severity of a pandemic situation and identify areas which need immediate attention.

While precision in COVID-19 descriptive statistics is paramount for researchers and decision makers, access and equity among the tested is equally important. Without proper access in testing, individuals in the population are unable to make the difficult decisions necessary to navigate a pandemic. Equity in testing ensures vulnerable communities receive the aid they need to avoid disproportionate harm from the pandemic. However, there is evidence that COVID-19 test site allocation throughout the United States resulted in test sites located in predominantly Black and Hispanic neighborhoods to experience higher demand compared to those located in whiter neighborhoods28. Symptoms of high demand include long wait times, test shortages, and understaffed healthcare facilities. Considering the evidence of disparities in COVID-19 outcomes by race, ethnicity, and socioeconomic status29, it is likely the placement of test sites during the early stages of the pandemic did not reach vulnerable populations in need of COVID-19 support. Access and equity of testing must be prioritized alongside the precision criteria more typically seen in the disease model and optimization literature.

Fig. 1
figure 1

Epidemic curve for COVID-19 cases in Atlanta from 2020 to 2021. The shaded pink area represents the time period used in the simulation.

Full size image

In this paper, we borrow from the adaptive design MBG literature by using a Bayesian areal spatiotemporal disease model to capture the dynamic spread of COVID-1930, and incorporate it into a multi-objective optimization solved by the linear combination of weights and interior point method31,32. To validate our approach we use COVID-19 case data in Atlanta, Georgia to simulate real-time test site placement during the pandemic and compare to five other allocation methods. We track each allocation over a month long period starting in December 2020 during the peak of the COVID-19 Delta wave (Fig. 1) and calculate three performance metrics in access, precision, and equity, plus an aggregate metric equal to their sum, which we refer to as the total score. We also compare the number of test sites and time needed for each adaptive approach to achieve the same total score as a uniformly random non-adaptive allocation. We show the proposed multi-objective adaptive approach saves considerable resources relative to non-adaptive allocation, and does not suffer drastically in single-objective performance when compared to other adaptive designs. Although the proposed framework has been validated by COVID-19 incidence, it has broad applications in pandemic disease surveillance, policy making and resource management.

Results

In our study, we sought to answer the following three questions.

  1. 1.

    How does the performance of the proposed multi-objective adaptive allocation compare to that of benchmark methods like single-objective and non-adaptive random allocations?

  2. 2.

    How do the spatial distributions between allocation methods differ?

  3. 3.

    How many more (or less) test sites are required for the single-objective and random allocations to reach the same performance as our proposed allocation?

Fig. 2
figure 2

Objective function score over time for the total and individual components as defined in Eq. (4) for each of the allocation methods under study.

Full size image

To answer the first question, we compared our proposed approach balancing access, precision, and equity to the 1) single-objective adaptive allocations for access, precision, and equity, 2) simultaneous access and equity (AE) adaptive allocation, 3) a random adaptive allocation, in which at each update step new locations are chosen uniformly at random, and 4) a one-shot non-adaptive allocation, a one-time design in which all locations are selected uniformly at random. We considered 1,217 candidate locations for test sites corresponding to the total number of 2020 census tracts covered by the eleven counties in our study region representing the metropolitan Atlanta area. Fig. 2 shows the average of the access (Eq. 1), precision (Eq. 2), and equity (Eq. 3) metrics, and total (Eq. 4) scores over 100 simulations over time (Methods). Each simulation starts with a different set of original test sites, and all allocation methods with the exception of the one-shot allocation (which selects 100 test sites at random at the beginning of the study period) adaptively add a batch of five new test sites to the original set at every time point, according to their designed objectives. The proposed method is competitive with each of the single objective methods for all component scores, and outpaces all other methods for the total score. It is only second to the single objective allocation optimizing over that exact same metric. In particular, the equity metric is achieved close to its maximum and maintained throughout the allocation for the proposed, equity, and AE allocations.

Fig. 3
figure 3

Empirical distribution curve (ECDF) of the nearest distance to a test site by race/ethnicity for one run out of 100 total simulations for the final allocation decided by each plotted method at the end of the study period. Colors differentiate race/ethnicity and line type differentiates whether the ECDF is under the proposed multi-objective adaptive allocation or random. Because test sites are located at tract centroids and each individual is associated with a census tract, each ECDF curve starts at a positive value.

Full size image

In addition to the objective function metrics, we assessed access and equity of the test site allocations through empirical distribution curves (ECDF) of distance to the nearest test site by race and ethnicity. We consider four racial ethnic groups: non-Hispanic white, non-Hispanic black, non-Hispanic other, and Hispanic. Figure 3 shows the ECDF curves for the final allocation under the proposed and random methods for one simulation in the experiment described in the Methods. Each proposed ECDF curve is higher than that of the random ECDF, suggesting more people overall are located closer to test sites, a sign of better access to testing. In addition, the ECDF’s for the proposed method are closer together than the ECDF’s for the random method, implying greater equity in testing access between the four racial/ethnic groups. Figure 4 maps the final test allocation scheme for each of the studied allocation methods for a given simulation. Allocations which include the access score in their objective criteria contain an even coverage of test sites across Atlanta. In contrast, the equity and precision allocations exhibit more clustering. Visually, our proposed method achieves a balance between the even coverage of the access allocation, and the more targeted areas in the precision and equity allocations.

Fig. 4
figure 4

Final set of test sites chosen by each allocation method for one run out of 100 total simulations. Grey polygons delineate Atlanta county borders, and red points symbolize test site locations chosen by the algorithm.

Full size image
Table 1 Summary of the minimum number of test sites needed for each allocation method to outperform proposed multi-objective adaptive allocation as measured by the sum of the evaluation metrics. Column \(\Vert {a} \Vert\) indicates the batch size or number of new test sites added at each time index. We fixed the One-Shot design to 100 sites and terminated the proposed design once it allocated more than 50% of that capacity. For the other adaptive designs, column \(N\) shows how many test sites are needed to either exceed the proposed design’s total score \(\sum _i f_i\) or, if that threshold cannot be reached, to attain the highest achievable total score below it. Column \(f_i\) is the individual score for the component. \(f_1\) is the access score, \(f_2\) is the precision score, and \(f_3\) is the equity score. Note that for each score, higher is better.All listed methods select test sites adaptively, except for the “One-Shot (non-adaptive)” approach. The “Random” method is adaptive in the sense that it selects new test sites at each time point, but unlike the other adaptive methods–which use criteria such as access, precision, equity, or a combination thereof–it selects locations entirely at random.
Full size table

The single-objective and random allocations also required more test sites and resources to achieve similar outcomes to our proposed multi-objective approach. Table 1 displays the number of sites needed for each method to achieve a similar total score to our proposed method for a 55 site allocation. For example, for a batch size of five, the access-only method required 195 test sites and the equity-only method required 105 test sites to achieve the same performance as the proposed method for 55 test sites.

We found that the performance of our proposed allocation varied based on the choice of weights (denoted as \(\lambda_1, \lambda_2, \lambda_3\) for access, precision, and equity respectively) placed on each individual objective (Methods). Methods with equal weights achieved the highest total scores regardless of number of total sites selected, indicating strong performance when balancing all objectives upon appropriate scaling (Tables S1, S2, and S3). We selected \(\lambda _1 = 1\), \(\lambda _2 =1\), and \(\lambda _3 = 1\) for use in our proposed method. A sensitivity analysis demonstrated that increasing the weight of an individual objective corresponded to higher scores for that objective, reflecting our method’s flexibility in prioritizing specific objectives through weight selection (Figs. S1 and S2).

We also assessed the robustness of our method to the assumption that COVID-19 risk is uniformly distributed within counties, meaning that county-level case counts from the Department of Public Health can be allocated to census tracts proportionally based on population, as was done in the main analysis. To do this, we repeated the analysis using a combined weighting scheme based on both population size and the CDC Social Vulnerability Index (SVI), allowing for differential risk by tract, with larger and more vulnerable tracts assigned a higher proportion of cases. Figure S3 compares the performance of our proposed approach under both assumptions. The results show that our method is robust to this modeling choice, consistently outperforming the alternative allocations under both assumptions and yielding similar trends in objective scores.

Discussion

The proposed multi-objective adaptive allocation displayed clear improvement over non-adaptive and single-objective test site allocation strategies. After a 30-day period in our experiment, the proposed allocation attained a higher total score compared to random allocation, without sacrificing performance in any single objective. It is also more efficient in terms of the number of test sites required to achieve relevant outcomes compared to the single objective allocations, with important implications for resource management. Access and equity in testing was also much improved for the proposed method compared to allocations which did not prioritize said objectives. For practical purposes, the algorithm only takes a few hours to run lending itself well to real-time applications, so long as COVID-19 case data are available and up-to-date.

When comparing the spatial distribution of test sites we noted how prioritizing access manifested in an even distribution of test sites across Atlanta while prioritizing equity resulted in many more clusters of test sites. The wide difference in allocation between the access and equity allocations, coupled with the compromise given by the multi-objective allocations is evidence that access and equity are indeed competing priorities and require a systematic approach to achieve optimal balance.

To our knowledge, this is the first application of an adaptive design to multi-objective test site allocation. While adaptive designs and location allocation solutions are both recognized methodologies in their respective fields, they had not been combined effectively in previous disease surveillance applications. We show despite the consideration of multiple objectives, the proposedallocation achieves access, precision, and equity on par with single-objective methods optimized exclusively for each metric. It also consistently outperforms and requires less resources than non-adaptive random designs, especially in the long run.

While our proposed allocation places test sites at census tract centroids, the approach remains relevant for practical planning, particularly when outcomes of interest are defined areally. Because our model defines coverage by census tract and evaluates access, equity, and precision based on tract-level areal data, placing a test site anywhere within a designated tract would likely be sufficient when areal outcomes are the primary concern. However, we acknowledge that the model does not explicitly account for logistical constraints involved in setting up physical testing sites including availability of necessary infrastructure or public accessibility, which may limit the feasibility of implementation in some settings.

Our method has several limitations. First, our method relies on county case counts reported by the Georgia Department of Public Health. COVID-19 case counts have been noted to be unreliable relative to COVID-19 hospitalization and deaths due to different reporting standards across multiple agencies, delays in testing, and general under-ascertainment of COVID-19 cases33. Despite these concerns, our method is designed to support quick decision making in the midst of a pandemic, which requires real-time data as opposed to waiting for higher quality but less timely data. A potential improvement of the proposed method could be to use past hospitalizations and deaths to adjust for the bias in case data before input into the allocation model.

Second, higher resolution spatial and demographic case information would be better suited for multi-objective allocation (particularly for the equity metric) compared to county case counts. Since we placed candidate test sites at the centroid of each census tract, there was a discrepancy between the geographic level of the case data and the unit of analysis. We addressed the issue by assuming COVID-19 risk within a county was homogeneous, and assigned cases to tracts within each county in proportion to the tract population. However this assumption is difficult to verify in practice. We hope national reporting standards for epidemic and pandemic data continue to improve to allow the collection of more detailed information conducive for detailed test site allocation.

A third limitation is the inherent subjectivity of selecting objective function weights in Eq. (4). Each component objective function is assigned a weight which represents the relative importance of that objective. Ideally the decision-maker has enough information to choose those weights effectively, but multiple competing objectives can complicate weight selection. Improper scaling of the single objective components can also disrupt the optimization. Our sensitivity analysis provides guidance on what magnitude of weights may be suitable for users with different priorities for the three evaluation metrics. We found that balanced weights achieve high performance, and that increasing the weight does prioritize that objective, but possibly at the expense of the other objectives (Fig. S1). While subjectivity may be unavoidable when it comes to multi-objective decision making, our method combined with a thorough sensitivity analysis provides guidance for weight selection under a wide variety of possible scenarios.

Finally, while our method contains a parameter for test site capacity, several other factors affecting accessibility were not accounted for. We assumed all test sites had the same capacity, even though capacity most likely varies based on the type of testing site (government mobile pop-up site, pharmacy store, physician office, urgent care clinic, hospital, etc.). Staffing, insurance requirements, and especially mobility are also unique determining factors for each test site’s accessibility. Our method serves as an approximation to the true scenario to demonstrate its practicality, and future extensions of the allocation could more thoroughly account for these differences between test sites.

While precision in testing is important for decision-makers and researchers to gather the best information available to guide the pandemic response, access and equity of testing are equally important for the population to guide their own individual pandemic response and make safe decisions in their work and personal lives. Our study has demonstrated the value of the proposed multi-objective adaptive allocation in simultaneously achieving the key objectives of access, precision, and equity in COVID-19 testing. The adaptive selection of sites can further reduce the resources required to set up testing for future administrations. By adaptively balancing multiple competing objectives in a principled manner, we hope better and fairer outcomes can be realized for all stakeholders under future pandemic scenarios.

Methods

Data

We obtained daily confirmed case counts of COVID-19 from eleven counties in Georgia (Fulton, Cherokee, Forsyth, Gwinnett, DeKalb, Clayton, Fayette, Coweta, Carroll, Douglas, Cobb) between March 2, 2020 and July 13, 20211. The case data were only reported at the county level, however, we defined candidate locations for testing sites at the census tract level, totaling 1,217 locations. To allocate county-level case counts to census tracts, we proportionally distributed cases based on each tract’s share of the total county population as reported in the 2020 American Community Survey. For each date and county, we calculated the expected number of cases in each tract as the product of the county’s case count and the tract’s population weight. These expected values were then floored to ensure integer counts, and any remaining cases (due to rounding) were allocated to the tracts with the largest fractional remainders. This approach ensures that the total number of cases assigned across tracts matches the rounded county total while maintaining proportionality to the tract-level population. The resulting tract-level case counts were then used in subsequent modeling steps. The assumption is that the COVID-19 cases are distributed uniformly at random within each county, i.e., we define \(\hat{Y}_{ijk} = Y_{i..} (N_{ijk} / N_{i..})\), for county i, tract j, and demographic group k where Y represents case counts and N represents population as measured by the U.S. Census. The dot notation indicates a sum over the respective subscript.

Optimization criteria and formulation

We propose a test allocation strategy balancing three key objectives: (i) access of the population to COVID-19 testing (ii) precision of disease models for COVID-19 incidence and (iii) equity across sociodemographic lines. Constraints for the optimization are defined through the number and available capacity of test sites. We quantitatively define each of these three criteria in the following sections. Candidate locations for test sites were restricted to the centroid of each census tract.

Access score

Suppose there are I candidate test site locations and J demand points to be serviced (in this study, demand points represent census tracts). We define an allocation plan \({a}\in \{0,1\}^I\), with \(a_i = 1\) representing a test site to be set up at a candidate testing location i. We assume that individuals always choose the closest available test site to their census tract of residence. Define indicator variable \(e_j(\boldsymbol{a})=1\) if demand point j is covered by at least one test center, under allocation plan \(\boldsymbol{a}\), and \(e_j(\boldsymbol{a})=0\) otherwise. A demand point is considered covered if a user-defined proportion of the demand point’s population, denoted \(p_j\), is smaller than the capacity of the nearest test site. We define the access score, i.e., the first component of the objective function, as \(f_1\), which takes as input an allocation plan \({a}\):

$$\begin{aligned} f_1({a})=\sum _{j=1}^J\frac{e_j({a})p_j}{\sum _k p_k}. \end{aligned}$$
(1)

Precision score

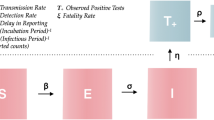
The second component of the objective function addresses the precision in COVID-19 incidence estimates. Intuitively, new test sites should be placed in areas with the most uncertain COVID-19 incidence estimates to increase precision of future estimates. Assuming again that individuals always choose the closest available test site to their residence, the test centers serve as point-referenced data in a statistical model for COVID-19 incidence. Under our proposed multi-objective adaptive approach, any model capable of producing posterior variance estimates at unknown locations can be used. In this study we adopt a Bayesian spatiotemporal count model30 as follows.

$$\begin{aligned}& Y_{it}|\beta _0,S_i,\epsilon _i, \gamma _t, \alpha _t, \delta _{it}, \sim Pois(P_ie^{\beta _0+S_i+\epsilon _i+\gamma _t + \alpha _t + \delta _{it}}), \\& S_i|\sigma ^2_s \sim ICAR(\sigma ^2_s), \\& \epsilon _i|\sigma ^2_\epsilon \sim N(0, \sigma ^2_\epsilon ), \\ &\gamma _t | \sigma ^2_\gamma \sim RW2(\sigma ^2_\gamma ), \\& \alpha _t | \sigma ^2_\alpha \sim N(0, \sigma ^2_\alpha ), \\& \delta _{it} | \sigma ^2_\delta \sim N(0, \sigma ^2_\delta ), \\& \beta _0 \sim N(0, \infty ), \\ &\sigma ^2 \sim LogGamma(0.5, 0.001). \end{aligned}$$

here, \(Y_{it}\) represents the COVID-19 case counts for census tract i at time t, \(P_i\) is the population of census tract i, \(S_i\) is a structured spatial intrinsic conditional autoregressive random (ICAR) effect, \(\epsilon _i\) is an unstructured spatial effect, \(\gamma _t\) is a structured 2nd order random walk temporal effect, \(\alpha _t\) is an unstructured temporal effect, \(\delta _{it}\) is an unstructured spatiotemporal interaction effect, and \(\beta _0\) is an overall intercept. Unstructured terms refer to independent and identically distributed terms indexed by either space or time to account for any variation unexplained by the structured spatiotemporal terms (ICAR and random walk). Lastly, each \(\sigma ^2\) variance parameter has the same weakly informative log-gamma prior. All random effects are designed to induce correlation and borrow strength between all census tracts in a principled manner.

An attractive feature of this model is its ability to take advantage of assumed spatiotemporal correlations to smooth areal rates without reliance on external covariates. We estimated the model using integrated nested Laplace approximation34 implemented in the R-INLA package. The variance of the posterior estimates of Y for each tract in candidate locations were then input into the second objective criteria as follows

$$\begin{aligned} f_2({a})=\sum _{i}{\text {Var}}(Y_i|{\textbf {Y}}_{\varvec{a}^-}), \end{aligned}$$
(2)

where \({\textbf {Y}}_{\varvec{a}^-}\) represents the data obtained from the current allocation plan, \({a}^-\), to be fed into the disease model. Our objective function is based on previous work on sequential design / active learning in Gaussian processes35. In our case, candidate test site locations with high posterior variance in case count estimates are prioritized by our precision score, as they represent areas where model uncertainty is greatest. Typically, these are locations with sparse or unreliable data where the model has little information to work with, forcing the allocation to explore and expand within the study region. Selecting these sites for new test centers enables targeted data collection to reduce uncertainty and refine future predictions.

Equity score

We assume there are u categories of subgroups, e.g., sex and race and ethnicity, and within each categories there are \(V_u\) sub-populations. Then, our equity score is evaluated by the discrepancy of coverage between sub-populations, at each demand point:

$$\begin{aligned} f_3({a})= -1000 \sum ^{V_1}_{v_1=1} \dots \sum ^{V_u}_{v_u=1} \left( \left( \sum _{j=1}^J\frac{p_{v_1,...,v_u,j}e_j({a})}{\sum _k p_{v_1,...,v_u,k}}\right) - \left( \sum _{j=1}^J\frac{p_je_j({a})}{\sum _kp_k}\right) \right) ^2, \end{aligned}$$
(3)

where the first term in parentheses represents the empirical conditional probability of being covered for a given sub-population, and the second term represents the marginal probability of being covered across the entire population. Under this definition, maximum equity is achieved when \(f_3(a) = 0\), meaning that the conditional probability of being covered by a test site for every sub-population is equal to the marginal probability of coverage for the overall population36. This condition implies that access to testing is entirely independent of local sociodemographic characteristics. In other words, no subgroup has a higher or lower likelihood of access due to their demographic composition. Therefore, we aim to maximize \(f_3\) to obtain an equitable allocation plan.

We found that while \(f_1\) and \(f_2\) tend to have relatively similar magnitudes, \(f_3\) can be much smaller than the other two objectives due to the sum of squares expression. The linear scaling factor of 1000 is designed to put \(f_3\) at a similar scale as \(f_1\) and \(f_2\).

In this study, race and ethnicity classifications follow those reported by the U.S. 2020 Census. Group labels included non-Hispanic white, non-Hispanic black, non-Hispanic other, and Hispanic.

Constraints

We assume that individuals choose the test site closest to their resident census tract, and enforce two constraints in our optimization. The first constraint limits the number of total test sites in an allocation plan, i.e., \({a}^\top \textbf{1} \le K\) where \({a}\in \{0,1\}^I\). Here, \(a_i\) is a decision whether to put a testing site at location i and K is the maximum number of test sites. The second constraint forces that if a demand point j is covered, then there must be at least one testing location i covering it. This if-then condition is modeled by the “big-M” method in the optimization problem. Specifically, first denote coverage matrix \({Z}\in \{0,1\}^{I\times J}\) with each element \(z_{ij}\) representing whether demand point j can be covered by potential test site i. This coverage matrix indicates exactly which demand points each test site location can cover when it prioritizes nearest neighbors and respects its testing-volume limit. Then, whether or not the demand point j can be covered with an allocation plan \({a}\) can be modeled by

$$\begin{aligned}& {Z}^\top {a} \le M{e},\\ & {Z}^\top {a} \ge \epsilon - M (1-{e}). \end{aligned}$$

Here \(M>0\) represents an finite upper bound of \({Z}^\top {a}\), e.g., K in our case. Additionally, \(\epsilon >0\) represents a small value between 0 and 1. In this case, we set \(\epsilon = 0.0001\). The first big-M rule states that if a demand point j is uncovered (\(e_j=0\)), it forces the sum of in-range selected sites \(\sum_i z_{ij}a_i\) to zero, so no test site location can cover it. The second big-M rule states that if a demand point j is covered (\(e_j=1\)) then \(\sum_i z_{ij}a_i\) is forced to be positive, so that at least one selected site must cover it.

Importantly, the matrix \({Z}\) can be pre-computed based on the testing capability of a testing site, the demands of a demand point, and the distance between candidate testing locations and demand points. We assume that each test site, i, can perform up to 1, 000 tests and it will first serve the nearest demand point. Moreover, if a demand point j finds that the nearest test site runs out of capacity, it will resort to the second nearest test site.

Final objective function

We seek to maximize the overall access of the testing sites \((f_1)\), precision of the disease model \((f_2)\), and equity of the allocation plan \((f_3)\). Therefore, the problem statement for our optimization, for a single location-allocation step is

$$\begin{aligned} \max _{{a}} \left\{ \lambda _1f_1({a}) + \lambda _2f_2({a}) +\lambda _3f_3({a})\right\} , \end{aligned}$$
(4)

where the parameters \(\lambda _1\), \(\lambda _2\), and \(\lambda _3 \ge 0\) reflect the relative priority of these objectives, to be determined by the decision makers. The choice of weights are crucial hyperparameters in our optimization framework, and we discuss this choice in detail in the next section.

Optimization

Combining all the objectives and the constraints yields the following optimization problem:

$$\begin{aligned} \begin{aligned}\max \quad &\left\{ \lambda _1f_1({a}) + \lambda _2f_2({a}) +\lambda _3f_3({a})\right\} \\s.t. \quad & {a}^\top \textbf{1} \le K\\ & {Z}^\top {a} \le M{e}\\ & {Z}^\top {a} \ge \epsilon - M (1-{e})\\ &{a}\in \{0,1\}^I; {e} = \{0,1\}^J \end{aligned} \end{aligned}$$

We note that this problem can be categorized as a multi-objective quadratic optimization problem, which can be efficiently solved by the interior-point method37. This optimization algorithm is implemented in Python with the Gurobi environment.

We note that Zhong et al.38 worked on a similar test-site allocation problem with one time period and implemented via a Genetic Algorithm (GA) using the \(\texttt {gramEvol}\) R package39. However, a key disadvantage of GA is its inability to reveal the quality of any solution40. Although it is generally believed that GA can generate high-quality solutions, it is not clear how close the current solution is to the optimum and whether all the available resources are fully utilized41. The interior-point method avoids these issues by utilizing the geometric properties of our optimization problem to control the optimality gap of the returned solutions.

Weight selection and sensitivity analysis

Weight selection in our optimization is a critical procedure as it directly influences the balance between competing objectives in our problem. Other location allocation methods rely on frameworks that clearly delineate between the “objective” optimization and “subjective” preference of the user. For example, the decision making frameworks TOPSIS42,43 and AHP44 operate by first providing a solution set and then asking the decision maker to choose a solution based on the user’s preferences codified into a series of weights. Our method directly integrates these weights into the optimization. While different from traditional multi-criteria decision making frameworks, this makes our weight selection procedure not much different from “hyperparameter selection” in statistical and machine learning methods. We acknowledge traditional methods allow for clear, separate stages between optimization and preference specification and allow the decision maker to consider multiple solutions. However, we believe our method may be more appropriate in situations like test site allocation during COVID-19, where streamlining decision-making is important and evaluating multiple solutions may be inefficient.

Unfortunately, choosing weights in this scenario lacks a universally accepted method. An added difficulty is, unlike most statistical problems where cross-validation procedures can be used to evaluate performance over a single metric, our evaluation metrics are multi-dimensional and can be in conflict, making an optimal choice difficult. Any choice of weights will inevitably reflect trade-offs between competing objectives and have large downstream effects on the optimization. In order for decision makers to feel confident in this procedure, understanding of its behavior in a wide range of scenarios is critical to advise users. To address these challenges in a robust fashion, we conducted a large sensitivity analysis to identify a “region” of weights where the solution was stable, as measured by the individual objective functions. The scale of the analysis allowed us to carefully balance the competing objectives without oversimplifying the problem into a single evaluation metric.

We first defined a grid of weights and let \(\lambda _1, \lambda _2,\) and \(\lambda _3\) be any of the values in \(\{10^{-4}, 10^{-2}, 10^0, 10^2\}\), giving us a total of 64 scenarios. For each scenario, we used our proposed method to conduct the sequential location allocation and compute each of the three evaluation metrics and the total score, and did this for a final allocation of 100, 200, and 500 test sites. The identification of stable solution sets was made visually and the weights that balanced good performance and stability in the evaluation metrics were selected.

In another sensitivity analysis assessing the robustness of our assumption of homogeneous risk of COVID-19 within a county, we repeated the tract-level case allocation procedure mentioned in the Data section, but instead of weighting tracts by population, we used the CDC’s Social Vulnerability Index (SVI) as the basis for allocation. As a sensitivity analysis, we repeated the tract-level case allocation procedure using a combined weighting scheme based on both population size and SVI. After merging tract-level case and population data, we joined SVI scores by census tract. For each tract, a raw weight was computed as the product of population and SVI, reflecting both the size and vulnerability of the tract. Larger and more vulnerable tracts were assigned a higher proportion of cases These raw weights were normalized within each county to form tract-level allocation weights. County-level case counts were then distributed proportionally according to these weights. As in the main analysis, expected counts were floored to integer values, and any remaining cases (due to rounding) were allocated to tracts with the largest fractional remainders.

All results for sensitivity analyses are reported in the Supplement.

Adaptive design

Once we establish the optimization approach for determining test site locations, we then define the follow approach as a way to use the information in an adaptive design. This contrasts with a non-adaptive allocation design, which selects all test sites at once without accounting for the evolving nature of the pandemic or incorporating incoming data streams such as case counts.

We first assign a uniform selection of initial testing site locations. This assignment defines step 0, and reflects the first test site allocation under complete lack of knowledge regarding the spatial distribution of the disease. In actual testing scenarios, the initial design is likely informed by expert opinion and not completely uniform in space. We then set two parameters for the method: batch size - the number of testing sites we add or re-arrange at each step denoted by \(\Vert {a_i} \Vert\) for new locations \({a_i}\), and time step - the amount of time that passes in between each iteration of testing site allocation. We then run the optimization procedure on the current selection of testing sites. The method will output an optimal set of locations, based on the testing data provided by the initial random design. This optimal set is the testing site allocation for step 1. The next step then proceeds in the exact same way, only now the new set of locations in addition to the original set replaces the role of the initial random design. Observational data are now collected from the updated set of locations as we move forward in time, and the process repeats itself until we achieve a stopping criteria. In the current study, we stopped after a time length of 30 days, but the criteria are not subject to strictly temporal limits.

Experiment

We compared the proposed multi-objective adaptive approach with a benchmark non-adaptive random approach, and several single-objective adaptive approaches. We decided that the multi-objective function itself was best to measure performance in all categories of interest simultaneously. Other metrics like mean squared error (MSE) do not capture the multi-objective nature of the problem, and classic classification metrics do not apply since the goal of the model is to predict case counts, not a binary variable.

Our experimental procedure to measure the performance of our proposed approach consisted of a series of pseudo-simulation studies aimed at comparing the proposed method to several other allocation approaches. The dataset comprised of tract-level COVID-19 daily case counts, broken down by race and ethnicity. Each of the methods under investigation were used to solve for a final testing allocation, during the peak of the Delta variant COVID-19 epidemic in the United States during the winter of 2020–2021. The time period for the experiment is shown in Fig. 1.

For the first experiment, to determine which method performed best over time within a fixed time period, each adaptive method was used to add five new test sites every day over the course of the 30 days. The same initial allocation of five test sites was used for each method. Scores calculated from the multi-objective function were compared over time to examine performance in the long run. Results are reported in Fig. 2.

For the second experiment we determined how many test sites were required to achieve similar performance to our proposed approach. First, 100 test sites were randomly selected out of all possible test locations to represent a non-adaptive random approach denoted as the ”One-Shot (non-adaptive)” allocation. These test sites were designated all at once at the beginning of the study period and no sequential adding or rearrangement of test site locations was involved. The overall and individual scores for access, precision, and equity score were recorded. Then for each adaptive method, starting from zero test sites, five test sites were added each day. We also ran a version adding ten test sites a day. Since the non-adaptive design can yield negative total scores, we terminated the proposed design once it allocated more than \(50\%\) of the testing sites used by the non-adaptive design (over 50 sites out of the 100 selected by the one-shot non-adaptive allocation). Then, the other methods under investigation were stopped once the overall score for the adaptive method exceeded the score of the proposed design. If a design did not achieve a higher total score than the target, we report the results corresponding to the score closest to the target. The number of sites required to achieve the target was recorded. Results are reported in Table 1.

We replicated each experiment 100 times. The stochastic nature of the results originates solely from the location of the initial test sites—all other elements of the method are deterministic.