A graph attention network-based multi-agent reinforcement learning framework for robust detection of smart contract vulnerabilities

Abstract

Smart contracts have revolutionized decentralized applications by automating agreement enforcement on blockchain platforms. However, detecting vulnerabilities in smart contract interactions remains challenging due to complex state interdependencies. This paper presents a novel approach using multi-agent Reinforcement Learning (MARL) to identify smart contract vulnerabilities. We integrate a Hierarchical Graph Attention Network (HGAT) into a Multi-Agent Actor-Critic framework, decomposing vulnerability detection into complementary policies: a high-level policy encoding historical interactions and a low-level policy capturing structured actions within contract state spaces. By modeling interactions as multistep reasoning paths, our MARL framework effectively navigates complex transaction sequences and resolves semantic ambiguities across different contract states. Experimental evaluations on real-world blockchain datasets demonstrate significant improvements in detecting multiple vulnerability types. For reentrancy attacks, our model achieves 93.8% accuracy and an 89.8% F1 score. The framework also performs strongly in detecting front running (88.9% accuracy), denial-of-service attacks (91.2% accuracy), and unchecked low-level vulnerabilities (91.6% accuracy), outperforming existing approaches across all vulnerability categories.

Introduction

Blockchain technology has profoundly reshaped the digital economy by introducing decentralized frameworks that ensure secure and transparent transactions, particularly within cryptocurrency ecosystems^1,2. A key development in this domain is the emergence of smart contracts, which are self-executing digital agreements with embedded predefined operational logic. Decentralized Autonomous Organizations (DAOs) leverage smart contracts to define operational rules and decision-making processes, facilitating transparent and decentralized governance. These programmable protocols have gained widespread adoption in various sectors, including decentralized finance (DeFi), supply chain management, and healthcare data administration, due to their ability to streamline operations and eliminate intermediaries³.

Smart contracts hold transformative potential but face significant technical challenges that threaten their security and reliability. Persistent vulnerabilities in their design and coding pose considerable risks, including financial theft and systemic instability, which can erode trust in blockchain-based infrastructures⁴. Common security flaws include coding errors such as integer overflows and underflows^5,6, reentrancy attacks^7,8, weak access controls⁹, and reliance on insecure third-party libraries¹⁰. These issues are exacerbated by the immutable and transparent nature of blockchain, making deployed contracts difficult to update or patch¹¹.

Traditional approaches to vulnerability detection, such as static and dynamic code analysis^12,13,14,15, provide foundational tools for identifying security flaws in smart contracts. However, these approaches cannot capture the nuanced and evolving nature of contract interactions in decentralized applications (DApps). As smart contracts interact with both on-chain and off-chain entities, understanding these interactions’ contextual and sequential behavior becomes vital. Static analysis, while effective in identifying code-level issues, may overlook vulnerabilities that emerge during runtime or in complex operational scenarios¹⁶.

Recent improvements in machine learning, particularly Reinforcement Learning (RL)¹⁷, present an advantageous pathway for the detection of vulnerabilitiestracts¹⁸. By framing vulnerability detection as a sequential decision-making problem, RL can analyze the evolving states of contract execution and predict potential risk scenarios. Unlike traditional RL methods, which often treat each decision in isolation, modern hierarchical RL approaches can effectively leverage contextual information and hierarchical relationships to navigate large action spaces. This ability to model and adapt to complex contract behaviors makes RL a powerful tool for mitigating security risks in smart contracts¹⁹.

Inspired by human cognitive processes, Hierarchical Reinforcement Learning (HRL) has emerged as an effective approach for addressing complex reasoning tasks. By decomposing tasks into sub-tasks, HRL facilitates structured decision-making, allowing models to manage large action spaces and ambiguous semantics through layered policies²⁰. These frameworks have demonstrated notable success in domains such as knowledge graph reasoning, where multi-step inference is required to establish connections between entities across diverse contexts²¹.

To improve reasoning capabilities, we incorporate a Hierarchical Graph Attention Network (HGAT) into the Multi-Agent Actor-Critic framework. The HGAT enables efficient representation learning by capturing complex relationships between entities and actions within smart contract interactions. The hierarchical nature of HRL consists of high-level policies that encode historical context and low-level policies responsible for executing structured actions. The integration of graph attention mechanisms allows the model to focus on the most relevant interactions, improving predictive accuracy in smart contract vulnerability detection.

Our proposed framework leverages the strengths of HRL and Graph Attention Networks (GAT) to enhance predictive analytics in smart contracts. The high-level policy captures past interaction sequences to provide contextual awareness, while the low-level policy focuses on fine-grained contract actions, thereby reducing ambiguity and improving decision-making precision. Our key contributions are as follows:

• We propose a novel graph attention network-based multi-agent reinforcement learning approach for detecting vulnerabilities and conducting predictive analytics in smart contract interactions. Our approach employs hierarchical policies and graph-based representations to model complex contract behaviors and potential outcomes.

• We address the challenges of multi-action sequences, state dependencies, and relational complexities inherent in smart contracts through a multi-hop reasoning approach, improving predictive accuracy and robustness.

• We evaluate our proposed framework on real-world blockchain datasets, demonstrating its effectiveness in identifying high-risk scenarios and predicting contract outcomes with superior accuracy compared to existing methods.

This paper is organized as follows. In Section, we review related work on smart contract analysis, reinforcement learning, and hierarchical models. Section provides the background on theories and concepts of reinforcement learning, and Section presents the smart contract vulnerabilities under study and the problem statement. Sections and 0.0.2 detail our proposed methodology, experimental setup, and performance evaluation, respectively. Finally, Section 0.0.2 concludes with potential applications and future research directions in smart contract predictive analytics.

Related work

The application of reinforcement learning (RL) in smart contract analysis is an emerging field that aims to address the limitations of traditional smart contract analysis techniques, particularly regarding dynamic interactions in blockchain environments. This section reviews relevant studies in three categories: traditional vulnerability detection methods, RL-based approaches, and recent advancements in deep learning techniques.

Traditional smart contract vulnerability detection methods

Traditional methods for detecting smart contract vulnerabilities have largely focused on static and symbolic analysis, which are effective for identifying syntax-based errors and ensuring correctness prior to deployment¹⁹. These methods translate Solidity code and Ethereum Virtual Machine (EVM) bytecode into formal verification systems to detect vulnerabilities before contracts are executed^22,23,24. However, these techniques are limited in handling the evolving nature of contracts once deployed, where interactions may introduce unforeseen vulnerabilities.

Tools such as Oyente²⁵, Securify²⁶, and Zeus²⁷ have advanced symbolic analysis to detect potential vulnerabilities in smart contracts. However, they suffer from high false negative rates due to the difficulty of exploring all possible execution paths. To address this, dynamic execution approaches like ContractFuzzer²⁸ and Sereum²⁹ have been introduced, enabling runtime monitoring of data flows. These tools provide a more comprehensive vulnerability assessment but often require hand-crafted agent contracts to detect specific issues, such as reentrancy vulnerabilities, limiting their generalizability and scalability in complex contract environments.

Reinforcement learning approaches for smart contract analysis

In response to the limitations of static and symbolic methods, several studies have investigated using RL to predict outcomes and detect anomalies in smart contract executions. Chen et al.¹⁶ proposed an RL-based framework where an agent, trained on historical transaction data, simulates contract interactions to anticipate outcomes that static methods might overlook. Although this approach captures historical behavioral patterns effectively, it faces scalability challenges when applied to large contract networks with vast action spaces. This issue highlights a core challenge in adapting RL to decentralized blockchain systems, where numerous possible states and actions complicate accurate predictions.

Some RL applications outside the smart contract domain, such as DeepPath²¹, offer insights into handling complex dependencies in sequential actions. Originally designed for knowledge graph reasoning, DeepPath applies multi-hop reasoning to connect entities across a sequence of actions. However, its adaptation to smart contract analysis presents difficulties; the large action spaces and complex state transitions in blockchain data often result in suboptimal predictions and inefficiencies. These limitations underscore the need for more tailored RL approaches to address the unique requirements of smart contract interactions.

To address scalability and complexity challenges, hierarchical reinforcement learning (HRL) has been proposed as a more structured approach. HRL divides the decision-making process into a hierarchy of high-level and low-level policies, allowing for refined control over extensive action spaces. Barto and Mahadevan²⁰ demonstrated the advantages of HRL in layered decision tasks, suggesting its potential for smart contract analysis, where contextual awareness across sequences of states and actions is crucial. By structuring decision processes hierarchically, HRL offers significant advantages over standard RL methods in complex contract environments.

Deep learning for vulnerability detection

Recent advancements in deep learning, particularly graph neural networks (GNNs), have introduced new techniques for vulnerability detection in smart contracts. GNNs are effective at processing graph-structured data, making them suitable for representing relationships within contracts. Approaches include spectral-based methods like GCN³⁰, which generalize convolutional neural networks for graph data, and spatial-based methods that use message passing for graph convolutions^31,32. For example, Zhuang et al.³³ converted smart contract source code into graph structures and applied GNNs for vulnerability detection, capturing dependencies that traditional methods might miss.

Liu et al.³⁴ further enhanced GNN-based detection by integrating expert rules, which improved accuracy but presented challenges in explainability and interpretability. These advancements in GNNs represent a significant shift toward more complex, data-driven approaches to vulnerability detection. However, issues such as feature significance and model transparency remain, particularly in high-stakes domains like blockchain security.

Tranformer-based vulnerability detection

Guo et al.³⁵ introduced GraphCodeBERT, a pre-trained model that jointly learns code semantics and data flow structures to improve code understanding tasks such as vulnerability detection and clone identification. Its novel lies in integrating data flow graphs with masked language modeling, demonstrating superior performance on code summarization and classification benchmarks. Koreeda and Manning³⁶ proposed ContractNLI, a dataset and benchmark for document-level natural language inference on legal contracts. The work emphasizes clause-level entailment reasoning and highlights challenges in understanding legal semantics, providing a foundational resource for NLP models in legal AI applications.

Wang et al.³⁷ developed TMF-Net, a multimodal smart contract vulnerability detection framework based on multiscale transformer fusion of code tokens, abstract syntax trees, and control flow graphs. Their fusion mechanism outperformed single-modality baselines on vulnerability classification tasks, particularly for reentrancy and timestamp dependence. Shang et al.³⁸ introduced CEGT, a hybrid architecture combining Connectivity-Enhanced Graph Convolutional Networks (GCN) and Transformers to capture long-range dependencies and code execution paths in smart contracts. The model achieved state-of-the-art accuracy on real-world datasets by effectively modeling both structural and sequential code features.

Despite these advances, several key challenges remain. Existing approaches often lack resilience to real-world obfuscation, suffer from high false-positive rates in dynamic execution contexts, or do not adequately model the hierarchical and relational semantics across multi-contract ecosystems. Furthermore, reward shaping and model interpretability are frequently underexplored in RL-based detection settings. These limitations motivate our proposed GANS-MARL framework, which integrates hierarchical multi-agent reinforcement learning with graph attention to improve robustness, semantic reasoning, and predictive accuracy in smart contract vulnerability detection.

Background

Partially observable Markov game formulation for smart contract vulnerability detection

Smart contract vulnerability detection can be effectively modelled as a Partially Observable Markov Game (POMG), providing a framework for the multi-agent reinforcement learning approach. A POMG extends the conventional Markov Decision Process to accommodate multiple agents operating with partial observations of the environment state, which accurately reflects the nature of smart contract analysis where different vulnerability detection components observe different aspects of the contract code and execution state. A POMG for N agents is defined by the tuple $\langle S, \{A_i\}_{i=1}^N, \{O_i\}_{i=1}^N, T, \{r_i\}_{i=1}^N, \gamma , \rho \rangle$, where each component has a specific interpretation in the vulnerability detection context:

• S represents the complete state space of the smart contract environment, encompassing the full bytecode, storage variables, execution state, transaction history, and all potential execution paths. The state space is typically high-dimensional and complex, containing all information about contract vulnerabilities, manifest or latent.

• $A_i$ denotes the action space available to agent i. In vulnerability detection, actions correspond to various analysis techniques, code transformations, state explorations, or detection heuristics that can be applied to identify specific vulnerability patterns. For instance, an action might involve examining the control flow after external calls to detect reentrancy vulnerabilities or analyzing transaction ordering dependencies to identify front-running vulnerabilities.

• $O_i$ represents the observation space of agent i. Since the complete state $s \in S$ is typically too complex to observe fully, each agent receives a partial observation $o_i \in O_i$ based on its specialized focus. These observations might include code segments, execution traces, data flow patterns, or specific contract properties relevant to the agent’s vulnerability detection domain.

• $T: S \times A_1 \times \cdots \times A_N \rightarrow \Delta (S)$ is the state transition function that maps the current state and joint actions to a probability distribution over the next states. In the vulnerability detection framework, this represents how the analysis state evolves as different detection techniques are applied, with the next state potentially revealing new aspects of the contract’s behavior or vulnerability status.

• $r_i: S \times A_1 \times \cdots \times A_N \rightarrow \mathbb {R}$ is the reward function for agent i, which quantifies the effectiveness of detection actions. The reward structure is fundamental to guiding the learning process toward successful vulnerability detection. For reentrancy vulnerability detection, the reward function might assign high values when the agent identifies a state modification pattern after an external call without proper guards. For unchecked low-level calls, rewards might correspond to discovering call operations whose return values are not properly checked. Front-running vulnerability detection rewards would emphasize identifying time-sensitive operations with transaction ordering dependencies. Denial of service detection rewards would focus on recognizing patterns that could lead to resource exhaustion or blocking of contract execution.

• $\gamma \in [0,1]$ is the discount factor that balances the importance of immediate versus future rewards, allowing the agent to consider the long-term consequences of its detection strategies rather than merely focusing on immediate indicators.

• $\rho : S \rightarrow [0,1]$ defines the initial state distribution, which in our context represents the starting point of the analysis, typically the initial state of the smart contract before any vulnerability detection techniques are applied.

In this framework, each agent i aims to learn a policy $\pi _i: O_i \rightarrow \Delta (A_i)$ that maximizes its expected discounted return:

$$\begin{aligned} V_i^{\pi } = \mathbb {E}_{\pi , T, \rho }\left[ \sum _{t=0}^{\infty } \gamma ^t r_i^t\right] \end{aligned}$$

(1)

where $r_i^t$ represents the reward received by agent i at time step t. The expectation is taken over the trajectories generated by the joint policy $\pi = (\pi _1, \ldots , \pi _N)$, the transition dynamics T, and the initial state distribution $\rho$.

The POMG formulation capture the complexity of vulnerability detection, where multiple specialized agents must coordinate their analysis strategies to uncover different types of vulnerabilities while operating with incomplete information about the smart contract’s full state.

Deterministic policy gradient

At its core, MADDPG builds upon the Deterministic Policy Gradient (DPG) framework, which aims to learn a deterministic policy $\mu _\theta : S \rightarrow A$ parameterized by $\theta$ that directly maps states to actions. The objective is to maximize the expected return:

$$\begin{aligned} J(\theta ) = \mathbb {E}_{s \sim \rho ^{\mu }}\left[ R(s, \mu _\theta (s))\right] \approx \mathbb {E}_{s \sim \rho ^{\mu }}\left[ Q^{\mu }(s, \mu _\theta (s))\right] \end{aligned}$$

(2)

where $\rho ^{\mu }$ is the state distribution induced by policy $\mu$, and $Q^{\mu }(s, a)$ is the action-value function that estimates the expected return when taking action a in state s and following policy $\mu$ thereafter.

In the DPG framework, the policy parameters $\theta$ are updated using the gradient:

$$\begin{aligned} \nabla _\theta J(\theta ) = \mathbb {E}_{s \sim \rho ^{\mu }}\left[ \nabla _\theta \mu _\theta (s) \nabla _a Q^{\mu }(s, a)|_{a=\mu _\theta (s)}\right] \end{aligned}$$

(3)

This gradient comprises two components: $\nabla _\theta \mu _\theta (s)$, which represents how the policy’s action changes with respect to the policy parameters, and $\nabla _a Q^{\mu }(s, a)|_{a=\mu _\theta (s)}$, which indicates how the Q-value changes with respect to the action. Together, they guide the policy toward actions that maximize the expected return.

Deep deterministic policy gradient

Deep Deterministic Policy Gradient (DDPG) extends DPG by approximating both the policy $\mu _\theta$ and the Q-function $Q^{\mu }(s, a)$ using deep neural networks. DDPG employs an actor-critic architecture where:

• The actor network $\mu _\theta : S \rightarrow A$ represents the policy, mapping states to deterministic actions.

• The critic network $Q_\phi (s, a)$ estimates the action-value function, evaluating the quality of state-action pairs.

• DDPG incorporates several techniques to stabilize learning:

• Experience Replay: Transitions $(s, a, r, s')$ are stored in a replay buffer D and randomly sampled for training, breaking the temporal correlations in sequential experiences.

• Target Networks: Separate target networks $\mu _{\theta '}$ and $Q_{\phi '}$ with delayed parameters are used to compute the target values, reducing the non-stationarity of the learning targets.

• The critic is updated by minimizing the temporal difference error:

  $$\begin{aligned} L(\phi ) = \mathbb {E}_{(s, a, r, s') \sim D}\left[ (Q_\phi (s, a) - y)^2\right] \end{aligned}$$

  (4)

where $y = r + \gamma Q_{\phi '}(s', \mu _{\theta '}(s'))$ is the target value.

The actor is updated using the deterministic policy gradient:

$$\begin{aligned} \nabla _\theta J(\theta ) = \mathbb {E}_{s \sim D}\left[ \nabla _\theta \mu _\theta (s) \nabla _a Q_\phi (s, a)|_{a=\mu _\theta (s)}\right] \end{aligned}$$

(5)

Smart contract vulnerabilities

Vulnerability definitions

Reentrancy vulnerability

Reentrancy vulnerabilities occur when an external call is made before state variables are updated, allowing an attacker to recursively re-enter the calling function and manipulate the contract’s state. This vulnerability was famously exploited in the 2016 DAO attack³⁹, resulting in a loss of approximately $60 million. The fundamental issue lies in the execution order of operations within a function, where premature external calls provide an opportunity for malicious contracts to exploit partially updated states.

Definition 1

(Reentrancy Vulnerability) Given a contract C with state variables $\mathscr {S} = \{s_1, s_2, \ldots , s_n\}$ and functions $\mathscr {F} = \{f_1, f_2, \ldots , f_m\}$, a function $f_i \in \mathscr {F}$ has a reentrancy vulnerability if: $\exists$ execution trace $\tau = \{op_1, op_2, \ldots , op_k\}$ of $f_i$ such that $\exists j, l \in \{1, 2, \ldots , k\}$ where $j < l$ and $op_j = \text {ExternalCall}(addr, val, data)$ and $op_l = \text {StateUpdate}(s_p) \text { with } s_p \in \mathscr {S}$

Here, $\text {ExternalCall}(addr, val, data)$ represents a call to an external contract at address addr, with value val and calldata data, while $\text {StateUpdate}(s_p)$ represents a modification to state variable $s_p$. The attack vector emerges when the external contract called can execute malicious code that re-enters the original function before the state update occurs, allowing multiple withdrawals or other state manipulations. This pattern is particularly dangerous in financial contracts, as it can lead to unauthorized fund drainage through repeated calls to withdrawal functions.

Unchecked low-level call vulnerability

Unchecked low-level calls occur when return values from external calls such as send, call, or delegatecall are not properly verified, allowing execution to continue even when the external call has failed. This can lead to inconsistent contract state and unexpected behavior. The vulnerability stems from Ethereum’s design choice to continue execution after a failed call unless explicitly checked, contrasting with the automatic reversion behavior of high-level interface calls.

Definition 2

(Unchecked Low-Level Call Vulnerability) For a function $f_i \in \mathscr {F}$ containing low-level calls $\mathscr {L} = \{l_1, l_2, \ldots , l_q\}$, an unchecked low-level call vulnerability exists if: $\exists l_j \in \mathscr {L}$ such that $\not \exists$ condition c in the control flow graph after $l_j$ where c depends on the return value of $l_j$.

This vulnerability can lead to silent failures where important operations like payments fail without the contract recognizing the failure, potentially causing funds to be locked or accounting to become inconsistent. Smart contracts often use these low-level calls for Ether transfers or contract interactions, and failure to verify their success can break the fundamental assumptions of business logic. The disconnect between expected and actual behavior creates a security gap that can be exploited or can simply result in broken contract functionality that becomes apparent only under specific conditions.

Front-running vulnerability

Front-running vulnerabilities arise when the order of transaction execution can be manipulated by miners or other participants to gain an unfair advantage. In blockchain systems, transactions wait in a memory pool before being selected and ordered by miners, creating an opportunity for adversaries to observe pending transactions and insert their own transactions ahead of them. This vulnerability exploits the time gap between transaction submission and confirmation, a fundamental characteristic of decentralized systems.

Definition 3

(Front-running vulnerability) For a set of transactions $\mathscr {T} = \{t_1, t_2, \ldots , t_r\}$ that interact with contract C, a front-running vulnerability exists if: $\exists (t_i, t_j) \in \mathscr {T} \times \mathscr {T}, i \ne j$ such that Outcome $(t_i \rightarrow t_j) \ne$ Outcome$(t_j \rightarrow t_i)$ and $\exists$ party P that can profit from controlling execution order.

Here, $\text {Outcome}(t_i \rightarrow t_j)$ represents the resulting state after executing transaction $t_i$ followed by $t_j$, and P represents any participant in the system who can observe pending transactions. Common instances of front-running vulnerabilities occur in decentralized exchanges, NFT minting, and auction mechanisms where transaction ordering directly impacts asset prices or availability. The economic incentives for front-running can be substantial, making this attack particularly common in high-value markets. The strategy typically involves observing profitable pending transactions and submitting competing transactions with higher gas prices to ensure earlier execution.

Denial of service vulnerability

Denial of Service (DoS) vulnerabilities allow attackers to render contracts inoperable by exploiting resource limitations or control flow dependencies. These vulnerabilities can completely halt contract operations, preventing legitimate users from accessing services or funds. The immutable nature of blockchain makes these attacks particularly severe, as vulnerable contracts often cannot be easily modified once deployed.

Definition 4

(Denial of service vulnerability) For a function $f_i \in \mathscr {F}$, a denial of service vulnerability exists if either: $\exists$ execution path p in $f_i$ such that GasConsumption(p) scales unboundedly with input or state parameters. Or: $\exists$ control flow condition c in $f_i$ such that c depends on actions of external actors who can force c to always evaluate to false.

DoS vulnerabilities can manifest through several mechanisms. Gas limit exploitation forces loops to iterate over large data structures, potentially exceeding block gas limits. External call dependencies make critical functions rely on external contracts that can be disabled. Block stuffing prevents specific transactions from being included in blocks by manipulating gas prices and network congestion. Poison data attacks supply input that causes excessive computation or storage, rendering functions unusable. These attack vectors are particularly problematic in smart contracts due to their autonomous nature and the lack of administrative intervention capabilities in truly decentralized applications.

Challenge formulation

Problem statement

Given the formal vulnerability definitions above, we formulate the challenge of automated vulnerability detection in smart contracts as follows:

Definition 5

(Smart contract vulnerability detection) For a given smart contract C with state variables $\mathscr {S}$ and functions $\mathscr {F}$, identify the set of vulnerabilities $\mathscr {V} = \{v_1, v_2, \ldots , v_p\}$ present in C, where each $v_i$ is an instance of one of the defined vulnerability types. Each identified vulnerability should specify the vulnerable function $f_j \in \mathscr {F}$, the vulnerability type (reentrancy, unchecked call, front-running, or DoS), the specific execution path or condition that triggers the vulnerability, and the potential impact of successful exploitation.

Computational challenges

The detection of these vulnerabilities presents several significant computational challenges. State space explosion represents a fundamental obstacle, as the number of possible execution paths grows exponentially with contract complexity. For a contract with n branches, there can be up to $O(2^n)$ distinct execution paths, making exhaustive analysis computationally intractable for complex contracts. This combinatorial explosion limits the effectiveness of brute-force verification approaches and necessitates more sophisticated techniques.

Partial observability further complicates detection, as no single analysis technique can observe all aspects of contract behavior. Static analysis may miss dynamic vulnerabilities that only manifest during specific execution conditions, while dynamic analysis cannot guarantee complete coverage of all execution paths. This limitation forces detection systems to balance different analysis methods, each with their own blind spots and strengths.

Semantic complexity introduces another layer of difficulty, as vulnerabilities often depend on subtle semantic properties and inter-contract interactions. The context in which a contract operates, including its interaction with other contracts and the underlying blockchain protocol, can introduce vulnerabilities that are not apparent from analyzing the contract in isolation. The meaning and implications of certain operations change based on the broader ecosystem, requiring analyzers to account for this contextual information.

The challenge of adaptive adversaries stems from the evolving nature of vulnerability patterns as attackers develop new exploitation techniques. New vulnerability classes emerge as the ecosystem evolves, requiring detection systems to adapt to previously unknown patterns. This cat-and-mouse game between attackers and defenders means that detection mechanisms must generalize beyond known vulnerability patterns to identify novel variations.

The false positive/negative trade-off presents a practical challenge for deployment, as increasing detection sensitivity typically leads to more false positives while reducing sensitivity increases the risk of missing vulnerabilities. Finding the optimal balance between these competing objectives depends on the specific security requirements and risk tolerance of the contract being analyzed.

Multi-agent reinforcement learning approach

We propose formulating the detection task as a multi-agent reinforcement learning problem where specialized agents focus on different vulnerability types while sharing information to build a comprehensive understanding of contract security.

Definition 6

(MARL vulnerability detection framework) We define a multi-agent system $\mathscr {M} = \{A_1, A_2, \ldots , A_w\}$ where each agent $A_i$ specializes in detecting a specific vulnerability type. The state space $\mathscr {S}_i$ for agent $A_i$ includes relevant contract features and execution traces. The action space $\mathscr {A}_i$ consists of vulnerability detection decisions and information sharing. The reward function $\mathscr {R}_i: \mathscr {S}_i \times \mathscr {A}_i \rightarrow \mathbb {R}$ incentivizes correct vulnerability identification while penalizing false positives. A communication protocol $\mathscr {P}$ facilitates information sharing between agents to improve collective detection accuracy.

This approach enables specialization, as each agent can develop expertise in a specific vulnerability pattern. Knowledge transfer becomes possible as agents share insights about contract behavior to improve collective detection. The system gains adaptability by learning to recognize new vulnerability patterns through reinforcement learning. Comprehensive coverage is achieved as multiple agents working in parallel examine different aspects of contract security. The ultimate goal is to develop a robust, adaptive system that can identify both known vulnerability patterns and novel variations, providing developers with actionable security insights before contracts are deployed to production networks. By leveraging the collective intelligence of specialized agents, this approach addresses the computational challenges inherent in vulnerability detection while maintaining flexibility to evolve alongside the smart contract ecosystem.

Method: hierarchical graph attention-based multi-agent actor-critic framework

Our proposed model integrates hierarchical graph representation learning with multi-agent reinforcement learning. The unique contributions of each component of our proposed framework are:

• 1. Multi-Agent Reinforcement Learning (MARL): Conventional single-agent models, such as standard hierarchical Graph Attention Networks (GAT), encounter significant scalability issues and limitations in parallel exploration within the context of smart contracts, which involve multiple interacting entities and concurrent transactions. In contrast, our multi-agent reinforcement learning (MARL) framework effectively addresses these challenges by partitioning the action space among multiple agents. Each agent can focus on specific aspects of contract behavior, such as fund flow, function invocation, and external call interactions. This approach mirrors the decentralized nature of Decentralized Autonomous Organizations (DAOs) and Decentralized Applications (DApps), where actions are both distributed and interdependent. Additionally, MARL facilitates parallelized learning, which improves convergence rates and enhances robustness in environments characterized by sparse reward signals.

• 2. Hierarchical Reinforcement Learning (HRL): The hierarchical decomposition of tasks elucidates the compositional attributes of vulnerabilities in smart contracts. At the high level, policies encapsulate overarching patterns, such as execution context variables and trends derived from historical behavior, whereas low-level policies delve into specific actions, including sequences of reentrancy calls. Hierarchical Reinforcement Learning (HRL) enhances temporal abstraction and structured exploration, thereby reducing sample complexity when compared to traditional flat Reinforcement Learning approaches. This hierarchical architecture is crucial for detecting vulnerabilities that emerge across multiple transactions or contract invocations, which are often overlooked by more simplistic, monolithic frameworks, as highlighted in²¹.

• 3. Graph Attention Networks (GAT): The components of smart contracts–encompassing functions, storage variables, and external calls–naturally configure into a graph structure. While both DA-GNN and DR-GCN provide fundamental message-passing capabilities, they generally operate on the premise that all neighboring interactions hold equal importance. In contrast, the Graph Attention Network (GAT) introduces a dynamic attention mechanism that allows the model to selectively weigh interactions based on their relevance, particularly concerning known attack vectors such as reentrancy or unauthorized access patterns. This targeted approach is especially effective in mitigating the effects of irrelevant or noisy nodes and edges within the graph, improving overall model performance in the context of security analyses.

Foundation

The foundation consists of a multi-dimensional graph representation pipeline that transforms smart contract bytecode and source code into four specialized graph structures. The Control Flow Graph (CFG) maps execution pathways and branching logic, capturing the runtime traversal of code. The Data Flow Graph (DFG) traces variable dependencies and state mutations, revealing how values propagate through the contract. The Function Call Graph (FCG) documents the invocation hierarchy between methods, exposing potential callback chains. The Inter-Contract Graph (ICG) models cross-boundary interactions, essential for detecting vulnerabilities that manifest only in the complex interplay between multiple contracts. Together, these graph representations form a comprehensive computational model of smart contract behavior suitable for deep structural analysis.

Building on this graph-theoretic foundation, we implement a dual-level attention mechanism within our neural architecture. This hierarchical graph attention network functions as a trainable feature extractor that automatically identifies vulnerability-relevant subgraphs within the contract’s structure. At the micro level, intra-graph attention weights emphasize critical nodes and edges that exhibit vulnerability signatures. At the macro level, inter-graph attention mechanisms establish cross-references between the four graph representations, enabling the model to correlate execution paths with data dependencies and cross-contract calls. This multi-resolution approach facilitates both fine-grained bytecode-level scrutiny and high-level architectural pattern recognition, mirroring the multi-faceted analysis performed by expert security auditors.

To operationalize vulnerability detection, we implement a distributed multi-agent system where agents are partitioned into specialized detection clusters. Each cluster employs domain-specific neural network architectures tailored to particular vulnerability classes. The reentrancy detection cluster utilizes recursive neural networks to identify unsafe state modifications following external calls. The unchecked-call cluster employs control-dependency analysis to trace return value propagation through execution paths. The front-running vulnerability cluster implements temporal logic verification to detect transaction-ordering dependencies. The denial-of-service cluster applies resource consumption modeling to identify unbounded operations and potential execution blockages. This modular design allows each agent cluster to optimize its neural architecture for specific vulnerability patterns.

These components are orchestrated through a multi-agent actor-critic reinforcement learning framework. The system employs centralized training with a decentralized execution paradigm, where each agent maintains an independent policy (actor) for local decision-making while sharing a vulnerability-specific critique that evaluates joint actions. During training, agents interact with a diverse corpus of smart contracts, receiving positive reinforcement signals for correctly identified vulnerabilities and negative feedback for false alarms. Through gradient-based policy optimization, the framework evolves increasingly refined detection strategies without requiring hard-coded heuristics. This self-improving architecture continuously adapts to novel vulnerability patterns, achieving a level of detection sophistication that surpasses static analysis approaches.

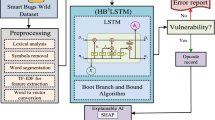
System architecture

As illustrated in Fig. 1, our approach consists of four primary components: (1) smart contract graph representation, (2) hierarchical graph attention network, (3) multi-agent actor-critical framework and (4) vulnerability detection mechanism. These components work in concert to identify complex vulnerability patterns across multiple contract interactions.

Fig. 1

System architecture for smart contract vulnerability detection using hierarchical graph network.

Smart contracts are transformed into graph-based representations that capture their structural and semantic properties. Given a smart contract C, we construct four complementary graph representations:

Control flow graph

The Control Flow Graph (CFG) $G_{CF} = (V_{CF}, E_{CF})$ represents the execution paths within the contract, where $V_{CF}$ is the set of basic blocks (consecutive statements without branching) and $E_{CF} \subseteq V_{CF} \times V_{CF}$ is the set of possible control transfers between blocks. Thus: $E_{CF} = \{(v_i, v_j) \mid \text {execution can transfer from block } v_i \text { to block } v_j\}$.

Data flow graph

The Data Flow Graph (DFG) $G_{DF} = (V_{DF}, E_{DF})$ models data dependencies, where $V_{DF}$ represents variables and operations, and $E_{DF}$ indicates data dependencies. For variables or operations $v_i, v_j \in V_{DF}$: $(v_i, v_j) \in E_{DF} \iff \text {value of } v_i \text { affects value of } v_j$

Function call graph

The Function Call Graph (FCG) $G_{FC} = (V_{FC}, E_{FC})$ represents the call relationships between functions, where $V_{FC}$ corresponds to the functions in the contract, and $(f_i, f_j) \in E_{FC}$ indicates that function $f_i$ calls function $f_j$.

Inter-contract graph

The Inter-Contract Graph (ICG) $G_{IC} = (V_{IC}, E_{IC})$ models interactions between multiple contracts, where $V_{IC}$ represents contracts and $(C_i, C_j) \in E_{IC}$ indicates that contract $C_i$ interacts with contract $C_j$.

These graph representations collectively capture the structural, behavioral, and semantic properties of smart contracts necessary for vulnerability detection.

Hierarchical graph attention network

The core of our approach is the Hierarchical Graph Attention Network (HGAT), which processes the graph representations to extract vulnerability-relevant patterns. The HGAT consists of two key components: agent clustering and hierarchical attention mechanisms.

Agent clustering

We organize detection agents into K specialized groups $\{C^1, C^2, \ldots , C^K\}$, where each group $C^k$ focuses on a specific vulnerability type:

$C^1$: Reentrancy vulnerability detection agents $C^2$: Unchecked low-level call detection agents $C^3$: Front-running vulnerability detection agents $C^4$: Denial of service detection agents

This clustering introduces an inductive bias that reflects the natural grouping of vulnerability patterns, allowing agents to develop specialized expertise.

Node embedding with inter-agent attention

For each vulnerability group k and agent i, HGAT computes embeddings between the agent and code components in its observation range. Given a local observation $o_i = \{s_j \mid j \in V(i)\}$, where $s_j$ is the local state of code component j and V(i) defines the observation range of agent i, we compute:

$$\begin{aligned} h_{ij}^k = f_M^k(s_i, s_j; w_M^k) \quad \forall j \in C^k \cap V(i) \end{aligned}$$

(6)

Where $f_M^k$ is a neural network parameterized by $w_M^k$ that captures vulnerability-specific relationships.

These embeddings are aggregated using an inter-agent attention mechanism:

$$\begin{aligned} \bar{h}_i^k = \sum _{j \in C^k \cap V(i)} \alpha _{ij}^k h_{ij}^k \end{aligned}$$

(7)

The attention weight $\alpha _{ij}^k$ quantifies the importance of code component j to agent i in the context of vulnerability type k:

$$\begin{aligned} \alpha _{ij}^k = \frac{\exp (e_{ij}^k)}{\sum _{l \in C^k \cap V(i)} \exp (e_{il}^k)} \end{aligned}$$

(8)

Where $e_{ij}^k = f_\alpha ^k(s_i, s_j; w_\alpha ^k)$ is computed by a neural network $f_\alpha ^k$.

Hierarchical state representation with inter-group attention

The group-level embeddings $\{\bar{h}_i^1, \bar{h}_i^2, \ldots , \bar{h}_i^K\}$ are further aggregated through an inter-group attention mechanism:

$$\begin{aligned} h_i = \sum _{k=1}^K \beta _i^k \bar{h}_i^k \end{aligned}$$

(9)

The inter-group attention weight $\beta _i^k$ determines the focus on each vulnerability type given the current code context:

$$\begin{aligned} \beta _i^k = \frac{\exp (q_i^k)}{\sum _{l=1}^K \exp (q_i^l)} \end{aligned}$$

(10)

Where $q_i = [q_i^1, \ldots , q_i^K] = f_\beta ([\bar{h}_i^1, \ldots , \bar{h}_i^K]; w_\beta )$ is computed by a neural network $f_\beta$.

This hierarchical attention mechanism enables the model to adaptively focus on different vulnerability types based on the specific code characteristics, producing a comprehensive embedding $h_i$ that captures vulnerability-relevant patterns at multiple levels of abstraction.

Multi-agent actor-critic framework

The HGAT embeddings feed into a Multi-Agent Actor-Critic (MAAC) framework that learns vulnerability detection policies. The MAAC follows the Centralized Training with Decentralized Execution paradigm, where agents share information during training but act independently during deployment.

Dual embeddings for critic and actor

For each agent i, we compute two separate embeddings:

$h_i^C$: Used for critic computation, capturing information needed to evaluate state-action pairs.

$h_i^A$: Used for actor computation, focusing on information needed for action selection.

These embeddings are computed by two separate HGAT instances, allowing specialization for different purposes.

Centralized critics and decentralized actors

The critic for agent i in vulnerability group c(i) evaluates state-action pairs:

$$\begin{aligned} Q_{c(i)}(o, a) \approx Q_{c(i)}(h_i^C; \phi _{c(i)}) \end{aligned}$$

(11)

Where $\phi _{c(i)}$ are the critic network parameters for vulnerability group c(i).

The actor for agent i determines actions based solely on local observations:

$$\begin{aligned} a_i = \mu _{c(i)}(o_i) \approx \mu _{c(i)}(h_i^A; \theta _{c(i)}) \end{aligned}$$

(12)

Where $\theta _{c(i)}$ are the actor network parameters for vulnerability group c(i).

Agents within the same vulnerability group share networks, enhancing generalization and knowledge transfer.

Training procedure

The training procedure utilizes an Experience Replay Buffer D to store interaction histories. The critic is trained by minimizing:

$$\begin{aligned} L(\phi _k) = \mathbb {E}_{(o, a, r_i, o') \sim D}\left[ (Q_k^\mu (o, a; \phi _k) - y_i)^2\right] \end{aligned}$$

(13)

Where $y_i = r_i + \gamma Q_k^{\mu '}(o', a'; \phi' _k)|_{a'_j = \mu '(o'_j; \theta ')}$ is the target value and reward $r_i$ is formulated to reflect detection performance:

$$\begin{aligned} r_i = w_{TP} \cdot \mathbb {I}_{TP} - w_{FP} \cdot \mathbb {I}_{FP} - w_{FN} \cdot \mathbb {I}_{FN} \end{aligned}$$

(14)

where $\mathbb {I}_{TP}$, $\mathbb {I}_{FP}$, and $\mathbb {I}_{FN}$ are indicator functions for true positives, false positives, and false negatives respectively, and $w_{TP}$, $w_{FP}$, and $w_{FN}$ are their corresponding weights. The actor is updated using the deterministic policy gradient:

$$\begin{aligned}&\nabla _{\theta _k} J(\theta _k) \nonumber \\&= \mathbb {E}_{(o, a) \sim D}\left[ \nabla _{\theta _k} \mu _k(o_i; \theta _k) \nabla _{a_i} Q_k^\mu (o, a; \phi _k)|_{a_i = \mu _k(o_i; \theta _k)}\right] \end{aligned}$$

(15)

The training procedure is summarized in Algorithm 1.

Algorithm 1

GANS-MARL Training Procedure

As shown in Fig. 1, each vulnerability-specific agent cluster produces actions that contribute to the final vulnerability assessment. These actions correspond to detecting specific patterns associated with each vulnerability type:

Reentrancy detection

Reentrancy detection agents identify functions where state modifications occur after external calls. The action space includes flagging suspicious control flow patterns, identifying state variables modified after calls, and detecting missing reentrancy guards. The detection mechanism forms a binary classification for each function $f_i$:

$$\begin{aligned} R(f_i) = {\left\{ \begin{array}{ll} 1 & \text {if } \exists \text { path with state } \\ & \text {modification after external call}\\ 0 & \text {otherwise} \end{array}\right. } \end{aligned}$$

(16)

Unchecked call detection

Unchecked call detection agents identify low-level calls whose return values aren’t properly verified. The action space includes analyzing error handling patterns, tracking return value propagation, and identifying critical operations that proceed without verification. For each low-level call $l_j$, the detection produces:

$$\begin{aligned} U(l_j) = {\left\{ \begin{array}{ll} 1 & \text {if return value not checked} \\ 0 & \text {otherwise} \end{array}\right. } \end{aligned}$$

(17)

Front-running detection

Front-running detection agents identify operations vulnerable to transaction ordering manipulation. The action space includes analyzing time-sensitive operations, identifying value calculations dependent on the state that could be front-run, and detecting missing commit-reveal patterns. For transaction-sensitive operations $t_k$:

$$\begin{aligned} F(t_k) = {\left\{ \begin{array}{ll} 1 & \text {if operation vulnerable to front-running} \\ 0 & \text {otherwise} \end{array}\right. } \end{aligned}$$

(18)

Denial of service detection

DoS detection agents identify patterns that could lead to resource exhaustion or execution blocking. The action space includes analyzing loop conditions, identifying gas-intensive operations, and detecting control flow dependencies that could be manipulated. For each potential DoS vector $d_m$:

$$\begin{aligned} D(d_m) = {\left\{ \begin{array}{ll} 1 & \text {if vector can cause denial of service} \\ 0 & \text {otherwise} \end{array}\right. } \end{aligned}$$

(19)

The final vulnerability assessment combines these individual detections to provide a comprehensive security analysis of the smart contract.

Reward processing and learning mechanism

The reward mechanism plays a crucial role in guiding our multi-agent framework toward effective vulnerability detection. We define rewards based on detection accuracy, with positive reinforcement for correctly identified vulnerabilities and penalties for false positives and false negatives.

Reward processing and learning mechanism

Our framework employs a reward processing mechanism to guide the multi-agent system toward effective vulnerability detection. For each vulnerability group k and agent i, reward $r_i$ in equation (14) quantifies detection performance by balancing true positives against false positives and negatives. These rewards directly inform the learning process through an Experience Replay Buffer D that stores interaction histories, as described in Eq. (13). The critic networks are trained by minimizing the loss function $L(\phi _k)$ shown in equation (13), which measures the temporal difference error between predicted and target Q-values. This approach enables our agents to learn from past experiences and generalize to new smart contract instances.

The reward signals play a crucial role in shaping the hierarchical attention mechanisms that form the core of our detection system. As agents receive rewards for successful detections, the attention weights $\alpha _{ij}^k$ and $\beta _i^k$ defined in Equations (8) and (10) adapt dynamically. The inter-agent attention weights $\alpha _{ij}^k$ gradually concentrate on code components that consistently contribute to accurate vulnerability identification, while the inter-group attention weights $\beta _i^k$ shift focus toward vulnerability types where the detection performance is strongest. This adaptive attention mechanism allows the system to efficiently allocate computational resources to the most promising aspects of code analysis.

The actor networks, which determine the detection actions, are updated using the deterministic policy gradient approach specified in Equation (14). This gradient-based optimization reinforces actions that yield higher expected rewards according to the critic’s evaluation. As training progresses, the agents develop increasingly sophisticated detection strategies that can identify subtle vulnerability patterns across different smart contract structures. The entire reward processing pipeline creates a positive feedback loop where successful detection behaviors are reinforced, allowing our framework to continuously improve its capability to identify complex vulnerability patterns while maintaining high detection accuracy across different smart contract architectures and programming patterns.

Experimental setup and performance evaluation

In this section, we conduct extensive experiments to evaluate the performance of our Graph Attention Network-Based Multi-Agent Reinforcement Learning approach for robust smart contract vulnerability detection (GANs-MARL). Our simulation aims to determine how effectively the GANs-MARL framework detects vulnerabilities through real-time node communications and monitors dynamic interactions within a blockchain network. Specifically, we address the following:

• 1. Dynamic Exploitation: How can the vulnerability detection module capture and exploit the dynamic interdependencies among blockchain entities to enhance vulnerability detection?

• 2. Context-Dependent Analysis: Can the proposed method dynamically analyze context-dependent vulnerabilities in smart contracts to improve early detection and mitigation?

These investigations comprehensively assess GANs-MARL’s capability in real-time vulnerability detection and response in blockchain environments.

Experimental setup

We evaluated our GANs-MARL framework using two smart contract datasets: the SB Curated Dataset, which contains 69 vulnerable contracts totaling 3,799 lines of code, and the SB Wild Dataset, which includes 47,518 contracts totaling approximately 9.7 million lines of code⁴⁰. We synthetically expanded these datasets; the SB Curated Dataset now comprises over 16,761 functions from 5,170 contracts, while the SB Wild Ethereum Dataset obtained from Etherscan includes over 437,696 functions from 50,332 contracts. This expansion involved pattern matching, static analysis, cross-referencing with vulnerability databases to identify relevant contracts, and blockchain scanning, deduplication, and filtering based on complexity, interaction, transaction behavior, and code uniqueness.

To further explain, the SB Curated Dataset was expanded by leveraging a combination of pattern-based vulnerability detection, static analysis tools (eg, Slither and SmartCheck), and cross-referencing with established vulnerability databases such as SmartBugs⁴¹, SolidiFI⁴², and DASP⁴³. To identify functions indicative of known exploit classes, we applied custom pattern-matching rules that targeted specific vulnerability signatures, including reentrancy call patterns, unchecked call value usage, and improper access modifiers. In parallel, the SB Wild dataset was filtered using a set of heuristics derived from contract interaction graphs, code complexity metrics, and transaction behavior. This process ensured that the extracted contract samples represented diverse and realistic deployment scenarios, improving the dataset’s quality and its alignment with real-world smart contract ecosystems.

In our extended datasets, vulnerabilities were classified into four categories using pattern matching, static analysis, database cross-referencing, blockchain scans, deduplication and intelligent filtering. For reentrancy, i.e., recursive calls and cyclic interactions, the curated dataset contains about 32 instances, and the wild dataset contains about 1,000. Unchecked low-level calls where external calls (e.g., call() and delegate call ()) create time-varying dependencies, comprising about 26 instances in the curated dataset and 900 in the wild dataset. Front-running, which results from the sequence of transactions and the mutual dependency within a block, comprises about 29 instances in the curated data set and almost 850 in the wild data set. Denial of service, characterized by computational overload and dynamic interaction propagation, comprises about 28 cases in the curated dataset and about 1,050 in the wild dataset.

Implementation details

All experiments were conducted on an Intel${\circledR }$ Xeon${\circledR }$ W-2255 CPU with 256GB RAM and 2 $\times$ GeForce RTX 3090 GPUs running Ubuntu 20.04. Our vulnerability detection system comprises three main components: Graph Generation, Node Embedding using a Graph Attention Network (GAT), and a Multi-Agent Actor-Critic Deep Q Network. All code is implemented in Python, with the deep learning modules built using the PyTorch framework.

Parameter settings

The GANs-MARL framework combines multi-agent actor-critic deep reinforcement learning with a GAT to analyze smart contract interactions⁴⁴. The architecture features a GAT module that transforms 128D vectors into 64D embeddings, which feed into dual networks: an actor for vulnerability detection and a critic for state value estimation. Both networks use two hidden layers (256/128 neurons). Optimization employs Adam (learning rate: $10^{-4}$, $\beta _1=0.9$, $\beta _2=0.999$) with key hyperparameters including a 0.99 discount factor, 128 batch size, and 1M replay buffer. Training uses 80% of data with epsilon-greedy exploration decreasing from 1.0 to 0.1⁴⁴.

Benchmarks

We compare GANs-MARL with several state-of-the-art smart contract vulnerability detection methods, encompassing both traditional analysis tools and machine learning approaches:

• Mythril⁴⁵: A symbolic execution and taint analysis tool that systematically explores execution paths to detect security flaws.

• Slither⁴⁶: A static analysis framework that constructs and inspects data/control flow graphs to uncover vulnerability patterns without executing the code.

• MythSlith⁴⁵: A hybrid solution combining Mythril’s dynamic techniques with Slither’s static analysis for more comprehensive detection.

• Graph Neural Network (GNN)⁴⁷: Processes contracts as graphs, iteratively propagating information between nodes to learn vulnerability patterns from structural and data-flow relationships.

• Graph Convolutional Network (GCN)⁴⁸: An extension of GNNs that applies convolutional operations on graph data, capturing local neighborhoods for semi-supervised tasks.

• Degree-Free Graph Convolutional Network (DR-GCN)⁴⁹: Improves on GCN by accommodating variable node degrees and multi-relational graphs, enhancing feature propagation in complex structures.

• Dual Attention Graph Neural Network (DA-GNN)⁵⁰: Transforms the control-flow graph into node-level features, then employs a dual attention mechanism within a graph attention network. The final embeddings are aggregated via self-attention to detect security vulnerabilities.

Table 1 Performance comparison of vulnerability detection methods across different vulnerability types.

Detection performance across multiple vulnerability categories

In this section, we compare our proposed GANs-MARL with 4 smart contract vulnerability detection tools (Smartcheck, Mythril, Slither, and MythSlith) and 4 neural network based methods (GNN, GCN, DR-GCN, and DA-GNN) under four critical vulnerability categories: Reentrancy, Unchecked Low Level Calls, Front Running, and Denial of Service. In this experiment, we evaluate the performance in terms of accuracy, recall, precision, and F1-score, which are widely adopted metrics in vulnerability detection tasks. Accuracy measures the overall correctness of detection, recall indicates the model’s ability to identify all existing vulnerabilities, precision reflects the reliability of positive predictions, and F1-score provides a balanced measure between precision and recall.

As shown in Table 1, our evaluation across four critical smart contract vulnerability types reveals that neural network-based methods consistently outperform conventional detection tools. For Reentrancy vulnerabilities, which represent one of the most sophisticated attack vectors in smart contracts, GANs-MARL achieves a remarkable accuracy of 93.8%, substantially surpassing traditional tools like Smartcheck (62.5%) and Mythril (75.3%). This significant performance gap demonstrates GANs-MARL’s enhanced capability in capturing complex patterns of recursive calls and state-dependent vulnerabilities. In detecting Unchecked Low-Level Calls, GANs-MARL maintains its superior performance with 91.6% accuracy, while conventional methods like Slither and MythSlith achieve only 76.1% and 79.8% accuracy, respectively, highlighting the advantages of our approach in analyzing cross-contract interactions. The results from Table 1 further indicate GANs-MARL’s robust performance in detecting Front Running vulnerabilities, achieving 88.9% accuracy compared to traditional tools that struggle to surpass 80%. For Denial of Service detection, GANs-MARL sets a new benchmark with 91.2%

Analysis of recall metrics in Table 1 reveals the superior capability of GANs-MARL in identifying actual vulnerabilities across all categories. For Reentrancy detection, GANs-MARL achieves a recall of 90.7%, significantly outperforming traditional tools like Smartcheck (58.3%) and Mythril (71.8%). This substantial improvement demonstrates GANs-MARL’s enhanced ability to capture complex vulnerability patterns that conventional static analysis often misses. In detecting Unchecked Low-Level Calls, GANs-MARL maintains its strong performance with 88.4% recall. At the same time, conventional tools like Smartcheck and Mythril achieve only 54.1% and 68.7%, respectively, indicating their limitation in identifying vulnerabilities within low-level contract interactions. The performance gap becomes even more pronounced for Front Running vulnerabilities, where GANs-MARL achieves 85.8% recall, substantially surpassing traditional methods like Slither (69.5%) and MythSlith (73.2%). Similarly, in Denial of Service detection, GANs-MARL sets a new benchmark with 88.1% recall, compared to conventional tools that struggle to exceed 70% recall rates.

Precision metrics in Table 1 demonstrate GANs-MARL’s superior ability to minimize false positives across all vulnerability types. For Reentrancy detection, GANs-MARL achieves 88.9% precision, substantially outperforming both traditional tools like Smartcheck (55.7%) and advanced approaches like DA-GNN (86.2%). In detecting Unchecked Low-Level Calls, GANs-MARL maintains high precision at 86.1%, significantly above conventional methods like Slither (69.1%) and Mythril (65.2%). Similar performance gaps are observed in Front Running and Denial of Service detection, where GANs-MARL achieves 83.2% and 85.4% precision respectively, demonstrating its robust capability to accurately identify legitimate vulnerabilities while minimizing false alerts. The F1-scores in Table 1 provide a balanced assessment of GANs-MARL’s overall detection capability. For Reentrancy, GANs-MARL achieves an F1-score of 89.8%, significantly surpassing both traditional tools (Smartcheck: 57.0%, Mythril: 70.3%) and other neural network approaches. This superior performance extends to Unchecked Low-Level Calls (87.2% F1-score), Front Running (84.5%), and Denial of Service (86.7%), consistently demonstrating GANs-MARL’s balanced approach in vulnerability detection.

Fig. 2

Convergence performance.

Convergence performance for neural network detection approaches

Figure 2a illustrates the progression of mean reward over iterations for different vulnerability detection models in smart contracts. The trends indicate how well each model optimizes its performance as learning progresses. Among the models, GANs-MARL exhibits a unique trajectory, where its hierarchical structure initially limits its performance, resulting in a slower reward accumulation in the early stages. This is likely due to the multi-level learning approach, where different layers must coordinate effectively before achieving optimal results. However, once the model fully adapts to the vulnerability patterns, GANs-MARL outperforms all other models in the later iterations, demonstrating its superior learning capability and adaptability.

DR-GCN shows the fastest initial improvement, achieving high mean rewards early in the training process. This suggests that decentralized graph convolutional networks can effectively learn from contract vulnerabilities in a structured way, quickly optimizing decision-making. However, its performance stabilizes and fluctuates in later iterations, indicating possible limitations in long-term learning efficiency or generalization. On the other hand, DA-GNNs and GCNs exhibit moderate performance growth, with steady improvements but without surpassing GANs-MARL in the final stages. This suggests that while graph-based models can efficiently extract vulnerability structures, they lack the adaptive learning capability of reinforcement-learning-driven models. Overall, GANs-MARL achieves the highest final mean reward, reinforcing the effectiveness of hierarchical learning combined with reinforcement optimization. Although its performance was initially constrained by complex learning dependencies, its ability to refine strategies over time allows it to surpass other models in the long run. This highlights the advantage of hierarchical reinforcement learning in smart contract vulnerability detection, where early-stage inefficiencies are compensated by enhanced long-term performance and adaptability.

Figure 2b also shows the performance in terms of loss reduction across different models over training iterations. The loss function represents the error between predicted vulnerability classifications and actual vulnerabilities in smart contracts. As seen in the figure, all models experience a sharp decline in loss in the initial training phases, indicating rapid learning and adaptation. However, GANs-MARL achieves the lowest final loss, demonstrating its superior ability to generalize and optimize during training. Initially, GNNs and GCNs exhibit relatively high loss values, suggesting that their structural learning approaches require more training to converge. Although GNNs show an early decline, they eventually stabilize at a higher loss value compared to GANs-MARL and DR-GCN. DA-GNNs and DR-GCNs demonstrate faster convergence than GNNs and GCNs, showing strong adaptability in smart contract vulnerability detection. The GANs-MARL model, despite starting with a higher loss due to its hierarchical complexity, achieves the most stable and lowest loss across iterations, indicating improved optimization and feature extraction. A key observation is the final stabilization of loss values. GANs-MARL and DR-GCN achieve the lowest final loss, suggesting they have effectively minimized misclassification errors. On the other hand, GNNs and GCNs settle at relatively higher loss values, reinforcing their limitations in vulnerability detection compared to reinforcement-learning-based methods. This confirms that models integrating hierarchical learning (GANs-MARL) and decentralized decision-making (DR-GCN) yield more precise and reliable vulnerability detection in smart contracts, as they consistently maintain lower loss values across extended training iterations.

Fig. 3

Training convergence under different reward configurations, showing average episode reward progression over 2000 episodes. Precision-focused rewards suppress false positives while recall-focused rewards encourage detection of rare vulnerabilities.

Table 2 Effect of reward weight configurations on detection performance.

Reward sensitivity analysis

We conducted a reward weight sensitivity study by varying the reward weights ($w_{TP}$, $w_{FP}$, $w_{FN}$) across three configurations:

• Balanced: $w_{TP}$ = 1.0, $w_{FP}$ = 1.0, $w_{FN}$ = 1.0

• Precision-Focused: $w_{TP}$ = 1.0, $w_{FP}$ = 1.5, $w_{FN}$ = 1.0

• Recall-Focused: $w_{TP}$ = 1.0, $w_{FP}$ = 0.5, $w_{FN}$ = 1.5

The results, shown in Fig. 3 and Table 2 of the revised manuscript, indicate that:

• The precision-focused configuration improved the F1-score by  2% in low-FP scenarios.

• The recall-focused setting enhanced vulnerability recall by  4%.

Analyzing the convergence using the mean episode reward and loss trajectory across 2,000 iterations. The recall-focused setting led to slower early convergence but better final performance, while the balanced reward configuration yielded faster convergence with robust but slightly less specialized detection results, as shown in Fig. 3.

Fig. 4

ROC curves comparing the performance of different graph neural network architectures (GNNs, GCNs, DA-GNNs, DR-GCN, and GANs-MARL) across four smart contract vulnerability detection tasks.

Fig. 5

Time to detect vs. false positive rate for smart contract vulnerability detection tasks per Vulnerability Type.

ROC performance for vulnerability detection

In this section, we analyze the Receiver Operating Characteristic (ROC) curves to evaluate the performance of different models in detecting various types of software vulnerabilities. Using the ROC curve, we can determine the trade-off between the true positive rate (TPR) and the false positive rate (FPR) and gain insight into the effectiveness of each model in distinguishing between vulnerable and non-vulnerable instances. Using the ROC curves, we can assess which models achieve high detection accuracy with minimal false positives, ultimately identifying the most robust approaches for detecting vulnerabilities. Figure 4a shows that for reentrancy detection, GANs-MARL quickly reaches a high TPR with a low FPR, outperforming DR-GCN, while traditional GNNs lag. DA-GNNs and GCNs perform moderately, with DA-GNNs leading. In Fig. 4b, all models improve on front-running detection. It is noteworthy that GANs-MARL once more exhibits superior performance, attaining a near-perfect true positive rate (TPR) over 0.9 alongside minimal false positive rates. This is followed by DR-GCN, with DA-GNNs demonstrating a marked improvement over GCNs. In the context of DoS detection, as illustrated in Fig. 4c, both GANs-MARL and DR-GCN achieve TPR values exceeding 0.9 and false positive rates (FPR) below 0.2, with DA-GNNs effectively narrowing the performance disparity.

Nevertheless, GNNs and GCNs exhibit limitations, particularly in addressing the intricate decision boundaries required for effective DoS detection. In the context of Unchecked Low-Level vulnerability detection, as depicted in Fig. 4d, the disparity in performance is negligible, indicating that this particular vulnerability is more readily identifiable. While GANs-MARL remains the preeminent approach, its advantage diminishes, given that all models attain a high TPR (> 0.8) with an FPR of 0.2. Traditional GNNs perform optimally compared to historical benchmarks, yet they remain the least efficacious in a comparative analysis. The ROC analysis delineates a distinct hierarchy: GANs-MARL leads, followed by DR-GCN, with DA-GNNs being moderately effective, whereas GCNs and traditional GNNs are notably less effective, particularly for complex vulnerabilities such as reentrancy and front running.

Detection speed analysis (time-to-detection per vulnerability type)

This experiment evaluates model speed in identifying vulnerabilities, balancing precision and recall, as shown in Fig. 5. Detection time is plotted against the FPR, revealing that increased FPR reduces detection time. At an FPR of 0.05, GNNs require about 80 time units, whereas GANs-MARL need only 10 units, showing their efficiency. Allowing a slight increase in false positives leads to faster detection. GANs-MARL consistently demonstrates the quickest detection across scenarios, followed by DR-GCN, excelling in early detection, particularly in Reentrancy and Front Running, detecting vulnerabilities under 5-time units at an FPR above 0.2. This highlights the benefits of hierarchical reinforcement learning and adversarial training in speeding up detection while maintaining high precision. In Fig. 5a, GANs-MARL show the fastest detection times for Reentrancy vulnerabilities across all FPRs, detecting them in 5-time units at an FPR of 0.1, compared to 8-time units for DR-GCN. DA-GNNs, GCNs, and GNNs are much slower, with GNNs taking up to 50 time units. Similar results occur in Front Running detection (Fig. 5b), where GANs-MARL and DR-GCN maintain low FPR and quick detection. At an FPR of 0.15, DR-GCN detects vulnerabilities in 7-time units, while DA-GNNs need about 15, and GNNs over 40-time units. This indicates that GANs-MARL and DR-GCN are optimized for fast vulnerability patterns.

In Fig. 5c, the DoS detection experiment shows a clustered performance among top models, with GANs-MARL and DR-GCN leading. DA-GNNs narrow the gap, detecting vulnerabilities in 18-time units at an FPR of 0.1, compared to 6-time units for GANs-MARL and 10 for DR-GCN. In contrast, GCNs and GNNs take over 40-time units, rendering them less effective for real-time applications. For Unchecked Low-Level vulnerability detection shown in Fig. 5d, the performance gap is smaller, indicating easier detectability. Although GANs-MARL remains the most efficient–detecting vulnerabilities in 4-time units at an FPR of 0.2–the differences among models are less pronounced, with DR-GCN at 6-time units, DA-GNNs at 12, and GNNs at up to 25-time units. ‘The link between detection speed and FPR shows that GANs-MARL and DR-GCN offer quick and accurate detection, suitable for real-time security. Meanwhile, traditional GCNs and GNNs detect more slowly, especially with complex vulnerabilities such as reentrancy, highlighting the advantages of using GANs-MARL, where the graph module enables the efficient extraction of intricate dependency patterns and the MARL allows each agent to dynamically optimize detection strategies based on evolving threat scenarios.

Fig. 6

Detection performance with varying window sizes and detection-reward trade-offs.

Detection latency performance analysis

In this section, we analyze the detection time for various models in identifying smart contract vulnerabilities, as shown in Fig. 6a. The graph plots detection time versus window size, highlighting performance differences. GANs-MARL uses a hierarchical approach to decompose complex decisions, improving scalability and generalization. Graph Attention Networks (GATs) enhance this by prioritizing key interactions, while reinforcement learning continuously refines detection based on past behaviors. Consequently, GANs-MARL exhibits the lowest detection times, outperforming traditional GNNs and centralized GCN-based models. At a window size of 30, GANs-MARL achieves a detection time of approximately 0.2, compared to 10.05 for DR-GCN, 20.11 to 25 steps for DA-GNNs and GCNs, and 46.26 to 53.73 steps for traditional GNNs. The effectiveness of GANs-MARL can be attributed to its multi-agent architecture, which facilitates parallel processing of contract interactions, while its attention mechanism effectively filters out irrelevant information. Conversely, traditional models are required to process the entire contract graph sequentially, resulting in computational bottlenecks with increasing window sizes. Moreover, the experience replay mechanism in GANs-MARL enables the utilization of previously acquired patterns, thereby substantially diminishing redundant computations when examining similar vulnerability structures across various contracts.

Figure 6b shows the tradeoff between “normalized reward” and detection rate for vulnerability detection using hierarchical reinforcement learning with graph attention networks (GANs-MARL). The graph reveals that combining hierarchical attention with reinforcement learning forms a more robust and adaptable detection system compared to traditional methods. GANs-MARL excels by analyzing smart contracts at various levels, from individual operations to overarching vulnerabilities. Traditional GNNs, with their centralized processing, cannot effectively optimize reward signals across levels, leading to rapid performance degradation and a drop to 0.1 reward at a 2.0 detection rate due to their monolithic structure. GANs-MARL successfully integrates local and global contract features through hierarchical attention, dynamically adjusting detection strategies based on past performance. This enhances detection accuracy and surpasses the limitations of centralized GNNs, especially in identifying complex or novel vulnerabilities requiring an understanding of both local and global contract aspects.

Table 3 Ablation study of GANs-MARL model variations across different vulnerability types.

Ablation study

Table 3 presents an ablation study of our GANs-MARL architecture over different vulnerability types. The complete model consistently achieves better performance in all categories and metrics. For reentrancy detection, the most complex type of vulnerability, our complete model achieves an accuracy of 93.8% and F1 score of 89.8%, with performance gradually decreasing as key components are removed. The sharpest drop in performance occurs when the reinforcement learning component is removed, resulting in an 8.1% drop in accuracy for reentrancy detection. Front running detection shows similar trends, with the full model achieving 88.9% accuracy and performance dropping to 80.4% without reinforcement learning. DoS and Unchecked Low-Level vulnerabilities continue to exhibit robust performance within the comprehensive model, achieving 91.2% and 91.6% accuracy, respectively. The performance demonstrates the model’s resilience to several vulnerabilities. Each component of the proposed architecture significantly increases the efficiency of the model, and their integration leads to superior results. The Graph Attention Network selectively prioritizes critical interactions by filtering out noise and highlighting important structural patterns, while the Reinforcement Learning Agent dynamically adjusts the detection strategy based on evolving threat scenarios.

Table 4 Model performance on obfuscated and perturbed smart contracts.

Robustness to obfuscation and code perturbations

To assess GANS-MARL’s resilience against real-world obfuscation tactics, we constructed an adversarial contract evaluation set using the following transformations:

• Minification: Removal of all comments and whitespaces.

• Block Reordering: Reordering of non-dependent code blocks (eg, function declarations).

• Variable Renaming and Literal Shuffling: Using semantic-preserving transformations.

This test set includes 320 obfuscated contracts from EtherScan (https://etherscan.io/) covering Unchecked Low Level Calls vulnerability types.

Results: As shown in Table 4, the model retains strong accuracy and F1-score, only marginally lower than on the canonical SB Wild dataset. This suggests that GANS-MARL effectively captures semantic and relational structure rather than superficial syntax.

False-positive analysis and case examples

We reviewed predictions on 150 manually validated clean contracts (verified on Etherscan) to quantify and explain false positives.

False Positive Rate: 6.8% overall, primarily in complex multi-contract systems.

Common Patterns:

• Contracts using custom proxy patterns or inline assembly triggered false alarms due to novel execution traces.

• Mislabeling occurred when internal function invocations mimicked known vulnerability paths.

We included two anonymous case studies below detailing why GANS-MARL flagged these benign contracts and proposed model adjustments (eg, integrating proxy detection heuristics).

Case 1—Proxy Contract Misclassification: The model flagged a verified upgradable proxy contract that included fallback functions and delegate calls. While safe by design, its structure mimicked known reentrancy attack patterns. The model over-relied on control flow similarity between benign and malicious contracts. Future improvements will integrate proxy-aware logic to reduce such confusion.

Case 2—Inline Assembly Confusion: The contract used inline assembly for gas optimization and low-level call management. These patterns activated the model’s path attention mechanism due to their syntactic overlap with low-level exploit routines. We hypothesize that this confusion arose from sparse training samples featuring safe inline assembly. Augmenting the training set with verified assembly-based contracts is planned as future work.

Overall, these false positives illustrate that while GANS-MARL generalizes well, some semantic-rich patterns still challenge its interpretability.

Table 5 Impact of training under imbalanced class distribution (1:5 ratio).

Impact of class imbalance

We conducted an imbalanced setting test by training on downsampled vulnerability subsets (ratio 1:5, vulnerable : clean ). The model was then evaluated on the full SB Wild dataset.

Findings (see Table 5):

• F1-score dropped, mainly due to reduced recall.

• Precision remained above, showing the model’s robustness to class skew.

Cross-validation performance analysis

To address the issue of overfitting, we conducted 5-fold cross-validation on the complete dataset. The performance metrics for both training and validation, specifically accuracy and F1 score, are presented comprehensively in Table 6 across all folds.

From Table 6 the key observations include:

• Small generalization gap: Mean training-validation accuracy difference is only 0.6%

• Low variance across folds: Standard deviation $< 0.3\%$ for all metrics

• Consistent F1-score performance: Training and validation F1-scores differ by only 0.3%

Table 6 5-Fold cross-validation results for GANs-MARL.

Generalization gap analysis across vulnerability types

The data presented in Table 7 indicates only minimal overfitting across the different vulnerability categories. The consistently low generalization gaps, remaining under 1% for all vulnerability types, imply robust generalization capabilities rather than a susceptibility to overfitting on specific patterns.

Table 7 Generalization gap analysis across vulnerability types.

Conclusion

In this paper, we presented the GANS-MARL framework, a novel hierarchical reinforcement learning approach for smart contract vulnerability detection. Our model integrates high-level strategic policies with low-level execution tactics to capture long-term dependencies and immediate action requirements in complex contract interactions. The framework’s key innovation lies in its two-tier policy structure. The high-level policy analyzes the historical context to establish strategic sub-goals, while the low-level policy efficiently executes targeted actions within contextually relevant clusters. This architecture reduces decision-making complexity and enhances interpretability, making GANS-MARL particularly valuable for real-world blockchain applications where transparency is crucial. GANS-MARL effectively detects complex vulnerabilities like reentrancy and front-running, overcoming challenges of contextual dependencies faced by traditional methods. Its multi-agent architecture and efficient attention mechanism enable faster detection than conventional GNN approaches. Future research will focus on improving adaptability with real-time feedback, expanding blockchain compatibility, and using adversarial training for robustness. GANS-MARL lays a groundwork for hierarchical reinforcement learning in decentralized environments, enhancing smart contract security systems.