Monitoring and investigation to control the brain network disease under immunotherapy by using fractional operator

Abstract

Parkinson’s disease (PD) is one of the well-known neurodegenerative diseases. The main reason is the death of dopaminergic neurons that release dopamine in the brain region known as the Substantia Nigra pars Compacta (SNc). In this study, we developed a mathematical model of Parkinson’s disease incorporating a fractal-fractional operator with the Mittag–Leffler kernel to capture the complex, memory-dependent dynamics of the disease. We conduct a qualitative analysis to explore the existence and uniqueness of solutions and examine both disease-free and endemic equilibrium states. Stability conditions are explored using fixed-point theory and Lyapunov functions, while the dynamics are further analyzed through sensitivity analysis to identify the parameters most influential to the basic reproduction number. Additionally, chaos control is investigated using PID feedback strategies, and a Newton polynomial-based numerical method is implemented to simulate the system’s behavior. This approach enhances our understanding of Parkinson’s disease progression and offers a foundation for developing personalized therapeutic strategies.

Introduction

Parkinson’s disease (PD) is recognized as a prominent neurodegenerative disorder and mental health. The main reason involves the degeneration of dopaminergic neurons that are responsible for the secretion of dopamine in the brain region identified as the Substantia Nigra pars Compacta (SNc). Furthermore, the presence of Lewy bodies, which are aggregates of misfolded alpha-synuclein ($\alpha$-syn) protein, has been observed in the post-mortem examinations of individuals diagnosed with Parkinson’s disease^1,2. The demise of neurons ensues when the $\alpha$-syn protein accumulates within a neuron, thereby obstructing the cellular autophagic processes^3,4. As a result, the protein is released into the extracellular milieu, contributing to additional neuronal degeneration^5,6. As a prion-like protein, the pathogenic $\alpha$-syn spreads from cell to cell^7,8 and causes toxicity in recipient cells^9,10. The body is protected from foreign antigens by the immune system. The central nervous system (CNS) contains innate immune cells called microglia, which continuously monitor the environment around the brain^11,12 and respond to viruses immediately and non-selectively^13,14. Anti-inflammatory cytokines are released when microglia are activated, protecting and warning nearby cells¹⁵. Additionally, they take quick action to absorb and eliminate misfolded $\alpha$-syn^16,17 to stop neurodegeneration. But when inflammation is severe, active microglia might not be controlled, harming healthy neurons¹⁵.

In order to comprehend the dynamics of neurodegenerative disorders, mathematical models were used^18,19. Puri and Li²⁰, developed a model to investigate the interactions of amyloid-$\beta$, neurons, microglia, and astrocytes in Alzheimer’s disease. They discovered that activated microglia are important in the development of neuropathy. Hao and Friedman described the interactions between neurons, microglia, astrocytes, amyloid-$\beta$ aggregation, macrophages, and hyperphosphorylated tau proteins using nonlinear partial differential equations in²¹. To halt the disease’s course, they proposed a treatment strategy. A model explaining the accumulation of $\alpha$-syn within a neuron cell was proposed in²² for PD models. They determined that a lack of effective degradation mechanisms is the main reason for the accumulation of $\alpha$-syn. Furthermore, as demonstrated in²³, they employed two models, diffusive and active $\alpha$-syn transmission, in both healthy and diseased axons. They observed that damaged axons exhibit $\alpha$-syn clumping in Lewy bodies. In²⁴, a model was constructed to explain the connection between $\alpha$-syn aggregation and proteasome activity. They found that $\alpha$-syn aggregation is blocked when the proteasome to $\alpha$-syn ratio falls below a critical threshold. The study²⁵ employs Hybrid NAR-RBFs networks integrated with fractional operators to analyze the dynamics of a complex non-linear COVID-19 model, enhancing predictive accuracy and system understanding. In²⁶ explores computational techniques for monitoring a fractional-order type-1 diabetes mellitus model, aiming to optimize feedback design for artificial pancreas systems. The importance of using generalized fractal fractional operators to understand the complex dynamics of Chlamydia infection and vaccination strategies²⁷, offering insights for effective disease control. The fractal-fractional model effectively captures the complex dynamics of tuberculosis prevalence²⁸, demonstrating how sensitivity and stability analyses, combined with simulations under feasible scenarios, can guide optimized control strategies. A comprehensive understanding of disease dynamics across different infection stages²⁹, offering deeper insights into transmission patterns and potential control measures. The piecewise hybrid fractional operator enhances the computational and stability analysis of the Ebola virus epidemic model³⁰, accurately capturing the disease’s complex transmission dynamics and aiding in the design of effective control strategies. The use of fractional-order mathematical models to describe tumor dynamics under chemotherapy³¹. A reaction-diffusion model for Hepatitis B using real data from Thailand³² confirms stability, estimates $R_0$, and evaluates vaccination and hospitalization impacts. A convex incidence model³⁴ and a fractional-order norovirus model with vaccination and asymptomatic carriers³³ further validate equilibrium stability and highlight key outbreak drivers through sensitivity analysis. For Ebola, the integration of vaccination within a Caputo–Fabrizio framework³⁵ and a co-infection model with malaria³⁶ both emphasize memory effects and targeted interventions. A dual-dosage vaccination model for Lassa fever³⁷ and a fractional-order formulation using the Laplace-Adomian Decomposition Method³⁸ enhance understanding of disease control. Similarly, fractional models address malaria with combined enlightenment and therapy strategies³⁹, measles with strategic vaccination⁴⁰, and computer virus spread⁴¹, highlighting the role of memory-based interventions. Within-host Chikungunya dynamics⁴² are also explored, revealing the impact of immune response on viral load and progression. In⁴³ incorporates both singular and non-singular kernels to represent memory effects and the disease dynamics more accurately. The study emphasizes the impact of fractional parameters on disease progression, providing insights into control measures and the role of fractional operators in capturing real-world epidemiological trends. Recent research highlights the effectiveness of fractional and numerical modeling in understanding COVID-19 dynamics. It has been shown⁴⁴ that a more transmissible SARS-CoV-2 variant will eventually outcompete less transmissible strains, and complete eradication is only possible when both variants have basic reproduction numbers below one. In a related work⁴⁵, a fractional-order model using the Haar wavelet collocation method was employed to simulate the spread of Omicron in Pakistan, confirming model stability and identifying key parameters through sensitivity analysis. Similarly,⁴⁶ applied finite difference and meshless methods to solve a COVID-19 model, yielding accurate estimates of the reproduction number and validating the model s stability. Additionally, a non-integer time fractional model developed in⁴⁷ captures the long-term societal and economic impacts of the pandemic in Nigeria, emphasizing the value of fractional dynamics in representing persistent effects and some key factors related neural network for nonlinear system are also studied in^48,49.

The study⁵¹ offers key insights into neurodegenerative disease dynamics, but most rely on classical models that overlook memory effects. In contrast, our fractal-fractional model incorporates both innate and adaptive immunity, capturing long-term biological feedback. This approach enhances realism, enables threshold analysis for disease control, and improves understanding of Parkinson s disease progression. The specific novelty of this model lies in its incorporation of a fractal-fractional operator with the Mittag–Leffler kernel, which captures the memory-dependent and complex dynamics of Parkinson’s disease more accurately than traditional integer-order models. Unlike previous models, it integrates both innate and adaptive immune responses under immunotherapy, providing a comprehensive framework to study the interplay between neurons, extracellular $\alpha$-syn, and immune cells. Additionally, the model employs advanced stability analysis and chaos control techniques, such as Lyapunov functions and PID controllers, to explore disease progression and therapeutic strategies. This approach offers a more nuanced understanding of PD pathophysiology and potential personalized treatment options. The fractal-fractional operator with a Mittag–Leffler kernel is employed to capture the memory and hereditary properties inherent in neurodegenerative processes like Parkinson’s disease. Biologically, it reflects the long-term interactions between neuronal damage and immune responses. Mathematically, the Mittag–Leffler kernel offers a more accurate representation of non-local dynamics and anomalous diffusion compared to classical exponential kernels, enhancing the model’s realism and analytical depth. One of the main challenges in this study lies in accurately capturing the complex, memory-dependent interactions between neuronal degeneration and immune responses. Additionally, implementing and solving the fractal-fractional model with Mittag–Leffler kernels requires advanced numerical techniques, posing both analytical and computational difficulties. The primary objective of this study is to develop a mathematically tractable model that captures the memory-dependent and nonlinear dynamics of Parkinson s disease by incorporating both neuronal degeneration and immune responses under immunotherapy. Specifically, the research seeks to address the following questions: (i) How do interactions between neurons, a-synuclein, and immune cells influence disease progression? (ii) Can fractional-order operators with Mittag–Leffler kernels better represent the long-term memory effects observed in neurodegenerative processes? (iii) What are the stability conditions and control strategies that can inform effective therapeutic interventions?

The research presents a unique model combining fractals, fractional calculations, and the Mittag–Leffler kernel for analyzing Parkinson’s disease. The structure includes: In “Introduction”, an overview of the study goals. “Preliminaries”, definitions of the operator used. “Model formulation” introduces a mathematical model for studying Parkinson’s disease. An in-depth examination of the proposed model is discussed in “Existence and uniqueness”. Stability analysis using the Lyapunov function is explained in “Stability analysis”. Chaos Control is explored in “Chaos control”. Numerical findings and results and discussion are in “Numerical scheme” and “Results of proposed scheme”. Summarizes findings in section “Conclusion”.

Preliminaries

In this section, we present several essential definitions that can significantly simplify the process of system analysis. Understanding these key concepts will help in grasping the complexities of the system.

Definition 2.1

⁵⁰ According to the Atangana-Baleanu approach, which uses a generalized Mittag–Leffler type kernel, the fractal-fractional derivative of a function $\mathfrak {U}$ belonging to $\textbf{C}((a, b), \textbf{R})$ can be formulated as follows: it is fractally differentiable on the interval (a, b) with a fractal dimension $0 < \vartheta \le 1$ and a fractional order $0 < \varpi \le 1$.

$$_{0}^{{{\mathcal{F}\mathcal{F}\mathcal{M}}}} {\mathbb{D}}_{t}^{{\varpi ,\vartheta }} {\mathfrak{U}}(t) = \frac{{{\mathbb{A}\mathbb{B}}(\varpi )}}{{(1 - \varpi )}}\frac{d}{{dt^{\vartheta } }}\int_{0}^{t} {\mathfrak{U}} (\chi ){\mathcal{W}}_{\varpi } \left[ { - \frac{\varpi }{{1 - \varpi }}(t - \chi )^{\varpi } } \right]d\chi ,{\text{ }}$$

(1)

where $\mathbb{A}\mathbb{B}(\varpi )=1-\varpi +\frac{\varpi }{\Gamma (\varpi )}$.

Definition 2.2

⁵⁰ As previously indicated, the Atangana–Baleanu technique, using a Mittag–Leffler type kernel, may calculate the fractal-fractional integral of the function $\mathfrak {U}$ with a fractional order $0 < \varpi \le 1$.

$$_{0}^{{{\mathcal{F}\mathcal{F}\mathcal{M}}}} {\mathbf{I}}^{{\varpi ,\vartheta }} {\mathfrak{U}}(t) = \frac{{\vartheta (1 - \varpi )t^{{\vartheta - 1}} {\mathfrak{U}}(t)}}{{{\mathbb{A}\mathbb{B}}(\varpi )}} + \frac{{\varpi \vartheta }}{{{\mathbb{A}\mathbb{B}}(\varpi )\Gamma (\varpi )}}\int_{0}^{t} {(t - \chi )^{{\varpi - 1}} } \chi ^{{\vartheta - 1}} {\mathcal{F}}(\chi )d\chi .{\text{ }}$$

(2)

Model formulation

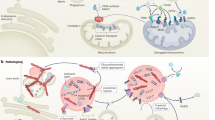
The dynamics of the interaction between neurons, extracellular $\alpha$-syn, and innate and adaptive immune cells are described in⁵¹. The proposed model comprises five distinct compartments: the density of functionally intact neurons, denoted as N(t); the density of neurons infected in the brain, I(t); the density of extracellular $\alpha$-syn, indicated as $\alpha S(t)$; the density of activated microglia, referred to as M(t); and the density of activated T cells, T(t). The model is based on biologically informed assumptions that simplify the complex neuroimmune dynamics of Parkinson’s disease to enable tractable mathematical analysis. These include constant recruitment and decay rates for neurons and immune cells, and homogeneous mixing of compartments. While these assumptions facilitate analytical and numerical treatment, they can be relaxed in future work by incorporating time-dependent or spatially heterogeneous parameters. The parameter values were selected based on existing literature⁵¹ and calibrated to reflect biologically plausible behavior under both disease-free and endemic scenarios. Neurons and $\alpha$-syn capture disease spread, while microglia and T-cells reflect the innate and adaptive immune responses. The interaction terms model activation, apoptosis, and immune regulation based on established neuroinflammatory mechanisms in PD. The schematic diagram of model show in Fig. 1 the interaction terms $\beta N \alpha S$ for neuron infection, $ed_1I$ for $\alpha$-syn release, and $a_1 I$ + a$\alpha$ S for microglial activation reflect experimentally observed mechanisms, such as $\alpha$-syn propagation, neuroinflammation, and immune clearance. These terms align with prior biological studies⁵¹ and ensure the model captures critical PD dynamics, including neuronal loss and immune response modulation. Parameters value display in Table 1. The two cases in Table 1 represent distinct disease dynamics: $R_0 < 1$ corresponds to a controlled or eradicated state, while $R_0 > 1$ indicates disease persistence. These parameter sets were used in simulations to illustrate the model’s behavior under varying transmission intensities, enabling comparative analysis of stability and progression outcomes. The fractal-fractional operator as conceptualized within the Atangana-Baleanu framework, which is introduced in the current study, serves as an effective instrument for comprehending the dynamics of epidemics and the transmission of diseases, in addition to facilitating the modeling of complex systems and phenomena.

This set of non-linear fractal-fractional differential equations represents the updated fractional model, concerning the Atangana–Baleanu approach for values of $0 < \varpi ,\vartheta \le 1$.

$$\begin{aligned} \left\{ \begin{array}{l}{}^{FFM}D_{0,t}^{\varpi ,\vartheta }N\left( t \right) = \sigma - \beta N\alpha S - {a_1}N - {a_2}N - {\mu _1}N,\\ {}^{FFM}D_{0,t}^{\varpi ,\vartheta }I\left( t \right) = \beta N\alpha S - {d_1}I - {a_1}I - {a_2}I,\\ {}^{FFM}D_{0,t}^{\varpi ,\vartheta }\alpha S\left( t \right) = e{d_1}I - {a_1}\alpha S - {a_2}\alpha S,\\ {}^{FFM}D_{0,t}^{\varpi ,\vartheta }M\left( t \right) = {a_1}I + {a_1}\alpha S - {\mu _2}M,\\ {}^{FFM}D_{0,t}^{\varpi ,\vartheta }T\left( t \right) = {a_1}I + \left( {{a_1} + {a_2}} \right) \alpha S - {\mu _3}T,\end{array} \right. \end{aligned}$$

(3)

with the initial conditions

$$\begin{aligned} N(0)\ge 0 \, \ \ \ I(0)\ge 0 \, \ \ \ \alpha S(0)\ge 0, \ \ \ M(0)\ge 0, \ \ \ T(0)\ge 0. \end{aligned}$$

Fig. 1

Schematic diagram of Parkinson’s disease model.

Table 1 Description of model parameters and their corresponding values.

Positive bounded solutions

Given that the operations delineated in the suggested model are constrained and exhibit positive outcomes with a degree of certainty, we examine the specific conditions under which its application may be relevant to significant real-world situations. Regarding derivatives, for every $\forall t \ge 0$, we have the following:

$$\begin{aligned} \begin{array}{l}I\left( t \right) \ge I\left( 0 \right) {e^{ - \left( {{d_1} + {a_1} + {a_2}} \right) t}},\\ \alpha S\left( t \right) \ge \alpha S\left( 0 \right) {e^{ - \left( {{a_1} + {a_2}} \right) t}},\\ M\left( t \right) \ge M\left( 0 \right) {e^{ - \left( {{\mu _2}} \right) t}},\\ T\left( t \right) \ge T\left( 0 \right) {e^{ - \left( {{\mu _3}} \right) t}}.\end{array} \end{aligned}$$

To find out the norm, we need to: ${\left\| \mathfrak {V} \right\| _\infty } = {\sup _{t \in {D_\mathfrak {V}}}}\left| {\mathfrak {V}\left( t \right) } \right| .$ Next, we find

$$\begin{aligned} \begin{aligned}^{FFM}D_{0,t}^{\varpi ,\vartheta }N\left( t \right)&= \sigma - \left( {\beta \alpha S\left( t \right) + {a_1} + {a_2} + {\mu _1}} \right) N\left( t \right) \\ &\ge - \left( {\beta \alpha S\left( t \right) + {a_1} + {a_2} + {\mu _1}} \right) N\left( t \right) \\ &\ge - \left( {\beta \left| {\alpha S\left( t \right) } \right| + {a_1} + {a_2} + {\mu _1}} \right) N\left( t \right) \\ &\ge -\left( {\beta {\sup }_{t \in \alpha S} \left| {\alpha S\left( t \right) } \right| + {a_1} + {a_2} + {\mu _1}} \right) N\left( t \right) \\ &\ge - \left( {\beta {{\left| {\alpha S\left( t \right) } \right| }_\infty } + {a_1} + {a_2} + {\mu _1}} \right) N\left( t \right) ,\end{aligned} \end{aligned}$$

(4)

then

$$\begin{aligned} N\left( t \right) \ge N\left( 0 \right) {e^-{\left( {\beta {{\left| {\alpha S\left( t \right) } \right| }_\infty } + {a_1} + {a_2} + {\mu _1}} \right) t}},{\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} {\hspace{0.55542pt}} \forall t \ge 0. \end{aligned}$$

According to⁵², system (3) solutions are always positive $\forall t \ge 0$.

$$\begin{aligned} \left\{ {\begin{array}{l}{N\left( t \right) \ge N\left( 0 \right) {E_\varpi }\left[ { - \frac{{{\wp ^{1 - \vartheta }}\varpi \left( {\beta {{\left| {\alpha S\left( t \right) } \right| }_\infty } + {a_1} + {a_2} + {\mu _1}} \right) {t^\varpi }}}{{AB\left( \varpi \right) - \left( {1 - \varpi } \right) \left( {\beta {{\left| {\alpha S\left( t \right) } \right| }_\infty } + {a_1} + {a_2} + {\mu _1}} \right) }}} \right] ,}\\ {I\left( t \right) \ge I\left( 0 \right) {E_\varpi }\left[ { - \frac{{{\wp ^{1 - \vartheta }}\varpi \left( {{d_1} + {a_1} + {a_2}} \right) {t^\varpi }}}{{AB\left( \varpi \right) - \left( {1 - \varpi } \right) \left( {{d_1} + {a_1} + {a_2}} \right) }}} \right] ,}\\ \begin{array}{l}\alpha S\left( t \right) \ge \alpha S\left( 0 \right) {E_\varpi }\left[ { - \frac{{{\wp ^{1 - \vartheta }}\varpi \left( {{a_1} + {a_2}} \right) {t^\varpi }}}{{AB\left( \varpi \right) - \left( {1 - \varpi } \right) \left( {{a_1} + {a_2}} \right) }}} \right] ,\\ M\left( t \right) \ge M\left( 0 \right) {E_\varpi }\left[ { - \frac{{{\wp ^{1 - \vartheta }}\varpi \left( {{\mu _2}} \right) {t^\varpi }}}{{AB\left( \varpi \right) - \left( {1 - \varpi } \right) \left( {{\mu _2}} \right) }}} \right] ,\\ T\left( t \right) \ge T\left( 0 \right) {E_\varpi }\left[ { - \frac{{{\wp ^{1 - \vartheta }}\varpi \left( {{\mu _3}} \right) {t^\varpi }}}{{AB\left( \varpi \right) - \left( {1 - \varpi } \right) \left( {{\mu _3}} \right) }}} \right] .\end{array}\end{array}} \right. \end{aligned}$$

Equilibrium points

The model’s equilibrium points (3) are determined by setting the equations on the right side to zero. Thus, the model has a free equilibrium point.

$$\begin{aligned} {E_ \oplus } = \left( {{N_ \oplus },{I_ \oplus },\alpha {S_ \oplus },{M_ \oplus },{T_ \oplus }} \right) = \left( {\frac{\sigma }{{{a_1} + {a_2} + {\mu _1}}},0,0,0,0} \right) . \end{aligned}$$

The model endemic point is

$$\begin{aligned} {E^ \oplus } = \left( {{N^ \oplus },{I^ \oplus },\alpha {S^ \oplus },{M^ \oplus },{T^ \oplus }} \right) , \end{aligned}$$

where

$$\begin{aligned} & {N^ \oplus } = \frac{{ed\sigma \beta - ({a_1} + {a_2} + {\mu _1})({a_1} + {a_2})({d_1} + {a_1} + {a_2}) + \beta ({a_1} + {a_2})({d_1} + {a_1} + {a_2})({a_1} + {a_2} + {\mu _1})}}{{\sigma ({a_1} + {a_2})({d_1} + {a_1} + {a_2})}},\\ & \quad {I^ \oplus } = - \frac{{\sigma \left( {({a_1} + {a_2})({a_1} + {a_2} + {d_1})({a_1} + {a_2} + {\mu _1}) - \beta {d_1}e\sigma } \right) }}{{({a_1} + {a_2})\left( {{{({a_1} + {a_2} + {d_1})}^2}} \right) \left( {{a_1} + {a_2} + {\mu _1} - \frac{{({a_1} + {a_2})({a_1} + {a_2} + {d_1})({a_1} + {a_2} + {\mu _1}) - \beta {d_1}e\sigma }}{{({a_1} + {a_2})({a_1} + {a_2} + {d_1})}}} \right) }}, \\ & \quad \alpha {S^ \oplus } = \frac{{e{d_1}\sigma \beta - \left( {{a_1} + {a_2} + {\mu _1}} \right) \left( {{a_1} + {a_2}} \right) \left( {{d_1} + {a_1} + {a_2}} \right) }}{{\beta \left( {{a_1} + {a_2}} \right) \left( {{d_1} + {a_1} + {a_2}} \right) }}, \\ & \quad {M^ \oplus } = - \frac{{{a_1}\left( {{a_1} + {a_2} + {d_1}e} \right) \mathfrak {R}}}{{({a_1} + {a_2})\left( {\beta d_1^2e{\mu _3} + {a_1}\beta {d_1}e{\mu _3} + {a_2}\beta {d_1}e{\mu _3}} \right) }},\\ & \quad {T^ \oplus } = - \frac{{\mathfrak {G} + {\mathfrak {G}_1}}}{{\beta d_1^2e{\mu _3} + {a_1}\beta {d_1}e{\mu _3} + {a_2}\beta {d_1}e{\mu _3}}}, \\ & \quad \begin{aligned}\mathfrak {R}&= 3{a_1}a_2^2 + 3a_1^2{a_2} + a_1^2{d_1} + a_2^2{d_1} + a_1^2{\mu _1} + a_2^2{\mu _1} + a_1^3 + a_2^3 + 2{a_1}{a_2}{d_1} + 2{a_1}{a_2}{\mu _1} + {a_1}{d_1}{\mu _1}\\&+ {a_2}{d_1}{\mu _1} - \beta {d_1}e\sigma ,\end{aligned} \\ & \quad \begin{aligned}\mathfrak {G}&= a_1^4 + 3a_1^3{a_2} + a_1^3{d_1}e + a_1^3{d_1} + {\mu _1}a_1^3 + 3a_1^2a_2^2 + 3a_1^2{a_2}{d_1}e + 2a_1^2{a_2}{d_1} + 2{\mu _1}a_1^2{a_2} + a_1^2d_1^2e\\&+ {\mu _1}a_1^2{d_1}e + {\mu _1}a_1^2{d_1} + {a_1}a_2^3 + 3{a_1}a_2^2{d_1}e + {a_1}a_2^2{d_1},\end{aligned} \\ & \quad \begin{aligned}{\mathfrak {G}_1}&= {\mu _1}{a_1}a_2^2 + 2{a_1}{a_2}d_1^2e + 2{\mu _1}{a_1}{a_2}{d_1}e + {\mu _1}{a_1}{a_2}{d_1} + {\mu _1}{a_1}d_1^2e - \beta \sigma {a_1}{d_1}e + a_2^3{d_1}e + a_2^2d_1^2e\\&+ {\mu _1}a_2^2{d_1}e + {\mu _1}{a_2}d_1^2e - \beta \sigma d_1^2{e^2}.\end{aligned} \end{aligned}$$

The disease-free equilibrium represents a healthy brain state with no infection or immune activation, indicating successful control of pathological processes. In contrast, the endemic equilibrium reflects persistent $\alpha$-syn accumulation and immune activity, corresponding to sustained neuroinflammation and disease progression. These states help assess long-term outcomes under different biological conditions.

Next, we use the next-generation approach and the free equilibrium point to determine the basic reproduction number. The following matrices, F and V, are obtained by evaluating the Jacobian at the free equilibrium point:

$$\begin{aligned} F = \begin{bmatrix} 0 & \frac{\beta \sigma }{a_1 + a_2 + \mu _1} \\ 0 & 0 \end{bmatrix}, \quad V = \begin{bmatrix} d_1 + a_1 + a_2 & 0 \\ -e d_1 & a_1 + a_2 \end{bmatrix}. \end{aligned}$$

Therefore, the matrix for the next generation is

$$\begin{aligned} FV^{-1} = \begin{bmatrix} \frac{\beta d_1 e \sigma }{(a_1 + a_2)(a_1 + a_2 + d_1)(a_1 + a_2 + \mu _1)} & \frac{\beta \sigma }{(a_1 + a_2)(a_1 + a_2 + \mu _1)} \\ 0 & 0 \end{bmatrix}. \end{aligned}$$

Therefore, $R_0$, the fundamental reproduction number, is provided by

$$\begin{aligned} R_0 = \frac{\beta d_1 e \sigma }{(a_1 + a_2)(a_1 + a_2 + d_1)(a_1 + a_2 + \mu _1)}. \end{aligned}$$

(5)

The effect of parameters on reproduction number show in Fig. 2.

Fig. 2

Analysis the effect of parameters on $R_0$.

Sensitivity analysis examines how variations in input parameters influence model outcomes, identifying the most impacting factors. It is widely used to improve model accuracy, prioritize interventions, and guide decision-making in complex systems. Sensitivity analysis of key parameters affecting model are shown in Table 2 and Fig. 3. Parameter ranges for sensitivity analysis were chosen based on existing literature on Parkinson’s disease⁵¹. These ranges represent biologically plausible variations in key parameters. Figure 3 illustrates that parameters $\mu _1, a_1$ and $a_2$ have negative sensitivity indices, indicating their suppressive effect on the basic reproduction number $R_0$, while parameters $\beta$, e, $\sigma$ and $d_1$ positively influence $R_0$. Among these, $\beta$, e, and d1 most strongly influence R0, highlighting their critical roles in disease progression.

Table 2 Effect of changes in parameter values.

Fig. 3

The impact of key parameters on model.

Existence and uniqueness

The primary objective of the analysis is to utilize fixed point theorems to establish the existence of solutions for nonlinear systems. In the realm of nonlinear functional analysis, fixed-point contractions are employed to substantiate the existence of solutions within specific systems. Within the context of Banach spaces, fixed point mappings facilitate a more profound understanding of the matter at hand. One must ascertain whether a solution exists and whether it possesses uniqueness. According to a theorem pertaining to fixed point mappings, the model represented by Eq. (3) will yield a singular solution within the interval $[0, \mathbb {T}]$. By considering Eq. (3), we may interpret it as

$$\begin{aligned} \left\{ \begin{array}{l}{}^{FFM}D_{0,t}^{\varpi ,\vartheta }N\left( t \right) = \sigma - \beta N\alpha S - {a_1}N - {a_2}N - {\mu _1}N,\\ {}^{FFM}D_{0,t}^{\varpi ,\vartheta }I\left( t \right) = \beta N\alpha S - {d_1}I - {a_1}I - {a_2}I,\\ {}^{FFM}D_{0,t}^{\varpi ,\vartheta }\alpha S\left( t \right) = e{d_1}I - {a_1}\alpha S - {a_2}\alpha S,\\ {}^{FFM}D_{0,t}^{\varpi ,\vartheta }M\left( t \right) = {a_1}I + {a_1}\alpha S - {\mu _2}M,\\ {}^{FFM}D_{0,t}^{\varpi ,\vartheta }T\left( t \right) = {a_1}I + \left( {{a_1} + {a_2}} \right) \alpha S - {\mu _3}T.\end{array} \right. \end{aligned}$$

(6)

Mittag–Leffler kernel transforms equation into Fractal Fractional integral.

$$\begin{aligned} & \begin{aligned}&N(t)= N(0)+\frac{\vartheta (1-\varpi ) t^{\vartheta -1}}{{\mathbb{A}\mathbb{B}}(\varpi )}\bar{N}(t,N(t))+\frac{\varpi \vartheta }{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )} \int ^t_0 (t-\chi )^{\varpi -1} \chi ^{\vartheta -1}\bar{N}(\chi ,N(\chi )) d\chi ={J_1}+{J_2},\\ &I(t)= I(0)+\frac{\vartheta (1-\varpi ) t^{\vartheta -1}}{{\mathbb{A}\mathbb{B}}(\varpi )}\bar{I}(t,I(t))+\frac{\varpi \vartheta }{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )} \int ^t_0 (t-\chi )^{\varpi -1} \chi ^{\vartheta -1}\bar{I}(\chi ,I(\chi )) d\chi ={K_1}+{K_2},\\ &\alpha S(t)= \alpha S(0)+\frac{\vartheta (1-\varpi ) t^{\vartheta -1}}{{\mathbb{A}\mathbb{B}}(\varpi )}\bar{\alpha S}(t,\alpha S(t))+\frac{\varpi \vartheta }{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )} \int ^t_0 (t-\chi )^{\varpi -1} \chi ^{\vartheta -1}\bar{\alpha S}(\chi ,\alpha S(\chi )) d\chi ={L_1}+{L_2},\\ &M(t)= M(0)+\frac{\vartheta (1-\varpi ) t^{\vartheta -1}}{{\mathbb{A}\mathbb{B}}(\varpi )}\bar{M}(t,M(t))+\frac{\varpi \vartheta }{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )} \int ^t_0 (t-\chi )^{\varpi -1} \chi ^{\vartheta -1}\bar{M}(\chi , M(\chi )) d\chi ={O_1}+{O_2},\\ &T(t)= T(0)+\frac{\vartheta (1-\varpi ) t^{\vartheta -1}}{{\mathbb{A}\mathbb{B}}(\varpi )}\bar{T}(t,T(t))+\frac{\varpi \vartheta }{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )} \int ^t_0 (t-\chi )^{\varpi -1} \chi ^{\vartheta -1}\bar{T}(\chi ,T(\chi )) d\chi ={P_1}+{P_2}, \end{aligned} \end{aligned}$$

(7)

$$\begin{aligned} & \quad \begin{aligned} {J_1} = N(0) + \frac{{\vartheta (1 - \varpi ){t^{\vartheta - 1}}}}{{\mathbb{A}\mathbb{B}(\varpi )}}{\bar{N}}(t,N(t)),&\\{K_1} = I(0) + \frac{{\vartheta (1 - \varpi ){t^{\vartheta - 1}}}}{{\mathbb{A}\mathbb{B}(\varpi )}}{\bar{I}}(t,I(t)),&\\{L_1} = \alpha S(0) + \frac{{\vartheta (1 - \varpi ){t^{\vartheta - 1}}}}{{\mathbb{A}\mathbb{B}(\varpi )}}\bar{\alpha }S(t,\alpha S(t)),&\\{O_1} = M(0) + \frac{{\vartheta (1 - \varpi ){t^{\vartheta - 1}}}}{{\mathbb{A}\mathbb{B}(\varpi )}}{\bar{M}}(t,M(t)),&\\{P_1} = T(0) + \frac{{\vartheta (1 - \varpi ){t^{\vartheta - 1}}}}{{\mathbb{A}\mathbb{B}(\varpi )}}{\bar{T}}(t,T(t)),\end{aligned} \end{aligned}$$

(8)

$$\begin{aligned} & \quad \begin{aligned}&{J_2} = \frac{{\varpi \vartheta }}{{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )}} \int _0^t {{{(t - \chi )}^{\varpi - 1}}} {\chi ^{\vartheta - 1}}{\bar{N}}(\chi ,N(\chi ))d\chi ,\\ &{K_2} = \frac{{\varpi \vartheta }}{{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )}}\int _0^t {{{(t - \chi )}^{\varpi - 1}}} {\chi ^{\vartheta - 1}}{\bar{I}}(\chi ,I(\chi ))d\chi ,\\ &{L_2} = \frac{{\varpi \vartheta }}{{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )}}\int _0^t {{{(t - \chi )}^{\varpi - 1}}} {\chi ^{\vartheta - 1}}\bar{\alpha }S(\chi ,\alpha S(\chi ))d\chi ,\\ &{O_2} = \frac{{\varpi \vartheta }}{{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )}}\int _0^t {{{(t - \chi )}^{\varpi - 1}}} {\chi ^{\vartheta - 1}}{\bar{M}}(\chi ,M(\chi ))d\chi ,\\ &{P_2} = \frac{{\varpi \vartheta }}{{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )}}\int _0^t {{{(t - \chi )}^{\varpi - 1}}} {\chi ^{\vartheta - 1}}{\bar{T}}(\chi ,T(\chi ))d\chi .\end{aligned} \end{aligned}$$

(9)

We show the basic idea behind the governing formulas (6) applying the fixed point theorem of Krasnoselski: ${\Phi }({J_1},{K_1},{L_1},{O_1},{P_1})$ as maps of contractions and ${\Psi }({J_2},{K_2},{L_2},{O_2},{P_2})$ as compact, continuous integrated elements.

Theorem 4.1

This non-linear mapping ${\Phi }({J_1},{K_1},{L_1},{O_1},{P_1}): [0,\textbf{T}]\rightarrow \textbf{R}^5$ given in (8)–(9) certify that constants satisfy the Lipschitz contractive requirement ${Q}_{{J}}$, ${Q}_{{K}}$, ${Q}_{L}$,${Q}_{{O}}$,${Q}_{{P}}$ $>0$

Proof

Examine ${\Phi }({J_1},{K_1},{L_1},{O_1},{P_1}) : [0,\textbf{T}]\rightarrow \mathbb {R}^5$ in the form of a completely normed space

$$\begin{aligned} \Vert (N,I,\alpha S,M,T)\Vert =\max _{t\in [0,\textbf{T}]}\big \Vert N(t)+I(t)+\alpha S(t)+M(t)+T(t)\big \Vert , \end{aligned}$$

(10)

$$\begin{aligned} N,I,\alpha S,M,T \in [0,\textbf{T}]. \end{aligned}$$

(i) Initially, we will show that the details of a mapping of contractions is ${\Phi }({J_1},{K_1},{L_1},{O_1},{P_1})$. For N and ${\bar{N}}$

$$\begin{aligned} \begin{aligned}&\left\| {J\left( {N,I,\alpha S,M,T} \right) \left( t \right) - J\left( {{\bar{N}},I,\alpha S,M,T} \right) \left( t \right) } \right\| \\ &= \left\| {\left( {\sigma - \left( {\beta \alpha S + {a_1} + {a_2} + \mu } \right) N} \right) - \left( {\sigma - \left( {\beta \alpha S + {a_1} + {a_2} + \mu } \right) {\bar{N}}} \right) } \right\| \\ &= \left\| {\left( {\beta \alpha S + {a_1} + {a_2} + \mu } \right) \left( {N - {\bar{N}}} \right) } \right\| \\ &\le \left\| {\left( {\beta \left\| {\alpha S} \right\| + {a_1} + {a_2} + \mu } \right) } \right\| \left\| {\left( {N - {\bar{N}}} \right) } \right\| \\ &\le {Q_J}\left\| {\left( {N - {\bar{N}}} \right) } \right\| ,\end{aligned} \end{aligned}$$

(11)

where ${Q_J} = \left\| {\left( {\beta \left\| {\alpha S} \right\| + {a_1} + {a_2} + \mu } \right) } \right\|$. By employing this method, we get

$$\begin{aligned} \begin{aligned}&\big \Vert {K}(N,I,\alpha S,M,T)(t)-{K}(N,\bar{I},\alpha S,M,T)(t)\big \Vert \ \le \ Q_{{K}}\Vert ({I}-\bar{{I}})\Vert ,\\ &\big \Vert {L}(N,I,\alpha S,M,T)(t)-{L}(N,I,\bar{\alpha S},M,T)(t)\big \Vert \ \le \ Q_{{L}}\Vert ({\alpha S}-\bar{{\alpha S}})\Vert ,\\ &\big \Vert {O}(N,I,\alpha S,M,T)(t)-{O}(N,I,{\alpha S}, \bar{M},T)(t)\big \Vert \ \le \ Q_{{O}}\Vert ({M}-\bar{{M}})\Vert ,\\ &\big \Vert {P}(N,I,\alpha S,M,T)(t)-{O}(N,I,{\alpha S}, M,\bar{T})(t)\big \Vert \ \le \ Q_{{P}}\Vert ({T}-\bar{{T}})\Vert , \end{aligned} \end{aligned}$$

(12)

where ${Q_K} = \left\| {{d_1} + {a_1} + {a_2}} \right\| ,$ ${Q_L} = \left\| {{a_1} + {a_2}} \right\| ,$ ${Q_O} = \left\| {{\mu _2}} \right\| ,$ ${Q_P} = \left\| {{\mu _3}} \right\| .$

The following is clearly derivable for ${\Phi }(N,I,\alpha S,M,T)$.

$$\begin{aligned}&\big \Vert {\Phi }(N,I,\alpha S,M,T)(t)-{\Phi }(\bar{N}, \bar{I},\bar{\alpha S}, {\bar{M}}, {\bar{T}})(t)\big \Vert \nonumber \\&= \frac{\vartheta (1-\varpi ) t^{\vartheta -1}}{\mathbb{A}\mathbb{B}(\varpi )}\displaystyle \max _{t\in [0,\textbf{T}]}\big |(N,I,\alpha S,M,T)(t)-(\bar{N},\bar{I}, \bar{\alpha S}, {\bar{M}}, {\bar{T}})(t) \big | \nonumber \\ &\le \frac{\vartheta (1-\varpi ) t^{\vartheta -1}}{\mathbb{A}\mathbb{B}(\varpi )}\big \Vert (N,I,\alpha S)(t)-(\bar{N},\bar{I}, \bar{\alpha S}, {\bar{M}}, {\bar{T}})(t)\big \Vert \nonumber \\ &\le \frac{\vartheta (1-\varpi ) t^{\vartheta -1}}{\mathbb{A}\mathbb{B}(\varpi )}{Q}, \end{aligned}$$

(13)

where

$Q=\max [Q_{{J}},Q_{{K}},Q_{{L}},Q_{{O}},Q_{{P}}]<1$ ensures the Lipschitz constant. In this sense, the operator ${\Phi }({J},{K},{L},O,P)$ is implied to be non-expansive.

(ii) We shall then demonstrate the continuous compactness of ${\Psi }({J_2},{K_2},{L_2},{O_2},{P_2})$.

Bounded operators absolute modulus J, K,L,O  and  P specified in (10)–(11) non-zero positive constants ${\eta _{J}},{\eta _{K}},{\eta _{L}},{\eta _{O}},{\eta _{P}},{\zeta _{J}},{\zeta _{K}},{\zeta _{L}},{\zeta _{O}}~ and ~{\zeta _{P}}$ proving the operator’s compactness by satisfying the following bounded-ness inequalities

${\Psi }({J_2},{K_2},{L_2},{O_2},{P_2})$.

$$\begin{aligned} \begin{aligned}&\left| {J(t,N)} \right| \; \le \;{\eta _J}\left\| N \right\| + {\zeta _J},\\ &\left| {K(t,I)} \right| \; \le \;{\eta _K}\left\| I \right\| + {\zeta _I},\\ &\left| {L(t,\alpha S)} \right| \; \le \;{\eta _L}\left\| \alpha S \right\| + {\zeta _\alpha S},\\ &\left| {O(t,M)} \right| \; \le \;{\eta _O}\left\| M \right\| + {\zeta _M},\\ &\left| {P(t,T)} \right| \; \le \;{\eta _P}\left\| T \right\| + {\zeta _T}.\end{aligned} \end{aligned}$$

(14)

$\mathscr {B}$ represents a closed subset of $\mathfrak {Z}$.

$$\begin{aligned} \mathscr {B}=\big \{({J},{K},{L},O,P)\in \mathfrak {Z}/\Vert {J},{K},{L},O,P\Vert \le \varpi , \ \varpi >0 \big \}. \end{aligned}$$

(15)

For $({J},{K},{L},O,P)\in \mathscr {B}$, we find

$$\begin{aligned} \Vert {J_2}(t,N)\Vert&= \displaystyle \max _{t\in [0,\mathbb {T}]}\Big |\frac{\varpi \vartheta }{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )} \int ^t_0 (t-\chi )^{\varpi -1} \chi ^{\vartheta -1}{J}(\chi ,N(\chi )) d\chi \Big |\nonumber \\ &\le \frac{\gimel ^{\varpi ,\vartheta }}{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )} \int ^{\gimel }_0 (\gimel -\chi )^{\varpi -1} \chi ^{\vartheta -1}\big |{J}(\chi ,N(\chi ))\big |d\chi \nonumber \\ &\le \frac{\gimel ^{\varpi ,\vartheta }}{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )}\eta _{{J}}\xi +\zeta _{{J}}. \end{aligned}$$

(16)

The same is shown for additional elements. Finding the maximum norm continues $\Vert \psi ({J_2},{K_2},{L_2},{O_2},{P_2})\Vert$ as,

$$\begin{aligned}&\Vert \psi ({J_2},{K_2},{L_2},{O_2},{P_2})\Vert \nonumber \\&\le \Big \{\big [\eta _{{J}}+\eta _{{K}}+\eta _{{L}}+\eta _{{O}}+\eta _{{P}}\big ]\xi +\zeta _{{J}}+\zeta _{{K}}+\zeta _{{L}}+\zeta _{{O}}+\zeta _{{P}}\Big \}=\phi , \end{aligned}$$

(17)

where a positive constant is denoted by $\phi$. A uniformly bounded operator, is

$$\begin{aligned} \Vert \psi (N,I,\alpha S, M,T)\Vert \le \phi \ \Rightarrow \ \psi . \end{aligned}$$

We shall now demonstrate that $t_x<t_y \in [0,\mathbb {T}]$, h is uniformly continuous. We have for $t_1<t_2 \in [0,\mathbb {T}]$ for this purpose.

$$\begin{aligned} \begin{aligned}&|{J_2}(t_2,N)-{J_2}(t_1,N)|\\ &~~~~~~~~~ =\frac{\varpi \vartheta }{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )} \Big |\int _0^{t_y} (t-\chi )^{\varpi -1} \chi ^{\vartheta -1}{J}(\chi ,N(\chi )) d\chi - \int _0^{t_x} (t-\chi )^{\varpi -1} \chi ^{\vartheta -1}{J}[\chi ,N(\chi )] d\chi \Big |\\ &~~~~~~~~~ \le \frac{\varpi \vartheta }{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )} \Big [\int _0^{t_y} (t-\chi )^{\varpi -1} \chi ^{\vartheta -1}-\int _0^{t_x} (t-\chi )^{\varpi -1} \chi ^{\vartheta -1}\Big ]\Big (\eta _{{J}} \xi +\zeta _{{J}}\Big ) \\ &~~~~~~~~~ \le \frac{\eta _{{J}}\vartheta +\zeta _{{J}}}{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )} \Big [t_2^{\varpi ,\vartheta }-t_1^{\varpi ,\vartheta }\Big ]. \end{aligned} \end{aligned}$$

(18)

Similarly,

$$\begin{aligned} \begin{aligned}&\big |{K_2}(t_2,I)-{K_2}(t_1,I)\big | ~ \le ~ \frac{\eta _{{K}}\varpi +\zeta _{{K}}}{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )} \big (t_2^{\varpi ,\vartheta }-t_1^{\varpi ,\vartheta }\big ),\\ &\big |{L_2}(t_2,\alpha S)-{L_2}(t_1,\alpha S)\big | ~ \le ~ \frac{\eta _{{L}}\varpi +\zeta _{{L}}}{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )} \big (t_2^{\varpi ,\vartheta }-t_1^{\varpi ,\vartheta }\big ),\\ &\big |{O_2}(t_2,M)-{O_2}(t_1,M)\big | ~ \le ~ \frac{\eta _{{O}}\varpi +\zeta _{{O}}}{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )} \big (t_2^{\varpi ,\vartheta }-t_1^{\varpi ,\vartheta }\big ),\\ &\big |{P_2}(t_2,T)-{P_2}(t_1,T)\big | ~ \le ~ \frac{\eta _{{P}}\varpi +\zeta _{{P}}}{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )} \big (t_2^{\varpi ,\vartheta }-t_1^{\varpi ,\vartheta }\big ). \end{aligned} \end{aligned}$$

(19)

As $t_2\rightarrow t_1$ is independent of $(N,I,\alpha S, M,T)$. This implies that

$$\begin{aligned} \big \Vert \psi ({J_2},{K_2},{L_2},{O_2},{P_2})(t_2) -\psi ({J_2},{K_2},{L_2},{O_2},{P_2})(t_1)\big \Vert \rightarrow \ 0. \end{aligned}$$

(20)

$\Rightarrow \psi ({J_2},{K_2},{L_2},{O_2},{P_2}),$ represents an operator that is equi-continuous and complete.

$\Rightarrow \psi ({J_2},{K_2},{L_2},{O_2},{P_2}),$ it is reasonably concise, according to Arzela’s theorem.

The existence of a unique singular solution is guaranteed by the compactness of the operators ${\Phi }$ and ${\Psi }$, according to the Krasnoselski theorem. $\square$

Theorem 4.2

The model solution (3) is regarded as unique if

$$\begin{aligned} \frac{\wp ^{\varpi ,\iota }}{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )}Q \le 1, \end{aligned}$$

(21)

where $Q=\max \{\mathscr {W}_{{J}},\mathscr {W}_{{K}},\mathscr {W}_{{L}},\mathscr {W}_{{O}},\mathscr {W}_{{P}}\}.$

Proof

Establish an operator $\beth =(\beth _1,\beth _2,\beth _3,\beth _4,\beth _5): \mathfrak {Z}\rightarrow \mathfrak {Z}$ utilizing (20) as:

$$\begin{aligned} \begin{aligned}&\beth _1(N)(t)= N(0)+\frac{\vartheta (1-\varpi ) t^{\vartheta -1}}{\mathbb{A}\mathbb{B}(\varpi )}{J}(t,N(t)) +\frac{\varpi \vartheta }{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )} \int ^t_0 (t-\chi )^{\varpi -1}\chi ^{\vartheta -1}{J}(\chi ,N(\chi )) d\chi ,\\ &\beth _2(I)(t)= I(0)+\frac{\vartheta (1-\varpi ) t^{\vartheta -1}}{\mathbb{A}\mathbb{B}(\varpi )}{K}(t,I(t)) +\frac{\varpi \vartheta }{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )} \int ^t_0 (t-\chi )^{\varpi -1}\chi ^{\vartheta -1}{K}(\chi ,I(\chi )) d\chi ,\\ &\beth _3(\alpha S)(t)= \alpha S(0)+\frac{\vartheta (1-\varpi ) t^{\vartheta -1}}{\mathbb{A}\mathbb{B}(\varpi )}{L}(t,\alpha S(t)) +\frac{\varpi \vartheta }{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )} \int ^t_0 (t-\chi )^{\varpi -1}\chi ^{\vartheta -1}{L}(\chi ,\alpha S(\chi )) d\chi ,\\ &\beth _4(M)(t)= M(0)+\frac{\vartheta (1-\varpi ) t^{\vartheta -1}}{\mathbb{A}\mathbb{B}(\varpi )}{O}(t,M(t)) +\frac{\varpi \vartheta }{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )} \int ^t_0 (t-\chi )^{\varpi -1}\chi ^{\vartheta -1}{O}(\chi ,M(\chi )) d\chi ,\\ &\beth _5(T)(t)= T(0)+\frac{\vartheta (1-\varpi ) t^{\vartheta -1}}{\mathbb{A}\mathbb{B}(\varpi )}{P}(t,T(t)) +\frac{\varpi \vartheta }{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )} \int ^t_0 (t-\chi )^{\varpi -1}\chi ^{\vartheta -1}{P}(\chi ,T(\chi )) d\chi . \end{aligned} \end{aligned}$$

(22)

For $(N,I,\alpha S)$, $(\bar{N},\bar{I},\bar{\alpha S}),{\bar{M}},{\bar{T}}$ $\in \mathfrak {Z}$, and utilizing (22) we have,

$$\begin{aligned} \big \Vert \beth _1(N)(t)-\beth _1(\bar{N})(t)\big \Vert&=\frac{\vartheta (1-\varpi ) t^{\vartheta -1}}{\mathbb{A}\mathbb{B}(\varpi )}\Vert {J}(t,N(t)) -{J}(t,\bar{N}(t))\Vert \nonumber \\ &+ \frac{\varpi \vartheta }{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )}\int ^t_0 \Vert {J}(\chi ,N(\chi )) -{J}(\chi ,\bar{N}(\chi ))\Vert (t-\chi )^{\varpi -1}\chi ^{\vartheta -1}{J}(\chi ,J(\chi )) d\chi \nonumber \\ &\le \frac{\vartheta (1-\varpi ) t^{\vartheta -1}}{\mathbb{A}\mathbb{B}(\varpi )}Q_{{J}} \Vert N-\bar{N}\Vert +\frac{\chi ^{\varpi ,\vartheta }}{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )}Q_{{J}}\Vert N-\bar{N}\Vert \nonumber \\&\le \Big [\frac{\vartheta (1-\varpi ) t^{\vartheta -1}}{\mathbb{A}\mathbb{B}(\varpi )} +\frac{\chi ^{\varpi ,\vartheta }}{ \mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )}\Big ]Q_{{J}}\Vert N-\bar{N}\Vert . \end{aligned}$$

(23)

$\Vert N-\bar{N}\Vert \rightarrow 0$ when $N\rightarrow \bar{N}$. Hence

$$\begin{aligned} \big \Vert \beth _1(N)(t)-\beth _1(\bar{N})(t)\big \Vert \le \Big [\frac{\vartheta (1-\varpi ) t^{\vartheta -1}}{\mathbb{A}\mathbb{B}(\varpi )} +\frac{\chi ^{\varpi ,\vartheta }}{ \mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )}\Big ]Q_{{J}} \le 1, \end{aligned}$$

with

$$\begin{aligned} \big \Vert \beth _1(N)(t)-\beth _1(\bar{N})(t)\big \Vert \Big [1-\Big (\frac{\vartheta (1-\varpi )t^{\vartheta -1}}{\mathbb{A}\mathbb{B}(\varpi )} +\frac{\chi ^{\varpi ,\vartheta }}{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )}\Big )Q_{{J}}\Big ]\le 0. \end{aligned}$$

(24)

Using this approach, we find

$$\begin{aligned}&\big \Vert \beth (N,I,\alpha S)(t) - \beth (\bar{N}, \bar{I},\bar{\alpha S},{\bar{M}},{\bar{T}})(t)\big \Vert \nonumber \\ &\le \big (\frac{\vartheta (1-\varpi )t^{\vartheta -1}}{\mathbb{A}\mathbb{B}(\varpi )} +\frac{\chi ^{\varpi ,\vartheta }}{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )}\big ) Q\big \Vert (N,I,\alpha S,M,T)-(\bar{N},\bar{I},\bar{\alpha S}, {\bar{M}},{\bar{T}})\big \Vert . \end{aligned}$$

(25)

The model unique fixed-point solution is confirmed using $\beth$, combining Schauder and Krasnoselski theorems. $\square$

Stability analysis

Local stability analysis

Theorem 5.1

 When ${R_0} < 1$, the Parkinson disease free equilibrium ${E_\oplus }$ is asymptotically locally stable. There is unstable if ${R_0} > 1$.

Proof

For the system (3) at ${E_\oplus }$, the Jacobian can be expressed as

$$\begin{aligned} J(E_\oplus )= \begin{bmatrix} -a_1 - a_2 - \mu _1 & 0 & -\frac{\sigma }{a_1 + a_2 + \mu _1} \beta & 0 & 0 \\ 0 & -a_1 - a_2 - d_1 & \frac{\sigma }{a_1 + a_2 + \mu _1} \beta & 0 & 0 \\ 0 & d_1 e & -a_1 - a_2 & 0 & 0 \\ 0 & a_1 & a_1 & -\mu _3 & 0 \\ 0 & a_1 & a_1 + a_2 & 0 & -\mu _3 \end{bmatrix} \end{aligned}$$

The following are the resultant eigenvalues when the parameter values from Table (1) are substituted into the Jacobian matrix: ${\lambda _1} = - 0.0402$, ${\lambda _2} = - 0.0150$, ${\lambda _3} = - 0.0150$, ${\lambda _4} = -0.0407$, ${\lambda _5} = -0.0397$. Hence, the point $E_\oplus$ is locally asymptotically stable. $\square$

Global stability analysis

Global stability, in this context, ensures that the system will converge to the endemic equilibrium regardless of initial conditions, reflecting the irreversible progression of Parkinson’s disease once it surpasses a critical threshold. Biologically, this highlights the importance of early intervention to prevent the system from settling into a persistent diseased state.

First derivative of Lyapunov

For the endemic Lyapunov function, $\{ N, I, \alpha S, M, T\},$ ${}^{FFM}D_{0,t}^{\varpi ,\vartheta }L$ < 0, is the endemic equilibrium ${E^\oplus }$.

Theorem 5.2

Global asymptotic stability is achieved by the model endemic equilibrium points ${E^ \oplus }$ when the reproduction number $R_0$ > 1.

Proof

The following is a representation of the Lyapunov function:

$$\begin{aligned} \begin{aligned}L({N^*},{I^*},\alpha {S^*},{M^*},{T^*})&= \left( {N - {N^*} - {N^*}\ln \frac{N}{{{N^*}}}} \right) + \left( {I - {I^*} - {I^*}\ln \frac{I}{{{I^*}}}} \right) + \left( {\alpha S - \alpha {S^*} - \alpha {S^*}\ln \frac{{\alpha S}}{{\alpha {S^*}}}} \right) \\ &+ \left( {M - {M^*} - {M^*}\ln \frac{M}{{{M^*}}}} \right) + \left( {T - {T^*} - {T^*}\ln \frac{T}{{{T^*}}}} \right) .\end{aligned} \end{aligned}$$

(26)

Differentiating both sides with respect to t.

$$\begin{aligned} \begin{aligned}{}^{FFM}D_{0,t}^{\varpi ,\vartheta }L&\le \left( {\frac{{N - {N^*}}}{N}} \right) {}^{FFM}D_{0,t}^{\varpi ,\vartheta }N + \left( {\frac{{I - {I^*}}}{I}} \right) {}^{FFM}D_{0,t}^{\varpi ,\vartheta }I + \left( {\frac{{\alpha S - \alpha {S^*}}}{{\alpha S}}} \right) {}^{FFM}D_{0,t}^{\varpi ,\vartheta }\alpha S\\ &+ \left( {\frac{{M - {M^*}}}{M}} \right) {}^{FFM}D_{0,t}^{\varpi ,\vartheta }M + \left( {\frac{{T - {T^*}}}{T}} \right) {}^{FFM}D_{0,t}^{\varpi ,\vartheta }T.\end{aligned} \end{aligned}$$

The following is now an expression for their derivative:

$$\begin{aligned} \begin{aligned}{}^{FFM}D_{0,t}^{\varpi ,\vartheta }L&\le \left( {\frac{{N - {N^*}}}{N}} \right) \left( {\sigma - \beta N\alpha S - {a_1}N - {a_2}N - \mu _1 N} \right) + \left( {\frac{{I - {I^*}}}{I}} \right) \left( {N\alpha S - {d_1}I - {a_1}I - {a_2}I} \right) \\ &+ \left( {\frac{{\alpha S - \alpha {S^*}}}{{\alpha S}}} \right) \left( {e{d_1}I - {a_1}\alpha S - {a_2}\alpha S} \right) + \left( {\frac{{M - {M^*}}}{M}} \right) \left( {{a_1}I + {a_1}\alpha S - {\mu _2}M} \right) \\ &+ \left( {\frac{{T - {T^*}}}{T}} \right) \left( {{a_1}I + \left( {{a_1} + {a_2}} \right) \alpha S - {\mu _3}T} \right) .\end{aligned} \end{aligned}$$

(27)

Putting $N = N - {N^ * }$, $I = I - {{I}^ * }$, $\alpha S = \alpha S - {{\alpha S}^ * }$, $M = M - {{M}^ * }$  and  $T = T - {T^ * }$ leads to.

$$\begin{aligned} \begin{aligned}{}^{FFM}D_{0,t}^{\varpi ,\vartheta }L&\le \left( {\frac{{N - {N^*}}}{N}} \right) \left( {\sigma - \beta \left( {N - {N^ * }} \right) \left( {\alpha S - \alpha {S^ * }} \right) - {a_1}\left( {N - {N^ * }} \right) - {a_2}\left( {N - {N^ * }} \right) - \mu _1 \left( {N - {N^ * }} \right) } \right) \\ &+ \left( {\frac{{I - {I^*}}}{I}} \right) \left( {\left( {N - {N^ * }} \right) \left( {\alpha S - \alpha {S^ * }} \right) - {d_1}\left( {I - {I^ * }} \right) - {a_1}\left( {I - {I^ * }} \right) - {a_2}\left( {I - {I^ * }} \right) } \right) \\ &+ \left( {\frac{{\alpha S - \alpha {S^*}}}{{\alpha S}}} \right) \left( {e{d_1}\left( {I - {I^ * }} \right) - {a_1}\left( {\alpha S - \alpha {S^ * }} \right) - {a_2}\left( {\alpha S - \alpha {S^ * }} \right) } \right) \\ &+ \left( {\frac{{M - {M^*}}}{M}} \right) \left( {{a_1}\left( {I - {I^ * }} \right) + {a_1}\left( {\alpha S - \alpha {S^ * }} \right) - {\mu _2}\left( {M - {M^ * }} \right) } \right) \\ &+ \left( {\frac{{T - {T^*}}}{T}} \right) \left( {{a_1}\left( {I - {I^ * }} \right) + \left( {{a_1} + {a_2}} \right) \left( {\alpha S - \alpha {S^ * }} \right) - {\mu _3}\left( {T - {T^ * }} \right) } \right) ,\end{aligned} \end{aligned}$$

after some computational

$$\begin{aligned} & {}^{FFM}D_{0,t}^{\varpi ,\vartheta }L \le {\mathfrak {A}_1} - {\mathfrak {A}_2}. \\ & \begin{aligned}\mathfrak {A}_1&= \sigma + \beta \alpha {S^ * }\frac{{\left( {N - {N^*}} \right) }^2}{N} + N\alpha S + {N^*}\alpha {S^*} + N\alpha {S^*}\frac{{{I^*}}}{I} + {N^*}\alpha S\frac{{{I^*}}}{I} + e{d_1}I + e{d_1}{I^*}\frac{{\alpha {S^*}}}{{\alpha S}} + {a_1}I \\&+ {a_1}I\frac{{{M^*}}}{M} + {a_1}\alpha S + {a_1}\alpha {S^*}\frac{{{M^*}}}{M} + {a_1}I + {a_1}{I^*}\frac{{{T^*}}}{T} + {a_1}\alpha S + {a_2}\alpha S + {a_1}\alpha {S^*}\frac{{{T^*}}}{T} + {a_2}\alpha {S^*}\frac{{{T^*}}}{T}.\end{aligned}\\ & \quad \begin{aligned}{\mathfrak {A}_2}&= \sigma \frac{{{N^*}}}{N} + \beta \alpha S\frac{{{{\left( {N - {N^*}} \right) }^2}}}{N} + {a_1}\frac{{{{\left( {N - {N^*}} \right) }^2}}}{N} + {a_2}\frac{{{{\left( {N - {N^*}} \right) }^2}}}{N} + \mu _1 \frac{{{{\left( {N - {N^*}} \right) }^2}}}{N} + N\alpha {S^*} + {N^*}\alpha S\\ &+ N\alpha S\frac{{{I^*}}}{I} + {N^*}\alpha {S^*}\frac{{{I^*}}}{I} + {d_1}\frac{{{{\left( {I - {I^*}} \right) }^2}}}{I} + {a_1}\frac{{{{\left( {I - {I^*}} \right) }^2}}}{I} + {a_2}\frac{{{{\left( {I - {I^*}} \right) }^2}}}{I} + e{d_1}{I^*} + e{d_1}I\frac{{\alpha {S^*}}}{{\alpha S}}\\ &+ {a_1}\frac{{{{\left( {\alpha S - \alpha {S^*}} \right) }^2}}}{{\alpha S}} + {a_2}\frac{{{{\left( {\alpha S - \alpha {S^*}} \right) }^2}}}{{\alpha S}} + {a_1}{I^*} + {a_1}I\frac{{{M^*}}}{M} + {a_1}\alpha {S^*} + {a_1}\alpha S\frac{{{M^*}}}{M} + {\mu _2}\frac{{{{\left( {M - {M^*}} \right) }^2}}}{M}\\ &+ {a_1}{I^*} + {a_1}I\frac{{{T^*}}}{T} + {a_1}\alpha {S^*} + {a_2}\alpha {S^*} + {a_1}\alpha S\frac{{{T^*}}}{T} + {a_2}\alpha S\frac{{{T^*}}}{T} + {\mu _3}\frac{{{{\left( {T - {T^*}} \right) }^2}}}{T}.\end{aligned} \end{aligned}$$

It is achieved that if $\mathfrak {A}_1 < \mathfrak {A}_2$, this yields ${}^{FFM}D_{0,t}^{\varpi ,\vartheta } L < 0$, however when $N = {N^*},I = {{I}^*},\alpha S = {{\alpha S}^*},M = {M^*} ~ and ~ T = {T^*}.$

$$\begin{aligned} 0 = \mathfrak {A}_1 - \mathfrak {A}_2 \,\,\,\, \Rightarrow \,\,\,{}^{FFM}D_{0,t}^{\varpi ,\vartheta } L = 0. \end{aligned}$$

(28)

The proposed model is shown to have the biggest compact invariant set.

$$\begin{aligned} \left\{ {\left( {{N^*},{{I}^*},{{\alpha S}^*},M^*,T^*} \right) } \right\} . \end{aligned}$$

Thus, if ${\mathfrak {A} _1} < {\mathfrak {A} _2}$, then the endemic equilibrium points $E^\oplus$ are asymptotically stable globally within the invariant region. $\square$

The analysis confirms that when the basic reproduction number $R_0<1$, the disease-free equilibrium is locally asymptotically stable, indicating eradication. Conversely, if $R_0>1$, the endemic equilibrium is globally asymptotically stable, indicating the persistence of the disease.

Chaos control

In this section, we use the linear feedback control strategy to stabilize the system (3) at equilibrium positions. The fractional-order system depicted in its controlled state (3) will be the focus of the following analysis:

$$\begin{aligned} \left\{ \begin{array}{l}{}^{FFM}D_{0,t}^{\varpi ,\vartheta }N\left( t \right) = \sigma - \beta N\left( t \right) \alpha S\left( t \right) - {a_1}N\left( t \right) - {a_2}N\left( t \right) - {\mu _1}N\left( t \right) + {\varepsilon _1}\left( {{N_t} - N} \right) ,\\ {}^{FFM}D_{0,t}^{\varpi ,\vartheta }I\left( t \right) = \beta N\left( t \right) \alpha S\left( t \right) - {d_1}I\left( t \right) - {a_1}I\left( t \right) - {a_2}I\left( t \right) + {\varepsilon _2}\left( {{I_t} - I} \right) ,\\ {}^{FFM}D_{0,t}^{\varpi ,\vartheta }\alpha S\left( t \right) = e{d_1}I\left( t \right) - {a_1}\alpha S\left( t \right) - {a_2}\alpha S\left( t \right) + {\varepsilon _3}\left( {\alpha {S_t} - \alpha S} \right) ,\\ {}^{FFM}D_{0,t}^{\varpi ,\vartheta }M\left( t \right) = {a_1}I\left( t \right) + {a_1}\alpha S\left( t \right) - {\mu _2}M\left( t \right) + {\varepsilon _4}\left( {{M_t} - M} \right) ,\\ {}^{FFM}D_{0,t}^{\varpi ,\vartheta }T\left( t \right) = {a_1}I\left( t \right) + \left( {{a_1} + {a_2}} \right) \alpha S\left( t \right) - {\mu _3}T\left( t \right) + {\varepsilon _5}\left( {{T_t} - T} \right) ,\end{array} \right. \end{aligned}$$

(29)

where $E_\oplus$ represents the system equilibrium point and $\varepsilon _1$, $\varepsilon _2$, $\varepsilon _3$, and $\varepsilon _4$ are control variables. For the system (29), the Jacobian matrix at $E_\oplus$ is built as

$$\begin{aligned} J(E_\oplus ) = \begin{bmatrix} - a_1 - a_2 - \varepsilon _1 - \mu _1 & 0 & -\frac{\sigma }{{{a_1} + {a_2} + {\mu _1}}} \beta & 0 & 0 \\ 0 & - a_1 - a_2 - d_1 - \varepsilon _2 & \frac{\sigma }{{{a_1} + {a_2} + {\mu _1}}} \beta & 0 & 0 \\ 0 & d_1 e & - a_1 - a_2 - \varepsilon _3 & 0 & 0 \\ 0 & a_1 & a_1 & - \varepsilon _4 - \mu _3 & 0 \\ 0 & a_1 & a_1 + a_2 & 0 & - \varepsilon _5 - \mu _3 \end{bmatrix} \end{aligned}$$

$\varepsilon _1=1,\varepsilon _2=2,\varepsilon _3=3,\varepsilon _4=4, \varepsilon _5=5$ is the selection. The polynomial roots related to equilibrium point $E_\oplus$ are determined.

$$\begin{aligned} C\left( \lambda \right) = {\lambda ^5} - 289.557{\lambda ^4} - 233.419{\lambda ^3} - 86.890{\lambda ^2} - 15.150{\lambda } -129.910. \end{aligned}$$

(30)

Moreover, $\lambda _1= -1.0402$, $\lambda _2= -4.0150$, $\lambda _3= -5.0150$, $\lambda _4= -2.0403$ and $\lambda _5= -3.0400$ are computed as the characteristic roots of Eq. (30). Given that each of the eigenvalues is a negative real number, $E_\oplus$ is an asymptotically stable equilibrium point. The chaotic behavior of the Proposed model show in Figs. 4, 5 and 6.

Fig. 4

The chaotic interactions between model compartments under the influence of extracellular $\alpha$-syn.

Fig. 5

The chaotic interactions between model compartments under the influence of extracellular $\alpha$-syn.

Fig. 6

The chaotic interactions between model compartments under the influence of extracellular $\alpha$-syn.

Numerical scheme

In this section, we will solve the system (3) numerically using the Newton polynomial.

$$\begin{aligned} \left\{ \begin{array}{l}{}^{FFM}D_{0,t}^{\varpi ,\vartheta }N\left( t \right) = \sigma - \beta N\alpha S - {a_1}N - {a_2}N - {\mu _1}N,\\ {}^{FFM}D_{0,t}^{\varpi ,\vartheta }I\left( t \right) = \beta N\alpha S - {d_1}I - {a_1}I - {a_2}I,\\ {}^{FFM}D_{0,t}^{\varpi ,\vartheta }\alpha S\left( t \right) = e{d_1}I - {a_1}\alpha S - {a_2}\alpha S,\\ {}^{FFM}D_{0,t}^{\varpi ,\vartheta }M\left( t \right) = {a_1}I + {a_1}\alpha S - {\mu _2}M,\\ {}^{FFM}D_{0,t}^{\varpi ,\vartheta }T\left( t \right) = {a_1}I + \left( {{a_1} + {a_2}} \right) \alpha S - {\mu _3}T.\end{array} \right. \end{aligned}$$

(31)

Simplifying the given system

$$\begin{aligned} \begin{aligned}&{}^{FFM}\textrm{D}_{0,t}^{\varpi ,\vartheta }N(t)= \Upsilon _1[t,N,I,\alpha S,M,T],\\ &{}^{FFM}\textrm{D}_{0,t}^{\varpi ,\vartheta }I(t)= \Upsilon _2[t,N,I,\alpha S,M,T],\\ &{}^{FFM}\textrm{D}_{0,t}^{\varpi ,\vartheta }\alpha S(t)= \Upsilon _3[t,N,I,\alpha S,M,T],\\ &{}^{FFM}\textrm{D}_{0,t}^{\varpi ,\vartheta }M(t)= \Upsilon _4[t,N,I,\alpha S,M,T],\\ &{}^{FFM}\textrm{D}_{0,t}^{\varpi ,\vartheta }T(t)= \Upsilon _5[t,N,I,\alpha S,M,T]. \end{aligned} \end{aligned}$$

(32)

Fractal-fractional integral with Mittag–Leffler kernel yields:

$$\begin{aligned} N(t_{q} +1)&= N(0)+\frac{1-\varpi }{\mathbb{A}\mathbb{B}(\varpi )} t_{q}^{1-\vartheta } \Upsilon _1\big [t_{q},N(t_{q}),I(t_{q}),\alpha S(t_{q}),M(t_{q}),T(t_{q})))\big ] \nonumber \\ &+ \frac{\varpi }{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )}\displaystyle \sum _{v=2}^{q} \int _{t_v}^{t_{v+1}} \Upsilon _1(t,N,I,\alpha S, M,T)\chi ^{1-\vartheta }(t_{{q}+1}-\chi )^{\varpi -1}d\chi . \end{aligned}$$

(33)

Reviewing the Newton polynomial

$$\begin{aligned} W(t,N,I,\alpha S,M,T)&\simeq ~ W(t_{q-2},N_{q-2},I_{q-2},\alpha S_{q-2},M_{q-2},T_{q-2})+\frac{1}{\Delta t}\Big [W(t_{q-1},N_{q-1},I_{q-1},\alpha S_{q-1},M_{q-1},N_{q-1})\nonumber \\&-W(t_{q-2},G_{q-2},I_{q-2},\alpha S_{q-2},M_{q-2},T_{q-2})\Big ] \nonumber \\ &\times (\chi -t_{{q}-2})+\frac{1}{2{\Delta t}^2}\Big [W(t_{q},N_{q},I_{q},\alpha _{q},M_{q},T_{q})-2W(t_{q-1},N_{q-1},I_{q-1},\alpha _{q-1},M_{q-1},T_{q-1}) \nonumber \\ &-W(t_{q-2},N_{q-2},I_{q-2},\alpha S_{q-2},M_{q-2},T_{q-2})\Big ]\times (\chi -t_{{q}-2})(\chi -t_{{q}-1}). \end{aligned}$$

To solve equations (33), the Newton polynomial can be utilized. This provides us

$$\begin{aligned} \begin{aligned} N_{(q +1)}&= N(0)+ \frac{1-\varpi }{\mathbb{A}\mathbb{B}(\varpi )} t_{q}^{1-\vartheta } \Upsilon _1\big (t_{q},N(t_{q}),I(t_{q}), \alpha S(t_{q}),M(t_{q}),T(t_{q})\big )\\ &+\frac{\varpi }{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )}\sum _{v=2}^{q}\Upsilon _1\big (t_{v-2},N^{v-2},I^{v-2},\alpha S^{v-2},M^{v-2},T^{v-2}\big )t_{v-2}^{1-\vartheta }\times \int _{t_v}^{t_{v+1}}(t_{{q}+1}-\chi )^{\varpi -1}d\chi \\ &+\frac{\varpi }{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )}\sum _{v=2}^{q} \frac{1}{\Delta t} \Big [t_{v-1}^{1-\vartheta }\Upsilon _1\big (t_{v-1},N^{v-1},I^{v-1},\alpha S^{v-1},M^{v-1},T^{v-1}\big )\\ &-t_{v-2}^{1-\vartheta }\Upsilon _1\big (t_{v-2},N^{v-2},I^{v-2},\alpha S^{v-2})\Big ] \times \int _{t_v}^{t_{v+1}} (\chi -t_{v-2})(t_{{q}+1}-\chi )^{\varpi -1}d\chi \\ &+\frac{\varpi }{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi )}\sum _{v=2}^{q} \frac{1}{2\Delta t^2} \Big [t_v^{1-\vartheta }\Upsilon _1\big (t_{v},N^{v},I^{v},\alpha S^{v},M^{v},T^{v}\big ) \\ &-2t_{v-1}^{1-\vartheta }\Upsilon _1\big (t_{v-1},N^{v-1},I^{v-1},\alpha S^{v-1},M^{v-1},T^{v-1}\big )\\ &+t_{v-2}^{1-\vartheta }\Upsilon _1\big (t_{v-2},N^{v-2},I^{v-2},\alpha S^{v-2},M^{v-2},T^{v-2}\big )\Big ]\times \int _{t_v}^{t_{v+1}} (\chi -t_{v-2})(\chi -t_{v-1})(t_{{q}+1}-\chi )^{\varpi -1}d\chi . \end{aligned} \end{aligned}$$

(34)

To determine the integrals in the equations (34), perform the following calculations.

$$\begin{aligned}&\int _{t_{v}}^{t_{{v}+1}}(t_{{q}+1}-\chi )^{\varpi -1}d\chi = \frac{(\Delta t)^{\varpi }}{\varpi }\Big [({q}-{v}+1)^{\varpi } -({q}-{v})^{\varpi } \Big ]\nonumber \\ &\int _{t_{v}}^{t_{{v}+1}} (\chi -t_{{v}-2})(t_{{q}+1}-\chi )^{\varpi -1}d\chi = \frac{(\Delta t)^{\varpi +1}}{\varpi (\varpi +1)}\Big [({q}-{v}+1)^\varpi ({q}-{v}+3+2\varpi ) -({q}-{v})^{\varpi }({q}-{v}+3+3\varpi ) \Big ]\nonumber \\ &\int _{t_{v}}^{t_{{v}+1}} (\chi -t_{{v}-2})(\chi -t_{{v}-1})(t_{{q}+1}-\chi )^{{\varpi }-1}d\chi = \frac{(\Delta t)^{\varpi +2}}{\varpi (\varpi +1)(\varpi +2)}\times \Big [({q}-{v}+1)^{\varpi }\Big \{2({q}-{v})^2 +(3\varpi +10)\nonumber \\ &({q}-{v})+2\varpi ^2+9\varpi +12\Big \}-({q}-{v})^{\varpi }\Big \{2({q}-{v})^2 +(5\varpi +10)({q}-{v})+6\varpi ^2+18\varpi +12\Big \}\Big ]. \end{aligned}$$

(35)

As a result, we finally get

$$\begin{aligned} \begin{aligned} N{(q +1)}&= N(0)+ \frac{1-\varpi }{\mathbb{A}\mathbb{B}(\varpi )} t_q^{1-\vartheta } \Upsilon _1\big [t_q,N(t_q),I(t_q),\alpha S(t_q),M(t_q),T(t_q)\big ]\\ &+\frac{\varpi (\Delta t)^{\varpi }}{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi +1)}\sum _{v=2}^q\Upsilon _1\big [t_{v-2},N^{v-2},I^{v-2},\alpha S^{v-2},M^{v-2},T^{v-2}\big ]t_{v-2}^{1-\vartheta }\times \daleth \\ &+\frac{\varpi (\Delta t)^{\varpi }}{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi +2)}\sum _{v=2}^q\Big \{t_{v-1}^{1-\vartheta }\Upsilon _1\big [t_{v-1},N^{v-1},I^{v-1}, \alpha S^{v-1},M^{v-1},T^{v-1}\big ]\\&-t_{v-2}^{1-\vartheta }\Upsilon _1\big [t_{v-2},N^{v-2},I^{v-2},\alpha S^{v-2},M^{v-2},T^{v-2}\big ]\Big \} \times \daleth _1\\ &+\frac{\varpi (\Delta t)^{\varpi }}{2\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi +3)}\sum _{v=2}^q \Big \{t_v^{1-\vartheta }\Upsilon _1\big [t_{v},N^v,I^v, \alpha S^v,M^v,T^v\big ]\\ &-2t_{v-1}^{1-\vartheta }\Upsilon _1\big [t_{v-1},N^{v-1},I^{v-1},\alpha S^{v-1},M^{v-1},T^{v-1}\big ]\\ &+t_{v-2}^{1-\vartheta }\Upsilon _1\big [t_{v-2},N^{v-2},I^{v-2},\alpha S^{v-2},M^{v-2},T^{v-2}\big ]\Big \}\times \daleth _2. \end{aligned} \end{aligned}$$

(36)

Similarly solve for I, $\alpha S$, T, M.

$$\begin{aligned} & \begin{aligned} I{(q +1)}&= I(0)+ \frac{1-\varpi }{\mathbb{A}\mathbb{B}(\varpi )} t_q^{1-\vartheta } \Upsilon _2\big [t_q,N(t_q),I(t_q),\alpha S(t_q),M(t_q),T(t_q)\big ]\\ &+\frac{\varpi (\Delta t)^{\varpi }}{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi +1)}\sum _{v=2}^q\Upsilon _2\big [t_{v-2},N^{v-2},I^{v-2},\alpha S^{v-2},M^{v-2},T^{v-2}\big ]t_{v-2}^{1-\vartheta }\times \daleth \\ &+\frac{\varpi (\Delta t)^{\varpi }}{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi +2)}\sum _{v=2}^q \Big \{t_{v-1}^{1-\vartheta }\Upsilon _2\big [t_{v-1},N^{v-1},I^{v-1}, \alpha S^{v-1},M^{v-1},T^{v-1}\big ]\\&-t_{v-2}^{1-\vartheta }\Upsilon _2\big [t_{v-2},N^{v-2},I^{v-2},\alpha S^{v-2},M^{v-2},T^{v-2}\big ]\Big \} \times \daleth _1\\ &+\frac{\varpi (\Delta t)^{\varpi }}{2\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi +3)}\sum _{v=2}^q \Big \{t_v^{1-\vartheta }\Upsilon _2\big [t_{v},N^v,I^v, \alpha S^v,M^v,T^v\big ]\\ &-2t_{v-1}^{1-\vartheta }\Upsilon _2\big [t_{v-1},N^{v-1},I^{v-1},\alpha S^{v-1},M^{v-1},T^{v-1}\big ]\\ &+t_{v-2}^{1-\vartheta }\Upsilon _2\big [t_{v-2},N^{v-2},I^{v-2},\alpha S^{v-2},M^{v-2},T^{v-2}\big ]\Big \}\times \daleth _2. \end{aligned} \end{aligned}$$

(37)

$$\begin{aligned} & \quad \begin{aligned} \alpha S{(q +1)}&= \alpha S(0)+ \frac{1-\varpi }{\mathbb{A}\mathbb{B}(\varpi )} t_q^{1-\vartheta } \Upsilon _3\big [t_q,N(t_q),I(t_q),\alpha S(t_q),M(t_q),T(t_q)\big ]\\ &+\frac{\varpi (\Delta t)^{\varpi }}{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi +1)}\sum _{v=2}^q\Upsilon _3\big [t_{v-2},N^{v-2},I^{v-2},\alpha S^{v-2},M^{v-2},T^{v-2}\big ]t_{v-2}^{1-\vartheta }\times \daleth \\ &+\frac{\varpi (\Delta t)^{\varpi }}{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi +2)}\sum _{v=2}^q \Big \{t_{v-1}^{1-\vartheta }\Upsilon _3\big [t_{v-1},N^{v-1},I^{v-1}, \alpha S^{v-1},M^{v-1},T^{v-1}\big ]\\&-t_{v-2}^{1-\vartheta }\Upsilon _3\big [t_{v-2},N^{v-2},I^{v-2},\alpha S^{v-2},M^{v-2},T^{v-2}\big ]\Big \} \times \daleth _1\\ &+\frac{\varpi (\Delta t)^{\varpi }}{2\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi +3)}\sum _{v=2}^q \Big \{t_v^{1-\vartheta }\Upsilon _3\big [t_{v},N^v,I^v, \alpha S^v,M^v,T^v\big ]\\ &-2t_{v-1}^{1-\vartheta }\Upsilon _3\big [t_{v-1},N^{v-1},I^{v-1},\alpha S^{v-1},M^{v-1},T^{v-1}\big ]\\ &+t_{v-2}^{1-\vartheta }\Upsilon _3\big [t_{v-2},N^{v-2},I^{v-2},\alpha S^{v-2},M^{v-2},T^{v-2}\big ]\Big \}\times \daleth _2. \end{aligned} \end{aligned}$$

(38)

$$\begin{aligned} & \begin{aligned} M{(q +1)}&= M(0)+ \frac{1-\varpi }{\mathbb{A}\mathbb{B}(\varpi )} t_q^{1-\vartheta } \Upsilon _4\big [t_q,N(t_q),I(t_q),\alpha S(t_q),M(t_q),T(t_q)\big ]\\ &+\frac{\varpi (\Delta t)^{\varpi }}{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi +1)}\sum _{v=2}^q\Upsilon _4\big [t_{v-2},N^{v-2},I^{v-2},\alpha S^{v-2},M^{v-2},T^{v-2}\big ]t_{v-2}^{1-\vartheta }\times \daleth \\ &+\frac{\varpi (\Delta t)^{\varpi }}{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi +2)}\sum _{v=2}^q\Big \{t_{v-1}^{1-\vartheta }\Upsilon _4\big [t_{v-1},N^{v-1},I^{v-1}, \alpha S^{v-1},M^{v-1},T^{v-1}\big ]\\&-t_{v-2}^{1-\vartheta }\Upsilon _4\big [t_{v-2},N^{v-2},I^{v-2},\alpha S^{v-2},M^{v-2},T^{v-2}\big ]\Big \} \times \daleth _1\\ &+\frac{\varpi (\Delta t)^{\varpi }}{2\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi +3)}\sum _{v=2}^q\Big \{t_v^{1-\vartheta }\Upsilon _4\big [t_{v},N^v,I^v, \alpha S^v,M^v,T^v\big ]\\ &-2t_{v-1}^{1-\vartheta }\Upsilon _4\big [t_{v-1},N^{v-1},I^{v-1},\alpha S^{v-1},M^{v-1},T^{v-1}\big ]\\ &+t_{v-2}^{1-\vartheta }\Upsilon _4\big [t_{v-2},N^{v-2},I^{v-2},\alpha S^{v-2},M^{v-2},T^{v-2}\big ]\Big \}\times \daleth _2. \end{aligned} \end{aligned}$$

(39)

$$\begin{aligned} & \begin{aligned} T{(q +1)}&= T(0)+ \frac{1-\varpi }{\mathbb{A}\mathbb{B}(\varpi )} t_q^{1-\vartheta } \Upsilon _5\big [t_q,N(t_q),I(t_q),\alpha S(t_q),M(t_q),T(t_q)\big ]\\ &+\frac{\varpi (\Delta t)^{\varpi }}{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi +1)}\sum _{v=2}^q\Upsilon _5\big [t_{v-2},N^{v-2},I^{v-2},\alpha S^{v-2},M^{v-2},T^{v-2}\big ]t_{v-2}^{1-\vartheta }\times \daleth \\ &+\frac{\varpi (\Delta t)^{\varpi }}{\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi +2)}\sum _{v=2}^q\Big \{t_{v-1}^{1-\vartheta }\Upsilon _5\big [t_{v-1},N^{v-1},I^{v-1}, \alpha S^{v-1},M^{v-1},T^{v-1}\big ]\\&-t_{v-2}^{1-\vartheta }\Upsilon _5\big [t_{v-2},N^{v-2},I^{v-2},\alpha S^{v-2},M^{v-2},T^{v-2}\big ]\Big \} \times \daleth _1\\ &+\frac{\varpi (\Delta t)^{\varpi }}{2\mathbb{A}\mathbb{B}(\varpi )\Gamma (\varpi +3)}\sum _{v=2}^q \Big \{t_v^{1-\vartheta }\Upsilon _5\big [t_{v},N^v,I^v, \alpha S^v,M^v,T^v\big ]\\ &-2t_{v-1}^{1-\vartheta }\Upsilon _5\big [t_{v-1},N^{v-1},I^{v-1},\alpha S^{v-1},M^{v-1},T^{v-1}\big ]\\ &+t_{v-2}^{1-\vartheta }\Upsilon _5\big [t_{v-2},N^{v-2},I^{v-2},\alpha S^{v-2},M^{v-2},T^{v-2}\big ]\Big \}\times \daleth _2. \end{aligned} \end{aligned}$$

(40)

Where

$$\begin{aligned} \daleth= & (q-v+1)^{\varpi } -(q-v)^{\varpi }\nonumber \\ \daleth _1= & (q-v+1)^{\varpi } (q-v+3+2\varpi )-(q-v)^{\varpi }(q-v+3+3\varpi ) \nonumber \\ \daleth _2= & (q-v+1)^{\varpi }\Big [2(q-v)^2+(3\varpi +10)(q-v)+2\varpi ^2+9\varpi +12\Big ]\nonumber \\ & -(q-v)^{\varpi }\Big [2(q-v)^2+(5\varpi +10)(q-v)+6\varpi ^2+18\varpi +12\Big ]. \end{aligned}$$

(41)

Remark: The Newton polynomial method is chosen for its superior accuracy in approximating solutions of fractional-order systems with memory effects, especially under the Mittag–Leffler kernel. Its higher-order interpolation capability ensures better convergence and computational efficiency compared to conventional methods when modeling complex neurodegenerative dynamics.

Results of proposed scheme

A mathematical analysis of Parkinson’s disease’s non-linear model has been explained. To observe the sound affects of the parameters used in this Parkinson’s disease model, several of numerical simulations based on the parameter values are carried out to validate the effect of the fractional derivative on the compartments. The Fractal fractional derivative is used to generate the model’s numerical results for different fractional values according to the steady-state point. The graphs of the approximate solutions against different fractional-order $\varpi$ are provided as in Figs. 7, 8, 9, 10, 11, 12, 13, 14, 15 and 16. In Fig. 7 lower fractional orders $\varpi$ slow the decline of N(t), indicating prolonged neuron survival compared $\varpi =1$. This show that memory effects preserve neuron functionality for longer, delaying the onset of severe neurodegeneration. Smaller $\varpi$ values delay the rise and reduce the peak of I(t) in Fig. 8, indicating a slower infection progression. This reflects a moderated infection spread, likely due to the influence of immune defenses or slower neuronal susceptibility to infection. In Fig. 9 when decreasing fractional order then results in a slower buildup and reduced maximum of extracellular $\alpha$-synuclein. This indicates reduced aggregation of toxic proteins, potentially limiting their harmful effects on neurons. Smaller fractional order values delay and moderate microglial activation in Fig. 10, resulting in a less aggressive inflammatory response. This suggests that inflammation is better regulated, reducing collateral damage to healthy neurons. In Fig. 11 decreasing fractional order value slows the activation of T cells, leading to a delayed and less intense immune response. This controlled immune activation reduces the risk of chronic inflammation and neurodegeneration. In Fig. 12$R_0>1$, decreasing fractional order still slows neuron degradation, though the disease progression state accelerates overall decline. Slower degradation reflects improved resilience even in a worsening disease environment. Lower $\varpi$ delays the peak of infection and reduces its intensity in Fig. 13, even in an active disease state. The slower spread of infection provides a buffer against rapid neurodegeneration. Decreasing fractional order values slow down protein aggregation and reduce toxic buildup in Fig. 14. Slower accumulation of $\alpha$-synuclein reduces its neurotoxic effects in disease progression. Microglial activation Fig. 15 is delayed and reduced for smaller $\varpi$, even with disease progression. A moderated inflammatory response minimizes further neuronal damage. Decrease $\varpi$ delays and moderates T cell activation in Fig. 16, even under worsening disease dynamics. Controlled immune activation prevents excessive inflammation, reducing overall tissue damage.

Fractional-order models capture real-world phenomena like prolonged inflammatory responses, delayed disease recovery, and memory-dependent dynamics that integer-order models cannot. They are particularly suited to biological systems with feedback loops and time-dependent processes. The fractal-fractional derivative with the Mittag-Leffler kernel effectively models the memory-dependent and prolonged dynamics of Parkinson s disease. Its non-local properties capture the slow accumulation of $\alpha$-synuclein and persistent immune activation, offering deeper insights into neurodegenerative processes.

Fig. 7

Simulation of N(t) at different fractional order values for $R_0<1$.

Fig. 8

Simulation of I(t) at different fractional order values for $R_0<1$.

Fig. 9

Simulation of $\alpha S(t)$ at different fractional order values for $R_0<1$.

Fig. 10

Simulation of M(t) at different fractional order values for $R_0<1$.

Fig. 11

Simulation of T(t) at different fractional order values for $R_0<1$.

Fig. 12

Simulation of N(t) at different fractional order values for $R_0>1$.

Fig. 13

Simulation of I(t) at different fractional order values for $R_0>1$.

Fig. 14

Simulation of $\alpha S(t)$ at different fractional order values for $R_0>1$.

Fig. 15

Simulation of M(t) at different fractional order values for $R_0>1$.

Fig. 16

Simulation of T(t) at different fractional order values for $R_0>1$.

Conclusion

A nonlinear compartmental model was developed in order to have a better understanding of the dynamics of Parkinson’s disease. There are five separate compartments in this model. Additionally, a fractional-order model was developed using fundamental mathematical methods. The well-posedness of the model’s nonlinear ordinary differential equations was confirmed by a thorough investigation. The Banach fixed-point theorem was utilized in the nonlinear functional analysis to ensure the existence and positivity of solutions. Finding the fractional-order Parkinson’s disease model’s equilibria required both a qualitative assessment and a quantitative investigation. Local Stability is explored, to determine the global stability of the fractional order Parkinson s disease model, a Lyapunov function was utilized. The use of PID controllers and chaos control further demonstrates the model’s applicability for exploring therapeutic interventions. Numerical simulations using Newton polynomial schemes validated the model’s behavior across disease-free and endemic states. This framework not only enhances understanding of Parkinson’s disease dynamics but also provides a robust basis for designing personalized control strategies. Future work may involve extending the model to include stochastic effects or spatial heterogeneity for more comprehensive insights.