Dynamic fractional-order ISDR rumor propagation model incorporating refutation mechanism in complex networks

Abstract

Rumor spreading has been posing a significant threat to maintain the normal social order. In this paper, we propose a ISDR rumor propagation model on scale-free networks that considers fractional-order and refutation mechanism. we acquire basic reproduction number ${R_0}$ based on the rumor equilibrium point ${E^*}$, which thoroughly characterizes the dynamics of rumor propagation. we have demonstrated that when ${R_0}<1$, the rumor-free equilibrium point is globally asymptotically stable; when ${R_0}>1$, the rumor equilibrium point is globally asymptotically stable. Numerical simulations are provided to illustrate the main theoretical results. By analyzing the existence and uniqueness of the equilibrium solution, we demonstrate the superiority of fractional-order dynamics and refutation mechanism in the rumor propagation model. Our findings are crucial for understanding the impact of network structure on the dynamics of fractional-order systems.

Introduction

Rumors are defined as unconfirmed elaborations or annotations related to common interests and are widely spread by online social media¹. The convenience of social media, with its low barriers to entry and instantaneous communication capabilities, facilitates extensive user engagement in information dissemination processes. However, rumor spreading may cause a serious threat to society. For example, rumors during COVID-19 outbreaks can quickly trigger a mass effect, causing some people to believe and propagate these rumors through various channels. Therefore, studying the spreading process of rumors can provide insights into the influence of different factors and significantly reduce the adverse effects of rumors, leading to the development of better control strategies to restrain rumor propagation².

Numerous rumor models concerning transmission mechanism and forecasting the spread of rumors across populations have been proposed. In the early days, the D-K model, a classic rumor propagation model put forward by Daley and Kendall, was introduced³. In this D-K model, the population is grouped into three classes: people who contact with nothing of the rumor, people who push to spread the rumor, and people who know but will never spread the rumor. Based on the D-K model, Maki and Thomson proposed the M-K model which assumes that a spreader can change into a stifler who stops spreading the rumor⁴. Based on these two models, many extended rumor propagation models have been proposed and studied^5,6,7. However, these rumor propagations are not appropriate for a social network environment, as they do not consider the influence of complex network topologies, such as regular networks, random networks, homogeneous networks and heterogeneous networks^8,9,10,11. Zanette first researched the dynamic behavior of rumor spreading and found that the spreading threshold is observably influenced by the network topologies, especially in small- world networks⁸. Moreno et al. developed the mean-field theory in the scale-free network⁹. Zhu et al. proposed a rumor propagation model with a silence-forcing function and it was proven that optimal control can reduce the scale of rumor spreading in online social networks¹⁰. Yu et al. researched new 2I2SR rumor propagation models with and without time-delay based on multilingual environment and proposed a real-time optimization method that minimizes the cost of restraining rumors to eliminate them within an expected time period¹¹. Ai et al. improved the traditional Barabasi-Albert scale-free network and proposed a network topology model that conforms to the characteristics of sharing social networks, based on complex network theory and the actual characteristics of sharing social networks¹².

In recent years, a multitude of rumor propagation models have been proposed, aiming to gaining insight into the influence of different factors on the prevalence of rumors such as heterogeneity of transmission and network^13,14, the hesitating mechanism¹⁵, the memory¹⁶, the skepticism and denial¹⁷, the education or scientific knowledge^18,19, the latency²⁰, super spreading effect²¹ and others^22,23. Based on different rumor spreading models, true information or positive news is also an important factor affecting rumor spreading. Refutation mechanism can be the truth of the rumor released by the government or media in an emergency. There are many studies of true information²⁴. Yang et al. proposed a competitive diffusion model to regulate rumors by propagating true information on social networks²⁵. Tian et al. proposed a novel rumor spreading model that considering debunking behavior to describe the rumor dynamics in OSNs under emergencies²⁶. Jiang et al. put forward a Spreading–debunking competitive model based on data from the real-world rumor case²⁷. Zhang et al. came up with two-stage model and refutation mechanism with time delay on the different network topologies²⁸. Huo et al. established a ISTR model of rumor by including influencing factors of true information spreader and social reinforcement in Heterogeneous Networks²⁹. Thus, motivated by these aspect, it is more suitable to add a refutation mechanism into the rumor propagation model to improve the image of the relevant authorities and to strengthen other positive effects on social stability.

Fractional differential equations can depict the dynamics of plentiful physical systems in a more precise way than integer order method³⁰. Many scholars have recommended fractional-order to describe real-life problems with a fractional order Caputo derivative^{31,32,33,34,35,36,37,38}. Angstman et al. concluded a fractional-order SIR model with a stochastic process that contains Infectious individual along with a time effect³¹. Huo et al. studied a fractional-order SIR model by means of birth and death rates on heterogeneous networks³². Alzahrani et al. proposed fractional-order derivative for the dynamical analysis of Hepatitis E model and optimal control³³. Kheiri et al. studied a multi-patch model with fractional-order derivative to reveal the impact of human behavior on the HIV/AIDS propagate³⁴. Singh et al. researched the dynamic model of rumor propagation associated with non-integer order in a social network³⁵. Jajarmi et al. extended a fractional version of SIRS model to investigate the HRSV disease involving a new derivative operator with Mittag-Leffler kernel in the Caputo sense³⁶. Ali et al. addressed the fractional mathematical model which describes the transmission dynamics of zika virus infection³⁷. Alzahrani et al. utilized proportional fractional-order differential equations with time dela to predict each fractional change more realistically³⁸. Although there have been numerous integer-order models to describe the dynamics of rumor propagation, few individuals probe into fractional-order rumor models on complex networks. Inspired by the above analysis, we will adopt Caputo derivative and propose a fractional-order ISDR rumor propagation model incorporating refutation mechanism on scale-free networks based on^26,32.

The rest of this paper is organized as follows. In Sect. 2, fractional-order ISDR rumor model incorporating refutation mechanism on scale-free networks is represented and some properties of the fractional calculus are provided. In Sect. 3, on account of the existence of rumor equilibrium point, the threshold is proven. In Sect. 4, the stability of equilibrium point is shown. In Sect. 5, the influences of two immunization strategies are proposed and compared. In Sect. 6, Sensitivity analysis and several numerical simulations are proposed. Finally, several conclusions are given at the end of this paper.

The fractional-order ISDR rumor propagation model and basic properties of fractional calculus

The fractional-order ISDR rumor propagation model

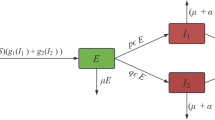
In this section, we build a novel fractional-order ISDR rumor propagation model incorporating refutation mechanism on scale-free networks. The flow diagram of the model is shown in (Fig. 1). We have divided the total population into four categories: ignorants who have never known the rumor and consequently are open to trust the rumor, denoted by I; spreaders who know and spread the rumor actively, denoted by S; debunkers who know the true information about the rumor and become the debunker under social reinforcement, denoted by D; resisters who have contacted the spreaders or debunkers but resist and do not spread it, denoted by R. On scale-free networks, every individual represents for a node of the network and the connections are deemed to the relations between individuals meanwhile which the rumor can transmit. let ${I_k}\left( t \right)$, ${S_k}\left( t \right)$, ${D_k}\left( t \right)$ and ${R_k}\left( t \right)$ be the relative densities of ignorants, spreaders, debunkers and resisters by means of the degree $k=1,2, \ldots ,n$ at time t respectively.

Fig. 1

The flow diagram of the model.

The transition among these states is subjected to the following rules.

(1) When the ignorants are connected to the spreaders, they will know the rumor thus become the spreaders with a probability of $\left( {1 - p} \right)\beta$ and become the debunkers with a probability of $p\beta$. p is used to describe the attractive degree of the debunkers and$\beta$ is the infection rate.

(2) The parameter $\gamma$ is the recovery rate of the spreaders under the influence of forgetting mechanism. When the spreaders get in touch with debunkers, it will become a debunker with probability $\varepsilon$. Moreover, the debunker is likely to be a resister in the probability $\delta$.

(3) We assume that the immigrate rate is $\Lambda$ and emigrate rate is $\mu$. All the newly added nodes are classified as ignorants. The parameters are all nonnegative.

According to the mean-field theory on complex networks³⁹, we can obtain the equations of propagate dynamics as follows:

$$\left\{ \begin{gathered} {D^\alpha }{I_k}\left( t \right)=\Lambda - \beta k{I_k}\left( t \right)\Theta \left( t \right) - \mu {I_k}\left( t \right), \hfill \\ {D^\alpha }{S_k}\left( t \right)=\left( {1 - p} \right)\beta k{I_k}\left( t \right)\Theta \left( t \right) - \varepsilon {S_k}\left( t \right) - \gamma {S_k}\left( t \right) - \mu {S_k}\left( t \right), \hfill \\ {D^\alpha }{D_k}\left( t \right)=p\beta k{I_k}\left( t \right)\Theta \left( t \right)+\varepsilon {S_k}\left( t \right) - \delta {D_k}\left( t \right) - \mu {D_k}\left( t \right), \hfill \\ {D^\alpha }{R_k}\left( t \right)=\gamma {S_k}\left( t \right)+\delta {D_k}\left( t \right) - \mu {R_k}\left( t \right),k=1,2, \ldots ,n. \hfill \\ \end{gathered} \right.$$

(1)

where ${D^\alpha }$ is the Caputo derivative, $\alpha \left( {0<\alpha \le 1} \right)$ is the order parameter on the system (1). $\Theta \left( t \right)$ is the probability that a random selection ignorant from a node of degree k refers to a spreader with node of degree ${k^{^\prime}}$, which meets $\sum\nolimits_{{{k^{^\prime}}}} {p\left( {\left. {{k^{^\prime}}} \right|k} \right){S_{{k^{^\prime}}}}}$, and $p\left( {\left. {{k^{^\prime}}} \right|k} \right)$ is assumed to the probability that a node with k degree refers to a node with ${k^{^\prime}}$ degree. The relationship of nodes is supposed to be uncorrelated for simplicity, so $p\left( {\left. {{k^{^\prime}}} \right|k} \right)=\frac{{{k^{^\prime}}p\left( {{k^{^\prime}}} \right)}}{{\sum\nolimits_{k} {kp\left( k \right)} }}$, satisfying the relation as follows:

$$\Theta \left( t \right)=\frac{{\sum\limits_{{{k^{^\prime}}=1}}^{n} {{k^{^\prime}}p\left( {\left. {{k^{^\prime}}} \right|k} \right){S_{{k^{^\prime}}}}} }}{{\left\langle k \right\rangle }}.$$

(2)

where $\left\langle k \right\rangle =\sum\limits_{{{k^{^\prime}}=1}}^{n} {kp\left( k \right)}$ is the average degree in regard to the network and $p\left( k \right)$ stands for the degree of distribution.

Basic properties of fractional calculus

We firstly give the definitions of fractional-order integration and some properties of the fractional-order differential equation, since those have the advantages of dealing properly with initial value problems³⁹. The Riemann–Liouville and the Caputo formula are two kinds of crucial and well-studied definitions^{40,41,42,43,44}.

Definition 2.1

The Riemann–Liouville fractional integral of order $\alpha >0$ of a function $f:{R^+} \to R$ is provided by.

${I^\alpha }f\left( x \right)=\frac{1}{{\Gamma \left( \alpha \right)}}\int_{0}^{x} {{{\left( {x - t} \right)}^{\alpha - 1}}f\left( t \right)} dt.$

Definition 2.2

The Riemann–Liouville fractional derivative of order $\alpha >0$ of a function $f:{R^+} \to R$ is provided by.

${D^\alpha }f\left( x \right)={\left( {\frac{{\text{d}}}{{{\text{d}}x}}} \right)^n}{I^{n - \alpha }}f\left( x \right)=\frac{1}{{\Gamma \left( {n - \alpha } \right)}}{\left( {\frac{{\text{d}}}{{{\text{d}}x}}} \right)^n}\int_{0}^{x} {{{\left( {x - t} \right)}^{n - \alpha - 1}}f\left( t \right)} dt,n=\left[ \alpha \right]+1.$

Definition 2.3

The Caputo fractional derivative of order $\alpha \in \left( {n - 1,n} \right)$ of a continuous function $f:{R^+} \to R$ is provided by.

${D^\alpha }f\left( x \right)={I^{n - \alpha }}{D^n}f\left( x \right)=\frac{1}{{\Gamma \left( {n - \alpha } \right)}}\int_{0}^{x} {\frac{{{f^n}\left( \tau \right)d\tau }}{{{{\left( {t - \tau } \right)}^{\alpha +1 - n}}}}.}$

While when $\alpha \to n$, the Caputo fractional derivative of function $f:{R^+} \to R$ is given by.

$\mathop {\lim }\limits_{{\alpha \to n}} {D^\alpha }f\left( x \right)={f^n}\left( 0 \right)+\int_{0}^{t} {{f^{n+1}}\left( \tau \right)} d\tau ={f^n}\left( x \right),n=1,2, \ldots .$

Definition 2.4

When function.

is a constant function $f$ $\left( {i.e.f\left( x \right)=u} \right)$, the Riemann–Liouville fractional derivative and Caputo fractional derivative are respectively provided by

$\begin{gathered} {D^\alpha }u=\frac{u}{{\Gamma \left( {n - \alpha } \right)}}{x^{ - \alpha }},x>0. \hfill \\ {D^\alpha }u=0. \hfill \\ \end{gathered}$

Consider the following autonomous system.

${D^\alpha }x\left( t \right)=f\left( x \right),f\left( 0 \right)=0.$

To prove the globally asymptotical stability of equilibrium points, we proposed the following lemma.

Lemma 2.5

Let D is a positive invariant set. If the following conditions $\exists V\left( x \right):D \to R$ with continuous first partial derivatives are satisfied:

${\left. {{D^\alpha }V} \right|_{\left( 5 \right)}} \le 0.$

Let $E=\left\{ {{{\left. {{D^\alpha }V} \right|}_{\left( 5 \right)}}=0,x \in D} \right\}$ and M be the largest invariant set of E. Then every solution $x\left( t \right)$ originating in D tends to M as $t \to \infty$. Particularly, when $M=\left\{ 0 \right\}$, then $x \to \infty$, as $t \to \infty$.

Lemma 2.6

Suppose $x\left( t \right) \in {R^+}=\left[ {0,+\infty } \right)$ be a continuous and derivable function. Accordingly, for any time instant$t \ge {t_0}$.

${D^\alpha }\left[ {x\left( t \right) - {x^*} - {x^*}\ln \frac{{{x^*}}}{{x\left( t \right)}}} \right] \le \left( {1 - \frac{{{x^*}}}{{x\left( t \right)}}} \right){D^\alpha }x\left( t \right).$

Equilibrium points and basic reproduction number

Due to the total number of nodes remains invariant, the normalization condition meets ${D^\alpha }{I_k}\left( t \right)+{D^\alpha }{S_k}\left( t \right)+{D^\alpha }{D_k}\left( t \right)+{D^\alpha }{R_k}\left( t \right) \equiv 1$ at any t. We obtain ${R_k}\left( t \right)=$$1 - {I_k}\left( t \right) - {S_k}\left( t \right) - {T_k}\left( t \right)$ at any t. So, system (1) can be written as the following model:

$$\left\{ \begin{gathered} {D^\alpha }{I_k}\left( t \right)=\Lambda - \beta k{I_k}\left( t \right)\Theta \left( t \right) - \mu {I_k}\left( t \right), \hfill \\ {D^\alpha }_{k}S\left( t \right)=\left( {1 - p} \right)\beta k{I_k}\left( t \right)\Theta \left( t \right) - \varepsilon {S_k}\left( t \right) - \gamma {S_k}\left( t \right) - \mu {S_k}\left( t \right), \hfill \\ {D^\alpha }{D_k}\left( t \right)=p\beta k{I_k}\left( t \right)\Theta \left( t \right)+\varepsilon {S_k}\left( t \right) - \delta {D_k}\left( t \right) - \mu {D_k}\left( t \right),k=1,2, \ldots ,n, \hfill \\ \end{gathered} \right.$$

(3)

Note that the equilibrium points of system (1) should satisfy

$$\left\{ \begin{gathered} \Lambda - \beta kI_{k}^{*}{\Theta ^*} - \mu I_{k}^{*}=0, \hfill \\ \left( {1 - p} \right)\beta kI_{k}^{*}{\Theta ^*} - \varepsilon S_{k}^{*} - \gamma S_{k}^{*} - \mu S_{k}^{*}=0, \hfill \\ p\beta kI_{k}^{*}{\Theta ^*}+\varepsilon S_{k}^{*} - \delta D_{k}^{*} - \mu D_{k}^{*}=0,k=1,2, \ldots ,n, \hfill \\ \end{gathered} \right.$$

(4)

The rumor-free equilibrium point${E_0}$of system (1) corresponds to $I_{k}^{*}=0,$$\left( {k=1,2, \ldots ,n} \right)$, substituting them into Eq. (1), we have

$$\left\{ \begin{gathered} I_{k}^{*}=\frac{\Lambda }{\mu }, \hfill \\ D_{k}^{*}=0,k=1,2, \ldots ,n, \hfill \\ \end{gathered} \right.$$

(5)

So system (3) always exists a unique rumor-free equilibrium point${E_0}\left( {I_{1}^{0},0,0, \ldots ,I_{k}^{0},0,0, \ldots ,} \right)$, where $I_{k}^{0}=\frac{\Lambda }{\mu },k=1,2, \ldots ,n$. The rumor equilibrium point of the system (1) is equal to the case which the rumor prevails among population $\left( {I_{k}^{*} \ne 0,k=1,2, \ldots ,n} \right)$. So, the equilibrium point ${E^*}\left( {I_{k}^{*},S_{k}^{*},D_{k}^{*}} \right)$ has the form

$$\left\{ \begin{gathered} I_{k}^{*}=\frac{\Lambda }{{\beta k{\Theta ^*}+\mu }}, \hfill \\ S_{k}^{*}=\frac{{\left( {1 - p} \right)\Lambda \beta k{\Theta ^*}}}{{\left( {\varepsilon +\gamma +\mu } \right)\left( {\beta k{\Theta ^*}+\mu } \right)}}, \hfill \\ D_{k}^{*}=\frac{{\Lambda k{\Theta ^*}}}{{\rho +\mu }}\left[ {\frac{{p\beta }}{{\beta k{\Theta ^*}+\mu }}+\frac{{\left( {1 - p} \right)\varepsilon \beta }}{{\left( {\varepsilon +\gamma +\mu } \right)\left( {\beta k{\Theta ^*}+\mu } \right)}}} \right],k=1,2, \ldots ,n. \hfill \\ \end{gathered} \right.$$

(6)

Put the second equation of (6) into (2), we obtain the self-consistency equality

$${\Theta ^*}=\frac{1}{{\left\langle k \right\rangle }}\sum\limits_{{{k^{^\prime}}=1}}^{n} {{k^{^\prime}}p\left( {\left. {{k^{^\prime}}} \right|k} \right)S_{{{k^{^\prime}}}}^{*}} =\sum\limits_{{{k^{^\prime}}=1}}^{n} {\frac{{{k^{^\prime}}p\left( {{k^{^\prime}}} \right)}}{{\left\langle k \right\rangle }}\frac{{\left( {1 - p} \right)\Lambda \beta {k^{^\prime}}{\Theta ^*}}}{{\left( {\varepsilon +\gamma +\mu } \right)\left( {\beta {k^{^\prime}}{\Theta ^*}+\mu } \right)}} \triangleq F\left( {{\Theta ^*}} \right).}$$

(7)

To demonstrate the existence and uniqueness of equilibrium point ${E^*}$, we define a function.

$F(\Theta )=\frac{1}{{\left\langle k \right\rangle }}\sum\limits_{{{k^\prime }=1}}^{n} {{k^{^\prime}}p\left( {\left. {{k^{^\prime}}} \right|k} \right){S_{{k^\prime }}}} - \Theta =$$\frac{{\left( {1 - p} \right)\Lambda \beta }}{{\left\langle k \right\rangle \left( {\varepsilon +\gamma +\mu } \right)}}$$\sum\limits_{{{k^{^\prime}}=1}}^{n} {\frac{{{k^{^\prime}}p\left( {{k^{^\prime}}} \right){k^{^\prime}}{\Theta ^{}}}}{{\left\langle k \right\rangle \left( {\beta {k^{^\prime}}\Theta +\mu } \right)}} - \Theta .}$

It is easy to see that ${\Theta ^*}=0$ is a solution of (7), then $I_{k}^{*}=\frac{\Lambda }{\mu }$ and $S_{k}^{*}=D_{k}^{*}=0$,which is a rumor-free equilibrium of system (1). so as to guarantee Eq. (7) has a nontrivial solution, i.e., ${\Theta ^*} \in \left( {0,} \right.\left. 1 \right]$, the following situations must be met:

${\left. {\frac{{dF\left( {{\Theta ^*}} \right)}}{{d{\Theta ^*}}}} \right|_{{\Theta ^*}=0}}={\left. {\frac{{dF\left( {{\Theta ^*}} \right)}}{{d{\Theta ^*}}}\left[ {\frac{{\left( {1 - p} \right)\Lambda \beta }}{{\left\langle k \right\rangle \left( {\varepsilon +\gamma +\mu } \right)}}\sum\limits_{{{k^{^\prime}}=1}}^{n} {\frac{{{k^{^\prime}}p\left( {{k^{^\prime}}} \right){k^{^\prime}}{\Theta ^*}}}{{\beta {k^{^\prime}}{\Theta ^*}+\mu }}} } \right]} \right|_{{\Theta ^*}=0}}>1$ and $F\left( 1 \right) \le 1$.

Thus, we can obtain.

${R_0}=\frac{{\left( {1 - p} \right)\Lambda \beta \left\langle {{k^2}} \right\rangle }}{{\mu \left( {\varepsilon +\gamma +\mu } \right)\left\langle k \right\rangle }}.$

Where $\left\langle {{k^2}} \right\rangle =\sum\limits_{{k=1}}^{n} {{k^2}p\left( k \right)}$. Therefore, if ${R_0}>1$, then system (1) has a unique rumor equilibrium point ${E^*}$.

Theorem 3.1

Closed set $\Omega =\left\{ {\left. {\left( {{I_k},{S_k},{D_k},{R_k}} \right) \in R_{+}^{{4n}},k=1,2, \ldots ,n} \right|0 \le {N_k}={I_k}+} \right.$$\left. {{S_k}+{D_k}+{R_k} \le \frac{\Lambda }{\mu }} \right\}$ is a positive invariant set and global attractivity set of system (1).

Proof

Based on three equations of system (1), we get.

${D^\alpha }{N_k}\left( t \right)=\Lambda - \mu \left( {{I_k}+{S_k}+{D_k}+{R_k}} \right)=\Lambda - \mu {N_k}.$

Solving this equation, we have.

${N_k}\left( t \right)=\left( { - \frac{\Lambda }{\mu }+{N_k}\left( 0 \right)} \right){E_\alpha }\left( { - \mu {t^\alpha }} \right)+\frac{\Lambda }{\mu },k=1,2, \ldots ,n.$

Especially, if ${N_k}\left( 0 \right) \le \frac{\Lambda }{\mu }$, then ${N_k}\left( t \right) \le \frac{\Lambda }{\mu }$, hence closed set $\Omega$ is the positive invariant set of system (1). Additionally, due to $\mathop {\lim }\limits_{{t \to \infty }} {E_\alpha }\left( { - \mu {t^\alpha }} \right)=0$, if ${N_k}\left( 0 \right)>\frac{\Lambda }{\mu }$, accordingly the solution of system (1) is inclined to $\frac{\Lambda }{\mu }$ when time turns to infinity. Therefore, closed set $\Omega$ attracts all the solution of $R_{+}^{{4n}}$, and $\Omega$ is the global attracting set of the system (1).

The stability of the equilibrium point

In this section, we will provide evidence of the stability of ${E_0}$ and ${E^*}$, which is one of the most crucial topics in the research of rumor spreading. Specifically, we will study the local asymptotic stability and then the global attractivity of the rumor-free equilibrium point${E_0}$. That is to say, the threshold value is ${R_0}<1$, and ${E_0}$ is globally asymptotically stable.

The dynamic of rumor-free equilibrium point ${E_0}$

Theorem 4.1

The rumor-free equilibrium point ${E_0}$ of system (1) is locally asymptotically stable if ${R_0}<1$, or unstable if ${R_0}>1$.

Proof

First of all, we linearize system (1) at${E_0}$

$$\left\{ \begin{gathered} {D^\alpha }{I_k}\left( t \right)=\Lambda - \beta kI_{k}^{0}{\Theta ^*} - \mu I_{k}^{*}, \hfill \\ {D^\alpha }{S_k}\left( t \right)=\left( {1 - p} \right)\beta kI_{k}^{0}{\Theta ^*} - \varepsilon S_{k}^{*} - \gamma S_{k}^{*} - \mu S_{k}^{*}, \hfill \\ {D^\alpha }{D_k}\left( t \right)=p\beta kI_{k}^{0}{\Theta ^*}+\varepsilon S_{k}^{*} - \delta D_{k}^{*} - \mu D_{k}^{*},k=1,2, \ldots ,n, \hfill \\ \end{gathered} \right.$$

(8)

That is,${D^\alpha }{\left( {{I_1}, \ldots ,{I_n},{S_1}, \ldots ,{S_n},{D_1}, \ldots ,{D_n}} \right)^T}=J\left( {{E_0}} \right){\left( {{I_1}, \ldots ,{I_n},{S_1}, \ldots ,{S_n},{D_1}, \ldots ,{D_n}} \right)^T}$, where.

$J\left( {{E_0}} \right)={\left( \begin{gathered} - \mu \;\;\; \cdots \;\;\;\;0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \beta I_{1}^{0}g\left( 1 \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdots \;\;\;\;\;\;\;\;\;\; - \beta I_{1}^{0}g\left( n \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0\;\;\;\; \cdots \;\;\;\;0\; \hfill \\ \; \vdots \;\;\;\;\; \ddots \;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\; \ddots \;\;\;\; \vdots \;\; \hfill \\ \;0\;\;\;\; \cdots \;\;\; - \mu \;\;\;\;\;\;\;\;\;\;\;\; - \beta nI_{n}^{0}g\left( 1 \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdots \;\;\;\;\;\;\;\;\;\; - \beta nI_{n}^{0}g\left( n \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0\;\;\;\; \cdots \;\;\;\;0\; \hfill \\ \;0\;\;\; \cdots \;\;\;\;\;0\;\;\;\;\; - \varepsilon - \gamma - \mu +\left( {1 - p} \right)\beta I_{1}^{0}g\left( 1 \right)\;\;\; \cdots \;\;\;\;\;\;\;\;\;\left( {1 - p} \right)\beta I_{1}^{0}g\left( n \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0\;\;\;\; \cdots \;\;\;\;0\; \hfill \\ \; \vdots \;\;\;\;\; \ddots \;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\; \ddots \;\;\;\; \vdots \;\; \hfill \\ \;0\;\;\;\; \cdots \;\;\;\;0\;\;\;\;\;\;\;\;\;\;\;\;\left( {1 - p} \right)\beta nI_{n}^{0}g\left( 1 \right)\;\;\;\;\;\;\;\;\;\;\;\;\; \cdots \;\;\; - \varepsilon - \gamma - \mu +\left( {1 - p} \right)\beta nI_{n}^{0}g\left( n \right)\;\;\;\;\;\;\;0\;\;\;\;\; \cdots \;\;\;0\; \hfill \\ 0\;\;\; \cdots \;\;\;\;\;\;0\;\;\;\;\;\;\;\;\;\;\;\;\;\varepsilon +p\beta I_{1}^{0}g\left( 1 \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;p\beta I_{1}^{0}g\left( n \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \rho - \mu \;\; \cdots \;\;\;0\; \hfill \\ \; \vdots \;\;\;\;\; \ddots \;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\; \ddots \;\;\;\;\; \vdots \;\; \hfill \\ \;0\;\;\;\; \cdots \;\;\;\;0\;\;\;\;\;\;\;\;\;\;\;\;\;\;p\beta nI_{n}^{0}g\left( 1 \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdots \;\;\;\;\;\;\;\;\;\;\;\varepsilon +p\beta nI_{n}^{0}g\left( n \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0\;\;\; \cdots \;\; - \rho - \mu \hfill \\ \end{gathered} \right)_{3n \times 3n}}$

$g\left( {{k^{^\prime}}} \right)=\frac{{{k^{^\prime}}p\left( {{k^{^\prime}}} \right)}}{{\left\langle k \right\rangle }},\left\langle k \right\rangle =\sum\limits_{{{k^{^\prime}}=1}}^{n} {{k^{^\prime}}p\left( {{k^{^\prime}}} \right).}$

We primarily give the following lemma so as to demonstrate the stability of equilibrium point.

Lemma 4.2

The equilibrium point of system (1) is locally asymptotically stable, provided that all the eigenvalues ${\lambda _i}\left( {i=1,2, \ldots ,3n} \right)$ of the corresponding Jacobian matrix are equal to the following condition.

$\left| {\arg \left( {{\lambda _i}} \right)} \right|>\frac{{\alpha \pi }}{2},i=1,2, \ldots ,3n.$ The characteristic polynomial of linear system (8) is.

${\left( {\lambda +\mu } \right)^n}{\left( {\lambda +\rho +\mu } \right)^n}\left| {\lambda E - F} \right|=0,$

where.

$F={\left( \begin{gathered} - \varepsilon - \gamma - \mu +\left( {1 - p} \right)\beta nI_{1}^{0}g\left( 1 \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {1 - p} \right)\beta nI_{1}^{0}g\left( 2 \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdots \;\;\;\;\;\;\;\;\;\;\;\left( {1 - p} \right)\beta nI_{1}^{0}g\left( n \right)\; \hfill \\ \;\;\;\;\;\;\;\;\left( {1 - p} \right)\beta 2I_{2}^{0}g\left( 1 \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \varepsilon - \gamma - \mu +\left( {1 - p} \right)\beta 2I_{2}^{0}g\left( 2 \right)\;\;\;\; \cdots \;\;\;\;\;\;\;\;\;\;\;\left( {1 - p} \right)\beta nI_{2}^{0}g\left( n \right) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \ddots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\; \hfill \\ \;\;\;\;\;\;\;\;\;\;\left( {1 - p} \right)\beta nI_{n}^{0}g\left( 1 \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {1 - p} \right)\beta nI_{n}^{0}g\left( 2 \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdots \;\;\;\; - \varepsilon - \gamma - \mu +\left( {1 - p} \right)\beta nI_{n}^{0}g\left( n \right) \hfill \\ \end{gathered} \right)_{n \times n}}$ It is quite obvious to obtain that the Jacobian matrix $J\left( {{E_0}} \right)$ has n eigenvalues equivalent to $- \rho - \mu$, and n eigenvalues equivalent to $- \mu$. And the last n eigenvalues of matrix $J\left( {{E_0}} \right)$ are the eigenvalues of matrix F. The characteristic polynomial of matrix F is given by.

$\begin{gathered} \left| {\lambda E - F} \right|=\left| \begin{gathered} \lambda +\varepsilon +\gamma +\mu - \left( {1 - p} \right)\beta nI_{1}^{0}g\left( 1 \right)\;\;\;\;\;\;\;\;\;\; - \left( {1 - p} \right)\beta nI_{1}^{0}g\left( 2 \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdots \;\;\;\;\;\;\;\;\;\;\; - \left( {1 - p} \right)\beta nI_{1}^{0}g\left( n \right)\; \hfill \\ \;\;\;\;\;\;\;\; - \left( {1 - p} \right)\beta 2I_{2}^{0}g\left( 1 \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\lambda +\varepsilon +\gamma +\mu - \left( {1 - p} \right)\beta 2I_{2}^{0}g\left( 2 \right)\;\;\;\;\; \cdots \;\;\;\;\;\;\;\;\;\;\; - \left( {1 - p} \right)\beta nI_{2}^{0}g\left( n \right) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \ddots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\; \hfill \\ \;\;\;\;\;\;\;\; - \left( {1 - p} \right)\beta nI_{n}^{0}g\left( 1 \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \left( {1 - p} \right)\beta nI_{n}^{0}g\left( 2 \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdots \;\;\;\;\lambda +\varepsilon +\gamma +\mu - \left( {1 - p} \right)\beta nI_{n}^{0}g\left( n \right) \hfill \\ \end{gathered} \right| \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;=\left| \begin{gathered} \lambda +\varepsilon +\gamma +\mu \;\;\;\;\;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;\;\;\;\; \cdots \;\;\;\;\;\;\;\;\;\;\;\;\; - \left( {1 - p} \right)\beta nI_{1}^{0}g\left( n \right)\; \hfill \\ \;\;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;\;\;\;\lambda +\varepsilon +\gamma +\mu \;\;\;\; \cdots \;\;\;\;\;\;\;\;\;\;\;\;\; - \left( {1 - p} \right)\beta nI_{2}^{0}g\left( n \right) \hfill \\ \;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\; \ddots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\; \hfill \\ \;\;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;\;\;\;\; \cdots \;\;\;\;\lambda +\varepsilon +\gamma +\mu - \left( {1 - p} \right)\beta \sum\limits_{{k=1}}^{n} {\left[ {kI_{k}^{0}g\left( k \right)} \right]} \hfill \\ \end{gathered} \right| \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;={\left( {\lambda +\varepsilon +\gamma +\mu } \right)^{n - 1}}\left( {\lambda +\varepsilon +\gamma +\mu - \left( {1 - p} \right)\beta \sum\limits_{{k=1}}^{n} {\left[ {kI_{k}^{0}g\left( k \right)} \right]} } \right). \hfill \\ \end{gathered}$ Obviously, the matrix F has $n - 1$ eigenvalues equal to $- \varepsilon - \gamma - \mu$. The nth eigenvalue is ${\lambda _n}= - \varepsilon - \gamma - \mu +\left( {1 - p} \right)\beta \sum\limits_{{k=1}}^{n} {\left[ {kI_{k}^{0}g\left( k \right)} \right]} =\left( {\varepsilon +\gamma +\mu } \right)\left( {{R_0} - 1} \right).$ Therefore, on account of Lemma 4.2, the rumor-free equilibrium point ${E_0}$ is locally asymptotically stable if ${R_0}<1$, and unstable if ${R_0}>1$.

Theorem 4.3

If ${R_0}<1$, then ${E_0}$ is the unique equilibrium point of system (1), and it is globally asymptotically stable.

Proof

For system (1), we construct the following Lyapunov function:

$V\left( t \right)=\sum\limits_{{k=1}}^{n} {{a_k}\left( {{I_k} - I_{k}^{0} - I_{k}^{0}\ln \frac{{{S_k}}}{{S_{k}^{0}}}} \right)} +\sum\limits_{{k=1}}^{n} {{a_k}{S_k},}$

where ${a_k}=\frac{{kp\left( k \right)}}{{\left\langle k \right\rangle }},\left\langle k \right\rangle =\sum\limits_{{{k^{^\prime}}=1}}^{n} {kp\left( k \right).}$.

By Lemma 2.6, we have

$$\begin{gathered} {\left. {{D^\alpha }V} \right|_{\left( 1 \right)}}=\sum\limits_{{k=1}}^{n} {{a_k}{D^\alpha }{I_k}} - \sum\limits_{{k=1}}^{n} {{a_k}I_{k}^{0}{D^\alpha }\ln \frac{{{I_k}}}{{I_{k}^{0}}}+\sum\limits_{{k=1}}^{n} {{a_k}{D^\alpha }{S_k}} } \hfill \\ \;\;\;\;\;\;\;\;\;\; \le \sum\limits_{{k=1}}^{n} {{a_k}\left( {1 - \frac{{I_{k}^{0}}}{{{I_k}}}} \right){D^\alpha }{S_k}} +\sum\limits_{{k=1}}^{n} {{a_k}{D^\alpha }{S_k}} \hfill \\ \;\;\;\;\;\;\;\;\;\;=\sum\limits_{{k=1}}^{n} {{a_k}\left( {1 - \frac{{I_{k}^{0}}}{{{I_k}}}} \right)\left( {\Lambda - \beta k{I_k}\Theta \left( t \right) - \mu {I_k}} \right)} +\sum\limits_{{k=1}}^{n} {{a_k}\left( {\left( {1 - p} \right)\beta k{I_k}\left( t \right)\Theta \left( t \right) - \varepsilon {S_k}\left( t \right) - \gamma {S_k}\left( t \right) - \mu {S_k}\left( t \right)} \right),} \hfill \\ \end{gathered}$$

(9)

Based on the first equation of system (1), we have $\Lambda =\mu I_{k}^{0}$, substituting into (9).

$\begin{gathered} {\left. {{D^\alpha }V} \right|_{\left( 1 \right)}}=\sum\limits_{{k=1}}^{n} {{a_k}\left( {1 - \frac{{I_{k}^{0}}}{{{I_k}}}} \right)\left( {\mu I_{k}^{0} - \beta k{I_k}\Theta \left( t \right) - \mu {I_k}} \right)} +\sum\limits_{{k=1}}^{n} {{a_k}\left( {\left( {1 - p} \right)\beta k{I_k}\left( t \right)\Theta \left( t \right) - \varepsilon {S_k}\left( t \right) - \gamma {S_k}\left( t \right) - \mu {S_k}\left( t \right)} \right)} \hfill \\ \;\;\;\;\;\;\;\;\;\; \le - \sum\limits_{{k=1}}^{n} {{a_k}\left( {1 - \frac{{I_{k}^{0}}}{{{I_k}}}} \right)\left( {\beta k{I_k}\Theta \left( t \right)+\mu {I_k}} \right)+\left( {\varepsilon +\gamma +\mu } \right)\left( {{R_0} - 1} \right)\Theta \left( t \right).} \hfill \\ \end{gathered}$

When ${R_0}<1,{D^\alpha }V<0$ and we infer the only compact invariant set is the singleton $\left\{ {{E_0}} \right\}$ for $\left\{ {{D^\alpha }V=0} \right\}$. Through the use of Lemma 2.5 and Theorem 4.1, the rumor-free equilibrium point ${E_0}$ is globally asymptotically stable when ${R_0}<1$, which means the rumor will fall into extinct ultimately in spite of the initial density of spreader.

Next, we will demonstrate the global asymptotical stability of the rumor equilibrium point ${E^*}$ of system (1) identical to the rumor-free equilibrium point ${E_0}$.

The dynamic of rumor equilibrium point ${E^*}$

Theorem 4.4

If ${R_0}>1$, then the rumor equilibrium point ${E^*}$ is locally asymptotically stable.

Proof

In a similar way, we linearize the system (1) at ${E^*}$, and acquire the corresponding Jacobian matrix$J\left( {{E^*}} \right)$.

$J\left( {{E^*}} \right)={\left( \begin{gathered} - \mu - \beta {p_1}\;\; \cdots \;\;\;\;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;\;\;\;\; - \beta {m_1}g\left( 1 \right)\;\;\;\;\;\; \cdots \;\;\;\; - \beta {m_n}g\left( n \right)\;\;\;\;\;\;\;\;0\;\;\;\; \cdots \;\;\;0\; \hfill \\ \;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\; \ddots \;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\; \ddots \;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\; \ddots \;\;\;\; \vdots \;\; \hfill \\ \;\;\;\;\;0\;\;\;\;\;\;\;\;\; \cdots \;\;\; - \mu - \beta {p_n}\;\;\;\;\; - \beta {m_n}g\left( 1 \right)\;\;\;\;\;\;\; \cdots \;\;\;\; - \beta {m_n}g\left( n \right)\;\;\;\;\;\;\;\;0\;\;\;\; \cdots \;\;\;0\; \hfill \\ \;\;\;b{p_1}\;\;\;\;\;\;\;\; \cdots \;\;\;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;\; - c+b{m_1}g\left( 1 \right)\;\;\;\;\;\; \cdots \;\;\;\;\;\;\;b{m_n}g\left( n \right)\;\;\;\;\;\;\;\;\;0\;\;\;\; \cdots \;\;\;0\; \hfill \\ \;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\; \ddots \;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\; \ddots \;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\; \ddots \;\;\;\; \vdots \;\; \hfill \\ \;\;\;\;0\;\;\;\;\;\;\;\;\; \cdots \;\;\;\;\;\;\;\;b{p_n}\;\;\;\;\;\;\;\;\;\;\;\;b{m_n}g\left( 1 \right)\;\;\;\;\;\;\;\;\; \cdots \;\;\; - c+b{m_n}g\left( n \right)\;\;\;\;\;\;0\;\;\; \cdots \;\;\;0\; \hfill \\ \;p\beta {p_1}\;\;\;\;\;\; \cdots \;\;\;\;\;\;\;\;\;0\;\;\;\;\;\;\;\;\;\;\varepsilon +\;p\beta {m_1}g\left( 1 \right)\;\;\;\;\; \cdots \;\;\;\;\;p\beta {m_n}g\left( n \right)\;\;\;\;\;\; - d\;\; \cdots \;\;\;0\; \hfill \\ \;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\; \ddots \;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\; \ddots \;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\; \ddots \;\;\;\; \vdots \; \hfill \\ \;\;\;\;0\;\;\;\;\;\;\;\;\; \cdots \;\;\;\;\;\;\;p\beta {p_n}\;\;\;\;\;\;\;\;p\beta {m_n}g\left( 1 \right)\;\;\;\;\;\;\;\; \cdots \;\;\;\varepsilon +\;p\beta {m_n}g\left( n \right)\;\;\;\;\;0\;\; \cdots \;\; - d \hfill \\ \end{gathered} \right)_{3n \times 3n}}$${p_k}=k{\Theta ^*},{m_k}=kS_{k}^{*},b=\left( {1 - p} \right)\beta ,c=\varepsilon +\gamma +\mu ,d=\delta +\mu ,g\left( {{k^{^\prime}}} \right)=\frac{{{k^{^\prime}}p\left( {{k^{^\prime}}} \right)}}{{\left\langle k \right\rangle }}.$

The characteristic equation of Jacobian matrix $J\left( {{E^*}} \right)$ is.

${\left( {\lambda +\mu } \right)^n}{\left( {\lambda +\delta +\mu } \right)^n}\left| {\lambda E - H} \right|=0,$

where.

$H={\left( \begin{gathered} - \varepsilon - \gamma - \mu - {h_1}+\left( {1 - p} \right)\beta {m_1}g\left( 1 \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {1 - p} \right)\beta {m_1}g\left( 1 \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {1 - p} \right)\beta {m_n}g\left( n \right)\; \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\left( {1 - p} \right)\beta {m_2}g\left( 1 \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; - \varepsilon - \gamma - \mu - {h_2}+\left( {1 - p} \right)\beta {m_2}g\left( 2 \right)\;\;\;\;\;\; \cdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {1 - p} \right)\beta {m_n}g\left( n \right)\;\; \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \ddots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\; \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\left( {1 - p} \right)\beta {m_n}g\left( 1 \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {1 - p} \right)\beta {m_n}g\left( 2 \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdots \;\;\;\;\; - \varepsilon - \gamma - \mu - {h_n}+\left( {1 - p} \right)\beta {m_n}g\left( n \right) \hfill \\ \end{gathered} \right)_{n \times n}}$

${h_k}=\frac{{\beta \left( {\varepsilon +\gamma +\mu } \right)}}{\mu }k{\Theta ^*}$

Clearly, matrix $J\left( {{E^*}} \right)$ has 2n negative eigenvalues. Following, we calculate the last n eigenvalues of matrix $J\left( {{E^*}} \right)$.

$\left| {\lambda E - H} \right|=\left| \begin{gathered} \lambda +\varepsilon +\gamma +\mu +{h_1} - \left( {1 - p} \right)\beta {m_1}g\left( 1 \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {1 - p} \right)\beta {m_1}g\left( 1 \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {1 - p} \right)\beta {m_n}g\left( n \right)\; \hfill \\ \;\;\;\;\;\;\;\;\;\;\left( {1 - p} \right)\beta {m_2}g\left( 1 \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\lambda +\varepsilon +\gamma +\mu +{h_2} - \left( {1 - p} \right)\beta {m_2}g\left( 2 \right)\;\;\;\; \cdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {1 - p} \right)\beta {m_n}g\left( n \right) \hfill \\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \ddots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\; \hfill \\ \;\;\;\;\;\;\;\;\;\;\left( {1 - p} \right)\beta {m_n}g\left( 1 \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left( {1 - p} \right)\beta {m_n}g\left( 2 \right)\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \cdots \;\;\;\;\lambda +\varepsilon +\gamma +\mu +{h_n} - \left( {1 - p} \right)\beta {m_n}g\left( n \right) \hfill \\ \end{gathered} \right|=0$

Consider the following two cases:

• (1) If $\lambda +\varepsilon +\gamma +\mu +{h_i}=0$, namely, ${\lambda _i}= - \varepsilon - \gamma - \mu - {h_i}\left( {i=1,2, \ldots ,n} \right)$, then.

$\left| {\lambda E - H} \right|={\left( {\left( {1 - p} \right)\beta } \right)^n}\left| \begin{gathered} - {m_1}g\left( 1 \right)\;\;\;\; - {m_1}g\left( 1 \right)\;\;\; \cdots \;\; - {m_n}g\left( n \right)\; \hfill \\ - {m_2}g\left( 1 \right)\;\;\;\; - {m_2}g\left( 2 \right)\;\; \cdots \;\; - {m_n}g\left( n \right) \hfill \\ \;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\;\; \ddots \;\;\;\;\;\;\;\; \vdots \;\;\;\;\;\;\;\; \hfill \\ - {m_n}g\left( 1 \right)\;\;\;\; - {m_n}g\left( 2 \right)\;\; \cdots \;\;\; - {m_n}g\left( n \right) \hfill \\ \end{gathered} \right| \equiv 0.$

Therefore, we obtain n eigenvalues ${\lambda _i}= - \varepsilon - \gamma - \mu - {h_i}<0,i=1,2, \ldots ,n$.

• (2) If $\lambda +\varepsilon +\gamma +\mu +{h_i} \ne 0$, then.

$\left| {\lambda E - H} \right|=\prod\limits_{{i=1}}^{n} {\left( {\lambda +\varepsilon +\gamma +\mu +{h_i}} \right)\left( {1 - \sum\limits_{{i=1}}^{n} {\frac{{\left( {1 - p} \right)\beta {m_i}g\left( i \right)}}{{\lambda +\varepsilon +\gamma +\mu +{h_i}}}} } \right)} .$

Let $\varphi \left( x \right)=\prod\limits_{{i=1}}^{n} {\left( {\lambda +\varepsilon +\gamma +\mu +{h_i}} \right)\left( {1 - \sum\limits_{{i=1}}^{n} {\frac{{\left( {1 - p} \right)\beta {m_i}g\left( i \right)}}{{\lambda +\varepsilon +\gamma +\mu +{h_i}}}} } \right)}$, then.

$\begin{gathered} \varphi \left( x \right)=\left( {x+\varepsilon +\gamma +\mu +{h_1}} \right)\left( {x+\varepsilon +\gamma +\mu +{h_2}} \right) \cdots \left( {x+\varepsilon +\gamma +\mu +{h_n}} \right) \hfill \\ \;\;\;\;\;\;\;\;\;\; - \left( {1 - p} \right)\beta {m_1}g\left( 1 \right)\left( {x+\varepsilon +\gamma +\mu +{h_2}} \right)\left( {x+\varepsilon +\gamma +\mu +{h_3}} \right) \cdots \left( {x+\varepsilon +\gamma +\mu +{h_n}} \right) \hfill \\ \;\;\;\;\;\;\;\;\;\; - \left( {1 - p} \right)\beta {m_2}g\left( 2 \right)\left( {x+\varepsilon +\gamma +\mu +{h_1}} \right)\left( {x+\varepsilon +\gamma +\mu +{h_3}} \right) \cdots \left( {x+\varepsilon +\gamma +\mu +{h_n}} \right) \hfill \\ \;\;\;\;\;\;\;\;\;\; - \cdots - \left( {1 - p} \right)\beta {m_n}g\left( n \right)\left( {x+\varepsilon +\gamma +\mu +{h_1}} \right)\left( {x+\varepsilon +\gamma +\mu +{h_2}} \right) \cdots \left( {x+\varepsilon +\gamma +\mu +{h_{n - 1}}} \right). \hfill \\ \end{gathered}$ Since $\varphi \left( x \right)$ is continuous, ${h_k}$is increasing and note that.

$\varphi \left[ { - \left( {\varepsilon +\gamma +\mu +{h_i}} \right)} \right]\varphi \left[ { - \left( {\varepsilon +\gamma +\mu +{h_{i+1}}} \right)} \right]<0,i=1,2, \ldots ,n - 1.$

Hence, it exists at least one root in $\left[ { - \left( {\varepsilon +\gamma +\mu +{h_i}} \right), - \left( {\varepsilon +\gamma +\mu +{h_{i+1}}} \right)} \right]$. in another word, there exist $n - 1$ negative roots in $\left[ { - \left( {\varepsilon +\gamma +\mu +{h_n}} \right), - \left( {\varepsilon +\gamma +\mu +{h_1}} \right)} \right]$.

On the other hand, $\varphi \left( { - \left( {\varepsilon +\gamma +\mu +{h_1}} \right)} \right)<0$, and.

$\begin{gathered} \varphi \left( 0 \right)=\prod\limits_{{i=1}}^{n} {\left( {\varepsilon +\gamma +\mu +{h_i}} \right)\left( {1 - \sum\limits_{{i=1}}^{n} {\frac{{\left( {1 - p} \right)\beta {m_i}g\left( i \right)}}{{\varepsilon +\gamma +\mu +{h_i}}}} } \right)} \hfill \\ \;\;\;\;\;\;\;\;=\prod\limits_{{i=1}}^{n} {\left( {\varepsilon +\gamma +\mu +{h_i}} \right)\left( {1 - \sum\limits_{{i=1}}^{n} {\frac{{\left( {1 - p} \right)\beta iS_{i}^{*}ip\left( i \right)}}{{\left\langle k \right\rangle \left( {\varepsilon +\gamma +\mu +\frac{{\beta \left( {\varepsilon +\gamma +\mu } \right)}}{\mu }i{\Theta ^*}} \right)}}} } \right)} \hfill \\ \;\;\;\;\;\;\;\;>\prod\limits_{{i=1}}^{n} {\left( {\varepsilon +\gamma +\mu +{h_i}} \right)\left( {1 - \sum\limits_{{i=1}}^{n} {\frac{{\left( {1 - p} \right)\beta iS_{i}^{*}ip\left( i \right)}}{{\left\langle k \right\rangle \left( {\varepsilon +\gamma +\mu +\frac{{\beta \left( {\varepsilon +\gamma +\mu } \right)}}{\mu }i{\Theta ^*}} \right)}}} } \right)} \hfill \\ \;\;\;\;\;\;\;=0. \hfill \\ \end{gathered}$

Hence, the matrix N has n negative roots in $\left[ { - \left( {\varepsilon +\gamma +\mu +{h_n}} \right),0} \right]$. It is manifested that all the eigenvalues of the Jacobian matrix $J\left( {{E^*}} \right)$ are negative so far. That is to say, the rumor equilibrium point ${E^*}$ is locally asymptotically stable.

Theorem 4.5

Suppose that $\left( {{I_k}\left( t \right),{S_k}\left( t \right),{D_k}\left( t \right)} \right)$ is a solution of system (1) satisfying initial conditions ${S_k}\left( t \right)>0$ or ${D_k}\left( t \right)>0$. If ${R_0}>0$, then $\mathop {\lim }\limits_{{x \to \infty }} \left( {{I_k}\left( t \right),{S_k}\left( t \right),{D_k}\left( t \right)} \right)=$$\left( {I_{k}^{*}\left( t \right),S_{k}^{*}\left( t \right),T_{k}^{*}\left( t \right)} \right)$ is the rumor-prevailing equilibrium of (1) satisfying for $k=1,2, \ldots ,n$.

Proof

In the following, k is fixed to be any integer in $\left( {1,2, \ldots ,n} \right)$. By Theorem 4, there exists a sufficiently small constant $\xi \left( {0<\xi <1} \right)$ and a larger enough constant $T>0$ such that ${T_k}\left( t \right) \ge \xi$ for $t>T$, therefore $\Theta \left( t \right)>\xi \Theta$ for $t>T$. Submit this into the equation of (8) gives.

${D^\alpha }{I_k}\left( t \right) \le \Lambda - \mu {I_k}\left( t \right) - \beta k\Theta \xi {I_k}\left( t \right),t>T.$

By means of the standard comparison theorem, for any given constant $0<\xi <\frac{{\beta k\Theta \xi }}{{2\left( {\mu +\beta k\Theta \xi } \right)}}$, there exists a ${t_1}>T$, such that ${S_k}\left( t \right) \le A_{k}^{{\left( 1 \right)}} - {\xi _1}$ for $t>{t_1}$, where.

$A_{k}^{{\left( 1 \right)}}=\frac{r}{{\mu +\beta k\Theta \xi }}+2{\xi _1}<1.$

From the second equation of (1), it follow that.

${D^\alpha }{S_k}\left( t \right) \le \left( {1 - p} \right)\beta k\Theta \left( {1 - {S_k}\left( t \right)} \right) - \left( {\varepsilon +\gamma +\mu } \right){S_k}\left( t \right),t>{t_1}.$

Hence, for any given constant $0<{\xi _2}<\hbox{min} \left\{ {\frac{1}{2},{\xi _1},\frac{{\varepsilon +\gamma +\mu }}{{2\left( {\varepsilon +\gamma +\mu +\left( {1 - p} \right)\beta k\Theta } \right)}}} \right\}$, there exists a ${t_2}>{t_1}$, such that ${I_k}\left( t \right) \le B_{k}^{{\left( 1 \right)}} - {\xi _2}$ for $t>{t_2}$, where.

$B_{k}^{{\left( 1 \right)}}=\frac{{\beta k\Theta }}{{\left( {1 - p} \right)\beta k\Theta +\varepsilon +\gamma +\mu }}+2{\xi _2}<1.$

Then, it follows from the third equation of (1),

${D^\alpha }{D_k}\left( t \right) \le p\beta k\Theta \left( {1 - {D_k}\left( t \right)} \right)+\varepsilon \left( {1 - {D_k}\left( t \right)} \right) - \left( {\delta +\mu } \right){D_k}\left( t \right),t>{t_2}.$

Similarly, for any given constant $0<{\xi _3}<\hbox{min} \left\{ {\frac{1}{3},{\xi _2},\frac{{\delta +\mu }}{{2\left( {\varepsilon +\delta +\mu +p\beta k\Theta } \right)}}} \right\}$, there exists a ${t_3}>{t_2}$, such that ${D_k}\left( t \right) \le D_{k}^{{\left( 1 \right)}} - {\xi _3}$ for $t>{t_3}$, where.

$D_{k}^{{\left( 1 \right)}}=\frac{{p\beta k\Theta +\varepsilon }}{{p\beta k\Theta +\varepsilon +\delta +\mu }}+2{\xi _3}<1.$

Since $\Theta \left( t \right) \le \frac{1}{{\left\langle k \right\rangle }}\sum\limits_{{i=1}}^{n} {ip\left( i \right)=:H}$, we substitute this into the first equation of (1).

${D^\alpha }{I_k}\left( t \right) \ge \Lambda - \mu {I_k}\left( t \right) - \beta kH{I_k}\left( t \right),t>T.$

So for any given enough small constant $0<{\xi _4}<\hbox{min} \left\{ {\frac{1}{4},{\xi _3},\frac{r}{{2\left( {\mu +\beta kH} \right)}}} \right\}$, there exists a ${t_4}>{t_3}$, such that ${I_k}\left( t \right) \ge a_{k}^{{\left( 1 \right)}}+{\xi _4}$,for $t>{t_4}$, where.

$a_{k}^{{\left( 1 \right)}}=\frac{r}{{\mu +\beta kH}} - 2{\xi _4}>0.$

It follows that.

${D^\alpha }{S_k}\left( t \right) \ge \left( {1 - p} \right)\beta k\Theta a_{k}^{{\left( 1 \right)}} - \left( {\varepsilon +\gamma +\mu } \right){S_k}\left( t \right),t>{t_4}.$

So for any given enough small constant $0<{\xi _5}<\hbox{min} \left\{ {\frac{1}{5},{\xi _4},\frac{{\left( {1 - p} \right)\beta k\Theta a_{k}^{{\left( 1 \right)}}}}{{2\left( {\varepsilon +\gamma +\mu } \right)}}} \right\}$, there exists a ${t_5}>{t_4}$, such that ${I_k}\left( t \right) \ge b_{k}^{{\left( 1 \right)}}+{\xi _5}$ for $t>{t_5}$, where.

$b_{k}^{{\left( 1 \right)}}=\frac{{\left( {1 - p} \right)\beta k\Theta a_{k}^{{\left( 1 \right)}}}}{{\varepsilon +\gamma +\mu }} - 2{\xi _5}>0.$

From the third equation of (1) implies that.

${D^\alpha }{D_k}\left( t \right) \ge p\beta k\Theta \xi a_{k}^{{\left( 1 \right)}}+\varepsilon b_{k}^{{\left( 1 \right)}} - \left( {\delta +\mu } \right){D_k}\left( t \right),$

So for any given enough small constant $0<{\xi _6}<\hbox{min} \left\{ {\frac{1}{6},{\xi _5},\frac{{p\beta k\Theta \xi a_{k}^{{\left( 1 \right)}}+\varepsilon b_{k}^{{\left( 1 \right)}}}}{{2\left( {\delta +\mu } \right)}}} \right\}$, there exists a ${t_6}>{t_5}$, such that ${T_k}\left( t \right) \ge d_{k}^{{\left( 1 \right)}}+{\xi _6}$ for $t>{t_6}$.

As a result of $\xi$ is a small positive constant, we can deduce that $0<a_{k}^{{\left( 1 \right)}}<A_{k}^{{\left( 1 \right)}}<1,$ $0<b_{k}^{{\left( 1 \right)}}<B_{k}^{{\left( 1 \right)}}<1$ and $0<d_{k}^{{\left( 1 \right)}}<D_{k}^{{\left( 1 \right)}}<1$.

Let.

${q^{\left( j \right)}}=\frac{1}{{\left\langle k \right\rangle }}\sum\limits_{{j=1}}^{n} {ip\left( i \right)d_{i}^{{\left( j \right)}}} ,{Q^{\left( j \right)}}=\frac{1}{{\left\langle k \right\rangle }}\sum\limits_{{j=1}}^{n} {ip\left( i \right)D_{i}^{{\left( j \right)}}} ,j=1,2, \ldots ,n.$

We can easily get $0<{q^{\left( j \right)}} \le \Theta \left( t \right) \le {Q^{\left( j \right)}}<H,t>{t_4}.$.

Again, from the first equation of (8), it has.

${D^\alpha }{I_k}\left( t \right) \ge \Lambda - \mu {I_k}\left( t \right) - \beta k{q^{\left( 1 \right)}}{I_k}\left( t \right),t>{t_4}.$

Hence, for any given constant $0<{\xi _7}<\hbox{min} \left\{ {\frac{1}{7},{\xi _6}} \right\}$, there exists a ${t_7}>{t_6}$, such that.

${D^\alpha }{S_k}\left( t \right) \le A_{k}^{{\left( 2 \right)}} \triangleq \hbox{min} \left\{ {A_{k}^{{\left( 1 \right)}} - {\xi _1},\frac{r}{{\mu +\beta k{q^{\left( 1 \right)}}}}+{\xi _7}} \right\},t>{t_7}.$

Then, from the second equation of (8), we have.

${D^\alpha }{S_k}\left( t \right) \le \left( {1 - p} \right)\beta k{Q^{\left( 1 \right)}}A_{k}^{{\left( 1 \right)}} - \left( {\varepsilon +\gamma +\mu } \right){S_k}\left( t \right),t>{t_7}.$

So, for any given constant $0<{\xi _8}<\hbox{min} \left\{ {\frac{1}{8},{\xi _7}} \right\}$, there exists a ${t_8}>{t_7}$, such that.

${D^\alpha }{I_k}\left( t \right) \le B_{k}^{{\left( 2 \right)}} \triangleq \hbox{min} \left\{ {B_{k}^{{\left( 1 \right)}} - {\xi _2},\frac{{\left( {1 - p} \right)\beta k{Q^{\left( 1 \right)}}A_{k}^{{\left( 2 \right)}}}}{{\varepsilon +\gamma +\mu }}+{\xi _8}} \right\},t>{t_8}.$

Consequently, from the third equation of (8), we have.

${D^\alpha }{D_k}\left( t \right) \le p\beta k{Q^{\left( 1 \right)}}A_{k}^{{\left( 2 \right)}}+\varepsilon B_{k}^{{\left( 1 \right)}} - \left( {\delta +\mu } \right){D_k}\left( t \right),t>{t_8}.$

Hence, for any given constant $0<{\xi _9}<\hbox{min} \left\{ {\frac{1}{9},{\xi _8}} \right\}$, there exists a ${t_9}>{t_8}$, such that.

${D^\alpha }{I_k}\left( t \right) \le D_{k}^{{\left( 2 \right)}} \triangleq \hbox{min} \left\{ {D_{k}^{{\left( 1 \right)}} - {\xi _3},\frac{{p\beta k{Q^{\left( 1 \right)}}A_{k}^{{\left( 2 \right)}}+\varepsilon B_{k}^{{\left( 1 \right)}}}}{{\delta +\mu }}+{\xi _9}} \right\},t>{t_8}.$

Turning back, one has.

${D^\alpha }{I_k}\left( t \right) \ge \Lambda - \mu {I_k}\left( t \right) - \beta k{Q^{\left( 2 \right)}}{I_k}\left( t \right),t>{t_9}.$

So, for any given enough small constant $0<{\xi _{10}}<\hbox{min} \left\{ {\frac{1}{{10}},{\xi _9},\frac{r}{{2\left( {\mu +\beta k{Q^{\left( 2 \right)}}} \right)}}} \right\}$, there exists a ${t_{10}}>{t_9}$, such that ${T_k}\left( t \right) \ge a_{k}^{{\left( 2 \right)}}+{\xi _{10}}$ for $t>{t_{10}}$, where.

$a_{k}^{{\left( 2 \right)}}=\hbox{max} \left\{ {a_{k}^{{\left( 1 \right)}}+{\xi _4},\frac{r}{{\mu +\beta k{Q^{\left( 2 \right)}}}} - 2{\xi _{10}}} \right\}.$

It follows that.

${D^\alpha }{S_k}\left( t \right) \ge \left( {1 - p} \right)\beta k{q^{\left( 1 \right)}}a_{k}^{{\left( 2 \right)}} - \left( {\varepsilon +\gamma +\mu } \right){S_k}\left( t \right),t>{t_{10}}.$

So, for any given enough small constant $0<{\xi _{11}}<\hbox{min} \left\{ {\frac{1}{{11}},{\xi _{10}},\frac{{\beta k{q^{\left( 1 \right)}}a_{k}^{{\left( 2 \right)}}}}{{2\left( {\varepsilon +\gamma +\mu } \right)}}} \right\}$, there exists a ${t_{11}}>{t_{10}}$, such that ${C_k}\left( t \right) \ge b_{k}^{{\left( 2 \right)}}+{\xi _{11}}$ for $t>{t_{10}}$, where

$$b_{k}^{{\left( 2 \right)}}=\hbox{max} \left\{ {b_{k}^{{\left( 1 \right)}}+{\xi _5},\frac{{\left( {1 - p} \right)\beta k{q^{\left( 1 \right)}}a_{k}^{{\left( 1 \right)}}}}{{\varepsilon +\gamma +\mu }} - 2{\xi _{11}}} \right\}$$

From the third equation of (8) implies that.

${D^\alpha }{D_k}\left( t \right) \ge p\beta k{q^{\left( 1 \right)}}a_{k}^{{\left( 2 \right)}}+\varepsilon b_{k}^{{\left( 2 \right)}} - \left( {\delta +\mu } \right){D_k}\left( t \right),t>{t_{11}}.$

So, for any given enough small constant $0<{\xi _{12}}<\hbox{min} \left\{ {\frac{1}{{12}},{\xi _{11}},\frac{{p\beta k{q^{\left( 1 \right)}}a_{k}^{{\left( 2 \right)}}+\varepsilon b_{k}^{{\left( 2 \right)}}}}{{2\left( {\delta +\mu } \right)}}} \right\}$, there exists a ${t_{10}}>{t_9}$, such that ${D_k}\left( t \right) \ge d_{k}^{{\left( 2 \right)}}+{\xi _{12}}$ for $t>{t_{12}}$, where.

$d_{k}^{{\left( 2 \right)}}=\hbox{max} \left\{ {d_{k}^{{\left( 1 \right)}}+{\xi _6},\frac{{p\beta k{q^{\left( 1 \right)}}a_{k}^{{\left( 2 \right)}}+\varepsilon b_{k}^{{\left( 2 \right)}}}}{{\sigma +\mu }} - 2{\xi _{12}}} \right\}.$

Repeating the above analyses and calculation, we acquire six sequences $A_{k}^{{\left( i \right)}},B_{k}^{{\left( i \right)}},D_{k}^{{\left( i \right)}},$$a_{k}^{{\left( i \right)}},b_{k}^{{\left( i \right)}},d_{k}^{{\left( i \right)}},i=1,2, \ldots ,n$. The first three sequences are monotone decreasing continuous function, and the other three sequences are monotone increasing function, it exists a large positive integer $L>2$, as $l \ge L$:

$$\begin{gathered} A_{k}^{{\left( l \right)}}=\frac{r}{{\mu +\beta k{q^{\left( {l - 1} \right)}}}}+{\xi _{6l - 5}},B_{k}^{{\left( l \right)}}=\frac{{\left( {1 - p} \right)\beta k{Q^{\left( {l - 1} \right)}}A_{k}^{{\left( l \right)}}}}{{\varepsilon +\gamma +\mu }}+{\xi _{6l - 4}}, \hfill \\ D_{k}^{{\left( l \right)}}=\frac{{p\beta k{Q^{\left( {l - 1} \right)}}A_{k}^{{\left( l \right)}}+\varepsilon B_{k}^{{\left( l \right)}}}}{{\delta +\mu }}+{\xi _{6l - 3}},a_{k}^{{\left( l \right)}}=\frac{r}{{\mu +\beta k{Q^{\left( l \right)}}}} - 2{\xi _{6l - 2}}, \hfill \\ b_{k}^{{\left( l \right)}}=\frac{{\left( {1 - p} \right)\beta k{q^{\left( {l - 1} \right)}}a_{k}^{{\left( {l - 1} \right)}}}}{{\varepsilon +\gamma +\mu }} - 2{\xi _{6l - 1}},d_{k}^{{\left( l \right)}}=\frac{{p\beta k{q^{\left( 1 \right)}}a_{k}^{{\left( 2 \right)}}+\varepsilon b_{k}^{{\left( 2 \right)}}}}{{\delta +\mu }} - 2{\xi _{6l}}. \hfill \\ \end{gathered}$$

(10)

We can easy get that

$$a_{k}^{{\left( l \right)}} \le {I_k}\left( t \right) \le A_{k}^{{\left( l \right)}},b_{k}^{{\left( l \right)}} \le {S_k}\left( t \right) \le B_{k}^{{\left( l \right)}},d_{k}^{{\left( l \right)}} \le {D_k}\left( t \right) \le D_{k}^{{\left( l \right)}},t>{t_{6l}}.$$

(11)

Since the sequential limits of (10) exist, let $\mathop {\lim }\limits_{{x \to \infty }} \Delta _{k}^{{\left( l \right)}}={\Delta _k}$,where $\Delta _{k}^{{\left( l \right)}} \in \left\{ {A_{k}^{{\left( l \right)}},B_{k}^{{\left( l \right)}},D_{k}^{{\left( l \right)}},a_{k}^{{\left( l \right)}},b_{k}^{{\left( l \right)}},d_{k}^{{\left( l \right)}}} \right\}$ and ${\Delta _k} \in \left\{ {{A_k},{B_k},{D_k},{a_k},{b_k},{d_k}} \right\}$.

Noting that $0<{\xi _1}<\frac{1}{l}$, one has ${\xi _1} \to 0$ as $l \to \infty$. In the six sequences of (10), by taking $l \to \infty$, it follows from (10) that

$$\begin{gathered} A_{k}^{{\left( l \right)}}=\frac{r}{{\mu +\beta kq}},B_{k}^{{\left( l \right)}}=\frac{{\beta kQ{A_k}}}{{\varepsilon +\gamma +\mu }},D_{k}^{{\left( l \right)}}=\frac{{p\beta kQ{A_k}+\varepsilon {B_k}}}{{\delta +\mu }}, \hfill \\ a_{k}^{{\left( l \right)}}=\frac{r}{{\mu +\beta kQ}},b_{k}^{{\left( l \right)}}=\frac{{\left( {1 - p} \right)\beta kq{a_k}}}{{\varepsilon +\gamma +\mu }},d_{k}^{{\left( l \right)}}=\frac{{p\beta kq{a_k}+\varepsilon {b_k}}}{{\delta +\mu }}. \hfill \\ \end{gathered}$$

(12)

where,

$q=\frac{1}{{\left\langle k \right\rangle }}\sum\limits_{{i=1}}^{n} {ip\left( i \right)} {d_i},Q=\frac{1}{{\left\langle k \right\rangle }}\sum\limits_{{i=1}}^{n} {ip\left( i \right)} {D_i}.$

further,

$$\begin{gathered} D_{k}^{{\left( l \right)}}=\frac{{\left( {\left( {\varepsilon +\mu } \right)\eta +\beta \varepsilon } \right)rkQ}}{{\left( {\delta +\mu } \right)\left( {\varepsilon +\gamma +\mu } \right)\left( {\mu +\beta kq} \right)}}, \hfill \\ d_{k}^{{\left( l \right)}}=\frac{{\left( {\left( {\varepsilon +\mu } \right)\eta +\beta \varepsilon } \right)rkq}}{{\left( {\delta +\mu } \right)\left( {\varepsilon +\gamma +\mu } \right)\left( {\mu +\beta kQ} \right)}}. \hfill \\ \end{gathered}$$

(13)

Substituting (13) into q and Q, respectively, one has

$$1=\frac{{\left( {\left( {\varepsilon +\mu } \right)\eta +\beta \varepsilon } \right)r}}{{\left\langle k \right\rangle \left( {\rho +\mu } \right)\left( {\varepsilon +\gamma +\mu } \right)}}\sum\limits_{{i=1}}^{n} {{i^2}p\left( i \right)} \frac{{\mu +\beta iQ}}{{\left( {\mu +\left( {\beta +\eta } \right)iq} \right)\left( {\mu +\left( {\beta +\eta } \right)iQ} \right)}},$$

(14)

$$1=\frac{{\left( {\left( {\varepsilon +\mu } \right)\eta +\beta \varepsilon } \right)r}}{{\left\langle k \right\rangle \left( {\rho +\mu } \right)\left( {\varepsilon +\gamma +\mu } \right)}}\sum\limits_{{i=1}}^{n} {{i^2}p\left( i \right)} \frac{{\left( {\mu +\beta iq} \right)}}{{\left( {\mu +\left( {\beta +\eta } \right)iQ} \right)\left( {\mu +\left( {\beta +\eta } \right)iq} \right)}}.$$

(15)

By subtracting (14) and (15), it arrives at.

$0=\frac{{\left( {\left( {\varepsilon +\mu } \right)p\beta +\beta \varepsilon } \right)p\beta \left( {Q - r} \right)}}{{\left\langle k \right\rangle \left( {\delta +\mu } \right)\left( {\varepsilon +\gamma +\mu } \right)\left( {\mu +\beta iQ} \right)\left( {\mu +\beta iq} \right)}}\sum\limits_{{i=1}}^{n} {{i^3}p\left( i \right)}$

It is obviously that $q=Q$, so $\frac{1}{{\left\langle k \right\rangle }}\sum\limits_{{i=1}}^{n} {{i^3}p\left( i \right)} \left( {{D_i} - {d_i}} \right)=0$, which sees that ${D_i}={d_i}$, for $i=1,2, \ldots ,n$. From (9) and (11), it follows that.

$\mathop {\lim }\limits_{{x \to \infty }} {I_k}\left( t \right)={A_k}={a_k},\mathop {\lim }\limits_{{x \to \infty }} {S_k}\left( t \right)={B_k}={b_k},\mathop {\lim }\limits_{{x \to \infty }} {D_k}\left( t \right)={D_k}={d_k}.$

Finally, substituting $q=Q$ into (11), in view of (4) and (12), it obtains ${I_k}=I_{k}^{*},{S_k}=S_{k}^{*}$, and ${T_k}=T_{k}^{*}$. The proof is completed.

Rumor control strategies

Rumor spreading can have incredible damage to maintain the normal social order, we need to take effective measures to control rumor propagation. Rumor control strategies are an important issue. The uniform immunization and the acquaintance immunization were adopted through immunizing a portion of the population based on different rumor transmission characteristics and channels⁴⁵. Hence, we suppose immunization is effective completely, that is to say, the immunized nodes cannot be transmit rumors to their neighbors. In this case, two useful strategies to control the spreading of rumors and the effectiveness of these control strategies will be discussed and compared.

Uniform immunization control

Firstly, we consider the artificial immunization which should be carried out to reduce the transmission of the rumors, in other words, a certain percentage of the population is randomly chosen to be immunized⁴⁶. In this section, for given transmission rates $\beta$, let $0<\sigma <1$ be the immunization rate through adding the suitable parameter $\sigma$ to reduce the number of ${I_k}$. By substituting $\beta \to \beta \left( {1 - \sigma } \right)$ into system (2), we now give an uniform control system as

$$\left\{ \begin{gathered} {D^\alpha }{I_k}\left( t \right)=\Lambda - \beta \left( {1 - \sigma } \right)k{I_k}\left( t \right)\Theta \left( t \right) - \mu {I_k}\left( t \right), \hfill \\ {D^\alpha }{S_k}\left( t \right)=\left( {1 - p} \right)\beta \left( {1 - \sigma } \right)k{I_k}\left( t \right)\Theta \left( t \right) - \varepsilon {S_k}\left( t \right) - \gamma {S_k}\left( t \right) - \mu {S_k}\left( t \right), \hfill \\ {D^\alpha }{D_k}\left( t \right)=p\beta \left( {1 - \sigma } \right)k{I_k}\left( t \right)\Theta \left( t \right)+\varepsilon {S_k}\left( t \right) - \delta {D_k}\left( t \right) - \mu {D_k}\left( t \right),k=1,2, \ldots ,n. \hfill \\ \end{gathered} \right.$$

(16)

By arguments similar to those in Sect. 3 and calculating the basic reproduction number of system (16), the basic reproduction $\overline {{{R_0}}}$ can be determined by the following inequality.

${\left. {\frac{{d\overline {{F\left( \Theta \right)}} }}{{d\Theta }}} \right|_{\Theta =0}}>0,$

where,

$\overline {{F\left( \Theta \right)}} =\frac{{\left( {1 - p} \right)\beta \Lambda \left( {1 - \sigma } \right)}}{{\left\langle k \right\rangle \left( {\varepsilon +\gamma +\mu } \right)}}\sum\limits_{{k=1}}^{n} {\frac{{kp\left( k \right)k\Theta }}{{\left( {1 - p} \right)\beta k\left( {1 - \sigma } \right)\Theta +\mu }}} - \Theta .$

Hence, we obtain the basic reproduction number as.

$\overline {{{R_0}}} =\frac{{\left( {1 - p} \right)\beta \Lambda \left( {1 - \sigma } \right)\left\langle {{k^2}} \right\rangle }}{{\mu \left( {\varepsilon +\gamma +\mu } \right)\left\langle k \right\rangle }}=\left( {1 - \sigma } \right){R_0}.$

In particular, when $\sigma =0$, that is, no immunization is performed, then $\overline {{{R_0}}} ={R_0}$; When $0<\sigma <{\sigma _c}$, namely, $0<\overline {{{R_0}}} <{R_0}$, which means that the immunization strategy makes sense to reduce the transmission of the rumors. As $\sigma \to 1,\overline {{{R_0}}} \to 0$, regarding the full immunization, it would be possible for the rumor to vanish in the network.

Acquaintance immunization control

Though the uniform immunization control is available, there is a more effective immune mechanism to regulate rumor propagation. The acquaintance immunization control strategy aimed at the heterogeneity of the complex network⁴⁷. The core idea of the acquaintance immunization is to randomly select a new node with a ratio of $\vartheta$ from N nodes. In order to avoid the problem of a demand for knowing degree of each node in target immunization, The adjacent individuals are randomly selected for immunizing individuals with degree k among their neighbors by the probability $\frac{{kp\left( k \right)}}{{N\left\langle k \right\rangle }}$.Thus, the individuals with degree k in the complex networks are immunized by the probability$\vartheta k$, which is equal to $\frac{{\vartheta kp\left( k \right)}}{{\left\langle k \right\rangle }}$. The basic idea is to randomly select a new node with a ratio of $\vartheta$ from N nodes. And then, for each selected node, another adjacent node is randomly selected, which can skillfully avoid the problem of a demand for knowing degree of each node in target immunization. The adjacent individuals with degree k can be selected for immunization by the probability $\frac{{kp\left( k \right)}}{{N\left\langle k \right\rangle }}$. Therefore, the individuals with degree k in the network are immunized among their neighbors by ${\vartheta _k}=\vartheta N \times \frac{{kp\left( k \right)}}{{N\left\langle k \right\rangle }}=\frac{{\vartheta kp\left( k \right)}}{{\left\langle k \right\rangle }}$. Considering the acquaintance immunization control, system (1.2) can be given as

$$\left\{ \begin{gathered} {D^\alpha }{I_k}\left( t \right)=\Lambda - \beta \left( {1 - {\vartheta _k}} \right)k{I_k}\left( t \right)\Theta \left( t \right) - \mu {I_k}\left( t \right), \hfill \\ {D^\alpha }{S_k}\left( t \right)=\left( {1 - p} \right)\beta \left( {1 - {\vartheta _k}} \right)k{I_k}\left( t \right)\Theta \left( t \right) - \varepsilon {S_k}\left( t \right) - \gamma {S_k}\left( t \right) - \mu {S_k}\left( t \right), \hfill \\ {D^\alpha }{D_k}\left( t \right)=p\beta \left( {1 - {\vartheta _k}} \right)k{I_k}\left( t \right)\Theta \left( t \right)+\varepsilon {S_k}\left( t \right) - \delta {D_k}\left( t \right) - \mu {D_k}\left( t \right),k=1,2, \ldots ,n. \hfill \\ \end{gathered} \right.$$

(17)

Similarly, we obtain the basic reproduction number as.

$\widetilde {{{R_0}}}={R_0} - \frac{{\left( {1 - p} \right)\beta \Lambda \left\langle {{\vartheta _k}{k^2}} \right\rangle }}{{\mu \left( {\varepsilon +\gamma +\mu } \right)\left\langle k \right\rangle }},$

where $0<\vartheta \le 1$, $\overline {\vartheta } =\sum\limits_{{k=1}}^{n} {\vartheta \left( k \right)p\left( k \right)}$ is the average immunization rate.$\left\langle {{\vartheta _k}{k^2}} \right\rangle =\frac{{\vartheta \left\langle {{k^3}p\left( k \right)} \right\rangle }}{{\left\langle k \right\rangle }}=\left\langle {{\vartheta _k}} \right\rangle \left\langle {{k^2}+\operatorname{cov} \left( {{\vartheta _k},{k^2}} \right)} \right\rangle =\overline {\vartheta } \left\langle {{k^2}} \right\rangle +\left\langle {\left( {{\vartheta _k} - \overline {\vartheta } } \right)\left( {{k^2} - \left\langle {{k^2}} \right\rangle } \right)} \right\rangle .$

For appropriately small k, ${\vartheta _k} - \overline {\vartheta }$ and ${k^2} - \left\langle {{k^2}} \right\rangle$ have the same signs, then $\operatorname{cov} \left( {{\vartheta _k},{k^2}} \right)>0$.

It is prone to infer that $\widetilde {{{R_0}}}<{R_0}$, which means that targeted immunization is valid, and $\widetilde {{{R_0}}}<\frac{{1 - \overline {\vartheta } }}{{1 - \vartheta }}\overline {{{R_0}}} .$ If $0<\overline {\vartheta } =\vartheta <1$, then $\widetilde {{{R_0}}}<\overline {{{R_0}}}$. Hence, based on same average immunization rate, the effect of the targeted immunization strategy is superior to the uniform immunization strategy.

Numerical simulations

In this section, we provide some numerical simulations to explain the main theoretical results on scale-free networks with $p\left( k \right)=\left( {{\gamma _1} - 1} \right){m^{{\gamma _1} - 1}}{k^{ - {\gamma _1}}}$, where parameter m represents the smallest degree of the network nodes, parameter ${\gamma _1}$ is the variable of power law exponent. Suppose $m=2,{\gamma _1}=3$ and the number of the nodes on scale-free networks is N, let $N=100$.

The effect of network structure on rumor propagation

Consider system (2.1) with the following parameters $\Lambda =0.02,\beta =0.05,$ $\varepsilon =0.28,$$\mu =0.28,\gamma =0.18,\delta =0.3,p=0.1,\alpha =0.98$, With this choice of parameter values and a simple calculation, one has the basic reproduction number ${R_0}=0.1229<1$. In terms of Theorem 4.1, the unique rumor-free equilibrium point ${E_0}$ is locally asymptotically stable as Fig. 2 show. These figures show that when ${R_0}<1$, the rumor-spreading will ultimately disappear, and the spreaders will ultimately extend to the maximum value, which indicates that rumor will disappear from society.

Fig. 2

Each compartment population changes over time when ${R_0}<1$.

Here, we choose$\Lambda =0.05,\beta =0.5,\varepsilon =0.38,\mu =0.3,\gamma =0.3,\delta =0.3,p=0.1,$ $\alpha =0.98$, By calculating, ${R_0}=2.1219>1$, which suggests that system (1) also has a rumor equilibrium point ${E^*}$ and the rumor-free equilibrium point ${E_0}$. In terms of Theorem 4.4, the rumor equilibrium point ${E^*}$ is locally asymptotically stable as Fig. 3 shows.

Fig. 3

Each compartment population changes over time when ${R_0}>1$.

The above figures prove that when ${R_0}>1$, the rumor maintains and the density of spreaders will converge to a positive constant. Namely, it is also proved that the larger the degree number is, the wider the spread of rumors will be, which implies the more individuals contact, the more people get rumors.

Global dynamics of system (1) with different initial values

Without loss of generality in system (1), we set $\Lambda =0.03,\beta =0.05,$ $\varepsilon =0.28,$$\mu =0.28,\gamma =0.18,\delta =0.3,p=0.1,\alpha =0.98$. That is, the basic reproduction number is${R_0}={\text{0}}{\text{.1843}}<1$. According to Remark 4.5, the rumor-free equilibrium point ${E_0}$ is globally asymptotically stable. Next, we provide the image of $k=30$. Figure 4 shows the global dynamics of ${E_0}$ in Ω for the case ${R_0}<1$. It indicates that the rumor-spreading vanishes with time, and the rumor will vanish ultimately.

Fig. 4

Profile of individual notes with ${I_k}\left( 0 \right)=1 - 0.05i,i=1,2, \ldots ,10$${S_k}\left( 0 \right)=0.05i,i=1,2, \ldots ,10.$.

Without loss of generality in system (1), we take$\Lambda =0.1,\beta =0.2,$ $\varepsilon =0.32,$ $\mu =0.28,$$\gamma =0.28,\delta =0.2,p=0.1,\alpha =0.98$. That is, the basic reproduction number is ${R_0}=2.0667>1$. On the basis of Theorem 4.5, the rumor equilibrium point ${E^*}$ is globally asymptotically stable. simultaneously, we only provide the profile of $k=30$. Figure 5 shows the global dynamics of ${E^*}$ in ${\Omega ^*}$ for the case ${R_0}>1$. It indicates that the rumor-spreading persists at a rumor equilibrium level if it initially exists.

Fig. 5

Profile of individual notes with ${I_k}\left( 0 \right)=1 - 0.05i,i=1,2, \ldots ,10$${S_k}\left( 0 \right)=0.05i,i=1,2, \ldots ,10.$.

The effect of parameter $\alpha$ in rumor propagation

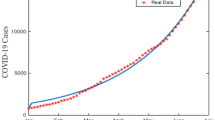
Reference⁴⁸ verified the effects of parameter $\alpha$ on the dynamic of the rumor propagation. Next, we will investigate the influences of the parameter in system (1) on scale-free networks, following the same approach as in³². We demonstrate some numerical simulations for different values of the parameter $\alpha$. As Fig. 6 shows, the numerical results show that the lower values of parameter $\alpha$, the peak of rumor propagation is wider and lower, which implies a more precise conclusion that fits the real data^49,50,51. A wider rumor peak implies a longer period along with numerous spreaders, which can probably cause panic and unnecessary losses to the society. Therefore, we should implement appropriate control measures to block the spread of rumors.

Fig. 6

Profile of individual notes with (${S_k}\left( t \right)$ and ${D_k}\left( t \right)$).

The effectiveness of immunization strategy on rumor propagation

In this section, we will compare system (1) with and without immunization strategies on spread of rumors to prove the effectiveness of control strategy. To demonstrate the effectiveness of optimal control, we adopt the uniform immunization control as an example. Choose $\Lambda =0.1,\beta =0.2,\varepsilon =0.32,$$\mu =0.28,\gamma =0.28,\delta =0.2,$ $p=0.1,\alpha =0.98$ and immunization control proportion $\sigma =0.2,0.4,0.6$, respectively. Figure 7 shows that the controlled system (17) can increase the density of spreaders, and decrease the density of resisters compared with the uncontrolled system (1). And the higher the immunization control proportion $\sigma$ is, the lower the level of rumor propagation is. In fact, the rumor propagation can be eliminated if we make effort s to take immunization strategies actively.

Fig. 7

(a) The density of spreaders with degree $k=30$ and $\alpha =0.98$; (b) The density of resisters with degree $k=30$ and $\alpha =0.98$.

Conclusions

In this paper, we have investigated the rumor dynamics of the fractional-order ISDR rumor propagation model incorporating a refutation mechanism on scale-free networks. We have established that there exists a basic reproduction number${R_0}$, which determines not only the prevalence of the rumor equilibrium point ${E^*}$, but also the eradication of the rumor. Firstly, through simple calculations, we derived basic reproduction number${R_0}$ based on the rumor equilibrium point ${E^*}$, which thoroughly characterizes the dynamics of rumor propagation. Secondly, using the Lyapunov function, we analyzed the stability of the rumor-free equilibrium point ${E_0}$ and the existence of rumor equilibrium point ${E^*}$. when ${R_0}<1$, the rumor-free equilibrium point ${E_0}$ is globally asymptotically stable and the rumor always vanishes in community, in other words, the rumor will eventually disappear regardless of the initial density of spreaders; when ${R_0}>1$, the rumor-free equilibrium point ${E_0}$ comes unstable and there exists a unique rumor equilibrium point ${E^*}$, which is globally asymptotically stable and the rumor will continue, in other words, spreaders will sustain at an rumor equilibrium level on condition that it initially exists. Numerical simulations are provided to demonstrate the main theoretical results. The influences of the parameter α on the dynamics of rumor propagation has been confirmed. Finally, two control strategies are studied and compared. Simulations prove that targeted immunization strategy is more efficient.

Our research provides a quantifiable intervention framework for the governance of social network rumors. The immune strategy simulation in our research provides a direct basis for the containment of rumors in reality, Public health departments can refer to this threshold (such as σ = 0.4) to formulate a resource allocation plan for rumor-refuting, such as allocating 40% of official accounts to disseminate authoritative information during emergencies. The fractional-order parameter α in our research reveals the “memory effect” mechanism of social media, the platform can optimize the content attenuation algorithm based on this (such as reducing the α value), and shorten the life cycle of old rumors by reducing their exposure.

At the same time, the model in this paper can be more perfect, such as considering time delay, nonlinear incidence rate and so on, These work will be analyzed in more detail in the future research.