Introduction

In modern medical environments, the rapid growth of telemedicine and big data technologies has significantly transformed diagnostic workflows. For each patient, multiple scans across various imaging modalities and time points such as MRI, CT, and OCT are commonly acquired, resulting in high-resolution, large-scale datasets that contain highly sensitive medical information 1. Following the COVID-19 pandemic, there has been an accelerated shift toward the use of cloud-based platforms for transmitting these medical images, enabling remote diagnosis and consultation. Telemedicine has proven instrumental in minimizing physical contact and maintaining continuity of care during times of healthcare system strain. However, the adoption of cloud-based remote diagnostics within distributed healthcare infrastructures also introduces critical challenges related to data confidentiality, integrity, and computational efficiency 2,3. Consequently, ensuring secure and efficient transmission of medical images remains a paramount concern in contemporary healthcare systems 4.

Traditional steganographic techniques, such as Least Significant Bit (LSB) and Pixel Value Differencing (PVD), have served as baseline methods for embedding information within medical images. However, their limited resilience to noise, compression, and transformation renders them unsuitable for real-world applications in telehealth, where images are routinely subjected to varied transmission conditions. Moreover, these approaches often compromise the balance between embedding capacity and image quality—an unacceptable trade-off in diagnostic imaging contexts where visual fidelity is non-negotiable.

Recent advancements in Deep Learning (DL) offer promising avenues for adaptive and robust steganographic systems. Deep neural networks, particularly convolutional encoder-decoder architectures, have demonstrated the ability to embed and reconstruct hidden data with high imperceptibility and robustness. Despite these capabilities, most current DL-based steganographic methods are computationally intensive and poorly suited for edge deployment, limiting their practical application in low-power medical environments.

To overcome these limitations, we propose a hybrid steganographic framework that integrates residual connections, Squeeze-and-Excitation (SE) attention mechanisms, and Inception modules to optimize both encoding and decoding performance. The proposed model is designed for real-time deployment on resource-constrained device NVIDIA Jetson TX2 platform, ensuring feasibility in edge computing environments. By using multi-scale feature extraction and channel-wise recalibration, our method enhances both the imperceptibility and robustness of medical image embedding.

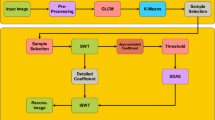
The overall architecture of the proposed steganography framework is illustrated in Fig. 1. The system takes two input repositories: cover images dataset and secret medical images dataset. These datasets are divided into training and testing subsets to enable robust model development and evaluation. The encoder module comprises multiple 2D convolutional layers and Squeeze-and-Excitation (SE) blocks, which collaboratively extract and recalibrate essential features. These components ensure high-fidelity embedding while preserving the visual quality of the cover images. The output of the encoder is a set of stego images, which visually resemble the original cover images but contain the embedded secret information. The decoder receives these stego images and reconstructs the hidden medical data using a deep convolutional structure enhanced with residual connections and inception blocks. These layers help preserve spatial integrity and ensure accurate recovery of the embedded content. The trained model is deployed on the NVIDIA Jetson TX2 platform, a power-efficient edge computing device equipped with a CUDA-enabled GPU, which facilitates real-time inference and secure medical data transmission in low-resource settings. Also, performance evaluation is conducted using standard steganography metrics such as Peak Signal-to-Noise Ratio (PSNR), Mean Squared Error (MSE), Normalized Cross-Correlation (NCC), Average Difference (AD), Structural Similarity Index (SSIM) and Laplacian Mean Squared Error (LMSE) to assess image quality, embedding success, and reconstruction accuracy. The key contributions of our work are:

  • A hybrid encoder-decoder architecture is implemented, integrating Squeeze-and-Excitation (SE) blocks, dilated convolutions, and Inception modules to enhance embedding robustness and reconstruction fidelity in medical image steganography.

  • The decoder network employs residual connections and multi-scale feature extraction to recover secret images with minimal distortion under challenging conditions (e.g., noise, compression).

  • Our model is optimized for edge deployment on the NVIDIA Jetson TX2 platform, enabling real-time, low-power operation for telemedicine and teleradiology.

  • Extensive experiments conducted on Brain MRI and OCT glaucoma datasets demonstrate superior performance in terms of PSNR, SSIM, NCC, and LMSE, validating the framework’s applicability to practical healthcare scenarios.

  • The proposed method outperforms traditional spatial and transform domain steganography techniques in imperceptibility, payload capacity, and robustness to perturbations.

Fig. 1
figure 1

Architecture of the proposed steganography approach.

Full size image

Recent works

Steganography, as a technique for embedding information within images, has evolved significantly in recent years to address increasing demands for data confidentiality in domains such as telemedicine and medical diagnostics. Classical spatial-domain methods like Least Significant Bit (LSB) substitution and Pixel Value Differencing (PVD) have been widely adopted due to their simplicity and low computational overhead. LSB-based approaches operate by modifying the least significant bits of pixel intensity values to conceal secret data, utilizing the human visual system’s insensitivity to small changes 5. These methods provide minimal visual distortion and are useful in controlled environments. However, their vulnerability to statistical attacks, noise, format conversions, and compression artifacts restricts their use in real-world healthcare settings where robustness is essential 6,7.

To overcome these limitations, several enhancements to LSB have been proposed, such as LSB matching, adaptive embedding based on image intensity or edge features 6,7, and learning-based optimization strategies 8,9. While some methods attempt to increase embedding capacity by expanding into multiple LSB planes 10, these often compromise imperceptibility which is an unacceptable trade-off in clinical imaging where even minor distortions may impact diagnosis.

Pixel Value Differencing (PVD) methods, in contrast, utilize differences between adjacent pixel values for embedding, offering improved imperceptibility by aligning with human visual sensitivity. Adaptive PVD schemes have further refined these techniques by predicting optimal embedding positions using various neighbourhoods models 11. Yet, PVD remains vulnerable to histogram-based steganalysis and often lacks sufficient randomness in its embedding strategy. Security-enhanced variations such as improved rightmost digit replacement (iRMDR), Parity-Bit PVD (PBPVD) 12, and pseudo-random block selection 13 have been introduced to mitigate these issues. Hybrid models combining LSB and PVD 14,15 offer incremental improvements, but many still fall short of the robustness required for modern medical data transmission.

Transform-domain steganography techniques offer greater resilience against noise and signal processing operations. Methods such as Discrete Cosine Transform (DCT), Discrete Wavelet Transform (DWT), and Discrete Fourier Transform (DFT) embed data in the frequency components of images to improve imperceptibility and robustness 16. DCT-based techniques embed data in mid-frequency components to balance robustness and visual fidelity, particularly in JPEG-compressed images 17. But, conventional DCT approaches are prone to blocking artifacts and limited payload capacities. Adaptive DCT methods, which leverage coefficient variations across blocks, attempt to improve performance, but still face limitations in robustness and embedding efficiency.

DWT-based steganography decomposes images into multi-resolution sub-bands, embedding data in high-frequency components where alterations are less perceptible 18. This makes DWT especially suitable for high-resolution modalities like CT and MRI, where structural fidelity is essential. Hybrid DWT-DCT methods combine the advantages of both transforms to further enhance security and efficiency. But they remain susceptible to geometric distortions and may introduce perceptual artifacts in sensitive regions of medical scans. DFT-based approaches manipulate phase and magnitude components for embedding. While phase modification is often imperceptible to the human eye, the global nature of the Fourier transform means that minor frequency changes can have broad spatial impact, making DFT less effective for localized or structure-preserving medical applications 19.

Recent advances in deep learning have opened new possibilities for adaptive, robust, and high-capacity steganographic systems. Convolutional neural networks (CNNs), attention mechanisms, and encoder-decoder frameworks enable content-aware embedding that maintains the diagnostic quality of medical images. These methods provide improved imperceptibility, robustness to distortions, and generalization across modalities such as CT, MRI, and ultrasound, making them well-suited for telemedicine and electronic health record (EHR) systems. Baluja 20 pioneered deep learning-based image steganography, demonstrating that a complete image can be hidden within another. In contrast, the resulting stego images often exhibited poor visual fidelity. Duan et al. 21 addressed this limitation using a U-Net architecture to extract and integrate hierarchical features, improving visual quality 22. Yu et al. 23 introduced attention masks to identify optimal embedding regions, further enhancing imperceptibility.

Despite these advances, conventional CNNs often struggle with extracting fine-grained secret features, leading to distortions in reconstructed images. To mitigate this, Lu et al. 24 proposed the Invertible Steganography Network (ISN), employing parameter-sharing mechanisms for efficient embedding and extraction. Jing et al. 25 integrated a wavelet loss to guide embedding into high-frequency regions, preserving structural details. On the other hand, the lack of explicit attention mechanisms limited their ability to emphasize task-relevant features. Subsequent works, incorporated channel attention mechanisms to highlight salient features, while Li et al. 26 introduced spatial-channel joint attention within an invertible framework to minimize distortion. Still, many of these models rely on fixed-kernel convolutional attention, which limits their receptive field and adaptability. To overcome these constraints, we adopt Squeeze-and-Excitation (SE) blocks 27, which dynamically recalibrate channel-wise feature activations, enabling the model to focus on the most relevant information during both encoding and decoding. This improves the robustness of the embedded content while preserving the quality of both the stego and extracted medical images. Table 1 summarizes the strengths, weaknesses, and evaluation metrics of the major steganographic techniques discussed.

Table 1 Comparison of Steganographic Techniques in Medical Imaging.
Full size table

Methodology

This section describes the proposed deep learning-based steganography framework designed for secure, high-fidelity medical image embedding and reconstruction. Our model adopts a hybrid encoder–decoder architecture incorporating residual connections, Squeeze-and-Excitation (SE) blocks, dilated convolutions, and Inception modules to improve robustness, embedding accuracy, and imperceptibility. The entire system is optimized for real-time deployment on the NVIDIA Jetson TX2 edge computing platform. The notations used throughout this paper are summarized in Table 2.

Table 2 Summary of notations used in the proposed model.
Full size table

Overall architecture

The proposed steganographic system comprises two core modules: an encoder network that embeds secret medical images into natural cover images, and a decoder network that reconstructs the hidden images with minimal perceptual distortion Both the encoder and decoder are built using deep convolutional operations augmented with attention and multi-scale feature learning techniques. Figure 2 shows the block diagram of the overall architecture and we give a detailed description of each module in subsequent sections.

Fig. 2
figure 2

Block diagram of the proposed encoder-decoder architecture.

Full size image

Encoder architecture

The encoder receives a pair of inputs: a cover image \({I}_{c}\) and a secret medical image \({I}_{s}\), each resized to the same spatial dimensions. The two inputs are then concatenated along the channel axis to form a unified tensor:

$${I}_{concat}={\text{Concat}}({I}_{c},{I}_{s})$$
(1)

This tensor is passed through a sequence of convolutional layers initialized with \(3\times 3\) kernels and 64 filters. These layers extract low-level features from the combined representation. Each convolution operation is followed by ReLU activation, batch normalization, and, in some blocks, residual skip connections to preserve gradient flow. Figure 3 shows the different layers in the encoder network.

Fig. 3
figure 3

Encoder Architecture.

Full size image

Squeeze-and-excitation attention mechanism: To recalibrate channel-wise feature responses, SE blocks are integrated within the encoder. Given an intermediate feature map \(F\in {\mathbb{R}}^{H\times W\times C}\), SE attention performs the following steps:

Squeeze: Apply global average pooling to obtain a channel descriptor:

$$z_{c} = \frac{1}{H \times W}\mathop \sum \limits_{i = 1}^{H} \mathop \sum \limits_{j = 1}^{W} F_{i,j,c}$$
(2)

Excitation: Pass through two fully connected layers with non-linear activation:

$$s=\sigma ({W}_{2}\cdot \delta ({W}_{1}\cdot z))$$
(3)

Scaling: Rescale the original feature map:

$${\widehat{F}}_{i,j,c}={s}_{c}\cdot {F}_{i,j,c}$$
(4)

This attention module enhances the model’s ability to focus on semantically meaningful features relevant for embedding. Figure 4 shows the different elements in the Squeeze and Excitation module.

Fig. 4
figure 4

Squeeze and Excitation Attention mechanism.

Full size image

Dilated convolutions: To capture multi-scale spatial information without significantly increasing computational cost, dilated convolutions are employed with rates \(r=\{2,4,8\}\). These increase the receptive field and enable the model to encode contextual features at varying levels:

$${F}_{dilated}^{(r)}={\text{Conv}}_{3\times 3}^{(dilation=r)}(F)$$
(5)

Smaller rates capture texture and edges, while larger ones encode global patterns. Outputs from different dilation levels are combined using summation with residual projections.

Skip connections and feature aggregation: To facilitate deeper learning and enhance training stability, residual skip connections are introduced between intermediate feature maps. Intermediate outputs \({F}_{1},{F}_{2}\) are aligned using \(1\times 1\) convolutions and aggregated as:

$${F}_{agg}={\text{Conv}}_{1\times 1}({F}_{1})+{\text{Conv}}_{1\times 1}({F}_{2})$$
(6)

This aggregation improves feature fusion and gradient propagation, preserving both local and global features critical to accurate embedding.

Encoded output generation: The aggregated features are passed through a final convolutional layer followed by a sigmoid activation to produce the stego image \({I}_{encoded}\):

$${I}_{encoded}=\sigma ({\text{Conv}}_{3\times 3}({F}_{agg}))$$
(7)

The stego image retains the same shape as the cover image and visually resembles it while imperceptibly containing the embedded medical content.

Decoder architecture

The decoder module reconstructs the hidden medical image from the encoded stego image while preserving its structural and visual integrity. This ensures that the embedded diagnostic data is accurately recovered, with minimal distortion or loss of information. Figure 5 shows the different layers in the decoder architecture.

Fig. 5
figure 5

Decoder Architecture.

Full size image

Initial feature extraction: The decoding process begins by passing the encoded image \({I}_{stego}\) into a convolutional layer with a \(3\times 3\) kernel and 64 filters. This operation captures low-level spatial patterns required for subsequent reconstruction. The ReLU activation function introduces non-linearity, enhancing the feature representation. The transformation is mathematically expressed as:

$${F}_{1}={\text{ReLU}}({W}_{1}*{I}_{stego}+{B}_{1})$$
(8)

Residual feature mapping: To improve gradient flow and learning stability, residual blocks are incorporated into the decoder. Each residual unit contains two convolutional layers with ReLU activations and a shortcut connection. This structure enables identity mappings that help preserve fine-grained details during decoding. The residual transformation can be described as follows:

$${F}_{r1}={\text{ReLU}}({W}_{r1}*{F}_{in}+{B}_{r1})$$
(9)
$${F}_{r2}={W}_{r2}*{F}_{r1}+{B}_{r2}$$
(10)

If the input and output dimensions differ, a \(1\times 1\) convolution is applied to align the channel dimensions before the residual summation:

$${F}_{out}={F}_{r2}+{\text{Conv1x1}}({F}_{in})$$
(11)

This residual structure facilitates effective feature learning and reconstruction of complex anatomical structures from the stego image. Figure 6 shows the architecture of the residual block.

Fig. 6
figure 6

Architecture of a Residual block.

Full size image

Multi-scale decoding via inception modules: Following residual mapping, the decoder employs Inception modules to extract multi-scale spatial features. These blocks apply convolutional filters of varying kernel sizes (\(1\times 1\), \(3\times 3\), and \(5\times 5\)) in parallel, enabling the model to capture both fine and coarse details within the image which is shown in Fig. 7. The individual operations are defined as:

Fig. 7
figure 7

Architecture of an Inception module.

Full size image
$${F}_{1x1}={\text{ReLU}}({W}_{1x1}*F+{B}_{1x1})$$
(12)
$${F}_{3x3}={\text{ReLU}}({W}_{3x3}*F+{B}_{3x3})$$
(13)
$${F}_{5x5}={\text{ReLU}}({W}_{5x5}*F+{B}_{5x5})$$
(14)

These feature maps are concatenated along the channel dimension to form the final multi-scale representation:

$${F}_{concat}=[{F}_{1x1},{F}_{3x3},{F}_{5x5}]$$
(15)

The use of inception structures ensures that relevant spatial patterns at multiple resolutions are incorporated into the reconstruction process, improving robustness to variations in medical image structure.

Final reconstruction and output: A final \(3\times 3\) convolutional layer, followed by a sigmoid activation function, is applied to generate the output secret image. This ensures that the reconstructed pixel values remain within the normalized range \([0,1]\), suitable for grayscale medical imaging:

$${I}_{decoded}=\sigma ({W}_{f}*{F}_{concat}+{B}_{f})$$
(16)

Decoder enables precise and high-fidelity reconstruction of the embedded medical image, making it suitable for telemedicine and real-time diagnostic applications on edge devices.

Experiments and results

This section presents the experimental evaluation of the proposed deep learning-based steganography model, focusing on reconstruction fidelity, robustness, and computational efficiency. A series of experiments were conducted to validate the performance of the proposed architecture on diverse datasets and under varying perturbation scenarios. Metrics such as Peak Signal-to-Noise Ratio (PSNR), Structural Similarity Index Measure (SSIM), Mean Squared Error (MSE), and Normalized Cross-Correlation (NCC) were employed to quantify performance.

Hardware and software configuration

All experiments were implemented in Python 3.8 using the PyTorch framework. The model was trained and tested on a workstation equipped with an NVIDIA Jetson TX2 platform, a power-efficient embedded system featuring a 256-core Pascal GPU and a quad-core ARM CPU. CUDA and cuDNN were used to enable hardware acceleration. Hyperparameter tuning and training monitoring were conducted using PyTorch Lightning and TensorBoard.

Datasets

To evaluate the performance of the proposed model, three distinct datasets were utilized. The cover images comprised 600 natural flower images 28,29, serving as the visual medium for embedding. Two types of medical datasets were employed as secret images: 600 MRI brain scans used for tumour detection 30, and 600 Optical Coherence Tomography (OCT) eye images used for glaucoma detection 31.

All images were pre-processed to a standardized resolution of 256 × 256 × 3 pixels to ensure uniformity in input dimensions and compatibility with the encoder-decoder framework. The datasets were partitioned into training and testing subsets using an 80:20 split. The network was trained for 200 epochs using a batch size of 8. Optimization was performed using the Adam algorithm, with an initial learning rate set to 0.0001. Figure 8 shows sample images- cover image, secret MRI image, stego image and decoded secret image corresponding to three samples from MRI brain dataset and Fig. 9 shows three samples from OCT Glaucoma dataset.

Fig. 8
figure 8

Cover image, secret image, stego image & decoded secret image of three MRI Brain images.

Full size image
Fig. 9
figure 9

Cover image, secret image, stego image & decoded secret image of three OCT Glaucoma images.

Full size image

Quantitative evaluation

The effectiveness of the model was evaluated using a range of standard metrics including PSNR, MSE, Structural Content (SC), Normalized Cross-Correlation (NCC), Maximum Difference (MD), Laplacian Mean Squared Error (LMSE), Normalized Absolute Error (NAE), and Structural Similarity Index (SSIM). These metrics were computed for all test images and box plots were plotted across 25 randomly selected test images from the brain MRI dataset to assess distortion, similarity, and structural preservation.

Peak signal-to-noise ratio (PSNR): PSNR is a widely used metric that quantifies the reconstruction fidelity by measuring the pixel-level distortion introduced during embedding.

$${\text{PSNR}}=10\cdot {\text{log}}_{10}\left(\frac{{\text{MAX}}^{2}}{\text{MSE}}\right)$$
(17)

where MAX is the maximum pixel value (255 for 8-bit images), and MSE denotes the Mean Squared Error between the secret and reconstructed images.

Our model achieved average PSNR values of 39.02 dB (brain MRI) and 38.75 dB (glaucoma), indicating high-fidelity reconstruction. Figure 10a shows the box plot of PSNR values obtained for MRI Brain image dataset for 25 test images. The median is centered around 39 dB, with most values falling in the 38–40 dB range. A single upper outlier above 42 dB is observed, suggesting occasional enhanced reconstruction due to variations in embedding strength.

Fig. 10
figure 10

Box plots of (a) PSNR (b) MSE and (c) SC for 25 MRI brain test images.

Full size image

Mean squared error (MSE): MSE measures the average squared difference between the original and decoded pixel intensities.

$${\text{MSE}} = \frac{1}{MN}\mathop \sum \limits_{i = 1}^{M} \mathop \sum \limits_{j = 1}^{N} \left( {I_{s} \left( {i,j} \right) - I_{decoded} \left( {i,j} \right)} \right)^{2}$$
(18)

Lower MSE values indicate minimal distortion. Figure 10b shows a median value of ~ 9, with most values ranging from 7 to 12 obtained for MRI Brain image dataset for 25 test images. The absence of extreme outliers reflects the stability of the model.

Structural content (SC): SC assesses structural preservation by comparing the energy of the original and decoded images.

$${\text{SC}}=\frac{\sum {I}_{s}(i,j{)}^{2}}{\sum {I}_{decoded}(i,j{)}^{2}}$$
(19)

Values close to 1 indicate minimal deviation. As seen in Fig. 10c, the majority of SC values are centered around 1.05, indicating excellent preservation of structural content, which is very important for medical imaging.

Normalized cross-correlation (NCC): NCC measures pixel-level similarity between the secret and decoded images:

$${\text{NCC}}=\frac{\sum {I}_{s}(i,j)\cdot {I}_{decoded}(i,j)}{\sum {I}_{s}(i,j{)}^{2}}$$
(20)

Ideal values are close to 1. Figure 11a illustrates NCC values predominantly above 0.96, with a median near 0.97 and a single upper outlier at 1.0, confirming excellent reconstruction fidelity.

Fig. 11
figure 11

Box plots of (a) NCC (b) MD and (c) LMSE for 25 MRI brain test images.

Full size image

Maximum difference (MD): MD quantifies the largest absolute pixel-wise difference:

$${\text{MD}}=\underset{i,j}{\text{max}}\left|{I}_{s}(i,j)-{I}_{decoded}(i,j)\right|$$
(21)

Lower values are preferred for medical images. As shown in Fig. 11b, most MD values lie between 25 and 35, with a median around 30. A few samples exhibit higher deviation, likely due to localized image complexity.

Laplacian mean squared error (LMSE): LMSE evaluates edge-based distortion using the Laplacian of the image:

$${\text{LMSE}}=\frac{\sum {\left[{\nabla }^{2}{I}_{s}(i,j)-{\nabla }^{2}{I}_{decoded}(i,j)\right]}^{2}}{\sum {\left[{\nabla }^{2}{I}_{s}(i,j)\right]}^{2}}$$
(22)

A low LMSE (< 0.1) signifies excellent structural preservation. Figure 11c shows LMSE values predominantly in the 0.09–0.15 range, with a median near 0.11.

Normalized absolute error (NAE): NAE measures perceptual distortion between the secret and decoded image.

$${\text{NAE}}=\frac{\sum \left|{I}_{s}(i,j)-{I}_{decoded}(i,j)\right|}{\sum \left|{I}_{s}(i,j)\right|}$$
(23)

NAE values < 0.05 are considered excellent. Figure 12a shows a median NAE of ~ 0.06 with low variability, indicating good imperceptibility across test cases.

Fig. 12
figure 12

Box plot on brain MRI images (a) NAE values (b) SSIM values for 25 MRI brain test images.

Full size image

Structural similarity index measure (SSIM): SSIM evaluates perceptual similarity based on luminance, contrast, and structure.

$${\text{SSIM}}({I}_{s},{I}_{d})=\frac{(2{\mu }_{s}{\mu }_{decoded}+{C}_{1})(2{\sigma }_{s,decoded}+{C}_{2})}{({\mu }_{s}^{2}+{\mu }_{decoded}^{2}+{C}_{1})({\sigma }_{s}^{2}+{\sigma }_{decoded}^{2}+{C}_{2})}$$
(24)

with \(\mu ,\sigma\), and \({\sigma }_{sd}\) representing means, variances, and covariances, respectively.

As shown in Fig. 12b, the SSIM values for the proposed model are consistently high, with a median near 0.98 and a minimum above 0.95. These results confirm minimal perceptual distortion and excellent structural consistency.

Robustness analysis under common image perturbations

To evaluate the robustness of the proposed method against common image distortions, we applied four types of perturbations- JPEG compression, Gaussian noise, cropping with resizing, and salt & pepper noise. The quantitative results are summarized in Fig. 13 which presents a heatmap comparing PSNR and SSIM across these perturbations. It illustrates that the model maintains high perceptual similarity and signal fidelity even under moderate perturbations.

  • JPEG Compression (Q = 75) yields the highest PSNR (39.02 dB) and SSIM (0.975), indicating minimal perceptual degradation which suggests that our technique is highly resilient to lossy compression artifacts.

  • Gaussian Noise (σ = 0.01) moderately impacts performance, with a PSNR of 37.55 dB and SSIM of 0.963, reflecting slight pixel-level perturbations but relatively preserved structural integrity.

  • Cropping + Resizing resulted in a more noticeable degradation (PSNR = 36.10 dB, SSIM = 0.950), likely due to interpolation and information loss at borders.

  • Salt & Pepper Noise imposes the greatest challenge, with the lowest PSNR (34.70 dB) and SSIM (0.931), attributable to the high-intensity, localized nature of the noise.

Fig. 13
figure 13

Heatmap of PSNR (dB) and SSIM values across four perturbation types. Darker blue indicates higher PSNR, while lighter shades in SSIM indicate higher structural similarity.

Full size image

So, our model is robust especially under realistic distortions like compression and Gaussian noise. But the performance slightly degrades under spatial transformations and impulsive noise, warranting future improvements in noise-aware training schemes.

Ablation study

To evaluate the individual contributions of key architectural components within the proposed steganographic model, an ablation study was performed. In each experiment, one or more components were removed or modified while keeping the remaining architecture unchanged. The effect of each modification was assessed based on the average PSNR and SSIM values over the test set, allowing for a quantitative analysis of image fidelity and structural preservation.

Model A: removal of residual connections—Residual connections were excluded from the encoder-decoder architecture to assess their influence on feature propagation. The absence of skip connections resulted in a PSNR of 34.12 dB and SSIM of 0.915. The degradation in performance highlights the critical role of residual learning in maintaining deep feature retention and facilitating gradient flow, which are essential for accurate reconstruction.

Model B: exclusion of squeeze-and-excitation (SE) blocks—SE blocks were removed while preserving all other architectural elements. The modified model yielded a PSNR of 35.05 dB and SSIM of 0.927. This decline demonstrates the importance of channel-wise attention in recalibrating feature responses, allowing the network to selectively emphasize salient features during both embedding and decoding.

Model C: replacement of dilated convolutions with standard convolutions—In this variant, all dilated convolutions were substituted with standard convolutions. A significant drop in performance was observed, with PSNR falling to 33.80 dB and SSIM to 0.910. These results suggest that dilated convolutions are instrumental in expanding the receptive field without increasing the parameter count, thereby enhancing spatial feature extraction necessary for effective steganographic encoding.

Model D: removal of inception modules—The inception blocks responsible for multi-scale feature extraction were eliminated. The resulting model achieved a PSNR of 34.50 dB and SSIM of 0.918. This indicates that the parallel use of multiple kernel sizes contributes substantially to the model’s adaptability in capturing hierarchical spatial patterns, which supports better feature representation across varied image textures.

Model E: Joint removal of SE blocks and dilated convolutions—To assess the combined effect of removing both channel attention and spatial context mechanisms, SE blocks and dilated convolutions were jointly removed. The model’s performance further deteriorated, with PSNR at 33.30 dB and SSIM at 0.905. The result underscores the complementary role these components play in balancing local emphasis and global context, both crucial for accurate and imperceptible data embedding.

Model F: elimination of all attention mechanisms—All attention mechanisms, including SE blocks and channel-based recalibration layers, were removed in this configuration. The performance declined to a PSNR of 32.90 dB and SSIM of 0.895. These findings emphasize the role of attention in enhancing discriminative features, improving the network’s capability to recover fine details from stego images.

Model G: removal of residual and attention mechanisms—In the most constrained configuration, both residual connections and all attention mechanisms were removed. This led to the most pronounced performance degradation, with a PSNR of 32.20 dB and SSIM of 0.880. The simultaneous exclusion of deep feature retention and selective attention mechanisms severely impacted the model’s ability to reconstruct the hidden content, reaffirming their synergistic importance in achieving high-fidelity steganography.

Hardware implementation and deployment feasibility

The proposed steganography model was deployed on the NVIDIA Jetson TX2 platform to evaluate its real-time processing capability, energy efficiency, and suitability for edge applications in telemedicine and medical imaging. The Jetson TX2 is equipped with a 256-core Pascal GPU, a 6-core ARM CPU, and 8 GB of LPDDR4 RAM, making it a compact yet powerful embedded system ideal for low-power, real-time AI tasks.

The architecture’s integration of residual connections, squeeze-and-excitation (SE) blocks, inception modules, and dilated convolutions enables high-capacity embedding while maintaining visual fidelity. Residual learning facilitates deep feature propagation, SE blocks enhance attention-based refinement, and inception modules allow multi-scale spatial feature extraction all of which are essential for robust and accurate reconstruction of medical images.

During inference, convolutional operations, adaptive embedding, and decoding tasks were significantly accelerated by the Jetson TX2’s parallel CUDA cores. The system consistently achieved a processing time of 25–35 ms per image and a throughput of approximately 25–30 images per second. These results demonstrate the feasibility of deploying the model for real-time steganographic operations in mobile or low-resource medical environments. Table 3 summarizes the computational resource usage and environmental suitability of the proposed model on the Jetson TX2 platform.

Table 3 Computational Resource Consumption and Real-World Feasibility of the Proposed Model on NVIDIA Jetson TX2.
Full size table

Benchmarking with State-of-the-Art Techniques

To evaluate the performance of the proposed steganographic model, we conducted a comparative analysis with recent state-of-the-art methods, including HiDDeN 32, SteganoGAN 33, HCISNet 34, and AVGGAN 35. The comparison was performed using three widely adopted image quality metrics- PSNR, MSE, and SSIM-on both the brain MRI and OCT glaucoma datasets. Table 4 shows the corresponding metric values obtained for three sample images from MRI Brain image datset.

Table 4 Comparison of Key metrics with State-of-the-Art Techniques.
Full size table

The proposed model consistently achieved the highest or near-highest PSNR values, ranging from 38.51 dB to 41.96 dB, indicating excellent reconstruction fidelity. SSIM values remained above 0.96 for all test cases, with peaks of 0.99 for brain MRI samples, highlighting strong preservation of structural information. While MSE values were slightly higher in some OCT cases compared to AVGGAN, the overall visual quality remained high, as reflected by superior SSIM and PSNR values.

To further assess model generalizability and average performance across a broader test set, we computed the mean PSNR and SSIM values over 25 randomly selected images from each dataset. As shown in Table 5, the proposed method consistently outperformed SteganoGAN, HCISNet, and CSIS on both brain MRI and glaucoma OCT datasets. Its performance closely matched AVGGAN, achieving competitive SSIM and PSNR values while maintaining lower model complexity and real-time deployability.

Table 5 Average SSIM and PSNR values over 25 test images for brain MRI and glaucoma OCT datasets.
Full size table

Conclusion and future works

In this research, we introduced a novel deep learning-based steganographic framework designed specifically for secure medical image transmission in telemedicine and teleradiology applications. By using Squeeze-and-Excitation (SE) blocks, Inception modules, and residual connections within an encoder-decoder architecture, the proposed model effectively balances embedding capacity, imperceptibility, and reconstruction accuracy. Experimental results on MRI brain scans and OCT glaucoma datasets demonstrated high visual fidelity of the stego images and successful reconstruction of secret image, with average PSNR values exceeding 39 dB and SSIM values approaching 0.98. Unlike traditional steganographic techniques, our model is robust against various perturbations and is optimized for real-time edge deployment on NVIDIA Jetson TX2, addressing the practical constraints of clinical environments. The integration of dilated convolutions and multi-scale feature extraction further enhances the system’s ability to capture spatial context and maintain diagnostic integrity, making it suitable for high-resolution medical imagery.

This work establishes a viable pathway for implementing secure, lightweight, and scalable steganographic solutions in resource-constrained settings, where both data confidentiality and real-time processing are critical. Future research may explore integrating transformer-based attention mechanisms and cross-modality steganography to further increase adaptability across diverse medical imaging standards.