Introduction

As the automotive industry advances toward electrification, intelligence, and high performance1,2, vehicle operating conditions have grown increasingly demanding. The suspension system, a core component of the vehicle chassis3, connects the body to the wheels through a combination of damping devices, elastic members, and guiding mechanisms4,5. It functions to transmit vertical, longitudinal, and lateral forces, as well as associated moments, from the road to the vehicle, thereby ensuring safe and stable operation6. Among various independent suspension types, the torsion bar double-wishbone configuration stands out for enabling independent wheel movement and offering a short, efficient force transmission path. Compared to dependent suspensions, this design improves ride quality and handling7 by lowering floor height, reducing turning radius, and minimizing body roll and vibration8. The lower control arm, a vital component within this suspension layout, plays a crucial role in guiding motion and transferring loads. Its structural integrity directly affects vehicle handling stability and overall safety9. During real-world driving, this component endures complex and variable loading conditions, particularly at its hinge points, which are subjected to extreme and random cyclic stresses10,11. Over time, such stress cycles result in cumulative fatigue damage, potentially leading to structural failure, degraded driving performance, and, in severe cases, safety hazards to occupants12. Since both material properties and structural geometry exert significant influence over fatigue resistance 13,14, the early-stage prediction and evaluation of fatigue life for suspension components has become a focal point in automotive design research.

Related works on fatigue life of lower control arm

The finite element simulation method has been effectively applied in the fatigue performance research of the lower control arm. Sun et al.15 investigated the lower control arm of a MacPherson suspension, conducting finite element analysis on the modal and stiffness, and employed the nominal stress method to predict fatigue life. Abebe et al.16 built a finite element model to predict the fatigue life of the control arm under bump-loading conditions and developed a method for systematic uncertainty quantification. Gonsalves et al.17 presented a numerical framework to perform fatigue high-fidelity simulations of vehicle chassis components. The results evidence the predictive capabilities of this numerical framework in performing fatigue high-fidelity simulations of metallic structures at engineering-relevant scales. Most critically, the accurate acquisition of fatigue loads determines the confidence level in the fatigue life prediction of the control arm. The fatigue loads describe the load variation conditions of the component, which depend on the vehicle’s operating conditions. Liu et al.18 finished the load test on the vehicle structure of the control arm under the vehicle proving ground combination road containing 8 cases and computed equivalent coefficients of failure damage on the vehicle structure. Zou et al.19 collected load spectra through vehicle road tests to obtain force load signals of the suspension lower control arms and performed fatigue life calculations. Santharaguru et al.20 determined the appropriate frequency domain methods for durability predictions of lower suspension arms based on real-life random vibration data. They obtained the power spectral densities of the vibration signals via vehicle tests based on vibration acceleration sensors. However, these methods require extensive vehicle or rig tests, which involve long cycles and high costs, thereby reducing the efficiency of control arm development and optimization21. Therefore, the key lies in developing a simulation model that can accurately obtain fatigue loads on the control arm and predict its fatigue life.

There are multiple approaches to improve the fatigue performance of vehicle control arms. Some researchers have improved fatigue life by optimizing the structural configuration of the control arm and have developed relevant optimization algorithms. Yoo et al.22 conducted the topology optimization of the lower control arm. Mohamed Attia et al.23 proposed different designs of a suspension control arm developed, concerning its strength to weight ratio. Ren et al.24 calculated the stress distribution and lowest point of lifetime of the control arm under fatigue load and presented the optimization scheme according to the structure characteristics of components. Jiang et al.25 carried out the multi-objective optimization design of the control arm based on the Kriging surrogate model and NSGA-II algorithm. The optimization results show that the mass of the control arm was reduced by 4.1% and the fatigue life was increased by 215.8% while its reliability increased by 7.8%. Meanwhile, other researchers have explored novel high-strength materials as replacements for conventional control arm materials to improve fatigue performance. Ragab et al.26 developed and designed much lighter and better fatigue resistant metal of semisolid A357 aluminum alloys to replace steel suspension control arms. The research results show a clear improvement of the fatigue curve towards the experimental curve performed on the samples of aluminum alloy A357 compared with the same analytical curve for the same alloy. Oruc et al.27 investigated and compared the buckling behavior of control arms which are produced with Si particle reinforced aluminum-based metal composite material and standard aluminum alloy material. Wei et al.28 conducted lightweight development of an aluminum alloy control arm using carbon fiber materials. The results demonstrate that the carbon fiber control arm exhibits superior stiffness, strength, and fatigue resistance, while achieving significant weight reduction. However, these methods would significantly alter the original composition of control arms. Topology optimization substantially impacts production costs for automotive manufacturers, which means the existing structural molds would become obsolete. Moreover, the application of expensive advanced materials is often impractical for mass-produced vehicles.

With the continuous emergence of smart materials and the mature application of piezoelectric ceramics29,30,31, it has the characterized of smaller size, lighter weight, controllable frequency bandwidth, and high electromechanical conversion efficiency32. Piezoelectric ceramics can adjust the vibration characteristics of beam structures33,34,35, providing a new guiding direction for active vibration control and even fatigue life control. Some researchers have conducted relevant research on the active control of automobile vibration. Zhou et al.36 performed the anti-vibration active control test of a car roof using an LMS adaptive filtering method. In the field of noise control, Xu et al.37 developed an active vehicle interior noise control system based on piezoelectric ceramic elements. The system simplifies the vehicle cavity model into plate components as the research object, with vibration reduction as the objective, ultimately achieving active interior noise control. Although these large-scale structures may appear complex, they fundamentally consist of basic components such as rods, plates, and beams. Meanwhile, current applied research predominantly focuses on noise and vibration control based on simplified structural models, with limited reported research on piezoelectric coupling models specifically targeting active fatigue life control. Therefore, the key challenge lies in developing a reasonable piezoelectric material and structural configuration to optimize the fatigue life of the lower control arm based on the piezoelectric effect.

Analysis of related works

According to the above analysis, many studies have implemented the prediction and optimization of lower control arm fatigue life and have achieved effective results; however, the following common problems remain:

  1. 1.

    The fatigue load data of lower control arms obtained via vehicle tests are accurate and effective, but they have the problems of high cost and low efficiency. Meanwhile, in the fatigue life calculation of the lower control arm, both rig test and accelerated fatigue methods lead to reduced prediction efficiency.

  2. 2.

    Current optimization methods for lower control arm fatigue life still face critical limitations. First, the topology optimization of the lower control arm has the problem of increasing the production cost for the automotive manufacturers. Second, the application of expensive advanced materials (such as aluminum alloy materials and carbon fiber materials) is often impractical for mass-produced vehicles.

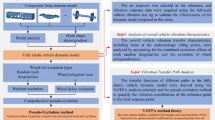
To overcome the aforementioned problems, this paper combined the finite element method and multi-body dynamics method and developed a rigid-flexible coupling model, which is applied to the fatigue life prediction and optimization for the lower control arm. This paper has two main contributions: (1) A rigid-flexible coupling dynamics model of the independent suspension system is developed, which includes a finite element flexible body model of the lower control arm and a multi-rigid body model of the suspension system. (2) The piezoelectric ceramic-lower control arm coupling model is developed. Based on this, the fatigue performance active control methods based on piezoelectric ceramic for the lower control arm are proposed, which employ bonded piezoelectric ceramic and embedded piezoelectric ceramic to enhance the static and dynamic performance of the lower control arm, respectively, and thus optimize the fatigue life. The research process of fatigue life analysis and piezoelectric active control for vehicle suspension lower control arm is shown in Fig. 1.

Fig. 1
figure 1

Research process of fatigue life analysis and piezoelectric active control for vehicle suspension lower control arm.

Full size image

The remainder of this paper is organized as follows. In Section “Development of rigid-flexible coupling dynamic model for independent suspension system”, a rigid-flexible coupling dynamics model of the independent suspension system is established and validated. In Section “Analysis of fatigue life and influence regularity”, the fatigue life of the lower control arm is predicted and the influence regularity is analyzed. In Section “Presentation of piezoelectric active control method for fatigue performance of lower control arm”, a piezoelectric ceramic-based active control method is proposed. The fatigue performance active control methods based on piezoelectric ceramic are proposed. Section “Conclusions” summarizes the conclusions of this paper.

Development of rigid-flexible coupling dynamic model for independent suspension system

Establishment of finite element model for lower control arm

The structure of the torsion bar double-wishbone independent suspension is shown in Fig. 2a. The main components of the suspension system include the upper control arm, lower control arm, steering knuckle, torsion bar, damper, stabilizer bar, and various bracket structures. Among them, the lower control arm, as the core component of the suspension system, is connected to the steering knuckle, torsion bar, damper, lateral stabilizer bar and bushing. Considering the geometry and dimensions of the lower control arm38, a 10-node tetrahedral element is selected as the solid element type. In addition, to account for the computational iteration capacity during structural optimization, the element size is set to 15 mm, with local mesh refinement applied to stress concentration-prone regions such as bolt connections and bushings. The finite element model of the lower control arm is shown in Fig. 2b.

Fig. 2
figure 2

Torsion bar double-wishbone independent suspension system and lower control arm: (a) Independent suspension system; (b) Finite element model of lower control arm.

Full size image

The total mesh element number is 90,595. The solid structure of the lower control arm and the bracket are simulated using tetrahedral Solid185 element. The connection between the lower control arm and the vehicle body is achieved through bushings, with three linear and three rotational stiffness simulated using the linear spring Combin14 element. The bushing stiffnesses are shown in Table 1. The torsion rod bracket and the lower control arm are connected using Beam188 element representing bolted joint, with a cross-sectional diameter of 15 mm. To accurately reproduce the mechanical load transfer path of the torque, the finite element model of the torsion rod bracket is retained. In addition, the material used for the suspension system is 42CrMoA, and the material property is shown in online Table A1.

Table 1 Front independent suspension system bushing stiffness.
Full size table

Establishment of rigid-flexible coupling suspension system model

In a multibody system, the components are connected through kinematic joints, which constrain certain relative motions between them. The dynamic characteristics of such systems must be described using differential and algebraic equations39. The dynamic equations of the multibody system, established using the Lagrange multiplier method, are expressed in Eq. (1):

$$\begin{aligned} \frac{{\text{d}}}{{{\text{d}}t}}\left( {\frac{{\partial {\varvec{T}}}}{{\partial \dot{\user2{q}}}}} \right)^{{\text{T}}} - \left( {\frac{{\partial {\varvec{T}}}}{{\partial {\varvec{q}}}}} \right)^{{\text{T}}} + f_{q}^{T} {\varvec{\rho}} + g_{{\dot{q}}}^{T} {\varvec{\mu}} = & {\varvec{Q}} \\ {\text{Complete}}\,{\text{constraint}}\,{\text{equation: }}f({\varvec{q}},t) = & 0 \\ {\text{Incomplete}}\,{\text{constraint}}\,{\text{equation: }}g({\varvec{q}},\dot{\user2{q}},t) = & 0 \\ \end{aligned}$$
(1)

where,\({\varvec{T}}=\frac{({\dot{{\varvec{q}}}}^{T}{\varvec{M}}\dot{{\varvec{q}}})}{2}\) is the kinetic energy of the system; q is the generalized coordinate matrix, describing the Cartesian coordinates of rigid-body centers of mass and the Euler angles representing body orientations; \(\dot{{\varvec{q}}}\) is the generalized velocity matrix; M is the mass matrix of the system; Q is the generalized force matrix; ρ and μ are the Lagrange multiplier matrices for holonomic constraints and nonholonomic constraints, respectively.

Flexible multibody system dynamics is a research methodology developed from rigid multibody system dynamics. It not only considers the deformation of flexible components themselves, but also accounts for their coupling effects with rigid-body motions. The generalized coordinates of any point on a flexible-body can be expressed in Eq. (2):

$${\varvec{\xi}} = \left( {\begin{array}{*{20}c} {x,y,z,\phi ,\theta ,\varphi ,p_{i,m} } \\ \end{array} } \right)^{{\text{T}}} = \left( {\begin{array}{*{20}c} {{\varvec{R}},{\Psi },{\varvec{p}}} \\ \end{array} } \right)^{{\text{T}}}$$
(2)

where, x, y, z, ϕ, θ, φ represent the position and Euler angles of the local coordinate system in the global coordinate frame; pi,m is the mode shape component of the mth modal amplitude for node i of the flexible-body; R and Ψ are the vector representations of coordinates; p is the vector representation of pi,m, i.e., the modal amplitude vector.

The kinetic energy and potential energy of the system are expressed in Eq. (3):

$$\begin{array}{*{20}c} {{\varvec{T}} = \frac{1}{2}\dot{\user2{\xi }}^{{\text{T}}} \user2{M\dot{\xi }}} \\ {{\varvec{V}} = \frac{1}{2}\dot{\user2{\xi }}^{{\text{T}}} \user2{K\dot{\xi }}} \\ \end{array}$$
(3)

By substituting the kinetic and potential energy formulations into Lagrange’s equations, the dynamic equations of the flexible multibody system can be expressed in Eq. (4):

$$\user2{M\dot{\xi }} + \user2{\dot{M}\dot{\xi }} - \frac{1}{2}\left( {\frac{{\partial {\varvec{M}}}}{{\partial {\varvec{\xi}}}}\dot{\user2{\xi }}} \right)^{{\text{T}}} \dot{\user2{\xi }} + \user2{K\xi } + {\varvec{G}} + \user2{C\dot{\xi }} + \left( {\frac{{\partial {{\varvec{\Omega}}}}}{{\partial {\varvec{\xi}}}}} \right)^{{\text{T}}} \lambda = {\varvec{Q}}$$
(4)

where, K and C are the modal stiffness matrix and modal damping matrix of the flexible-body, respectively; G represents the gravity force vector of the flexible-body; λ is the Lagrange multiplier associated with the constraint equations.

The load spectra borne by the suspension lower control arm under actual working conditions are a critical factor in fatigue analysis. Therefore, the accurate acquisition of the load time course on the lower control arm is essential for fatigue life prediction. Considering the stiffness and actual working conditions of the suspension lower control arm, the fatigue life prediction accuracy can be greatly improved by treating the lower arm as a flexible body to establish a rigid-flexible coupling dynamics model of the independent suspension system. The finite element model of the lower control arm has been established in HyperMesh software. Subsequently, the material properties are assigned. Finally, the modal analysis of the lower control arm is conducted, and the results are imported into ADAMS dynamics software40. The front independent suspension system rigid-flexible coupling dynamics model is shown in Fig. 3.

Fig. 3
figure 3

Front independent suspension system rigid-flexible coupling dynamics model.

Full size image

Model validation

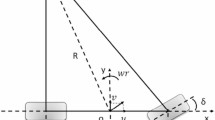
To validate whether the front suspension subsystem model can accurately represent the actual suspension system, a kinematic simulation analysis was conducted and compared with Kinematic and Compliance (K&C) test results41. The suspension K&C tests were performed using a standard twin-axle suspension parameter measurement machine (SPMM) manufactured by UK-based ABD Company, which can realistically simulate vehicle motions such as bounce, roll, and pitch during road operation. Prior to testing, comprehensive preparatory work was required, including: positioning the vehicle on the test rig; securing the vehicle in place; connecting all necessary wiring; and performing initial value calibration. During testing, all measurement data were acquired through the SPMM’s integrated measurement system, as shown in Fig. 4.

Fig. 4
figure 4

Schematic diagram of front suspension K&C characteristic testing.

Full size image

The SPMM conducts parallel wheel travel tests by applying vertical motion inputs to the entire vehicle. Simultaneously, the test rig applies lateral forces and aligning torques to the tire contact patch to complete lateral force tests and aligning torque tests, respectively. In the ADAMS software, the actual test conditions were simulated to calculate the variation patterns of K&C parameters for the front suspension system. The comparison curves between simulation and test results are shown in Figs 5, 6 and 7 (taking the left front wheel as an example).

Fig. 5
figure 5

Parallel wheel travel test: (a) Toe angle variation; (b) Camber angle variation; (c) Wheel center lateral displacement; (d) Wheel center longitudinal displacement; (e) Suspension stiffness.

Full size image
Fig. 6
figure 6

Lateral force test: (a) Toe angle variation; (b) Camber angle variation; (c) Wheel center lateral displacement.

Full size image
Fig. 7
figure 7

Aligning torque test: (a) Toe angle variation; (b) Camber angle variation.

Full size image

The comparative results demonstrate that, apart from minor discrepancies between simulated and test values for some K&C characteristics, the simulation curves generally agree well with the test curves. The accuracy of the simulation curves was evaluated by calculating the Root Mean Square (RMS) errors. The comparison results show that the RMS errors of all evaluation metrics are less than 10%, which falls within the allowable range of engineering error. It is worth noting that, due to the elastic property of the rubber bushing stiffness, certain test curves exhibit a degree of hysteresis; however, the overall error still meets the required standards. Overall, the established rigid-flexible coupling suspension system model can effectively predict the K&C characteristics of the studied vehicle’s front suspension, thereby validating the correctness of the front suspension dynamic model.

Analysis of fatigue life and influence regularity

The nominal stress refers to the condition in which the stress–strain relationship follows Hooke’s law when the stress is below the yield limit, such that the nominal stress and the true stress are identical. The fatigue life prediction of the lower cross arm is conducted based on the nominal stress method and Miner’s cumulative damage theory. Meanwhile, the nominal stress method is the simplest and most widely used approach for evaluating the fatigue life of welded joints42. Among them, the fatigue analysis of the lower cross arm requires three key factors: the actual fatigue load spectra43, the analysis results of stress–strain under unit load, and the material property. The fatigue analysis process of the lower control arm is shown in Fig. 8.

Fig. 8
figure 8

Fatigue analysis process of the lower control arm.

Full size image

Fatigue life analysis

Load spectrum acquisition

To ensure the accuracy and applicability of fatigue life prediction, relatively severe working conditions experienced in actual operation are applied. The simulation analysis is conducted in Adams/Car44,45 for the suspension system rigid-flexible coupling dynamics model on both B and C road levels, respectively. The working conditions are set to travel straight at 40 km/h for 20 s. The load time courses are extracted from four critical positions: the steering knuckle link joint, the stabilizer bar link joint, the damper link joint and the torsion bar to bracket link joint. Take the C road level as an example, the fatigue load spectra are shown in Fig. 9. It can be observed that, among the four load positions on the lower control arm, the steering knuckle link joint exhibits the most significant influence on suspension fatigue failure, with the contribution of the Z-direction load being the predominant factor. The damper connection link joint and stabilizer bar link joint demonstrate relatively minor contributions.

Fig. 9
figure 9

Fatigue load spectra: (a) Triaxial load spectra at steering knuckle link joint on C road level; (b) Triaxial load spectra at stabilizer bar link joint on C road level; (c) Triaxial load spectra at damper link joint on C road level; (d) X-direction load spectrum at torsion bar to bracket link joint on C road level.

Full size image

Stress–strain analysis

During vehicle operation, the lower control arm is subjected to four forces and torque. Before performing the fatigue life analysis, the inertia relief method is employed to determine the stress–strain states under unit load conditions. Unit loads (forces/torques) are sequentially applied along the X-, Y-, and Z-directions at four critical joint positions: the steering knuckle link joint, the stabilizer bar link joint, the damper link joint, and the torsion bar to bracket link joint. The stress–strain results unit loads are obtained (for the first three critical load positions, the Z-direction is presented as an example), as shown in Fig. 10.

Fig. 10
figure 10

Stress contour plots of the lower cross arm: (a) At steering knuckle link joint under Z-direction unit load; (b) At stabilizer bar link joint under Z-direction unit load; (c) At damper link joint under Z-direction unit load; (d) At torsion bar link joint under X-direction unit load.

Full size image

Fatigue life calculation

The S–N curve describes the relationship between cyclic stress level and fatigue life46. The structural material of the lower control arm is 42CrMoA, with a tensile strength of 1080 MPa. The base S–N curve for this material is in red, as shown in Fig. 11. To account for post-manufacturing component condition, a surface roughness of Ra3.2 is applied with a finish factor of 0.72. The modified S–N curve of the lower control arm is shown in blue.

Fig. 11
figure 11

S–N curves of 42CrMoA material before and after modification.

Full size image

Given that the number of cycles before fatigue fracture of the lower control arm in the distributed-drive bus studied in this paper is far greater than 105, the problem falls within the high-cycle fatigue category. Therefore, considering the actual service conditions of the bus and the characteristics of the load-induced failure, the fatigue life analysis of the lower control arm was conducted based on the Goodman method. When conducting the fatigue life analysis for the lower control arm, the primary step involves inputting both the finite element results under unit load conditions and the time course of the load spectra47. Meanwhile, the S–N curve is applied and the Goodman method is selected to correct for mean stress effects48. The material survival rate is set to 95%. The fatigue life contour plots of the lower cross arm are shown in Fig. 12. The results demonstrate that under B and C road levels, the most of nodes on the lower control arm fall within the infinite-life region, and the weak locations are the same. Under the B road level, the lower control arm exhibits infinite fatigue life, with a minimum cycle count of 8.353 × 1010 at Node 101,221. Under the C road level, the minimum cycle count is 5.293 × 106, equivalent to the mileage of 1.176 × 106 km.

Fig. 12
figure 12

Fatigue life contour plots of the lower cross arm: (a) On B road level; (b) On C road level.

Full size image

Influence regularity analysis

Single factor influence regularity analysis

Based on the above analysis, bushing stiffness, load magnification factor, surface roughness and material tensile strength are selected from structural design, service environment considerations, manufacturing processes and material properties to investigate the single factor influence regularity of the lower control arm fatigue life.

The bushing stiffness significantly influences the structural mechanical performance, especially the load transfer path. Under actual working conditions, the dominant factors affecting the lower control arm performance are the linear stiffness in the X-direction and the torsional stiffness in the X-, and Y-direction. In this study, the X-directional linear stiffness of the front bushing is selected as the research parameter. The stiffness values are set to 3700, 4100, 4500, 4900, and 5300 N/mm, and the corresponding fatigue life is calculated, as shown in Fig. 13a. The results indicate that as the X-directional linear stiffness of the front bushing increases, the fatigue life also increases, while the absolute variation rate (sensitivity magnitude) gradually decreases.

Fig. 13
figure 13

Fatigue life influence regularity: (a) The relationship between cycle count and bushing stiffness; (b) The relationship between cycle count and load magnification factor; (c) The relationship between cycle count and surface roughness; (d) The relationship between cycle count and tensile strength.

Full size image

The load amplification factor modifies the scale of the input loads. In this study, the input loads are scaled by ± 10% increments (0.9, 1.0, 1.1, 1.2, 1.3 multiples of the original load), and the corresponding fatigue life is calculated, as shown in Fig. 13b. The results indicate that as the load amplification factor increases, the fatigue life decreases, while the absolute variation rate gradually decreases.

Among various manufacturing factors, surface roughness is the only quantifiable parameter. Surface roughness of 0.8 μm, 3.7 μm, 6.6 μm, 9.5 μm, and 12.4 μm are selected to approximate the four standard roughness grades (Ra0.8, Ra3.2, Ra6.3, and Ra12.5). This surface roughness range covers a wide spectrum of manufacturing processes, from precision machining to coarse casting. The lower control arm investigated in this paper has a measured surface roughness of Ra3.2, which is consistent with the typical roughness of CNC-machined 42CrMoA forged components49. The corresponding fatigue life is calculated, as shown in Fig. 13c. The results indicate that as surface roughness increases, the fatigue life decreases, while the absolute variation rate gradually decreases.

Different materials correspond to distinct S–N curves that directly influence the fatigue life of the lower control arm. Tensile strength of 1040 MPa, 1060 MPa, 1080 MPa, 1100 MPa, and 1120 MPa are selected, and the corresponding fatigue life is calculated, as shown in Fig. 13d. The results indicate that as the tensile strength increases, the fatigue life decreases, while the absolute variation rate gradually decreases. This phenomenon is observed because for medium- and high-strength steels, the fatigue limit Sbe increases linearly with the tensile strength Su, i.e., Sbe /Su = constant. However, this proportional relationship has a limit, known as the critical ultimate strength. When a material tensile strength exceeds this critical value, the fatigue limit ceases to increase.

Sensitivity Analysis

For the orthogonal experimental design, four influence factors are similarly selected: bushing stiffness, load amplification factor, surface roughness and tensile strength. Each factor is assigned five equally spaced levels. Considering the existing orthogonal tables and selecting L25(54) form, which contains the 4-factor and 5-level. The confidence interval is set at 95%. The factors and levels of orthogonal experiment design are shown in Table 2 and the results of orthogonal experiment design are shown in online Table A2.

Table 2 The factors and levels of orthogonal experiment design.
Full size table

Sensitivity analysis of lower control arm fatigue life based on analysis of variance50,51, and the significance level of 0.05 is selected for the analysis. Based on the F value, when F > F0.05, it indicates that the factor has a significant influence on the fatigue life, and vice versa. The fatigue life variance analysis results are shown in Table 3. It can be observed that the F values of bushing stiffness, surface roughness and tensile strength are 0.73, 2.74 and 1.11, respectively, all lower than F0.05(4.8) = 3.84, indicating these three factors have insignificant influence on the fatigue life of the lower control arm. In contrast, the load amplification factor has an F value of 6.62, significantly higher than F0.05, demonstrating its more pronounced influence on fatigue life. Comparing the F values of these four factors, the order of the sensitivity to fatigue life is: load amplification factor, surface roughness, tensile strength and bushing stiffness.

Table 3 Fatigue life variance analysis results.
Full size table

Presentation of piezoelectric active control method for fatigue performance of lower control arm

Piezoelectric materials are the class of innovative materials exhibiting mechanical–electrical-thermal coupling characteristics52,53,54. Their inverse piezoelectric effect refers to the phenomenon where polarization under an electric field causes displacement of charge centers, resulting in structural deformation and strain generation55, thereby converting electrical energy into mechanical energy. Piezoelectric ceramics demonstrate exceptional piezoelectric performance and stability, including high piezoelectric constants, strong coupling coefficients, and superior dielectric characteristics56. Therefore, in this paper, piezoelectric ceramic is selected as the piezoelectric material to develop a piezoelectric ceramic-lower control arm (PC-LCA) coupling model for active fatigue life control research of the lower control arm.

When utilizing the inverse piezoelectric effect, the piezoelectric materials will produce a certain deformation under voltage application, generating significant counterforces when deformation is constrained. When the electric field direction is consistent with the deformation direction of piezoelectric material, the relationship is expressed in Eq. (5) 57:

$$\varepsilon = d_{33} \frac{{V_{P} }}{d} + \frac{{F_{r} }}{{A_{P} E_{P} }}$$
(5)

where ε represents the strain of the piezoelectric material under non-rigid constraint; d₃₃ is the piezoelectric strain constant; d denotes the distance between electrodes; Vp is the applied voltage; Ap is the area of the force; Ep is the elastic modulus of the piezoelectric material; Fr is the reaction force induced by the constraint. Meanwhile, for fully rigid constraints (ε = 0), the actuation force of the piezoelectric material actuator is expressed in Eq. (6):

$$F_{r} = (\frac{{d_{33} }}{d}E_{P} A_{P} )V_{P}$$
(6)

Bonded piezoelectric ceramic active control method

Due to significant variations in performance among different piezoelectric ceramic materials, this paper selects piezoelectric ceramic material with a high dielectric constant to generate large strains for active fatigue life control. PIC-151 is a modified lead zirconate-titanate material with a high dielectric constant, high coupling coefficient, and high piezoelectric charge constant. Therefore, PIC-151 is selected as the piezoelectric ceramic actuator. The material property and the piezoelectric characteristics parameters of PIC-151 are shown in online Tables A3 and A4.

The geometry of piezoelectric ceramic materials and their adhesive position significantly influence the piezoelectric effect. At present, determining the optimal adhesive position of piezoelectric ceramic based on the modal strain distribution of the base structure has become a widely adopted and effective methodology. Therefore, this paper conducts modal analysis using the established finite element model of the lower control arm. The arrangement strategy for piezoelectric actuators is determined by observing the modal strain results, as shown in Fig. 14.

Fig. 14
figure 14

Strain contour plots of the lower cross arm: (a) First-order modal; (b) Second-order modal.

Full size image

The piezoelectric materials are directly bonded to the maximum stress–strain surface of the lower control arm first-order modal58. Based on the original finite element model, piezoelectric patches are applied at two critical positions identified from the modal strain results: both sides of the bushing with the main body connection. The piezoelectric patches are meshed with an element size of 2 mm and divided into two layers, totaling 13,439 mesh elements. After completing the mesh, the bonding form of the piezoelectric patches is simulated using the Tie contact. The bonded piezoelectric ceramic positions and finite element mesh are shown in Fig. 15.

Fig. 15
figure 15

The bonded piezoelectric ceramic positions and finite element mesh.

Full size image

After completing the above piezoelectric characteristics configurations, a static analysis is performed on the PC-LCA coupling model59. The static loads for all directions at the four joint positions of the lower control arm are obtained through suspension strength analysis conditions and evaluation criteria, as shown in online Table A5. Different voltage loads are applied to the piezoelectric ceramic patches to analyze the stress distribution of the coupling model under varying voltages. The relationship between the input voltage and the maximum stress of the PC-LCA coupling model is shown in Fig. 16.

Fig. 16
figure 16

The relationship between the input voltage and the maximum stress of the PC-LCA coupling model.

Full size image

The results show that as the input voltage increases, the maximum stress of the bonded PC-LCA coupling model gradually decreases, exhibiting an inverse proportional relationship with a consistent rate of decrease. When the input voltage is 0 V, the maximum stress of the coupling model is 891.7 MPa. This result is found because the bonded piezoelectric ceramic patch alters the original local configuration, consequently inducing minor changes in the stress distribution. Upon increasing the voltage to 100 V, the maximum stress of the PC-LCA coupling model is 880.4 MPa, representing a decrease of 11.3 MPa, with a 1.3% improvement. The stress contour plots of the PC-LCA coupling model at input voltages of 0 V, 10 V, 50 V, and 100 V are shown in Fig. 17. The results demonstrate that the introduction of piezoelectric ceramic materials can reduce the maximum stress of the suspension lower control arm under extreme working conditions. Meanwhile, a mesh refinement and stress concentration analysis near the bonded boundary is conducted. The results show that peak von Mises stress at the patch edge is 8.1% higher than in the adjacent base material under maximum load conditions. The gradient of stress is localized within 3 mm of the edge zone, indicating a narrow but potentially critical zone for adhesive integrity. Therefore, to mitigate potential debonding risks in practical applications, the tapered patch edges or fillet-bonding transitions can be used to reduce stress discontinuities, and the toughened structural adhesives can be used to enhance fatigue endurance.

Fig. 17
figure 17

Stress contour plots of the bonded PC-LCA coupling model: (a) At 0 V input voltage; (b) At 10 V input voltage; (c) At 50 V input voltage; (d) At 100 V input voltage.

Full size image

Embedded piezoelectric ceramic active control method

Due to the load conditions of the lower control arm during actual operation being extremely complex, with each link joint position continuously subjected to complex random dynamic loads, the static analysis cannot thoroughly reflect the operation conditions of the lower control arm. Therefore, dynamic analysis is performed on the PC-LCA coupling model. Since bonded piezoelectric ceramic patches would increase the total mass of the lower control arm, the dynamic analysis is conducted using embedded piezoelectric ceramic to obtain the voltage–time course curves of piezoelectric material. Then, the reverse voltage is applied and the stress states before and after voltage application are compared to provide a basis for fatigue life analysis.

Same as the bonded PC-LCA coupling model, the embedded piezoelectric ceramic model needs to be established based on the original lower control arm finite element model. Referring to the modal analysis results in Fig. 14, the embedded positions of the piezoelectric material should be as close as possible to the maximum strain energy locations of the lower control arm. The embedded piezoelectric ceramic position and finite element mesh are shown in Fig. 18.

Fig. 18
figure 18

The embedded piezoelectric ceramic position and finite element mesh.

Full size image

The upper surface of the piezoelectric ceramic is configured as an equipotential surface, while the lower surface is set to ground (0 V potential). Consistent with the bonded piezoelectric ceramic, PIC-151 is selected as the piezoelectric material for the dynamic analysis, completing the establishment of the embedded PC-LCA coupling model. The fatigue load spectra extracted from the C road level in subsection “Load spectrum acquisition” are applied as dynamic load input, and the voltage–time response curve of the piezoelectric ceramic is shown in Fig. 19a. Meanwhile, this response result is multiplied by a negative coefficient (− 10) to generate a new voltage–time load, as shown in Fig. 19b, which is applied to the upper surface of the piezoelectric ceramic as a dynamic load. The factor is determined based on previously established parameters and consistent trends reported in the literature, which indicate that such an amplification can achieve localized stress reduction without exceeding material limits, thereby improving the fatigue life of the control arm60,61. The transient response of the embedded PC-LCA coupling model is recalculated to compare the maximum stress in the lower control arm, as shown in Fig. 20. The results show that the maximum stress of the PC-LCA coupling model without applied voltage is 281.8 MPa and occurs at 13.048 s. After applying reverse voltage, the maximum stress is 274.9 MPa and occurs at 7.08 s, representing a 2.4% reduction compared to the original state.

Fig. 19
figure 19

The voltage–time course curves of piezoelectric ceramic: (a) Response result; (b) After multiplying by the inverse coefficient result.

Full size image
Fig. 20
figure 20

Stress contour plots of the embedded PC-LCA coupling model: (a) Without active control; (b) With active control (reverse voltage applied).

Full size image

Comparison of fatigue performance

Fatigue life calculation is conducted based on the results of the two transient analyses, and the fatigue life of the PC-LCA coupling model is shown in Fig. 21. The results indicate that both before and after applying the reverse voltage, the critical danger of the PC-LCA coupling model remains at Node 142,306, which is situated on the outer side of the right bushing. In particular, the minimum cycle count of the PC-LCA coupling model without applying voltage is 4.075 × 107 cycles, and the minimum cycle count after applying reverse voltage is 5.076 × 107 cycles, which is a 24.5% improvement in fatigue life. This finding is obtained because the S–N curve for 42CrMoA has a steep slope in the high-cycle fatigue region, and even a slight decrease in stress amplitude can result in a significant increase in fatigue life. Piezoelectric actuation reduced the peak local stress gradient, which significantly alters the damage accumulation rate62. At the same time, the drive response time of the system is analyzed. The actuation delay primarily arises from: signal generation time, amplifier rise time, and piezoelectric actuator response. The total effective control delay is less than 1 ms, which indicates that real-time or near-real-time control is feasible. The average power of each active piezoelectric control structure is approximately 0.243 W, and the total power of each vehicle (four actuators) is approximately 0.97 W, which is far below the power budget of modern semi-active and active suspension systems63,64. Therefore, the system can be powered by a 12 V vehicle system with minimal load. In addition, the added mass of a single piezoelectric ceramic structure is approximately 2.8 g, and the total added mass (including adhesive and encapsulation) represents less than 0.8% of the original lower control arm mass. These findings indicate that the piezoelectric control elements have a negligible impact on the suspension dynamics, including the vehicle ride smoothness and comfort. In conclusion, the proposed piezoelectric active control method greatly enhances the fatigue life of the lower control arm, and demonstrates remarkable effectiveness.

Fig. 21
figure 21

Fatigue life of the PC-LCA coupling model: (a) Without active control; (b) With active control (reverse voltage applied).

Full size image

Conclusions

In this paper, we combined the finite element method and multi-body dynamics method and developed a rigid-flexible coupling model, which includes a finite element flexible body model of the lower control arm and a multi-rigid body model of the suspension system and is applied to the fatigue life prediction and optimization for the lower control arm.

  1. 1.

    The fatigue load spectra were extracted from four critical positions: the steering knuckle link joint, the stabilizer bar link joint, the damper link joint and the torsion bar to bracket link joint. Meanwhile, the stress–strain results of the lower control arm under 10 unit loads were analyzed, and the fatigue was calculated, which has the minimum cycle count of 5.293 × 106, equivalent to the mileage of 1.176 × 106 km. Sensitivity analysis results show that as bushing stiffness increases (load magnification factor, surface roughness, material tensile strength) increases, the fatigue life decreases (decreases, decreases, increases). The order of the sensitivity to fatigue life is load amplification factor, surface roughness, tensile strength, and bushing stiffness.

  2. 2.

    The PC-LCA coupling model was developed. Based on this, the fatigue performance active control methods based on piezoelectric ceramic for the lower control arm were proposed, which employ bonded piezoelectric ceramic and embedded piezoelectric ceramic to enhance the static and dynamic performance of the lower control arm, respectively. The results show that as the input voltage increases, the maximum stress of the bonded PC-LCA coupling model gradually decreases, exhibiting an inverse proportional relationship with a consistent rate of decrease. When the input voltage is 0 V, the maximum stress of the bonded coupling model is 891.7 MPa. This result is found because the bonded piezoelectric ceramic patch alters the original local configuration, consequently inducing minor changes in the stress distribution. Upon increasing the voltage to 100 V, the maximum stress of the PC-LCA coupling model is 880.4 MPa, representing a decrease of 11.3 MPa, with a 1.3% improvement.

  3. 3.

    Same as the bonded piezoelectric material, the embedded positions of the piezoelectric material should be as close as possible to the maximum strain energy locations of the lower control arm. The transient response of the embedded PC-LCA coupling model was recalculated under the C road level. The results show that the maximum stress of the coupling model without applied voltage is 281.8 MPa and occurs at 13.048 s. After applying reverse voltage, the maximum stress is 274.9 MPa and occurs at 7.08 s, representing a 2.4% reduction compared to the original state.

  4. 4.

    Then, the fatigue life calculation was conducted based on the results of the two transient analyses. The results show that the minimum cycle count of the PC-LCA coupling model without applying voltage is 4.075 × 107 cycles, and the minimum cycle count after applying reverse voltage is 5.076 × 107 cycles, which is a 24.5% improvement in fatigue life.

  5. 5.

    Finally, to integrate the proposed smart material approach into mass-produced vehicles, it is recommended to place piezoelectric patches in regions with high modal strain energy density to maximize the performance enhancement of the control arm while minimizing the amount of piezoelectric material required. Surface-bonded patches offer easier retrofit and adjustment potential but may be susceptible to durability issues. In contrast, embedded ceramics provide greater robustness and improved protection. Meanwhile, voltage control should be integrated into the existing suspension ECU to enable adaptive control based on onboard sensor data.

In conclusion, the proposed piezoelectric active control method greatly enhances the fatigue life of the lower control arm, demonstrating remarkable effectiveness.