Introduction

With the rapid advancement of technology, magnetic field sensors have become integral both directly and indirectly in facilitating global progress. Therefore, it is essential to provide a precise measurement of magnetic fields across a wide range of research areas and practical applications, including industrial manufacturing, medical diagnostics, national defense, and resource exploration1,2,3,4. In this regard, numerous methods have been introduced for sensing the magnetic field such as Hall Effect, electromagnetic induction, tunnel magnetoresistance, giant magnetoresistance, anisotropic magnetoresistance, magneto-optical effect, nuclear precession, and superconducting quantum interface2,4,5. Conventional magnetic field sensing techniques rely on electromagnetic principles to convert magnetic signals into electrical signals. However, these electrically based sensors are suffering from several limitations, including large physical size, high fabrication costs, complex structural designs, integration challenges, susceptibility to electromagnetic interference, and the requirement for temperature control systems. In contrast, sensors based on the magneto-optical effect effectively address these issues, offering significant advantages such as high sensitivity, compatibility with large-area distributed sensing, a broad dynamic range, inherent multiplexing capabilities, and strong adaptability to varying environmental conditions3,6.

Magneto-optical effect (MOE) refers to the interaction between electromagnetic waves (EMWs) and material placed in an external of magnetic field. The MOE is categorized into several distinct phenomena, including the Faraday, cotton-Mouton, Voigt, Magneto-Optical Kerr Effect (MOKE)1,7,8,9. These effects are promising to alter the optical properties specifically the permittivity of the material like metals and doped semiconductors10. In the last two decades, the Faraday effect emerges as an effective technique for envisaging the sensing applications1,11,12. Notably, Faraday geometry provides a significant contribution to tuning the optical characteristics of the dispersive media. In Faraday effect, the direction of the external magnetic field must be parallel to the direction of the propagation of the EMW causing either left or right circular polarization for the eigenmodes. Accordingly, the influence of the Faraday effect has been incorporated into the design of our proposed magnetic field sensor. In contrast, under the Voigt effect, the eigenmodes remain linearly polarized due to the orientation of the external magnetic field being normal to the propagation direction of the electromagnetic wave10,13, whereas, in MOKE method, the polarization is elliptical1. In recent years, there has been a growing interest in applying magneto-optical effects in periodic structures like photonic crystals (PhCs).

PhCs are artificial designed periodic multilayers structures comprising at least two or more materials of different optical properties in each unit cell14,15. The periodicity of PhC structures can be implemented in one (1D), tow (2D), or three-dimensions (3D)16. One of the distinguishing characteristics of PhCs is the emergence of photonic band gaps (PBGs), which arises due to Bragg scattering of incident waves at the interfaces between different layers of the designed structure. PBGs are defined as bands of frequencies in which the propagation of the EMWs of similar frequencies is prohibited17. Therefore, this unique property allows for PhCs to control the propagation of the incident EMWs17,18. Consequently, the PBG has enabled a wide range of applications for PhCs, such as optical isolators, optical fibers, and integrated photonic circuits19,20,21. Moreover, the inclusion of a layer with different optical or geometrical characteristics as a defect inside PhC structure leads to breaking its periodicity which gives rise to the localization of some frequency modes known as defect modes inside the PBG20,21. Meanwhile, the optical properties of these modes including their number, position and full width are significantly dependent on the thickness and refractive index of the defect layer.

As the defect layer is localized between symmetric structures of a 1D PhC structure, the modes decay rapidly and the EMWs are trapped in the distance between these mirrors16. Due to the combarable between this distance and the wavelengh, the allowed modes are quantized. As a result, resonant states are created within the PBG. The resonant states are very sensitive to a small change of refractive index of the defect layer and its thickness as well, which makes the defect-based PhC as the suitable candidate for realizing sensing applications.

This work presents a theoretical analysis of high-sensitive magnetic field sensor utilizing the Transfer Matrix Method (TMM). Here, we have introduced a defect layer of an n doped Si inside a 1D PhC structure designed from 8-unit cells. Here, each unit cell comprises two layers of SiO2 and GaAs. The main novelty of this work lies in exploiting the enhanced Faraday effect in n-doped Si to achieve highly sensitive and tunable magnetic field sensing within a 1D PhC structure. Unlike previous magnetic field sensors based on 1D PCs, which primarily use magneto-optical materials, our design integrates precisely engineered doping levels in Si to significantly boost its magneto-optical response through free-carrier interactions. This enables a pronounced, magnetic-field-induced shift in the photonic bandgap and transmission spectrum. Further, all the geometrical parameters are meticulously optimized to achieve a maximum sensitivity. The results revealed that the optimized structure has a very good performance for example the sensitivity reaches 2.91 μm/Tesla and detection limit decreases to 0.0041 Tesla. Moreover, to our knowledge, this is the first demonstration where n-doped Si Faraday effect is studied for high-performance magnetic field sensing in a 1D PhC framework. Additionally, the numerical findings demonstrate that the tolerance in the thicknesses of PhC constituent materials is almost unaffected on the sensitivity and may be on the overall performance of the designed sensor as well. Therefore, we believe that our designed sensor is robust against the structural disorders and the geometrical variations as well.

Structure design and mathematical model

Fig. 1
figure 1

3D schematic description of the designed magnetic field sensor in which an n doped Si defect layer is embedded between two identical 1D PhC structure comprising two layers of SiO2 and GaAs in each unit cell.

Full size image

Structure design

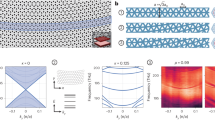
In this section, we present the structural design of the proposed sensor, which consists of 1D defective PhC. As illustrated in Fig. 1, the structure is envisaged with SiO2 as a first layer and GaAs as a 2nd layer, and the total number of periods is N = 4 as along the x-direction. The thickness of SiO2 and GaAs are taken as d1 = 19 μm and d2 = 8.5 μm, respectively, whereas the refractive index of SiO2 and GaAs are considered as n1 and n2, respectively. The lattice constant (d) of each unit cell is denoted as, d = d1 + d2. The defect layer, which is sandwiched between the two identical PhCs, is designed from an n-doped Si layer of carrier concentration (ni) = 1.5\(\:\times\:\)1016 m− 3 and doping concentration (Nd) = 1023 m− 3. The dielectric constant of the material is ε∞ = 11.7, while the effective masses of electron and holes are me = 0.26m0 and mh = 0.34m0, respectively, where m0 represents the free electron mass, m0 = 9\(\:\times\:\)10−31 Kg. Additionally, the thickness of the defect layer (dd) is selected as 40 μm and the damping frequencies γe = 7.35\(\:\times\:\)109 Hz, γh = 8.75\(\:\times\:\)109 Hz. Wherein, the final layer in the structure is the glass substrate, which has a refractive index ns = 1.5210. Here, the electromagnetic waves (EMWs) in range between 55 THz and 120 THz incident normally onto the structure.

Materials selection

The selection of SiO2 and GaAs for the proposed design is driven by their complementary physical, acoustic, and electronic properties, which are critical for achieving high-performance sensing at the targeted frequencies. SiO2 offers low acoustic impedance, low density, and high transparency to surface acoustic waves, making it ideal for enhancing wave confinement and minimizing propagation losses45. Its amorphous structure also provides mechanical stability and excellent thermal insulation, which is beneficial for maintaining consistent performance over temperature variations. On the other hand, GaAs is a piezoelectric semiconductor with high electron mobility and strong electromechanical coupling, which enables efficient detection46. Its crystalline structure supports precise photonic bandgap engineering, which allows the device to operate effectively at specific frequencies. Moreover, GaAs substrates are well-established in microfabrication, ensuring compatibility with existing semiconductor processing technologies. The combination of SiO2 and GaAs enables a high acoustic impedance contrast, which is essential for strong photonic bandgap formation and improved wave scattering, which directly enhances the sensitivity.

The defect layer is designed with n-doped Si to exploit its tunable free-carrier concentration, which directly affects its refractive index and conductivity through the plasma dispersion effect. Under an applied magnetic field, the charge carriers experience the magneto-optic (Hall) effect, leading to measurable changes in optical and electrical properties. N-doped Si offers high carrier mobility, compatibility with standard microfabrication processes, and low-cost integration with other semiconductor components47. Its adjustable doping level enables precise control over sensitivity and operating range. This makes n-doped Si an ideal choice for achieving strong magnetic field responsiveness while maintaining the structural stability and fabrication feasibility in the proposed sensor.

Mathematical model

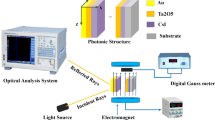
Under the influence of an external magnetic field, the mathematical analysis of the interaction of the EMWs with the 1D defective PhCs is formulated based on the transfer matrix method (TMM) and the Faraday geometry. TMM is widely regarded as an effective approach to study the reflection and the transmission coefficients for multilayer structures10,16,23,24,25. Using TMM, it is easy to study the electric (TE) and magnetic (TM) amplitudes associated with both incident and transmitted EMWs at the boundaries of the whole structure17,23,26. Subsequently, we have introduced the total transfer matrix (A) according to TMM as following10,24:

$$\:\text{A}\:=\:\left(\text{Z}\right)\text{N}\:\text{D}\:\left(\text{Z}\right)\text{N}\:=\:\left(\begin{array}{cc}{A}_{11}&\:{A}_{12}\\\:{A}_{21}&\:{A}_{22}\end{array}\right)$$
(1)

Where (Z)N and D represent matrices that describe the whole structure of PhCs and the defect layer, respectively. The terms \(\:{A}_{11}\), \(\:{A}_{12}\), \(\:{A}_{21}\), and \(\:{A}_{22}\) constitute the total transfer matrix (A). Meanwhile, the transfer matrix for one period of the PhC structure is given by:

$$\:\left(\text{Z}\right)\:=\:\left(\begin{array}{cc}cos\left({}_{1}\right)&\:(-i/{p}_{1})sin\left({}_{1}\right)\\\:-i{p}_{1}sin\left({}_{1}\right)&\:cos\left({}_{1}\right)\end{array}\right)\left(\begin{array}{cc}cos\left({}_{2}\right)&\:(-i/{p}_{2})sin\left({}_{2}\right)\\\:-i{p}_{2}sin\left({}_{2}\right)&\:cos\left({}_{2}\right)\end{array}\right)$$
(2)

Hence, \(\:{\phi\:}_{\iota\:}\) is the wave vector (\(\:{\phi\:}_{\iota\:}=\frac{2\pi\:{d}_{\iota\:}\:{n}_{\iota\:}}{\lambda\:}\text{cos}{\theta\:}_{\iota\:})\), and \(\:{p}_{\iota\:}\)is the effective optical impedance (\(\:{p}_{\iota\:}={n}_{\iota\:}\text{c}\text{o}\text{s}\:{\theta\:}_{\iota\:}\)), for the TE polarization10,25 \(\:\iota\:=1,\:2\).

Then, according to Chebyshev polynomials the transfer matrix for N periods of the 1D PhC structure can be expressed as24:

$$\begin{gathered} \left( {\text{Z}} \right){\text{N}}=\left( {\begin{array}{*{20}{c}} {{z_{11~}}{\beta _{N - 1}}\left( {\text{\varvec{\updelta}}} \right) - {\beta _{N - 2}}\left( {\text{\varvec{\updelta}}} \right)}&{{z_{12}}{\beta _{N - 1}}\left( {\text{\varvec{\updelta}}} \right)~} \\ {{z_{21}}{\beta _{N - 1}}\left( {\text{\varvec{\updelta}}} \right)~}&{{z_{22}}~{\beta _{N - 1}}\left( {\text{\varvec{\updelta}}} \right) - {\beta _{N - 2}}\left( {\text{\varvec{\updelta}}} \right)} \end{array}} \right) \hfill \\ ~~~~~~~=~\left( {\begin{array}{*{20}{c}} {{z_{11}}}&{{z_{12}}} \\ {{z_{21}}}&{{z_{22}}} \end{array}} \right) \hfill \\ \end{gathered}$$
(3)
$$\:\text{H}\text{e}\text{r}\text{e},\:{\beta\:}_{N}=\frac{\text{s}\text{i}\text{n}\left[\right(\text{N}+1\left)\:{\text{c}\text{o}\text{s}}^{-1}\:\right({\updelta\:}\left)\right]}{\sqrt{1-{\delta\:}^{2}}}\:\text{a}\text{n}\text{d}\:\delta\:=\frac{{z}_{11\:}+{z}_{22}}{2}.$$

.

Therefore, the transfer matrix of the defect layer can be written as:

$$\:\text{D}\:=\:\left(\begin{array}{cc}cos\left({}_{d}\right)&\:(-i/{p}_{d})sin\left({}_{d}\right)\\\:-i{p}_{d}sin\left({}_{d}\right)&\:cos\left({}_{d}\right)\end{array}\right)= \:\left(\begin{array}{cc}{d}_{11}&\:{d}_{12}\\\:{d}_{21}&\:{d}_{22}\end{array}\right)$$
(4)

Hence, \(\:{\phi\:}_{d}=\frac{2\pi\:{d}_{d}\:{n}_{d}}{\lambda\:}\text{cos}{\theta\:}_{d}\), and \(\:{p}_{d}={n}_{d}\text{c}\text{o}\text{s}\:{\theta\:}_{d}\). The transmission coefficient (t), which is a function in elements of the characteristic matrix, can be given as27,28:

$$\:t=\frac{2{p}_{0}}{\left({A}_{11}+{A}_{12}{p}_{s}\right){p}_{0}+({A}_{21}+{A}_{22}{p}_{s})}$$
(5)

Where, \(\:{p}_{0}\) and \(\:{p}_{s}\) are the effective optical impedance for air and substrate layer, respectively. Finally, the transmissivity (T) of the structure can be calculated based on the following formula29:

$$\:T=\frac{{p}_{0}}{{p}_{s}}{\left|t\right|}^{2}$$
(6)

Additionally, according to the Faraday geometry, the relative permittivity (\(\:\epsilon\:\)) of a n-doped semiconductor material can be calculated as10,13,19,30,31:

$$\:{\epsilon\:}_{\pm\:}\:\left(\right)=\:{\upepsilon\:}{\infty\:}(1-\frac{{\omega\:}_{pe}^{2}}{\omega\:(\omega\:\mp\:{\omega\:}_{c}-\mathcal{i}{\gamma\:}_{e})}-\frac{{\omega\:}_{pe}^{2}}{\omega\:\left(\omega\:\mp\:{\omega\:}_{c}-\mathcal{i}{\gamma\:}_{h}\right)})$$
(7)

Where, \(\:{\omega\:}_{pe\left(h\right)}^{2}\:\)is the electrons (holes) plasma frequency32 that can be written as:

$$\:{\omega\:}_{pe\left(h\right)}^{2}=\frac{{n}_{e\left(h\right)}{e}^{2}}{{m}_{e\left(h\right)}{\epsilon\:}_{0}{\epsilon\:}_{\infty\:}}$$
(8)

Here, e and \(\:{\epsilon\:}_{0}\) represent the electron charge and the permittivity of the vacuum, respectively. Meanwhile, the cyclotron frequency \(\:{\omega\:}_{c}\) is determined as a function of the magnetic field intensity B, given by33:

$$\:{\omega\:}_{c}=\frac{e}{{m}_{e}}B$$
(9)

Subsequently, the refractive index of the n-doped semiconductor material is calculated as:

$$\:{n}_{d}=\sqrt{{\epsilon\:}_{\pm\:}\:\left(\right)\:}$$
(10)

Results and discussions

We employ Faraday effect in n-doped silicon to accomplish highly tunable magnetic field sensor using 1D PhC. The Faraday effect was chosen because it offers a strong, linear magneto-optical response in transmission geometry, which perfectly matches the operating principle of 1D PhC. Unlike MOKE, which is reflection-based, and the Voigt effect, which is weaker and quadratic with field strength, the Faraday effect enables efficient, high-sensitivity modulation48]– [49. In n-doped Si, the free carriers significantly enhance this effect and produce a noticeable change in the refractive index and photonic bandgap. Moreover, Faraday effect avoids reliance on exotic materials, ensuring CMOS compatibility and easy integration. These factors make the Faraday effect the most effective choice for our magnetic field sensor design. In this section, we present the optimization of the designed sensor structure and thoroughly analyzed its performance to verify the ability and the accuracy of the proposed magnetic field sensor.

Optimization of sensor parametars

To achieve highest performance, we optimize the sensor parametars according to the performance tools. Initially, we consider the sensor structure as [ (MgF2 + GaAs)N=10/ n-doped Si / (MgF2 + GaAs)N=10]. Here, MgF2 and GaAs layers form the unit cell of the PhC with periodicity N = 10, and atomic density of the defect layer Nd=1 × 1023 m-3 in case of normal incedance of EMWs. All pararmeters of the sensor including the thicknesses of different layers, Nd and the incident angle of EMWs are optimized. The structure optimization is extensively studied in the following subsections.

Optimization of the doping concentration and thickness of the defect layer

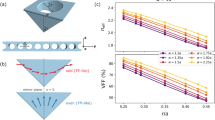
Here, we start the optimization process by checking the effect of doping concentration of the n-doped Si on the sensor sensitivity as shown in Fig. 2. Specifically, we took the values of Nd =[7, 8, 9, 10] ×1022 m-3 and observed the variation in the sensitivity. As seen in Fig. 2, the sensitivity increases gradually with increase in the atomic density, and the maximum sensitivity reaches upto 0.0324 THz/Tesla at Nd = 1023 m-3. Therfore, Nd = 1023 m-3 is selected as the optimal value for our magnetic field sensor.

Then, we survey the impact of defect layer thickness (da) on the sensitivity of the structure. According to Fig. 3, the sensitivity is affected by changing the thickness of the defect layer. In particual, when da = 25 μm, the sensitivity = 0.0226 THz/Tesla and by increasing (da) the sensitvity keeps increasing until the optimal thickness of 40 μm is reached. This confirms that the highest sensitivity (0.0324 THz/Tesla) occurred at Nd = 1023 m-3 and defect layer thickness da = 40 μm.

Fig. 2
figure 2

The sensitivity response versus the impact of different values of doping concentration of the n-doped Si.

Full size image
Fig. 3
figure 3

The effect of the defect layer thickness on the sensor’s sensitivity.

Full size image

Optimization of the typs of material of phc unit cell

Futhermore, we optimize the unit cell of PhC by checking the types of the dielectric layers, periodicity and its thickness for each one according to the highest sensitivity.

The Frist layer of the unit cell

Firstly, we fix the second layer as GaAs, and then change the dielecric type of the first layer. Notably, we select different dielecric materials like MgF2, SiO2, Al2O3, and SrF2 based on their refractive index contrast, because the high contrast between the constitunet dielectric materials must be sufficiently large to enhance the Bragg reflection and form a wide PhC band gap34.

In this regard, we have optmized different dielectric materials to be embedded as the first layer of the designed PhC structure. Here, the mainsty towards the dependence on a specified material is mainly based on the recorded sensitvity. Meanwhile, Table 1 summerizes the indices of refraction for the selected materials within the frequencies of interest35,50,51,52,53,54,55,56. Here, the selected materials provide a stable response for their indices of refraction over the operating wavelengths of the designed sensor as listed in Table 1. This response could be of a potential interest through the expermental verfication of the designed sensor. Then, Fig. 4 displays the different values of the senstivity based the inclusion of some different dielectric materials as a first layer inside each unit cell of the designed PhC structure. In contrast, the sencond layer in each unit cell of the designed PhC structure is kept as GaAs. In this regard, the inclusion SiO2 as the first layer of PhC design gives rise to some signficant improvements on the sensitvity of the designed sensor compared to other materials such as MgF2, Al2O3 and SrF2. Here, the sensitvity of the designed structure increases to 0.0342 THz/Tesla copmared to the results investigated in Figs. 2 and 3. Therefore, SiO2 presents the optimum choice as the first layer in each unit cell of the designed PhC towards the largest sensitvity.

Table 1 The refractive indices of the different dielectric materials through the operting wavelengths of the designed sensor35,50,51,52,53,54,55,56.
Full size table
Fig. 4
figure 4

The role of the refractive index of the 1st layer in each unit cell of PhC structure on the sensitvity of the designed sensor.

Full size image
The second layer of the unit cell

Following a similar optimization procedure, we analyzed the second layer of the photonic crystal (PhC) unit cell. The first layer was fixed as SiO₂, having previously been identified as the optimal configuration. To determine the most suitable material for the second layer, we evaluated the sensor’s sensitivity using various dielectric materials including GaAs, GdF₃, and SrF₂ whose refractive indices are listed in Table 1. The results, as illustrated in Fig. 5, indicate that GaAs yields the highest sensitivity, while SrF₂ demonstrates the lowest. Consequently, GaAs was selected as the optimal material for the second layer in the PhC design. Thus, the unit cell of the PhC is designed using SiO2 and GaAs due to their high effectiveness in enhancing the sensor’s sensitivity.

Fig. 5
figure 5

The role of the refractive index of the 2nd layer in each unit cell of PhC structure on the sensitivity of the designed sensor.

Full size image

Optimization of the periodic number of the phc unit cell

Moreover, we study the effect of the number of periods of the unit cell (SiO2/ GaAs) on the sensor sensitivity. It can be seen from the Fig. 6 that the sensitivity increases from 0.0342 THz/Tesla to 0.0352 THz/Tesla by decreasing the number of periods from 10 to 4. As a result, the sensor performance is enhanced at 4 periods of the unit cell, therefore we selected this optimal value to design our structure.

Fig. 6
figure 6

The impact of using different numbers of periods on the sensitivity of the sensor.

Full size image

Optimization of the layers’ thickness of the phc unit cell

Following the optimization of unit cell materials and its periodicity, we optimize the layers’ thickness which plays a critical role as a lattice constant of the structure’s unit cell.

The thickness of SiO2

Initially, we optimize the thickness of the first layer (SiO2) by checking the impact of different thicknesses like 16 μm, 18 μm, 19 μm, and 20 μm on the sensitivity, while keeping the other geometrical parameters as constant. As illustrated in Fig. 7, the sensitivity at 16 μm is 0.0352 THz/Tesla. Then, it increases with thickness and reaches a maximum of 0.0368 THz/Tesla at 19 μm. Beyond this thickness, the sensitivity begins to decrease. Therefore, 19 μm is identified as the most effective thickness based on the sensor sensitivity results.

Fig. 7
figure 7

The effect of different thicknesses of the SiO2 layers on the sensor sensitivity.

Full size image
The thickness of GaAs

The thickness of the second layer (GaAs) is optimized by following the same procedure as the thickness of the first layer. Specifically, we observed the effect of thicknesses like 7, 7.5, 8, and 8.5 μm on the sensor’s sensitivity and it is found that the sensitivity gradually increases with the thickness as illustrated in Fig. 8. This led to select 8.5 μm as the optimal thickness for the second layer (d2). Finally, the optimal thickness of the structure unit cell is found to be a = 19 μm + 8.5 μm = 27.5 μm. This thickness significantly enhances the sensor’s sensitivity, raising it to a high value of 0.0368 THz/Tesla.

Fig. 8
figure 8

The effect of different thicknesses of the GaAs layer on the sensor sensitivity.

Full size image
Fig. 9
figure 9

The role of the angle of incident on the sensitivity of the designed structure.

Full size image

Optimization of the incident angle of the interacting electromagnetic waves

Finally, we optimize the angle of the incidence. That is an important factor, which greatly affects sensor performance. We measured the sensitivity at different angles such as 0°, 20°,40°, and 60°, which is demonstrated in Fig. 9. We observed that the sensitivity decreases to 0.034 THz/Tesla by increasing the incident angle from 0° to 60°. So, it is confirmed that a maximum sensitivity of 0.0368 THz/Tesla is attained in case of the normal incident of the interacting EMWs.

From the above results, we concluded that optimal value of sensitivity is accomplished by designing the structure with SiO2 and GaAs as the dielectric layers, each with a thickness 19 μm and 8.5 μm, respectively. Moreover, the optimum thickness of the defect layer and its atomic density are found to be 40 μm and 1023 respectively. The number of the periodicity of the structure unit cell is 4, and the optimized incident angle is 0°. This optimization achives a maximum sensitivity of 0.0368 THz/Tesla.

Numerical analysis and the discussion

Depending on the optimization of the geometrical parameters, the overall performance of the sensor is presented in this section in detail. Consequently, the performance parameters which we measured include sensitivity (S), quality factor (Q), signal-to-noise ratio (SNR), detection limit (DL), sensor resolution (SR), and figure of merit (FOM) to evaluate the performance of the sensor30,36,37,38,39. Meanwhile, the sensitivity, quality factor, and figure of merit are considered key parameters, as their calculations depend on the resonance position, which shifts with varying magnetic field strength40,41.

To begin with, the sensitivity (S) determines the difference of the resonant wavelength according to change the strength of the magnetic field, and can be expressed as:

$$\:\text{S}\:=\frac{{\Delta\:}\lambda\:res}{{\Delta\:}B}$$
(11)

Where, Δλres is the change in the resonant wavelength, and ΔB is the change of the magnetic field strength. Futhermore, quality factor (Q) is defined as the ratio of λres to the full width at half maximum (FWHM) of the defect mode resonant wavelength. Based on this, Q is given by:

$$\:\text{Q}\:=\:\frac{\lambda\:res}{FWHM}$$
(12)

Anther, important parameter of the sensor is the figure of merit (FOM), and it is calculated as following:

$$\:\text{F}\text{O}\text{M}=\:\frac{\text{S}}{\varDelta\:\text{F}\text{W}\text{H}\text{M}}$$
(13)

Moreover, the signal-to-noise ratio (SNR) is another performance parameter, which we are interested to measure. SNR is calculated as the ratio between the resonance signal and the background noise. We can calculate it using the following formula:

$$\:\text{S}\text{N}\text{R}\:=\frac{{\Delta\:}\lambda\:res}{{\Delta\:}FWHM}$$
(14)

In addition to that, the detection limit (DL) is a significant parameter, which indicates the ability of the sensor to detect the smallest variation in the magnetic field, expressed as:

$$\:\text{D}\text{L}\:=\:\left(\frac{2}{S}\right)\left(\frac{\text{F}\text{W}\text{H}\text{M}}{3{\left(SNR\right)}^{0.25}}\right)$$
(15)

Futhermore, the sensor resolution (SR) is defined as following:

$${\text{SR }}={\text{ }}\left( {{\text{DL}}} \right)\left( {\text{S}} \right)$$
(16)

Owing to the presence of a defect layer in the proposed 1D PhC structure, a resonant state is appeared with in the bandgap (defect modes), which can be seen in Fig. 10. These modes help in measuring the sensor performance due to the shift of the resonant state that caused by changing the strength of the magnetic field. Then, we have considered in Fig. 11 the gegnetic field distribution through the designed PhC structure. In Fig. 11, a comprehensive analysis of the magnetic field distribution within our optimized structure is conducted, comprising 1D PhCs integrated with a defect layer fashioned from n-doped silicon. Figure 11a elucidates the precise localization of the magnetic field within the defect layer derived from n-doped silicon, under the compelling influence of an incident frequency of\(\:\:1.09\times\:{10}^{12}\:THz\). Subsequently, in Fig. 11b, the incident frequency is heightened to\(\:\:1.27\times\:{10}^{12}\:THz\), thereby effecting a notable transference of the magnetic field localization from the defect layer towards the layer of lower refractive index, specifically\(\:\:Si{O}_{2}\). The progression of this phenomenon is meticulously charted. Lastly, Fig. 11c demonstrates a further escalation in the incident frequency to\(\:\:2.28\times\:{10}^{12}\:THz\), instigating a consequential shift in the magnetic field localization from the lower refractive index layer (\(\:Si{O}_{2}\)) to the layer of higher refractive index, denoted as GaAs. This distinctive relocation of the magnetic field is brightly represented in the reduced graphical representation.

Fig. 10
figure 10figure 10

The light transmission spectrum of the 1D PhC magnetic field sensor versus the frequency of the propagating EMWs at the optimum values of the governing parameters.

Full size image
Fig. 11
figure 11

The magnetic field distribution for the optimum structure at different incident frequencies, (a) the frequency\(\:\:=\:1.09\times\:{10}^{12}\:THz\), (b) the frequency =\(\:\:1.27\times\:{10}^{12}\:THz\), and (c): the frequency =\(\:\:2.28\times\:{10}^{12}\:THz\).

Full size image

In greater depth, the optical characteristics of the transmission spectrum are depicted in Fig. 12. The transmission spectrum is clearly affected as the external applied magnetic field which increases from 0 Tesla to 10 Tesla. As can be observed from the figure, the position of the defect mode is shifted towards the higher frequencies, and the intensity decreases by increasing the strength of the magnetic field above 5 Tesla (T). The nature of shift of defect mode frequency can be described using standing wave condition41,

$$\:\gamma\:=p{\lambda\:}_{res}={n}_{eff}\tau$$
(17)

Where, \(\:\gamma\:\) and τ denote the optical and geometrical path difference respectively. The notion p indicates an integer, \(\:{\lambda\:}_{res}\) represents the resonance wavelength, and \(\:{n}_{eff}\:\)stands for the effective refractive index. The value of \(\:{n}_{eff}\) increases when the defect layer is exposed to the high intensity of magnetic field, which results in shift in \(\:{\lambda\:}_{res}\) towards higher value to keep \(\:\gamma\:\) fixed.

Fig. 12
figure 12

The light transmission spectrum of the defective 1D PhC sensor as a function of the frequency at different magnetic field intensities.

Full size image

Here, the resonant wavelength for 3 T, 5 T, 7 T, and 10 T is 155.5 μm, 149.6 μm, 143.4 μm, and 134.2 μm, respectively. By applying these values in Eq. 11 to Eq. 16, we measured the performance parameters like S, FWHM, Q, FOM, SNR, DL, and SR, which are listed in Table 2. It was observed that the sensor’s sensitivity increases with the strength of the applied magnetic field, reaching a maximum value of 2.91 μm/Tesla, which underscores its strong responsiveness to magnetic field variations. Furthermore, high quality factor (Q-factor) values of 1633 were recorded at magnetic field strengths of 7 T and 10 T, indicating narrow resonance linewidths and enhanced signal selectivity. The figure of merit (FOM) also exhibited significant improvement, validating the effectiveness of the optimized structural design. Additionally, a high signal-to-noise ratio (SNR) of 291 was achieved at 10 T, demonstrating the sensor’s capability to reliably differentiate signal from background noise. With a detection limit (DL) of 0.0055 Tesla and a spectral resolution (SR) of 0.016 μm, the sensor exhibits exceptional precision and can identify minute variations in the magnetic field, thereby confirming its high-performance potential.

Table 2 The performance of the 1D D-PhC sensor at different values of the applied magnetic field.
Full size table

Fabrication tolerance

Now, we turn our attention to discussing the role of thickness tolerance on the sensitivity of the designed sensor. Notably, fabrication tolerance could have a distinct effect on both optical response of the designed structure and detection accuracy as well in many diverse applications. Actually, the tolerance in the thickness of a distinct layer is described as the range of an acceptable change in the thickness of this layer. Meanwhile, we have considered the role of thickness tolerance on the different layers of our designed magnetic field sensor. Here, Table 3 demonstrates the changes in the sensitivity of the designed sensor due to the tolerance in the thickness of GaAs. In this regard, the changes in the thickness of GaAs layers vary from – 100 nm to + 100 nm. The results investigated in Table 3 show that the tolerance in the thickness of GaAs layers provides a little effect on the sensitivity of the designed sensor. This effect appears in a small variation of 0.0004 THz/Tesla at maximum through the sensitivity of the designed magnetic field sensor. In contrast, Table 4 investigates the same effect for SiO2 layers. The behavior of sensitivity for tolerance of SiO2 is like that of GaAs layers. Finally, Table 5 investigates the same role for n doped Si layers. The results obtained for n doped Si are like those investigated for GaAs and SiO2. To sum up, the tolerance in the thicknesses of PhC constituent materials is almost unaffected on the sensitivity and may be on the overall performance of the designed sensor as well. Therefore, we believe that our designed sensor is robust against the structural disorders and the geometrical variations as well. Moreover, we believe that tolerance of 100 nm during the manufacturing process is a very large value. In particular, some fabrication techniques such as the atomic layer deposition (ALD) could be promising for sufficient control of very small thicknesses which in turn may be of a significant contribution towards achieving precise tailoring of interfaces with great accuracy for fabricating thin films with tight tolerances57,58.

Table 3 The role of fabrication tolerance of GaAs layers thickness on the sensitivity of the designed sensor.
Full size table
Table 4 The role of fabrication tolerance of SiO2 layers thickness on the sensitivity of the designed sensor.
Full size table
Table 5 The role of fabrication tolerance of n doped Si layers thickness on the sensitivity of the designed sensor.
Full size table

Comparative analysis

We compare the sensor’s performance with recently published different photonic structures for magnetic field sensing applications, which is given in Table 6. From this table, it is confirmed that the magnetic field sensitivity of the proposed sensor exceeds that of most previous works by approximately two orders of magnitude. In addition to the high sensitivity, the use of n-doped Si in our design enhances the Q-factor up to 1633 at 7 T and 10 T due to the lower optical absorption of doped semiconductors in the THz region. The high sensitivity of 2.91 μm/T arises mainly due to the combined effects of the enhanced Faraday response in heavily n-doped Si and the strong field coupling provided by the optimized 1D PhC. The high doping level significantly increases the magneto-optical coefficient, producing a larger refractive index change under a given magnetic field. This, in turn, results in a more pronounced photonic bandgap shift compared to conventional designs. Additionally, careful optimization of layer thicknesses and other geometrical parameters maximizes the sensitivity. The proposed sensor design has demonstrated high performance efficiency, while also offering a cost-effective and structurally simple configuration. This added simplicity in fabrication and integration enhances its appeal for practical applications in magnetic field sensing systems.

Table 6 A brief comparison with the available published papers in the vicinity of the investigated sensitivity.
Full size table

Conclusion

In summary, the proposed magnetic field sensor designed based on the Faraday effect influencing the permittivity of n-doped silicon, which functions as a defect layer in a 1D PhC operating in the far-infrared range has been comprehensively investigated. Numerical analysis, conducted using the transfer matrix method within the Faraday geometry, was employed to examine the shift in the defect mode frequency under varying magnetic field intensities. To maximize performance, the sensor’s structural parameters and the incident angle of the interacting electromagnetic waves were systematically optimized by evaluating sensitivity. Parameters such as layer thicknesses, number of periods, doping concentration, and incident angle were fine-tuned. Based on the optimization results, the final sensor configuration is defined as [ (SiO2 + GaAs) N=4/ n-doped Si / (SiO2 + GaAs) N=4]​, with Nd=1 × 1023 m− 3, da = 40 μm, d1 = 19 μm, d2 = 8.5 μm, at normal incidence. The optimized sensor exhibits excellent performance metrics, achieving a sensitivity of 2.91 μm/Tesla, a quality factor (Q) of 1633, a signal-to-noise ratio (SNR) of 291, a detection limit (DL) of 0.0055 Tesla, a spectral resolution (SR) of 0.016 μm, and a figure of merit (FOM) of 29.1 Tesla⁻¹ highlighting its strong potential for high-precision magnetic field sensing applications. Additionally, the designed sensor is robust against the structural disorders and the geometrical variations as well. In particular, the decrements in the sensitivity of the designed sensor are not exceeding over 0.0004 THz/Tesla for tolerance of a tolerance of 100 nm in the thickness of the considered materials.