Calculation of nonlimit active earth pressure of retaining walls based on curved sliding surface

Abstract

The shape of the sliding surface and the displacement of the wall have important effects on the earth pressure of retaining walls. Taking the cohesive backfill behind the inclined retaining wall as the research object, the relationship between the displacement ratio of the wall and the internal friction angle, the external friction angle, the cohesion and the wall-soil adhesion were build up. The potential slip surface behind the wall was assumed to be a cycloid curve, establishing the force balance and moment balance equations of the horizontal differential soil element, the distribution of the non-limit active earth pressure was obtained. The reliability of the proposed method is verified by two model tests and some theoretical results. The parametric research indicates that with the increase of displacement ratio and internal friction angle, the range of potential sliding body decreases gradually, and the non-limit active earth pressure decreases accordingly, presenting a convex curve distribution with the peak value in the middle and lower part of the wall; With the increase of cohesion, the range of potential sliding body increases slightly, and the non-limit active earth pressure near the wall bottom gradually transitions from positive value to negative. With the increase of the inclination of the wall back, the range of potential sliding body increases, and the shape of non-limit active earth pressure curve gradually transitions from convex curve to concave curve. The theoretical method proposed in this paper can provide reference for the research of earth pressure of retaining walls under translational mode.

Introduction

The correct calculation of earth pressure plays an important role in the rational design of retaining walls. The traditional Coulomb theory and Rankine theory are widely used in retaining walls design because of their simple calculation and clear force. The two traditional theories assume that the backfill behind the wall is in a state of limit equilibrium, the sliding surface is a plane, and the distribution of earth pressure is linear along the wall. However, a large number of experiments^{1,2,3,4,5,6,7,8,9} showed that, the distribution of earth pressure behind the wall is nonlinear, whether it is cohesive fill or cohesionless fill, and the earth pressure varies with the displacement of the wall. In order to make the calculated earth pressure closer to the measured value, scholars have done a lot of research.

Paik & Salgado¹⁰ assumed that the slip surface was Rankine slip surface, considering the soil arching effect, according to the horizontal layer analysis method, deriving the formula for calculating the active earth pressure of sandy soil, and the calculated results were in good agreement with the measured values. On this basis, Peng and Zhu¹¹ considered the influence of shear stress between soil layers and gave the calculation formula of active earth pressure of cohesive fill. Zheng et al.¹² further considered the influence of the back inclination of the wall. Rao et al.¹³ assumed that the sliding surface of fill was a plane, obtaining the expression of the slip surface inclination and the formula of active earth pressure distribution of cohesive soil by using the central arc arch trace method. Chen et al.¹⁴ established the energy conservation equations, deriving the calculation formulas of crack depth, slip surface inclination and active earth pressure which can consider the basement reverse slope.

The above theories are all based on planes assumption, which were different from the curve failure surface obtained from experiments^1,7. Gnanapragasam¹⁵, Peng¹⁶ confirmed that the slip surface of soil is a curved surface by limit Mohr stress circle and slip line method, respectively, but the equation of curved failure surface is not given, and the obtained active earth pressure distribution is linear. For the convenience of research, different scholars assume that the slip surface is a curve, including logarithmic spirals^17,18, parabolas^8,19, cycloids^20,21,22, the obtained active earth pressure has a nonlinear distribution, which are basically consistent with the measured value. In order to further consider the influence of the displacement effect on the earth pressure, Bang et al.²³ thought that the internal friction angle of the fill behind the wall gradually developed from zero to the maximum before the wall reached the limit displacement. On this basis, Chang²⁴ established the relationship between internal friction angle, external friction angle and wall displacement, extending Coulomb theory. Tang et al.²⁵ According to the wedge element method, the distribution solution of the non-limit active earth pressure of sand is studied. According to the stress-strain relationship proposed by Duncan-Chang, Tang & Chen²⁶ obtained the formulas for calculating the non-limit active and passive earth pressure under different displacement, but there are many empirical parameters in the formulas, which are not convenient for application. Xu et al.²⁷ studied the relationship between internal friction angle and displacement of cohesive soil by using the hyperbolic relationship between radial stress and radial strain, assuming Coulomb slip surface, giving the calculation formula of non-limit active earth pressure of cohesive fill. Li et al.⁷ considered both soil arching effect and shear effect between soil layers, and obtained the numerical solution of non-limit active earth pressure of backfill through iterative calculation. Zhang et al.²⁸ extended Rankine theory to the calculation of non-limit earth pressure based on the linear elastic constitutive theory.

To sum up, the research on the active earth pressure of cohesive fill in non-limit state is not sufficient, which is embodied in that most theories can only be applied to solve the earth pressure when the back of the wall is vertical, and the influence of the shape of the curved slip surface and the displacement of the wall on the active earth pressure cannot be considered at the same time. In view of this, this paper establishes the relationship between the wall displacement ratio and the internal friction angle, external friction angle, cohesion and wall-soil adhesion. Assuming that the potential slip surface is a cycloid, the horizontal layer analysis method is used to establish the force balance and moment balance equations of the soil differential element, and the theoretical method for determining the distribution of non-limit active earth pressure is obtained. The calculation method of non-limit active earth pressure obtained in this paper is more widely used, and the effects of displacement ratio η, internal friction angle φ_m, external friction angle δ_m, cohesion force c_m, wall-soil adhesion c_wm and wall back inclination ε can be considered at the same time. The rationality of this method is verified by the measured values of sand test and clay test respectively, and the influence of related parameters on the shape of slip surface and the distribution of non-limit active earth pressure is explored.

Theoretical derivation

Relationship between wall displacement and friction angle and cohesion

The process that the backfill behind the retaining wall is failed by the change of the displacement of the wall is a gradual process. Some scholars^{10,13,14,16,17,19,22} have deduced the calculation formulas of active earth pressure by assuming that the wall reaches the limit displacement and the fill behind the wall is in the limit equilibrium state, that is, the internal friction angle and cohesion are constant. In practical engineering, the allowable displacement of the wall is often less than the limit displacement, and the internal friction angle of the soil is not fully exerted, but is between the initial value and the limit value (the shear strength index obtained by triaxial shear test). At this time, the backfill behind the wall is in the non-limit state, and the earth pressure acting on the wall is called the non-limit earth pressure.

Fig. 1

Mohr stress circle and shear strength envelope of cohesive soil.

Figure 1 is the Mohr stress circle of clay, σ₁ is the major principal stress, σ₀ is the minor principal stress in the initial state (S = 0), and the initial value of internal friction angle is φ₀; σ_am is the minor principal stress in the non-limit active state (0 < S < S_a), at which the internal friction angle is φ_m; σ_a is the minor principal stress in the limit active state (S = S_a), at which the limit value of internal friction angle is φ. Where S is the actual displacement of the wall and S_a is the ultimate displacement of the fill, which is related to the type of the fill and can be obtained through experiments.

According to the geometric relationship, there is the following relationship between the internal friction angle φ_m and the wall displacement S ^7,26,27, that is

$$\sin {\varphi _m}=\frac{{(1 - {R_f}+\eta {R_f})(1 - {K_0})(1+\sin \varphi )+\eta \sin \varphi (1+{K_0}) - \eta (1 - {K_0})}}{{(1 - {R_f}+\eta {R_f})(1 - {K_0})(1+\sin \varphi ) - \eta \sin \varphi (1+{K_0})+\eta (1 - {K_0})}}$$

(1)

Where η = S/S_a, φ is the internal friction angle when the soil reaches the ultimate displacement, which can be measured by experiments; R_f is the failure ratio, with the value ranging from 0.75 to 1, and 0.85 can be taken when there is no measured datas; K₀ is the coefficient of static earth pressure. For cohesive soil, Federico et al.²⁹ statistically analyzed the measured values of 59 cases of static earth pressure and satisfied the following relationship:

$${K_0}=(1 - \sin 0.64\varphi )/(1+\sin 0.64\varphi )$$

(2)

Fang & Ishibashi² found through experiments and Matsuzawa & Hazarika³⁰ through numerical simulation that the external friction angle and displacement are approximately linear. On this basis, Chang²⁴ established the relationship between the external friction angle and displacement:

$$\tan {\delta _{\text{m}}}=\tan {\delta _0}+\eta (\tan \delta - \tan {\delta _0})$$

(3)

δ and δ₀ respectively correspond to the external friction angle when the wall reaches the limit displacement and when the wall is at rest. When there is no measured data, δ₀ can be φ/2, and δ can be 2φ/3. For the selection of the cohesive force exertion value cm of fill and cwm of wall and soil, according to the assumptions of Xu et al.²⁷ and Li et al.⁷, namely

$$\left\{ \begin{gathered} {c_{{\text{wm}}}}={c_{\text{w}}}\tan {\varphi _{\text{m}}}/\tan \varphi \hfill \\ {c_{\text{m}}}=c\tan {\varphi _{\text{m}}}/\tan \varphi \hfill \\ \end{gathered} \right.$$

(4)

c and c_w are the cohesion of the fill and the wall-soil adhesion when the wall reaches the ultimate displacement, respectively. If there is no measured value, c_w=2/3c.

Assumption of potential slip surface

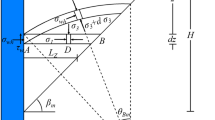
The shape of slip surface is an important factor affecting the magnitude of earth pressure. At present, most scholars^{10,13,14,16,25} assumes that the shape of the sliding surface of the backfill behind the retaining wall is a plane, but this is different from the curved failure surface in the test. When the backfill behind the wall is in the non-limit active state, the rectangular coordinate system x-o-y as shown in Fig. 2 is established. Based on the fact that the potential slip surface is a cycloid curve passing through the bottom of the wall^20,21,22, which is used to study the non-limit active earth pressure, and its parameter equations are

$$\left\{ \begin{gathered} x=R(\theta - \sin \theta ) \hfill \\ y=R(1 - \cos \theta ) \hfill \\ \end{gathered} \right.$$

(5)

Where R represents the radius of the cycloidal wheel and θ represents the rotation angle of the cycloidal wheel.

Fig. 2

Schematic diagram of calculation model.

The slope at any point on the cycloidal curve is tanζ, Its expression is

$$\tan \zeta =\frac{{{\text{d}}y}}{{{\text{d}}x}}=\frac{{R\sin {\text{d}}\theta }}{{R(1 - \cos \theta ){\text{d}}\theta }}=\tan \left( {\frac{\pi}{2} - \frac{\theta }{2}} \right)$$

(6)

The included angle between the tangent of this point and the horizontal direction is ζ = π/2-θ/2.

When the cycloidal curve passes through the bottom of the wall, its rotation angle θ = θ_am and y = H(H is the height of the wall), and the expression of the cycloidal wheel radius R can be obtained.

$$R=\frac{H}{{1 - \cos {\theta _{{\text{am}}}}}}$$

(7)

The value of θ at any point on the potential failure surface is

$$\theta =\arccos \left( {1 - \frac{y}{R}} \right)$$

(8)

Through the above analysis, as long as θ_am is determined, the parameter equation of the cycloid can be uniquely determined, and the value of θ_am will be determined by force balance analysis below.

Force balance analysis of infinitesimal elements

In the following mechanical analysis process, the author ignores the influence of soil arching effect on non-limit active earth pressure. There are two reasons. First, this paper studies the earth pressure of retaining wall in translation mode. Compared with the retaining wall in rotation mode, the soil arching effect of the backfill behind the wall is even less obvious². Second, although the existing earth pressure theory^{7,10,13,14,16,19,22} considered the influence of soil arching, the moment balance of soil can not be considered in the analysis process.

As shown in Fig. 2, the potential sliding soil element adeg behind the wall is selected, and the length of e.g. is b, and the expression of b can be obtained from the geometric relationship as follows

$$b=(H - y)\tan \varepsilon +\frac{{H({\theta _{{\text{am}}}} - \sin {\theta _{{\text{am}}}})}}{{1 - \cos {\theta _{{\text{am}}}}}} - \frac{{y(\theta - \sin \theta )}}{{1 - \cos \theta }}$$

(9)

Where ε represents the inclination of the wall back, and y represents the distance from e.g. to x axis.

The force analysis of the infinitesimal body is shown in Fig. 3, ignoring the second-order trace, and its gravity is

$${\text{d}}W=\frac{\gamma }{2}(b+b - \tan \alpha {\text{d}}y - \tan \frac{\theta }{2}{\text{d}}y)\frac{{\cos \alpha }}{{\cos \varepsilon }}{\text{d}}y=\gamma b{\text{d}}y$$

(10)

Where, γ is the unit weight of soil.

Fig. 3

Schematic diagram of stress analysis of horizontal differential soil element.

Establish the balance equation for horizontal force, that is $\sum {{F_x}=} 0$, we can obtain

$${p_{{\text{am}}}}\frac{{{\text{d}}y}}{{\cos \varepsilon }}\cos ({\delta _{\text{m}}}+\varepsilon ) - {c_{{\text{wm}}}}{\text{d}}y\tan \varepsilon - N\frac{{{\text{d}}y}}{{\cos \frac{\theta }{2}}}\cos (\frac{\theta }{2}+{\varphi _{\text{m}}})+{c_{\text{m}}}{\text{d}}y\tan \frac{\theta }{2}=0$$

(11)

Establish equilibrium equation for vertical force, that is $\sum {{F_y}=} 0$, we can obtain

$$\begin{gathered} {p_{{\text{am}}}}\frac{{{\text{d}}y}}{{\cos \varepsilon }}\sin ({\delta _{\text{m}}}+\varepsilon )+{c_{{\text{wm}}}}{\text{d}}y+N\frac{{{\text{d}}y}}{{\cos \frac{\theta }{2}}}\sin (\frac{\theta }{2}+{\varphi _{\text{m}}})+{c_{\text{m}}}{\text{d}}y+(q+{\text{d}}q)(b - \hfill \\ \tan \varepsilon {\text{d}}y - \tan \frac{\theta }{2}{\text{d}}y) - qb - {\text{d}}W=0 \hfill \\ \end{gathered}$$

(12)

In the formula, p_am is the non-limiting active earth pressure acting on the wall back, the angle between its direction and the normal direction of wall back is δ_m, and N is the reaction force of the potential sliding body.

By solving Eqs. (11) and (12) simultaneously, we can have

$${\text{d}}q=\gamma {\text{d}}y+\frac{{Lq - J{c_{\text{m}}} - K{c_{{\text{wm}}}} - I{p_{{\text{am}}}}}}{b}{\text{d}}y$$

(13)

Where L, J, K and I satisfy the following formulas:

$$\left\{ \begin{gathered} L=\tan \varepsilon +\tan \frac{\theta }{2} \hfill \\ J=1+\tan \frac{\theta }{2}\tan (\frac{\theta }{2}+{\varphi _{\text{m}}}) \hfill \\ K=1 - \tan \varepsilon \tan (\frac{\theta }{2}+{\varphi _{\text{m}}}) \hfill \\ I=\frac{{\cos (\varepsilon +{\delta _{\text{m}}})}}{{\cos \varepsilon }}[\tan (\frac{\theta }{2}+{\varphi _{\text{m}}})+\tan (\varepsilon +{\delta _{\text{m}}}) \hfill \\ \end{gathered} \right.$$

(14)

When all the forces on the micro-element exert moments about the middle point of ed, the moment balance equation $\sum {{M_0}=} 0$can be gived, namely

$$\begin{gathered} qb(\frac{b}{2} - \frac{{\tan \frac{\theta }{2}}}{2}{\text{d}}y)+\frac{{b{\text{d}}W}}{2}+\frac{{(q+{\text{d}}q)(b - \tan \varepsilon {\text{d}}y)}}{2}(b - \tan \varepsilon {\text{d}}y - \tan \frac{\theta }{2}{\text{d}}y) \hfill \\ - {p_{{\text{am}}}}\frac{{{\text{d}}y}}{{\cos \varepsilon }}\sin (\varepsilon +{\delta _{\text{m}}})(b - \frac{{\tan \varepsilon +\tan \frac{\theta }{2}}}{2}{\text{d}}y) - {c_{{\text{wm}}}}(b - \frac{{\tan \varepsilon +\tan \frac{\theta }{2}}}{2}{\text{d}}y)=0 \hfill \\ \end{gathered}$$

(15)

Simplify the formula (15)

$${\text{d}}q=\gamma {\text{d}}y+\frac{{2q\tan \varepsilon }}{b}{\text{d}}y - \frac{{2{p_{{\text{am}}}}\sin (\varepsilon +{\delta _{\text{m}}})}}{{b\cos \varepsilon }}{\text{d}}y - \frac{{2{c_{{\text{wm}}}}}}{b}{\text{d}}y$$

(16)

Solving Eqs. (13) and (16) simultaneously, we can get

$${p_{{\text{am}}}}=Qq - U{c_{\text{m}}}+Q{c_{{\text{wm}}}}$$

(17)

Where,

$$\left\{ \begin{gathered} Q=\lambda (\tan \frac{\theta }{2} - \tan \varepsilon ) \hfill \\ U=\lambda \left[ {1+\tan \frac{\theta }{2}\tan \left( {\frac{\theta }{2}+{\varphi _{\text{m}}}} \right)} \right] \hfill \\ V=\lambda \left[ {1+\tan \varepsilon \tan \left( {\frac{\theta }{2}+{\varphi _{\text{m}}}} \right)} \right] \hfill \\ \end{gathered} \right.$$

(18)

where, $\lambda =\frac{{\cos \varepsilon }}{{\cos (\varepsilon +{\delta _{\text{m}}})\tan \left( {\frac{\theta }{2}+{\varphi _{\text{m}}}} \right) - \sin (\varepsilon +{\delta _{\text{m}}})}}$

Substituting formula (17) into formula (13), we can get the differential equation about q, that is

$$\frac{{{\text{d}}q}}{{{\text{d}}y}}=\gamma +\frac{A}{b}q+\frac{B}{b}({c_{\text{m}}} - {c_{{\text{wm}}}})$$

(19)

where,

$$\left\{ \begin{gathered} A=L - QI \hfill \\ B=UI - J \hfill \\ D=VI+K \hfill \\ \end{gathered} \right.$$

(20)

According to formula (17), the magnitude of non-limit active earth pressure can be calculated. First, the value of q should be found by Eq. (19). However, the differential Eq. (19) cannot be solved analytically, and only a numerical solution can be obtained.

For the solution of non-limit active earth pressure under a certain working condition, H, ε, η, φ, δ, c and c_w are known, θ_am can be assumed in advance, and R and θ value corresponding to Y point can be obtained by formulas (7) and (8) respectively, and then L, J, K, I, Q, U, V, λ, A, and V can be obtained. And y∈[0,H], by assuming different Y, different p_am can be obtained, and the distribution curve of p_am along the wall height can be obtained. According to the integral knowledge, the resultant force E_am of non-limit active pressure can be obtained. Assuming different θ_am, a series of E_am can be obtained, and the maximum value E_am(max) can be selected, and the corresponding θ_am is the demand. Calculation program diagram is shown in Fig. 4.

Fig. 4

Calculation program diagram.

To ensure calculation accuracy, the thickness of soil stratification can be taken as 0.001H, that is, n = 1000.

The horizontal component of non-limit active earth pressure can be calculated according to the following formula.

$${p_{{\text{ahm}}}}={p_{{\text{am}}}}\cos ({\delta _{\text{m}}}+\varepsilon )$$

(21)

For sandy soil and cohesive backfill with tensile strength, the resultant force of non-limit active earth pressure E_am is

$${E_{{\text{am}}}}=\frac{{\sum\limits_{{i=1}}^{n} {{p_{{\text{ami}}}}\Delta y} }}{{\cos \varepsilon }}$$

(22a)

For backfill without considering tensile strength, the resultant force of non-limit active earth pressure E_am is

$${E_{{\text{am}}}}=\frac{{\sum\limits_{{i={i_0}}}^{{{n_0}}} {{p_{{\text{ami}}}}\Delta y} }}{{\cos \varepsilon }}$$

(22b)

Where, i₀ and n₀ can be derived by setting p_am=0 in Eq. (17).

The moment M of the resultant force about the bottom of the wall is

$$M=\sum\limits_{{i=1}}^{n} {{p_{{\text{ami}}}}\cos {\delta _{\text{m}}}\frac{{\Delta y}}{{\cos \varepsilon }}[H - (i - 0.5)\frac{{\Delta y}}{{\cos \varepsilon }}]}$$

(23)

The vertical distance h_am between the resultant force action point and the bottom of the wall is

$${h_{{\text{am}}}}=\frac{{M\cos \varepsilon }}{{{E_{{\text{am}}}}\cos {\delta _{\text{m}}}}}$$

(24)

If the influence of tensile strength of cohesive fill is not considered, the backfill will develop a tensile crack with a certain depth down the top of the wall, and its value can be obtained by making Eq. (17) equal to 0.

Comparison between theoretical solution and experimental value

Test one

Li et al.⁷ studied the distribution law of sandy soil pressure through indoor tests. The test parameters are: the height of retaining wall H = 0.8 m, the inclination of wall back ε = 0, φ = 30.2°, δ = 2/3φ, γ = 15.7kN/m³, and S_a=1 mm. Figure 5a,b are comparative analysis diagrams of theoretical solutions and measured values when the wall displacement is S = 0.2 mm and S = 1 mm, respectively. As can be seen from Fig. 4, when S = 0.2 mm and S = 1 mm, the distribution law of earth pressure obtained by Tang et al.²⁵ is linear, which is quite different from the measured value. The reason is that the Coulomb theory is directly applied to the non-limit state by Tang et al.²⁵, which leads to the linear distribution of earth pressure under any displacement. When S = 1 mm, the solution in this paper is in good agreement with Paik and Salgado¹⁰ solution, Xie and Leshchisk¹⁷ solution, Tang & Chen²⁶ solution and Li et al.⁷ solution, which shows the reliability of theoretical derivation in this paper. However, there are still some differences in the distribution of earth pressure obtained by several theories. The main reason is that Paik and Salgado¹⁰ solution is based on Rankine slip surface, considering soil arching effect, and the formula of active earth pressure is derived. Xie and Leshchisk¹⁷ solution takes into account the slip surface of logarithmic spiral and soil arching effect; Tang and Chen²⁶ solution is derived directly from Coulomb slip surface; Li et al.⁷ solution considers the shear force between soil layers and uses an iterative method to solve the earth pressure. The solution in this paper is based on the cycloid curve, considering the influence of displacement, deriving the numerical solution of non-limit active earth pressure. Moreover, Paik & Salgado¹⁰ solution and Xie & Leshchisk¹⁷ solution can only determine the active earth pressure when the sand reaches the limit state, while Tang and Chen²⁶ solution can only calculate the non-limit active earth pressure of sand, and the solution in this paper can also be applied to solve the non-limit active earth pressure of cohesive soil. It shows that the proposed method in this paper is more widely used.

Fig. 5

Comparison between theoretical solution and experimental value of non-limit active earth pressure of sand under different displacements. (a) S = 0.2 mm, (b) S = 1 mm.

Test two

Zhou and Ren³ explored the distribution law of clay soil pressure through indoor tests. The test parameters are: retaining wall height H = 4.45 m, wall back inclination ε = 0, φ = 24.3, δ = 21.4, γ = 14.27kN/m³, c = 1.472kPa, c_w=0.98 kPa, and S_a = 1 mm. Figures 4 and 6 are comparative analysis diagrams of the theoretical solution and the measured values when the wall displacement is S = 0.2 mm and S = 1 mm respectively. S_a=39.4 mm. Figure 6a,b are comparative analysis diagrams of theoretical solutions and measured values when the wall displacement is S = 0.2 mm and S = 1 mm, respectively. As can be seen from Fig. 4, when S = 0 mm and S = 39.4 mm, the non-limit active earth pressure obtained by Zhang et al.⁹ is approximately linearly distributed, which is quite different from the measured value, mainly because its theoretical formula is derived based on Rankine theory. When S = 39.4 mm, although Peng and Zhu¹⁶ solution and Rao et al.¹³ solution are also nonlinear, they are quite different from the measured values, mainly because Peng and Zhu¹⁶ solution exaggerates the shear force between soil layers when analyzing soil differential elements; Rao et al.¹³ consider that the slip surface is a plane through the soil arching effect. Moreover, Peng and Zhu¹⁶ solution and Rao et al.¹³ solution can not determine the distribution of non-limit active earth pressure. When S = 0 mm, the distribution of earth pressure gived by the proposed solution is very close to that obtained by Li et al.⁷, and both of them are in good agreement with the measured values. When S = 39.4 mm, the earth pressure distribution gived by the proposed solution is closer to the experimental value than that obtained by Li et al.⁷. The main reason is that this paper directly assumes that the potential sliding surface is a cycloid curve, while the solution of Li et al.⁷ is deduced by iterative calculation by considering the soil arching effect and interlayer shear stress. It shows that the assumption of slip surface in this paper is reasonable and the theoretical analysis is effective. Moreover, Li et al.⁷ cannot consider the influence of the wall back inclination on the non-limit active earth pressure, but the proposed solution can consider it, which shows that the application range of this method is wider.

Fig. 6

Comparison between theoretical solution and experimental value of non-limit active earth pressure of clay under different displacements. (a) S = 0 mm, (b) S = 39.4 mm.

Through the comparative analysis of the above two tests, it is found that the earth pressure obtained in this paper is non-negative, but not the maximum, which is consistent with the measured earth pressure law, which is different from the existing theory, mainly due to the geometric characteristics of the cycloid. There is a small gap between the distribution of non-limit active earth pressure obtained in this paper and the experimental value, which may be caused by the size effect or experimental error of model test.

Numerical simulation

To verify the rationality of active earth pressure under different wall back inclinations (ε = 0°, ε = 10°, ε = 20°) proposed in this paper, the ABAQUS software was used for numerical simulation. The relevant parameters are set as H = 5 m, φ = 40°, c = 0 kPa, δ = 20°, γ = 16kN/m³. As shown in Fig. 7, the distribution laws of the theoretical solutions and numerical solutions are basically the same, which verifies the rationality of the method proposed in this paper. There is still a certain gap between the theoretical values and numerical solutions, mainly because the determination of boundary conditions, parameter settings, and mesh division in the numerical simulation process have a certain impact on the earth pressure values. Therefore, experiments on earth pressure under different wall back inclinations will be carried out in the future to further verify the correctness of the theory proposed in this paper.

Fig. 7

Comparison analysis curves of numerical solutions and theoretical values under different inclination angles.

Parameter sensitivity analysis

The following mainly explores the influence of displacement ratio η, wall back inclination angle ε, internal friction angle φ and cohesion c on the morphology of potential slip surface and the distribution of non-limit active earth pressure. In order to study the influence of parameters on the shape of slip surface, the X-O-Y rectangular coordinate system as shown in Fig. 2 is established, and the relationship with the x-o-y coordinate system is as follows:

$$\left\{ \begin{gathered} {X_\theta }=H\tan \varepsilon +{x_{{\theta _{{\text{am}}}}}} - {x_\theta } \hfill \\ {Y_\theta }=H - {y_\theta } \hfill \\ \end{gathered} \right.$$

(25)

x_θam, x_θ, y_θ can be found by formula (5).

In the process of analysis, the unified values of parameters are: H = 10 m, γ = 15 kN/m³, c_w=2/3c, δ = 2/3φ, δ₀ = 1/2φ, and R_f = 0.85.

4.1 influence of displacement ratio η

Taking ε = 0°, φ = 36°, and c = 5 kPa for analysis, the potential slip surface shape and non-limit active earth pressure distribution curves under different displacement ratios are gived, as shown in Figs. 8 and 9 respectively. It can be seen that with the increase of η, the overall shape of the potential slip surface tends to be steeper, and the volume of the sliding soil is decreasing, indicating that the internal friction angle of the soil is gradually exerting, which leads to the decrease of the non-limit active earth pressure acting on the back of the wall. With the increase of η, the decreasing trend of both potential slip surface and non-limit active earth pressure is nonlinear, mainly because the internal friction angle φ and η are nonlinear relation. When the displacement ratio is the same, the distribution of non-limit active earth pressure along the wall height is a convex curve, and the earth pressure at the bottom of the wall is not zero.

Fig. 8

Potential slip surface shapes under different η.

Fig. 9

Distribution of non-limit active earth pressure under different η.

Influence of wall back inclination ε

Taking η = 0.2, φ = 36°, and c = 5 kPa for analysis, the potential slip surface shape and non-limit active earth pressure distribution curve under different wall back inclination angles are obtained, as shown in Figs. 10 and 11 respectively. It can be seen that with the increase of the back inclination angle of the wall, the shape of the sliding surface basically remains unchanged, while the sliding range expands, the earth pressure on the upper part of the wall gradually decreases, the earth pressure on the lower part gradually increases, and the distribution curve of the non-limit earth pressure gradually changes from convex curve to concave curve. The reason is that, because the fill has certain cohesion, the greater the inclination angle of the back of the wall, the greater the tensile stress will be, which will lead to the decrease of the earth pressure on the upper part of the wall, while the lower part will be subjected to greater soil weight, which will increase the earth pressure. The main causes of the morphological changes in the earth pressure distribution curve come from two aspects. First, the change in the wall back inclination leads to changes in the shape, position, and geometric boundaries of the cycloid slip surface, affecting the transmission path and distribution of earth pressure. Second, the change in the wall back inclination alters the way of soil constraint and support, and the earth pressure acting on the wall back and its distribution are adjusted accordingly.

Fig. 10

Potential slip surface shapes under different.

Fig. 11

Distribution of non-limit active earth pressure under different ε.

Influence of internal friction angle φ

Taking η = 0.2, ε = 0°, and c = 5 kPa for analysis, the potential slip surface shape and non-limit active earth pressure distribution curve under different internal friction angles are obtained, as shown in Figs. 12 and 13 respectively. It can be seen that with the increase of internal friction angle, the dip angle of potential slip surface becomes steeper as a whole, and the range of sliding soil becomes smaller, which leads to the decrease of non-limit earth pressure acting on the back of the wall, but the position of the peak value of distribution curve from the bottom of the wall remains basically unchanged. The reason is that the smaller the internal friction angle, the lower the soil strength, the worse the ability to maintain its own stability, and the greater the thrust on the back of the wall. The variation of the peak value of earth pressure with the change of the internal friction angle is uneven, mainly because the earth pressure distribution is a non-linear function of the internal friction angle φ.

Fig. 12

Potential slip surface shapes under different φ.

Fig. 13

Non-limit active earth pressure distribution under different φ.

Influence of cohesion c

Taking η = 0.2, ε = 0° and φ = 36° for analysis, the shape of potential slip surface and the distribution curve of unlimited active earth pressure under different cohesion are obtained, as shown in Figs. 14 and 15 respectively. It can be seen that with the increase of cohesion, the range of potential sliding soil increases slightly, while the earth pressure acting on the back of the wall decreases, and tensile stress will appear at the top and bottom of the wall. This is because cohesion, as an important strength parameter index of fill, the greater its value, it shows that it can support more potential sliding soil on its own, which leads to less external support for fill, that is, less earth pressure acting on the back of the wall. As the cohesion increases, the tensile stress also increases. When the tensile stress exceeds the compressive stress generated by the soil’s unit weight, the soil will exhibit a tensile state, resulting in negative values.

Fig. 14

Potential slip surface shapes under different c.

Fig. 15

Non-limit active earth pressure distribution under different c.

From the above analysis, it is found that the potential sliding surface of the fill is a cycloid curve with steep top and gentle bottom, which is basically consistent with most of the measured phenomena, which proves that the sliding surface of the cycloid can be used as the basis of non-limit earth pressure analysis of the retaining wall and can be further extended to the study of earth pressure in other displacement modes. The distribution of non-limit active earth pressure is generally convex curve, but it may be concave curve when there is a certain inclination angle at the back of the wall. The non-limit earth pressure at the bottom of retaining wall is generally positive, but when the cohesion of fill is large, it may be negative, that is, it is subjected to tensile stress.

Conclusions

(1) In this paper, it is assumed that the potential sliding surface of the backfill behind the wall is a cycloid curve, setting up the force balance and moment balance equations of the differential soil element, and the calculation method of the non-limit active earth pressure is obtained. Generally speaking, compared with the existing theory, the non-limit active earth pressure obtained by this method is in better agreement with the measured value, which verifies the rationality of this assumption and the correctness of theoretical derivation. The theoretical method in this paper can provide reference for the study of earth pressure of retaining wall under rotating modes.

(2) The calculation method obtained in this paper can take into account the influence of wall displacement ratio η, internal friction angle φ_m, external friction angle δ_m, cohesion c_m, wall-soil adhesion c_wm and wall back inclination ε on non-limit active earth pressure at the same time, and has a wide application range.

(3) The potential slip surface behind the wall always show a feature with a steep upper section and a gentle lower section. The range of potential sliding body behind the wall decreases with the increase of displacement ratio and internal friction angle, and decreases with the increase of wall back inclination angle and cohesion of the wall.

(4) Non-limit active earth pressure is generally distributed in a convex curve, but with the increase of the wall back inclination angle, its distribution curve will decrease in the upper part and increase in the lower part, and gradually transition to a concave curve.

(5) With the increase of displacement ratio and internal friction angle, the non-limit active earth pressure will decrease. With the increase of the cohesion of the fill, the height of the tensile stress zone at the top of the wall will increase, and the non-limit active earth pressure at the bottom of the wall will change from positive to negative.