Energy consumption minimisation at edge node using $C_cBPS$ approach in predicting sensor parameters in WSNs

Abstract

Owing to limited storage and battery power, wireless sensor nodes often face challenges in maintaining long-term energy sustainability. To address this, only a subset of sensors remains active to monitor different sensor parameters while others get predicted to minimize sensor node energy consumption. In prediction, not all active parameters are equally important, as low-correlated parameters increase computational complexity and decrease accuracy. Researchers use highly correlated active parameters, though existing solutions often use polynomial time and don’t ensure optimal parameter set. This paper proposes a cross-correlation-based parameter selection $(C_cBPS)$ approach, ensuring the selected parameter set is stable and Pareto-optimal. Simulations are performed on nine publicly available datasets of environmental data collected from different places and at different sampling intervals to validate the effectiveness of the $C_cBPS$ approach. It has been observed that $C_cBPS$ approach selects a subset of active parameters faster than existing approaches and reduces energy consumption at the edge node ranges from $6.5\%$ - $34.2\%$ in the prediction of sleep sensor parameters on various datasets.

Introduction

The rapidly growing Internet of Things (IoT) technology aims to connect millions of devices that are becoming an integral part of daily life. IoT sensor nodes, equipped with multiple sensors to monitor various parameters, are commonly deployed in diverse applications and are expanding rapidly. These sensor nodes are wirelessly connected to a central entity, forming wireless sensor networks (WSNs). WSNs play a crucial role in industrial monitoring, smart city management, agriculture, hospital monitoring, and border surveillance. However, the sensor nodes in WSNs typically have limited computing power and energy resources, which makes it challenging to process and analyze the collected data locally. As a result, this task is often offloaded to the cloud¹. Unfortunately, relying solely on cloud services can introduce unpredictable delays due to the involvement of the core network, which also increases energy consumption and bandwidth usage². Edge computing addresses these limitations by providing computing resources closer to the WSN, thereby reducing latency, energy consumption, and bandwidth requirements.

Different sensors of each sensor node of the WSN measure their respective parameters at predefined intervals known as measurement cycles {Measurement Cycle: A measurement cycle is a recurring process in a Wireless Sensor Network (WSN) that involves data sensing and transmission for monitoring the physical environment}. These parameters exhibit correlations among them^3,4. Consequently, some parameters are directly measured, while others are predicted at the edge node using these correlations. An edge intelligence-based sensing strategy is employed to reduce the energy consumption of sensor nodes in WSNs^3,5. In this strategy, the edge node selects an optimal subset of sensors to remain active for sensing environmental parameters in the measurement cycle while the rest of the parameters are in sleep mode. A Gaussian process regression (GPR)-based machine learning prediction model predicts sleep sensor parameters at edge node using correlated active sensor parameter^5,6,7. Using this strategy, the researcher minimized the energy consumption of the sensor node but did not consider the computational complexity and energy consumption of edge nodes during the prediction of sleep sensor parameters. The edge node’s computational complexity and energy consumption are also important factors. Therefore, for the efficient performance of the edge node, it is evident that computational complexity and energy consumption should be minimized while predicting sleep sensor parameters.

In the prediction of sleep sensor parameters, it is observed that not all active parameters contribute equally to the prediction process, as they do not exhibit the same level of correlation. Using active parameters with low correlation to the sleep sensor parameters adds unnecessary complexity to the prediction process and degrades the accuracy of predicted sleep sensor parameters^8,9. Bhuyan et al.¹⁰ used the correlation coefficient among parameters and the gradient descent technique to select the parameters from the active parameter set. In their approach, first, they assign the weight value $w \in [0,1]$ to each active parameter and then use the gradient descent technique to select the parameters. Tripathi et al.¹¹ used the chi-square parameter selection technique to select the parameter from the active parameter set. They considered positive and negative chi-square values for parameters and then used the probabilistic chi-square value to select the parameter from the active parameter set.

In the above parameter selection approach, Bhuyan et al.¹⁰ used the gradient descent technique to optimize the parameter selection process, which takes many iterations to optimize the weights for each parameter. Tripathi et al.¹¹ select the static number of parameters that limit their ability to ensure the best parameters for each sleep sensor parameter. All these approaches take polynomial time to select parameters from the active parameter set, and these approaches do not ensure whether the selected parameter set is an optimal parameter set {Optimal Parameter Set: A parameter set is optimal among all possible parameter sets if it has a higher correlation with the predicted parameter and the prediction model consumes less energy in prediction using this set.} of active sensor parameters.

In this paper, we propose a cross-correlation-based parameter selection $(C_cBPS)$ approach that selects optimal parameters from active parameter set to predict each sleep parameter. The $C_cBPS$ approach selects those active parameters that exhibit either high correlation or correlation greater than or equal to the average correlation of all active parameters with the sleep sensor parameter. By selecting the optimal parameters from the active sensor parameter set, the proposed approach reduces the computational complexity and energy consumption of the edge nodes in the prediction of sleep sensor parameters. Furthermore, by eliminating low-correlated parameters from the active parameter set, our method improves the accuracy of predicted sleep sensor parameters. Simulations are conducted to validate the effectiveness of the $C_cBPS$ approach using nine environmental datasets. These datasets were collected from different geographical locations and time intervals and are publicly available. These datasets consist of nine sensors designed to monitor specific environmental parameters, including $\text {PM}2.5, \text {PM}10, \text {NO}, \text {CO}, \text {NO}2, \text {NH}3, \text {SO}2, \text {Ozone}$, and $\text {Benzene}$.

The main contributions of this paper are as follows:

• 1. An algorithm based on $C_cBPS$ is proposed to select the optimal parameter set $\mathbb {K}$ from the active sensor parameter set to predict each sleep parameter at the edge node.

• 2. The $C_cBPS$ approach is theoretically analyzed and observed that the selected parameter set is both stable and Pareto optimal.

• 3. The time complexity of the proposed parameter selection algorithm is calculated and compared with the existing state-of-the-art parameter selection approaches.

• 4. Simulations are performed on various datasets to validate the effectiveness of the proposed approach. Simulation results show that the proposed approach selects the smallest parameter set from active sensor parameters and reduces energy consumption at the edge node ranges from $6.5 \%$ - $34.2 \%$ in the prediction of sleep sensor parameters on various datasets.

The paper is structured as follows: The literature review is presented in Section 2, followed by a description of the system model in Section 3. Section 4 discusses the cross-correlation-based optimal parameter selection approach, followed by Section 5, which presents the experimental setup for the simulation. Section 6 combines the results and discussion, while Section 7 provides the conclusion.

Literature Review

Parameter selection is an important approach in prediction because it reduces the dimensionality of the parameter, simplifying the predictive model while retaining the most relevant information. By eliminating less significant parameters, the parameter selection approach minimizes the prediction’s computational load and enhances the accuracy of predicted parameters. The authors utilized parameter selection strategies to improve the model’s efficiency and minimize energy consumption and computational costs. Bhuyan et al.¹⁰ used the correlation coefficient among data and the gradient descent technique to select the parameter from the parameter set. In their approach, first, they assign the weight value $w \in [0,1]$ to each active parameter and then use the gradient descent technique to select the parameters. Tripathi et al.¹¹ used the chi-square parameter selection technique to select the parameters from the dataset. They considered positive and negative chi-square values for parameters and then used the probabilistic chi-square value to select the parameter from the dataset. Tu et al.¹² proposed an enhanced approach for Cross-Validated Recursive Feature Elimination (RFECV) by randomly sampling different data, building multiple models, and comparing their scores to improve the robustness of the optimal parameter subset. Belhaouari et al.¹³ proposed the bird’s eye view parameter selection technique, which incorporated elements of evolutionary algorithms, genetic algorithms, dynamic Markov chain, and reinforcement learning to improve classification performance and reduced the number of parameters compared to conventional methods. Alhussan et al.¹⁴ used the binary waterwheel plant optimization technique for the selection of parameters in classification problems. Zhan et al.¹⁵ proposed a PD-based parameter selection technique that uses Possibility Degrees (PDs) to indicate parameter significance and mitigate data uncertainty. They used Gini entropy minimization to prioritize informative parameters, maximum correlation parameter selection to assure high relevance and minimal redundancy, and multisource information fusion to improve parameter informativeness and confidence. Fan et al.¹⁶ introduced an LCIFS technique that improves multi-label learning by capturing label correlations and managing parameter redundancy using information entropy and Pearson correlation analysis. It uses a manifold-based regression model and adaptive spectral graphs to discover accurate structural label correlations. In the above studies, either authors^12,13,14 are utilizing machine learning or optimization techniques to get the optimal parameters or authors^10,11,15,16 do not ensure that the selected parameter set in an optimal parameter set.

To the best of our knowledge, the existing studies either did not ensure that the selected parameter set is optimal parameter set or may take a long computational time to select the optimal parameter set from the active parameters. Therefore, we propose a $C_cBPS$ approach that relies on cross-correlations among sensor parameters to select the optimal parameter set from the active sensor parameter set to predict sleep sensor parameters faster than the existing parameter selection approaches. As a result, the proposed approach reduces computational complexity and energy consumption at the edge nodes in the prediction of sleep sensor parameters while improving the accuracy of predicted sleep sensor parameters.

System model

As shown in Figure 1, consider a sensor node with $\textsc {S}$ sensors where every sensor monitors one environmental parameter such that the parameter set $\mathbb {S} = \{ i; 1 \le \; i \le \; \textsc {S} \}$ contains all the parameters measured by the sensor node, where every i is an integer number and it represents a parameter of the sensor node. Assume a set $\mathbb {Q} = \{q_1, q_2,...,q_\textsc {S}\}$ such that $q_i = 1$ for every $i \in \textsc {S}$ if $i^{th}$ parameter is active, otherwise $q_i=0$. Set $\mathbb {G} = \{i \;|\; \forall q_i = 1, \;q_i \in \mathbb {Q}\}$ contains the active sensor parameters, and set $\mathbb {H} = \mathbb {Q}\; -\; \mathbb {G} = \{i \;|\; \forall q_i = 0, \; q_i \in \mathbb {Q}\}$ contains the sleep sensor parameters. The cardinalities of $\mathbb {G}$ and $\mathbb {H}$ are denoted by $\textsc {G}$ and $\textsc {H}$, respectively. If set $\mathbb {Z} = \{\mathbb {G}_{1}, \mathbb {G}_{2}, \ldots \mathbb {G}_{X} \}$, where $X = 2^{\textsc {S}}-1$, contains all subsets of active sensor parameter set excluding null set, then set $\mathbb {U} = \{ (\mathbb {G}_k, \mathbb {H}_{k}): 1 \le k \le X \}$ contains all pairs of active-sleep sensor parameters, where $\mathbb {U}_{i}$ represents the $i^{th}$ pair of active-sleep sensor parameters and it is defined as $\mathbb {U}_{i} = (\mathbb {G}_{i}, \mathbb {H}_{i})$. The matrix $\textbf{CC} \in \mathrm{I\!R}^{\textsc {S} \times \textsc {S}}$ represents the cross-correlation coefficient between all parameters of the parameter set $\mathbb {S}$. The matrix is defined as follows:

$$\begin{aligned} \textbf{CC} = \begin{bmatrix} {C}_{S_{1}S_{1}} & {C}_{S_{1}S_{2}} & \ldots & {C}_{S_{1}S_{S}} \\ {C}_{S_{2}S_{1}} & {C}_{S_{2}S_{2}} & \ldots & {C}_{S_{2}S_{S}} \\ \vdots & \ddots & & \vdots \\ {C}_{S_{S-1}S_{1}} & {C}_{S_{S-1}S_{2}} & \ldots & {C}_{S_{S-1}S_{S}} \\ {C}_{S_{S}S_{1}} & {C}_{S_{S}S_{2}} & \ldots & {C}_{S_{S}S_{S}} \end{bmatrix} \end{aligned}$$

where ${C}_{S_iS_j} = \textbf{CC}[S_i][S_j]$ represents the value of the cross-correlation coefficient between any pairs ($S_i$ , $S_j$) $\in \mathbb {S}$.

Figure 1

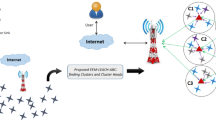
Environmental Data Collection and Transmission in Wireless Sensor Network via Edge Node. {Created using draw.io, Version: 24.7.17, https://www.drawio.com/}.

Problem Definition

In environmental data collection, some sensors become active to sense environmental parameters, while the rest parameters are in sleep mode in the measurement cycle. The sleep parameters in that measurement cycle are predicted at the edge node by utilizing the cross-correlation among parameters⁵. However, this prediction process also includes those active parameters that exhibit weak correlations with the sleep parameters, directly impacting the edge node’s computational complexity and energy consumption. The sleep sensor parameters are predicted by using the GPR-based prediction model^3,5. In the GPR-based prediction model, the covariance matrix computation notably influences the model’s computation and energy consumption. Therefore, reducing the energy consumption of the edge nodes is directly proportional to reducing the energy consumption of covariance matrix computation in the GPR prediction model. The covariance matrix computation is defined as follows:

$$\begin{aligned} k(x_i, x_j) = \exp \left( \dfrac{-1}{2l^{\prime 2}} \Vert x_i - x_j\Vert ^2 \right) +\, \beta ^{2} \times \rho _{ij} \end{aligned}$$

(1)

where $\beta ^{2}$ represents the variance of noise vector and $\rho _{ij}$ is the kronecker delta function. Here $\Vert x_i - x_j\Vert$ quantifies the pairwise euclidean distance in the original $\textsc {G}$ - dimensional space, computed as:

$$\begin{aligned} \Vert x_{i} - x_{j}\Vert = \sqrt{ \sum _{g=1}^{\textsc {G}} (x_{i,g} - x_{j,g})^{2} }. \end{aligned}$$

(2)

where $\textsc {G}$ represents the number of active parameters.

From Equation (1), to reduce the energy consumption in covariance matrix computation, it is necessary to minimize the number of active parameters. This paper aims to select the optimal parameter set $\mathbb {K}$ from the active parameter set $\mathbb {G}$ that will be used in the prediction of sleep sensor parameter h. The optimal set $\mathbb {K}$ from the active parameter set for predicting the sleep parameter $h (h \in \mathbb {H})$ is defined as follows:

$$\begin{aligned} \mathbb {K}_h = \{\, { k \,|\, \;\forall \; k \in \textbf{K}[h] \;\;and\; \; \textbf{K}[h][k] = 1} \} \end{aligned}$$

(3)

where $\textbf{K}$ represents the matrix that contains all the optimal parameters used in the prediction of each sleep sensor parameter and $\textbf{K}[h][k]$ represents the value of matrix $\textbf{K}$ at the position h and k, where h and k represents the sleep and active parameters, respectively. By finding this optimal parameter set $\mathbb {K}_h$ from the active parameters, the proposed approach effectively minimizes the computational complexity and energy consumption of the edge node in the prediction of sleep sensor parameter h.

GPR-Based Cross-Correlated Parameter Prediction Model

The sleep sensor parameters are predicted using Gaussian Process Regression (GPR)-based prediction models at the edge node. By harnessing the predictive capabilities of GPR, the edge node adeptly fills in data gaps, thereby ensuring a comprehensive dataset for subsequent analysis¹⁷. The GPR model is comprised of a total of $\textsc {U} (\textsc {U}= |\mathbb {U}|)$ sub-models, corresponding to $\textsc {U}$ active-sleep pairs of sensor parameters. Each sub-model is designed to include $\textsc {H}_{i}$ where $(1 \le i \le \textsc {U})$ number of the regressor, aimed at predicting each parameter of $\mathbb {H}_{i}$. When the subset $\mathbb {G}_{j}$ is active during the measurement cycle, the selection of the $j^{th}$ sub-model becomes pertinent, as it is tailored to estimate each parameter of $\mathbb {H}_j$. Notably, in the GPR model, the prediction of each parameter h within $\mathbb {H}_j$ is done by strategically choosing an optimal parameter set $\mathbb {K}_h$ from the active sensor parameters. If $p^{th}$ parameter collected $N_p$ number of samples, then $\mathcal {Z}_p = \mathrm{I\!R}^{N_p \times 1}$ denotes the temporal measurement values of $p^{th}$ parameter and can be formulated as follows:

$$\begin{aligned} \mathcal {Z}_p = \mathcal {Y}_p + \mathcal {\eta }_p \end{aligned}$$

(4)

where $\mathcal {Y}_p$ is the actual signal vector and $\mathcal {\eta }_p$ represents the measurement noise vector associated with the $p^{th}$ sensor parameter. The noise vector components are independent and identically distributed, where $\mathcal {\eta } = N(0,\rho )$ for all sensor parameters.

In GPR prediction model the input matrix of the $h^{th}$ regressor of the $i^{th}$ submodel is $\textbf{I}^{i}_{\mathbb {K}_h} \in \mathrm{I\!R}^{m \times \textsc {K}_h}$ and the output vector is ${I}^{i}_{\mathbb {H}_h} \in \mathrm{I\!R}^{m \times 1}$, where m represents the number of collected samples by the sensor parameters. Each row of the matrix $\textbf{I}^{i}_{\mathbb {K}_h}$ contains one parameter vector. The $j^{th}$ row of the matrix $\textbf{I}^{i}_{\mathbb {K}_h}$ is represented as ${I}^{i,j}_{\mathbb {K}_h} = \{ {I}_{\mathbb {K}_h}(j,1), {I}_{\mathbb {K}_h}(j,2), \ldots \ldots {I}_{\mathbb {K}_h}(j, \textsc {K}) \}$. The Equation (4) for the active parameter $\textbf{I}^{i}_{\mathbb {K}_h}[j]$ and sleep sensor parameter ${I}^{i}_{\mathbb {H}_h}(j)$ can be written as, $\mathcal {Z}_{\textbf{I}^{i}_{\mathbb {K}_h}}(j) = \mathcal {Y}_{\textbf{I}^{i}_{\mathbb {K}_h}}(j) + \mathcal {\eta }_{\textbf{I}^{i}_{\mathbb {K}_h}}(j)$ and $\mathcal {Z}_{{I}^{i}_{\mathbb {H}_h}}(j) = \mathcal {Y}_{{I}^{i}_{\mathbb {H}_h}}(j) + \mathcal {\eta }_{{I}^{i}_{\mathbb {H}_h}}(j)$, respectively. For the test vector ${I}^{i}_{\mathbb {K}_h} (*)$, GPR finds the underlying function $\mathcal {F}^{i}_{h,*}$ for the $h^{th}$ regressor as:

$$\begin{aligned} \mathcal {Y}^{i}_{\mathbb {H}_h} (*) = \mathcal {F}_h(\textbf{I}^{i}_{\mathbb {K}_h}(*)) = \mathcal {F}^{i}_{h,*} \in \mathrm{I\!R} \end{aligned}$$

(5)

where $\mathcal {F}^{i}_{h} \sim N(0, \textbf{K}_{m \times m})$. $\textbf{K}_{m \times m}$ is the covariance matrix whose elements are derived from the Radial Basis Function (RBF) kernel. $\textbf{K}_{m \times m} = [k(x_i, x_j)]_{m\times m}$, where $k(x_i, x_j)$ represents the $i^{th}$ and $j^{th}$ sampling instance of the input matrix $\textbf{I}^{i}_{\mathbb {K}_h}$. The RBF kernel for the $h^{th}$ regressor is derived as follows:

$$\begin{aligned} k(x_i, x_j) = \exp \left( \dfrac{-1}{2l^{\prime 2}} \sum _{k=1}^{\textsc {K}_h} (x_{i,k} - x_{j,k})^{2} \right) +\, \beta ^{2} \times \rho _{ij} \end{aligned}$$

(6)

Now, the GPR prediction model is given by $\mathcal {F}^{i}_{h,*} \,\,| \,\, \textbf{I}^{i}_{\mathbb {K}_h}, {I}^{i}_{\mathbb {H}_h}, \textbf{I}^{i}_{\mathbb {K}_h}(*) \sim N ( \overline{\mathcal {F}^{i}_{h,*}}, Cov (\mathcal {F}^{i}_{h,*}) )$, where $\overline{\mathcal {F}^{i}_{h,*}}$ and $Cov (\mathcal {F}^{i}_{h,*}) )$ represents the mean function and covariance function and are derived from (A.1) and (A.2) of Appendix. The mean $(\overline{\mathcal {F}^{i}_{h,*}})$ and covarience $(Cov (\mathcal {F}^{i}_{h,*}) )$ are expressed^3,5,18,19 as:

$$\begin{aligned} \overline{\mathcal {F}^{i}_{h,*}}= & \textbf{K} \big ( \textbf{I}^{i}_{\mathbb {K}_h}, \textbf{I}^{i}_{\mathbb {K}_h}(*) \big ) \big [\textbf{K}( \textbf{I}^{i}_{\mathbb {K}_h}, \textbf{I}^{i}_{\mathbb {K}_h}) + \beta ^{2}I \big ]^{-1} ({I}^{i}_{\mathbb {H}_h}) \end{aligned}$$

(7)

$$\begin{aligned} Cov (\mathcal {F}^{i}_{h,*})= & k(\textbf{I}^{i}_{\mathbb {K}_h}(*), \textbf{I}^{i}_{\mathbb {K}_h}(*)) + \textbf{K} \big ( \textbf{I}^{i}_{\mathbb {K}_h}(*), \textbf{I}^{i}_{\mathbb {K}_h} \big ) \big [\textbf{K}( \textbf{I}^{i}_{\mathbb {K}_h}, \textbf{I}^{i}_{\mathbb {K}_h}) + \beta ^{2}I \big ]^{-1} \textbf{K} \big ( \textbf{I}^{i}_{\mathbb {K}_h}, \textbf{I}^{i}_{\mathbb {K}_h}(*) \big ) \end{aligned}$$

(8)

This GRP prediction model will be used in Section 4 to predict the sleep sensor parameter values at the edge node using the cross-correlated optimal parameters selected from active sensor parameters.

PROPOSED APPROACH

This section presents a $C_cBPS$ approach for selecting the optimal parameter set from active sensor parameters to predict sleep sensor parameter at the edge node. The edge node selects the optimal parameter set $\mathbb {K} \subseteq \mathbb {G}$, which has a strong correlation with sleep parameter $h (h \in \mathbb {H})$. The edge node predicts the sleep parameter h using the set $\mathbb {K}$ and employing the GPR prediction model.

Assume two sensing parameters a and b. If $|\textbf{CC}[a][b]| \ge 0.5$³, the parameters a and b are considered as correlated. The cross-correlation factor $\delta (\mathbb {G},h)$ determines the degree of cross-correlation of the active parameter set $\mathbb {G}$ with sleep parameter $h \; ( h \in \mathbb {H})$. The cross-correlation factor $\delta (\mathbb {G},h)$ is defined as follows:

$$\begin{aligned} \delta (\mathbb {G},h) = \dfrac{1}{\textsc {G}} \sum _{i=1}^{\mathbb {G}} |\textbf{CC}[i][h]|; \forall \; i \in \; \mathbb {G}. \end{aligned}$$

(9)

The performance of $C_cBPS$ approach is evaluated using the reconstruction error of the sensing parameters at the edge node. The reconstruction error for parameter s in the measurement cycle x is $Se_s^x$, then the reconstruction error of all parameters is as follows:

$$\begin{aligned} SE^x = \dfrac{1}{\textsc {S} \times Z} \sum _{s=1}^{\textsc {S}} \sum _{z=1}^{Z} Se_{s,z}^x\; \forall \; s \in \; \mathscr {S} \end{aligned}$$

(10)

where Z represents the number of the measurement cycle.

Table 1 Comparison of Computational Time Complexity of Different Parameter Selection Approaches.

Table 2 Description of Datasets used in the Experiments.

Table 3 Maximum, minimum, and average number of selected parameters from active sensor parameters using different non-optimal parameter selection approaches among all datasets.

Table 4 Comparison of performance metrics for different non-optimal parameter selection approaches with $C_cBPS$ approach among all datasets.

Table 5 Comparison of maximum, minimum, and average energy consumption at edge node using different parameter selection approaches among All Datasets.

Table 6 Statistical measures of actual vs predicted sleep sensor parameters value using $C_cBPS$ approach among all datasets.

Table 7 Categorization of actual vs. predicted graphs based on their average prediction error among all datasets.

Optimal subset of active parameters set

This section presents the proposed approach for selecting the optimal parameter set from active sensor parameters for each sleep sensor parameter as given in Algorithm 1. This algorithm iteratively selects an optimal parameter set for every sleep sensor parameter $i (i \in \mathbb {H})$ (Lines 2-27). In an iteration, first, we select two sets of active sensor parameters $\mathbb {X}$ and $\mathbb {W}$ that have a cross-correlation coefficient greater than or equal to 0.9 and 0.5 with sleep parameter i, respectively (Lines 5-12), as shown in Equations (11) and (12).

$$\begin{aligned} \begin{aligned} \mathbb {X} = \{ x \;|\; \forall \; x \in \mathbb {G} \wedge \; |\textbf{CC}[i][x]| \ge 0.9 \} \end{aligned} \end{aligned}$$

(11)

and

$$\begin{aligned} \begin{aligned} \mathbb {W} = \{ w \;|\; \forall \; w \in \mathbb {G} \wedge \; |\textbf{CC}[i][w]| \ge 0.5 \} \end{aligned} \end{aligned}$$

(12)

The reason for selecting the parameter set $\mathbb {W}$ is that only the active parameters with a correlation coefficient greater than or equal to 0.5 with i are considered in the prediction of the parameter i, and the parameters that exhibit a correlation less than 0.5 are discarded³ and parameter set $\mathbb {X}$ contains the active parameters that exhibit high correlation with the sleep sensor parameter i²⁰. In Equations (11) and (12), to get the correlation coefficient between parameters, we use the correlation matrix $\textbf{CC} \in \mathrm{I\!R}^{\textsc {S} \times \textsc {S}}$ which is already available for the given data samples of the parameter set.

Algorithm 1

Selection of active parameter for prediction of sleep sensor parameter

The proposed approach first checks whether there exist parameters that are highly correlated with sleep sensor parameter i; if yes, then it uses all the highly correlated active parameters to predict the sleep parameter i (Lines 14-18). Otherwise, it selects parameters from set $\mathbb {W}$, ensuring that the selected subset is small in size and captures the maximum information about the sleep sensor parameter (Lines 19-25). To select such parameters, we find the average of selected parameters using Equation (13) (Line 13).

$$\begin{aligned} \delta (\mathbb {W},i) = \dfrac{1}{\textsc {W}} \sum _{w=1}^{\mathbb {W}} \left| \textbf{CC}[i][w] \right| ; \forall \; w \in \; \mathbb {W} \; \end{aligned}$$

(13)

where $i \in \; \mathbb {H}$. This average will be a new threshold, and we will identify those parameters whose correlation with sleep sensor parameter i is greater than or equal to this threshold (Lines 20-25).

For other sleep sensor parameters, this algorithm will select the optimal active parameter set in a similar way. In this way, the algorithm returns matrix $\textbf{K}$, which contains optimal active parameters corresponding to each sleep sensor parameter.

Theoretical Analysis of Proposed Approach

In this section, the proposed approach is theoretically analyzed, and it is observed that the selected parameter set is both stable and Pareto optimal. The optimal parameter set $\mathbb {K}$ to predict the sleep sensor parameter $h (h \in \mathbb {H})$ is defined as follows:

$$\begin{aligned} \mathbb {K} = \{\, { k \,|\, \;\forall \; k \in \textbf{K}[h] \;\;and\; \; \textbf{K}[h][k] = 1} \} \end{aligned}$$

(14)

The $C_cBPS$ approach is analyzed using the Shapley value from the cooperative game. Shapley value is the contribution of each player based on their marginal contributions to all possible coalitions. Therefore, the allocation of Shapley value in the coalition is stable because the contribution value of each player in the coalition is greater than or equal to their worth. The Shapley value of player i is defined as follows:

$$\begin{aligned} \phi _{i} = \sum _{k \subseteq K \setminus \{i\}} \dfrac{|k|!(n-|k|-1)!}{n!} (v(k \cup \{i\})-v(k)) \end{aligned}$$

(15)

where $\mathbb {K}$ represents the set of all players and n is the total number of players in the cooperative game. v(k) represents the value/worth of the coalition of the set of players in the cooperative game.

Theorem 1

The allocation of sensors in sensor set $\mathbb {K} ( \mathbb {K} \subseteq \mathbb {G} \}$ using $C_cBPS$ approach is a stable allocation.

Proof

The allocation of sensors in the sensor set is considered a stable allocation if each sensor k of sensor set $\mathbb {K}$ has a Shapley value greater than or equal to their individual worth.

All the sensors of the sensor set $\mathbb {K}$ are considered the players of the cooperative game. The action profile of each player is the decision that the player takes to participate (play) in the coalition or not to participate (pass). The action profile of each player is defined as:

$$\begin{aligned} \text {Action} = \{ \text {Play}, \text {Pass} \} \end{aligned}$$

The worth function is the value of the coalition of the game. The worth function of the coalition depends on the factors that determine how strong the coalition can get the degree of cross-correlation while expanding the energy consumption in the prediction. This also includes the number of active parameters that strongly correlate with the sleep parameter. The worth function v(k) of any correlation k in the game is defined as follows:

$$\begin{aligned} v(k) = \rho (k,h) \times {\Psi (k)}^2- {e_h(k)} \end{aligned}$$

(16)

where $k \subseteq \mathbb {K}$. Terms $\rho (k,h) = \sum _{a \in k} \textbf{CC}[h][a]$ and $\Psi (k) = \Vert \{k \;|\; k \in \mathbb {K} \} \Vert$ represent the sum of the cross-correlation coefficient of all parameters and the total number of parameters in the coalition k, respectively. The term $e_h(k)$ represents the energy consumption in the prediction of sleep parameter h using k active parameter set.

The Shapley value of player i is determined as ;

$$\begin{aligned} \phi _{i}= & \sum _{k \subseteq \mathbb {K} \setminus \{i\}} \dfrac{|k|!(n-|k|-1)!}{n!} (v(k \cup \{i\})-v(k)) \end{aligned}$$

(17)

$$\begin{aligned} \phi _{i}= & \, \frac{|k_1|!(n-|k_1|-1)!}{n!} \big (v(k_1 \cup \{i\}) - v(k_1)\big ) + \frac{|k_2|!(n-|k_2|-1)!}{n!} \big (v(k_2 \cup \{i\}) - v(k_2)\big )\nonumber \\ & + \dots + \frac{|k_m|!(n-|k_m|-1)!}{n!} \big (v(k_m \cup \{i\}) - v(k_m)\big ). \end{aligned}$$

(18)

$$\begin{aligned} \phi _{i}= & \, \alpha _{1} \bigg [ \rho (k_1\cup \{i\}, h) \times {\Psi (k_1\cup \{i\})}^2- {e_h(k_1\cup \{i\})} - \left( \rho (k_1, h) \times {\Psi (k_1)}^2- {e_h(k_1)} \right) \bigg ]\nonumber \\ & + \, \alpha _{2} \bigg [ \rho (k_2\cup \{i\}, h) \times {\Psi (k_2\cup \{i\})}^2- {e_h(k_2\cup \{i\})} - \left( \rho (k_2, h) \times {\Psi (k_2)}^2- {e_h(k_2)} \right) \bigg ]\nonumber \\ & + \ldots \; \; \ldots \nonumber \\ & + \, \alpha _{m} \bigg [ \rho (k_m\cup \{i\}, h) \times {\Psi (k_m\cup \{i\})}^2- {e_h(k_m\cup \{i\})} - \left( \rho (k_m, h) \times {\Psi (k_m)}^2- {e_h(k_m)} \right) \bigg ] \end{aligned}$$

(19)

where $k_m \subseteq \mathbb {K} \setminus \{i\}$. The weight factor $\alpha _{i}$ is defined as:

$$\begin{aligned} \alpha _{i} = \frac{|k_i|!(n-|k_i|-1)!}{n!} \end{aligned}$$

(20)

from Equation (19);

Consider the $m_{th}$ term as an empty set, then the Shapley value of player i is defined as:

$$\begin{aligned} \begin{aligned} \phi _{i} =&\, \alpha _{1} \bigg [ \rho (k_1\cup \{i\}, h) \times {\Psi (k_1\cup \{i\})}^2- {e_h(k_1\cup \{i\})} - \left( \rho (k_1, h) \times {\Psi (k_1)}^2- {e_h(k_1)} \right) \bigg ] \\ +&\ldots \; \; \ldots + \, \dfrac{1}{n} \left( \rho (\{i\}, h) \times {\Psi (\{i\})}^2- {e_h(\{i\})} \right) \\ \end{aligned} \end{aligned}$$

(21)

In Equation (16), since v(k) is a convex function, therefore from Equations (16) and (21), $\forall \; k \subseteq \mathbb {K} \setminus \{i\}$;

$$\begin{aligned} \begin{aligned}&\left( \rho (k\cup \{i\}, h) \times {\Psi (k\cup \{i\})}^2- {e_h(k\cup \{i\})} \right) \ge \left( \rho (k, h) \times {\Psi (k)}^2- {e_h(k)} \right) \end{aligned} \end{aligned}$$

(22)

and

$$\begin{aligned} \begin{aligned} v\{i\} = \rho (\{i\}, h) \times {\Psi (\{i\})}^2- {e_h(\{i\})} \end{aligned} \end{aligned}$$

(23)

therefore, from Equations (22) and (23);

$$\begin{aligned} \phi _{i} \ge v\{i\} \;; \; \forall \; i \in \mathbb {K}, \; ( \mathbb {K} \subseteq \mathbb {G} ). \end{aligned}$$

(24)

Equation (24) shows that the active parameter set $\mathbb {K} ( \mathbb {K} \subseteq \mathbb {G} )$ is stable. Therefore, no sensor from the active parameter set $\mathbb {K} ( \mathbb {K} \subseteq \mathbb {G} )$ of the proposed $C_cBPS$ approach leaves the coalition. $\square$

Theorem 2

The active parameter set $\mathbb {K} ( \mathbb {K} \subseteq \mathbb {G} )$ is a Pareto optimal set.

Proof

An active parameter set $\mathbb {K} ( \mathbb {K} \subseteq \mathbb {G} )$ is Pareto optimal if it is impossible to add or remove any sensor parameter from $\mathbb {K} ( \mathbb {K} \subseteq \mathbb {G} )$ without either increasing the energy consumption in prediction or reducing the average cross correlation between the active parameter set and sleep sensor parameter. It also means that no modification to the set can improve one criterion without worsening the other.

$\mathbf {CASE-1:}$ A set $\mathbb {K} ( \mathbb {K} \subseteq \mathbb {G} )$ is Pareto optimal if there is no other set $\mathbb {K}' ( \mathbb {K}' \subseteq \mathbb {G} )$ $(\Vert \mathbb {K}'\Vert > \Vert \mathbb {K} \Vert )$, where the average cross-correlation of the selected active parameter set is higher and the energy consumption is equal to or lower as compared to the set $\mathbb {K} ( \mathbb {K} \subseteq \mathbb {G} )$.

Suppose that the active parameter set $\mathbb {K}$ is not Pareto optimal. Then there exists another set $\mathbb {K}'$ with;

$$\begin{aligned} \delta (\mathbb {K}', h) > \delta (\mathbb {K}, h) ;\; h\;\in \; \mathbb {H} \end{aligned}$$

(25)

and

$$\begin{aligned} e_{h}{(\mathbb {K}')} \le e_{h}{(\mathbb {K})} \end{aligned}$$

(26)

since prediction energy is a monotonic increasing function. Therefore, increasing the number of active parameters increases the prediction energy consumption. But, from our assumption,

$$\begin{aligned} \Vert \mathbb {K}'\Vert > \Vert \mathbb {K} \Vert \end{aligned}$$

(27)

from Equation (27):

$$\begin{aligned} e_{h}{(\mathbb {K}')} \quad > \quad e_{h}{(\mathbb {K})} \end{aligned}$$

(28)

Equation (28) contradicts our assumptions of Equation (26). Therefore, this concludes that there is no other set $\mathbb {K}'$ that has lower energy consumption compared to $\mathbb {K}$.

$\mathbf {CASE-2:}$ A set $\mathbb {K}$ is Pareto optimal if there is no other set $\mathbb {K}'$ $( \Vert \mathbb {K}'\Vert \le \Vert \mathbb {K} \Vert )$ where the degree of cross-correlation of the selected sensor is higher and the energy consumption is equal to or lower.

Assume that $\mathbb {K}$ is not Pareto optimal. Suppose that another set $\mathbb {K}'$ exists that achieves the same or lower energy consumption and a higher degree of cross-correlation as follows:

$$\begin{aligned} e_{h}{(\mathbb {K}')} \le e_{h}{(\mathbb {K})} \end{aligned}$$

(29)

and

$$\begin{aligned} \delta (\mathbb {K}', h) > \delta (\mathbb {K}, h); h \;\in \; \mathbb {H} \end{aligned}$$

(30)

since the sensor set is selected based on Equations (11)-(14), and the set $\mathbb {K}'$ and $\mathbb {K}$ both are the subsets of $\mathbb {G}$.

from Equation (13);

$$\begin{aligned} \delta (\mathbb {K}', h) \le \delta (\mathbb {K}, h) \end{aligned}$$

(31)

The above Equation (31) contradicts our assumption of Equation (30). Therefore, based on the studies of CASE-1 and CASE-2, this concludes that there is no other set $\mathbb {K}' (\mathbb {K}' \subseteq \mathbb {G})$ that has the degree of cross-correlation of the selected sensor is higher, and the energy consumption is equal to or lower. Therefore, the parameter set $\mathbb {K} ( \mathbb {K} \subseteq \mathbb {G} )$ is a Pareto optimal. $\square$

Figure 2

Heatmap of cross-correlation coefficient between all sensor parameters of all Datasets: (a) IESD-15, (b) IESD-30, (c) IESD-1H, (d) IESD-4H, (e) IESD-8H, (f) IESD-24H, (g) BTM-L-B, (h) IITM-D, (i) AN-RSPCB. {Created using Google Colab, Version: Python 3.10, https://colab.research.google.com/}.

Prediction of sleep parameter at edge node

In this section, we introduce an algorithm that uses an optimal parameter set to predict each sleep sensor parameter. As stated in the problem definition in Section III-B, the sensor node transmits active parameter data to the edge node at the end of each measurement cycle. After receiving data from the sensor node, the edge node applies Algorithm 1 to determine the matrix $\textbf{K}$, which contains the optimal active parameters used in the prediction of each sleep parameter.

Following the computation of $\textbf{K}$ using Algorithm 1, in Algorithm 2, the edge node predicts the sleep sensor parameters using optimal active parameters (Lines 1–24). To do this, first edge node sets the value of variable $u=1$ to train the model (Line 1). Now, the edge node selects the optimal active parameters from matrix $\textbf{K}$ for each sleep sensor parameter $h (h \in \mathbb {H})$ and trains the model using recently collected samples of optimal active parameters (Lines 3-10). After training the model for each sleep sensor parameter, change the value of variable $u=0$ (Line 12). Once the model gets trained for each sleep sensor parameter, the edge node uses the optimal parameter set $\mathbb {K}_h$ to predict the sleep sensor parameter h (Line 15-24).

Algorithm 2

Prediction of sleep parameter’s data at Edge Node

Computational complexity of $C_cBPS$ approach

In this section, the time complexity of the selection of an optimal parameter set from the active parameter set using proposed $C_cBPS$ approach is calculated and compared with other parameter selection approaches. $C_cBPS$ approach uses algorithm 1 to select the optimal parameter set to predict the sleep sensor parameter $h \; (h \in \mathbb {H})$.

Algorithm 1 consists of three FOR loops to select the optimal parameter set from the active sensor parameter set. The first FOR loop selects the predicted sleep sensor parameters, which takes $O(\textsc {H})$ time complexity. The second and third FOR are within the first for loop. The second FOR loop is used to select the intermediate set $\mathbb {W}$, which takes $O(\textsc {G})$ time complexity. The third FOR loop is for selecting the optimal parameters, which takes $O(\textsc {W})$ time complexity. Therefore, the overall time complexity of the proposed $C_cBPS$ approach to select the optimal parameter set is $O(\textsc {G}\textsc {H})$. Table 1 compares the time complexity of the proposed parameter selection approach with the state-of-the-art. In Table 1, $n_{iter}$ denotes the number of algorithm iterations, m represents the number of samples of the parameter set, and $\Vert S \Vert$ represents the number of unselected parameters from the parameter set. $n_{models}$ is the total number of machine learning models, C(M) represents the computational complexity of a machine learning model, and w represents the number of waterwheels in the waterwheel plant optimization technique.

Experimental setup

This section presents a description of dataset usage, data preprocessing methods, performance measure criteria, and a comparative analysis of various parameter selection approaches with the proposed approach.

Dataset description and prepossessing

Table 2 shows a description of the datasets used in this experiment, which were taken from different locations and at different sampling intervals²¹. Encompassing the timeframe spanning {To increase the dataset size in IESD-24H for effective model analysis, we include data from the last three months [1 November 2024 - 31 January 2025].} from 1 January 2025 to 31 January 2025, this dataset intricately examines various environmental parameters, notably concerning $\text {PM}2.5, \text {PM}10, \text {NO}, \text {CO}, \text {NO}2, \text {NH}3, \text {SO}2, \text {Benzene},$ and $\text {Ozone}$. It is acknowledged that the $\text {PM}2.5$ and $\text {PM}10$ sensors operate on a 60-minute interval. Therefore, to promise reliable data collection at 15 and 30-minute intervals, four and two identical $\text {PM}2.5$ and $\text {PM}10$ sensor values must be used. Initial preprocessing involves employing imputation techniques to address null values. The dataset is then partitioned into training and testing subsets. The training subset encompasses 24 days of data, while the testing subset includes 7 days of data. Ensuring dataset quality necessitates handling missing values, which is accomplished through data cleaning. To rectify missing attribute values, this process replaces them with the mean value of the attribute, ultimately contributing to a reliable dataset for analysis.

Performance measure

This study analyzed the performance of each approach using well-known assessment metrics including Mean Square Error (MSE), Mean Absolute Error (MAE), Root Mean Square Error (rMSE), and $R^2 \;\text {Score}$, which are summarized as follows:

Let $M_p$ and $\bar{M}_p$ represent the measurement vectors of the actual and predicted parameter sequences in connection to the parameter p.

MSE

It’s a commonly used metric to measure the average squared difference between actual and model-predicted data. The effectiveness of predictive models is frequently evaluated using it.

$$\begin{aligned} MSE = \frac{1}{N} \sum (M_p^x - \bar{M}_p^x)^2 \end{aligned}$$

(32)

rMSE

The accuracy of a prediction model is frequently assessed using the Root Mean Square Error (rMSE) statistic. It has the advantage of being expressed in the same unit as the original data, making it simpler to understand and compare to the actual values.

$$\begin{aligned} rMSE = \sqrt{\dfrac{1}{N} \sum (M_p^x - \bar{M}_p^x)^2} \end{aligned}$$

(33)

MAE

Mean Absolute Error (MAE) indicates the average absolute difference between predicted and actual values.

$$\begin{aligned} MAE = \dfrac{1}{N} \sum |M_p^x - \bar{M}_p^x| \end{aligned}$$

(34)

$R^2$ Score

It demonstrates how well the data adhere to the regression model.

$$\begin{aligned} R^2\; \text {Score} = 1 - \dfrac{\sum (M_p^x - \bar{M}_p^x)^2}{\sum ({M_p^x} - \hat{M}{_p^x} )^2} \end{aligned}$$

(35)

where $\hat{M}{_p^x}$ represents the mean of the actual data.

Comparison of Parameter Selection Approaches

The proposed parameter selection approach is compared to the traditional approach where all parameters are used to predict the sleep sensor parameters and other parameter selection approaches, including gradient descent (G.Descent)¹⁰, chi-squared (CHI-S)¹¹, binary water-wheel plant optimization (bWWPA)¹⁴, and cross-validated recursive feature elimination (RFECV)¹². In all the above parameter selection approaches, the chi-squared (CHI-S)¹¹ approach selects the static (fixed) number of active sensor parameters for each sleep sensor parameter. To ensure a fair and consistent comparative analysis, we set this fixed number equal to the average number of active parameters.

RESULTS AND DISCUSSION

This section discussed the comparative analysis of proposed $C_cBPS$ approach with the other state-of-the-art parameter selection approaches. Simulation results show that $C_cBPS$ approach performs superiorly in all comparison metrics.

Figure 3

Selected parameters from active sensor parameter by different non-optimal parameter selection approaches among all datasets: (a) IESD-15, (b) IESD-30, (c) IESD-1H, (d) IESD-4H, (e) IESD-8H, (f) IESD-24H, (g) BTM-L-B, (h) IITM-D, (i) AN-RSPCB. {Created using Google Colab, Version: Python 3.10, https://colab.research.google.com/}.

Figure 4

Total energy consumption comparison using different parameter selection approaches at edge node among all datasets: (a) IESD-15, (b) IESD-30, (c) IESD-1H, (d) IESD-4H, (e) IESD-8H, (f) IESD-24H, (g) BTM-L-B, (h) IITM-D, (i) AN-RSPCB. {Created using Google Colab, Version: Python 3.10, https://colab.research.google.com/}.

Figure 5

Graph of actual vs predicted sleep sensor parameters value using $C_cBPS$ approach on IESD-15 Dataset: (a) PM2.5, (b) PM10, (c) CO, (d) $\text {SO}2$. {Created using Google Colab, Version: Python 3.10, https://colab.research.google.com/}.

Figure 6

Graph of actual vs predicted sleep sensor parameters value using $C_cBPS$ approach on IESD-30 Dataset: (a) PM2.5, (b) PM10, (c) CO, (d) $\text {SO}2$, (e) $\text {NH}3$. {Created using Google Colab, Version: Python 3.10, https://colab.research.google.com/}.

Figure 7

Graph of actual vs predicted sleep sensor parameters value using $C_cBPS$ approach on IESD-1H Dataset: (a) PM2.5, (b) PM10, (c) CO, (d) $\text {SO}2$, (e) $\text {NH}3$. {Created using Google Colab, Version: Python 3.10, https://colab.research.google.com/}.

Figure 8

Graph of actual vs predicted sleep sensor parameters value using $C_cBPS$ approach on IESD-4H Dataset: (a) PM2.5, (b) PM10, (c) CO, (d) $\text {SO}2$, (e) NO, (f) $\text {NO}2$, (g) $\text {NH}3$. {Created using Google Colab, Version: Python 3.10, https://colab.research.google.com/}.

Figure 9

Graph of actual vs predicted sleep sensor parameters value using $C_cBPS$ approach on IESD-8H Dataset: (a) PM2.5, (b) CO, (c) $\text {SO}2$, (d) NO, (e) $\text {NO}2$, (f) $\text {NH}3$. {Created using Google Colab, Version: Python 3.10, https://colab.research.google.com/}.

Figure 10

Graph of actual vs predicted sleep sensor parameters value using $C_cBPS$ approach on IESD-24H Dataset (a) PM2.5, (b) PM10, (c) CO, (d) $\text {SO}2$, (e) NO, (f) $\text {NO}2$, (g) $\text {NH}3$. {Created using Google Colab, Version: Python 3.10, https://colab.research.google.com/}.

Figure 11

Graph of actual vs predicted sleep sensor parameters value using $C_cBPS$ approach on BTM-L-B Dataset: (a) NO (b) $\text {NO}2$, (c) $\text {SO}2$. {Created using Google Colab, Version: Python 3.10, https://colab.research.google.com/}.

Figure 12

Graph of actual vs predicted sleep sensor parameters value using $C_cBPS$ approach on IITM-D Dataset: (a) PM2.5, (b) PM10. {Created using Google Colab, Version: Python 3.10, https://colab.research.google.com/}.

Figure 13

Graph of actual vs predicted sleep sensor parameters value using $C_cBPS$ approach on AN-RSPCB Dataset: (a) PM2.5, (b) PM10, (c) CO, (d) NO, (e) $\text {NO}2$, (f) $\text {NH}3$ (g) Ozone (h) Benzene. {Created using Google Colab, Version: Python 3.10, https://colab.research.google.com/}.

Parameter setting

This part discusses the simulation results of proposed $C_cBPS$ approach on different datasets, as outlined in Part IV. To simulate the proposed approach, air pollution monitoring datasets²¹ composed of nine sensors measuring the unique parameters $( \text {PM}2.5, \text {PM}10, \text {NO}, \text {CO}, \text {NO}2, \text {NH}3, \text {SO}2, \text {Benzene},\text {Ozone} )$ from the environment is considered. Figure 2 shows the heat map of the cross-correlation coefficient between all sensor parameters that show how sensor parameters are correlated in the parameter set. The simulations are performed on a Dell Precision Workstation T7910, which is equipped with two CPU sockets containing eight Dual Intel Xeon Processors E5-2667 (8C 16HT, 20 MB Cache, 3.2 GHz) apiece and 256 GB of RAM. This workstation’s operating system, Ubuntu 20.4, was chosen for its dependability and performance. To validate the proposed strategy, simulations are conducted over 100 measurement cycles to mitigate the impact of extreme scenarios.

Performance analysis

This section analyses the performance of the proposed $C_cBPS$ parameter selection approach with state-of-the-art parameter selection approaches. The comparison is focused on three essential criteria: (1) the number of active sensor parameters selected by each approach, (2) the total energy consumption at the edge node, and (3) the accuracy in predicting sleep sensor parameter values using $C_cBPS$ approach. These metrics highlight the efficiency of the proposed $C_cBPS$ approach over other state-of-the-art parameter selection approaches.

Comparison of parameter selection approach

The performance of $C_cBPS$ approach is compared with the existing state-of-the-art parameter selection approach. Figure 3 compares the number of selected active parameters and Table 3 shows the maximum, average, and minimum number of selected active parameters used in the prediction of sleep sensor parameters using the proposed and other state-of-the-art parameter selection approaches on all datasets. From Figure 3 and Table 3, our observations are summarized as follows:

• 1. The motivation behind the $C_cBPS$ parameter selection approach is to select the highly correlated parameters for predicting sleep sensor parameters. When highly correlated parameters exist in predicting sleep sensor parameters, $C_cBPS$ selects all the highly correlated parameters for the prediction as shown in Equation 11. For example, in the IESD-4H dataset, Figure 3d, if NO, $\text {NH}3$, $\text {SO}2$, CO, Ozone, and Benzene are active to sense the environmental parameters in a measurement cycle, and PM2.5, PM10, and $\text {NO}2$ are in sleep mode. The proposed approach selects only CO to predict sleep parameter PM2.5 because among all active parameters, CO exhibits a high correlation with PM2.5. (Corr(PM2.5, CO) = 0.91). On the other hand, CHI-S¹¹ uses a static number of parameters, which limits their ability to capture dependencies. The G.Descent¹⁰ technique focuses on discarding disparaging parameters from the active parameter set. Therefore, to preserve the dependencies among parameters, the G.Descent technique requires more number of active parameters to predict the sleep sensor parameter.

• 2. In Figure 3a–f,i where parameters in the active parameter set exhibit a medium²⁰ correlation with the sleep sensor parameters, the proposed approach selects only those that exhibit a correlation greater than the average correlation with all active parameters to the sleep sensor parameters as shown in Equation 12. The number of selected parameters by the $C_cBPS$ approach is always less than or equal to the CHI-S and G.Descent approach. For example, in the IESD-1H dataset, Figure 3(c), if NO, $\text {NO}2$, $\text {NH}3$, $\text {SO}2$, Ozone, and Benzene are active to sense the environmental parameters in a measurement cycle, and PM2.5, PM10, and CO are in sleep mode. The proposed approach selects only $\text {SO}2$ to predict sleep parameter CO because, among all active parameters, $\text {SO}2$ exhibits a correlation greater than or equal to the average correlation of all active sensor parameters. Whereas in the CHI-S parameter selection approach, $\text {NH}3$, $\text {SO}2$, and Benzene have CHI-S values greater than the average CHI-S value of all active parameters, and similarly gradient descent approach, $\text {NH}3$, $\text {SO}2$, Benzene, and Ozone are selected to predict the sleep sensor parameter CO.

Table 4 shows the comparison of performance metrics of all parameter selection approaches on different datasets. The result shows that the $C_cBPS$ approach surpasses all error metrics, such as MSE, rMSE, MAE, and $R^2$ Score because among all the parameter selection approaches, the $C_cBPS$ approach selects the parameters that are highly correlated with the sleep sensor parameters, thus it reduces the errors in the prediction of sleep sensor parameters.

Comparison of total energy consumption at edge node

This section discusses the total energy consumption of all parameter selection approaches over all datasets. The energy consumption is defined as the sum of the amount of energy used to select the parameter set from the active sensor parameters and use those parameters to predict the sleep sensor parameter at the edge node. Let’s assume that processing speed or hardware performance remains constant or negligible in their variation to study the impact of the number of parameters in the prediction. Let us assume that $'\Delta '$ is the energy consumed in the computation in unit time. The prediction energy $(e_{pred})$ is defined as follows:

$$\begin{aligned} e_{pred} = \Delta \times N_{\mathbb {K}} (\mathbb {K} \times T_{dist} + T_{kernal} + T_{mv}) \end{aligned}$$

(36)

where $N_{\mathbb {K}}$ represents the number of samples collected by active sensors, $\mathbb {K}$ represents the number of parameters, and $T_{dist}, T_{kernal},$ and $T_{mv}$ represent the time to compute the distance of data points, kernel matrix, and mean and variance of new data points, respectively. Now, the total energy consumption at the edge node is defined as follows:

$$\begin{aligned} ENERGY_{Edge} = \Delta \times T_{selection} + e_{pred} \end{aligned}$$

(37)

where $T_{selection}$ is the time consumed to select the parameter set from the active sensor parameters. We assume the value of $\Delta$ =1mJ, which will be used as the basis for our calculations.

Figure 4 and Table 5 demonstrate the total energy consumption at the edge node by using different approaches on various datasets. The result is depicted by moving average with a window size of 10 to reduce the variations in the graph and make it more readable. The observations are summarized as follows:

• 1. The $C_cBPS$ approach takes minimum energy in the prediction of sleep sensor parameters compared to state-of-the-art parameter selection approaches.

• 2. The CHI-S approach selects the static parameters for the prediction of sleep sensor parameters, limiting their performance in the parameter selection. The G.Descent method eliminates only the parameters that do not exploit the dependencies within the input parameters and also takes more computational time to select the parameters from the active parameters. The RFECV method takes every pair of input data to select the best parameter set. Therefore, the RFECV method requires more computation in different machine learning model training, which increases its computation time and energy in the parameter selection process. The bWWPA algorithm optimizes the parameter selection problem using a binary waterwheel plant optimization algorithm. This algorithm itself can take more computation and energy in the optimization process. As a result, RFECV, and bWWPA approaches select parameters by increasing the energy at the edge node.

• 3. Considering Figure 3 and utilizing Equation (37), $C_cBPS$ the approach achieves approximately $\{30.90, 9.23, 16.17, 9,70, 8.10, 27.40, 6.50, 34.20, 7.50\}$ substantial energy reductions compared to the original approach, where all the active parameters are used in the prediction of the sleep sensor parameters on $\{$IESD-15, IESD-30, IESD-1H, IESD-4H, IESD-8H, IESD-24H, BTM-L-B, IITM-D, AN-RSPCB $\}$ datasets, respectively.

Accuracy of predicted sleep sensor parameters using $C_cBPS$ approach

This section assesses the accuracy of $C_cBPS$ parameter selection approach to predict sleep sensor parameters over all datasets. To evaluate prediction accuracy, we compare the actual (A) values of sleep sensor parameters to the predicted (P) values acquired by the proposed $C_cBPS$ approach. Figures 5, 6, 7, 8, 9, 10, 11, 12 and 13 visually depict the model’s accuracy of the actual vs. predicted parameters value graph in reconstructing the original parameter sequence using $C_cBPS$ approach on all the datasets. In these figures, we consider only those parameters that are in sleep mode in at least one measurement cycle. The parameters that are active in each measurement cycle are not considered in the graph. Table 6 shows the statistical measure of each predicted parameter compared to the actual parameter over all the datasets. This measure includes the minimum value (Min), maximum value (Max), mean value (Mean), median value (Median), standard deviation (std), and variance (Varience) of the distribution of the actual and predicted sleep sensor parameters. We study the performance of the $C_cBPS$ approach by dividing the graphs into the following categories which are summarized as follows:

• 1. The first category shows a high degree of alignment, with a significant match between the actual and the predicted sleep sensor parameter and having the average error between the actual and predicted parameters is less than $0.05\%$, showing an efficient model approximation.

• 2. The second category has a moderate fit, suggesting a good approximation with slight deviations that might be due to built-in difficulties in the dataset or modeling assumptions, and the average error between the actual and predicted parameters ranges from $0.05\% - 0.5\%$.

• 3. The third category shows a fair approximation, demonstrating the model’s ability to catch essential patterns despite inevitable differences and having the average error between the actual and predicted parameters greater than $0.5\%$.

Table 7 shows the parameters that lie within these categories over all the datasets. These results highlight the effectiveness of the proposed approach because it accomplishes precise signal reconstruction with minor errors for all sleep parameter values.

Conclusion

This paper presents a cross-correlation-based parameter selection $(C_cBPS)$ approach. The proposed approach utilizes parameter cross-correlation to select the highly correlated parameters to predict each sleep sensor parameter at the edge node. The effectiveness of the $C_cBPS$ approach has been validated theoretically. Simulations are also performed on nine publicly available environmental datasets, collected from different geographical locations and time intervals. The proposed approach outperforms the existing state-of-the-art parameter selection approaches and demonstrates an improvement of $6.5 \%$ - $34.2 \%$ in energy efficiency in the prediction of sleep sensor parameters at the edge node among all datasets.