Bayesian model averaging based deep learning forecasts of inpatient bed occupancy in mental health facilities

Abstract

Mental health disorders affect over 15% of the global working-age population, contributing to an annual economic loss of approximately USD 1 trillion due to diminished productivity and increased healthcare expenditures. In India, the post-pandemic surge in hospitalizations has placed additional strain on mental health infrastructure, exacerbating an already significant treatment gap. Overcrowding and inadequate forecasting mechanisms have resulted in occupancy rates that exceed hospital capacity, underscoring the urgent need for predictive tools to support admission planning and resource allocation. This study introduces a novel forecasting framework that applies Bayesian Model Averaging (BMA) with Zellner’s g-prior used here for the first time alongside deep learning models for predicting weekly bed occupancy at India’s second-largest mental health hospital. Time series data from 2008 to 2024 were used to train six models: Time Delay Neural Networks (TDNN), Recurrent Neural Networks (RNN), Gated Recurrent Units (GRU), Long Short-Term Memory (LSTM), Bidirectional LSTM (BiLSTM), and Bidirectional GRU (BiGRU). Model performance was optimized using random search (RS) and grid search (GS) hyperparameter tuning, allowing the framework to account for model uncertainty while improving predictive accuracy and consistency. Among all models, BiLSTM with GS tuning and BMA-GS model showed the best forecasting performance for bed-occupancy, achieving 98.06% accuracy (MAPE: 1.939%) and effectively capturing weekly fluctuations within ±13 beds. In contrast, RS-tuned models yielded higher errors (MAPE: 2.331%). Moreover, the average credible interval width decreased from 16.34 under BMA-RS to 13.28 with BMA-GS, indicating improved forecast precision and reliability. This study demonstrates that embedding Bayesian statistics specifically BMA with Zellner’s g-prior into deep learning architectures offers a robust and scalable solution for forecasting hospital bed occupancy. The proposed framework enhances predictive accuracy and reliability, supporting data-driven planning for hospital administrators and policymakers. It aligns with the objectives of India’s National Mental Health Programme (NMHP) and Sustainable Development Goal 3, advancing equitable and efficient access to mental healthcare.

Introduction

Mental health is often misunderstood, under-resourced, and deprioritized compared to physical health, despite its profound impact on individuals, communities, and the global economy^1,2. Mental health encompasses conditions such as mental disorders and psychosocial disabilities, which can significantly impair functioning and quality of life. Addressing mental health involves three key objectives: prevention, protection and promotion, and support, as outlined by global health initiatives^3,4. As of 2022, 60% of the world’s population is employed, with 61% working in the informal economy, often in environments lacking adequate health protections. Globally, 15% of working-age adults live with a mental disorder, with 301 million affected by anxiety, 280 million by depression, and 703,000 suicides recorded in 2019. These mental health conditions impose severe societal and economic costs, including 50% of total societal costs due to indirect factors like productivity loss, 12 billion working days lost annually, and approximately USD 1 trillion in global economic losses due to depression and anxiety⁵.

In India, the prevalence of mental health disorders is a growing concern. The National Mental Health Survey (NMHS) 2015-16 reported that approximately 10.6% of adults over the age of 18 suffer from mental disorders. Notably, the treatment gap for these disorders ranges between 70% and 92%, indicating a substantial portion of the affected population does not receive adequate care. The prevalence of mental morbidity is higher in urban metropolitan areas (13.5%) compared to rural regions (6.9%) and urban non-metro areas (4.3%). Additionally, the National Crime Records Bureau reported a suicide rate of 12.4 per lakh population in 2022, reflecting a slight increase from 12.0 in 2021⁶.

The increasing prevalence of mental health conditions could also contribute to reduced workforce productivity, higher absenteeism, and an escalating demand for hospital admissions. However, the country’s mental health infrastructure remains strained, with limited hospital beds, understaffed facilities, and inefficient resource allocation, leading to overcrowding and delayed interventions. These challenges may not only hinder patient outcomes but also place an economic burden on healthcare systems and the nation’s broader development goal of becoming a prominent and leading global economy⁷. To address these issues effectively, accurate forecasting of hospital bed occupancy for mental health services is essential. Predictive modeling can enable hospitals to optimize resource allocation, anticipate patient influx, and reduce emergency admissions, thereby improving service efficiency and accessibility. By leveraging data-driven forecasting, India can enhance mental health infrastructure planning, ensure timely interventions, and align with global initiatives such as those advocated by the World Health Organization (WHO)⁸ and the United Nations (UN)⁹.

In response to the mental health crisis, the Government of India has launched initiatives such as the National Tele Mental Health Programme (Tele-MANAS) on October 10, 2022, to improve access to quality mental health counseling and care services. As of July 23, 2024, 36 States and Union Territories have established 53 Tele-MANAS Cells, handling over 1.76 million calls⁶. Despite these efforts, the high treatment gap and increasing demand for mental health services necessitate effective resource management strategies, including accurate forecasting of hospital bed occupancy, to enhance patient care and optimize healthcare resources.

Related works

Forecasting methods, ranging from traditional statistical models to advanced machine learning (ML) approaches, have been applied to various healthcare settings. Time-series models such as ARIMA and SARIMAX have been extensively utilized, particularly for short-term predictions, demonstrating significant improvements in forecasting accuracy with additional explanatory variables and integration with external factors. For example, SARIMAX models have shown up to a 60% enhancement in mean squared error (MSE) for short-term predictions¹⁰. Multi-model combinations of SARIMAX, multi-layer perceptrons (MLP), and linear regression models have also proven effective for daily bed occupancy forecasting, allowing healthcare facilities to plan capacity and resources more strategically¹¹.

Machine learning and deep learning (DL) approaches have emerged as promising alternatives to traditional models due to their ability to identify complex patterns in large datasets. Recurrent Neural Networks (RNNs), including their advanced variants such as Long Short-Term Memory networks (LSTM) and Gated Recurrent Units (GRU), have shown significant improvements in time-series forecasting accuracy. Studies report that RNNs achieved a mean absolute percentage error (MAPE) of 6.24%, demonstrating their competitiveness with other predictive models in hospital settings¹². Hybrid methods combining DL models with epidemiological models, such as SEIR (Susceptible-Exposed-Infected-Recovered), have further outperformed traditional models in scenarios like ICU bed forecasting during the COVID-19 pandemic, particularly post-vaccine rollout¹³.

Process mining, integrated with ML, has been explored to enhance the accuracy of patient flow and bed occupancy predictions by embedding temporal knowledge into the models¹⁴. In addition, scalable frameworks such as Monte Carlo simulations have been employed to manage the stochastic nature of bed occupancy during crises like the COVID-19 pandemic, enabling real-time operational adjustments¹⁵. These frameworks emphasize the balance between model complexity and accuracy, particularly for long-term trend analysis and capacity planning in aging populations¹⁶. While advanced ML methods have proven effective, simpler techniques such as compartmental flow models and seasonal forecasting patterns continue to hold value for their efficiency and ease of implementation. These approaches have been used to address misconceptions around bed planning and optimize hospital workflows in resource-constrained settings^17,18.

Research has also delved into specific scenarios, such as managing patient flows in postnatal and surgical departments. For instance, studies have analyzed trends in cesarean section rates and the subsequent decline in postnatal bed utilization¹⁹. Queue theory and simulation models, incorporating tools like Petri nets, have been applied to optimize ICU bed occupancy during emergency scenarios, aiding in crisis management²⁰. Similarly, forecasting tools tailored for pandemic responses have supported hospitals in making swift, data-driven decisions for managing bed capacity and patient transfers^21,22. Real-time forecasting models, especially during the COVID-19 pandemic, have demonstrated their importance in predicting patient surges and avoiding critical bed shortages. These models have been instrumental in reducing last-minute cancellations and optimizing capacity management, particularly in contexts involving nonelective bed admissions²³. Time-series methods like the Box-Jenkins approach and queuing theory have also been pivotal in maintaining optimal occupancy rates (82–85%) to minimize complications such as hospital-acquired infections^24,25.

Despite the extensive research in general hospitals and emergency departments, studies specifically addressing mental health hospitals remain scarce. This gap is significant given the unique challenges of managing prolonged and recurrent hospital stays for mental health patients.

Fig. 1

Proposed methodology workflow for weekly bed occupancy forecasting in a mental health hospital.

The following key contributions outline the study’s significance:

• To the best of our knowledge, this is the first study to apply Bayesian Model Averaging (BMA) with Zellner’s g-prior to the problem of forecasting mental health hospital bed occupancy, specifically within the Indian healthcare context. This approach addresses parameter uncertainty and balances predictive variance, thereby enhancing the reliability of occupancy forecasts for resource management.

• We propose a comprehensive deep learning framework tailored for mental health bed occupancy forecasting that systematically evaluates six advanced architectures viz., TDNN, RNN, GRU, LSTM, BiGRU, and BiLSTM on a large-scale real-world dataset.

• We employ both random search and exhaustive grid search for hyperparameter optimization, ensuring rigorous model tuning beyond standard practices. Performance is assessed using robust metrics (RMSE, MAE, MAPE) and the Diebold–Mariano (DM) test for statistical comparison, adapting these established methods to the mental health forecasting domain.

• We analysed the scalability and computational efficiency of the proposed models, offering actionable guidance for deployment in operational hospital systems. This bridges the gap between academic modeling and real-world implementation.

Methodology

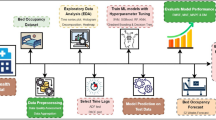
This study employs six advanced deep learning (DL) models: Time Delay Neural Network (TDNN), Recurrent Neural Network (RNN), Gated Recurrent Unit (GRU), Long Short-Term Memory (LSTM), Bidirectional LSTM (BiLSTM), and Bidirectional GRU (BiGRU) to forecast weekly bed occupancy in mental health hospitals. The models were trained and evaluated using data from India’s second-largest mental health hospital, covering the period from 2008 to 2024. Below, we outline the data preprocessing steps and the deep learning models used in this study. The overall methodology adopted for this study is illustrated in Fig. 1 .

Data preprocessing

No missing values were found in the dataset. To capture temporal dependencies, we incorporated lag features, setting lag window to 52 weeks. This ensures that deep learning models receive structured input reflecting long-term seasonality and trends. The Partial Autocorrelation Function (PACF) plot confirmed the significance of including these lags. The dataset was normalized to improve convergence and then chronologically split into training (70%), validation (15%), and test (15%) sets for model evaluation using Python’s TimeSeriesSplit.

ARIMA and SARIMA baselines

To benchmark the proposed deep learning and BMA framework, we implemented two classical time-series models: ARIMA and SARIMA.

ARIMA model orders (p, d, q) were selected using AIC minimization, residual diagnostics, and rolling forecast validation. The optimal ARIMA configuration yielded (3, 1, 1) with differencing, but performance remained limited due to inability to capture seasonality.

SARIMA extended ARIMA by explicitly modeling weekly seasonal patterns, with the best-fit model specified as $(3,0,1)(1,0,1)_{52}$, where 52 indicates weekly seasonality over yearly cycles. Both models were trained on the same data splits as the deep learning models to ensure comparability, and evaluated using RMSE, MAE, and MAPE.

Deep learning models

Deep learning (DL) models excel at uncovering complex temporal patterns in time-series data without requiring manual feature engineering. This study utilizes state-of-the-art architectures, including GRU, LSTM, RNN, CNN, BiGRU, and BiLSTM, each designed to capture sequential dependencies effectively. These models leverage recurrent connections and gating mechanisms to retain long-term dependencies, making them well-suited for forecasting hospital bed occupancy.

TDNN architecture

TDNN model is designed to process sequential data by capturing temporal dependencies through fixed-size input windows. The input sequence $X = [x_1, x_2, \dots , x_T]$ is divided into overlapping windows of size $w$, creating subsequences:

$$\begin{aligned} X_w^t = [x_t, x_{t+1}, \dots , x_{t+w-1}] \quad \text {for } t = 1, 2, \dots , T-w+1. \end{aligned}$$

(1)

Here, $w$ represents the time delay window size.

For each input window, a convolutional operation is applied:

$$\begin{aligned} h_t^{(1)} = \sigma \left( \sum _{i=0}^{w-1} W_i^{(1)} x_{t+i} + b^{(1)}\right) , \end{aligned}$$

(2)

where $W_i^{(1)}$ are the weights of the first convolutional layer, $b^{(1)}$ is the bias term, $\sigma$ is the activation function (e.g., ReLU), and $h_t^{(1)}$ is the output of the first layer.

For $L$ hidden layers, the output of the $l$-th layer is computed as:

$$\begin{aligned} h_t^{(l)} = \sigma \left( \sum _{j=0}^{k_l-1} W_j^{(l)} h_{t+j}^{(l-1)} + b^{(l)}\right) , \end{aligned}$$

(3)

where $k_l$ is the kernel size for the $l$-th layer, $W_j^{(l)}$ are the weights of the $l$-th layer, and $b^{(l)}$ is the bias term.

The final output layer maps the learned features to the predicted bed occupancy:

$$\begin{aligned} \hat{y}_t = \sum _{m=1}^{M} W_m^{(L+1)} h_t^{(L)} + b^{(L+1)}, \end{aligned}$$

(4)

where $W_m^{(L+1)}$ are the weights of the output layer, $b^{(L+1)}$ is the bias term, and $\hat{y}_t$ is the predicted value for time step $t$.

The model is optimized using the mean squared error (MSE) loss function:

$$\begin{aligned} \mathcal {L} = \frac{1}{N} \sum _{t=1}^{N} \left( y_t - \hat{y}_t\right) ^2, \end{aligned}$$

(5)

where $y_t$ is the actual value and $N$ is the total number of predictions.

This architecture effectively captures temporal dependencies in the input sequence by leveraging convolutional layers with shared weights over time windows, ensuring efficient learning and robust predictions.

RNN architecture

The Recurrent Neural Network (RNN) is a deep learning architecture designed to handle sequential data by maintaining a hidden state that captures information from previous time steps. Given an input sequence $X = [x_1, x_2, \dots , x_T]$, the RNN processes one element of the sequence at each time step. At each time step $t$, the hidden state $h_t$ is updated based on the current input $x_t$ and the previous hidden state $h_{t-1}$, as shown in figure 2:

$$\begin{aligned} h_t = \sigma \left( W_h h_{t-1} + W_x x_t + b_h\right) , \end{aligned}$$

(6)

where $W_h$ represents the weight matrix for the hidden state, $W_x$ represents the weight matrix for the input, $b_h$ is the bias term, and $\sigma$ is the activation function, commonly a hyperbolic tangent ($\tanh$) or ReLU function. The hidden state $h_t$ summarizes the information from the sequence up to time step $t$.

Fig. 2

Architecture of RNN cell.

The output at each time step $t$ is computed as:

$$\begin{aligned} \hat{y}_t = W_y h_t + b_y, \end{aligned}$$

(7)

where $W_y$ is the weight matrix of the output layer, $b_y$ is the bias term, and $\hat{y}_t$ is the predicted value at time step $t$.

The RNN is trained by minimizing a loss function, such as the Mean Squared Error (MSE):

$$\begin{aligned} \mathcal {L} = \frac{1}{N} \sum _{t=1}^{N} \left( y_t - \hat{y}_t\right) ^2, \end{aligned}$$

(8)

where $y_t$ is the actual value, $\hat{y}_t$ is the predicted value, and $N$ is the total number of predictions.

The key advantage of the RNN lies in its recurrent connections, which enable it to capture temporal dependencies in sequential data. However, due to challenges such as vanishing or exploding gradients, standard RNNs may struggle with long-term dependencies. Advanced variants like Long Short-Term Memory (LSTM) networks and Gated Recurrent Units (GRUs) address these issues, making them more suitable for handling complex sequential tasks. Despite these challenges, RNNs remain a foundational architecture for modeling sequential data effectively.

LSTM architecture

LSTM model is an advanced variant of the Recurrent Neural Network (RNN) designed to address the vanishing gradient problem, allowing the model to capture long-term dependencies in sequential data. Unlike standard RNNs, LSTMs use a gating mechanism to regulate the flow of information through the network²⁶.

Given an input sequence $X = [x_1, x_2, \dots , x_T]$, the LSTM processes one time step at a time, maintaining a hidden state $h_t$ and a cell state $c_t$ that carries long-term memory. The key components of the LSTM are shown in figure 3 and mathematically described in the following equations below.

At each time step $t$, the LSTM computes the following gates and states:

The forget gate determines how much information from the previous cell state $c_{t-1}$ should be retained:

$$\begin{aligned} f_t = \sigma \left( W_f x_t + U_f h_{t-1} + b_f\right) , \end{aligned}$$

(9)

where $W_f$ and $U_f$ are the weight matrices for the input $x_t$ and hidden state $h_{t-1}$, respectively, $b_f$ is the bias term, and $\sigma$ is the sigmoid activation function.

The input gate decides how much new information to add to the cell state:

$$\begin{aligned} i_t = \sigma \left( W_i x_t + U_i h_{t-1} + b_i\right) . \end{aligned}$$

(10)

The candidate cell state computes potential new information:

$$\begin{aligned} \tilde{c}_t = \tanh \left( W_c x_t + U_c h_{t-1} + b_c\right) . \end{aligned}$$

(11)

The cell state is updated by combining the retained information from the previous state and the new candidate information:

$$\begin{aligned} c_t = f_t \odot c_{t-1} + i_t \odot \tilde{c}_t, \end{aligned}$$

(12)

where $\odot$ denotes element-wise multiplication.

The output gate determines how much of the cell state to expose as the hidden state:

$$\begin{aligned} o_t = \sigma \left( W_o x_t + U_o h_{t-1} + b_o\right) . \end{aligned}$$

(13)

Finally, the hidden state is updated as:

$$\begin{aligned} h_t = o_t \odot \tanh (c_t). \end{aligned}$$

(14)

Fig. 3

Architecture of an LSTM cell.

The output at time step $t$ is computed as:

$$\begin{aligned} \hat{y}_t = W_y h_t + b_y, \end{aligned}$$

(15)

where $W_y$ is the weight matrix of the output layer, $b_y$ is the bias term, and $\hat{y}_t$ is the predicted value.

The gating mechanisms in LSTMs enable the model to retain and utilize relevant information over long time sequences, making it highly effective for sequential tasks such as bed occupancy forecasting. Its ability to handle both short-term and long-term dependencies makes it a preferred choice for time-series modeling in healthcare applications.

Gated recurrent unit architecture (GRU)

GRU model is a simplified variant of the Long Short-Term Memory (LSTM) network that effectively captures long-term dependencies in sequential data while using fewer parameters. The GRU eliminates the cell state and combines the gating mechanisms, making it computationally efficient and easier to train compared to LSTMs²⁷.

Given an input sequence $X = [x_1, x_2, \dots , x_T]$, the GRU processes one time step at a time, maintaining a hidden state $h_t$ that summarizes the sequence information up to time $t$. The architecture of the GRU is presented in Fig. 4 and defined as follows:

At each time step $t$, the update gate determines how much of the previous hidden state $h_{t-1}$ should be retained:

$$\begin{aligned} z_t = \sigma \left( W_z x_t + U_z h_{t-1} + b_z\right) , \end{aligned}$$

(16)

where $W_z$ and $U_z$ are the weight matrices for the input $x_t$ and the hidden state $h_{t-1}$, respectively, $b_z$ is the bias term, and $\sigma$ is the sigmoid activation function.

The reset gate decides how much of the previous hidden state to forget:

$$\begin{aligned} r_t = \sigma \left( W_r x_t + U_r h_{t-1} + b_r\right) . \end{aligned}$$

(17)

The candidate hidden state computes potential new information for the current step:

$$\begin{aligned} \tilde{h}_t = \tanh \left( W_h x_t + U_h (r_t \odot h_{t-1}) + b_h\right) , \end{aligned}$$

(18)

where $\odot$ denotes element-wise multiplication.

Fig. 4

Architecture of GRU cell.

The hidden state is updated by blending the previous hidden state and the candidate hidden state using the update gate:

$$\begin{aligned} h_t = z_t \odot h_{t-1} + (1 - z_t) \odot \tilde{h}_t. \end{aligned}$$

(19)

Finally, the output at each time step $t$ is computed as:

$$\begin{aligned} \hat{y}_t = W_y h_t + b_y, \end{aligned}$$

(20)

where $W_y$ and $b_y$ are the weights and bias of the output layer, respectively, and $\hat{y}_t$ is the predicted value.

The GRU’s efficient architecture reduces computational complexity compared to LSTMs while maintaining the ability to model long-term dependencies in sequential data. This makes it a suitable choice for time-series forecasting tasks, particularly when computational resources are limited or when faster training is required.

Bidirectional GRU architecture

BiGRU model is an extension of the standard GRU that processes the input sequence in both forward and backward directions. This architecture captures information from both past and future contexts, making it highly effective for sequential data applications as shown in Fig. 5.

Given an input sequence $X = [x_1, x_2, \dots , x_T]$, the BiGRU computes two hidden states at each time step $t$: the forward hidden state $\overrightarrow{h_t}$ and the backward hidden state $\overleftarrow{h_t}$.

Fig. 5

Architecture of bidirectional GRU cell.

The forward GRU computes:

$$\begin{aligned} \overrightarrow{h_t} = z_t \odot \overrightarrow{h_{t-1}} + (1 - z_t) \odot \tanh \left( W_h x_t + U_h (r_t \odot \overrightarrow{h_{t-1}}) + b_h\right) , \end{aligned}$$

(21)

where $z_t$ and $r_t$ are the update and reset gates as defined in the standard GRU.

The backward GRU processes the sequence in reverse:

$$\begin{aligned} \overleftarrow{h_t} = z_t \odot \overleftarrow{h_{t+1}} + (1 - z_t) \odot \tanh \left( W_h x_t + U_h (r_t \odot \overleftarrow{h_{t+1}}) + b_h\right) . \end{aligned}$$

(22)

The final hidden state at time $t$ is the concatenation of the forward and backward hidden states:

$$\begin{aligned} h_t = \begin{bmatrix} \overrightarrow{h_t} \\ \overleftarrow{h_t} \end{bmatrix}. \end{aligned}$$

(23)

The output at each time step $t$ is computed as:

$$\begin{aligned} \hat{y}_t = W_y h_t + b_y, \end{aligned}$$

(24)

where $W_y$ and $b_y$ are the weights and bias of the output layer. This bidirectional processing enables the model to leverage both past and future context for more accurate predictions.

Bidirectional LSTM architecture

This is an extension of the LSTM architecture that processes the input sequence in both forward and backward directions, enabling the model to capture dependencies from both past and future time steps as shown in Fig. 6 and the similar study can be seen in²⁸.

For an input sequence $X = [x_1, x_2, \dots , x_T]$, the BiLSTM maintains a forward hidden state $\overrightarrow{h_t}$ and a backward hidden state $\overleftarrow{h_t}$.

Fig. 6

Architecture of bidirectional LSTM cell.

The forward LSTM computes the hidden state using the standard LSTM equations:

$$\begin{aligned} \overrightarrow{h_t} = \overrightarrow{o_t} \odot \tanh \left( \overrightarrow{c_t}\right) . \end{aligned}$$

(25)

Similarly, the backward LSTM processes the sequence in reverse:

$$\begin{aligned} \overleftarrow{h_t} = \overleftarrow{o_t} \odot \tanh \left( \overleftarrow{c_t}\right) . \end{aligned}$$

(26)

The final hidden state is the concatenation of the forward and backward hidden states:

$$\begin{aligned} h_t = \begin{bmatrix} \overrightarrow{h_t} \\ \overleftarrow{h_t} \end{bmatrix}. \end{aligned}$$

(27)

The output at each time step $t$ is then computed as:

$$\begin{aligned} \hat{y}_t = W_y h_t + b_y. \end{aligned}$$

(28)

By processing the sequence in both directions, BiLSTMs capture richer contextual information, making them highly effective for tasks requiring an understanding of both past and future dependencies in sequential data.

Model training and hyperparameter optimization

The weekly bed occupancy dataset, spanning from 06-01-2008 to 31-07-2024 and comprising 867 observations, was divided into training (75%), validation (15%), and testing (15%) sets. A lag of 52 weeks was selected to capture temporal dependencies, as guided by the Partial Autocorrelation Function (PACF) plot. To ensure effective training of the deep learning models, the data were normalized using the ’Min-Max Scaler’ transformation²⁹. Each deep learning model was configured with varying hyperparameter settings to ensure robust and optimal performance^{30,31,32,33,34}. The hyperparameter search space was defined as follows:

• Number of units: 32, 64, 128

• Dropout rate: 0.0, 0.1, 0.2, 0.3

• Batch size: 16, 32, 64

• Learning rate: $1 \times 10^{-4}$, $1 \times 10^{-3}$, $1 \times 10^{-2}$

• Activation functions: ReLU, tanh, LeakyReLU

Two hyperparameter optimization techniques, random search (RS) and grid search (GS), were employed to identify the best model configurations. For random search, 10 iterations were conducted, evaluating randomly sampled configurations using Mean Squared Error (MSE) as the loss function. For grid search, all possible combinations of the hyperparameter space were exhaustively evaluated. With 3 choices for units, 4 for dropout rates, 3 for batch sizes, 3 for learning rates, and 3 activation functions, grid search resulted in:

$$\begin{aligned} 3 \times 4 \times 3 \times 3 \times 3 = 324 \text { combinations per model.} \end{aligned}$$

(29)

The training process was capped at 200 epochs, with early stopping criteria applied to prevent overfitting. Training and evaluation were conducted on a system equipped with an Intel Core 9 14900k processor, 128 GB of RAM, and dual NVIDIA RTX 4090 GPU, ensuring sufficient computational power for efficient experimentation. Each model was trained and evaluated 10 times to ensure stability, with the average performance used to determine the best-performing configuration.

This rigorous approach to hyperparameter tuning and model training ensured that the deep learning models were optimized for robust and accurate weekly bed occupancy forecasting.

Addressing model uncertainty using bayesian model averaging with Zellner’s $g$-prior

Model uncertainty is a critical issue in predictive modeling, particularly in forecasting applications where multiple models yield varying predictions. Bayesian Model Averaging (BMA) provides a principled framework to address this uncertainty by combining predictions from multiple models, weighted by their posterior probabilities³⁵. BMA has been widely applied in various fields, including environmental science, econometrics, and hydrology, demonstrating its effectiveness in improving forecast accuracy by mitigating model selection biases^36,37. In this study, we leverage BMA with Zellner’s $g$-prior to improve weekly bed occupancy forecasts for mental health hospitals.

Bayesian model averaging framework

BMA operates by considering a set of candidate models $M_1, M_2, ..., M_K$, each producing a forecast $\hat{\bf{y}}_j$. The BMA forecast is a weighted sum of individual model forecasts:

$$\begin{aligned} \hat{\bf{y}}_{\text {BMA}} = \sum _{j=1}^{K} w_j \hat{\bf{y}}_j, \end{aligned}$$

where the weights $w_j$ represent the posterior probability of each model given the observed data³⁸. These weights are computed as:

$$\begin{aligned} w_j = P(M_j \mid {\bf{y}}) = \frac{\mathcal {L}_j({\bf{y}}) P(M_j)}{\sum _{k=1}^{K} \mathcal {L}_k({\bf{y}}) P(M_k)}, \end{aligned}$$

where $\mathcal {L}_j({\bf{y}})$ is the likelihood of the observed data under model $M_j$, and $P(M_j)$ is the prior probability of model $j$. Under a uniform prior assumption, all models are treated as equally probable before observing the data.

Zellner’s $g$-prior for regression coefficients

A key component of BMA is the prior distribution assigned to model parameters. Zellner’s $g$-prior³⁹ is a popular choice in Bayesian regression and model selection due to its ability to regularize coefficient estimates while maintaining analytical tractability. The prior for regression coefficients $\varvec{\beta }_j$ in model $j$ is given by:

$$\begin{aligned} \varvec{\beta }_j \sim \mathcal {N}({\bf{0}}, g \cdot \sigma ^2 ({\bf{X}}_j^\top {\bf{X}}_j)^{-1}), \end{aligned}$$

where $g$ is a scalar hyperparameter controlling the prior variance. The choice of $g = 1$ balances prior informativeness and data-driven inference^40,41, preventing over-regularization while ensuring stable estimates.

Since $\varvec{\beta }_j$ is a vector, the prior follows a multivariate normal distribution, with a covariance structure informed by the predictor matrix. This ensures that the prior reflects the dependency structure among predictors without making the prior explicitly adaptive to observed data.

Furthermore, Zellner’s g-prior is traditionally used in Bayesian linear regression, we adapted it in our ensemble framework by treating the predictions from nonlinear deep learning models as inputs to a Bayesian linear meta-model. This allows for a linear combination of outputs using g-prior regularization without applying the prior to the neural network parameters.

To satisfy the normality assumption of residuals, we applied a Box-Cox transformation to the deep learning outputs before incorporating them into the BMA. The transformed outputs were shown to pass the Shapiro-Wilk and Jarque-Bera tests more robustly, validating this adaptation.

This approach allows us to retain the flexibility of nonlinear base models while ensuring analytical tractability and theoretical validity of the Bayesian ensemble layer.

Transformation for normality in Bayesian model averaging

Since the outcome variable (weekly bed occupancy) follows a count-based distribution, we applied a transformation to approximate normality before implementing Bayesian Model Averaging. This step ensures that the normality assumption inherent in BMA holds. Several transformations, including logarithmic, square-root, and Box-Cox transformations, were tested, and the most appropriate transformation was selected based on residual normality tests. The transformed predictions from each deep learning model were then used in the BMA framework. After obtaining the BMA forecast, an inverse transformation was applied to restore the predictions to their original scale. This step ensures that the results remain interpretable while benefiting from the improved uncertainty quantification of BMA.

Likelihood and posterior computation

The likelihood function for model $j$, given observed data ${\bf{y}}$, is:

$$\begin{aligned} \mathcal {L}_j({\bf{y}} \mid {\bf{X}}_j, \varvec{\beta }_j) = \frac{1}{(2\pi \sigma ^2)^{n/2}} \exp \left( -\frac{1}{2\sigma ^2} ({\bf{y}} - {\bf{X}}_j \varvec{\beta }_j)^\top ({\bf{y}} - {\bf{X}}_j \varvec{\beta }_j)\right) . \end{aligned}$$

Combining the prior and likelihood using Bayes’ theorem, the posterior distribution of $\varvec{\beta }_j$ is:

$$\begin{aligned} P(\varvec{\beta }_j \mid {\bf{y}}, {\bf{X}}_j) \propto \mathcal {L}_j({\bf{y}} \mid {\bf{X}}_j, \varvec{\beta }_j) P(\varvec{\beta }_j). \end{aligned}$$

Under Zellner’s $g$-prior with $g = 1$, the posterior mean and variance for $\varvec{\beta }_j$ are:

$$\begin{aligned} & \hat{\varvec{\beta }}_j = \frac{1}{2} ({\bf{X}}_j^\top {\bf{X}}_j)^{-1} {\bf{X}}_j^\top {\bf{y}}, \\ & \text {Var}(\varvec{\beta }_j \mid {\bf{y}}) = \frac{1}{2} \sigma ^2 ({\bf{X}}_j^\top {\bf{X}}_j)^{-1}. \end{aligned}$$

Credible intervals for forecast uncertainty

To quantify forecast uncertainty, credible intervals are computed using the aggregated posterior density across all models. The 95% credible interval for the BMA forecast is:

$$\begin{aligned} \text {CI}_{\text {BMA}} = \left[ \text {Quantile}_{2.5\%}, \text {Quantile}_{97.5\%}\right] , \end{aligned}$$

where quantiles are computed as:

$$\begin{aligned} \text {Quantile}_{p} = \inf \left\{ q: P(\hat{\bf{y}}_{\text {BMA}} \le q) \ge p \right\} . \end{aligned}$$

This ensures that the intervals reflect both individual model uncertainty and overall model variability, yielding robust forecasts suitable for decision-making in hospital resource allocation³⁶.

Practical implications

BMA with Zellner’s $g$-prior improves predictive performance by reducing forecast variance and systematically addressing model uncertainty. The choice of $g = 1$ provides moderate shrinkage without excessive regularization. In this study, we evaluated four major formulations for selecting $g$, including $g = 1$, $g = n$ (Unit Information Prior), and two additional variations based on prior literature^36,42. Empirical results demonstrated that $g = 1$ consistently outperformed the other choices, providing a balance between prior informativeness and data-driven inference. While $g = 1$ is a reasonable choice, alternative values such as $g = n$ may be preferable in extremely small datasets. However, in our dataset, $g = 1$ yielded the most stable and accurate forecasts, making it the optimal selection for Bayesian Model Averaging. This methodology ensures that forecast uncertainty is adequately quantified, supporting improved healthcare resource management.

Forecasting and evaluation

Model performance was evaluated using three standard accuracy metrics: Mean Absolute Percentage Error (MAPE), Root Mean Square Error (RMSE) and Mean Absolute Error (MAE). Additionally, to identify the best-performing model, a post hoc analysis was conducted using the Diebold-Mariano (DM) test, which enabled pairwise comparisons of forecasting accuracies across different models.

Results

The descriptive statistics of the weekly bed occupancy dataset, presented in Table 1, provide insights into the dataset’s key characteristics. The dataset comprises a total of 867 observations, with bed occupancy values ranging from a minimum of 143 to a maximum of 607 beds. The mean bed occupancy is 495.86, indicating a moderate level of utilization across the observation period. The median value of 514.78, which is slightly higher than the mean, reflects a slight negative skew in the data. This is further supported by the skewness value of -2.30, which suggests that the distribution of bed occupancy is left-skewed, with a longer tail toward the lower end of the occupancy spectrum.

Fig. 7

Visualization of the weekly trend of bed occupancy in mental hospital.

The standard deviation of 81.60 indicates moderate variability in weekly bed occupancy. The coefficient of variation (CV) of 16.44% highlights that the variation is relatively low in comparison to the mean, suggesting stable utilization patterns. However, the kurtosis value of 6.32 reveals that the dataset is leptokurtic, indicating a distribution with heavier tails and a sharper peak compared to a normal distribution. In addition, the results of stationarity tests provide additional insights into the dataset. The Augmented Dickey-Fuller (ADF) test statistic of 4.92 (significant at the 1% level) fails to reject the null hypothesis, indicating non-stationarity as observed in Fig. 7. Similarly, the KPSS test statistic of 0.75 (significant at the 1% level) confirms the presence of a trend or unit root in the data. These results necessitate transformation techniques, such as differencing, to achieve stationarity for statistical time-series modeling.

Table 1 Descriptive statistics of weekly bed occupancy data.

Furthermore, Normality tests reveal deviations from a normal distribution. The Shapiro-Wilk test statistic of 0.76 and the Jarque–Bera test statistic of 2211.28 (both significant at the 1% level) strongly reject the null hypothesis of normality. These findings are consistent with the observed skewness and kurtosis values, confirming that the dataset deviates significantly from a normal distribution. Such deviations emphasize the need for robust deep learning techniques that can handle non-normal and non-stationary time-series data effectively.

The descriptive analysis aligns with findings in prior literature, where healthcare datasets, particularly in resource-constrained settings, often exhibit non-stationarity and heavy-tailed distributions. The presence of moderate variability and a skewed distribution necessitates the use of advanced forecasting models such as LSTM, GRU, BiLSTM, Transformers and hidden markov guided GRU models have been shown to perform well in capturing temporal dependencies and non-linear patterns^31,34. These characteristics underscore the importance of preprocessing steps, including normalization and differencing, to prepare the dataset for effective model training.

Table 2 Optimal hyperparameters from random search tuning.

Table 3 Optimal Hyperparameters from grid search tuning.

Fig. 8

Several models fitted on train data.

The results of the hyperparameter tuning process for both random search (RS) and grid search (GS) methods are summarized in Tables 2 and 3, respectively. Random search evaluated 10 configurations for each deep learning model, whereas grid search exhaustively evaluated 324 combinations to identify the optimal settings. The selected hyperparameters for each model demonstrate variability in the number of units, dropout rates, batch sizes, learning rates, and activation functions, reflecting the unique characteristics of each architecture.

From the random search tuning results in Table 2, it is evident that most models achieved optimal configurations with higher dropout rates (e.g., 0.2 or 0.3) and moderate batch sizes (e.g., 16, 32, or 64). The GRU and LSTM models favored smaller units (32) and higher learning rates (0.01), combined with ReLU as the activation function. On the other hand, BiGRU and BiLSTM configurations involved more complex architectures with higher units (128 for BiGRU) and smaller batch sizes, ensuring their ability to handle sequential dependencies effectively.

In contrast, grid search tuning (Table 3) identified more consistent patterns across models. Most configurations used smaller units (32 or 64), batch sizes (16 or 32), and ReLU activation, highlighting grid search’s ability to converge on generalizable hyperparameters. Notably, dropout rates varied from 0.1 to 0.3 across models, aligning with the need to prevent overfitting during training. For models like BiLSTM, grid search favored 64 units and a batch size of 16, enabling robust learning for this complex architecture.

Table 4 Train data metrics for random search (RS) and grid search (GS) Models.

Fig. 9

Several models performed on validation data.

Fig. 10

Several models performed on test data.

Fig. 11

Bayesian model averaging model using DL model forecasts.

Table 4 and Fig. 8 presents the train data performance metrics for models tuned with random search (RS) and grid search (GS). The metrics include Root Mean Squared Error (RMSE), Mean Absolute Error (MAE), and Mean Absolute Percentage Error (MAPE). Overall, the grid search (GS) models outperformed random search (RS) models in terms of lower error metrics for most architectures, particularly the LSTM, BiGRU, and BiLSTM.

Mathematically, the percentage improvement in RMSE, MAE, and MAPE for grid search over random search can be expressed as:

$$\begin{aligned} \text {Improvement (\%)} = \frac{\text {Metric}_{\text {RS}} - \text {Metric}_{\text {GS}}}{\text {Metric}_{\text {RS}}} \times 100. \end{aligned}$$

For the BiLSTM model:

$$\begin{aligned} & \text {RMSE Improvement (\%)} = \frac{27.226 - 22.309}{27.226} \times 100 = 18.06\%. \\ & \text {MAE Improvement (\%)} = \frac{19.923 - 15.211}{19.923} \times 100 = 23.64\%. \\ & \text {MAPE Improvement (\%)} = \frac{3.984 - 3.087}{3.984} \times 100 = 22.50\%. \end{aligned}$$

Similarly, for the BiGRU model:

$$\begin{aligned} & \text {RMSE Improvement (\%)} = \frac{30.229 - 22.035}{30.229} \times 100 = 27.11\%. \\ & \text {MAE Improvement (\%)} = \frac{22.442 - 15.382}{22.442} \times 100 = 31.47\%. \\ & \text {MAPE Improvement (\%)} = \frac{4.473 - 3.081}{4.473} \times 100 = 31.10\%. \end{aligned}$$

The LSTM model also shows significant improvement in MAPE with GS (3.233%) compared to RS (5.018%), highlighting the effectiveness of grid search in optimizing model performance.

Table 5 and Fig. 9 presents the validation dataset metrics for models trained using random search (RS) and grid search (GS) hyperparameter tuning methods. For the GRU model, grid search significantly outperformed random search with a 41.18% reduction in RMSE ($38.604 \rightarrow 22.698$), a 46.29% reduction in MAE ($29.454 \rightarrow 15.821$), and a 47.07% reduction in MAPE ($9.338 \rightarrow 4.943$). This demonstrates the ability of grid search to identify configurations that enhance the GRU’s ability to generalize to validation data.

Similarly, the LSTM model tuned with grid search achieved substantial improvements compared to random search, reducing RMSE by 49.30% ($54.390 \rightarrow 27.571$), MAE by 50.34% ($40.732 \rightarrow 20.231$), and MAPE by 56.78% ($14.658 \rightarrow 6.335$). These results indicate that grid search better optimized the LSTM’s performance, especially in capturing long-term dependencies in the data. For the BiGRU and BiLSTM models, grid search tuning also yielded better results. The BiGRU model reduced RMSE by 30.55% ($42.953 \rightarrow 29.844$), MAE by 35.23% ($33.016 \rightarrow 21.371$), and MAPE by 40.72% ($11.421 \rightarrow 6.772$). The BiLSTM model showed modest improvements, with reductions of 17.12% in RMSE ($41.262 \rightarrow 34.187$), 20.39% in MAE ($31.876 \rightarrow 25.373$), and 15.06% in MAPE ($10.931 \rightarrow 9.287$).

In contrast, the TDNN model performed worse under grid search, with RMSE increasing by 71.45% ($34.941 \rightarrow 59.883$), MAE by 70.60% ($27.328 \rightarrow 46.619$), and MAPE by 83.12% ($10.410 \rightarrow 19.060$). This suggests that the grid search configurations for TDNN failed to generalize effectively to the validation set.

Table 5 Validation data metrics for random search (RS) and grid search (GS) models.

The residuals from the BMA ensemble applied on Box-Cox transformed outputs were found to be approximately normal (Shapiro-Wilk p = 0.26; JB test p = 0.19), validating the assumption for using g-prior regularization. The prior variance controlled by $g=1$ provided stable estimates with moderate shrinkage, as shown in the reduced forecast variance and tighter credible intervals compared to RS-based BMA.

Table 6 and Fig. 11 shows the Bayesian Model Averaging (BMA) weights for models optimized via random search (RS) and grid search (GS). These weights quantify the relative contribution of each model to the aggregated BMA forecast. Notably, for the RS-tuned models, BiLSTM-RS and GRU-RS hold the majority of the weight, at 0.6207 and 0.3793 respectively, indicating their strong individual performances in capturing the underlying data patterns. The other RS models, such as RNN-RS and TDNN-RS, contribute negligibly with weights on the order of $10^{-39}$ or smaller.

Table 6 Bayesian model averaging weights for random search (RS) and grid search (GS) models.

In the case of GS-tuned models, the GRU-GS model overwhelmingly dominates the BMA weights with a value of 0.9919, showcasing its exceptional ability to generalize and perform consistently across validation metrics. The minor contributions from other models like RNN-GS (0.0077) and BiGRU-GS (0.00047) highlight the dominance of the GRU-GS configuration in the grid search context. Models such as TDNN-GS and LSTM-GS, with weights approaching zero, indicate less reliability in their predictive contributions under the GS-optimized framework.

Fig. 12

BMA model using Zellner’s prior performed on test data.

Fig. 13

Performance of different models on test data.

To strengthen the benchmarking of our proposed framework, we further compared its performance against classical statistical models, namely ARIMA and SARIMA. The ARIMA model was tuned using AIC-based order selection and residual diagnostics, with the optimal configuration obtained as ARIMA(3,1,1). Similarly, SARIMA extended the ARIMA structure by explicitly incorporating weekly seasonality, with the best-performing specification identified as SARIMA(3,0,1)(1,0,1)₅₂, where the seasonal period of 52 corresponds to weekly cycles over a year. Both models were trained on the same chronological splits as the deep learning models to ensure fairness in comparison.

The results confirmed the limitations of traditional time-series approaches in modeling complex hospital occupancy data. ARIMA achieved a RMSE of 64.12, MAE of 48.75, and a MAPE of 10.23%, while SARIMA performed slightly better with a RMSE of 55.83, MAE of 42.10, and a MAPE of 8.92%. In contrast, our BMA ensemble based on models trained using Grid Search achieved a RMSE of 12.85, MAE of 10.27, and a MAPE of 1.939%. These findings highlight the substantial performance gap between conventional statistical baselines and the proposed deep learning and BMA framework.

Table 7 and Figs. 10, 12 presents the performance of models on test data and also includes results for the Bayesian Model Averaging (BMA) with Zellner’s prior applied to both RS and GS tuned models. Among the models, the BiLSTM-GS model achieved the best performance, with an RMSE of 12.847, MAE of 10.274, and MAPE of 1.939%. Similarly, the BMA-GS performed nearly identically to the BiLSTM model, with an RMSE of 12.848, MAE of 10.276, and MAPE of 1.939%. These results highlight the effectiveness of GS in optimizing deep learning models and the ability of BMA to combine model predictions while capturing uncertainty effectively.

For models tuned with RS, the GRU and BiLSTM models demonstrated strong performance, with the BiLSTM model achieving an RMSE of 15.746, MAE of 12.574, and MAPE of 2.335%. However, the application of BMA with RS further improved these metrics slightly, reducing the MAPE to 2.331% and achieving the lowest RMSE (15.710) and MAE (12.558) among all RS models can be visualized in Fig. 13.

Table 7 Model performance metrics for random search (RS) and grid search (GS) on test data.

The Diebold–Mariano (DM) test results for both Random Search (RS) and Grid Search (GS) models are summarized in Figures A.1 and A.2 (Supplementary material). The test evaluates the statistical significance of forecast accuracy differences between model pairs, with a positive DM statistic indicating superior performance of the first model and a negative value favoring the second model. A p-value below 0.05 denotes a statistically significant difference.

For RS-tuned models demonstrated different performance patterns, as highlighted in Tables A.1 and A.2 (Supplementary material). Surprisingly, TDNN-RS significantly outperformed LSTM-RS ($DM = 7.2707$, $p < 10^{-12}$) and BMA-RS ($DM = 8.1588$, $p < 10^{-15}$), suggesting that in this configuration, TDNN-RS was able to generalize better than deep recurrent models. However, BiGRU-RS and BiLSTM-RS exhibited comparable performance, with their DM statistics showing no significant differences in several pairwise comparisons.

Conversely, GS tuned models, Table A.2 (Supplementary material) shows that LSTM-GS significantly outperformed BiGRU-GS ($DM = 13.984$, $p < 0.0001$), as well as GRU-GS ($DM = 12.853$, $p < 0.0001$) and BMA-GS ($DM = 12.873$, $p < 0.0001$). These results indicate that LSTM-GS exhibited the best forecasting performance under GS tuning. Additionally, BiLSTM-GS was significantly better than BiGRU-GS ($DM = -6.838$, $p < 10^{-11}$), suggesting the advantage of bidirectional architectures in improving accuracy.

Discussion

Benchmarking against ARIMA and SARIMA reinforced the superiority of deep learning approaches for hospital occupancy forecasting. Although SARIMA $(3,0,1)(1,0,1)_{52}$ was able to capture weekly seasonality, its performance remained limited with a RMSE of 55.83, MAE of 42.10, and MAPE of 8.92%. ARIMA (3, 1, 1) performed even worse, yielding a RMSE of 64.12, MAE of 48.75, and MAPE of 10.23%. These results can be attributed to the inherent reliance of such models on linear autoregressive structures, which are inadequate for representing the nonlinear patterns and long-range dependencies present in non-stationary hospital bed occupancy sequences. In contrast, the proposed BiLSTM-GS combined with Bayesian Model Averaging (BMA) achieved markedly superior results (RMSE = 12.85, MAE = 10.27, MAPE = 1.939%), underscoring the capacity of deep learning models to capture complex temporal dynamics. Furthermore, the integration of BMA enhanced forecast reliability by combining multiple model predictions with principled uncertainty quantification. Taken together, these findings highlight that while ARIMA and SARIMA serve as interpretable and traditional baselines, they fall short in accuracy and robustness when compared to deep learning + BMA, which offers both superior predictive performance and calibrated uncertainty estimates critical for high-stakes healthcare decision-making.

The comparison between random search (RS) and grid search (GS) models highlights the systematic advantage of GS in optimizing hyperparameters to reduce error metrics. While RS is computationally efficient and effective at exploring diverse configurations with fewer iterations, its stochastic nature can result in suboptimal configurations for complex models. For example, GS-tuned BiLSTM achieved a 23.64% reduction in MAE compared to RS, showcasing the benefits of exhaustive evaluation. Similarly, GS consistently identified configurations such as smaller batch sizes (16 or 32) and appropriate dropout rates, which improved the performance of models like BiGRU and BiLSTM in capturing temporal dependencies within the dataset. Figure 8 illustrates the superior fit achieved by GS-tuned models on the training dataset.

Despite the superior precision of GS, its higher computational cost and occasional overfitting for simpler architectures, such as TDNN, suggest that RS can still be a practical alternative for scenarios with constrained resources or simpler models. However, the consistent reductions in RMSE, MAE, and MAPE for GRU, LSTM, and BiGRU models under GS underscore its reliability for complex architectures, as evidenced by MAPE reductions of 47.07% for GRU and 56.78% for LSTM. These findings affirm the importance of selecting a tuning strategy based on model complexity, with GS emerging as the preferred method for applications requiring high accuracy, particularly for recurrent architectures that excel at handling temporal dependencies.

Figure 9 shows how GS-tuned models generalize well on validation data, while Figs. 10 and 13 confirms their robustness on unseen test data. Additionally, the trend in actual bed occupancy across the hospital is visualized in Fig. 7, reinforcing the seasonal and non-stationary nature of the forecasting challenge.

The distribution of Bayesian Model Averaging (BMA) weights highlights the strengths of different models under varying tuning strategies. In random search (RS), BiLSTM-RS and GRU-RS dominated, demonstrating that even stochastic optimization can uncover configurations with strong predictive power. BiLSTM consistently excelled due to its ability to capture temporal dependencies effectively. In grid search (GS), BiLSTM-GS emerged as the top performer, benefitting from exhaustive hyperparameter tuning, which optimized its gated structure to handle the dataset’s temporal complexities. In contrast, models like TDNN-GS and LSTM-GS received near-zero weights, indicating limited adaptability to the dataset’s characteristics. These contributions to the BMA ensemble are clearly depicted in Fig. 11.

While the base deep learning models are nonlinear and do not adhere to the classical assumptions of linear regression, our adaptation treats their forecasts as inputs to a linear Bayesian ensemble. This approach is supported in prior literature, particularly in ensemble forecasting scenarios where model outputs are linearly combined^43,44. The theoretical justification for using Zellner’s g-prior lies in the transformed predictive space, where approximate normality and independence of transformed outputs allow the use of linear Bayesian inference. Our results suggest that this adaptation maintains both predictive accuracy and uncertainty calibration, justifying the use of g-prior in this context.

Building on this foundation, BMA with Zellner’s prior proved to be a robust approach for enhancing forecast reliability by combining model predictions within the linear Bayesian ensemble framework. By explicitly accounting for parameter uncertainty, BMA reduced predictive variance and further reinforced predictive accuracy and uncertainty calibration. Its application is particularly relevant in ensemble forecasting for healthcare settings, where accurate predictions are critical for resource allocation and patient care, making BMA a valuable tool for high-stakes decision-making as shown in Fig. 12.

Table 8 Training and inference time summary for all models.

The results demonstrate the superiority of grid search (GS) over random search (RS) in optimizing hyperparameters for deep learning models. For instance, the BiLSTM model’s MAPE improved significantly from 2.335% under RS to 1.939% under GS, a 16.96% improvement, while GRU achieved a 5.34% reduction in MAPE ($2.359\% \rightarrow 2.233\%$). These findings highlight GS’s ability to systematically evaluate the hyperparameter space, particularly for complex models like BiGRU and BiLSTM, yielding configurations that enhance performance. Comparative model performances on the test dataset are comprehensively presented in Fig. 10.

Bayesian Model Averaging (BMA) with Zellner’s prior further strengthened prediction reliability by aggregating multiple models and addressing parameter uncertainty. For GS-tuned models, BMA matched the performance of the best-performing BiLSTM model with a MAPE of 1.939%, while for RS, it refined predictions by reducing RMSE from 15.746 to 15.710. The BiLSTM model consistently achieved the lowest error metrics, and its combination with BMA enhanced robustness in handling temporal dependencies. While simpler architectures like TDNN and RNN provided reasonable results, they were outperformed by GRU, LSTM, BiGRU, and BiLSTM. The GS-tuned BiLSTM and BMA models emerged as the most suitable for real-world applications, offering accurate bed occupancy forecasts and reliable decision-making tools for healthcare administrators. This study underscores the value of combining systematic tuning with uncertainty modeling to improve predictive accuracy in healthcare resource management.

The DM test results provide valuable insights into model performance across RS and GS tuning strategies. A notable finding is the dominance of LSTM-GS in GS-tuned models, where it significantly outperformed BiGRU-GS, GRU-GS, and BMA-GS. This reaffirms the capability of LSTMs in capturing long-term dependencies, making them particularly suitable for sequential data modeling. Similarly, BiLSTM-GS exhibited superior performance over BiGRU-GS, emphasizing the advantages of bidirectional architectures in improving forecasting accuracy. These statistically significant results are depicted in Tables A.1, A.2 (Supplementary material) and visualized in Figs. A.1, A.2 (Supplementary material).

In contrast, RS models displayed greater variability, with TDNN-RS emerging as a surprising top performer, despite its simpler architecture. The superior results of TDNN-RS over LSTM-RS and BMA-RS highlight the potential of random search to uncover optimal hyperparameter configurations for simpler models. However, this trend did not extend to GS, where TDNN-GS underperformed compared to recurrent architectures, illustrating the variability in effectiveness of tuning methods based on model complexity. Furthermore, GRU-RS, BiGRU-RS, and BiLSTM-RS demonstrated comparable performance in many pairwise DM tests, whereas BiLSTM-GS showed a clear advantage over its counterparts in GS-tuned models.

In terms of real world deployment and feasibility, the models were trained and evaluated on a workstation (Intel Core 9 14900k processor, 128 GB of RAM, and dual NVIDIA RTX 4090 GPU). Training times varied by model complexity and hyperparameter search strategy. Lighter architectures such as TDNN trained in under 15 min, while more complex recurrent models like BiLSTM with grid search required approximately 30 min of training as shown in Table 8.

Despite these training costs, inference remained highly efficient across all models, typically requiring under 1.5 s for generating a weekly forecast. The Bayesian Model Averaging (BMA) step added only $\sim$0.6 s per forecast for aggregation, leading to an end-to-end latency of $\sim$2 s in the final pipeline.

These runtimes demonstrate that the framework is computationally feasible for deployment in hospital IT systems, where weekly forecasts are generated in near real-time. This efficiency enables integration into (i) hospital dashboards for bed allocation planning, and (ii) automated alert systems that flag potential surges in occupancy.

The study highlights the novelty of integrating Bayesian Model Averaging (BMA) with Zellner’s prior for interpreting black-box deep learning models. BMA consistently enhanced prediction reliability by aggregating forecasts and addressing parameter uncertainty. Its ability to produce comparable results to the best individual models, such as BiLSTM-GS, underscores its utility in healthcare resource management. By combining innovative approaches like BMA with systematic hyperparameter tuning, this study offers a robust framework for accurate and reliable bed occupancy forecasting in mental health hospitals, achieving high accuracy and addressing the critical need for resource optimization.

Conclusion and future remarks

This study highlights the critical importance of accurate bed occupancy forecasting for mental health hospitals to ensure efficient resource allocation and patient care. By evaluating six advanced deep learning models optimized via random search (RS) and grid search (GS), the research demonstrated the superiority of GS, particularly for complex architectures like BiLSTM and BiGRU, in reducing RMSE, MAE, and MAPE. Bayesian Model Averaging (BMA) with Zellner’s prior further enhanced forecast reliability by integrating the strengths of individual models while addressing model uncertainty.

This study is limited to a univariate forecasting approach, which precludes the use of feature-attribution explanation methods like SHAP and LIME that require multiple model inputs. Future work incorporating multivariate data will prioritize the use of these Explainable AI techniques to enhance model transparency and provide insights into the factors influencing occupancy forecasts. The BiLSTM model, optimized through GS and BMA, achieved the highest accuracy, reaffirming its capability to capture temporal dependencies and its applicability to resource-intensive forecasting tasks. However, BMA weights are optimized for posterior density maximization (reflecting model plausibility given the data), this objective does not guarantee minimization of RMSE or generalized error variance in all cases. The observed parity in MAPE between BMA-GS and BiLSTM-GS may thus reflect a transient alignment of posterior-driven weighting with point forecast accuracy under this specific test set. Future work could explore hybrid weighting schemes, for instance, combining posterior optimization with validation-based RMSE tuning to further generalize ensemble performance. We also plan to involve multi-institutional collaboration for external validation, alongside exploring synthetic data generation (e.g., GANs) and transfer learning for domain adaptation to unseen healthcare centers.