Introduction

Emotion drives the common decision-making of humans in their daily activities. Additionally, emotional conditions can indirectly affect human attention, communication, and the ability to remember information1. However, the detection and understanding of emotional states often come naturally to humans; these task poses critical challenges to computational sequences. The term affective computing denotes the models for identifying, predicting, and detecting human emotions, such as anger, joy, trust, sadness, anticipation, and surprise, to adjust computational methods to these states2. Emotional information is transferred through a diversity of physiological and physical features3. Emotions play a significant role in the survival and the overall individual makeup4. They observe information relating to our existing state and well-being. For people and businesses to offer optimal services to customers, they have to detect the diverse emotions expressed by individuals with disabilities and utilize the source to provide bespoke suggestions to meet the individual necessities of their customers5. Emotion recognition for individuals with disabilities will play a favourable role in human-computer interaction and the field of artificial intelligence (AI)6.

Several kinds of models were utilized to identify emotions from humans, such as body movements, facial expressions, textual information, heartbeat, and blood pressure. In computational linguistics, human emotion recognition in a text for disabled individuals is becoming progressively significant from an applicative viewpoint7. Currently, there is a massive amount of textual information. It is captivating to remove emotion from many targets, such as those in business. Numerous studies have attained acceptable outcomes in the emotion recognition field from text8. Most ML approaches excessively depend on handcrafted aspects that necessitate extensive manual design and adjustment, and it is cost-intensive and time-consuming9. Nevertheless, this concern is assisted prominently by the application of deep learning (DL) recently. DL models have effectively addressed difficulties in multiple fields, like machine translation, image classification, text-to-speech generation, speech recognition, and other relevant ML fields10. Likewise, extensive performance improvements are attained when DL models are utilized for statistical speech processing.

This paper introduces a novel Sustainable Emotion Recognition System for Disabled Persons Using Deep Learning and Equilibrium Optimiser for Real-Time Communication Enhancement (SERDP-DLEOCE) approach. The SERDP-DLEOCE approach is designed as an advanced approach for emotion recognition in text to facilitate enhanced communication for people with disabilities. The process begins with text pre-processing, which involves multiple distinct stages to convert the raw text into a more suitable format for analysis. Furthermore, Word2Vec is employed for word embedding to capture semantic meaning by mapping words to dense vector representations. Moreover, the Elman neural network (ENN) model is used for emotion recognition in the test. Finally, the equilibrium optimizer (EO) model adjusts the hyperparameter values of the ENN model optimally and results in greater classification performance. The experimental validation of the SERDP-DLEOCE methodology is performed under the Emotion detection from text dataset. The key contribution of the SERDP-DLEOCE methodology is highlighted below.

  • The SERDP-DLEOCE approach applies a comprehensive text pre-processing to clean, normalize, and structure raw text data, thus improving its suitability for analysis. This process ensures that the irrelevant and noise are removed, enabling more precise word embedding and overall performance of the emotion recognition model.

  • The SERDP-DLEOCE methodology employs the Word2Vec model for generating meaningful word embeddings, which effectually captures semantic relationships within the text, thus enhancing the word representation in a dense vector space. This improves the capability of the model in comprehending context and subtle variances, resulting in more accurate emotion recognition and better overall classification performance.

  • The SERDP-DLEOCE technique implements the ENN model for robustly recognizing textual emotions by effectively capturing temporal dependencies in sequential data, which also improves the sensitivity of the model to contextual cues in text. This approach enhances the accuracy and reliability of emotion classification across diverse samples.

  • The SERDP-DLEOCE model applies the EO technique for effectually tuning the hyperparameters, thus enhancing the performance of the model by finding optimal settings that efficiently balance accuracy and computational efficiency. This step ensures more stable and effective training outcomes, contributing to an improved emotion recognition output.

  • The integration of Word2Vec embeddings with the ENN and EO models forms a novel unified framework that improves emotion recognition accuracy. This methodology uniquely balances semantic understanding and dynamic modelling with optimized hyperparameters, resulting in enhanced performance. Additionally, it maintains computational efficiency, making it appropriate for real-world applications.

Literature works

Tanabe et al.11 proposed a concept for emotion recognition methods that depend on AI employing motion and physiological signals. Primarily, the heartbeat interval of a child with PIMD was determined, and the correlation between the emotion and RRI was shortly examined in a primary experiment. Afterwards, an emotion recognition method for children with PIMD was formed employing motion and physiological signals by applying an RF classifier. Chhimpa et al.12 advanced a video-oculography (VOG) based method under natural head movements for cursor movement and eye-tracking. Furthermore, a GUI is designed to analyze the fulfilment and performance of the day-to-day essential needs of disabled people. Komuraiah et al.13 developed a web-based facial emotion recognition method intended to aid ASD children with ASD in understanding and recognizing emotions in others, finally improving their social skills. This method was applied by utilizing the CNN and Flask web structure, offering a user-friendly interface for both children and therapists or caregivers. This work utilizes DL to identify faces and investigate facial expressions and precisely classify emotions. In14, an Inception-based CNN structure is developed for emotion prediction. The presented technique has attained better precision, resulting in a six per cent enhancement around the current network structure for emotion classification.

This technique is tested over seven diverse datasets to verify its sturdiness. Furthermore, the real-world performance abilities of the verified humanoid robot NAO. Priya and Sandesh15 focused on increasing communication for the speech and hearing-impaired communities by detecting alphabets and ISL digits of static images in either offline or real-time situations. This work utilized both DL and ML with CNN to classify the ISL numbers and alphabets. In the ML method, image pre-processing models like skin mask generation, HSV conversion, Gabor filtering and skin portion extraction were utilized to divide the region of interest (ROI) that is fed into 5 ML methods for sign prediction. Conversely, the DL method applied CNN techniques. The authors16 developed a multimodal emotion recognition platform (MEmoRE) approach. MEmoRE utilizes advanced emotion recognition models, incorporating textual sentiment analysis, vocal intonation, and facial expression, to extensively recognize stakeholder emotions. This technique is additionally designed to be employed. Nie et al.17 developed an avant-garde pig FER method called CReToNeXt-YOLOv5. The presented approach comprises multiple refinements modified for adeptness and heightened precision in detection.

The existing studies exhibit various limitations and research gaps in emotion recognition. Several techniques heavily depend on controlled environments or specific signal types, restricting generalizability across diverse real-world scenarios and sensor modalities. The model also lacks effective fusion models to capture complementary emotional cues. The integration of multimodal data (e.g., physiological, motion, facial, and vocal) also remains underexplored. Furthermore, additional refinement is required for real-time implementation and user-friendly interfaces for individuals with varied disabilities. Various techniques concentrate on isolated datasets or specific disabilities, illustrating a research gap in developing robust, scalable models adaptable to varied populations and varying data quality. Addressing these gaps is significant for enhancing the accuracy, accessibility, and practical applicability of emotion recognition systems.

The proposed model

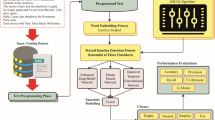
In this paper, a novel SERDP-DLEOCE method is introduced. The SERDP-DLEOCE method is designed as an advanced approach for emotion recognition in text to facilitate enhanced communication for people with disabilities. Figure 1 portrays the workflow of the SERDP-DLEOCE technique.

Fig. 1
figure 1

Workflow of SERDP-DLEOCE method.

Full size image

Text pre-processing

Text pre-processing is an essential stage in emotion recognition, as it prepares raw textual data for analysis by eliminating noise and normalizing the input18. Efficient pre-processing guarantees that the text data is in a systematic format appropriate for feature classification and extraction. The method typically includes many phases, all intended to deal with particular challenges in textual data.

  1. 1.

    Tokenization: This phase splits the input text into small components, like sentences or words, to enable study. It assists in breaking down composite sentences into controllable units for additional processing.

  2. 2.

    Lowercasing: To remove case sensitivity, each text is transformed to lowercase. This guarantees that words like \(\:Happy\) and \(\:happy\) are considered equal, minimizing redundancies in the data.

  3. 3.

    Removal of stop words: Normally applied words, namely, \(\:is\), \(\:and\), \(\:the\), and \(\:of\), are eliminated as they give little to the emotional or sentiment content. This decreases noise and concentrates on the words, which transfer meaningful context.

  4. 4.

    Removal of punctuation and special characters: Special characters and punctuation marks are eliminated to streamline the text and guarantee uniformity. Nevertheless, in similar cases, particular punctuation marks might be maintained after they convey emotion (for example, exclamation marks).

  5. 5.

    Lemmatisation and stemming: Words are limited to their root or base forms. For instance, \(\:running\) becomes\(\:\:run\), guaranteeing reliability in the example for related words.

  6. 6.

    Handling negations: Negations, namely \(\:not\:happy\), are recognized and considered as individual concepts for preserving the projected sentiments.

By performing these pre-processing methods, emotion recognition systems can successfully examine textual data, enhancing the precision of downstream tasks such as feature classification and extraction, and word embedding.

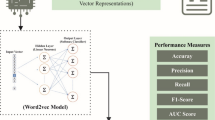
Word embedding process

Afterwards, the Word2Vec is employed for word embedding to capture semantic meaning by mapping words to dense vector representations19. This model effectually captures semantic relationships between words by mapping them into dense vector representations. This technique also provides a continuous, low-dimensional space that preserves meaningful linguistic patterns, allowing the model to comprehend context and similarity in language. The capability of the model in both syntactic and semantic information makes it superior to other embedding models. Furthermore, this is an ideal technique for balancing performance with resource constraints, and hence is computationally efficient and scalable for massive datasets. This balance between accuracy and efficiency justifies its use in the proposed framework.

Word2Vec is the word embedding approach commonly used in NLP for text classification. Its primary aim is to characterize words as dense vectors within the constant vector area. For numerous reasons, with its capability to capture semantic relationships among words, Word2Vec is confirmed as a valuable tool for text classification. Using Word2Vec for text classification provides many advantages, including its ability to determine semantic relations between words. Therefore, the classifier performs well on the tasks of classification as it may acquire a better knowledge of the meanings of words in the text. It is introduced to characterize a word as a constant-valued vector in this higher-dimensional vector space. The two main models are a Continuous Bag of Words (CBOW) and Skip-gram.

(i). CBOW: According to the contextual words near targeted words, it tries to predict such terms. For maximizing the probability of accurately forecasting the targeted word \(\:w\_t\) provided its contextual words \(\:w\_c\), whereas c travels from \(\:-C\) to \(\:C\) as exposed in Eq. (1)

$$Maximise~\left( {\frac{1}{T}} \right){\text{*}}\Sigma \left( {{\text{~Log~}}P\left( {{w_t}{\text{|}}{w_c}} \right)} \right)$$
(1)

\(\:\left(1\right)\)

Whereas T indicates each of the targeted words within the training data.

The likelihood of forecasting the targeted word, given its contextual words, is demonstrated by utilizing the functions of softmax exposed in Eq. (2):

$$P\left( {{w_ - }t{\text{|}}{w_ - }c} \right)=\frac{{exp\left( {{\theta _ - }{w_ - }t \cdot {\varphi _ - }{w_ - }c} \right)}}{{\Sigma \left( {exp\left( {{\theta _ - }w.{\varphi _ - }{w_ - }c} \right)} \right)}}~for~all~words~in~the~vocabulary$$
(2)

Here, \(\:{\theta\:}_{-}\)w_t: Target word embedding as vector representations of the targeted word \(\:w\_t\). \(\:{\phi\:}_{-}{w}_{-}c\): The contextual word \(\:w\_c\) (contextual word embedding) is characterized as vectors. Dot \(\:\left(\bullet\:\right)\) product among dual vectors.

b. Skip-gram: For estimating the contextual words for a targeted word, it is applied. The aim is to improve the probability of precisely forecasting the targeted word \(\:\left({w}_{-}t\right)\) specified by the contextual word \(\:\left({w}_{-}c\right)\) exposed in Eq. (3).

$$Maximize\left( {\frac{1}{T}} \right){\text{*}}\Sigma \left( {{\text{Log}}P\left( {{w_c}{\text{|}}{w_t}} \right)} \right)$$
(3)

The function of the SoftMax is applied to signify the probability of accurately guessing the contextual word given the target exposed in Eq. (4)

$$P\left( {{w_ - }c{\text{|}}{w_ - }t} \right)=\frac{{exp\left( {{\theta _ - }{w_ - }c \cdot {\varphi _ - }{w_ - }t} \right)}}{{\Sigma \left( {exp\left( {{\theta _ - }{w_ - }c \cdot {\varphi _ - }w} \right)} \right)}}~for~all~words~in~the~vocabulary$$
(4)

Emotion classification using ENN model

For the emotion recognition in text, the ENN model is utilized20. This model is chosen for its robust capability in capturing contextual data and temporal dependencies in sequential data. This technique effectually remembers prior inputs, making it significant in comprehending the flow and variances of language, unlike conventional feedforward networks. This methodology also presents a simple architecture with fewer parameters, making it computationally effective while still efficiently modelling short-term dependencies, compared to more intrinsic techniques such as LSTM or GRU. This balance between performance and efficiency makes ENN appropriate for emotion recognition tasks where capturing the sequence and context of words is crucial for accurate classification.

The ENN is a dynamical recurrent neural network (RNN) with local feedback networks. It usually contains four layers: the context, input, output layers, and hidden layer (HL). The contextual neuron layers relate one-to-one to the HL neurons. The HL output is generated in response to the HL input over the contextual layer’s storage and delay, attaining shorter-term memories and searching for local information. This tool characterizes a particular NN object, summarising the network’s weights, biases, training parameters, and structure, enabling fast utilization of the Elman code for calculation and investigation.

The mathematical formulation for its networking architecture is provided as shown:

$$y\left( k \right)=g\left( {{w_3} \cdot x\left( k \right)} \right)$$
(5)
$$x\left( k \right)=f\left( {{w_1} \cdot {x_C}\left( k \right)+{w_2}\left( {u\left( {k1} \right)} \right)} \right)$$
(6)
$${x_C}\left( k \right)=\alpha x\left( {k - 1} \right)+x\left( {k - 1} \right)$$
(7)

Here, \(\:x\) stands for an n-dimensional vector of the intermediate layer node unit; \(\:y\) refers to an m-dimensional vector of the output node. \(\:{x}_{c}\) denotes \(\:n\:\)dimensional feedback state vector;\(\:\:u\) signifies \(\:r\)-dimensional input vector;\(\:\:{w}_{1}\) characteristics connected weight; \(\:{w}_{2}\) symbolize connected weighting from an input to intermediate layers;\(\:{\:w}_{3}\) represents connected weighting from the middle layer to the output layer; \(\:0\le\:\alpha\:<1\) indicates the self‐feedback gain feature; \(\:f(\bullet\:)\) epitomizes the transfer function of the intermediate layer neuron, typically utilizing Sigmoid and\(\:\:g(\bullet\:)\) means an output neuron’s transfer function, demonstrating the linear mixture of the outputs of the intermediate layer.

Parameter optimizer using EO

Finally, the EO approach adjusts the hyperparameter values of the ENN approach optimally and results in greater classification performance21. This approach is chosen for its capability in effectually exploring and exploiting the search space, resulting in optimal parameter settings. This model also converges more efficiently and avoids getting trapped in local optima, unlike conventional techniques such as grid or random search, thus improving the overall performance of the model. The method also effectively balances exploration and exploitation dynamically, and its physics-inspired optimization mechanism allows for effective tuning. This results in an enhanced accuracy while mitigating the computational overhead, making EO appropriate and effective for improving the ENN model.

The EO is a heuristic optimizer algorithm. This theory is represented using the following equation: The rate of change in mass is computed as the rate of inflow minus the rate of outflow, resulting in the final mass.

During this EO model, particles characterize solutions, and their attentions are applied to searching parameters. All particles try to discover an equilibrium point arbitrarily from a particular collection of best solutions within the exploration area. Attention directs the location of the solution in this regard. The model effectively directs particles to this equilibrium place to discover optimum solutions. The equilibrium candidates are successively applied to build a vector, which imitates the set of equilibria that is theoretically described as demonstrated:

$$\left\{ {\begin{array}{*{20}{l}} {{X_{eq}}\left( {Iter} \right) \in \left\{ {{X_{eq1}}\left( {Iter} \right), \ldots ,~{X_{eq4}}\left( {Iter} \right),~{X_{eq,ave}}\left( {Iter} \right)} \right\}} \\ {D\left( {Iter} \right)=X\left( {Iter} \right) - {X_{eq}}\left( {Iter} \right)} \\ {{X_1}~(Iter={X_{eq}}\left( {Iter} \right) - D\left( {Iter} \right).F+\frac{{{G_\alpha }}}{{{\lambda _\alpha }}}.\left( {1 - {F_\alpha }} \right)} \end{array}} \right.$$
(8)

Here, \(\:{X}_{eq1}\left(Iter\right),\dots\:,{X}_{eq4}\left(Iter\right)\) represent controller variables similar to the four best-fitted people in generation \(\:Ite{r}^{th}\:{X}_{eq,ave}\left(Iter\right)\) specifies the average value of these four individuals. \(\:X\left(Iter\right)\) are selected arbitrarily amongst these individuals. In every cycle, all particle locations are upgraded by arbitrarily choosing one such option with equivalent likelihood. For instance, in the initial testing, the primary particle can update its position according to \(\:{X}_{eq1}\left(Iter\right)\), then in the next iteration, the average value \(\:{X}_{eq,ave}\left(Iter\right)\) may be applied. Using the result of the optimizer method, all particles should be upgraded to an equivalent repeatedly for each of the possible solutions. \(\:\lambda\:\) refers to a random vector distributed uniformly in the interval of \(\:\left[\text{0,1}\right],\) \(\:F\) denotes a randomly generated vector described by the relations provided in Eq. (9), and \(\:G\) is another arbitrary vector shown in Eq. (10).

$$F=2sign\left( {r - 0.5} \right).\left( {{e^{l\lambda }} - 1} \right)$$
(9)
$$\left\{ {\begin{array}{*{20}{c}} {G={G_0}.F} \\ {{G_0}=GCP.\left[ {{X_{eq}}\left( {Iter} \right) - \lambda .X~\left( {Iter} \right)} \right]} \\ {GCP=\left\{ {\begin{array}{*{20}{c}} {0.5{r_1}~~{r_2} \geqslant GP} \\ {0~~~~{r_2}<GP} \end{array}} \right.} \end{array}} \right.$$
(10)

\(\:r\) stands for a randomly generated vector by a uniform distribution across the component interval. \(\:{r}_{1}\) and \(\:{r}_{2}\) represent randomly formed values through a uniform distribution inside the component interval. \(\:l\) denotes the parameter presented by Eq. (11).

$$l={\left( {1 - \frac{{Iter}}{{{\text{~Max}} - iter}}} \right)^{\frac{{lter}}{{{\text{~Max}} - {\text{iter}}}}}}$$
(11)

The fitness selection refers to a substantial factor that manipulates the performance of the EO model. The hyperparameter range procedure comprises the solution-encoded technique for evaluating the effectiveness of the candidate solution:

$$Fitness~={\text{~max~}}\left( P \right)$$
(12)
$$P=\frac{{TP}}{{TP+FP}}$$
(13)

Here, \(\:TP\) and \(\:FP\) signify the true and false positive values.

Experimental result and analysis

The performance validation of the SERDP-DLEOCE methodology is verified under Emotion detection from text dataset22. The method runs on Python 3.6.5 with an i5-8600k CPU, 4GB GPU, 16GB RAM, 250GB SSD, and 1 TB HDD, using a 0.01 learning rate, ReLU, 50 epochs, 0.5 dropout, and batch size 5. The dataset contains 31,390 samples under seven sentiments as depicted in Table 1. Table 2 signifies the sample text.

Table 1 Details of the dataset.
Full size table
Table 2 Sample text.
Full size table

Table 3; Fig. 2 represent the emotion detection of the SERDP-DLEOCE technique under dissimilar epochs. The results imply that the SERDP-DLEOCE technique correctly identified the samples. On Epoch 500, the SERDP-DLEOCE technique attains an average \(\:acc{u}_{y}\) of 91.02%, \(\:pre{c}_{n}\) of 76.70%, \(\:rec{a}_{l}\) of 45.51%, \(\:F{1}_{score}\:\)of 44.85%, and \(\:{AUC}_{score}\) of 69.81%. Moreover, on Epoch 1000, the SERDP-DLEOCE technique attains an average \(\:acc{u}_{y}\) of 91.91%, \(\:pre{c}_{n}\) of 75.20%, \(\:rec{a}_{l}\) of 50.87 \(\:F{1}_{score}\:\)of 52.04%, and \(\:{AUC}_{score}\) of 72.79%. Besides, on Epoch 2000, the SERDP-DLEOCE methodology attains an average \(\:acc{u}_{y}\) of 93.05%, \(\:pre{c}_{n}\) of 78.07%, \(\:rec{a}_{l}\) of 57.81 \(\:F{1}_{score}\:\)of 61.15%, and \(\:{AUC}_{score}\) of 76.65%. Also, on Epoch 2500, the SERDP-DLEOCE methodology accomplishes attains an \(\:acc{u}_{y}\) of 93.93%, \(\:pre{c}_{n}\) of 78.89%, \(\:rec{a}_{l}\) of 63.48 \(\:F{1}_{score}\:\)of 67.14%, and \(\:{AUC}_{score}\) of 79.80%. At last, on Epoch 3000, the SERDP-DLEOCE methodology attains an average \(\:acc{u}_{y}\) of 95.15%, \(\:pre{c}_{n}\) of 80.95%, \(\:rec{a}_{l}\) of 71.65 \(\:F{1}_{score}\:\)of 75.00%, and \(\:{AUC}_{score}\) of 84.29%.

Table 3 Emotion detection of the SERDP-DLEOCE technique under dissimilar epochs.
Full size table
Fig. 2
figure 2

Average of SERDP-DLEOCE technique under dissimilar epochs.

Full size image

In Fig. 3, the training (TRA) \(\:acc{u}_{y}\) and validation (VAL) \(\:acc{u}_{y}\) analysis of the SERDP-DLEOCE technique below Epoch 3000 is illustrated. The \(\:acc{u}_{y}\:\)analysis is computed throughout 0-3000 epochs. The figure highlights that the TRA and VAL \(\:acc{u}_{y}\) analysis exhibits an increasing tendency, which informed the capacity of the SERDP-DLEOCE methodology with maximal outcomes over several iterations. Simultaneously, the TRA and VAL \(\:acc{u}_{y}\) remains closer across the epochs, which indicates inferior overfitting and exhibits better outcomes of the SERDP-DLEOCE methodology, assuring reliable prediction on hidden samples.

Fig. 3
figure 3

\(\:Acc{u}_{y}\) curve of SERDP-DLEOCE model under Epoch 3000.

Full size image

In Fig. 4, the TRA loss (TRALOS) and VAL loss (VALLOS) curve of the SERDP-DLEOCE approach under Epoch 3000 is shown. The values of loss are computed across the range of 0-3000 epochs. The TRALOS and VALLOS analysis exhibits a decreasing trend, demonstrating the capacity of the SERDP-DLEOCE method in balancing a trade-off between simplification and data fitting. The continuous reduction in values of loss moreover guarantees the maximum outcomes of the SERDP-DLEOCE method and tunes the prediction results over time.

Fig. 4
figure 4

Loss curve of SERDP-DLEOCE technique under Epoch 3000.

Full size image

In Fig. 5, the precision-recall (PR) curve results of the SERDP-DLEOCE methodology below Epoch 3000 present clarification into its results by plotting Precision alongside Recall for all the classes. The steady increase in PR analysis across all class labels illustrates the efficacy of the SERDP-DLEOCE model in the classification procedure.

Fig. 5
figure 5

PR curve of SERDP-DLEOCE technique under Epoch 3000.

Full size image

In Fig. 6, the ROC graph of the SERDP-DLEOCE technique below Epoch 3000 is examined. The outcomes imply that the SERDP-DLEOCE technique accomplishes maximal ROC outcomes across all classes, demonstrating an essential capacity for discriminating the classes. This dependable trend of maximal ROC analysis across several classes indicates the capable outcomes of the SERDP-DLEOCE approach on predicting classes, highlighting the robust nature of the classification procedure.

Fig. 6
figure 6

ROC graph of SERDP-DLEOCE technique below Epoch 3000.

Full size image

Table 4; Fig. 7 present a comparison of the SERDP-DLEOCE methodology with the existing techniques23,24,25. The results emphasized that the CGT-2, AraBERT, DenseNet201, EfficientNet-B3, ResNet50, and NB + lexicon methods have reported worse performance. Meanwhile, the MGT-2 model has gotten closer to outcomes. Furthermore, the SERDP-DLEOCE technique reported superior performance with higher \(\:pre{c}_{n}\), \(\:rec{a}_{l},\) \(\:acc{u}_{y},\:\)and \(\:{F1}_{score}\) of 80.95%, 71.65%, 95.15%, and 75.00%, respectively.

Table 4 Comparative results of SERDP-DLEOCE model with existing techniques.
Full size table
Fig. 7
figure 7

Comparative analysis of SERDP-DLEOCE model with existing techniques.

Full size image

In Table 5; Fig. 8, the comparative results of the SERDP-DLEOCE methodology are identified in terms of execution time (ET). The results imply that the SERDP-DLEOCE methodology gets maximum performance. Depending on ET, the SERDP-DLEOCE model delivers a lower ET of 1.01 min, whereas the MGT-2, CGT-2, AraBERT, DenseNet201, EfficientNet-B3, ResNet50, and NB + lexicon models achieve better ET values of 2.75 min, 3.37 min, 5.47 min, 5.21 min, 3.89 min, 4.57 min, and 5.45 min, disparately.

Table 5 ET outcome of SERDP-DLEOCE approach with existing models.
Full size table
Fig. 8
figure 8

ET outcome of SERDP-DLEOCE approach with existing models.

Full size image

Table 6; Fig. 9 specifies the error analysis of the SERDP-DLEOCE technique with existing methods. The MGT-2 and CGT-2 models exhibit better balance across metrics, with MGT-2 attaining a higher F1-Score of 33.45%, illustrating more stable classification. Additionally, the AraBERT, DenseNet201, and ResNet50 models illustrate robust representation learning. The NB + lexicon technique surpasses the SERDP-DLEOCE model by attaining an \(\:acc{u}_{y}\) of 30.15% and \(\:{F1}_{score}\) of 26.59%. The SERDP-DLEOCE model attains an \(\:acc{u}_{y}\) of 4.85%, \(\:pre{c}_{n}\) of 19.05%, \(\:rec{a}_{l}\) of 28.35%, and \(\:{F1}_{score}\) of 25.00%, underperforms significantly compared to other baseline models.

Table 6 Error analysis of SERDP-DLEOCE technique with existing methods.
Full size table
Fig. 9
figure 9

Error analysis of SERDP-DLEOCE technique with existing methods.

Full size image

Table 7; Fig. 10 indicates the ablation study of the SERDP-DLEOCE methodology. The SERDP-DLEOCE methodology attained the highest performance with an \(\:acc{u}_{y}\) of 95.15%, \(\:pre{c}_{n}\) of 80.95%, recall of 71.65%, and \(\:{F1}_{score}\) of 75.00%. When only the ENN model is used without the full integration, performance drops slightly to an \(\:acc{u}_{y}\) of 94.61% and \(\:{F1}_{score}\) of 74.21%, indicating the robust baseline capabilities of the ENN model. The EO method achieves an \(\:acc{u}_{y}\) of 94.02% and \(\:{F1}_{score}\) of 73.33%, illustrating its efficiency in optimization but also highlighting the necessity of integration with other components for best results. The Word2Vec technique achieves an \(\:acc{u}_{y}\) of 93.24% and \(\:{F1}_{score}\) of 72.66%, reflecting its contribution to semantic understanding. These results highlight the superior output of the SERDP-DLEOCE model.

Table 7 Result analysis of the ablation study of SERDP-DLEOCE methodology.
Full size table
Fig. 10
figure 10

Result analysis of the ablation study of SERDP-DLEOCE methodology.

Full size image

Conclusion

In this paper, a novel SERDP-DLEOCE method is introduced. The SERDP-DLEOCE method is designed as an advanced approach for emotion recognition in text to facilitate enhanced communication for people with disabilities. Initially, the SERDP-DLEOCE method begins with text pre-processing, which involves several distinct stages to transform the raw text into a more suitable format for analysis. Furthermore, Word2Vec is employed for word embedding to capture semantic meaning by mapping words to dense vector representations. For the emotion recognition in text, the ENN model is utilized. Finally, the EO technique adjusts the hyperparameter values of the ENN technique optimally and results in greater classification performance. The experimental validation of the SERDP-DLEOCE methodology is performed under the Emotion detection from text dataset. The comparison study of the SERDP-DLEOCE methodology portrayed a superior accuracy value of 95.15% over existing techniques.