Polarization-controlled coding metasurface with phase cancellation and diffusion for enhanced radar cross section reduction

Abstract

A novel metasurface design is presented integrating polarization conversion, diffusion, and phase cancellation mechanisms for broadband radar cross-section (RCS) reduction. The metasurface employs a rotationally symmetric configuration, enabling efficient dispersion of electromagnetic waves in x and y polarizations. By changing the unit cell size, polarization conversion optimization is accomplished. This results in a 180$\phantom{0}^{\circ }$ phase difference for the 1-bit design and 22.5$\phantom{0}^{\circ }$ for the 2-bit design, with reflection magnitudes surpassing 0.9 in the 11.2-20.2 GHz and 12.3-19.5 GHz frequency ranges, respectively. The genetic algorithm (GA) was employed to optimize the arrangement of unit cells, identifying the most effective configuration for scattering and RCS suppression. Simulation results under LP normal incidence demonstrate significant RCS reduction capabilities. The 1-bit metasurface achieves approximately 10 dB RCS reduction across 12.3-19.2 GHz, corresponding to a relative bandwidth of 43.81%. In contrast, the 2-bit metasurface achieves a 20 dB decrease inside 12-19.3 GHz (relative bandwidth 46.65%) and a wider 10 dB reduction over 11.1-20.3 GHz (relative bandwidth 58.60%), with a peak reduction of roughly 15 dB in the 13.5-15.4 GHz range. Additionally, co-polarized reflections produced by the Pancharatnam-Berry (PB) phase or unit cell rotation introduce continuous phase discrepancies, which aid in efficient wave manipulation. Under LP oblique incidence, the metasurface demonstrates robust performance. Over 12.3-18.9 GHz, the 1-bit design retains RCS reduction of 10 dB up to a 15$\phantom{0}^{\circ }$ incidence angle (relative bandwidth 42.3%), while the 2-bit design extends this capability up to a 30$\phantom{0}^{\circ }$ incidence angle across 12-19.3 GHz (relative bandwidth 46.65%). Both simulated and experimental results validate the metasurface’s ability to manipulate electromagnetic waves and achieve effective RCS reduction, highlighting its potential for advanced stealth and electromagnetic wave control applications.

Introduction

Engineered materials called metasurfaces are composed of subwavelength unit cells and are used to control electromagnetic (EM) waves. As radar technology continues to advance, these structures have become increasingly important in stealth applications due to their ability to control wave behavior effectively. By arranging unit cells in different patterns, the core characteristics of EM waves can be manipulated. Due to their diverse configurations, various types of metasurfaces have been developed¹, such as artificial magnetic conductors^2,3,4,5, absorptive metasurfaces, and coding metasurfaces employing different bits^{6,7,8,9,10,11,12,13}. The rapid development of metasurface technology has enabled extensive research into the artificial control of EM waves^14,15.

Metasurfaces have rapidly evolved into multifunctional platforms enabling a wide range of applications across the electromagnetic spectrum. For instance, in terahertz imaging, metasurfaces with engineered chromatic dispersion have been employed to achieve high-resolution 3D confocal imaging over a large depth-of-field, enabling rapid inspection of concealed objects in security screening and defect detection scenarios¹⁶. In the field of polarization manipulation, quarter-wave metasurfaces have demonstrated efficient linear-to-circular polarization conversion with broad bandwidth and compact form factors, offering significant advantages over conventional birefringent waveplates in terahertz spectroscopy and portable wireless communication systems¹⁷. Moreover, metasurfaces have shown promise in ultra-wideband absorption, as demonstrated by far-infrared absorbers based on nonresonant structures that maintain high absorptivity across an extremely broad spectral range, suitable for applications in detection, sensing, and stealth technologies¹⁸. These advances highlight the versatility of metasurfaces and motivate continued research into novel configurations and functional materials for electromagnetic wave manipulation.

Stealth technology is a highly promising area in the defense industry, where metasurfaces are used for practical applications, particularly for RCS¹⁹. RCS is a critical factor in many defense-related communication and sensor systems. The first coding metasurface was proposed in²⁰, introducing the concept of designing unit cells and arranging them in specific patterns to scatter EM waves. This metasurface employed basic unit cells with a constant phase difference within specified frequency bands, helping to weaken the signal and reduce RCS.

One approach to achieving different reflection phases is to use identical unit cells of varying sizes; however, this method is often inefficient and limited in bandwidth. A more effective alternative is to rotate an anisotropic structure, thereby achieving the PB phase. A reflection phase shift between $-2\pi$ and $+2\pi$ can be obtained by altering the metallic element’s rotation angle on the substrate^21,22. Digital bits are used to indicate elements having certain phase properties in the context of coding metasurfaces. For instance, in a 2-bit coding system, the codes ’00’, ’01’, ’10’, and ’11’ correspond to phase shifts of $0^\circ$, $90^\circ$, $180^\circ$, and $270^\circ$, respectively. The arrangement of these coded elements across the surface defines the overall phase distribution pattern of the metasurface.

Based on this understanding, the design process for a coding metasurface starts by creating unit cells that provide specific phase responses. By carefully arranging these elements, it is possible to induce phase cancellation a spatial method used to suppress RCS. This arrangement allows for either destructive interference or the formation of a phase gradient, enabling precise manipulation of the reflected beam’s direction. Several studies have proposed phase distribution methods using chessboard metasurfaces^5,19,23,24 and coding sequences^25,26,27,28. A checkerboard arrangement of unit cells disperses EM waves into two or four symmetrically reflected beams, reducing monostatic RCS. However, optimizing the coding sequence can scatter beams in multiple directions, leading to improved RCS reduction. The earlier research showed that the annealing procedure outperformed alternative optimization methods for efficient RCS reduction using PB metasurfaces over a broad bandwidth²⁹. Absorptive metasurfaces reduce RCS by dissipating incident electromagnetic energy through the inherent lossy characteristics of unit cells, such as resistive, dielectric, and magnetic losses^30,31,32. A single-band polarization conversion-coded design achieving a 10 dB reduction was presented in³³, while a dual-band design using the same technique was introduced in³⁴.

Some designs incorporate both absorption and phase cancellation mechanisms. For example,³⁵ presented an absorption mechanism using lumped resistors, achieving an 8 dB RCS reduction with a dual-band high-frequency random phase distribution. Another design³⁶ demonstrated RCS reduction from 1.55–19.2 GHz by employing multilayer phase cancellation and absorption mechanisms. Similarly, a wideband RCS reduction was proposed in³⁷ using a double-layered metasurface combining both mechanisms. However, these works do not achieve a lower RCS index with a dual mechanism. The design in³⁸ reduced RCS to 10 dB using absorption and phase diffusion principles but did not achieve a 20 dB reduction.

More recent advances in coding metasurfaces have enabled greater RCS reductions. A 1-bit coding metasurface uses two types of unit cells, ’0’ and ’1’^{13,39,40,41,42}. Phase cancellation reduces the RCS by 10 dB when the two unit cells have a phase difference of $180^\circ \pm 37^\circ$. A diffusion-type checkerboard technique that produced a 10 dB RCS reduction was described by⁴³. Diffusion, absorption, and polarization conversion methods were suggested in^44,45 to improve reduction even more.

A coding metasurface facilitates greater RCS reduction potential and advanced phase control by combining four distinct elements (’00’, ’01’, ’10’, and ’11’) in a 2-bit arrangement²⁰. According to⁴⁶, a 2-bit matrix-structured coding sequence in the 8–16 GHz frequency range was used to achieve a 10 dB RCS reduction. Additionally, a broad 10 dB RCS reduction was suggested utilizing phase cancellation metasurfaces in¹⁰, and an optimized 2-bit design achieved a 10 dB RCS reduction spanning the 7.5–17.5 GHz range in⁴⁷.

RCS is a critical factor in stealth applications, as it directly influences the detection range of a target. For example, reducing RCS by 10 dB can shorten the detection range from 100 miles to 56 miles, while a 20 dB reduction decreases it to 32 miles⁴⁸. A lower RCS shortens the reaction time available to enemy radar systems⁴⁹. While earlier designs focused on achieving 10 dB reduction, this is insufficient for modern stealth requirements. A 10 dB RCS reduction reduces energy by 90%, which is inadequate against advanced radar technologies. Few studies have investigated 20 dB reduction, and experimental characterization remains scarce. Only⁴⁸ reported experimental results using lumped resistors for absorption, a method unsuitable for practical applications. An absorption and diffusion mechanism achieving 20 dB reduction was proposed in⁵⁰ using a checkerboard metasurface. To the best of our knowledge, a 2-bit metasurface design achieving 20 dB reduction with combined polarization conversion, diffusion, and improved bandwidth has not yet been reported for defense applications.

We present RCS reduction strategies based on polarization loss, phase cancellation and diffusion methods for 1-bit and 2-bit coding metasurfaces. For efficient phase cancellation, the metasurface implements the PB phase using a three-layer structure. The 1-bit arrangement achieves a 10 dB RCS reduction by maintaining out-of-phase behavior within the intended frequency band by aligning unit cells of the same size and shape orthogonally. A 20 dB RCS decrease was obtained by optimizing the coding approach for the 2-bit metasurface using a GA. Both x- and y-polarized linear waves can behave consistently because of the unit cells’ anisotropic character. Computational simulations and experimental data confirm the performance and reliability of the designed metasurfaces. The 2-bit design demonstrates 20 dB RCS reduction, surpassing existing methods, while the 1-bit design achieves 10 dB reduction. This work offers significant potential for practical stealth applications.

Unit cell design

Unit cells ’0’ and ’1’ are arranged in a 1-bit configuration with a $180^\circ$ phase difference at the start of the design. ’00’, ’01’, ’10’, and ’11’ are bit patterns that are utilized in the same 2-bit coding metasurface architecture. The corresponding reflective phase angles for these bit patterns are $0^\circ$, $90^\circ$, $180^\circ$, and $270^\circ$. The construction of this metasurface involves a proposed broadband polarization conversion, which includes a metallic patch printed on an ultrathin Rogers RT-5880 substrate. The ultrathin height of this substrate facilitates easier usage of the material, avoiding the need for different materials.

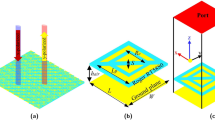
Figure 1 illustrates an example of one of the unit cells. To permit circular rotation to reach PB phase, the design has a circular gap in the patch with concentric incisions. The symmetrical character of the patch is indicated by a layer along the symmetric axes, ’j’ and ’k’. $\psi$ represents the rotation angle between the ’j-axis’ and the ’k-axis’. $p=7.3$ mm, $t=0.9$ mm, $c=4.3$ mm, $d=0.3$ mm, $u=1.34$ mm, $w=1.59$ mm, $l=0.51$ mm, $r=2.15$ mm, $f=0.95$ mm, $i=4$ mm, $h_1=0.25$ mm, and $h_2=2.3$ mm are the unit cell dimensions determined by careful analysis and simulations.

As a metallic patch on the substrate, the copper film has a thickness of 0.035 mm. The Rogers RT-5880 substrate’s ultrathin profile has a height of 0.25 mm. The ground plane is 2.3 mm above the substrate and has a thickness of 0.2 mm. The matrix for the LP wave is provided by the symmetrical properties of the metasurface structure ⁷:

$$\begin{aligned} R_{L-jk} = \begin{pmatrix} r_{jj} & 0 \\ 0 & r_{kk} \end{pmatrix} \end{aligned}$$

(1)

The $r_{jj}$ and $r_{kk}$ in Eq. (1) are both near to 1 because of the extremely low dielectric loss. Consequently, for smaller dielectric loss, the following formula is applicable:

$$\begin{aligned} r_{kk} = r_{jj} e^{-i \Delta \varphi _{jk}} \end{aligned}$$

(2)

The phase difference between $r_{jj}$ and $r_{kk}$ is $\Delta \varphi _{jk}$. The transformation of the jk-coordinate to the xy-coordinate system will be demonstrated when the patch is rotated at an angle $\psi$ as ⁷:

$$\begin{aligned} \begin{pmatrix} E_{x} \\ E_{y} \end{pmatrix} = \begin{pmatrix} \cos \psi & -\sin \psi \\ \sin \psi & \cos \psi \end{pmatrix} \begin{pmatrix} E_{j} \\ E_{k} \end{pmatrix} \end{aligned}$$

(3)

Therefore, the LP xy-coordinate can be calculated by the following equations:

$$\begin{aligned} \begin{pmatrix} E_{x}^{r} \\ E_{y}^{r} \end{pmatrix} = \begin{pmatrix} \cos \psi & -\sin \psi \\ \sin \psi & \cos \psi \end{pmatrix} \begin{pmatrix} r_{jj} & 0 \\ 0 & r_{kk} \end{pmatrix} \begin{pmatrix} \cos \psi & -\sin \psi \\ \sin \psi & \cos \psi \end{pmatrix} \begin{pmatrix} E_{x}^{i} \\ E_{y}^{i} \end{pmatrix} \end{aligned}$$

(4)

$$\begin{aligned} R_{L-xy} = \begin{pmatrix} r_{jj} \cos ^2 \psi + r_{kk} \sin ^2 \psi & (r_{jj} - r_{kk}) \cos \psi \sin \psi \\ (r_{jj} - r_{kk}) \cos \psi \sin \psi & r_{jj} \sin ^2 \psi + r_{kk} \cos ^2 \psi \end{pmatrix} \end{aligned}$$

(5)

For PB phase reflection coding metasurface, the magnitudes of $r_{++}$ and $r_{--}$ should be 1.The $r_{++}$ and $r_{--}$ denote the reflection coefficients for co-polarized components in the linear polarization basis. The PB metasurface phase difference between $r_{jj}$ and $r_{kk}$ should be equivalent to $180^\circ$, therefore $r_{jj}$ and $r_{kk}$ will both have magnitude 1, as indicated by the subsequent equation:

$$\begin{aligned} \left| r_{++} \right| = \left| r_{--} \right| = \sqrt{ \frac{1 - \cos \Delta \varphi _{jk}}{2} } \quad \text {or} \quad \left| r_{-+} \right| = \left| r_{+-} \right| = \sqrt{ \frac{1 + \cos \Delta \varphi _{jk}}{2} } \end{aligned}$$

(6)

Fig. 1

Proposed unit cell structure and side view.

Fig. 2

(a) LP normal incidence simulated reflection coefficient and phase difference of the unit cell. (b) Simulated phase results of $r_{++}$ under LP normal incidence. (c) Simulated phase results of $r_{--}$ under LP normal incidence.

In Eq. (6) the $r_{++}$ denotes the reflection when the incident and reflected waves are both x-polarized, and $r_{--}$ denotes the reflection when both are y-polarized. The cross-polarized components, where the polarization changes from x to y or vice versa, are notated separately as $r_{+-}$ and $r_{-+}$. The computational models were validated using CST Microwave Studio 2021 in order to improve comprehension of polarization conversion. The simulations demonstrated a $180^\circ$ phase difference and were carried out over a broad frequency range from 11.6 to 21.1 GHz using j and k polarized incidences. Between 11.6 and 21.1 GHz, the phase difference between $r_{++}$ and $r_{-+}$ is shown in Fig. 2. It is observed that while $|r_{-+}|$ approaches a value of 0 (linear scale) within this frequency range, $|r_{++}|$ remains close to 1 (linear scale). These results validate a strong agreement across the datasets and are in line with the calculated outcomes.

The unit cell was subjected to several simulations using a LP wave, with the metallic patch rotated at angles $\psi$ from $0^\circ$ to $157.5^\circ$ in steps of $22.5^\circ$. Figure 2 shows that as the rotation angle step increases, $r_{++}$ steadily increases, while $r_{--}$ gradually decreases within the designated frequency band. At a $45^\circ$ rotation angle, the PB phase of $r_{++}$ and $r_{--}$ is denoted as $\varphi _{++}$ and $\varphi _{--}$, respectively. Rotating the metallic patch from $0^\circ$ to $157.5^\circ$ in $22.5^\circ$ increments produces a phase difference at each step, enabling the unit cell’s use in 1-bit to 3-bit metasurface designs.

In Table 1, PCM is used to design different bit-coding metasurfaces with specified reflection phases. The primary emphasis is on the designs of 1-bit and 2-bit metasurfaces. Consequently, $\theta$ will be set at $0^\circ$ and $90^\circ$ for the 1-bit design, while for the 2-bit design, it will be $0^\circ$, $45^\circ$, $90^\circ$, and $135^\circ$.

Table 1 Multi-bit rotation angles, corresponding phase shifts, and bit encoding for the proposed unit cell designs.

Polarization loss of unit cell and current distribution

The designed unit cell is a periodic structure of subwavelength size; hence, effective medium theory can be employed to analyze its absorption properties. The absorption formula, as presented in⁵¹, is presented as:

$$\begin{aligned} A(\omega ) = 1 - R(\omega ) - T(\omega ) \end{aligned}$$

(7)

Angular frequency is denoted by $\omega$ in Eq. (7), while reflectivity and transmissivity are denoted by $R(\omega )$ and $T(\omega )$, respectively. However, $T(\omega )$ is near zero due to the metallic plate at the back, therefore our design does not employ a two-port analysis. Therefore, reflectivity is the only factor that affects the absorption equation⁵¹:

$$\begin{aligned} R(\omega ) = |r_{xx}|^2 + |r_{xy}|^2 \quad \text {or} \quad R(\omega ) = |r_{yy}|^2 + |r_{yx}|^2 \end{aligned}$$

(8)

According to Eq. (8), the reflection coefficients $r_{xx}$, $r_{yy}$, $r_{xy}$, and $r_{yx}$, which stand for the co-polarization and cross-polarization components, respectively, define the incident wave’s absorption. Both the co-polarization and cross-polarization components of these reflection coefficients must be considered when assessing absorption.

In this design, the absorption characteristics are not primarily due to ohmic losses, as the Rogers substrate possesses minimal ohmic loss. Specifically, energy is transferred from the incident polarization to cross-polarization components, which is significant in metasurfaces designed with anisotropic or polarization-converting elements. This phenomenon is supported by the substantial contribution of the cross-polarized reflection coefficients to the total reflectivity. Consequently, the reduction in reflectivity and the corresponding increase in absorption are largely governed by polarization effects rather than material losses. Three distinct resonance frequencies are observed at 13.6, 17.9, and 18.4 GHz, as shown in Fig. 3. These resonances originate from antiparallel surface currents between the top and bottom metallic layers, which are indicative of magnetic dipole responses rather than plasmonic resonances. This magnetic behavior is further illustrated by the surface current distributions in Fig. 3(b–d), which provide insight into the polarization conversion mechanism.

Fig. 3

(a) Simulated absorption and reflection coefficients for the designed unit cell under LP normal incidence. Surface current distributions under LP normal incidence for the top and bottom layers of the unit cell at (b) 13.6 GHz, (c) 17.6 GHz, and (d) 18.4 GHz.

The arrows in the surface current plots represent the dominant direction of current flow, extracted from the real part of the simulated complex surface current density vectors. These are highlighted in regions of high current magnitude to emphasize areas with significant resonant activity. At each of the three resonant frequencies, enhanced current densities are observed particularly around the patch circumference. These enhancements are attributed to edge effects and magnetic resonance phenomena, which are crucial to facilitating polarization conversion.

It is clearly evident from Fig. 3 that the surface currents are antiparallel in all three cases, confirming that the resonances at 13.6, 17.9, and 18.4 GHz from magnetic resonances. This behavior is distinct from plasmonic resonances, which are typically associated with collective electron oscillations and occur predominantly at optical or infrared frequencies.

Within the dielectric region of the structure, magnetic resonances enhance the effective magnetic permeability, thereby increasing the surface impedance relative to free space. This high-impedance characteristic is a key factor in achieving effective cross-polarization conversion. Thus, the magnetic nature of the observed resonances plays a pivotal role in the polarization manipulation capabilities of the proposed metasurface⁵².

Angular stability plays a crucial role in enabling bistatic applications, where incident EM waves strike the metasurface from various angles. For most practical applications, it is essential that the metasurface response remains invariant to the polarization of the incident wave. Therefore, the structure’s performance was evaluated under different polarization angles to assess its robustness. The PCR was analyzed under oblique incidence of LP EM waves, as illustrated in Fig. 4. Within the frequency range of 11.6–21.1 GHz, the PCR remains relatively stable for oblique incidence angles up to 30$\phantom{0}^\circ$. Although a slight frequency shift is observed along with some variation in PCR around the mid-frequency range, the conversion efficiency consistently exceeds 90%, indicating excellent performance. This angular stability is attributed to the low substrate thickness and compact unit cell dimensions. At lower frequencies, the unit cell dimension corresponds to 0.282$\lambda$, which is relatively small compared to the operational wavelength, ensuring minimal dispersion effects. However, at higher frequencies, some degradation in PCR is noted due to changes in the relative unit cell size with respect to the wavelength. Overall, the proposed metasurface demonstrates remarkable angular stability under LP wave oblique incidence up to 30$\phantom{0}^\circ$, making it a strong candidate for angularly robust polarization conversion in bistatic and other practical EM applications.

Fig. 4

Simulated PCR performance of the metasurface under oblique incidence ($\theta$) of linearly polarized EM waves for various incident angles.

RCS reduction for stealth applications

RCS reduction for stealth targets is a promising area in EM fields. Theoretically, the RCS expression of the scattering field is given as⁵³:

$$\begin{aligned} \sigma = \lim _{r \rightarrow \infty } 4 \pi r^2 \left| \frac{E_s}{E_i} \right| ^2 = \lim _{r \rightarrow \infty } 4 \pi r^2 \left| \frac{H_s}{H_i} \right| ^2 \end{aligned}$$

(9)

The incident and scattered electric field amplitudes in the far-field areas are denoted by $E_i$ and $E_s$, respectively, and the incident and scattered magnetic field amplitudes by $H_i$ and $H_s$. The RCS formula is given in⁵³ and is represented in dBsm:

$$\begin{aligned} \sigma \, (\textrm{dBsm}) = 10 \log \left| \sigma \, (m^2) \right| = 10 \log \left[ \lim _{r \rightarrow \infty } 4 \pi r^2 \left| \frac{E_s}{E_i} \right| ^2 \right] \end{aligned}$$

(10)

Practically, when the enemy target is distant from the radar, the incident waves can be approximated as plane waves. The incident wave can be practically described as a plane wave when the transmitter and receiver are far from the target. The incident or dispersed fields are hence independent of one another.

In random coding theory, a 1-bit design employs two configurations of the same anisotropic unit cell, typically rotated by $\psi = 0^\circ$ and $\psi = 90^\circ$, respectively, to achieve a phase difference of approximately $180^\circ$ in the cross-polarized reflection. These rotated configurations, referred to as unit cell ”0”and unit cell ”1”, enable the binary phase coding required for RCS reduction. Unlike traditional polarization-converting metasurfaces that rely on mirror-symmetric unit cells to achieve a $180^\circ$ phase difference, our design leverages the polarization-dependent anisotropic behavior of the unit cell. Although the rotated unit cells are not geometric mirror images, their polarization dependent anisotropic behavior results in a $180^\circ$ phase difference in the cross-polarized reflection coefficient when rotated $90^\circ$, functionally mimicking the mirror configuration commonly used in polarization-converting metasurfaces (PCM) designs. The RCS reduction in a 1-bit design (where 1-bit RCS refers to the RCS calculated for a metasurface composed of unit cells that can reflect waves with two discrete phase states, i.e., $0^\circ$ or $180^\circ$ of the reflected wave), compared to an identically sized copper plate, is expressed as⁵⁴:

$$\begin{aligned} \sigma _{\textrm{reduction}} = 10 \log \left| \frac{A_1 e^{j \varphi _1} + A_2 e^{j \varphi _2}}{2} \right| ^2 \end{aligned}$$

(11)

$A_1$ and $A_2$ represent the complex reflection coefficients of the unit cells, while $\varphi _1$ and $\varphi _2$ denote their respective phase shifts, typically exhibiting a phase difference of approximately $180^\circ$. In the case of polarization-converting metasurfaces, these reflection coefficients correspond to the cross-polarized reflected components, unless otherwise stated. A phase difference of about $180^\circ$ between the unit cells is required for efficient polarization conversion. Consequently, the RCS reduction is expressed as⁵⁴.

$$\begin{aligned} \sigma _{\textrm{reduction}} = 10 \log \left| \frac{1 + e^{j(\varphi _1 - \varphi _2)}}{2} \right| ^2 \end{aligned}$$

(12)

It is important to note that Eq. (12) is derived under ideal conditions, assuming a constant phase difference of $180^\circ$ between the unit cells and equal reflection amplitudes, that is, $A_1 = A_2 = 1$. However, in practical metasurface designs, the reflection amplitudes vary with frequency due to the dispersive nature of the structure. This frequency dependence significantly affects the RCS reduction performance. In PCM, the co-polarized reflection components (such as $R_{xx}$ or $R_{yy}$) are suppressed at specific frequencies, while the cross-polarized components (such as $R_{xy}$ or $R_{yx}$) are enhanced. As a result, the RCS reduction can exceed the 10 dB predicted by the theoretical model. The minima observed in the simulated RCS correspond to frequencies where the reflection amplitude variation is most pronounced, rather than being solely dictated by the phase behavior. In particular, within the operational bandwidth where the co-polarized reflection coefficient falls below 0.1, enhanced polarization conversion leads to improved RCS suppression, as confirmed by the simulation results.

A 90% decrease in the target’s radar reflectivity necessitates a phase difference between the unit cells of between $143^\circ$ and $217^\circ$¹². Eq. (12) results in a theoretical RCS reduction of approximately 10 dB under ideal phase difference conditions. For a 2-bit design of the metasurface, which consists of four unit cells with different phase values, the 2-bit RCS reduction formula is given as:

$$\begin{aligned} \sigma _{\textrm{reduction}} = 10 \log \left| \frac{A_{00} e^{j \varphi _{00}} + A_{01} e^{j \varphi _{01}} + A_{10} e^{j \varphi _{10}} + A_{11} e^{j \varphi _{11}}}{4} \right| ^2 \end{aligned}$$

(13)

The unit cell reflection coefficients are denoted by $A_{00}$, $A_{01}$, $A_{10}$, and $A_{11}$, and $\varphi _{00}$, $\varphi _{01}$, $\varphi _{10}$, and $\varphi _{11}$ represent their respective phases. These reflection coefficients correspond to the cross-polarized reflected field, consistent with the polarization conversion behavior of the metasurface. According to polarization conversion theory and typical 2-bit coding design practice, the amplitudes of specific unit cell pairs are assumed equal (i.e., $A_{00} = A_{10}$ and $A_{01} = A_{11}$), as they are designed to provide the same magnitude response in the cross-polarized reflected component, differing only in their phase response. This symmetry helps maintain uniform scattering strength while enabling phase manipulation for RCS reduction. According to polarization conversion theory, the following relations hold: $A_{00} = A_{10}$, $A_{01} = A_{11}$, and $\varphi _{00}$, $\varphi _{01}$, $\varphi _{10}$, $\varphi _{11}$ follow the corresponding phase relations. Therefore, the RCS reduction formula simplifies to:

$$\begin{aligned} \sigma _{\textrm{reduction}} = 10 \log \left| \frac{A_{00} \left( e^{j \varphi _{00}} + e^{j \varphi _{01}} \right) + A_{10} \left( e^{j \varphi _{10}} + e^{j \varphi _{11}} \right) }{4} \right| ^2 \end{aligned}$$

(14)

While Eqs. (13) and (14) apply to metasurfaces composed of unit cells with consistent polarization behavior (e.g., fully cross-polarized PCM structures), generalizing these expressions to a metasurface containing a mix of PCM and non-PCM unit cells (e.g., combining $R_{yx}$ and $R_{yy}$) is non-trivial. In such cases, the superposition principle used in Eq. (13) would not strictly hold due to differing polarization bases, and the total RCS reduction would need to account for the vectorial nature of the scattered fields and their interactions. This remains a potential area for extended theoretical and simulation-based investigation.

In this work, the reflection coefficients used in Eq. (13) and Eq. (14) represent the cross-polarized components of the reflected field, i.e., $R_{xy}$ or $R_{yx}$, which are dominant in PCM. For metasurfaces without polarization conversion (non-PCM), the co-polarized components such as $R_{xx}$ or $R_{yy}$ are dominant and would require separate treatment in the RCS reduction formulation.

As presented in the RCS reduction formulas above, the unit cell design, phase difference, and reflected magnitude play crucial roles in achieving RCS reduction. In particular, achieving a 20 dB reduction in RCS requires precise control over both the phase variation and the reflection coefficient amplitude to meet the desired suppression level.

1-Bit coding metasurface design for 10dB RCS reduction

Achieving a 90% reduction in radar waves has been the emphasis of low RCS in stealth technologies. The coding metasurface will scatter EM waves in different directions, thereby reducing the RCS. Our unit cell has polarization conversion properties; now, the coding arrangement will add diffusion properties, resulting in further RCS reduction. The metasurface design will be achieved by arranging different types of unit cells with varying phase values but nearly the same amplitude.

It is now possible to control the phase response of individual unit cells thanks to the development of PB phase technique. Because the unit cell design is symmetrical, rotating metallic structure is necessary to achieve a phase shift that is nearly $180^\circ$. Therefore, the metallic element inside each unit cell must rotate $90^\circ$ in order to build a 1-bit metasurface.

The author presents the far-field equation as follows²⁰:

$$\begin{aligned} F(\theta , \varphi ) = f_e(\theta , \varphi ) \cdot AF_{6 \times 6}(\theta , \varphi ) \end{aligned}$$

(15)

The elevation angle is $\theta$, while the azimuth angle is $\varphi$. $f_e(\theta , \varphi )$ describes the dispersion pattern of coding elements, and Eq. (16) gives the array factor. In this case, $k_0$ stands for the wave vector, and D indicates the separation between the metasurface’s elements. For most 1-bit and 2-bit designed coding elements, the reflection amplitude is about the same, but the reflection phases differ. After optimization, phase cancellation causes the highest RCS reduction as a result of this phase fluctuation.

$$\begin{aligned} AF_{6 \times 6} = \sum _{m=1}^{6} \sum _{n=1}^{6} \exp \left\{ -i \left[ \varphi (m, n) + k_0 D \sin \theta \left( (m - \tfrac{1}{2}) \cos \varphi + (n - \tfrac{1}{2}) \sin \varphi \right) \right] \right\} \end{aligned}$$

(16)

In a 1-bit metasurface design, the scattering phase at location (m, n), represented as $\varphi (m,n)$, assumes values of $0^\circ$ and $180^\circ$. According to²⁰, this binary phase modulation efficiently suppresses the main lobe, increasing the metasurface’s directivity.

$$\begin{aligned} Dir(\theta , \varphi ) = \frac{4 \pi \left| F(\theta , \varphi ) \right| ^2}{\int _{0}^{2\pi } \int _{0}^{\frac{\pi }{2}} \left| F(\theta , \varphi ) \right| ^2 \sin \theta \, d\theta \, d\varphi } \end{aligned}$$

(17)

The following is an expression for the metasurface’s lower RCS as compared to a typical metallic plate:²⁰:

$$\begin{aligned} RCS\_reduction = \frac{\lambda ^2}{4 \pi N^2 D^2} \cdot \max \left[ Dir(\theta , \varphi ) \right] \end{aligned}$$

(18)

Fig. 5

Proposed design: (a) arrangement of unit cells in the 1-bit metasurface, (b) layout of the 1-bit metasurface, (c) simulated RCS comparison under normal incidence for x- and y-polarized plane waves between the checkerboard and 1-bit metasurface designs, and (d) simulated RCS reduction results under x- and y-polarized normal incidence for both checkerboard and 1-bit metasurface configurations.

Based on Eqs. (15)–(17), it can be concluded that scattering control is achievable through appropriate coding of the metasurface elements. A similar strategy was applied in²⁰, where the meta-atoms were arranged using different matrix configurations to get 10 dB RCS reduction. This strategy was further validated in⁵⁵ using identical bit sequences in dual-band unit cell designs.

Utilizing Eqs. (15)–(18), effective scattering control can be realized in a 1-bit configuration. For example, metasurface arrangements such as 11/11 or 00/00 result in uniform phase distribution among unit cells, causing complete reflection of the incident EM waves characteristic of a perfect electric conductor. Consequently, these configurations are unsuitable for RCS reduction.

Alternatively, sequences like 01/01 or 10/10 produce two main scattering beams directed toward $90^\circ$ and $270^\circ$. In contrast, checkerboard patterns such as 01/10 or 10/01 distribute scattering into four directions: $45^\circ$, $135^\circ$, $225^\circ$, and $315^\circ$. This highlights the importance of a carefully designed coding scheme to induce diffuse reflection and cancel out scattered waves. To enhance scattering suppression, an aperiodic unit cell arrangement is proposed. Fig. 5(a) shows the construction of a metasurface layout made up of a $6 \times 6$ lattice consisting of $(4 \times 4)$ unit cells. In this configuration, black regions represent lattice ‘1’ (phase $0^\circ$), while gray regions represent lattice ‘0’ (phase $180^\circ$). Whereas Fig. 5(b) shows the simulated metasurface design.

Fig. 6

(a) Schematic diagram showing the optimized arrangement of unit cells in the 1-bit metasurface. (b) Layout of the optimized 1-bit metasurface design. (c) x-polarized and y-polarized normal incidence plane waves simulated RCS comparison between the checkerboard and optimized 1-bit metasurface designs. (d) Simulated x-polarized and y-polarized normal incidence plane waves RCS reduction results achieved by the checkerboard and optimized 1-bit metasurface designs.

For the RCS reduction evaluation, the metasurface was simulated using CST Microwave Studio with open boundary conditions and a plane wave excitation. The plane wave struck the metasurface from the direction of $-z$. Fig. 5(c) shows a comparison between the metallic plate and the intended 1-bit metasurface for x- and y-polarized waves. Fig. 5(d) displays the normalized RCS reduction for x- and y-polarized waves. It demonstrates that the symmetric layout of unit cells renders RCS reduction almost identical for both polarization states. Approximately 12.4–19.2 GHz is the frequency band where a 10 dB RCS drop is achieved. The reduction decreases slightly from 10 dB in the 13.7–14.4 GHz frequency. To solve this, as shown in the dual-band characteristic design was slightly altered in Fig. 6 to obtain a 10 dB drop across the range of frequency 12.3–19.2 GHz.

Fig. 7

(a) Simulated far-field RCS reduction comparison under various LP oblique incidences for the 1-bit metasurface design; (b) simulated 3D scattering RCS at a $15^\circ$ oblique LP incidence on the 1-bit metasurface at different frequencies; (c) simulated 3D scattering RCS at a $15^\circ$ oblique LP incidence on a copper plate of identical dimensions across the same frequency range.

Figure 7 (a) illustrates the LP oblique incidence far-field RCS reduction, and Fig. 7 (b-c) show the 3D scattering pattern (at $\theta = 15^\circ$) for an LP oblique incident wave in contrast to a metallic plate of the same size. The results show that the diffuse scattering characteristic is effectively achieved using a 1-bit metasurface up to $\theta = 15^\circ$. In the frequency range of 12.5–18.9 GHz, an RCS reduction of 10 dB is achieved by oblique incidence up to $15^\circ$. Furthermore, the bandwidth of RCS reduction decreases with increasing oblique incidence angles, which is evident due to decrease of PCR. In the whole frequency range when the PCR is above 90%, the RCS reduction is greater than 10 dB.

Figure  8 presents the simulated bistatic RCS performance of the 1-bit metasurface under LP normal incidence at selected frequencies of 13.1 GHz, 16 GHz, 18.9 GHz, and 20.1 GHz. Both x-polarized and y-polarized incident waves were considered, as shown in subfigures (a)–(d) and (e)–(h), respectively. The metasurface’s performance is compared against an identically sized metallic plate. At 13.1 GHz, 16 GHz, and 18.9 GHz, the metasurface demonstrates a significant reduction in bistatic RCS for both polarization cases. However, at 20.1 GHz, the reduction effect is less pronounced, likely due to decreased performance near the upper edge of the operating frequency band. The observed RCS reduction results from destructive interference between the scattered waves from the metasurface elements, redirecting energy into multiple directions rather than reflecting it coherently. This leads to up to a 10 dB reduction in RCS compared to the metallic reference. The simulations were conducted in CST Microwave Studio using the bistatic scattering template, which enables far-field data extraction over a wide angular range ($-90^\circ$ to $+90^\circ$ in the azimuthal plane). This template was preferred over the monostatic scattering template, as it is more suitable for evaluating wide-angle and broadband bistatic scattering behavior. A far-field monitor was configured to sweep across this angular range under normal incidence plane wave excitation for both x- and y-polarizations ($\phi = 0^\circ$ and $\phi = 90^\circ$). The time-domain solver was employed due to its broadband efficiency, with GPU acceleration enabling large-scale transient simulations. The metasurface was modeled as a large structure, and the simulation domain was defined using the “open (add space)” boundary condition to minimize artificial reflections and allow accurate representation of free-space propagation. A hexahedral mesh was applied, and adaptive mesh refinement (AMR) was used with strict settings: 2–10 passes, a mesh increment of 3, and a maximum delta of 0.01 over the frequency range of interest. The refinement strategy was set to “Expert system based,” with hexahedral refinement applied in the X, Y, and Z directions to ensure accurate resolution of the metasurface geometry and electromagnetic field discontinuities.

Fig. 8

Simulated bistatic RCS of the 1-bit metasurface design at 13.1 GHz, 16 GHz, 18.9 GHz, and 20.1 GHz for $\varphi = 0^\circ$ and $\varphi = 90^\circ$, under x-polarized (a–d) and y-polarized (e–h) incident waves.

Coding metasurface 2-bit design for 20dB RCS reduction

After achieving a 10 dB RCS reduction using a 1-bit coding metasurface, it becomes necessary to explore methods capable of attaining a further reduction, targeting 20 dB. The limitation of 1-bit coding lies in its binary phase control, offering only a $180^\circ$ phase difference. To overcome this limitation and enhance the efficacy of RCS reduction, a 2-bit coding metasurface is selected. This design utilizes a $4 \times 4$ unit cell arrangement to construct a $6 \times 6$ metasurface. In the 2-bit configuration, four distinct coding elements are introduced, each exhibiting unique reflection amplitudes while maintaining consistent phase differences. A random coding sequence is applied to these elements under various electromagnetic polarizations to analyze the scattering behavior. According to ¹⁰, the optimal unit cell configuration for maximal RCS reduction is determined using a GA. GA is a nature-inspired optimization technique based on the principles of biological evolution, incorporating mechanisms such as selection, crossover, and mutation. Through iterative refinement, less optimal configurations are eliminated, progressively leading toward an optimal solution. In this work, the metasurface’s coding sequence is optimized via GA. According to¹⁰, the far-field scattering pattern is used to assess each candidate configuration’s suitability.

$$\begin{aligned} fitness = \frac{1}{\max (F(\theta , \varphi ))} \end{aligned}$$

(19)

From Eq. (19), it can be observed that a larger fitness value corresponds to a smaller peak of the AF in Eq. (16). To optimize the coding sequence for maximum RCS reduction, a GA was employed with a mutation probability of 0.052, a population size of 300, and a crossover probability of 0.8. These parameters were selected based on empirical testing, where multiple GA configurations were evaluated using the array factor equation as the fitness function. The objective was to maximize RCS reduction reaching up to 20 dB while keeping computational time within practical limits. In the GA, the mutation probability introduces diversity into the population by randomly altering genes, helping the algorithm avoid local optima. The population size defines the number of candidate solutions in each generation, affecting both convergence reliability and computational cost. The crossover probability governs the frequency of recombination between individuals, encouraging the inheritance of favorable traits. Extensive testing showed that increasing the population size or mutation rate beyond the chosen values provided negligible improvements in RCS reduction, while significantly increasing runtime. As reported in¹⁰, the optimal 2-bit coding sequence was obtained after multiple iterations using these GA parameters. This arrangement was further validated by examining various mirror images of the unit cells, all of which produced the same results, demonstrating the practicality of the metasurface, as presented in Fig. 9.

Fig. 9

Schematic diagram (a) optimized arrangement of unit cells in 2-bit metasurface. (b) 2-bit metasurface design.

Simulated 2-bit results and discussion

As illustrated in Fig. 9(a), the RCS reduction performance of the 2-bit metasurface was evaluated using a $4 \times 4$ unit cell and a $6 \times 6$ arrangement of meta-atoms, whereas Fig. 9(b) presents the designed metasurface used to verify the RCS reduction. There are relatively little variations in the reflection amplitude across the frequency range, which is almost constant across the various coding parts. In contrast, the reflection phases exhibit notable differences. Specifically, the phase difference between the coding states 00 and 10, as well as between 01 and 11, is approximately $180^\circ$. Through a combination of polarization conversion, phase cancellation among unit cells, and absorption mechanisms, proves phase disparity facilitates efficient RCS reduction. When combined, these tactics can lower RCS by as much as 20 dB.

Fig. 10

(a) Simulated x- and y-polarized plane waves RCS of the 2-bit metasurface and metal plate. (b) Simulated RCS reduction for x- and y-polarized normal incidence plane waves, compared to the same size metal plate.

A 2-bit metasurface with the same dimensions as the metallic plate was simulated in order to evaluate RCS reduction under x- and y-polarized plane waves. The findings of the metasurface and metallic sheet simulated RCS are shown in Fig. 10. The monostatic RCS of the coding metasurface is nearly the same for both polarizations due to the symmetry of the cells. In contrast to the metallic plate, the RCS has dramatically dropped. There is a slight difference in RCS between x- and y-polarized waves because complete phase difference cancellation is not accomplished. This disparity is also caused by different unit cell phase arrangements throughout the metasurface.

The findings show that the suggested metasurface reduces the monostatic RCS by about 10 dB between 11.2–20.2 GHz and 20 dB between 12.3–19.5 GHz. For decreases of 10 dB and 20 dB, the corresponding relative bandwidths are 57.3% and 45.3%, respectively.The largest simulated RCS reductions are -36 dB at 13.1 GHz and -33 dB at 18.9 GHz. These results verify that the suggested coding metasurface successfully reduces RCS by 20 dB over a broad frequency range. A 20 dB drop is especially noteworthy since it indicates a mere 1% chance of radar detection in the designated frequency band.

To provide a more detailed performance assessment, Fig. 11 shows the bistatic RCS patterns under x- and y-polarized excitation across various frequencies, specifically 13.1 GHz, 16 GHz, 18.9 GHz, and 20 GHz. The frequencies 13.1 GHz and 18.9 GHz were selected due to the observed dips in the RCS reduction curve, indicating peak performance. The frequency 16 GHz was chosen to evaluate the metasurface’s behavior at a midway point between these dips, while 20 GHz was included to assess the upper boundary where RCS reduction begins to diminish, as shown in the reduction curve. Unlike the metallic plate, which produces significant backscattering, the metasurface redistributes energy onto the side lobes and significantly reduces the intensity of the main lobe. This confirms the metasurface’s effectiveness in suppressing RCS.

Further analysis is provided through the E-plane radiation patterns shown in Fig. 12 for 13.1 GHz, 16 GHz, 18.9 GHz, and 20.1 GHz. Due to their similarity, the corresponding H-plane patterns are omitted. Fig. 12(a–d) represent x-polarized normal incidence, while Fig. 12(e–h) correspond to y-polarized incidence. Effective RCS suppression is achieved by scattering energy into minor lobes, thus reducing the primary lobe in accordance with the principle of energy conservation. While the metallic plate shows strong directional scattering, the metasurface attenuates incident energy more uniformly through its encoded configuration. These observations confirm that the metasurface functions not only as a RCS-reducing structure but also as a diffusive scatterer.

Fig. 11

Simulated bistatic RCS comparison between the 2-bit metasurface design and a metallic plate at 13.1 GHz, 16 GHz, 18.9 GHz, and 20.1 GHz. (a) x-polarized incident plane waves at $\varphi = 0^\circ$ and $\varphi = 90^\circ$; (b) y-polarized incident plane waves at $\varphi = 0^\circ$ and $\varphi = 90^\circ$.

Fig. 12

Simulations of the 2-bit planar metasurface’s radiation patterns. (a–d) x-polarized incident plane waves at 13.1 GHz, 16 GHz, 18.9 GHz, and 20.1 GHz. (e–h) y-polarized incident plane waves at 13.1 GHz, 16 GHz, 18.9 GHz, and 20.1 GHz.

Figure 13(a) displays the oblique far-field RCS reduction, obtained through full-wave simulations in CST Microwave Studio by comparing the 2-bit coding metasurface to a metallic plate of identical size, without relying on Eq. (14) or any analytical approximation. TE-mode excitation was employed, with the electric field polarized along the y-axis and the wave propagating in the x–z plane. This configuration was selected to evaluate the polarization conversion and RCS reduction characteristics under fixed linear polarization, a common and effective approach for capturing the dominant scattering behavior. Reported RCS reduction corresponds to the co-polarized backscattered field, which is suppressed due to diffuse scattering and partial conversion into cross-polarized components. This aligns with monostatic radar detection scenarios, where backscatter reduction is critical. Fig. 13(b) and (c) present the 3D scattering patterns at $\theta = 30^\circ$ for the metasurface and metallic plate, respectively, under LP plane wave incidence. The results demonstrate that the metasurface enables effective diffuse scattering up to a $30^\circ$ oblique angle, achieving an RCS reduction exceeding 10 dB across 12.5–18.9 GHz. Beyond $30^\circ$, while the RCS reduction remains above 10 dB, the operational bandwidth and polarization conversion ratio decline. Compared to the 1-bit design, the 2-bit metasurface exhibits improved angular stability due to enhanced wave dispersion, as shown in Fig. 13.

Fig. 13

(a) LP simulated far-field RCS reduction comparison for various oblique incidences on the 2-bit metasurface design. (b) LP simulated 3D scattering RCS at a $30^\circ$ oblique incidence on the 2-bit metasurface design. (c) LP simulated 3D scattering RCS at a $30^\circ$ oblique incidence on a copper plate of the same size.

Fabrication and measurement

To demonstrate the functionality of the proposed 2-bit coding metasurface, a prototype was fabricated using traditional printed circuit board (PCB) technology, as shown in Fig. 14. The metasurface structure consists of a metallic ground plane, a dielectric substrate, and a top-layer metallic patch. The substrate material is Rogers RT5880, which has a relative permittivity of $\varepsilon _r = 2.2$ and a loss tangent of $\tan \delta = 0.0009$. The thicknesses of the ground plane, substrate, and top-layer copper are 0.2 mm, 0.25 mm, and 0.035 mm, respectively.

Experimental RCS measurements were carried out in an anechoic chamber, as illustrated in Fig. 14(c). The setup involved a pair of horn antennas (for transmission and reception) connected to a Keysight N5224A two-port vector network analyzer (VNA). Two types of horn antennas were used to cover the full frequency range: one operating from 10–18 GHz and another from 18–22 GHz. The measurement was performed under normal incidence using LP wave with the electric field aligned along the y-axis, consistent with the simulation configuration.

The monostatic backscattered signal was received in the co-polarization direction (i.e., same polarization as the incident wave). To suppress reflections from the chamber environment and enhance measurement accuracy, time-domain gating was applied using the VNA’s built-in functionality. The measured RCS values for the metasurface were compared to those of a same-sized copper plate under identical conditions. The RCS reduction was calculated by subtracting the metasurface RCS from the copper plate RCS in the dB scale, following the same methodology as in simulation.

The dimensions of the fabricated metasurface (175.2 mm $\times$ 175.2 mm) influenced the selection of horn antennas for the RCS measurement setup. Two standard gain horn antennas were used to cover the full frequency range: one operating from 1–18 GHz and another from 18–30 GHz. The primary selection criteria included aperture size, beamwidth, gain, and object capturing capability. The aperture dimensions of the horn antennas (approximately 160 mm $\times$ 241 mm) were large enough to fully illuminate the metasurface under test. The antennas exhibited a typical gain of $\sim$11 dBi and a VSWR of 2:1, ensuring efficient transmission and reception. The beamwidths (ranging from $\sim$20$\phantom{0}^\circ$ to 30$\phantom{0}^\circ$ across the band) enabled far-field coverage and ensured that the entire metasurface lay within the main lobe of the radiation pattern. This configuration provided reliable capture of the backscattered signals while minimizing diffraction and edge effects, thus maintaining consistency with the simulation setup.

With the exception of a slight dip between 13.5 and 15.4 GHz (where the reduction was approximately 15 dB), a reduction of about 20 dB was observed in the 12–19.3 GHz range, and around 10 dB in the 11.1–20.3 GHz range. Minor discrepancies between simulated and measured results are attributed to fabrication tolerances, finite-size effects, and alignment uncertainties in the measurement setup.

A comparative summary of this design and related works is presented in Table 2.

Fig. 14

(a) Measuring system schematic diagram. (b) Fabricated metasurface. (c) Experimental setup. (d) LP normal incidence simulated and experimental RCS reduction.

Figure 15 shows the 3D far-field scattering patterns for the proposed metasurface and a metallic plate of the same size under x- and y-polarized incident waves at 13.1 GHz, 16 GHz, 18.9 GHz, and 20.1 GHz. The metallic surface exhibits strong specular reflection, whereas the 2-bit metasurface disperses the reflected energy into multiple directions, indicating its diffusive scattering behavior.

Fig. 15

Simulated 3D far-field scattering pattern of 2-bit metasurface under frequencies of 13.1 GHz, 16 GHz, 18.9 GHz, and 20.1 GHz. (a) x-polarized plane wave metasurface, (b) x-polarized plane wave metallic plate, (c) y-polarized plane wave metasurface, (d) y-polarized plane wave metallic plate.

Conclusion

This work presents a coding metasurface design incorporating polarization conversion and diffusion mechanisms to achieve RCS reduction. A 1-bit metasurface was developed by adjusting unit cell dimensions to obtain a $180^\circ$ phase shift, ensuring a high 10dB RCS reduction across the 11.2–20.2 GHz range. Unit cell layouts on a 2-bit coding metasurface allow for a $22.5^\circ$ phase resolution was presented in order to further improve performance. Using a GA for optimization, the 2-bit design was able to achieve RCS reductions of around 10 dB and 20 dB across the frequency spectrum of 11.2–20.2 GHz and 12.3–19.5 GHz, respectively. A 2-bit metasurface prototype was created and put through experimental testing. The effectiveness of the metasurface in suppressing specular reflections was confirmed by comparing the observed RCS values with those of a reference metallic plate. The experimental results closely align with simulations, demonstrating the metasurface’s effectiveness in electromagnetic wave manipulation. The findings indicate that the proposed design offers a viable and efficient approach for RCS reduction, with promising potential for stealth and electromagnetic interference mitigation applications.

Table 2 Comparison with previous works.