Introduction

The atmosphere is a chaotic system with high nonlinearity and complexity1. The Lorenz system is a set of equations that simplifies the physical process of atmospheric heat convection motion. Although simple, the Lorenz system can qualitatively describe several key characteristics of atmospheric dynamics2. Hence, this system is often used in the field of atmospheric science when exploring chaos theory3,4,5, abrupt climate change6,7, predictability8,9,10, and data assimilation11. Research concerning the Lorenz system has considerable significance in terms of understanding the nonlinear dynamics and complex behavior of the atmosphere.

Causality refers to the way in which events or phenomena interact with each other, with cause followed by effect12. Causal relationships between variables are important in modern natural science research. Causal inference explores the cause of a specific finding and then predicts the future state of the system. Studies in the field of causality often rely on metrics such as the Pearson correlation coefficient13, transfer entropy14, and mutual information15 to quantify both the strength and direction of causal relationships between variables. It should be noted that traditional correlation does not mean causation16,18. Causality has been widely applied in neuroscience19,20, economics21, climatology22,23,24, and ecology25. The selection of atmospheric predictors is an example of application of causal inference26. Therefore, research on causal relationships is important in terms of both theoretical analysis and practical applications.

The methods used to identify causal relationships between variables include, but are not limited to, the Granger causality (GC) model, causal network learning, the information–theoretic approach, and the nonlinear state space model. The GC27 inference method is suitable for linear systems and strongly coupled nonlinear systems. However, for weakly coupled nonlinear systems, the GC algorithm fails to detect the existence of causal drivers. Therefore, researchers have developed nonlinear extensions of the GC algorithm using approaches such as kernel functions28, Copula functions29, and reservoir computing30. The Peter–Clark algorithm is a classical causal network learning method that has been confirmed to be effective in detection of instantaneous causal relationships between variables, but its computational complexity remains a limitation31,32. Subsequent improvements by Runge et al. addressed the critical issues of autocorrelation and nonlinearity of data33,34,35. Information–theoretic methods, such as those based on transfer entropy36, conditional entropy37, and conditional mutual information38,39, quantify causal strength by establishing evaluation metrics. However, in practical applications, computational estimation of high-dimensional probability density functions becomes prohibitive with increasing dimensionality of the input variables40. Sugihara et al. proposed a convergent cross-mapping (CCM)41 algorithm that has significant advantages for the detection of causal relationships within weakly coupled nonlinear systems. From a dynamical systems perspective, CCM effectively addresses the limitations of the GC algorithm by capturing causality under nonlinear, weakly coupled conditions42. Ye et al. extended the CCM method by considering time lag and distinguished between true bidirectional causality and the synchronization phenomenon caused by strong unidirectional forcing43. Building upon the CCM framework, Egbert et al. inferred from dynamical systems theory that climate dynamics are predominantly driven by internal mechanisms in the Earth system rather than by external forcing44. In view of the noise properties inherent in real-world systems, Mønster et al. suggested methods to overcome the weakness of this approach45.

The core principle of the CCM algorithm lies in translating causal relationships into geometric properties within the state space of a dynamical system. The associated algorithmic framework comprises three key steps: first, state space reconstruction; second, cross-mapping; and finally, convergence analysis. The CCM algorithm requires that the reconstructed attractor manifold is diffeomorphism with the original manifold and that the reconstructed manifold can fully reflect the dynamic characteristics of the original manifold41. Failure to satisfy this requirement may result in state superposition during phase space reconstruction, thereby violating the fundamental conditions for valid manifold reconstruction. Hu et al. used Takens’ theorem and the CCM algorithm to identify a significant asymmetric causal drive phenomenon during the causal testing of variables in the classical Lorenz system. They established that variables X and Y exhibit mutual (bidirectional) driving, while variable Z unilaterally drives both X and Y, and variables X and Y do not show a clear causal driving relationship with variable Z46,47. This finding is consistent with the observation of Sugihara et al. that “… in the canonical Lorenz system, variable Z fails to generate a valid attractor manifold.”41 Critically, the difference form of the Lorenz equations explicitly reveals mutual causal driving relationships among variables X, Y, and Z (a point that will be elaborated upon later). Given this discrepancy between the known dynamics and the CCM detection results for the Lorenz system, it is plausible that similar failures to detect existing causal relationships occur in general chaotic models. This indicates that the phenomenon is not unique to the Lorenz system, but rather exposes a potential systematic failure of the CCM algorithm to detect causality when the reconstructed manifold of the variable cannot fully reflect the dynamic characteristics of the original manifold. Such undetected causality is an inherent limitation within the CCM algorithm itself. This paper describes an improved CCM algorithm based on the Lorenz system that addresses this fundamental constraint.

Theory and methods

Lorenz equations

The Lorenz equations can be written in the form

$$\left\{ {\begin{array}{*{20}l} {\frac{dx}{{dt}} = 10( - x + y),} \hfill \\ {\frac{dy}{{dt}} = 28x - y - xz,} \hfill \\ {\frac{dz}{{dt}} = xy - \frac{8}{3}z,\quad \;\;} \hfill \\ \end{array} } \right.$$
(1)

where x is the turning velocity of the convection, y is the temperature ratio between the upper and lower fluids, and z is the vertical temperature gradient. System (1) has three equilibrium points, namely, the origin O (0,0,0), the left equilibrium point L \(( - 6\sqrt 2 , - 6\sqrt 2 ,27)\), and the right equilibrium point R \((6\sqrt 2 ,6\sqrt 2 ,27)\). The relationship between the difference and the derivative is as follows:

$$f^{(n)} (\xi ) = {{\Delta^{n} f_{k} } \mathord{\left/ {\vphantom {{\Delta^{n} f_{k} } {h^{n} }}} \right. \kern-0pt} {h^{n} }},\;\xi \in (x_{k} ,x_{k + 1} ),$$
(2)

where \(\Delta^{n} f_{k}\) is the n-order forward difference of \(f(x)\) at \(x_{k}\) with h as the step size. Based on the above relationship, the difference form of the Lorenz equation at the discrete time k can be obtained as

$$\left\{ {\begin{array}{*{20}l} {x_{k + 1} = (1 - 10h)x_{k} + 10hy_{k} ,\quad \quad } \hfill \\ {y_{k + 1} = (1 - h)y_{k} + 28hx_{k} - hx_{k} z_{k} ,} \hfill \\ {z_{k + 1} = z_{k} + hx_{k} y_{k} - ({8 \mathord{\left/ {\vphantom {8 3}} \right. \kern-0pt} 3})hz_{k} ,\quad \;} \hfill \\ \end{array} } \right.$$
(3)

Equation (3) implies that the evolution of each variable in the system is directly controlled by other variables. This cross-dependence is a mathematical explanation of mutual driving, and reveals the mutual driving relationship between the three variables of the Lorenz equations.

Decomposition of the Lorenz trajectory

The fourth-order Runge–Kutta algorithm can be used to find numerical solutions for system (1). The initial field is (3,5,9), the integral interval is [0,500], the integral step is \(\Delta \tau = 0.01\), and the truncation error is 0.013. The components x, y, and z of the numerical solution are denoted as the time series X, Y, and Z, respectively. Assume that the points on the corresponding trajectory are as follows:

$$P = \{ P_{1} (x_{1} ,y_{1} ,z_{1} ),P_{2} (x_{2} ,y_{2} ,z_{2} ), \ldots ,P_{n} (x_{n} ,y_{n} ,z_{n} )\} ,$$
(4)

The tangent vector of the trajectory at \(P_{i} (x_{i} ,y_{i} ,z_{i} )\) is denoted as \(\alpha_{i}\), and the vector connecting the left and right equilibrium points is \(\overrightarrow {LR}\). The cosine value of the angle \(\theta_{i}\) between the two vectors is denoted as

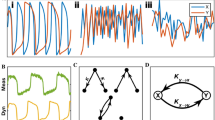
$$\lambda_{i} = \cos \theta_{i} = \frac{{ < \overrightarrow {LR} ,\alpha_{i} > }}{{\left\| {\mathop{LR}\limits^{\rightharpoonup} } \right\| \cdot \left\| {\alpha_{i} } \right\|}},$$
(5)

where \(< \cdot , \cdot >\) denotes the vector inner product and \(\left\| \cdot \right\|\) denotes the norm. From this, the time series \(\{ \lambda_{i} |i = 1,2,3, \cdots \}\) is obtained. Its positive minimal trajectory transitions from right to left, while the negative maximum segment trajectory transitions from left to right. From the end of the positive minimum segment to the start of the negative maximum segment, the trajectory is in the left equilibrium region; from the end of the negative maximum segment to the start of the positive minimum segment, the trajectory is in the region of the right equilibrium point48. Ma et al. used the angle between vectors and the extreme value principle to decompose the Lorenz trajectory into four parts, as shown in Fig. 1. The gray curves represent trajectories within the left equilibrium point region, the light blue curves depict trajectories in the right equilibrium point region, the red curves indicate transition trajectory segments from the right to left equilibrium regions, and the pink curves illustrate transition trajectory segments from the left to right equilibrium regions.

Fig. 1
figure 1

Decomposition of the Lorenz trajectory.

Full size image

CCM algorithm

Let time series X and Y of length L be represented as follows:

$$X = \left\{ {x_{1} ,x_{2} , \ldots ,x_{L} } \right\},$$
(6)
$$Y = \left\{ {y_{1} ,y_{2} , \ldots ,y_{L} } \right\},$$
(7)

where \(x_{i}\) is the value of function \(x(t)\) at time \(t_{i}\) (\(1 \le i \le L\)), which also represents the value of time series X at time \(t_{i}\) (i is a natural number), \(t_{i + 1} - t_{i} = \Delta \tau\); time series Y is similarly represented. To discuss the causal relationship between X and Y, the attractor manifolds MX and MY are reconstructed. At time \(t_{j}\), the vector \(X(t_{j} )\) is formed by E lag values of \(x_{j}\) as follows:

$$X(t_{j} ) = (x_{j} ,x_{j - k} ,x_{j - 2k} , \ldots ,x_{j - (E - 1)k} ),$$
(8)

where \(1 + (E - 1)k \le j \le L\) is for natural number k (i.e., lags of \(k\Delta \tau\), \(2k\Delta \tau\), and so on) and E is the reconstructed phase space dimension. There are three ways to select E and k: the simplex projection algorithm49, according to experience, and the collaborative selection method46. The reconstructed attractor manifold is obtained as

$$M_{X} = \{ X(t_{j} )|1 + (E - 1)k \le j \le L\} .$$
(9)

Similarly, the attractor manifold MY is

$$M_{Y} = \{ Y(t_{j} )|1 + (E - 1)k \le j \le L\} .$$
(10)

Using the reconstructed attractor manifold MX, the cross-mapping estimate \(\hat{Y}(t_{j} )|M_{X}\) of \(y_{j}\) in the time series Y can be calculated, and the E + 1 nearest neighbors of the vector \(X(t_{j} )\) in the reconstructed attractor manifold MX at time \(t_{j}\) can be found. The distance, from small to large, is measured by the indices j1, j2,…, j(E + 1). Therefore, the nearest neighbor of E + 1 is \(X(t_{j1} )\), \(X(t_{j2} )\),…,\(X(t_{j(E + 1)} )\). If the E + 1 nearest neighbors map to the time series Y as \(y_{j1}\), \(y_{j2}\), …, \(y_{j(E + 1)}\), it is possible to estimate \(\hat{Y}(t_{j} )|M_{X}\) as a locally weighted average of these E + 1 values:

$$\hat{Y}(t_{j} )|M_{X} = \sum\limits_{m = 1}^{E + 1} {w_{m} y_{jm} } ,$$
(11)

where \(w_{m}\) is the distance weight between vector \(X(t_{j} )\) and its l-th nearest neighbor \(X(t_{jl} )\) on manifold MX:

$$w_{m} = {{u_{m} } \mathord{\left/ {\vphantom {{u_{m} } {\sum\limits_{l = 1}^{E + 1} {u_{l} } }}} \right. \kern-0pt} {\sum\limits_{l = 1}^{E + 1} {u_{l} } }},\;u_{l} = e^{{ - \frac{{d(X(t_{j} ),X(t_{jl} ))}}{{d(X(t_{j} ),X(t_{j1} ))}}}} ,\;\;(1 \le m \le E + 1).$$
(12)

Here, \(d( \cdot , \cdot )\) is the Euclidean distance between two vectors. The cross-mapping from Y to X is similarly defined.

The Pearson correlation coefficient \(\rho\) for the relationship between time series \(y_{j}\) and the forecast value \(\hat{Y}(t_{j} )\left| {M_{X} } \right.\) is given by the following Eq. 13:

$$\rho (L) = \frac{{\sum\limits_{j = 1 + (E - 1)k}^{L} {(y_{j} - \overline{y})(\hat{Y}(t_{j} )|M_{X} - \overline{{\hat{Y}(t_{j} )|M_{X} }} )} }}{{\sqrt {\sum\limits_{j = 1 + (E - 1)k}^{L} {(y_{j} - \overline{y})^{2} } } \sqrt {\sum\limits_{j = 1 + (E - 1)k}^{L} {(\hat{Y}(t_{j} )|M_{X} - \overline{{\hat{Y}(t_{j} )|M_{X} }} )^{2} } } }},$$
(13)

where \(1 + (E - 1)k \le j \le L\), \(\overline{y}\) is the mean of time series \(y_{j}\) and \(\overline{{\hat{Y}(t_{j} )|M_{X} }}\) is the mean of the forecast value \(\hat{Y}(t_{j} )|M_{X}\). As the time series window length L increases, if

$$\mathop {\lim }\limits_{L \to \infty } \rho (L) = u,$$
(14)

the variable Y is called the driving factor for X, and the absolute value of u indicates the causal strength. The closer the absolute value of u is to 1, the stronger the ability to drive variable Y to X. Conversely, the further the absolute value of u is from 1, the less strong the causal relationship. Convergence in this context means that \(\rho (L)\) approaches a certain value as L increases.

Collection of meteorological data

The Western Pacific Subtropical High Index was obtained from the National Climate Center of China (http://cm-dp.ncc-cma.net/Monitoring/cn_index_130.php). Precipitation data for the middle–lower Yangtze River region (110–118° E, 28–32° N) were sourced from the Daily Dataset of Basic Meteorological Elements in China (V3.0), which is compiled and released by the National Meteorological Information Center, China Meteorological Administration. Both datasets cover the period from January 1961 to December 2024. Data for the Southern Oscillation Index and Niño 3.4 Index covering the period from January 1870 to December 2023 were obtained from the National Oceanic and Atmospheric Administration (https://psl.noaa.gov/data/timeseries/monthly/DS/).

An improved CCM attribution method

Detection of causality between variables of the Lorenz equations

From system (3), we can see that there must be a causal relationship between the solution components X, Y, and Z. The numerical solutions X, Y, and Z derived in section “Decomposition of the Lorenz trajectory” were obtained in the time interval [35, 50] and used as a test series to find the Pearson correlation coefficient \(\rho\) for the relationship between the time series. The results are shown in Fig. 2, where the horizontal coordinate represents the time series window length L. The green curve shows the evolution of the correlation coefficient \(\rho_{{(Y,\hat{Y}(t)|M_{X} )}}\) (indicated by the left ordinate) between \(y_{j}\) and the forecast value \(\hat{Y}(t_{j} )|M_{X}\) with respect to the time series length L, which is also the causal intensity of Y that drives X. The pink curve indicates the evolution of the correlation coefficient \(\rho_{{(X,\hat{X}(t)|M_{Z} )}}\) (indicated by the right ordinate) between \(x_{j}\) and the forecast value \(\hat{X}(t_{j} )|M_{Z}\) with respect to L, and is also the causal strength of X that drives Z, with \(1 + (E - 1)k \le j \le L\). This indicates that the CCM method detected a strong causal relationship in the direction from Y to X (causal strength, > 0.99). The causal relationship from X to Z is very weak (causal strength, ~ 0.14), clearly indicating that there is a missing detection situation when CCM detects the causal relationship between the variables in the Lorenz system. This is consistent with the failure of the study by Hu et al. to detect the unidirectional driving effect of X and Y on Z when investigating the causal relationship between the variables of the Lorenz system46. It also shows that the prediction effect is poor when the attractor manifold MZ is used to predict X. The present research investigated the causal problem of the driving effect of variables X and Y on variable Z, and the steps used to select the parameters are not discussed in detail (we set E = 3 and k = 146,49).

Fig. 2
figure 2

Use of the convergent cross mapping method to detect causality between variables in the Lorenz system (the green curve is the causal strength of Y driving X, corresponding to the left ordinate; the pink curve is the causal strength of X driving Z, corresponding to the right ordinate).

Full size image

Selection of nearest neighbors on the shadow manifold and mapping on the Lorenz trajectory

Suppose that the discrete points on the Lorenz trajectory form a set B:

$$B = \{ (x_{j} ,y_{j} ,z_{j} )|x_{j} \in X,y_{j} \in Y,z_{j} \in Z,{\kern 1pt} \,1 + (E - 1)k \le j \le L\} .$$
(15)

Based on the decomposition of the Lorenz trajectory in Fig. 1, the set B of points on this trajectory is divided into four subsets. The following notation is introduced for convenience: \(B_{R}\) denotes the points in the right equilibrium region, \(B_{R2L}\) denotes the points in the transition segment from the right equilibrium region to the left equilibrium region, \(B_{L}\) denotes the points in the left equilibrium region, and \(B_{L2R}\) denotes the points in the transition segment from the left equilibrium region to the right equilibrium region. The mapping F: \(M_{X} \to B\) between sets MX and B is

$$F((x_{j} ,x_{j - 1} ,x_{j - 2} )) = (x_{j} ,y_{j} ,z_{j} ),$$
(16)

which is a diffeomorphism; that is, MX and each point on B are in one-to-one correspondence with smoothness. Therefore, its preimage manifold MX can also be decomposed into four sets, denoted by \(B_{R}\), \(B_{R2L}\), \(B_{L}\) and \(B_{L2R}\); the color identification is completely consistent with Fig. 1 and is not repeated here.

Figure 3a shows the shadow manifold MX and its decomposition, as well as the points at time \(t_{240}\) (yellow points) and their nearest neighbors (four blue points). Figure 3a' shows the Lorenz trajectory and the image corresponding to mapping (16) with the yellow and blue points in Fig. 3a; the colors are consistent with the original image. Figure 3 indicates that the yellow point and its nearest neighbors (blue points) on the shadow manifold MX in Fig. 3a are in the left equilibrium point region; in Fig. 3a', the images of these points are in the left equilibrium point region of the Lorenz trajectory. By discussing the images of the points and their nearest neighbors at other time points on the Lorenz trajectory, the same conclusion can be reached, namely, that if the points in Fig. 3a and their nearest neighbors are in the left (right) equilibrium region, their images in Fig. 3a' are also in the left (right) equilibrium region of the Lorenz trajectory. If the point in Fig. 3a and its neighbor point are in the transition segment of the left (right) to right (left) equilibrium point region, its image in Fig. 3a' is also in the transition segment of the left (right) to right (left) equilibrium point region on the Lorenz trajectory, as shown in the animation provided in the Supplementary Video 1. The same conclusion can be reached for the shadow manifold MY, as shown in the animation provided in the Supplementary Video 2.

Fig. 3
figure 3

(a) Points on the shadow manifold MX and their nearest neighbors. (a') Image of a point on MX on the Lorenz trajectory.

Full size image

The shadow manifold MZ is now discussed. Consider the map F: \(M_{Z} \to B\) given by

$$F((z_{j} ,z_{j - 1} ,z_{j - 2} )) = (x_{j} ,y_{j} ,z_{j} ).$$
(17)

The preimage manifold MZ can also be decomposed into four sets: \(B_{R}\), \(B_{R2L}\), \(B_{L}\) and \(B_{L2R}\). The color identification is consistent with Fig. 1.

Figure 4a shows the shadow manifold MZ and its decomposition, as well as the points at time \(t_{711}\) (yellow points) and their nearest neighbors (four blue points). From the inset in Fig. 4a, it can be seen that the yellow point and its three nearest neighbors are on the gray track, while one nearest neighbor is on the light blue track. As a result, the position of the mapping image (17) in Fig. 4a' is not synchronized; that is, the yellow point is in the left balance point region of the Lorenz track, but the image of the nearest neighbor (the blue points) lies in the region of the right equilibrium point of the Lorenz track in Fig. 4a', as shown in the animation provided in the Supplementary Video 3. This phenomenon is completely different from that in Fig. 3, and can be observed for other time points. The reason is that the manifold in Fig. 3a has two equilibrium points, but the manifold in Fig. 4a has only one equilibrium point. This is caused by the overlap of the left and right equilibrium points of the manifold MZ, which cannot reproduce the complete dynamic characteristics of the Lorenz system41.

Fig. 4
figure 4

(a) Points on the shadow manifold MZ and their nearest neighbors; (a') Image of a point on MZ on the Lorenz trajectory.

Full size image

Scheme for selection of nearest neighbors on the shadow manifold based on decomposition of the Lorenz trajectory

In section "Selection of nearest neighbors on the shadow manifold and mapping on the Lorenz trajectory", manifold MZ was decomposed into sets \(B_{R}\), \(B_{R2L}\), \(B_{L}\), and \(B_{L2R}\). Accordingly, a new scheme for selecting nearest neighbor points on manifold MZ is now described. If the yellow point \((z_{j} ,z_{j - 1} ,z_{j - 2} ) \in B_{R}\), the search for its nearest neighbor (the blue points) is restricted to set \(B_{R}\); if the yellow point \((z_{j} ,z_{j - 1} ,z_{j - 2} ) \in B_{R2L}\), the search for its nearest neighbor (the blue points) is restricted to set \(B_{R2L}\). That is, when the yellow point is in the light blue region, its corresponding neighbor (the blue points) must be within the light blue region; if the yellow point is in the red region, its corresponding neighbor (the blue points) must also be within the red region, and similarly for other regions. This selection strategy ensures that the yellow point on manifold MZ and its nearest neighbor are on the same color track (the projection on the Lorenz track is in the same region), thereby guaranteeing that the dynamic characteristics of adjacent points on the attractor manifold MZ are consistent with the nearest neighbor points on the Lorenz track. A high degree of synchronization between the local dynamic behavior on manifold MZ and the structure of the Lorenz system is then maintained.

Figure 5 shows the images of points (in yellow) and their neighbors (four blue points) on manifold MZ and on the Lorenz trajectory at time \(t_{711}\) (Fig. 5a and a’), \(t_{551}\) (Fig. 5b and b’), \(t_{517}\) (Fig. 5c and c’), and \(t_{679}\) (Fig. 5d and d’). These points correspond to sets \(B_{L}\), \(B_{R}\), \(B_{L2R}\), and \(B_{R2L}\). Comparing Fig. 4a' with Fig. 5a', b', c', and d’, it can be seen that the selection of points and their nearest neighbors in Fig. 5 ensures that the point and its image on the Lorenz trajectory are in the same region at each moment in time.

Fig. 5
figure 5figure 5

(a–d) Points on the shadow manifold MZ and their nearest neighbors. (a'–d') Image of a point at MZ on the Lorenz trajectory.

Full size image

LdCCM method detects causality between variables in the Lorenz equations

The CCM using the nearest neighbor selection scheme in section “Scheme for selection of nearest neighbors on the shadow manifold based on decomposition of the Lorenz trajectory” is defined as the local dynamic behavior-consistent CCM (LdCCM), the LdCCM algorithm can be used to detect the causal relationship between the Lorenz numerical solutions for X, Y, and Z (Fig. 6).

Fig. 6
figure 6

Use of the local dynamic behavior-consistent convergent cross mapping method to detect the causality between variables in the Lorenz equations.

Full size image

In Fig. 6, all curves converge as the time series length L increases, and the convergence value is high. The yellow dotted line is above 0.94, and the others are above 0.98, indicating that the LdCCM algorithm based on decomposition of the trajectory detects the mutual driving relationship between X, Y, and Z with no detection missing. In particular, the convergence value of the pink solid and dotted lines is > 0.99, which is significantly higher than that in Fig. 2 (see Table 1). This means that a strong causal association of variables X and Y with Z has been detected, and indicating that the strategy of selection of the nearest neighbor points in section “Scheme for selection of nearest neighbors on the shadow manifold based on decomposition of the Lorenz trajectory” ensures that the attractor manifold MZ can predict variables X and Y with excellent effect.

Table 1 Comparison of causal strength before and after improvement of the convergent cross mapping algorithm.
Full size table

Effect of noise on the LdCCM method

The predicted value \(\hat{Y}(t)\) of Y is

$$\hat{Y}(t) = Y + e_{n} ,$$
(18)

Assuming that the estimation error \(e_{n}\) is of zero-mean and variance \(\sigma_{n}^{2}\), then

$$\rho (Y,\hat{Y}(t)\left| {M_{X} } \right.) \approx \rho (Y,\hat{Y}(t)) = \frac{{\sigma_{Y} }}{{\sigma_{{\hat{Y}(t)}}^{2} }} = \frac{{\sigma_{Y} }}{{\sqrt {\sigma_{Y}^{2} + \sigma_{n}^{2} } }}.$$
(19)

Here, \(\sigma_{Y}^{2}\) is the variance of Y. From formula (19), it can be seen that after adding Gaussian white noise, the variance of the predicted value \(\sigma_{n}^{2}\) will increase and the correlation between Y and \(\hat{Y}(t)\) will decrease; therefore, the causal strength of Y to X will decrease. Taking the noise-free state as a reference point, the LdCCM algorithm is used to detect the causal strength between the variables of the Lorenz equation at different signal-to-noise ratios (SNRs). The results are shown in Table 2. As the SNR increases from –10 dB to 20 dB, the causal strength gradually approaches the noise-free state, that is, the higher the SNR, the smaller the prediction error. When the SNR is > 10 dB, the detection result using the LdCCM method is reliable.

Table 2 Causal strength at various signal-to-noise ratios.
Full size table

Applications of measured data

In the Lorenz system, the trajectory jumps randomly between two chaotic attractors, and the behavior and statistical characteristics near each attractor are relatively stable. Similarly, driven by strong external forcing, observational atmospheric data often have obvious seasonal characteristics50,51. There are essential differences in the thermal and dynamic structure of the atmosphere between summer and winter. We can regard summer and winter as different equilibrium states, similar to the two lobes of the Lorentz attractor, and consider spring and autumn to be the transition between the two equilibrium states. Considering that the dynamic mechanisms governing the various seasons may be different, when a state point needs to find its nearest neighbor for prediction, finding the nearest neighbor point in the same “seasonal state” is more physically meaningful than finding the point in a completely different state dynamic mechanism. Although this analogy is simplified, it captures the key characteristics of atmospheric dynamics driven by seasonal external forcing. Therefore, the LdCCM algorithm can better adapt to the processing of seasonal changes and effectively reduce the interference of these changes on causal inference, thereby improving the accuracy of analysis of the causal relationship. Meteorological data show a certain linear trend that affects the correlation analysis between variables. Therefore, to test whether the linear trend of the data affects causality, the data are detrended before the causality test52. Improved detection using the LdCCM algorithm based on decomposition of the Lorenz trajectory is applicable to measured data. The proposed method can be summarized as follows:

Step 1: Time series X and Y are constructed by importing observational data

Step 2: The phase spaces MX and MY are reconstructed

Step 3: The manifold MX is used to predict Y (MY forecasts X); when selecting the best neighbor points on the shadow manifold, each season only selects the neighbor points in their respective time periods

Step 4: Evolution of causal strength over time is calculated, and the causal relationship between time series X and Y is identified.

Specific attention should be paid to noise and other confounding factors that may exist in the observational data because they may affect the results of causal analysis. Therefore, the influence of these factors on the inferred results should be identified and controlled when making causal inferences. To ensure the accuracy of causal inferences, the quality and integrity of the data must be ensured, and missing or erroneous data should be handled appropriately.

The Western Pacific Subtropical High (WPSH), a semi-permanent anticyclonic circulation system over the Pacific Ocean, serves as a critical component of the East Asian monsoon system. Variations in its position and intensity have profound impacts on precipitation patterns and climatic conditions across China, particularly the strong teleconnections with anomalous weather–climate events in the Yangtze River Basin53. Conversely, release of latent heat from precipitation events thermally excites the dynamics of the upper atmosphere, inducing anomalous atmospheric circulation patterns that subsequently modulate the intensity and spatial configuration of the WPSH. This bidirectional thermodynamic coupling constitutes a critical determinant of the formation and evolution of subtropical high-pressure systems across the northern hemisphere54. The bidirectional causal coupling between the intensity and precipitation of the WPSH in the middle–lower Yangtze River basin is shown in Fig. 7. The abscissa denotes the time series length L, while the ordinate quantifies the Pearson correlation coefficient for the relationship between temporal sequences. The gold curve delineates the causal influence of the intensity of the WPSH on precipitation, while the emerald curve characterizes the reverse causal influence of precipitation on modulation of the intensity of the WPSH.

Fig. 7
figure 7

Causal relationship between the intensity of the Western Pacific Subtropical High and precipitation. (a) Use of the convergent cross mapping method to detect causal strength. (b) Use of the local dynamic behavior-consistent convergent cross mapping method to detect causal strength.

Full size image

As the length of the time series increases, the two curves in Fig. 7a do not show obvious convergence, that is, the traditional CCM method fails to effectively identify the causal relationship between the intensity of the WPSH and precipitation in the middle and lower reaches of the Yangtze River. The two curves in Fig. 7b show excellent convergence characteristics. The causal strength of the intensity of the WPSH on precipitation is 0.32, and that of precipitation on the intensity of the WPSH is 0.61 (Table 3), and the 95% significance test is met. This observation indicates that the LdCCM method accurately captures the ability of the intensity of the WPSH to drive precipitation in the middle–lower reaches of the Yangtze River and reflects the fact that precipitation in these reaches of the Yangtze River has an obvious driving effect on the intensity of the WPSH (the driving mechanism of this conclusion is not explored here). This conclusion is consistent with the theory proposed by Liu et al.54, who stated that the WPSH regulates the intensity of precipitation over East Asia, while the latent heat released by precipitation has a significant effect on the intensity and location of the WPSH. This bidirectional coupling mechanism has been revealed at the causal level.

Table 3 Comparison of causal strength between the intensity of the Western Pacific Subtropical High and precipitation before and after improvement of the convergent cross mapping algorithm.
Full size table

The Niño 3.4 Index and Southern Oscillation Index jointly characterize the El Niño-Southern Oscillation (ENSO) phenomenon from oceanic and atmospheric perspectives, respectively. The Niño 3.4 Index quantifies anomalies in sea surface temperature in the central–eastern equatorial Pacific, whereas the Southern Oscillation Index measures atmospheric pressure differentials between Tahiti and Darwin, reflecting large-scale variations in circulation. These two indices show strong interdependencies through ocean–atmosphere coupling mechanisms55. Figure 8 delineates their bidirectional causal relationship: the yellow curve illustrates the influence of the causal strength of Niño 3.4 on the variability of the Southern Oscillation Index, whereas the green curve inversely maps the causal impact of fluctuations in the Southern Oscillation Index on the dynamics of the Niño 3.4 Index.

Fig. 8
figure 8

Causal relationship between the Niño 3.4 Index and the Southern Oscillation Index. (a) Use of the convergent cross mapping method to detect causal strength. (b) Use of the local dynamic behavior-consistent convergent cross mapping method to detect causal strength.

Full size image

In Fig. 8, the two curves converge as the length of the time series increases, indicating that both CCM and LdCCM can detect a bidirectional causal relationship between the Niño 3.4 Index and the Southern Oscillation Index and pass the 95% significance test. Compared with the traditional CCM method, the causal strength detected by LdCCM is slightly higher, but not significantly so (see Table 4). This is mainly because of the strong coupling of the ENSO system itself, leading to a limited increase in causal strength. This conclusion demonstrates strong concordance with those of previous studies56,57, while providing quantitative validation of the bidirectional causal coupling between the Niño 3.4 Index and Southern Oscillation Index through systematic causal inference.

Table 4 Comparison of causal strength between the Niño 3.4 Index and the Southern Oscillation Index before and after improvement of the convergent cross mapping algorithm.
Full size table

Discussion and conclusion

The CCM algorithm can detect a strong causal relationship between variables X and Y in the Lorenz system, but not the unidirectional driving effect of X (Y) on variable Z. The spatial structure is known to differ between attractor manifolds MZ and MX (MY), with the former having only one equilibrium point and the latter having two equilibrium points. In terms of CCM attribution and detection, we have shown that this difference in spatial structure means that the images mapped to the Lorenz orbitals by points on the attractor manifold MZ and their nearest neighbors may be distributed in different equilibrium regions. In contrast, the images of points on manifold MX (MY) and their nearest neighbors are in the same equilibrium region of the Lorenz orbitals. Therefore, selection of the best nearest neighbor points on manifold MZ is one of the reasons that CCM attribution and detection may be missed. Based on decomposition of the Lorenz trajectories, an LdCCM was proposed to improve the selection of the best nearest neighbor points on the attractor manifolds. The specific scheme is as follows: the attractor manifold MZ (MX, MY) is decomposed into four parts (\(B_{R}\), \(B_{R2L}\), \(B_{L}\) and \(B_{L2R}\)); assuming that a point belongs to \(B_{L}\) at time \(t_{j}\), when selecting the best nearest neighbor point on the attractor manifold at time \(t_{j}\) the search is restricted to \(B_{L}\), and similarly for other regions. Experiments on the detection of causal strength have demonstrated that the proposed LdCCM method effectively improves the ability of the attractor manifold MZ to forecast variable X (Y). The causal strength of X (Y) to Z is 0.99, which is a significant improvement over the original 0.14 (0.13). Consequently, the LdCCM method, which constrains the selection of optimal nearest neighbors, significantly enhances the sensitivity with which both causal directionality and strength can be detected. This approach represents a refinement of the established CCM causal attribution framework. Our improvement overcomes the systematic missed detection rate with the existing CCM algorithm, in which dynamic information for the variables overlaps, and significantly improves the ability of this algorithm to reveal causal relationships in complex systems, such as that from variables X and Y to variable Z in the Lorenz system. LdCCM also provides a reliable analytic tool for a more accurate understanding of the internal mechanism driving the system. The improvement in the causal inference rate in this paper is mainly based on the unique multi-equilibrium topological characteristics of the Lorenz system. In view of the fact that this multi-equilibrium state is a common feature of many chaotic systems, the nearest neighbor point selection strategy based on manifold decomposition provides a feasible approach for improving the causal detection ability of the CCM algorithm in complex systems. However, for more complex or high-dimensional systems, there may be multiple equilibrium states, which are difficult to identify or evolve over time and increase the complexity of manifold decomposition.

Compared with the Lorenz equation, the fundamental equations of atmospheric motion are more complex and highly nonlinear. Hence, they have multiple equilibrium points, which are reflected in atmospheric dynamics and the characteristics of the multi-equilibrium state of atmospheric motion. It is reasonable to believe that detection using the CCM algorithm will miss or generate false relationships between the variables of the Lorenz equation when detecting causality between atmospheric variables. When using conventional CCM to detect the causal relationships between the WPSH intensity index and precipitation in the middle–lower Yangtze River basin, the bidirectional causal coupling between these variables was not captured. In contrast, the LdCCM algorithm successfully identified mutual causal interactions between the intensity of WPSH and regional precipitation, while demonstrating enhanced capabilities to detect causal strength between the Niño 3.4 Index and Southern Oscillation Index when compared with the traditional CCM approach. Consequently, the LdCCM algorithm, as an enhanced variant of traditional CCM, has heightened precision for detection of causal linkages within observational data characterized by strong seasonal dependency and nonlinear feedback mechanisms.