Modelling of hybrid deep learning framework with recursive feature elimination for distributed denial of service attack detection systems

Abstract

Dealing with network security has always been a challenging task, particularly in the prevention and detection of distributed denial of service (DDoS) attacks. Attacks such as DDoS pose hazards to the system by compromising its accessibility to individuals who need to use a specific server. This type of cyberattack occurs when a system is overloaded with a massive amount of traffic, causing the network to become unavailable. This attack type focuses on engaging the service with correct operators without breaching safety parameters. Responsible artificial intelligence (AI) refers to the ethical development and deployment of AI systems that prioritise fairness, transparency, privacy, and accountability. Currently, the deep learning method is very effective in distinguishing DDoS traffic from harmless traffic by removing the representation of higher-level features from lower-level traffic. The study presented in this paper proposes a responsible artificial intelligence-based hybridisation framework for attack detection using recursive feature elimination (RAIHFAD-RFE) for cybersecurity systems. The study aimed to analyse and propose efficient cybersecurity tactics for preventing, mitigating and detecting DDoS attacks using advanced methods. As a primary step, the RAIHFAD-RFE technique utilises the Z-score standardisation method for the data pre-processing phase to clean, transform and organise raw data into a structured format. Furthermore, the recursive feature elimination (RFE) model is employed for feature selection (FS) to identify and retain the most essential features, thereby improving model performance and reducing model complexity. Moreover, the hybridisation of long short-term memory and bidirectional gated recurrent unit (LSTM-BiGRU) models was employed for classification. To optimise model performance, the improved orca predation algorithm (IOPA) is utilised for hyperparameter tuning to select the optimal parameters for enhanced accuracy. A comprehensive experimental analysis of the RAIHFAD-RFE approach was performed under the CIC-IDS-2017 and Edge-industrial internet of things (IIoT) datasets. A comparison study of the RAIHFAD-RFE approach provided superior accuracy values of 99.35% and 99.39%, respectively, compared to existing models on the dual dataset.

Introduction

The internet plays a vital role worldwide, serving as a global information resource for every user and making it essential. The internet is vast, providing access to data, resources and services for every domain¹. Currently, data security is given higher importance because everything is linked to the internet. To safeguard private and personal data against malicious cyberattacks, it is crucial to implement essential measures to ensure that strong and consistent security protocols are in place². As its needs increase, so do security concerns. There are numerous types of attacks affecting the internet that should be detected, identified and defended against by attackers. In particular, distributed denial of service (DDoS) is among the most prevalent assaults in cyberspace. A DDoS attack aims to utilise computing resources, thereby preventing standard work from continuing³. In contrast to denial of service (DoS) attacks, which do not attempt to corrupt or destroy information, DDoS attacks involve numerous resources that simultaneously assault the target systems.

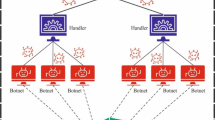
DDoS attacks have become a universal and disruptive threat in the cyberworld⁴. DDoS attacks are designed to overwhelm and disable targeted systems by rendering them inaccessible to legitimate users. By overloading a website, network or online service with malicious requests or excessive traffic, DDoS attacks disrupt standard functions, causing significant disruptions, damage and financial loss to a business’s reputation. DDoS assaults are noticeable in various methods, including volumetric, protocol and application layer attacks⁵. The DDoS attack is constantly evolving to keep pace with technological advances. Figure 1 illustrates the DDoS attack scenario. Attackers continually invent novel techniques to evade service provider defences driven by the development of DoS methods. As the complexity and scale of DDoS attacks continue to evolve, businesses should adopt proactive and robust defence strategies⁶. This involves applying anomaly detection (AD) and traffic monitoring methods, utilising mitigation models, and leveraging the services of specific DDoS mitigation providers. Furthermore, the effective detection and mitigation of DDoS attacks depends comprehensively on collaboration and the transfer of data between numerous entities⁷.

Fig. 1

DDoS attack scenario.

Recently, the DL approach has been highly effective in distinguishing DDoS traffic from benign traffic by removing representations of higher-level features from those of lower-level features. The effective nature of tools in security, such as malware identification, access control, secure uploading and cloud encryption, is attained by computers and DL⁸. It is suitable for modelling nonlinear complex relations by learning numerous phases of representation that relate to several phases of abstraction. A deep neural network (DNN) comprises an array of nonlinear layers of processing units capable of conversion and feature extraction, making it a suitable method for detecting threats on social networking sites⁹. Cyberattack identification shares features that are widespread with image recognition, harnessing novel DL features. Minor variations in the pixel are inclined to recognise image variations; there, an attack is identified in the same manner as more than 99% of new threats are tiny adaptations of earlier threats. This strengthens DL’s effectiveness in identifying slight variations in attack patterns. DL is implemented in cybersecurity due to its ability to self-learn and analyse¹⁰.

The study presented in this paper proposes a responsible artificial intelligence-based hybridisation framework for attack detection using recursive feature elimination (RAIHFAD-RFE) for cybersecurity systems. The study aimed to analyse and propose efficient cybersecurity tactics for preventing, mitigating and detecting DDoS attacks using advanced methods. The RAIHFAD-RFE technique utilises the Z-score standardisation method for the data pre-processing phase to clean, transform and organise raw data into a structured format. Furthermore, the recursive feature elimination (RFE) model is employed for feature selection (FS) to identify and retain the most essential features, thereby improving model performance and reducing model complexity. Moreover, the hybridisation of long short-term memory and bidirectional gated recurrent unit (LSTM-BiGRU) models was employed for classification. To optimise model performance, the improved orca predation algorithm (IOPA) is utilised for hyperparameter tuning to select the optimal parameters for enhanced accuracy. A comprehensive experimental analysis of the RAIHFAD-RFE approach was performed under the CIC-IDS-2017 and Edge-IIoT datasets. The key contribution of the RAIHFAD-RFE approach is listed below.

• The RAIHFAD-RFE model enhances pre-processing by applying Z-score standardisation to normalise input features, thereby improving learning efficiency and model convergence. This step ensures consistent feature scaling to reduce bias in training. It plays a significant role in stabilising and accelerating the overall detection process.

• The RAIHFAD-RFE method utilises the RFE technique to identify and retain the most relevant features, thereby improving the focus and interpretability of the model. This mitigates dimensionality and filters out noisy or redundant data. As a result, it improves classification accuracy and computational efficiency.

• The RAIHFAD-RFE approach integrates a hybrid LSTM-BiGRU classifier to effectively capture temporal patterns and contextual dependencies in network traffic data. This improves the accuracy and robustness of DDoS attack detection. The hybrid architecture facilitates better generalisation and learning from sequential behaviour.

• The RAIHFAD-RFE methodology utilises IOPA-based hyperparameter tuning to search intelligently for optimal parameter settings, thereby enhancing classification accuracy. This optimisation process ensures efficient model performance across a wide range of scenarios. It strengthens the adaptability and precision of the DDoS detection system.

• The integration of RFE-based feature selection (FS) with a hybrid LSTM-BiGRU classifier and IOPA-based tuning establishes a novel, responsible AI-based framework. This design uniquely integrates feature reduction, deep temporal learning and intelligent optimisation. It ensures high accuracy, efficiency and transparency in detecting DDoS attacks. The novelty lies in the unified approach to responsible, explainable and high-performance intrusion detection.

Related studies on DDoS attack detection

Alrumaih and Alenazi¹¹ presented a new model to enhance the resilience of industrial networks from DDoS attacks (ERINDA) to reduce downtime and uphold operations. It comprises a dual-step method that merges reactive and proactive approaches to mitigate DDoS attacks while effectively minimising network failures. Initially, network traffic is continuously examined to identify anomalies that represent probable intrusions. Next, response mechanisms are initiated in real-time threat detection to counteract the attack and reinstate network integrity rapidly. Hu and Shi¹² addressed the secure synchronisation issue for complex dynamical networks (CDNs) with an observer-enabled event-triggered communication strategy (ETCS) in multichannel DoS attacks (MCDSAs). Due to external environmental factors, viewers are expected to evaluate the network’s state accurately. Wang et al.¹³ proposed a framework named ARSAE-QGRU, which incorporates residual connections and attention mechanisms (AM) into a stacked autoencoder (SAE) for DDoS attack recognition. By presenting residual connections and AM in SAE, this technique efficiently transports valid data and enables the propagation of gradients, allowing for the effective learning of lower-dimensional models. Balamurugan et al.¹⁴ improved DDoS attack detection and mitigation by utilizing the Novel Attack Detection Protocol (NADP) and comparing its performance with dynamic source routing (DSR) model. Hnamte et al.¹⁵ proposed a groundbreaking technique to recognise DDoS attacks through a DNN framework depending on DL. This method presents an accessible and scalable model, enabling a thorough examination of network traffic data to distinguish composite formats that indicate DDoS attacks. To authenticate the method’s efficiency, precise assessments were done leveraging genuine actual traffic data. The outcomes demonstrate the supremacy of this DNN-aided method compared to conventional DDoS recognition methods. Martinez et al.¹⁶ proposed an innovative dual-space prototypical paradigm that utilises a specific dual-space function of loss to enhance recognition precision for various attack patterns as measured by angular and geometric metrics. This paradigm leverages the representation learning capabilities in the latent space, refining the paradigm’s flexibility and adaptability to counter DDoS attack vectors. Ahmed et al.¹⁷ presented a machine learning (ML)-driven trust-empowered routing protocol (TrustML-RP) model that classifies the attacking nodes accountable for packet suppression and DDoS attacks. This model implements a distributed trust model to establish trust factors between contributing nodes and then deploys an efficient integration of ML procedures, namely support vector machine (SVM) and artificial neural network (ANN), for finding the best and most secure path and identifying attacker nodes.

Hossain and Islam¹⁸ proposed ensemble-based random forest (RF) classifier integrated with advanced feature selection techniques such as principal component analysis (PCA), mutual information (MI), and correlation analysis with the Synthetic Minority Over-sampling Technique (SMOTE) to address class imbalance. Emirmahmutoğlu and Atay¹⁹ proposed a model to improve the performance of anomaly-based intrusion detection systems (IDS) by applying heuristic FS methods, namely particle swarm optimisation (PSO), flower pollination algorithm (FPA), and differential evolution (DE), integrated with various ML classifiers. Behiry and Aly²⁰ improved intrusion detection in WSNs by integrating FS models, namely singular value decomposition (SVD) and PCA, with K-means clustering improved by information gain (KMC-IG) technique for feature extraction and the synthetic minority oversampling technique (SMOTE) for data balancing. A DL-based feed-forward neural network (FNN) model was then employed to classify network traffic and detect cyberattacks accurately. Farid and Khalil²¹ improved intrusion detection in wireless sensor networks (WSNs) by integrating advanced ML techniques, such as decision trees (DTs), RF, SVM, k-nearest neighbours (KNN) and ensemble methods with the SMOTE-Tomek technique to address class imbalance. The framework also employs sequential backwards selection (SBS) for optimal FS and robust data pre-processing to improve detection accuracy and reduce false positives. AboulEla et al.²² reviewed and analysed AI-based cybersecurity methodologies for internet of medical things (IoMT) networks, focusing on ML, DL, hybrid ML-DL, transformer-based techniques and emerging approaches like graph-based and blockchain methods. Luthfi et al.²³ presented a method to improve software defect prediction by integrating advanced pre-processing techniques, such as Z-score standardisation and robust scaling, with the adaptive synthetic sampling (ADASYN) method for class imbalance. FS is optimised using the binary Harris Hawk Optimisation (BHHO) model, evaluated by kNN, and incorporated with ensemble learning (EL) models, such as RF, SVM and stacking, to improve classification performance. Al-Amiedy, Anbar and Belaton²⁴ detected selective forwarding (SF) attacks in low-power and lossy networks (LLNs) by integrating optimised data balancing using SMOTE, FS through binary particle swarm optimisation (BPSO) and attack detection with an optimised RF classifier tuned via GridSearchCV. Thamer Francis, Souri and İnanç²⁵ proposed an effective IDS for IIoT networks by utilising the split-point algorithm with attribute-reduced classifier (SPAARC) DT integrated with the firefly algorithm (FA) for FS. The proposed system utilises a software-defined networking (SDN) architecture to enhance centralised control and improve detection accuracy across IIoT environments.

Kocyigit et al.²⁶ presented a model to support phishing attack detection by employing a genetic algorithm (GA)-based FS method, integrated with local optimisation, to identify the most relevant URL features. This approach aims to enhance the performance of ML models by mitigating overfitting, computational cost and training time while maintaining high detection accuracy. Qiao et al.²⁷ developed a simple and efficient incentive mechanism for federated learning (FL) model in vehicular networks, thus improving clustering accuracy and mitigating network overhead and convergence time. Alfatemi et al.²⁸ improved DDoS attack detection by integrating diverse DNN models using combinatorial fusion analysis (CFA) to improve detection accuracy and robustness. Lv et al.²⁹ investigated a new front-end web attack by utilizing cloud object storage service vulnerabilities to bypass Content Security Policy (CSP), analyze its impact on real-world websites to eliminate the threat. Al-Shukaili, Kiah, and Ahmedy³⁰ improved detection of low-rate Distributed Denial of Service (LDDoS) attacks, specifically slowloris and slowhttptest, by optimizing feature selection using synthetic minority oversampling technique (SMOTE), recursive feature elimination, and DL models. Lu et al.³¹ proposed AutoD, an unpacking system using Java Native Interface (JNI) layer deception-calls in Android Runtime (ART) for restoring decrypted Dex files in reinforced blockchain-wallet applications for detecting hidden malicious code. Pradeesh, Jeyakarthic, and Thirumalairaj³² presented a sensor-enhanced hybrid framework using Adaptive Ensemble of Modular Classifiers (AEMC) and One-vs-Rest (OvR) classifiers for real-time multi-class detection and classification of DDoS attacks in SDNs. Lu et al.³³ presented DeepAutoD, a generic unpacking framework by utilizing deep deception call chains to restore original Dex files from reinforced Android apps, enabling accurate malicious code detection in distributed ML systems. Dilshad, Syed, and Rehman³⁴ improved DDoS attack detection in Internet of Vehicles (IoV) systems by employing the Gini index for feature selection and FL for decentralized, privacy-preserving model training. Gu et al.³⁵ proposed an interactive gradient shielding (IGS) and adaptive gradient shielding (AGS) methods to generate effective adversarial examples. Asuai et al.³⁶ developed an effective DDoS attack detection framework by utilizing a hybrid approach that combines the Three Conditions for Feature Aggregation (3ConFA) for robust feature selection and a 1D-CNN for deep temporal-spatial pattern learning. This integration seeks to improve detection accuracy while addressing class imbalance with the Adaptive Synthetic Sampling Approach (ADASYN). Table 1 summarises previous works on DDoS attacks.

Table 1 Comparison of existing studies on DDoS attacks using ML and DL models.

Despite crucial improvements in DDoS detection and mitigation, various limitations still exist. Various models face difficulty due to high computational complexity and increased communication overhead, restricting their scalability in distributed and resource-constrained environments like IoV and SDN. Few techniques encounter difficulty in balancing dimensionality reduction with maintaining critical data, affecting detection accuracy. Moreover, class imbalance issues still exist, despite oversampling methods like SMOTE and ADASYN. Various models highlight the need for decentralized models such as FL, and while hybrid and ensemble models enhance detection, their interpretability and real-time applicability require additional enhancement. This research gap calls for efficient, scalable, privacy-preserving frameworks with robust feature selection and balanced datasets, aiming to optimize detection accuracy while minimizing resource consumption.

Research design and methodology

In this study, the RAIHFAD-RFE model was proposed for cybersecurity systems. The study aimed to analyse and propose efficient cybersecurity strategies for detecting, mitigating and preventing DDoS attacks using advanced techniques. The model comprises data pre-processing, feature selection, attack classification and parameter tuning. Figure 2 illustrates the workflow of the RAIHFAD-RFE method.

Fig. 2

Work flow process of the RAIHFAD-RFE model.

Pre-processing using Z-score

As a primary step, the RAIHFAD-RFE technique utilises the Z-score standardisation method for the data pre-processing stage to clean, transform and organise raw data into a structured format³⁷. This technique was chosen for its efficiency in normalising features by centring data around a mean of zero and a standard deviation of one. It is specifically beneficial when features have varying scales; it ensures that each feature contributes equally to the learning process. The model is less sensitive to outliers, making it more robust for real-world network traffic data and is efficient in convergence speed and stability of gradient-based optimisation methods used in DL techniques, such as long short-term memory (LSTM) and bidirectional gated recurrent unit (BiGRU). This standardisation technique also helps prevent the model from being biased towards features with larger numerical ranges. Moreover, Z-score normalisation is widely applicable and consistent across datasets, thus enhancing generalisation.

The proposed model adjusts the features by subtracting the mean and then dividing them by the standard deviation, resulting in a standard deviation of 1 and a mean of 0. It is effective for models that typically assume distributed input features, such as logistic and linear regression. The z-score normalisation for feature $\:x$' is computed utilising the following equation:

$$\:{x}^{{\prime\:}}=\frac{x-mean\left(x\right)}{std\left(x\right)}\:\:$$

(1)

Here, $\:{x}^{{\prime\:}}$ depicts the normalised value, $\:x$ indicates the original value, $\:std\left(x\right)$ refers to the standard deviation of $\:x$ and mean $\:\left(x\right)$ denotes the average feature $\:x$. The other normalisation models include the interquartile range (IQR), which depicts the extent of statistical dispersion, denoting how spread out the data is. IQR is measured by the difference between the 75th and 25th percentiles. The quartiles are described as Q1 (lower quartile), Q2 (median), and Q3 (upper quartile); here, Q1 and Q3 are equivalent to the 25th and 75th percentiles. The following equation specifies the IQR:

$$\:IQR=Q3-Q1$$

(2)

Selecting a proper normalisation model plays an essential role in enhancing the performance of the LSTM-BiGRU method. Normalising input variables to a common scale might enhance the efficacy of learning models and improve the accuracy of predictions. Since a diverse normalisation model manages data scales and outliers, the selection of models can significantly influence how effectively the techniques acquire patterns in data. Determining the most appropriate methodology can necessitate empirical assessment or insights from preceding analysis utilising comparable datasets and DL frameworks.

Dimensionality reduction procedure

The RFE model is employed for the FS process to recognise and preserve the most significant features for increasing the model’s performance³⁸. This model was chosen for its capability in systematically selecting the most relevant features by recursively removing the least significant ones based on model performance. This method relies solely on statistical measures and considers feature importance within the learning algorithm, resulting in a more informed selection. It effectually mitigates dimensionality, which decreases overfitting and improves computational efficiency. Compared to embedded methods, RFE presents greater flexibility in pairing with diverse models. Its iterative nature ensures that optimal feature subsets are detected for improved model accuracy. RFE is particularly suitable for complex tasks, such as DDoS detection, where eliminating irrelevant features significantly enhances performance.

RFE is one of the FS approaches employed for recognising the essential features in a dataset by iteratively extracting less related aspects, depending on their performance. In this study, the datasets comprised higher-dimensional data, and RFE is specifically beneficial for reducing redundancy and enhancing the efficacy of ML techniques. To select only the most crucial features, RFE reduces computational overhead, creating methodologies that are more interpretable and faster, enhances precision and handles higher dimensions. Intrusion detection datasets frequently have a great number of attributes. RFE guarantees that only effectual aspects are retained. RFE is employed to pre-process and scale datasets for selecting the most substantial elements before training ML methodologies, such as RF, decision tree and logistic regression.

A base estimator was employed to assess significant features using an underlying technique. For instance, RF offers the significance of feature scores, depending on its DT. Primarily, the methodology is trained on the entire set of features. Assume that $\:X$ is the input feature matrix, $\:y$ indicates targeted labels, and $\:M$ signifies the ML technique employed in RFE. The significance of feature scores for the $\:ith$ feature is specified as follows:

$$\:{I}_{i}=Importance\:of\:feature\:{x}_{i}\:as\:determined\:by\:M$$

(3)

The least significant features were eliminated iteratively. This procedure repeats until the chosen feature count $\:k$ is designated. Let $\:{X}^{\left(T\right)}$ depict the feature matrix at iteration $\:t$. At all iterations, training $\:M$ on $\:{X}^{\left(T\right)}$ to calculate significant scores. Eliminate $\:r$ features with the least significant scores:

$$\:{X}^{(t+1)}={X}^{\left(t\right)}\setminus\:\left\{{x}_{1},\:{x}_{2},\dots\:,{x}_{n}\right\}$$

(4)

Now $\:\{{x}_{1},\:{x}_{2},\:\dots\:,{x}_{n}\}$ refers to less significant features. The procedure halts after the recollected feature counts achieve the preferred number $\:k$, halt

$$\:if\left|{X}^{\left(\tau\:+1\right)}\right|=k$$

(5)

The chosen features are employed for training the final model $\:{M}_{final}$:

$$\:{M}_{final}=Train\left(M,\:{X}^{\left(T\right)},\:y\right)$$

(6)

Once features are selected using RFE, datasets with reduced features are employed to train intrusion detection techniques, enhancing their computational efficacy and prediction accuracy. RF and DT classifiers were employed as the base techniques for RFE to effectively use their ability.

Algorithm 1: Pseudocode of RFE

Hybridisation of DDoS attack classification

For the DDoS attack classification procedure, the RAIHFAD-RFE model implements hybridisation of the LSTM-BiGRU technique³⁹. This hybrid model was chosen to employ the merits of both architectures in handling sequential network traffic data. LSTM outperforms at capturing long-term dependencies, while BiGRU processes data in both forward and backward directions for better context understanding. The capability of the model is improved by this integrated model for detecting complex and evolving attack patterns compared to standalone RNNs or CNNs. Unlike conventional ML models, hybrid DL models adapt better to temporal dynamics. It also enhances accuracy, robustness, and generalisation in imbalanced or noisy datasets. Overall, the hybrid model provides a more reliable and efficient solution for DDoS detection. Figure 3 specifies the framework of the LSTM-BiGRU model.

Fig. 3

Structure of the LSTM-BiGRU technique.

Generally, LSTM networks are efficient in predicting and modelling time-series data by presenting output, input, and forget gates. These gates help alleviate the gradient vanishing problems and gradient explosion to some extent. The forget gate, signified by $\:{f}_{t}$, controls whether the data must be forgotten. The input gate controls which novel information is added to the memory cell. The output gate, denoted as $\:{O}_{t}$, limits the output of the hidden layer (HL) vector. The reliable equations are presented in Eq. (7) to (12).

$$\:{f}_{t}=\sigma\:\left({W}_{f}\left[{h}_{t-1},\:{x}_{t}\right]+{b}_{f}\right)$$

(7)

$$\:{i}_{t}=\sigma\:\left({W}_{i}\left[{h}_{t-1},{x}_{t}\right]+{b}_{i}\right)\:\:$$

(8)

$$\:{o}_{t}=\sigma\:\left({W}_{o}\left[{h}_{t-1},{x}_{t}\right]+{b}_{o}\right)\:$$

(9)

$$\:{\stackrel{\sim}{C}}_{t}=\text{t}\text{a}\text{n}\text{h}\left({W}_{c}\left[{h}_{t-1},{x}_{t}\right]+{b}_{c}\right)\:$$

(10)

$$\:{C}_{t}={f}_{c}\odot\:{C}_{t-1}+{i}_{t}{\stackrel{\sim}{C}}_{t}\:\:$$

(11)

$$\:{h}_{t}={O}_{t}\odot\:\text{t}\text{a}\text{n}\text{h}\left({C}_{t}\right)\:$$

(12)

Whereas: $\:{x}_{t}$ denotes input at time step $\:t;{h}_{t}$ refers to HL at time step $\:t;{\stackrel{\sim}{C}}_{t}$ represents candidate cell state at time step $\:t$; $\:{C}_{t}$ signifies upgraded cell state at time step $\:t;{W}_{f},$ $\:{W}_{i},$ $\:{W}_{o}$, and $\:{W}_{c}$ designate the weighted matrices equivalent to every module; $\:{b}_{f},$ $\:{b}_{i},$ $\:{b}_{o}$, and $\:{b}_{c}$ represents bias matrices akin to every module; $\:\sigma\:$ characterises the activation function of the Sigmoid; and $\:\odot\:$ means Hadamard product.

Additionally, BiGRU is a neural network that incorporates a bidirectional GRU and RNN. Compared to conventional GRUs, RNNs better address the issues of explosion and gradient vanishing while capturing longer-term dependencies in sequences. The bidirectional RNN also increases the method by handling either past or future inputs, allowing improved sequence data processing. BiGRU handles data sequences by initially passing the input sequence through dual GRU networks, one in the forward direction and the other in the backward direction. The outputs from either direction are then connected to make the final output. Additionally, BiGRU is primarily beneficial in capturing dependencies within sequences, as it can consider either previous or future information. Therefore, adopting the BiGRU method to address the related intrusion of these features will enhance prediction precision by reducing the model’s error. The essential elements of a GRU consist of updates and reset gates that control the upgrading and use of the HL over nonlinear transformations. The consistent equations are presented in Eqs. (13) to (16).

$$\:{r}_{t}=\sigma\:\left({W}_{r}{x}_{t}+{U}_{r}{h}_{t-1}+{b}_{r}\right)\:$$

(13)

$$\:{z}_{t}=\sigma\:\left({W}_{Z}{x}_{t}+{U}_{z}{h}_{t-1}+{b}_{Z}\right)\:\:$$

(14)

$$\:{h}_{t}^{*}=\text{t}\text{a}\text{n}\text{h}\left({W}_{h}{x}_{t}+{r}_{t}{U}_{r}{h}_{t-1}+{b}_{h}\right)\:\:$$

(15)

$$\:{h}_{t}=\left(1-{z}_{t}\right){h}_{t}^{*}+{z}_{t}{h}_{t-1}\:$$

(16)

Here, $\:{r}_{t}\:$and $\:{z}_{t}$ denote reset and update gates; $\:\text{t}\text{a}\text{n}\text{h}$ represents the activation function of the hyperbolic tangent; $\:{h}_{t}^{*}$ signifies candidate HL at the time step$\:{;\:W}_{r},$ $\:{W}_{Z}$, and $\:{W}_{h}$ symbolise the weighted matrices for all modules; and $\:{b}_{r},$ $\:{b}_{Z}$, and $\:{b}_{h}$ illustrate bias matrices for all modules.

IOPA-based hyperparameter tuning model

To further optimise model performance, the IOPA is utilised for hyperparameter tuning to ensure that the best hyperparameters are chosen for enhanced accuracy⁴⁰. This model was selected for its superior balance between exploration and exploitation, which assists in avoiding local optima more effectively than conventional methods, such as grid search or GAs. The model performs efficient searching of the hyperparameter space, resulting in faster convergence and improved optimisation. Compared to other metaheuristic algorithms, it requires fewer iterations to achieve better performance, making it a computationally efficient approach. This results in improved model accuracy and robustness, especially crucial for complex architectures like the hybrid LSTM-BiGRU used in DDoS attack detection. Overall, IOPA presents a powerful and efficient approach for fine-tuning model parameters in dynamic network environments.

The orca predator algorithm (OPA) replicates the foraging behaviour of orcas (killer whales). The foraging tactic of the individual consists of three phases: attacking, driving, and surrounding prey. The presented model has improved the parameters for surroundings and drives for striking a balance between exploitation and exploration. During the attack phase, the best solution is recognised without offering the particle categories in consideration of numerous optimal orcas (candidates) in addition to those designated randomly. The presented OPA model is numerically described as follows:

1. The initial step is to assemble a group of orcas. The model recommends using $\:{N}_{n}$ individuals, all of whom are located in different dimensional areas. This process is verified by the succeeding Eq. (17):

$$\:X=\left[x1,\:x2,\:x3,\:\dots\:,\:x{N}_{n}\right]=\left[\begin{array}{cccc}{X}_{\text{1,1}}&\:{X}_{\text{1,2}}&\:\cdots\:&\:{X}_{1,Dim}\\\:{X}_{\text{2,1}}&\:{X}_{\text{2,2}}&\:\cdots\:&\:{X}_{2,Dim}\\\:\vdots &\:\vdots &\:\vdots &\: \vdots\\\:{X}_{{N}_{n},1}&\:{X}_{{N}_{n},2}&\:\cdots\:&\:{X}_{{N}_{n},Dim}\end{array}\right]\:\:$$

(17)

Whereas, the population candidate solution is represented by $\:X$. $\:x{N}_{n}$ establishes the $\:{N}^{th}$ candidate location. Dim has portrayed the population size.

• 1. 2. The second step is the chasing stage, which has two sub-steps: driving and encircling. The variable $\:{p}_{1}$ is used to improve the probability of individuals following these dual stages. Two conditions determine the choice between using the encircling or driving process. When the random number is improved, the driving process should be used for p1. Alternatively, the encircling process should be applied.

• 2. 3. The third step is the driving procedure, which is crucial for ensuring that group members maintain their primary position and remain close to the prey. The objective is to prevent individuals from travelling apart from their goals.

$$\:{V}_{chase,1,i}^{t}=a\times\:\left(d\times\:{x}_{best}^{t}-F\times\:\left(b\times\:{M}^{t}+c\times\:{x}_{i}^{t}\right)\right)\:\:$$

(18)

$$\:{V}_{chase,2,i}^{t}=e\times\:{x}_{best}^{t}-{x}_{i}^{t}\:\:$$

(19)

Whereas, the iterations’ numbers are represented by $\:t$. $\:{V}_{chase,1,\:i}^{t}$ and $\:{V}_{chase,2,}^{}$ specify the chasing speed following the choice of the first and second stages. The random amounts consist of $\:d$ and $\:b$, which are in the interval of $\:(0$,1), and $\:e$ signifies stochastic numbers that are in the range ($\:0$,2). For chasing tactic selection, $\:q$ is applied that varies among$\:\:(0$,1), and the $\:F$ value equivalents two. $\:M$ represents the orca population’s mean position.

$$\:M=\frac{{\sum\:}_{i=1}^{{N}_{n}}{x}_{i}^{t}}{{N}_{n}}\:\:$$

(20)

$$\:c=1-b\:$$

(21)

In this context, there are two different methods for chasing that depend significantly on the population size. The 1 st model is applied if $\:rand>q$, and the 2nd model is applied if $\:rand\le\:q$.

$$\:\left\{\begin{array}{l}{x}_{chase,1,i}^{t}={x}_{i}^{t}+{V}_{chase,1,i}^{t}\:\:if\:rand>q\\\:{x}_{chase,2,i}^{t}={x}_{i}^{t}+{V}_{chase,2,i}^{t}\:\:if\:rand\le\:q\end{array}\right.\:\:$$

(22)

4. The fourth step is to surround the prey. Here, the development of candidates utilising three arbitrary individuals is defined in Eqs. (23) and (24):

$$\:{x}_{chase,3,i,k}^{t}={x}_{d1,k}^{t}+u\times\:\:\left({x}_{d2,k}^{t}-{x}_{d3,k}^{t}\right)\:\:$$

(23)

$$\:u=2\times\:\left(randn-\frac{1}{2}\right)\times\:\frac{{\text{M}\text{a}\text{x}}_{itr}-t}{{\text{M}\text{a}\text{x}}_{itr}}\:\:$$

(24)

Now, the variable $\:{\text{M}\text{a}\text{x}}_{itr}$ exemplifies the maximal number of iterations. Candidates chosen at random are represented by $\:1,$ $\:d2$, and $\:d3$, and they are not equal. If the third chasing tactic is selected, the state is specified by $\:{x}_{ch\alpha\:se,3,i,k}^{t}.$.

5. The fifth step is to develop the surroundings of the victim, where every individual’s state has improved.

$$\:\left\{\begin{array}{ll}{x}_{chase,i}^{t}={x}_{chase,i}^{t}&\:if\:f\left({x}_{chase,i}^{t}\right)<f\left({x}_{i}^{t}\right)\\\:{x}_{chase,i}^{t}={x}_{i}^{t}&\:if\:f\left({x}_{chase,i}^{t}\right)\ge\:f\left({x}_{i}^{t}\right)\end{array}\right.$$

(25)

Whereas the cost function is associated with $\:{x}_{chase,\:i}^{t}$ was portrayed by $\:f\left({x}_{chase,\:i}^{t}\right)$, and the function of cost, which is associated with $\:{x}_{i}^{t}$ was established by $\:f\left({x}_{i}^{t}\right)$.

6. The sixth step is to attack on the prey. The best four individuals are positioned in the top-four places. The candidates’ locations and their speed of movement during the attack are verified utilising the equations below:

$$\:{V}_{\alpha\:ttack,1,i}^{t}=\frac{({x}_{1}^{t}+{x}_{2}^{t}+{x}_{3}^{t}+{x}_{4}^{t})}{4}-{x}_{chase,i}^{t}\:\:$$

(26)

$$\:{V}_{\alpha\:ttack,2,i}^{t}=\frac{\left({x}_{chase,d1}^{t}+{x}_{chase,d2}^{t}+{x}_{chase,d3}^{t}\right)}{3}-{x}_{i}^{t}\:\:$$

(27)

$$\:{x}_{attack,i}^{t}={x}_{chase,i}^{t}+{g}_{1}\times\:{V}_{attack,1,i}^{t}+{g}_{2}\times\:{V}_{attack,2,i}^{t}\:\:$$

(28)

Next, the vector speed is proven by $\:{V}_{attack\:2}^{}$ and $\:{V}_{attack}^{}$ 1. The best individuals in the optimal positions are identified by $\:{x}_{1}^{t},$ $\:{x}_{2}^{t},$ $\:{x}_{3}^{t}$, and $\:{x}_{4}^{t}$. The three randomly chosen individuals are demonstrated by $\:1,$ $\:d2$, and $\:d3$ to differ from each other. The state designated following the attacking stage is described by $\:{x}_{attack,i}^{t}$. The variables $\:{g}_{1}$ and $\:{g}_{2}$ specify a random value within the interval of $\:(0$, 2) and $\:-2.5$ to 2.5.

7. The seventh step is the attack stage. The orcas’ positions were verified by the lower boundary $\:\left(lb\right)$ problems.

As previously stated, the primary objective of this paper is to utilise OPA for optimal parameter selection. Selecting the best parameters is a complex task that involves numerous steps for the typical OPA to achieve accurate results and convergence rates in complex states. To address these difficulties, enhancements are made to increase the efficacy and robustness of the method, resulting in improvements in the IOPA. The establishment of the IOPA is the insertion of the removal stage. At the start of every iteration, the model tactically removes ineffective individuals to create space for unique individuals within the novel solution area. This new model significantly enhances the model’s ability to perform an exploration, enabling it to examine numerous pathways towards the optimal solution.

Eliminating the caught individuals in local ideals helps the model avoid suboptimal solutions and improves exploration in better ways. The characteristics of the IOPA technique are a dynamic area of exploration, frequently adding novel initial points. The adaptive feature enables the model to avoid getting caught in suboptimal solutions and expands its solution area. Removing the minimum efficient starting point’s assurances that computational sources are correctly concentrated on the more predictable regions within the solution area. The removal stage is an appropriate filter method that leads the model towards efficient solution spaces for exploration.

The projected developments offer various advantages, including improved precision and enhanced exploration capabilities. The IOPA examines different solutions by dynamically improving the solution area and giving new early points that reduce the probability of getting caught in local ideals. This model’s improved approach to its search method and exploration of dissimilar paths differentiates it from the standard OPA, making it particularly suitable for composite parameter identification challenges. Table 2 illustrates the comparative analysis of IOPA and advanced optimizers for hyperparameter tuning in DDoS detection. The key differences between IOPA and other optimizers such as Bayesian Optimization (BO) and covariance matrix adaptation evolution strategy (CMA-ES), particle swarm optimization (PSO), and genetic algorithm (GA) for DDoS tuning. It also highlights the faster convergence and better avoidance of local minima due to its iterative removal step, which slightly enhances computational overhead. This trade-off results in an enhanced accuracy, demonstrating the efficiency of the IOPA model for DDoS detection tasks.

Table 2 Comparison study of IOPA with advanced optimizers.

The IOPA technique creates a fitness function (FF) to achieve greater performance in classification. It defines an affirmative number to characterise the boosted outcome of the candidate solutions. The minimisation of the classification error rate was deliberated as the FF, as given in Eq. (29).

$$\:fitness\left({x}_{i}\right)=Classifier\:Error\:Rate\left({x}_{i}\right)$$

$$\:=\frac{number\:of\:misclassified\:samples}{Total\:no\:of\:samples}\times\:100\:$$

(29)

Results analysis and discussion

The performance simulation of the RAIHFAD-RFE model was evaluated using two datasets: CIC-IDS-2017⁴¹ and Edge-IIoT⁴². The CIC-IDS-2017 dataset comprises a total of 25,500 counts across 11 classes. Table 3 portrays the complete details of the CIC-IDS-2017 dataset. The complete number of attributes was 78, but only 32 attributes were selected.

Table 3 Details of the CIC-IDS-2017 dataset.

Figure 4 depicts the classifier results of the RAIHFAD-RFE technique on the CIC-IDS-2017 dataset. Figure 4a and c show the confusion matrices, demonstrating the accurate detection and classification of all classes on a 70:30 split. Figure 4b illustrates the PR examination, demonstrating the top performance for each class. Ultimately, Fig. 4d illustrates the ROC investigation, showing capable outcomes with higher ROC values to separate the classes.

Fig. 4

CIC-IDS-2017 dataset: (a, c) 70% and 30% confusion matrices and (b, d) PR and ROC curves.

Table 4; Fig. 5 illustrate the DDoS attack detection capabilities of the RAIHFAD-RFE approach using the CIC-IDS-2017 dataset. With 70% TRPHE, the proposed RAIHFAD-RFE model attains an average $\:acc{u}_{y}$ of 99.31%, $\:pre{c}_{n}$ of 96.15%, $\:rec{a}_{l}$ of 95.99%, $\:{F1}_{Score}\:$of 96.06%, and $\:MCC\:$of 95.68%. Finally, under 30% TSPHE, the proposed RAIHFAD-RFE model attains an average $\:acc{u}_{y}$ of 99.35%, $\:pre{c}_{n}$ of 96.36%, $\:rec{a}_{l}$ of 96.22%, $\:{F1}_{Score}\:$of 96.28%, and $\:MCC\:$of 95.93%.

Table 4 DDoS attack detection of the RAIHFAD-RFE model on the CIC-IDS-2017 dataset.

Fig. 5

Average values of the RAIHFAD-RFE model on the CIC-IDS-2017 dataset.

Figure 6 reveals the classifier results of the RAIHFAD-RFE methodology in the CIC-IDS-2017 dataset. Figure 6a illustrates the accuracy inspection of the RAIHFAD-RFE methodology. The figure indicates that the RAIHFAD-RFE methodology presents increasing values with increasing epoch counts. Additionally, the stable rise in validation over training demonstrates that the RAIHFAD-RFE technique efficiently learns from the test dataset. Figure 6b portrays the loss analysis of the RAIHFAD-RFE technique. The results specify that the RAIHFAD-RFE technique achieves close training and validation loss values. The RAIHFAD-RFE technique learns capably from the test dataset.

Fig. 6

(a) Accuracy and (b) loss curves on the CIC-IDS-2017 dataset.

Table 5; Fig. 7 present a comparative analysis of the RAIHFAD-RFE technique on the CIC-IDS-2017 dataset, along with current methods, using various measures^43,44,45. The table values indicate that the present methodologies, namely the KPCA-RN-SVM-LR, Naïve Bayes (NB), GRU-LSTM, PSO-LSTM, PRO-DLBIDCPS, BBFO-GRU and CO-Algorithm models, have shown the worst performance. However, the proposed RAIHFAD-RFE technique produced higher $\:acc{u}_{y}$, $\:pre{c}_{n}$, $\:rec{a}_{l}$ and $\:{F1}_{Score}$ of 99.35%, 96.36%, 96.22% and 96.28%, respectively.

Table 5 Comparative analysis of the RAIHFAD-RFE method on the CIC-IDS-2017 dataset^43,44,45.

Fig. 7

Comparative analysis of the RAIHFAD-RFE method on the CIC-IDS-2017 dataset.

Table 6; Fig. 8 specify the ablation study of the RAIHFAD-RFE technique. The ablation study highlights the individual and combined impacts of key components in the RAIHFAD-RFE technique on the CIC-IDS 2017 dataset. Using only RFE, the model achieved an $\:acc{u}_{y}$ of 97.50%, $\:pre{c}_{n}$ of 94.41%, $\:rec{a}_{l}$ of 94.08% and $\:{F1}_{Score}$ of 94.40%, illustrating the significance of effective FS. Incorporating IOPA for hyperparameter tuning improved performance to an $\:acc{u}_{y}$ of 98.20%, $\:pre{c}_{n}$ of 95.16%, $\:rec{a}_{l}$ of 94.79% and $\:{F1}_{Score}$ of 95.03%. The LSTM-BiGRU classifier additionally enhanced results, reaching an $\:acc{u}_{y}$ of 98.78%, $\:pre{c}_{n}$ of 95.75%, $\:rec{a}_{l}$ of 95.42% and $\:{F1}_{Score}$ of 95.62%. Finally, the RAIHFAD-RFE model integrating RFE, IOPA, and LSTM-BiGRU achieved the highest performance with an $\:acc{u}_{y}$ of 99.35%, $\:pre{c}_{n}$ of 96.36%, $\:rec{a}_{l}$ of 96.22% and $\:{F1}_{Score}$ of 96.28%, demonstrating the efficiency of each module and their synergistic impact when combined.

Table 6 Ablation study results comparing the RAIHFAD-RFE method on the CIC-IDS-2017 dataset.

Fig. 8

Ablation study results comparing the RAIHFAD-RFE method on the CIC-IDS-2017 dataset.

The Edge-IIoT dataset comprises 48,000 records across 12 distinct event types. The details of the Edge-IIoT dataset are shown in Table 7. This dataset contains 63 features, but only 27 features were selected.

Table 7 Details of the Edge-IIoT dataset.

Figure 9 illustrates the classifier outcomes of the RAIHFAD-RFE technique on the Edge-IIoT dataset. Figure 9a and c illustrates the confusion matrix, showing the correct detection and classification of each class at a 70:30 ratio. Figure 9b clarifies the PR analysis, specifying the maximal outcomes across each class. Ultimately, Fig. 9d illuminates the ROC evaluation, establishing efficacious results with superior ROC values for individual classes.

Fig. 9

Edge-IIoT dataset: (a, c) 70% and 30% confusion matrices and (b, d) PR and ROC curves.

Table 8; Fig. 10 describe the DDoS attack detection of the RAIHFAD-RFE technique at the Edge-IIoT dataset. Based on 70% TRPHE, the RAIHFAD-RFE technique achieved an average $\:acc{u}_{y}$ of 99.39%, $\:pre{c}_{n}$ of 96.37%, $\:rec{a}_{l}$ of 96.37%, $\:{F1}_{Score}\:$of 96.37% and $\:MCC\:$of 96.04%. Also, on 30% TSPHE, the RAIHFAD-RFE model attained an average $\:acc{u}_{y}$ of 99.38%, $\:pre{c}_{n}$ of 99.30%, $\:rec{a}_{l}$ of 96.29%, $\:{F1}_{Score}\:$of 96.29% and $\:MCC\:$of 95.96%.

Table 8 DDoS attack detection of the RAIHFAD-RFE technique on the Edge-IIoT dataset.

Fig. 10

Average values of the RAIHFAD-RFE model on the Edge-IIoT dataset.

Figure 11 depicts the classifier outcomes of the RAIHFAD-RFE method under the Edge-IIoT dataset. Figure 11a shows the accuracy examination of the RAIHFAD-RFE method. The figure suggests that the RAIHFAD-RFE method provides increasing values over successive epochs. In addition, the consistent progress in validation relative to training demonstrates that the RAIHFAD-RFE method effectively learns from the test dataset. Figure 11b reveals the loss analysis of the RAIHFAD-RFE method. The outcomes denote that the RAIHFAD-RFE method accomplishes similar training and validation loss values. It is highlighted that the RAIHFAD-RFE model learns effectively from the test dataset.

Fig. 11

(a) Accuracy and (b) loss curves on the Edge-IIoT dataset.

Table 9; Fig. 12 present a comparative analysis of the RAIHFAD-RFE approach on the Edge-IIoT dataset, along with existing techniques, using various metrics. The table values confirm that the current methods, such as the Shallow ANN, Isolated LSTM, CNN, RF, SVM, DNN and Inception Time techniques, illustrate the poorest performance. However, the RAIHFAD-RFE model achieved the highest $\:acc{u}_{y}$, $\:pre{c}_{n}$, $\:rec{a}_{l},$ and $\:{F1}_{Score}$ of 99.39%, 96.37%, 96.37% and 96.37%, respectively.

Table 9 Comparative study of the RAIHFAD-RFE model on the Edge-IIoT dataset^43,44,45.

Fig. 12

Comparative analysis of the RAIHFAD-RFE model on the Edge-IIoT dataset.

Table 10; Fig. 13 show the ablation study analysis of the RAIHFAD-RFE approach. Using RFE alone resulted in an $\:acc{u}_{y}$ of 97.38%, $\:pre{c}_{n}$ of 94.71%, $\:rec{a}_{l}$ of 94.30% and $\:{F1}_{Score}$ of 94.51%, indicating solid baseline performance from FS. When the IOPA was applied for hyperparameter tuning, the model achieved an $\:acc{u}_{y}$ of 98.14%, $\:pre{c}_{n}$ of 95.35%, $\:rec{a}_{l}$ of 95.08% and $\:{F1}_{Score}$ of 95.16%, confirming its tuning effectiveness. The LSTM-BiGRU classifier exhibits further improvements, providing an $\:acc{u}_{y}$ of 98.86%, $\:pre{c}_{n}$ of 95.86%, $\:rec{a}_{l}$ of 95.74% and $\:{F1}_{Score}$ of 95.83%, highlighting the power of temporal feature learning. The RAIHFAD-RFE model, which integrates RFE, IOPA and LSTM-BiGRU, delivered the highest performance with an $\:acc{u}_{y}$ of 99.39%, $\:pre{c}_{n}$ of 96.37%, $\:rec{a}_{l}$ of 96.37% and $\:{F1}_{Score}$ of 96.37%, confirming the superiority of the model.

Table 10 Results of the ablation study of the RAIHFAD-RFE technique on the Edge-IIoT dataset.

Fig. 13

Results of the ablation study of the RAIHFAD-RFE technique on the Edge-IIoT dataset.

Conclusion

The study presented in this manuscript, proposed the RAIHFAD-RFE technique for cybersecurity systems. The RAIHFAD-RFE technique utilises the Z-score standardisation method for the data pre-processing stage to clean, transform and organise raw data into a structured format. Furthermore, the RFE model was employed for the FS process to recognise and maintain the most essential features for improving the model’s performance. For the DDoS attack classification procedure, the RAIHFAD-RFE used hybridisation of the LSTM-BiGRU technique. To further optimises the model performance, the IOPA was utilised for hyperparameter tuning to ensure that the best hyperparameters are selected for enhanced accuracy. A comprehensive experimental analysis of the RAIHFAD-RFE model was performed under the CIC-IDS-2017 and Edge-IIoT datasets. The comparative analysis of the RAIHFAD-RFE approach provided superior accuracy values of 99.35% and 99.39%, respectively, compared to the existing models on the dual dataset.