Analytical modeling of coreless stator axial flux permanent magnet machines under no-load condition

Abstract

This paper presents three analytical techniques for 3D modeling and analysis of coreless stator axial flux permanent-magnet (CS-AFPM) machines under no-load condition. Quasi 3D analytical model based on Hague’s solution, magnetic equivalent circuit (MEC) model, and analytical model based on Fourier-Bessel series are used to calculate the components of air-gap magnetic flux density. In quasi 3D analytical model, the 3D geometry of CS-AFPM machine is transformed into the 2D geometries in different radii. Hague’s solution is used to calculate the tangential and axial components of air-gap flux density in corresponding radius. The law of superposition is then used to calculate the flux-linkage of stator phase. In the MEC model, the non-linear permeance network is used to calculate the axial component of air-gap flux density while considering the curvature effect, the fringing effect, and the leakage magnetic fluxes. In the proposed 3D analytical model, all components of air-gap flux density are calculated while considering the edge effect, the curvature effect, fringing and leakage fluxes, the magnetic saturation, and the skewed PMs. In final, the accuracy and capabilities of these techniques are verified through comparing with corresponding results obtained from 3D finite element method (FEM) and the experiment set-up.

Introduction

Coreless stator axial flux permanent magnet (CS-AFPM) machines have found many applications, such as electric vehicle and wind energy generation systems, due to their high power and torque density, low torque pulsation, and the absence of core losses in stator and cogging torque^1,2. The electromagnetic problems of CS-AFPM machines include the curvature effect, fringing effect, high leakage fluxes, and so on^3,4. For these reasons, the accurate 3D modeling of CS-AFPM machines is necessary for design, optimization, and analysis of them. The modeling techniques have two major categories: numerical and analytical methods. Undoubtedly, 3D finite element method (3D FEM) is the most accurate technique for the electromagnetic modeling and analysis of CS-AFPM machines^5,6,7,8,9. However, 3D FEM is so time-consuming, and it is better only used in the final stage to verify the 3D analytical results^3,4. To reduce the modeling and computation time by using 3D FEM, the quasi- 3D FEM was used in¹⁰ which acts based on dividing the 3D geometry of AFPM machine into the multi 2D linear FEM models in different radii. However, the curvature effect cannot be accurately considered by using this approximation. The analytical techniques have been introduced to more reduce the time computation while achieving the high precision, such as magnetic equivalent circuit (MEC) model, field reconstruction method (FRM), Hague’s solution, and sub-domain (S-D) model. The real and quasi 3D MEC models can be appropriate techniques for electromagnetic design and modeling the AFPM machines with iron core in the stator^11,12. In the case of CS-AFPM machines, the 3D MEC model is more complex due to the requirement to approximately consider the leakage, edge, and fringing effects of magnetic flux in the large air-gap between the rotor disks^4,13,14. 3D FRM was used to model one typical AFPM machine through applying the law of superposition on the basis functions obtained through 3D FEM¹⁵. For this reason, 3D FRM can be a suitable method for modeling the CS-AFPM machines due to its low level of magnetic saturation. However, 3D FRM is not a self-contained technique. A fast 2D analytical technique combining the MEC model and solving Laplace/Poisson equations has been introduced in^16,17 for axial-field flux-switching PM motors which approximate the inner PMs of stator and the rotor teeth to virtual surface PMs and currents, respectively. For the fast design of CS-AFPM machines, Hague’s solution was used to calculate the equivalent circuit parameters when considering one 2D linear model in the average radius¹⁸. S-D model divides the geometry of AFPM into several regions, including stator yoke, stator teeth, stator slot, PMs, air-gap and rotor yoke. Laplace or Poisson equations in terms of magnetic scalar potential or magnetic vector potential are then solved in each region while considering the boundary conditions¹⁹. The quasi-3D S-D model has been used to model and analysis the AFPM machines, frequently^{20,21,22,23,24,25,26,27,28,29}. The proposed analytical technique in²⁰ cannot consider the distribution of PM magnetization in radial direction. In²¹, one correction function was introduced to consider the curvature effect. The approximate models were used in^30,31 for optimal design of printed circuit board CS-AFPM machines. The proposed approach in²⁰ was used to optimal design of one typical CS-AFPM machine³². In³³, the complex Fourier series representation of scalar magnetic potential based on the linearization of the machine geometry to the mean radius has been used to calculate the 3D distribution of air-gap magnetic flux density. However, the radial variation of motor geometry cannot be accurately considered by using this complex Fourier series. The proposed 3D S-D model in³⁴ is very complicated and ambiguous to consider the different PM shapes in CS-AFPM machines. In this paper, a new 3D analytical technique based on Fourier-Bessel series is introduced which can consider different PM shapes in CS-AFPM machines, the magnetic saturation in rotor disks, the leakage, edge and fringing effects of air-gap magnetic flux, accurately and user-friendly. The quasi-3D analytical model and MEC model are also used to 3D model and analysis the studied CS-AFPM machine. This paper is organized as follows:

The rated parameters of studied CS-AFPM machine are introduced in section II. Quasi-3D model, MEC model, and proposed 3D analytical model are respectively presented in sections III-V. The electromagnetic results obtained through techniques are discussed in section V. The conclusions of work are presented in section VI.

Table 1 Parameters of analyzed CS-AFPM machine.

Rated parameters of studied machine

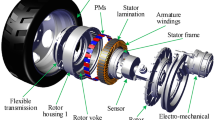
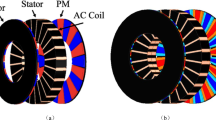
The parameters of studied CS-AFPM machine are introduced in Table 1¹⁸. This machine has two external rotors with trapezoid PMs and one internal stator, which is including the five-phase winding. The stator coils with planar structure are facing the air-gap. To increase the flux-linkage of planar coils, they have two layers pre-wound and placed in the plastic holder and then stacked in the axial direction, and all coils of one phase are connected in series. The stator coils are surrounded by plastics, air and PMs, which have very low relative magnetic permeability. The rotor disks are placed in a relatively big distance, and therefore the magnetic saturation can be weak. The 8 Nd-Fe-B PMs are mounted on the surface of each rotor disk. The 3D FEM model of analyzed CS-AFPM machine is shown in Fig. 1.

Quasi 3D model

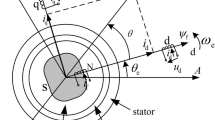
Due to the radial nonuniformity of AFPM machines and the time-consuming nature of 3D FEM, the quasi-3D models have been developed which slices the 3D geometry of AFPM machine into the individual cylindrical planes and then expanded into the Cartesian coordinate, as shown in Fig. 2¹⁸.

Fig. 1

3D FEM model.

Fig. 2

Simplified 2D model.

The main idea is to replace the PMs with equivalent virtual coils, as shown in Fig. 3 for one typical N-PM pole. The inactive parts of equivalent virtual coils only produce the leakage magnetic flux. For this reason, the active parts of equivalent virtual coils are only considered in the quasi-3D models. Considering n = 10 equivalent line currents for each side of equivalent virtual coils in active parts, formula (1)–(2) can be used to calculate the axial and tangential components of air-gap flux density in simplified 2D models (Fig. 2).

$$\:{B}_{z}\left(r,\alpha\:,z\right)=-\frac{{\mu\:}_{^\circ\:}}{4{h}_{z}}\sum\:_{i=1}^{8np}{I}_{i}\times\:\left[\frac{\text{sinh}\left(\frac{\pi\:}{{h}_{z}}r\left(\alpha\:-{\alpha\:}_{i}\right)\right)}{\text{cosh}\left(\frac{\pi\:}{{h}_{z}}r\left(\alpha\:-{\alpha\:}_{i}\right)\right)-\text{cos}\left(\frac{\pi\:}{{h}_{z}}\left(z+{z}_{i}\right)\right)}+\frac{\text{sinh}\left(\frac{\pi\:}{{h}_{z}}r\left(\alpha\:-{\alpha\:}_{i}\right)\right)}{\text{cosh}\left(\frac{\pi\:}{{h}_{z}}r\left(\alpha\:-{\alpha\:}_{i}\right)\right)-\text{cos}\left(\frac{\pi\:}{{h}_{z}}\left(z-{z}_{i}\right)\right)}\right]$$

(1)

$$\:{B}_{t}\left(r,\alpha\:,z\right)=\frac{{\mu\:}_{^\circ\:}}{4{h}_{z}}\sum\:_{i=1}^{8np}{I}_{i}\times\:\left[\frac{\text{sin}\left(\frac{\pi\:}{{h}_{z}}\left(z+{z}_{i}\right)\right)}{\text{cosh}\left(\frac{\pi\:}{{h}_{z}}r\left(\alpha\:-{\alpha\:}_{i}\right)\right)-\text{cos}\left(\frac{\pi\:}{{h}_{z}}\left(z+{z}_{i}\right)\right)}+\frac{\text{sin}\left(\frac{\pi\:}{{h}_{z}}\left(z-{z}_{i}\right)\right)}{\text{cosh}\left(\frac{\pi\:}{{h}_{z}}r\left(\alpha\:-{\alpha\:}_{i}\right)\right)-\text{cos}\left(\frac{\pi\:}{{h}_{z}}\left(z-{z}_{i}\right)\right)}\right]$$

(2)

Fig. 3

Equating one PM with virtual coil.

In (1)–(2), $\:r$ is the radius of the relevant 2D model, $\:{h}_{z}=2\times\:{h}_{m}+g$, and $\:{I}_{i}$ is the magnitude of i^th equivalent line current at the position of $\:{z}_{i}$ and $\:{\alpha\:}_{i}$. It should be noted that the formula (1)–(2) are extracted based on the image method^18,35.

Fig. 4

Main flux paths in CS-AFPM machine⁴.

Fig. 5

Reduced MEC model⁴.

MEC model

An improved MEC model⁴ which can consider the effects of leakage, fringing, and curvature is used to model and analysis the studied CS-AFPM machine under no-load condition. As shown in Figs. 4 and 5, the proposed MEC model in⁴ can consider all flux paths including the main air-gap flux, the leakage flux between adjacent PMs, PM to rotor yoke leakage flux at active parts, and at inner and outer radii of PMs. The reluctances shown in Fig. 5 can be calculated as follows⁴:

$$\:{R}_{m}=\frac{{h}_{m}}{{\mu\:}_{^\circ\:}{\mu\:}_{rm}\frac{\pi\:{\alpha\:}_{p}}{2p}\left({{r}_{mo}}^{2}-{{r}_{mi}}^{2}\right)}$$

(3)

$$\:{R}_{g}=\frac{g}{{\mu\:}_{^\circ\:}\frac{\pi\:{\alpha\:}_{p}}{2p}\left({{r}_{mo}}^{2}-{{r}_{mi}}^{2}\right)}$$

(4)

$$\:{R}_{r}=\frac{\frac{\pi\:}{2p}\left({r}_{mo}+{r}_{mi}\right)}{{\mu\:}_{^\circ\:}{\mu\:}_{rc}{l}_{r}\left({r}_{mo}-{r}_{mi}\right)}$$

(5)

$$\:{R}_{\sigma\:mm}=\frac{{h}_{m}}{{\mu\:}_{^\circ\:}{\mu\:}_{rm}\frac{g}{2}\left({r}_{mo}-{r}_{mi}\right)}$$

(6)

$$\:\frac{1}{{R}_{\sigma\:mg}}={\mu\:}_{^\circ\:}\underset{0}{\overset{0.5g}{\int\:}}\underset{{r}_{mi}}{\overset{{r}_{mo}}{\int\:}}\frac{drdz}{\frac{\pi\:}{p}\left(1-{\alpha\:}_{p}\right)r+\pi\:z}$$

(7)

$$\:{R}_{\sigma\:mr}=\frac{g+\frac{\pi\:}{2p}\left(1-{\alpha\:}_{p}\right)\left({r}_{mo}+{r}_{mi}\right)}{{\mu\:}_{^\circ\:}{\mu\:}_{rc}{l}_{r}\left({r}_{mo}-{r}_{mi}\right)}$$

(8)

$$\begin{aligned}{R}_{\sigma\:rm} & =\frac{{h}_{m}}{{\mu\:}_{^\circ\:}{\mu\:}_{rm}\underset{{r}_{mi}}{\overset{{r}_{mo}}{\int\:}}L\left(r\right)dr} \\ L\left(r\right) & =min\left\{0.5g,\frac{\pi\:r\left(1-{\alpha\:}_{p}\right)}{2p}\right\} \end{aligned}$$

(9)

$$\:\frac{1}{{R}_{\sigma\:rg}}={\mu\:}_{^\circ\:}\underset{{r}_{mi}}{\overset{{r}_{mo}}{\int\:}}\underset{0}{\overset{L\left(r\right)}{\int\:}}\frac{drdz}{\pi\:z+{h}_{m}}$$

(10)

$$\:\frac{1}{{R}_{\sigma\:rr}}={\mu\:}_{^\circ\:}{\mu\:}_{rc}\underset{{r}_{mi}}{\overset{{r}_{mo}}{\int\:}}\frac{{l}_{r}dr}{2L\left(r\right)}$$

(11)

$$\:{R}_{\sigma\:im}=\frac{{h}_{m}}{{\mu\:}_{^\circ\:}{\mu\:}_{rm}\frac{g}{2}{r}_{mi}\frac{\pi\:{\alpha\:}_{p}}{p}}$$

(12)

$$\:\frac{1}{{R}_{\sigma\:ig}}=\frac{2{\mu\:}_{^\circ\:}{\alpha\:}_{p}}{3p}\left[0.5g+\left({r}_{mi}-\frac{2{h}_{m}}{3\pi\:}\right)\text{ln}\left(1+\frac{3\pi\:g}{4{h}_{m}}\right)\right]$$

(13)

$$\:{R}_{\sigma\:ir}=\frac{0.5g}{{\mu\:}_{^\circ\:}{\mu\:}_{rc}{l}_{r}{r}_{mi}\frac{\pi\:{\alpha\:}_{p}}{p}}$$

(14)

$$\:{R}_{\sigma\:om}=\frac{{h}_{m}}{{\mu\:}_{^\circ\:}{\mu\:}_{rm}\frac{g}{2}{r}_{mo}\frac{\pi\:{\alpha\:}_{p}}{p}}$$

(15)

$$\:\frac{1}{{R}_{\sigma\:og}}=\frac{2{\mu\:}_{^\circ\:}{\alpha\:}_{p}}{3p}\left[-0.5g+\left({r}_{mo}+\frac{2{h}_{m}}{3\pi\:}\right)\text{ln}\left(1+\frac{3\pi\:g}{4{h}_{m}}\right)\right]$$

(16)

$$\:{R}_{\sigma\:or}=\frac{0.5g}{{\mu\:}_{^\circ\:}{\mu\:}_{rc}{l}_{r}{r}_{mo}\frac{\pi\:{\alpha\:}_{p}}{p}}$$

(17)

The magneto motive force (MMF) of one PM pole ($\:{F}_{m}$) can be calculated as follows:

$$\:{F}_{m}={H}_{c}\times\:{h}_{m}$$

(18)

The air-gap flux $\:{\varnothing\:}_{g}$ is calculated by applying the KVL and KCL laws to the MEC model (Fig. 5). The axial component of air-gap flux density is then calculated as follows⁴:

$$\:{B}_{z}\left(r,\alpha\:\right)=\frac{2p{\varnothing\:}_{g}}{\pi\:{\alpha\:}_{p}}\left({{r}_{mo}}^{2}-{{r}_{mi}}^{2}\right)\lambda\:\left(r,\alpha\:\right)\delta\:\left(r\right)$$

(19)

$$\:\delta\:\left(r\right)={\left(1+{\left|\frac{r-0.5\left({r}_{mi}+{r}_{mo}\right)}{{\beta\:}_{1}}\right|}^{{\beta\:}_{2}}\right)}^{-1}$$

$$\:{\beta\:}_{1}=0.5\left({r}_{mo}-{r}_{mi}\right)$$

$$\:{\beta\:}_{2}=\frac{6\left({r}_{mo}-{r}_{mi}\right)}{{g}^{0.77}}$$

(20)

$$\:\lambda\:\left(r,\alpha\:\right)=\left\{\begin{array}{c}0.5{e}^{\frac{r\alpha\:+\frac{r\pi\:{\alpha\:}_{p}}{2p}}{\sigma\:}}\:\:\:\:\:\:\:\:\:\:\:\alpha\:\in\:\left[-\pi\:,-\frac{\pi\:}{2p}{\alpha\:}_{p}\right]\\\:-0.5{e}^{\frac{-\left(r\alpha\:+\frac{r\pi\:{\alpha\:}_{p}}{2p}\right)}{\sigma\:}}+1\:\:\:\alpha\:\in\:(-\frac{\pi\:}{2p}{\alpha\:}_{p},0]\\\:-0.5{e}^{\frac{\left(r\alpha\:-\frac{r\pi\:{\alpha\:}_{p}}{2p}\right)}{\sigma\:}}+1\:\:\:\alpha\:\in\:(0,\frac{\pi\:}{2p}{\alpha\:}_{p}]\\\:0.5{e}^{\frac{-\left(r\alpha\:-\frac{r\pi\:{\alpha\:}_{p}}{2p}\right)}{\sigma\:}}\:\:\:\:\:\:\:\:\:\:\alpha\:\in\:(\frac{\pi\:}{2p}{\alpha\:}_{p},\pi\:]\end{array}\right.$$

$$\:\sigma\:=0.5\sqrt{0.5g(0.5g+\frac{{h}_{m}}{{\mu\:}_{rm}})}$$

(21)

where $\:\lambda\:\left(r,\alpha\:\right)$ and $\:\delta\:\left(r\right)$ are used to consider the fringing effect in tangential and radial directions.

Fig. 6

Different domains in r-z plane.

3D analytical model

The proposed 3D analytical model in this paper for analyzing the studied CS-AFPM machine acts based on dividing the 3D geometry into different layers (Fig. 6) including the rotor cores, two air-gaps, and the stator winding layer while considering the non-linear relative magnetic permeability for the rotor cores.

$$\:{\nabla\:}^{2}\psi\:\left(r,\alpha\:,z\right)=0$$

(22)

$$\begin{aligned}{\psi\:}_{i}\left(r,\alpha\:,z\right) & =\sum\:_{k}\sum\:_{l}\left[\left({L}_{i,(k,l)}{e}^{\frac{{j}_{(k,l)}}{{r}_{a}}z}+{M}_{i,(k,l)}{e}^{-\frac{{j}_{(k,l)}}{{r}_{a}}z}\right){J}_{l}\left(\frac{{j}_{(k,l)}}{{r}_{a}}r\right)\text{cos}\left(l\alpha\:\right) \right. \\ & \quad \left. +\left({N}_{i,(k,l)}{e}^{\frac{{j}_{(k,l)}}{{r}_{a}}z}+{O}_{i,(k,l)}{e}^{-\frac{{j}_{(k,l)}}{{r}_{a}}z}\right){J}_{l}\left(\frac{{j}_{(k,l)}}{{r}_{a}}r\right)\text{sin}\left(l\alpha\:\right)\right]\end{aligned}$$

(23)

$$\left\{ \begin{array}{c}\overrightarrow{H}\left(r,\alpha\:,z\right)=-\overrightarrow{\nabla\:}\psi\:={H}_{r}\overrightarrow{{a}_{r}}+{H}_{t}\overrightarrow{{a}_{t}}+{H}_{z}\overrightarrow{{a}_{z}}\\\overrightarrow{B}\left(r,\alpha\:,z\right)={\mu\:}_{^\circ\:}\times\:\overrightarrow{H}\left(r,\alpha\:,z\right)\end{array}\right.$$

(24)

$$\begin{aligned}{H}_{r,i}\left(r,\alpha\:,z\right) & =-\sum\:_{k}\sum\:_{l}\left(\frac{{j}_{(k,l)}}{{2r}_{a}}\right)\left[\left({L}_{i,(k,l)}{e}^{\frac{{j}_{(k,l)}}{{r}_{a}}z}+{M}_{i,(k,l)}{e}^{-\frac{{j}_{(k,l)}}{{r}_{a}}z}\right)F\left(\frac{{j}_{(k,l)}}{{r}_{a}}r\right)\text{cos}\left(l\alpha\:\right) \right. \\ & \quad \left. +\left({N}_{i,(k,l)}{e}^{\frac{{j}_{(k,l)}}{{r}_{a}}z}+{O}_{i,(k,l)}{e}^{-\frac{{j}_{(k,l)}}{{r}_{a}}z}\right)F\left(\frac{{j}_{(k,l)}}{{r}_{a}}r\right)\text{sin}\left(l\alpha\:\right)\right]\end{aligned}$$

(25)

$$\begin{aligned}{H}_{t,i}\left(r,\alpha\:,z\right) & =\sum\:_{k}\sum\:_{l}\left(\frac{l}{r}\right)\left[\left({L}_{i,(k,l)}{e}^{\frac{{j}_{(k,l)}}{{r}_{a}}z}+{M}_{i,(k,l)}{e}^{-\frac{{j}_{(k,l)}}{{r}_{a}}z}\right){J}_{l}\left(\frac{{j}_{(k,l)}}{{r}_{a}}r\right)\text{sin}\left(l\alpha\:\right) \right. \\ & \quad \left. -\left({N}_{i,(k,l)}{e}^{\frac{{j}_{(k,l)}}{{r}_{a}}z}+{O}_{i,(k,l)}{e}^{-\frac{{j}_{(k,l)}}{{r}_{a}}z}\right){J}_{l}\left(\frac{{j}_{(k,l)}}{{r}_{a}}r\right)\text{cos}\left(l\alpha\:\right)\right]\end{aligned}$$

(26)

$$\begin{aligned}{H}_{z,i}\left(r,\alpha\:,z\right) & =-\sum\:_{k}\sum\:_{l}\left(\frac{{j}_{(k,l)}}{{r}_{a}}\right)\left[\left({L}_{i,(k,l)}{e}^{\frac{{j}_{(k,l)}}{{r}_{a}}z}-{M}_{i,(k,l)}{e}^{-\frac{{j}_{(k,l)}}{{r}_{a}}z}\right){J}_{l}\left(\frac{{j}_{(k,l)}}{{r}_{a}}r\right)\text{cos}\left(l\alpha\:\right) \right. \\ & \quad \left. +\left({N}_{i,(k,l)}{e}^{\frac{{j}_{(k,l)}}{{r}_{a}}z}-{O}_{i,(k,l)}{e}^{-\frac{{j}_{(k,l)}}{{r}_{a}}z}\right){J}_{l}\left(\frac{{j}_{(k,l)}}{{r}_{a}}r\right)\text{sin}\left(l\alpha\:\right)\right]\end{aligned}$$

(27)

$$\left\{ \begin{array}{c}\overrightarrow{B}={\mu\:}_{0}\left(\overrightarrow{H}+\overrightarrow{M}\right)\\\overrightarrow{M}={M}_{z}\overrightarrow{{a}_{z}}=\frac{{B}_{R}}{{\mu\:}_{0}}\overrightarrow{{a}_{z}}\end{array}\right.$$

(28)

$$\left\{ \begin{array}{c}{M}_{z}\left(r,\alpha\:\right) =-0.5\sum_{k}{A}_{\left(k,0\right)}\:{J}_{l}\left(\frac{{j}_{\left(k,0\right)}}{{r}_{a}}r\right) +\sum_{k}\sum_{l}\left[{A}_{(k,l)}\:{J}_{l}\left(\frac{{j}_{(k,l)}}{{r}_{a}}r\right)\text{cos}\left(l\alpha\:\right)+{B}_{(k,l)}\:{J}_{l}\left(\frac{{j}_{(k,l)}}{{r}_{a}}r\right)\text{sin}\left(l\alpha\:\right)\right] \\\:{A}_{(k,l)}=\frac{2}{\pi\:{{r}_{a}}^{2}{\left[{J}_{l+1}\left({j}_{(k,l)}\right)\right]}^{2}}\underset{0}{\overset{2\pi\:}{\int\:}}\underset{0}{\overset{{r}_{a}}{\int\:}}r{M}_{z}{J}_{l}\left(\frac{{j}_{(k,l)}}{{r}_{a}}r\right)\text{cos}\left(l\alpha\:\right)drd\alpha\:\\\:{B}_{(k,l)}=\frac{2}{\pi\:{{r}_{a}}^{2}{\left[{J}_{l+1}\left({j}_{(k,l)}\right)\right]}^{2}}\underset{0}{\overset{2\pi\:}{\int\:}}\underset{0}{\overset{{r}_{a}}{\int\:}}r{M}_{z}{J}_{l}\left(\frac{{j}_{(k,l)}}{{r}_{a}}r\right)\text{sin}\left(l\alpha\:\right)drd\alpha\:\end{array}\right. $$

(29)

$$\:F\left(\frac{{j}_{(k,l)}}{{r}_{a}}r\right)={J}_{l-1}\left(\frac{{j}_{(k,l)}}{{r}_{a}}r\right)-{J}_{l+1}\left(\frac{{j}_{(k,l)}}{{r}_{a}}r\right)$$

(30)

$$\:z={z}_{4}\to\:\:\:{H}_{t,1}=0$$

(31)

$$\:z={z}_{3}\to\:\:\left\{\begin{array}{l}{H}_{t,1}={H}_{t,2}\\\:{B}_{z,1}={B}_{z,2}\to\:{\mu\:}_{r,1}\times\:{H}_{z,1}=\left({H}_{z,2}+{M}_{z}\right)\end{array}\right.$$

(32)

$$\:z={z}_{2}\to\:\:\left\{\begin{array}{l}{H}_{t,2}={H}_{t,3}\\\:{B}_{z,2}={B}_{z,3}\to\:\left({H}_{z,2}+{M}_{z}\right)={H}_{z,3}\end{array}\right.$$

(33)

$$\:z={-z}_{2}\to\:\:\:\left\{\begin{array}{l}{H}_{t,3}={H}_{t,4}\\\:{B}_{z,3}={B}_{z,4}\to\:{H}_{z,3}=\left({H}_{z,4}+{M}_{z}\right)\end{array}\right.$$

(34)

$$\:z={-z}_{3}\to\:\:\left\{\begin{array}{l}{H}_{t,4}={H}_{t,5}\\\:{B}_{z,4}={B}_{z,5}\to\:\left({H}_{z,4}+{M}_{z}\right)={\mu\:}_{r,5}\times\:{H}_{z,5}\end{array}\right.$$

(35)

$$\:z={-z}_{4}\to\:\:\:{H}_{t,5}=0$$

(36)

Maxwell’s equation in terms of the scalar magnetic potential (ψ) is used to calculate the all components of air-gap flux density under no-load condition as shown in (22).

Fig. 7

Distribution of M_z.

As shown in (23), the general solution of Laplace’s Eq. (22) in the i^th region can be obtained through using the method of separation of variables and by using the Fourier-Bessel series. Three components of air-gap flux density are then calculated by using (24)–(27). The vector of flux density in the region of PMs is defined as (28). As shown in (29), Fourier-Bessel series is used to express the distribution of PM magnetization. In aforementioned formulas, $\:{r}_{a}$ is the radial length of the domain of solution, $\:{j}_{(k,l)}$ is the k^th root of the first kind Bessel function ($\:{J}_{l}\left(r\right)$), and $\:F\left(\frac{{j}_{(k,l)}}{{r}_{a}}r\right)$ is defined as shown in (30). Figure 7 shows the high accuracy of Fourier-Bessel series to model the distribution of magnetization of trapezoid PMs (M_z).

$$\begin{aligned} & \left[\begin{array}{c}\begin{array}{ccc}{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{4}\right)}&\:{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{4}\right)}&\:zeros\left(\text{1,18}\right)\end{array}\\\:\begin{array}{ccc}zeros\left(\text{1,2}\right)&\:{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{4}\right)}&\:\begin{array}{cc}{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{4}\right)}&\:eros\left(\text{1,16}\right)\end{array}\end{array}\\\:\begin{array}{ccc}{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:\begin{array}{cc}zeros\left(\text{1,2}\right)&\:\begin{array}{ccc}-{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:-{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:zeros\left(\text{1,14}\right)\end{array}\end{array}\end{array}\\\:\begin{array}{ccc}zeros\left(\text{1,2}\right)&\:{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:\begin{array}{ccc}{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:zeros\left(\text{1,2}\right)&\:\begin{array}{ccc}{-e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:-{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:zeros\left(\text{1,12}\right)\end{array}\end{array}\end{array}\\\:\begin{array}{ccc}-{\mu\:}_{r,1}\times\:{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:{\mu\:}_{r,1}\times\:{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:\begin{array}{ccc}zeros\left(\text{1,2}\right)&\:{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:\begin{array}{cc}{-e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:zeros\left(\text{1,14}\right)\end{array}\end{array}\end{array}\\\:\begin{array}{ccc}zeros\left(\text{1,2}\right)&\:-{\mu\:}_{r,1}\times\:{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:\begin{array}{ccc}{\mu\:}_{r,1}\times\:{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:zeros\left(\text{1,2}\right)&\:\begin{array}{ccc}{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:-{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:zeros\left(\text{1,12}\right)\end{array}\end{array}\end{array}\\\:\begin{array}{ccc}zeros\left(\text{1,4}\right)&\:{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:\begin{array}{ccc}{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:zeros\left(\text{1,2}\right)&\:\begin{array}{ccc}{-e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:{-e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:zeros\left(\text{1,10}\right)\end{array}\end{array}\end{array}\\\:\begin{array}{ccc}zeros\left(\text{1,6}\right)&\:{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:\begin{array}{ccc}{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:zeros\left(\text{1,2}\right)&\:\begin{array}{cc}{-e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:\begin{array}{cc}-{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:zeros\left(\text{1,8}\right)\end{array}\end{array}\end{array}\end{array}\\\:\begin{array}{ccc}zeros\left(\text{1,4}\right)&\:-{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:\begin{array}{cc}{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:\begin{array}{ccc}zeros\left(\text{1,2}\right)&\:{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:\begin{array}{cc}-{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:zeros\left(\text{1,10}\right)\end{array}\end{array}\end{array}\end{array}\\\:\begin{array}{ccc}zeros\left(\text{1,6}\right)&\:-{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:\begin{array}{ccc}{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:zeros\left(\text{1,2}\right)&\:\begin{array}{ccc}{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:{-e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:zeros\left(\text{1,8}\right)\end{array}\end{array}\end{array}\\\:\begin{array}{ccc}zeros\left(\text{1,8}\right)&\:{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:\begin{array}{ccc}{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:zeros\left(\text{1,2}\right)&\:\begin{array}{cc}-{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:\begin{array}{cc}-{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:zeros\left(\text{1,6}\right)\end{array}\end{array}\end{array}\end{array}\\\:\begin{array}{ccc}zeros\left(\text{1,10}\right)&\:{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:\begin{array}{ccc}{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:zeros\left(\text{1,2}\right)&\:\begin{array}{ccc}{-e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:{-e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:zeros\left(\text{1,4}\right)\end{array}\end{array}\end{array}\\\:\begin{array}{ccc}zeros\left(\text{1,8}\right)&\:{-e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:\begin{array}{ccc}{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:zeros\left(\text{1,2}\right)&\:\begin{array}{ccc}{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:-{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:zeros\left(\text{1,6}\right)\end{array}\end{array}\end{array}\\\:\begin{array}{ccc}zeros\left(\text{1,10}\right)&\:{-e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:\begin{array}{ccc}{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:zeros\left(\text{1,2}\right)&\:\begin{array}{ccc}{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:-{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{2}\right)}&\:zeros\left(\text{1,4}\right)\end{array}\end{array}\end{array}\\\:\begin{array}{ccc}zeros\left(\text{1,12}\right)&\:{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:\begin{array}{ccc}{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:zeros\left(\text{1,2}\right)&\:\begin{array}{ccc}{-e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:-{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:zeros\left(\text{1,2}\right)\end{array}\end{array}\end{array}\\\:\begin{array}{ccc}zeros\left(\text{1,14}\right)&\:{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:\begin{array}{ccc}{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:zeros\left(\text{1,2}\right)&\:\begin{array}{cc}{-e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:-{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}\end{array}\end{array}\end{array}\\\:\begin{array}{ccc}zeros\left(\text{1,12}\right)&\:{-e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:\begin{array}{ccc}{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:zeros\left(\text{1,2}\right)&\:\begin{array}{ccc}{\mu\:}_{r,5}\times\:{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:-{\mu\:}_{r,5}\times\:{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:zeros\left(\text{1,2}\right)\end{array}\end{array}\end{array}\\\:\begin{array}{ccc}zeros\left(\text{1,14}\right)&\:{-e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:\begin{array}{ccc}{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:zeros\left(\text{1,2}\right)&\:\begin{array}{cc}{\mu\:}_{r,5}\times\:{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}&\:-{\mu\:}_{r,5}\times\:{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{3}\right)}\end{array}\end{array}\end{array}\\\:\begin{array}{ccc}zeros\left(\text{1,16}\right)&\:{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{4}\right)}&\:\begin{array}{cc}{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{4}\right)}&\:zeros\left(\text{1,2}\right)\end{array}\end{array}\\\:\begin{array}{ccc}zeros\left(\text{1,18}\right)&\:{e}^{-\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{4}\right)}&\:{e}^{\left(\frac{{j}_{\left(k,l\right)}}{{r}_{a}}{z}_{4}\right)}\end{array}\end{array}\right]\left[\begin{array}{c}{L}_{1,(k,l)}\\\:{M}_{1,(k,l)}\\\:\begin{array}{c}{N}_{1,(k,l)}\\\:{O}_{1,(k,l)}\\\:\begin{array}{c}{L}_{2,(k,l)}\\\:{M}_{2,(k,l)}\\\:\begin{array}{c}{N}_{2,(k,l)}\\\:\begin{array}{c}{O}_{2,\left(k,l\right)}\\\:{L}_{3,(k,l)}\\\:\begin{array}{c}{M}_{3,(k,l)}\\\:\begin{array}{c}{N}_{3,(k,l)}\\\:\begin{array}{c}{O}_{3,\left(k,l\right)}\\\:{L}_{4,(k,l)}\\\:\begin{array}{c}{M}_{4,(k,l)}\\\:{N}_{4,(k,l)}\\\:\begin{array}{c}{O}_{4,\left(k,l\right)}\\\:{L}_{5,(k,l)}\\\:\begin{array}{c}{M}_{5,(k,l)}\\\:{N}_{5,(k,l)}\\\:{O}_{5,\left(k,l\right)}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right] \\ & =\left(\frac{{r}_{a}}{{j}_{(k,l)}}\right)\left[\begin{array}{c}0\\\:0\\\:\begin{array}{c}0\\\:0\\\:\begin{array}{c}{A}_{(k,l)}\\\:{B}_{(k,l)}\\\:\begin{array}{c}0\\\:\begin{array}{c}0\\\:-{A}_{(k,l)}\\\:\begin{array}{c}-{B}_{(k,l)}\\\:0\\\:\begin{array}{c}0\\\:\begin{array}{c}{A}_{(k,l)}\\\:{B}_{(k,l)}\\\:\begin{array}{c}0\\\:0\\\:\begin{array}{c}-{A}_{(k,l)}\\\:-{B}_{(k,l)}\\\:\begin{array}{c}0\\\:0\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\end{array}\right] \end {aligned}$$

(37)

Fig. 8

B-H curve of core material.

The iron material of rotor disks is the non-grain-oriented silicon steel, which has the B-H curve as shown in Fig. 8. The function of relative magnetic permeability ($\:{\mu\:}_{r}$) for this material can be approximately defined as $\:{\mu\:}_{r}=10000\times\:{e}^{-0.8{B}^{2}}$³⁶. A proper rational expression of relative permeability ($\:{\mu\:}_{r}$) in terms of magnetic field intensity (H) can be also used to model the non-linearity effect of iron cores³⁷. The system of algebraic equations (37) is prepared through applying the boundary conditions (31)-(36) in Fig. 6 to determine the unknown constants $\:{L}_{i,(k,l)}$, $\:{M}_{i,(k,l)}$, $\:{N}_{i,(k,l)}$, and $\:{O}_{i,(k,l)}$ in (25)–(27) for every rotor position. An iterative algorithm should be used to consider the non-linear magnetization characteristic of the rotor core for every operating point (every rotor position). The non-linear iterative algorithm is shown in Fig. 9 (for k^th iteration). In Fig. 9, “$\:c$” is the correction factor, and the empirical value is $\:0.2\le\:c\le\:0.3$, ξ is the convergence criterion, and $\:{N}_{max}$ is the maximum allowed number of iterations.

Fig. 9

Non-linear iterative algorithm.

Fig. 10

Convergence path of $\:{\mu\:}_{r,1}$.

For an operating point, the result of iterative algorithm is shown in Fig. 10. As shown, the value of $\:{\mu\:}_{r,1}$ converges to the solution. Figure 10 also shows the magnetic saturation in the rotor core of CS-AFPM machines is negligible. After achieving the converged values of $\:{\mu\:}_{r,1}$and $\:{\mu\:}_{r,5}$ for relevant operating point, the distribution of air-gap flux density and the flux linkage of stator phases are obtained.

Fig. 11

3D plots of B_z.

To present the capability of proposed 3D analytical model, the 3D plots of air-gap field components due to PMs are illustrated in Figs. 11, 12 and 13 while considering the suitable values for constant parameters. The constant values in Figs. 11, 12 and 13 are selected based on the coordinate of center points in radial direction ($\:r=64.5\:\left(mm\right)$), in axial direction ($\:z=0\:\left(mm\right)$), and the center point of one pole pitch in circumferential direction ($\:\alpha\:={22.5}^{^\circ\:}\:(mech.\:deg.)$). Figure 11 shows the edge effect on $\:{B}_{z}$ in radial direction due to the unequal radial lengths of rotor and stator disks.

Figure 12b shows the edge effect on $\:{B}_{t}$ in axial direction and in the inter-pole region. Figure 13c also shows the edge effect on $\:{B}_{r}$ in axial and radial directions, simultaneously. In the case of CS-AFPM machines, it can be concluded from Figs. 12 and 13 that the magnitudes of $\:{B}_{t}$ and $\:{B}_{r}$ are negligible in the middle regions between two rotor disks. Figure 14 shows the 3D distribution of B_z obtained through the MEC and quasi-3D analytical models.

Fig. 12

3D plots of B_t.

Fig. 13

3D plots of B_r.

Fig. 14

Other 3D plots of B_z.

Fig. 15

Axial component of air-gap flux density.

Fig. 16

2D turn function of i^th coil.

As shown in Fig. 14, the quasi-3D model cannot consider the edge effect in the radial direction. The axial component of flux density ($\:{B}_{z}$) in the middle of air-gap ($\:z=0\:\left(mm\right)$ and $\:r=64.5\:\left(mm\right)$) obtained through the proposed and the quasi-3D analytical models, the MEC model, and 3D FEM are illustrated and compared in Fig. 15. As shown, there is a good agreement between the results obtained from the proposed 3D analytical model and 3D FEM.

Fig. 17

Phase flux-linkage.

Fig. 18

Phase back-EMF at 750 rpm.

It should be noted that the matrix of system of equations (37) is not very large. In real, for every value of “$\:k$” and “$\:l$”, a system of 20 equations with 20 unknowns should be solved, which is done very fast. In proposed 3D analytical model, for every operating point, the calculation of air-gap flux density distribution and the phase flux-linkage takes about 0.1 (s) while considering the magnetic saturation in the rotor disks. The flux-linkage with the i^th coil of stator can be calculated as follows:

$$\:{\lambda\:}_{i}\left({\theta\:}_{r}\right)=\underset{0}{\overset{2\pi\:}{\int\:}}\underset{{r}_{si}}{\overset{{r}_{so}}{\int\:}}{n}_{i}\left(r,\alpha\:\right)\times\:{B}_{z}\left(r,\alpha\:,{\theta\:}_{r}\right)\times\:ds\left(r,\alpha\:\right)$$

(38)

where $\:{\theta\:}_{r}$ is the rotor position, $\:{n}_{i}\left(r,\alpha\:\right)$ is the turn-function of the i^th coil, $\:{B}_{z}\left(r,\alpha\:\right)$ is the main component of the air-gap flux density, and $\:ds\left(r,\alpha\:,{\theta\:}_{r}\right)$ is the area of relevant differential element.

Fig. 19

Distribution of M_z with skewed PMs.

The 2D distribution of turn function of the i^th coil has been illustrated in Fig. 16 while considering the distribution of conductors in the coil sides. The flux-linkage with other stator coils can be easily calculated through shifting the result obtained from (38). In final, the flux-linkage and back-EMF of one stator phase is calculated through applying the law of superposition on the relevant results of two stator coils which belong to one stator phase as follows:

$$\:{\lambda\:}_{ph}\left({\theta\:}_{r}\right)=\sum\:_{i=1}^{2}{\lambda\:}_{i}\left({\theta\:}_{r}\right)$$

(39)

$$\:{E}_{ph}\left({\theta\:}_{r}\right)=\frac{d{\lambda\:}_{ph}\left({\theta\:}_{r}\right)}{dt}$$

(40)

The results of flux-linkage with the stator phase A and the back-EMF obtained through different techniques are illustrated and compared in Figs. 17 and 18. For studied CS-AFPM machine, Fig. 18c shows the relevant experiment result taken from¹⁸. As shown, the proposed 3D analytical model has excellent accuracy to calculate the phase flux-linkage and back-EMF.

Table 2 Comparison of techniques.

It can be also concluded that the flux-linkage with stator phases is over-estimated by using the quasi-3D analytical model because it cannot consider the edge effect in the radial direction. The key outputs of all techiques including the fundamental component of B_z, λ_A, E_A, total harmonic distortion (THD) of E_A, and the computation time are quantitatively compared in Table 2.

Fig. 20

Back-EMF with skewed PMs.

Table 3 Fourier analysis of back-EMF.

To prove the capability of proposed 3D analytical technique in modeling different PM shapes, the studied CS-AFPM machine is analyzed with skewed PMs. Figure 19 shows the real and approximate 3D distribution of skewed trapezoid PMs with skew angle ($\:{\theta\:}_{sk}$) of $\:{30}^{^\circ\:}$ obtained through Fourier-Bessel series with high accuracy. Figure 20 shows the phase back-EMF of analyzed CS-AFPM machine with skewed PMs. The results of Fourier analysis are presented in Table 3. As seen, THD of back-EMF are significantly reduced due to the skew effect of PM poles.

Conclusion

A new 3D analytical model was proposed in this paper for electromagnetic modeling the CS-AFPM machines which can consider the edge and curvature effects, and different PM shapes. The Fourier-Bessel series including the hyperbolic function, the Bessel function, and the Fourier series was used to consider the real geometry of PM poles including the effects of curvature, edge and skewed PMs. For this reason, the solutions of air-gap magnetic field were also expressed into the Fourier-Bessel series to accurately consider the edge effect in the radial and circumferential directions. In real, the edge effect in the circumferential direction is under-estimated by using the MEC and quasi-3D analytical models. In the case of radial direction, it is not considered by using the quasi-3D analytical model, and it can be approximately modeled through using the MEC model. It can be generally said that the proposed 3D analytical model can be used to accurately model and analysis the electric machines while considering all non-ideal effects as follows:

• Three components of air-gap magnetic field are considered and analyzed, simultaneously and accurately.

• The curvature effect in radial direction is considered, accurately.

• Different magnet shapes is considered, accurately.

• The magnetic saturation is considered, accurately.