Explainable AI for post-hoc and pseudo-post-hoc predictive maintenance of governor valve actuators

Abstract

The governor valve actuator (GVA), as the actuating mechanism of the steam turbine governing system, directly impacts production safety and economic efficiency. Its highly coupled nature leads to high-dimensional operational data, complex fault modes, and inherent opacity in diagnostic algorithms, posing significant challenges to the real-time performance, reliability, and generalizability of fault diagnosis and early warning tasks. To address these challenges in complex multi-sensor networks, this paper proposes a post-hoc and pseudo-post-hoc predictive maintenance (PPPM) framework leveraging advanced machine learning and SHapley Additive exPlanations, an XAI technology. The PPPM optimizes fault diagnosis and early warning models and provides interpretable attribution analysis to guide predictive maintenance workflows. Experimental results on the GVA fault testing platform prove the effectiveness of the proposed method. For the fault diagnosis and localization task, taking the random forest model as an example, PPPM achieves the optimization of 50% of the measurement points of the sensor network and the attribution analysis of fault localization, which improves the real-time, generality and reliability of the diagnosis model. For the warning task, PPPM carries out sensor network optimization and attribution analysis to improve the pseudo-supervised warning model through the pseudo-supervised learning method. Taking isolated forests as an example, the optimized model improves the W-F1 score by 5.997% and the AUC by 6.942%.

Introduction

Steam turbines are a critical system for converting thermal energy into electrical energy, playing a pivotal role in the power industry due to its high efficiency and advanced performance. Central to its operation is the turbine speed control system, for which the governor valve actuator (GVA) serves as the primary actuation mechanism¹. The GVA’s performance directly influences the unit’s operational economy, maneuverability, and reliability, thereby significantly impacting production safety and economic benefits. However, GVA systems are prone to faults, with statistics indicating that approximately one-third of all unplanned steam turbine unit shutdowns are attributable to failures within the GVA system. These failures not only disrupt power generation but also pose considerable safety risks.

The primary challenge in maintaining GVAs lies in their inherent operational complexity and the nature of their faults. GVAs are highly coupled with electro-mechanical-hydraulic systems, and their faults are often complex and diverse, including issues such as servo valve malfunctions, broken springs, solenoid valve issues, clogged throttle orifices, and cylinder leakages^2,3. This intricate nature significantly complicates manual fault diagnosis and maintenance, often leading to prolonged downtimes and increased operational costs. Consequently, there is a pressing need for advanced fault diagnosis and early warning systems to enhance GVA reliability and improve production efficiency.

Data-driven intelligent fault diagnosis (IFD) has emerged as a promising paradigm⁴, leveraging advancements in sensor and machine learning technologies. IFD approaches, encompassing supervised learning for fault classification^5,6,7 and unsupervised learning for anomaly detection^8,9,10 (i.e., early warning under conditions where the GVA appears to be operating normally but may exhibit incipient fault signatures), often utilize feature engineering from various data domains to map features to health states. While these methods have achieved notable success in many applications^11,12,13, their application to safety-critical systems like GVAs faces specific hurdles. Traditional machine learning models, particularly complex ones, often operate as “black boxes.” This lack of transparency can hinder operator trust, complicate the diagnosis of novel or unexpected fault manifestations, and make it difficult to derive actionable insights for targeted maintenance^{14,15,16,17,18}. Furthermore, issues such as large volumes of operational data, redundant information, and model complexity can negatively impact prediction accuracy and generalization performance in GVA applications, making efficient and reliable IFD an urgent practical need.

To address these limitations, particularly the opacity of “black-box” models in the context of critical GVA systems, Explainable Artificial Intelligence (XAI) offers a significant advancement¹⁹. XAI methods provide mechanisms to interpret model behavior, which is crucial for building trust and enhancing the utility of IFD systems. XAI can be categorized into intrinsic and post-hoc, or model-specific and model-agnostic approaches. Post-hoc, model-agnostic methods like Local Interpretable Model-Agnostic Explanations (LIME) and SHapley Additive exPlanations (SHAP) are particularly valuable as they can be applied to already trained models and offer insights into feature contributions at both local and global levels. For instance, SHAP-based methods have demonstrated superior diagnostic performance and can alleviate challenges in model training, such as class imbalance in fault diagnosis²⁰.

Local Interpretable Model-Agnostic Explanations (LIME) is a local interpretability method designed to elucidate the contribution of each feature to the prediction of individual samples, helping researchers determine whether to trust the predictions, how to improve classifiers, and why not to trust the classifiers²¹. Shreyas Gaw et al²². utilized LIME and Random Forest models to analyze multi-sensor feature sets, achieving fault diagnosis in rotating machinery. LIME has also been applied to the time-domain and frequency-domain feature selection of audio sensors in industrial fans, identifying the most relevant feature sets for fault characteristics to enhance the quality and reliability of fault diagnosis models²³. SHapley Additive exPlanations (SHAP) is a global interpretable artificial intelligence method that provides comprehensive and reliable decision analysis from both global and local perspectives to better achieve predictive maintenance^24,25. For instance, a feature selection method based on SHAP and ensemble learning models has been successfully applied to fault diagnosis in chillers²⁶. Mailson Ribeiro Santos et al²⁷. developed an efficient feature selection framework for rolling bearing fault detection, classification, and severity estimation using SHAP and Support Vector Machines (SVM). Studies have discussed various feature-level explanation methods, with results indicating that SHAP-based methods achieve the best diagnostic performance²⁸. Additionally, in extreme operating conditions, XAI methods can effectively alleviate the challenges faced during model training. Zhang et al²⁹. proposed a hybrid resampling and SHAP-based interpretability method that effectively addressed class imbalance issues in fault diagnosis.

This paper argues that for GVAs—where faults are diverse, requiring immediate localization upon occurrence, and where early warnings under seemingly normal operating conditions are vital for predictive maintenance — an XAI-enhanced approach is essential. The “complexity” in GVA operation addressed herein refers to the highly coupled nature of its electro-mechanical-hydraulic components and the diverse, often interacting, fault types. “Under normal conditions” for early warning refers to scenarios where the GVA is not in an overt fault state but may present subtle, incipient anomalies detectable by unsupervised methods, where XAI can clarify the basis for such warnings. Therefore, the motivation for this work is to develop an XAI-based predictive maintenance strategy that not only accurately diagnoses faults and provides early warnings for GVAs but also offers interpretable insights into its decisions. The problem statement addressed is the need for a trusted and transparent IFD system for GVAs that overcomes the “black box” limitations of conventional models, thereby improving diagnostic accuracy, maintenance efficiency, and overall system reliability.

To address this issue, we introduce the concept of pseudo-post-hoc explainability. In our framework, post-hoc refers to explanations of supervised diagnostic models trained with labeled fault categories, while pseudo-post-hoc refers to explanations anchored to anomaly scores or pseudo-labels derived from unsupervised detect$g\left( x \right)$ors. Specifically, given an anomaly scoring model and a calibrated threshold, we define pseudo-labels $y=\varvec{1}\left\{ {s\left( x \right) \geqslant \tau } \right\}$. Explanations computed with respect to the score itself or to a surrogate model trained on these pseudo-labels constitute pseudo-post-hoc attributions. Thus, the two notions are parallel: post-hoc focuses on model faithfulness in supervised classification, whereas pseudo-post-hoc aims at sensor optimization and uncertainty calibration in early-warning tasks. By aligning both under a unified attribution operator (SHAP), we establish a consistent analytical framework that integrates supervised and unsupervised stages of predictive maintenance.

To meet these needs, this study proposes an XAI-based post-hoc and pseudo-post-hoc predictive maintenance (PPPM) approach. The key contributions include:

(1) Designing a SHAP-based post-hoc analysis for multi-sensor networks to facilitate efficient and interpretable GVA fault diagnosis, guiding model enhancement and lightweighting.

(2) Developing a SHAP-based pseudo-post-hoc analysis to optimize unsupervised models for GVA early warning, providing interpretable attribution for anomalies.

(3) Proposing the PPPM method, integrating advanced machine learning with XAI, applicable to fault diagnosis and early warning in high-dimensional mechatronic and hydraulic systems like the GVA, validated on a specialized fault testing platform.

The remainder of this paper is structured as follows: Sect. 2 introduces foundational theories in feature engineering, fault diagnosis/prediction, and XAI. Section 3 details the proposed methods. Section 4 describes the experimental platform and data acquisition. Section 5 presents results and analysis. Finally, Sect. 6 concludes the paper.

Related works

Explainable artificial intelligence (XAI)

In many practical applications, understanding the underlying principles of a model’s decision-making process is essential. This understanding enables experts to confidently rely on prediction results or proactively engage in the decision optimization process. To address this necessity, a significant number of XAI methods have been proposed in recent years. XAI aims to demystify the inner workings of “black-box” models, and various techniques tailored to specific machine learning models can be employed to explain their behavior.

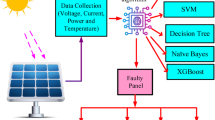
SHapley Additive exPlanations (SHAP) is a cutting-edge and model-agnostic technique for explaining machine learning predictions, applicable to both unsupervised and supervised learning tasks. By leveraging Shapley values from cooperative game theory, SHAP provides a measure of the contribution of each feature to the output prediction, as well as the interaction contributions between features, as shown in Fig. 1. This allows for the clarification of ML model predictions at the individual data point level. Specifically, for any high-dimensional feature set $\left\{ {{f_1},{f_2} \cdot \cdot \cdot {f_i}} \right\}$ and a prediction model P, the Shapley value of each feature is the contribution of that feature to the prediction, calculated as the weighted sum over all possible feature value combinations.

$${\Phi _i}(v)=\sum\nolimits_{{F \subseteq \left\{ {{f_1},{f_2} \cdot \cdot \cdot {f_i}} \right\}\backslash \left\{ {{f_i}} \right\}}} {\frac{{\left| F \right|!\left( {i - \left| F \right| - 1} \right)!}}{{i!}}} \left( {v\left( {F \cup \left\{ {{f_i}} \right\}} \right) - v\left( F \right)} \right)$$

(1)

where ${f_i}$ is the different high-dimensional features, F is the high-dimensional feature subset of the high-dimensional features, i is the number of features, ${{\left| F \right|!\left( {i - \left| F \right| - 1} \right)!} \mathord{\left/ {\vphantom {{\left| F \right|!\left( {i - \left| F \right| - 1} \right)!} {i!}}} \right. \kern-0pt} {i!}}$ is the weight of the feature subset, $v\left( F \right)$ and is the prediction value of the feature subset. Then for any two features i and j of the sample and their prediction models, SHAP feature interaction values can be expressed as Eq. 2.

$${\Phi _{i|j}}=\sum\nolimits_{{f \subseteq F\backslash \left\{ {i,j} \right\}}} {\frac{{\left| f \right|!\left( {\left| F \right| - \left| f \right| - 2} \right)!}}{{\left| F \right|!}}} \left( {P\left( {f \cup \left\{ {i,j} \right\}} \right) - P\left( {f \cup \left\{ i \right\}} \right) - P\left( {f \cup \left\{ j \right\}} \right)+P\left( f \right)} \right)$$

(2)

where f is the subset of high-dimensional features, F is the set of high-dimensional features, $F\backslash \left\{ {i,j} \right\}$ is the set of features in F except i and j, $P\left( {f \cup \left\{ {i,j} \right\}} \right)$ is the predicted value of the feature set after adding features i and j to the feature subset f, $P\left( {f \cup \left\{ i \right\}} \right)$ is the predicted value of the feature set after adding feature i to the feature subset f, $P\left( {f \cup \left\{ j \right\}} \right)$ is the predicted value of the feature set after adding feature j to the feature subset f, $P\left( f \right)$is the predicted value of the feature subset f.

Fig. 1

Schematic diagram of the SHAP framework.

Feature engineering

Feature selection is a crucial component of the machine learning workflow, aiming to identify and retain the core features that have a substantial impact on the target variable, ensuring strong mutual relevance among the selected features, thereby simplifying the model, enhancing its generalization capability, and accelerating the training process. While model-based and statistical methods (such as decision trees or Pearson correlation coefficient) can assess feature importance or analyze inter-feature correlations, they may have limitations in interpretability and capturing critical discriminative information. In contrast, XAI methods like SHAP enhance the interpretability and transparency of the decision-making process by visualizing the contribution of each feature to the model output, as well as the interactions and dependencies between features. SHAP-based feature selection effectively identifies key discriminative features with high contribution and strong relevance, eliminating redundant features to reduce model complexity, improve prediction accuracy, and accelerate training. The SHAP-based feature selection framework is illustrated in Fig. 2.

Fig. 2

SHAP-based feature selection.

Fault diagnosis and early warning

For complex electro-mechanical-hydraulic systems like the GVA, data-driven fault diagnosis and early warning are of paramount importance, as their regulation quality and response characteristics significantly impact on the operational economy, flexibility, and reliability of the turbine unit, thereby directly influencing production safety and economic benefits. Fault diagnosis typically utilizes supervised learning methods to identify and classify known fault types based on labeled fault data. Conversely, fault early warning, often framed as an anomaly detection (or outlier detection) problem, more commonly employs unsupervised learning methods to monitor and identify deviations from normal operating conditions, especially in real-world industrial environments where GVA faults are infrequent or sufficient labeled fault data is unavailable.

For the task of fault diagnosis in the GVA, this study employed several supervised learning models to classify and identify different fault types. Ensemble learning is a machine learning technique that combines the predictions of multiple base models (‘weak learners’) to enhance overall model performance³⁰. The goal of ensemble learning is to build a more accurate, stable, and robust model that generalizes better to unseen data. This approach reduces the risk of overfitting, enhances model generalization, and is a powerful tool for complex tasks such as fault diagnosis and early warning. These models learn from labeled fault data to establish a mapping between fault patterns and specific fault categories. Table 1 lists the supervised learning models used and their characteristics.

Table 1 Fault diagnosis model.

To support the analysis and validation of these fault diagnosis methods, a comprehensive GVA fault test platform was developed. This platform is capable of simulating six typical fault scenarios and collecting monitoring data under both normal and various faulty conditions. This data provided the basis for training and evaluating the diagnostic models.

Fault early warning aims to provide pre-emptive alerts for abnormal operating conditions, thereby facilitating predictive maintenance. Considering that GVA faults are infrequent or that sufficient labeled fault data is often unavailable in real-world industrial environments, this study employs unsupervised learning methods for early fault warning, also known as anomaly detection or outlier detection. These methods identify outliers or deviations from normal behavioral patterns by modeling the health status of multivariate systems. Table 2 presents a comparative analysis of advanced anomaly detection algorithms conducted in this study.

Table 2 Fault warning model.

The algorithmic principles and advantages of these eight anomaly detection methods involved in this study were systematically discussed, ensuring that the selected methods adequately consider the structure and distribution of the data, as well as the consumption of computational resources, thereby optimizing the balance between detection accuracy and computational efficiency.

Proposed methods

Formal definitions and theoretical framing

To unify supervised diagnosis and unsupervised early warning under the same interpretability paradigm, we introduce formal definitions and theoretical perspectives for both post-hoc and pseudo-post-hoc explainability.

Let the input be $x \in \mathcal{X} \subset {{\mathbb{R}}^p}$. In supervised fault diagnosis, a classifier $f:\mathcal{X} \to \left\{ {0,1, \ldots ,K} \right\}$ is trained using ground-truth labels y. Post-hoc explanations are then obtained by applying an attribution operator ${\Phi _i}(v)$ to produce per-feature contributions $\phi {}_{j}\left( x \right)$ and, optionally, interaction values $\phi {}_{{ij}}\left( x \right)$. These values indicate the marginal effect of each sensor on the model output, enabling transparent understanding of classification decisions.

In contrast, early-warning tasks often lack labeled faults. Here we define pseudo-post-hoc explainability. Let $g:\mathcal{X} \to {\mathbb{R}}$ denote an anomaly scoring model with score $s\left( x \right)=g\left( x \right)$. Given a calibrated threshold $\tau$, pseudo-labels are defined as $\tilde {y}=\varvec{1}\left\{ {s\left( x \right) \geqslant \tau } \right\}$. Explanations can then be derived in two ways: (i) directly with respect to the score function $s\left( \cdot \right)$, if the attribution operator supports it; or (ii) with respect to a surrogate classifier h trained on $\left\{ {\left( {x,\tilde {y}} \right)} \right\}$. In both cases, the resulting attributes are termed pseudo-post-hoc. Compared with standard post-hoc, which interprets predictions relative to true labels, pseudo-post-hoc interprets predictions relative to proxy labels, thus enabling interpretability in unsupervised anomaly detection.

Feature engineering

The GVA contains a vast amount of multimodal sensor data, which places significant pressure on servers. While this extensive data considers multiple influencing factors, it can lead to overfitting or feature redundancy in diagnostic models, resulting in poor generalization or negative transfer during training. Therefore, to improve the training efficiency and accuracy of the model, a series of feature engineering steps are necessary after data collection, including data preprocessing, feature selection, and feature extraction.

Data preprocessing

To enhance the algorithm’s generalization on unseen datasets and ensure its practical value in various operating conditions and scenarios of the oil actuator, we employ an overlapping sampling data augmentation method. Specifically, we apply a sliding window technique to the raw data with a window length of 1280 and a step size of 128. Each window containing 1280 data points is treated as a sample for subsequent feature extraction, as shown in Fig. 3.

Fig. 3

Sliding window sampling.

PPPM-based feature selection

To effectively identify redundant features and extract key features, thereby reducing model complexity, we employed the proposed global XAI method for feature selection. The XAI-ML based feature selection process is illustrated in Fig. 4.

Fig. 4

Feature selection process of PPPM-based approach.

The PPPM-based feature selection process employs post-hoc and pseudo-post-hoc explainability to analyze the contribution of multiple sensors points to fault condition identification and their interactions, enabling effective feature selection. Through this workflow, we achieved the selection of multi-modal sensor points, significantly reducing data collection pressure and server computational costs. The selected feature set, after feature extraction, allows for efficient fault diagnosis of the GVA, ensuring or even improving diagnostic accuracy and training speed. This provides a more robust foundation for predictive maintenance-related decision-making.

Feature extraction

To comprehensively capture signal information, a multi-dimensional set of features was extracted from each 1280-point time-series signal sample, encompassing time-domain, frequency-domain, and time-frequency domain characteristics. Specifically:

(1) Time-Domain Features: Seventeen common statistical features were extracted to characterize the amplitude distribution and temporal variation properties of the signal.

(2) Frequency-Domain Features: Thirteen statistical features were extracted from the frequency domain to describe the signal’s frequency structure and energy distribution.

(3) Time-Frequency Domain Health Indicators: A total of 30 health indicators were extracted to reveal local variations of the signal in both time and frequency, as detailed below:

① Wavelet Packet Decomposition³⁹ (WPD): The signal was decomposed using a four-level Wavelet Packet Decomposition (with the db6 wavelet basis). Energy was then extracted from each of the 16 terminal sub-bands as health indicators, yielding 16 indicators in total.

② Empirical Mode Decomposition (EMD): The signal was adaptively decomposed into a series of Intrinsic Mode Functions (IMFs). Several IMFs, determined at the point of maximum stable decomposition, were selected, and 6 health indicators (e.g., energy, kurtosis) were calculated from them.

③ Variational Mode Decomposition (VMD): A complete Variational Mode Decomposition was performed on the signal to obtain a predefined number of modes. From these modes, 8 health indicators (e.g., energy or specific statistical measures of each mode) were derived.

The specific names, calculation methods, and detailed parameters of all extracted features are provided in Appendix I.

PPPM-based fault diagnosis and early warnings

This study proposes a post-hoc and pseudo-post-hoc predictive maintenance (PPPM) methodology grounded in advanced machine learning techniques. By incorporating SHAP as an XAI approach, the framework establishes both post-hoc and pseudo-post-hoc predictive maintenance strategies. The PPPM method specifically addresses two critical aspects of equipment health management: (1) For fault diagnosis tasks, it develops an optimized fault localization system through efficient model refinement and comprehensive attribution analysis; (2) For early warning systems focusing on anomaly detection, it introduces a pseudo-post-hoc optimization design that provides interpretable attribution evidence for misclassified samples in pseudo-supervised learning scenarios. This approach enhances diagnostic accuracy and early warning reliability while maintaining model interpretability throughout the predictive maintenance process.

Fault diagnosis

The fault diagnosis workflow of the proposed PPPM-based approach is illustrated in Fig. 5.

Fig. 5

Process framework for fault diagnosis.

(1) Data Collection: Collect multimodal operational data from the GVA test platform under both healthy and faulty conditions to monitor system status.

(2) Feature Selection: Employ the PPPM-based feature selection method, as detailed in Sect. 3.2.2, to conduct a highly interpretable evaluation and attribution analysis, enabling the selection of important features while reducing redundant information.

(3) Feature Extraction: Extract health indicators from the optimized feature set across time, frequency, and time-frequency domains to reflect the machine’s operational status. This reduces computational costs, enhances model generalization, and maintains or improves diagnostic accuracy.

(4) Fault Diagnosis: Perform fault diagnosis using machine learning methods based on the optimized feature set.

Early warnings

The early warning workflow of the proposed PPPM-based approach is illustrated in Fig. 6.

Fig. 6

Process framework for early warning of malfunction.

(1) Data Collection: Gather many healthy signal samples from multimodal operational data as normal data and a small number of samples from different fault conditions as abnormal data for unsupervised fault early warning research.

(2) Pseudo-Labeling and Feature Selection: Use the pseudo-labels obtained from unsupervised fault early warning to conduct the PPPM-based attribution analysis detailed in Sect. 3.2.2. This allows for the selection of features most relevant to the occurrence of faults from a pseudo-post-hoc perspective.

(3) Feature Extraction: Extract health indicators from the feature set across time, frequency, and time-frequency domains to reflect the machine’s operational status, thereby enhancing prediction accuracy and model generalization.

(4) Early Warning: Perform early fault warning analysis using ML models based on the feature set. This effectively reduces redundant information, improves prediction accuracy, and reduces model complexity.

Experiments and data acquisition

The test platform of the GVA

The structure and hydraulic schematics of the GVA are depicted in Fig. 7, which created by SolidWorks 2016⁴⁰. To enable fault warning and monitoring within the expert system, sensor points are positioned to monitor the GVA’s operational status. Referring to Fig. 8, the decision has been made to retain measurement points indicated in green, while those in red are recommended for deletion to mitigate computational demands. The naming conventions and installation locations of the existing measurement points are summarized in Table 3.

Fig. 7

The internal structure diagram of the GVA. 1-Displacement sensor; 2-Cushion piston; 3-Piston rod; 4-AST solenoid valve; 5-Cartridge valve;6-Reset spring; 7-Oil inlet; 8-Pressure sensor; 9-Filter; 10-Oil outlet. This figure was created by Jun Tang of the study team.

Fig. 8

Hydraulic principle and sensor point layout diagram.

Table 3 Measurement point layout.

Experimental settings

The GVA fault test platform consists of GVA, sensors, a control industrial computer, a test industrial computer, and an electrical control cabinet. Figure 9 illustrates the framework of the platform.

To realistically simulate field fault modes and conditions, all operational evaluations utilize equipment and components that have been sourced from retired industrial assets. A detailed breakdown of the fault types is provided in Fig. 10. The simulated faults encompass servo valve malfunction (characterized by internal leakage), spring failure and fracture, AST solenoid valve failure (due to throttle hole clogging), C0 throttle hole clogging, as well as internal and external cylinder leakage. The test system is maintained at an operating pressure of 16 MPa via a plunger pump. The resulting fault dataset was acquired at a sampling frequency of 5.12 kHz.

Fig. 9

Measurement system arrangement of the GVA.

Fig. 10

Types of GVA faults. (a) Servo valve failure; (b) Broken springs; (c) Solenoid valve malfunction; (d) C0 Clogged throttle orifice; (e) Cylinder leakage; (f) Cylinder leakage.

All experiments were conducted on a Microsoft Windows 11 operating system, using an Nvidia RTX 3070 8G GPU and PyTorch 1.11 as the computational framework.

Results and discussion

Data description

In the fault diagnosis experiment, 200 samples from different health states were extracted to form the fault diagnosis dataset, which was used to evaluate the methods discussed in this paper. The fault diagnosis dataset, including all features, was split into an 80% training set and a 20% testing set for training and testing the baseline model. Details are provided in Table 4.

Table 4 Dataset for fault diagnosis.

For the fault early warning experiment, 20 samples from each of the six fault conditions were combined to form the abnormal data, which was then mixed with 200 healthy samples to create the fault early warning dataset. The dataset labels were not used during training but only in the evaluation phase. The dataset was split into a 70% training set and a 30% testing set for training and testing the baseline model. Details are provided in Table 5.

Table 5 Dataset for early warning of malfunction.

Evaluation metrics

In the diagnosis experiment, supervised learning methods are employed, with accuracy as the sole evaluation metric, as shown in Eq. 3:

$$Accuracy=\frac{{TP+TN}}{{TP+FP+TN+FN}}$$

(3)

where $TP$, $FP$, $TN$, and $FN$ represent the true positive, false positive, true negative, and false negative samples, respectively.

In the fault early warning experiment, an unsupervised learning method is used to compute anomaly scores at the end of the testing phase. Samples with higher anomaly scores are typically considered anomalies. To validate the performance of the proposed method, a threshold is defined based on the training set. Additionally, the performance of the unsupervised algorithm is evaluated using Weighted F1 Score and Area Under the Curve (AUC). These metrics provide a better assessment of the classifier’s performance in imbalanced datasets, as shown in Eqs. 4–6.

$$Weighted~ - F1~=\sum\limits_{{i=0}}^{n} {\left( {\frac{{N\left( {{C_i}} \right)}}{N} \times F1\left( {{C_i}} \right)} \right)}$$

(4)

$$F1({C_i})=2 \times \frac{{\frac{{T{P_i}}}{{T{P_i}+F{P_i}}} \cdot \frac{{T{P_i}}}{{T{P_i}+F{N_i}}}}}{{\frac{{T{P_i}}}{{T{P_i}+F{P_i}}}+\frac{{T{P_i}}}{{T{P_i}+F{N_i}}}}}$$

(5)

where n is the total number of categories, $N\left( {{C_i}} \right)$ is the number of samples in class i, N is the total sample size for all categories, $T{P_i}$, $F{P_i}$ and $F{N_i}$ are the number of true-positive cases, false-positive cases, and false-contrary cases of the class i category, respectively.

$$AUC=\frac{{\sum {_{{i \in P}}\sum {_{{i \in N}}I({P_i} {P_j})} } }}{{\left| P \right|\left| N \right|}}$$

(6)

where ${P_i}$ is the predicted probability of a positive sample i, ${P_j}$ is the predicted probability of a negative sample j, $\left| P \right|$ is the number of positive samples, $\left| N \right|$ is the number of negative samples, $I\left( \cdot \right)$ is a function, as shown in Eq. 10.

$$I\left( x \right)=\left\{ \begin{gathered} 1{\text{ }}if{\text{ }}{P_i} {P_j} \hfill \\ 0{\text{ }}else \hfill \\ \end{gathered} \right.$$

(7)

Fault diagnosis experiments

To better evaluate the effectiveness of the XAI-based PPPM fault diagnosis method for the governor valve actuator, we selected five machine learning models—Decision Tree, Random Forest, CatBoost, LightGBM, and XGBoost—as baseline models for fault diagnosis analysis. To achieve better learning performance and prevent overfitting, the hyperparameters were set based on preliminary experiments, as detailed in Table 6.

Table 6 Hyperparameter Settings.

To assess the training robustness of the dataset across these models, we introduced five-fold cross-validation and recorded the average training time for the entire process. The diagnostic results and training times for all models before introducing SHAP for feature selection are presented in Table 7. It is evident that all models achieved very high diagnostic accuracy, with the Random Forest and CatBoost models performing the best at 99.929%. In terms of training time, CatBoost’s model training time was significantly longer than the other models. This is due to its use of symmetric trees, which enhances performance but increases computational burden. Additionally, custom gradient statistics, Newton step methods, and unique encoding techniques for categorical variables further improve model performance while increasing computational costs. The achieved diagnostic accuracy confirms that these improvements indeed contribute to better model performance.

Table 7 Diagnostic results.

To more intuitively display and compare the diagnostic results, we introduce bar charts, line charts, and box plots to assist in the analysis, as shown in Figs. 11 and 12. From Fig. 11, it is evident that the Decision Tree model has a faster training speed compared to other ensemble tree models. However, due to its modeling approach, its diagnostic performance is slightly inferior to the other models. Figure 12 further illustrates that the training robustness of the Decision Tree model is also lower than that of the other ensemble tree models.

Fig. 11

Diagnostic accuracy versus training time.

Fig. 12

Diagnosis results from five-fold cross-validation.

Given the large volume of multimodal sensor data, which can introduce redundant features and significant computational costs, we will next conduct a global explainable fault diagnosis analysis using SHAP. Figure 13 shows the SHAP values of all features for different fault categories across various machine learning models. The SHAP values provide a clear indication of each feature’s contribution to the model output.

Based on the previous analysis, considering both diagnostic performance and model training time, we have selected the Random Forest (RF) model for more detailed global explainable fault diagnosis analysis. This will guide the optimization process of diagnostic model training.

Fig. 13

Feature contribution analysis based on SHAP-ML. (a) Decision tree; (b) Random Forest; (c) Catboost; (d) LightGBM; (e) XGboost.

To gain a more intuitive understanding of the contribution of all sensor data to different fault types, we calculated the Mean Absolute SHAP Values for all test samples, as shown in Fig. 14. It is evident that the sensor points M3, M4, M5, P6, P7, and P9 make a higher contribution to the fault diagnosis task, while the features from the two vibration sensors have the lowest contribution.

Fig. 14

Mean absolute SHAP values.

When analyzing a specific fault type, we introduce bar charts and box plots to visualize the contribution of all test sample features to a single fault category, as shown in Fig. 15. For example, for the normal condition (Category 0), we observe that M4 and M5 provide the highest contribution. The cluster points also reveal that many test samples have very high contributions from the M4 and M5 sensor points. With these global explainability analysis techniques, if the model fails to effectively distinguish a certain fault, we can delve into the high-contribution features to guide the model training towards more challenging areas, thereby improving model performance.

Fig. 15

Mean absolute SHAP values based on bar and box plots. (a) Class 0; (b) Class 1; (c) Class 2 (d) Class 3; (e) Class 4; (f) Class 5; (g) Class 6.

When discussing feature selection, the interaction contributions of features are also crucial. Ignoring these interactions can lead to a mechanical selection process that lacks interpretability and practical guidance. Traditional feature importance analysis methods can provide the contribution of features to the output, but they often lack a more intuitive and interpretable measure of feature interactions, such as the Pearson correlation coefficient matrix shown in Fig. 16. From Fig. 16, we can observe that the feature combinations M4-M5, P5-P6-P7-P8-P9, and M3-V1-V2 have high mutual dependencies.

Fig. 16

Feature correlation analysis based on Pearson.

The SHAP-based XAI approach can calculate the interaction contributions of all features for all samples from a post-hoc explainability perspective. To intuitively display these interaction contributions, we visualize the Mean Absolute SHAP Interaction Values for all samples, as shown in Fig. 17. First, we observe that M3-M5 has the highest interaction contribution, followed by M3-M4 and M4-M5. Additionally, M3-M4-M5, P6-P7-P9 and M3-M4-M5-P6-P7-P9 have high matching degrees and interaction contributions, while the relevance of the remaining measurement points is lower.

Fig. 17

Feature correlation analysis based on Pearson.

Force plots provide an intuitive explanation of the model’s predictions for individual data points, showing the contribution of all features to the prediction output under different operating conditions. The base value represents the baseline prediction, which is the final predicted value. For example, for the normal condition (Category 0), Fig. 18 illustrates the contribution of all features to the prediction output for seven test samples (1, 50, 100, 150, 200, 250, and 280) in the normal condition.

From the analysis, we observe that samples 150 and 200 have the highest overall contribution. Specifically, for sample 150, features M3, M4, M5 and P7 have a high contribution to the identification of the normal condition. For sample 200, features M3, M4, M5, P6, P7 and P9 have a high contribution to the normal condition. The analysis of these seven representative samples indicates that the feature set combination M3-M4-M5-P7-P9 shows a high contribution to the identification of the normal condition.

Fig. 18

SHAP force plot: (a) Sample 1; (b) Sample 50; (c) Sample 100; (d) Sample 150; (e) Sample 200; (f) Sample 250; (g) Sample 280.

Waterfall plots provide a structured view of how each feature incrementally changes the prediction value from the baseline to the final prediction, making the model’s predictions more transparent and easier to understand. As shown in Fig. 19, which presents the waterfall plot for the first sample under the Cylinder Leakage (internal leakage) condition (Class 5), $E[f(x)]=0.14$ is the baseline value, which is also the average prediction value. The final value is $f(x)=1$, which is the predicted value for this specific sample. The final prediction values for other samples are close to 0. This indicates that the first sample in the test set has a significant contribution to Category 5, while the contributions from other samples are minimal.

Based on this analytical framework, we have determined the contribution of different features from various samples to predictive maintenance decisions. From a global perspective, the feature set combination M3-M4-M5-P6-P7-P9 provides the highest contribution.

Fig. 19

Waterfall map. (a) Class 0; (b) Class 1; (c) Class 2 (d) Class 3; (e) Class 4; (f) Class 5; (g) Class 6.

Heatmaps can illustrate the positive or negative impact of different features on model predictions across various operating conditions, aiding in a deeper understanding of the model’s global explainability at the individual sample level. As shown in Fig. 20, which presents the heatmap for Class 3 (Solenoid Valve Malfunction, clogged throttle orifice), the features M3, M4, M5, P6, P7 and P9 exhibit the highest contribution to identifying the Solenoid Valve Malfunction across the 280 test samples. From the distribution of high-contribution samples, it is evident that the test samples in the 240–280 range show a higher contribution to the identification of the Solenoid Valve Malfunction.

Therefore, if the model fails to effectively identify a specific fault, we can use the heatmap to select appropriate sample and feature combinations, thereby effectively uncovering key discriminative features.

Fig. 20

Hit map: (a) Class 0; (b) Class 1; (c) Class 2; (d) Class 3; (e) Class 4; (f) Class 5; (g) Class 6.

Based on the comprehensive analysis, we can summarize five sensor selection schemes, as detailed in Table 8. Using these selected sensor methods, we conducted a new phase of fault diagnosis to demonstrate the superiority of our SHAP-based XAI fault diagnosis approach.

Table 8 Screening scheme for sensor measurement points.

The results of the new phase are presented in Table 9. It is evident that the two sensor selection schemes based on the SHAP method exhibit significantly better diagnostic performance. Specifically, by adopting the optimized sensor points from Group E, we achieved the same high level of diagnostic accuracy as before, despite reducing the number of sensors points by 50%. Additionally, the training speed improved by 17%. This confirms that the global explainable AI method plays a crucial role in guiding decision-making, offering high generalization and reliability. It significantly enhances the practical implementation of intelligent maintenance systems with high applicability and generalization in real-world scenarios.

Table 9 Diagnostic results.

To demonstrate the effectiveness of the proposed PPPM method in improving data cost, computational efficiency, and the generalization performance of machine learning models, we conducted comparative experiments using five machine learning models: Decision Tree, Random Forest, CatBoost, LightGBM, and XGBoost. The sensor points optimization, and diagnostic results are summarized in Table 10. From Table 10, it is evident that the proposed PPPM method significantly enhances the performance of all machine learning models in terms of data cost, computational efficiency, and diagnostic accuracy. Specifically, the optimization of sensor points and feature selection through the PPPM method leads to (1) The number of sensors points and data collection requirements are significantly reduced; (2) Training times are shortened, and computational resources are more efficiently utilized; (3) All models show improved diagnostic performance, with higher accuracy and robustness.

These results highlight the effectiveness of the PPPM approach in optimizing the training process and enhancing the generalization capabilities of machine learning models for predictive maintenance tasks.

Table 10 Diagnostic results.

Early warning experiments

To extract anomaly information from multiple anomaly detection modeling principles, we selected eight machine learning models—GMM, HBOS, IF, KNN, LOF, MCD, OCSVM, and PCA—to conduct the fault early warning task. The goal is to use the pseudo-labels generated by the highest-performing diagnostic model to conduct the early warning analysis based on the PPPM method. To achieve better learning performance and prevent overfitting, the hyperparameters were set based on preliminary experiments, as shown in Table 11.

Table 11 Hyperparameter Settings.

The Weight-F1-SCORE and AUC results of the above eight models for unsupervised fault diagnosis are shown in Table 12. We observed that the IF model achieved the best early warning accuracy. This is because the IF does not model normal data points to identify outliers; instead, it isolates each observation using independent tree structures. Anomalies are isolated first, making it effective in handling high-dimensional data and less sensitive to density variations. Benefiting from its tree structure, the IF offers strong flexibility and does not require strong correlations between features.

Table 12 Early warning results for anomaly detection models.

Figure 21 shows the confusion matrices for all models on the test dataset, with the x-axis representing the target labels and the y-axis representing the predicted labels. Overall, most misclassified samples are abnormal data points that are incorrectly classified as normal. This indicates that features related to normal samples play a more significant role in our unsupervised fault early warning task, leading the model to bias towards normal operating conditions during training.

Fig. 21

Confusion matrix: (a) GMM; (b) HBOS; (c) IF; (d) KNN; (e) LOF; (f) MCD; (g) OCSVM; (h) PCA.

Through the above early warning models, we obtained pseudo-labels for normal and abnormal conditions. Based on these pseudo-labels, we can conduct feature contribution analysis. Using the IF model, which achieved the best diagnostic performance, as an example, Fig. 22 shows the contribution of all features for all samples under normal and abnormal conditions. Red dots represent high contribution, while blue dots represent low contribution. Figure 23 presents the absolute average values of the contributions of all features under different conditions, providing a clear view of the contribution values of all features under different conditions. Through the Mean Absolute SHAP Values, we observe that sensors M3 and V1 exhibit higher contributions to the unsupervised fault early warning task, while the contributions of other sensors are minimal.

However, a more detailed examination of the scatter plots reveals that the number of red dots for sensors M4, M5 and V2 is significantly higher under normal conditions compared to abnormal conditions. Other features are either evenly distributed or more prevalent under abnormal conditions. This indicates that these three features (M4, M5 and V2) provide higher contributions to the identification of normal conditions compared to abnormal conditions. As mentioned in our earlier analysis, the diagnostic performance of unsupervised early warning is limited by the model’s tendency to overfit to normal data during training. Therefore, we plan to remove these sensor points and re-conduct the unsupervised early warning experiments.

Fig. 22

SHAP Values. (a) Normal; (b) Anomaly.

Fig. 23

Mean Absolutely SHAP Value.

As shown in Fig. 24, applying the Force plot visualization to the early warning results allows for an intuitive analysis of individual samples. The plots for TP samples are dominated by red bands, indicating a classification as normal, while the plots for PF samples are dominated by blue bands, indicative of a fault. The FP samples, which were incorrectly classified as normal, appear in a transitional state, though their contribution characteristics are closer to those of normal samples.

Fig. 24

Force plot visualization of TP, FP and TN samples.

The Waterfall plots in Fig. 25 provide a detailed breakdown of how each feature contributes to the model’s output for TP, FP, and TN samples. In the TP sample analysis, the M3 feature provides the largest contribution (+ 4.92) toward identifying the sample as normal, followed by V1 (+ 0.28). Conversely, in the TN (faulty) sample analysis, M3 demonstrates the greatest negative impact (−1.69), followed by V1 (−0.12). From an attributional analysis perspective, the misclassified FP samples clearly exhibit characteristics closer to those of the faulty samples.

Fig. 25

Waterfall plot visualization of TP, FP and TN samples.

Figure 26 presents the Heatmap plots, offering a global interpretation across samples. (1) Feature Influence (Horizontal Stripes): For TP (normal) samples, sensor M3 appears as a dark red stripe, indicating a significant positive influence, while V1 is light red, showing a weaker positive influence. For TN (faulty) samples, M3 is a dark blue stripe (significant negative influence) and V1 is light blue (weak negative influence). The FP samples show a blue layer for M3 and a mix of light blue and light red for V1, aligning them more closely with the interpretation of faulty samples. (2) Interactions (Vertical Stripes): A weak positive correlation between M3 and V1 is observed for both TP and TN samples, whereas for FP samples, this interaction is a mix of positive and negative correlations.

Fig. 26

Heatmap plot visualization of TP, FP and TN samples.

After going through the optimal design and attribution analysis of the XAI-based PPPM early warning process, we optimized all the sensor measurement points of the unsupervised fault warning model and re-conducted the unsupervised early warning experiments. The specific sensor point removal information and diagnostic results are shown in Table 13. The results indicate that, after targeted sensor point optimization, almost all models either improved or maintained their diagnostic accuracy. This is a significant improvement because we reduced the data collection burden while ensuring or enhancing the early warning accuracy of the GVA.

Table 13 Measurement points optimization scheme and its diagnosis results.

To more intuitively demonstrate the effectiveness of the proposed PPPM-based feature contribution analysis method, we visualized the evaluation metrics before and after optimization using a radar chart, as shown in Fig. 27. The radar chart clearly illustrates that the models optimized using the PPPM method achieved generally excellent diagnostic performance on the test set. This further validates the effectiveness and broad applicability of the PPPM-based early warning method.

Fig. 27

Radar chart: (a) Weight F1 scores; (b) AUC.

Figure 28 shows the confusion matrices for the early warning models after sensor point optimization. By examining the confusion matrices, we observe a reduction in the number of abnormal samples misclassified as normal. This indicates that the proposed PPPM-based early warning process effectively prevents the model from overfitting to one direction during training, thereby enhancing the reliability of early warning decisions. This improvement is consistent across all models, demonstrating the general applicability of our method.

Fig. 28

Confusion matrix. (a) GMM; (b) HBOS; (c) IF; (d) KNN; (e) LOF; (f) MCD; (g) OCSVM; (h) PCA.

Conclusions

In the industrial domain, the combination of feature engineering and machine learning has become an effective approach for intelligent fault diagnosis. However, complex data scenarios and the inherent opacity of machine learning algorithms pose significant limitations on the practical application and trustworthiness of health management systems in real-world settings. To address this challenge, this paper proposes a post-hoc and pseudo-post-hoc predictive maintenance (PPPM) approach based on eXplainable Artificial Intelligence (XAI), focusing on the optimization design and attribution analysis of fault diagnosis and early warning processes.

The proposed PPPM method follows a three-stage scheme in fault diagnosis tasks: first, conducting initial fault diagnosis and model optimization analysis using the PPPM approach; second, extracting core features (or sensor measurement points) with high contribution and strong correlation based on XAI attribution results; and finally, performing efficient and accurate fault diagnosis using the optimized feature set (or sensor configuration). Experimental results demonstrated that when applied to five typical machine learning models, the PPPM method, by optimizing sensor measurement points, significantly reduced data acquisition costs and computational expenses for model training (with an average training time reduction of 18.522%) while maintaining or even enhancing diagnostic accuracy, thereby effectively improving system real-time performance and generalization capability.

For early warning tasks, the PPPM method also employs a three-stage strategy: first, obtaining pseudo-labels through unsupervised learning; second, conducting pseudo-post-hoc early warning analysis by combining these pseudo-labels with the PPPM approach to optimize the warning model’s training process and perform attribution analysis, yielding an optimized feature set (or sensor configuration); and finally, executing unsupervised fault early warning using the optimized configuration. This approach successfully eliminated redundant or non-beneficial sensor measurement points, led to a general improvement in the performance of various unsupervised early warning models, and provided clear, interpretable attribution evidence for previously misclassified samples (particularly those with early fault indications that were initially judged as normal by the model). For instance, with the isolated forest model, removing the M4, M5, and V2 sensor points resulted in improvements of 6.057% and 6.942% in W-F1 scores and AUC metrics, respectively.

The core contribution of the proposed PPPM method lies in providing decision-making support for the predictive maintenance of complex electro-mechanical-hydraulic equipment from a post-hoc perspective. It optimizes the training and deployment of machine learning models guided by XAI, breaking open the “decision black box” and thereby enhancing system reliability and trustworthiness. Validation on the GVA fault test platform showed that the method exhibits superiority in data cost-effectiveness, computational efficiency, and diagnostic/warning performance when applied to various machine learning models for both fault diagnosis and unsupervised early warning tasks, and it possesses good generalization potential.

This research will further deepen the capabilities of the PPPM method in addressing unknown or novel fault modes, focusing on how to leverage XAI to assist in their detection, characterization, and adaptive learning, while also exploring the integration of online learning mechanisms to adapt to dynamic operating conditions. Concurrently, we will endeavor to extend the PPPM method to broader industrial domains such as rotating machinery, aerospace engines, and hydraulic pumps/valves, performing customized optimizations tailored to the unique data characteristics, fault mechanisms, and common challenges (e.g., data scarcity, class imbalance) of each domain. Ultimately, the aim is to promote the comprehensive validation of this method in real industrial production environments to assess its practical application value, robustness, and scalability, hoping to provide valuable insights for building more trustworthy and efficient intelligent health management systems.