Location optimization of cold chain logistics parks based on Bayesian probability theory and K-means clustering analysis in China

Abstract

The site selection of cold-chain logistics parks is an indispensable part of their planning and construction. This study aims to establish site selection model provide a scientific and sustainable for selecting and determining optimal cold chain logistics parks sites. Traditional site selection methods lacking quantitative standards for assessing the reliability of results. In response, this study introduces Bayesian probability theory to construct a Bayesian network model. This model selects and quantifies influencing factors for site selection, establishing a scientifically evaluation indicator system. Subsequently, utilizing K-means clustering analysis to develop a site selection model. The reliability of clustering results is verified using Bayesian discriminant analysis. Furthermore, a city within the first-class cluster is selected to construct a comprehensive suitability evaluation indicator system for cold-chain logistics park location using Geographic Information System (GIS) technology. Jiangsu Province is chosen as the study area to validate the model, and the analysis demonstrates that Suzhou is the most suitable location for establishing a cold-chain logistics park. The comprehensive suitability evaluation further divides Suzhou into five distinct zones, from which the optimal site is identified and confirmed. Overall, the established site selection model provides a scientific and reliable approach for selecting and determining optimal sites.

Introduction

Logistics, serving as an accelerator of economic growth, has increasingly gained prominence within the national economy. In recent years, China’s cold-chain logistics market has expanded rapidly, driven by rising consumer demand for high-quality products and market demand for superior logistics services. Nevertheless, the penetration rate of fresh food cold-chain distribution remains below 1%, indicating substantial room for growth in the cold-chain logistics market¹. To meet this burgeoning demand, China has formulated the “14th Five-Year Plan for Cold-chain Logistics Development,” aiming to facilitate healthy and rapid advancement within the sector, thereby presenting both new opportunities and challenges. Logistics parks, as key hubs for the centralized organization and management of logistics activities, play a critical role in logistics planning and development. Consequently, exploring optimal site selection for cold-chain logistics parks is crucial for enhancing China’s overall cold-chain logistics development.

Early scholars used Multi-Criteria Decision-Making (MCDM) methods to study the site selection of cold-chain logistics parks. MCDM methods are a class of decision-making tools used to select and rank alternatives under multiple conflicting evaluation criteria. Common methods include: AHP (Analytic Hierarchy Process), TOPSIS (Technique for Order Preference by Similarity to Ideal Solution), etc². Wang et al.³ utilized AHP to investigate the site selection issues for cold chain logistics centers, deriving a ranking of the importance of various factors. Zhao⁴ analyzed the current state of the cold chain market in Dongguan, utilizing both quantitative and qualitative methods to study the site selection for cold chain logistics distribution centers. Ultimately, AHP was employed to determine the location of the Dongguan cold chain logistics distribution center, providing a theoretical basis for the site selection of other distribution centers. Zhang and Luo⁵ analyzed the characteristics of the sales, production, and origin of fresh agricultural products in Hefei, employing AHP to analyze the factors influencing logistics center site selection, ranking potential addresses by weight, and conducting a comprehensive benefit evaluation to propose site selection recommendations for Hefei’s cold chain logistics center for fresh agricultural products. Although traditional MCDM methods have been widely applied in logistics and facility planning research, providing a systematic framework for multi-indicator evaluation and candidate scheme ranking, they usually rely on static weight allocation and assume that the indicators are independent of each other. Their analysis results tend to be a single ranking and are easily affected by subjective bias as well as the fuzziness and volatility of the objective data itself⁶. This limits the ability of traditional site selection methods to address the inherent uncertainty, interdependence, and incompleteness of many influencing factors in the site selection process of cold-chain logistics parks. Therefore, there are still limitations in establishing quantitative standards for the reliability of results⁷.

In the site selection methods of cold-chain logistics parks, some scholars use extended MCDM methods, such as Grey Relational Analysis (GRA)⁸ and Fuzzy Comprehensive Evaluation (FCE)⁹. They are widely applied in site selection and evaluation studies because they can handle multi-criteria problems under conditions of incomplete information (GRA) or linguistic/uncertain data (FCE). Zheng and Liu¹⁰ elucidated the fundamental meanings and characteristics of cold chain logistics and proposed a combined approach using Grey Relational Analysis and AHP to address the site selection of cold chain distribution centers. Cui et al.¹¹ proposed a site evaluation model based on the Ideal Solution Method and Grey Relational Analysis, validating its feasibility through case studies. Liao et al.¹² proposed an objective weight determination method applied under a Pythagorean fuzzy environment to eliminate the effects of criterion homogeneity, demonstrating the superiority of this method through comparative analysis. Huo et al.¹³, in consideration of the characteristics of the frozen seafood industry in Liaoning Province, designed a multi-tiered distribution network structure for frozen seafood sales. They analyzed the influencing factors for the site selection of frozen seafood distribution centers and summarized the evaluation indicators for determining the locations of cold chain distribution centers. Utilizing a fuzzy clustering evaluation method, they established an evaluation indicator model that allows for the identification of specific locations for cold chain distribution centers. Xia and Huang¹⁴ employed a fuzzy comprehensive evaluation method to establish a four-level assessment system. Through BP neural network training, they con-ducted a scientific site selection and verification analysis for alternative cities for cold chain logistics centers in Northwest China, ultimately deriving an optimal site selection plan for cold chain logistics centers in the region. However, these methods are still based on static weight allocation, mainly producing linear comprehensive scores or rankings. Therefore, they cannot explicitly capture the interdependence or causal relationships among the indicators.

Bayesian network model as a robust framework for decision-making under conditions of uncertainty. Bayesian Probability Theory is a reasoning method based on conditional probability and the updating of prior knowledge. Its core idea is to combine prior probability with observed data (likelihood) through Bayes’ formula to obtain posterior probability, thereby making inferences and decisions under conditions of uncertainty and incomplete information^7,15. By constructing a Bayesian network, the probabilistic dependencies among multiple influencing factors can be explicitly modeled, and their relative importance can be quantified. This advantage is particularly important for the site selection of cold-chain logistics parks, because the economic indicators, infrastructure conditions, and market demand of cold-chain logistics parks are interdependent and usually exhibit random fluctuations. Therefore, the Bayesian method not only enhances the scientific rigor of the evaluation indicator system, but also strengthens the reliability of the clustering results by providing probabilistic interpretations of factor interactions and outcome uncertainty¹⁶.

Based on existing studies, scholars typically determine the optimal site for cold chain logistics parks by selecting influencing factors and indicators within municipal level and below, or extended to the provincial level and even larger regions. However, there has been relatively little research combining these two researches scale. Accordingly, this study first draws on the characteristics and relevant literature of cold-chain logistics parks to compile an initial set of site-selection indicators. A Bayesian network model is then employed to quantify the significance of each indicator to establish a scientifically grounded indicator system for cold-chain logistics park location. Next, K-means clustering is applied to generate well-defined clusters with distinct attributes, thereby identifying provincial prefecture-level cities exhibiting higher overall development levels within the province, and used a Bayesian discriminant model to verify the reliability of the resulting site-selection scheme. Finally, Geographic Information System (GIS) technology will be utilized of one prefecture-level city of higher overall development for suitability evaluation and analysis of cold chain logistics park site selection, enabling a visual representation of site selection outcomes and making the results clearer and more intuitive. The resulting integrated methodological framework, compared with traditional MCDM methods, can more effectively address the complexity and spatial heterogeneity of cold-chain logistics park site selection¹⁷. Jiangsu Province was selected as the study area to verify the feasibility of the proposed method. This approach will further refine the theoretical framework and practical foundations related to the site selection of cold chain logistics parks (Fig. 1).

Fig. 1

Research framework.

Methods

Construction of a cold-chain logistics park location optimization model based on K-means clustering and bayesian discriminant analysis

Establishment of a Bayesian-based site selection evaluation indicator system

A well-constructed evaluation indicator system is essential for ensuring the scientific rigor of cold-chain logistics park site-selection decisions; however, existing indicator sets lack unified standards and appropriate weighting schemes. By performing probabilistic inference under uncertainty, Bayesian methods provide quantitative assessments of hypothesis-testing and estimation problems, thereby attenuating the impact of historical data volatility and ambiguity on evaluation outcomes. Moreover, they allow the systematic analysis of factor significance without requiring extensive regression analysis, facilitating a comprehensive quantification of each indicator’s influence¹⁸. In this study, a Bayesian network method is introduced to the domain of cold-chain logistics park site selection, optimizing conventional methodologies with quantitative analysis and good inference analysis of uncertainties, and ultimately constructing a scientific and reasonable site-selection evaluation indicator system.

• Selection of evaluation indicators.

Based on a broader regional perspective, the indicator system constructed for the evaluation of cold chain logistics park site selection in this study can be divided into two levels. Based on the macro-location factors and regional linkage elements that must be comprehensively considered in the site selection of cold-chain logistics parks, and drawing on existing research literature and relevant work reports, a series of site selection-related indicators were initially identified. From these, three primary categories—urban economic development, cold-chain market supply and demand, and infrastructure construction—were selected as the first-level indicators.

The preliminary selection of second-level indicators involved identifying and screening factors reported in the existing literature. These indicators represent the most specific and fundamental tier: they are taken directly from, or are closely aligned with, raw data and thus form the basis for the first-level indicators. Considering the current characteristics and development trends of urban economies and the cold-chain logistics sector, an evaluation framework comprising 11 s-level indicators was ultimately established. The identification and screening outcomes are summarized as: ① GDP^{12,15,18,19,20,21,22,23,24,25,26,27,28,29}, ② Fixed asset investment^{8,16,18,20,25}, ③ Per capita income of urban residents^{12,20,21,22,23,24,25,26}, ④ Per capita consumption expenditure of urban residents^19,20,21, ⑤ Gross import and export volume of foreign trade^12,18,20, ⑥ Proportion of the tertiary industry^20,25,27,28, ⑦ Value added of the tertiary industry^19,21,24, ⑧ Highway freight volume^{15,20,21,25,26,28}, ⑨ Total output value of agriculture, forestry, animal husbandry, and fishery^{15,20,24,27,29}, ⑩ Total retail sales^{12,13,18,19,20,21,23,26,27,29}, ⑪ Highway mileage^{12,15,19,20,21,25,27,29}. The indicator system is summarized in Fig. 2.

Fig. 2

Indicators system for cold chain logistics park site selection.

• Construction of a Bayesian network model.

Based on the selected influencing factors, a Bayesian network structure diagram (Fig. 2) was developed. Using GeNIe software in conjunction with the Expectation-Maximization (EM) algorithm, the conditional probability distributions of all nodes were determined. A Bayesian network model was established for the eleven second-level evaluation indicators of cold-chain logistics park site selection. We adopted the median split method, calculating the median of the basic data for each indicator, and used it as the benchmark to divide each indicator into “high” and “low” states. This method ensures classification balance and reduces the impact of outliers, and it has been widely applied in spatial and social science research in the absence of external standards. By performing reverse inference based on the structural model, the posterior probabilities of each evaluation indicator were obtained under the condition of a high planning level for cold-chain logistics park site selection. Combined with regional data, the statistical significance of each indicator was quantified, and those with a significance level of ≤ 0.05 were retained. These significant indicators, corresponding to the second-level evaluation indicators, were ultimately identified as the key factors influencing site selection, forming the basis for establishing the evaluation index system for cold-chain logistics parks^18,31.

Construction of a cold-chain logistics park site-selection model

The cold-chain logistics park site-selection model is primarily constructed using K-means clustering, which classifies prefecture-level cities within the province ac-cording to the concentration and dispersion of their indicator data. Based on the clustering results, a Bayesian discriminant analysis is then applied to assess the reliability of the site-selection clusters, ultimately yielding a robust site-selection model³².

• Construction of a site-selection model based on K-means clustering.

Clustering method is one of the key approaches for constructing site-selection models³³. K-means clustering quantitatively analyzes study objects through mathematical processing to generate clearly defined clusters with distinct attributes, ensuring high similarity within each cluster and marked differences between clusters³⁴. In addition to using K-means clustering, this study also introduced Ward’s hierarchical clustering as a comparative method³⁵. At each merging step, Ward’s method minimizes the increase of within-cluster variance, which is consistent with the optimization objective of K-means but does not rely on random initialization; meanwhile, it can generate a dendrogram to intuitively display the aggregation process, and therefore it has been widely used as a supplementary method in regional classification and site-selection studies. By comparing the results of the two methods, the robustness of the clustering conclusions can be effectively verified.

• Determine the optimal number of clusters.

In the K-means clustering algorithm, the core of classification lies in determining the optimal number of clusters K. Based on the density and dispersion of the indicator data, this study divides the prefecture-level cities within the province into three categories, namely K = 3. Through K-means clustering, a three-level urban cold-chain logistics network composed of logistics parks, logistics centers, and distribution centers³⁰ is constructed, enhancing the scientific rigor and practical feasibility of cold-chain logistics park site selection. To verify the rationality of the cluster number K, two commonly used data-driven methods, the Elbow Method³⁶ and the Silhouette Coefficient Method³⁷, are further employed for examination.

First, the Elbow Method is employed to calculate the Sum of Squared Errors (SSE) (Eq. 1), which is the sum of the squared distances from each point to its nearest cluster center, under different numbers of clusters. A curve of the number of clusters K versus SSE is then plotted. When choosing different numbers of clusters, the SSE usually decreases as the number of clusters increases, because more clusters mean that the points within each cluster are closer to their center. The “elbow” position, where the error reduction of the K-SSE curve begins to slow down, is identified as the balance point, which determines the efficiency inflection point by considering both clustering quality and model complexity.

$$\:SSE=\sum\:_{\text{i}=1}^{\text{k}}\:\sum\:_{p\in\:{C}_{i}}\:|p-{m}_{i}{|}^{2}\:\:$$

(1)

In cluster analysis, $\:{C}_{i}$​ denotes the k-th cluster, $\:p$ ​ represents a sample belonging to this cluster, and $\:{m}_{i}$​ refers to the centroid of the cluster.

Secondly, the Silhouette Coefficient is employed to comprehensively evaluate clustering quality from the two dimensions of internal compactness and external separation. The Silhouette Coefficient (Eq. 2) combines the degree of cohesion within clusters and the degree of separation between clusters, providing a measure for each sample. Its value ranges from [− 1, 1], with values closer to 1 indicating better clustering performance. It is often used in conjunction with the Elbow Method to verify clustering effectiveness.

$$\:s\left(i\right)=\frac{b\left(i\right)-a\left(i\right)}{\text{max}\left\{a\left(i\right),b\left(i\right)\right\}}\:\:$$

(2)

In the calculation of the silhouette coefficient, $\:a\left(i\right)$ denotes the average distance between sample $\:i$ and other points within the same cluster, which reflects intra-cluster cohesion, while $\:b\left(i\right)$ denotes the average distance between sample $\:i$ and all points in the nearest neighboring cluster (non-own cluster), which reflects inter-cluster separation.

Overall Silhouette Coefficient (Eq. 3):

$$\:S=\frac{1}{n}\sum\:_{i=1}^{n}\:s\left(i\right)\:$$

(3)

The calculation results first determine a K1 value by observing the inflection point of the Elbow Method, and then determine a K2 value by observing the change of the Silhouette Coefficient. If K1 = K2, it is regarded as the optimal number of clusters. If K1 ≠ K2, the average of the two can be taken as the optimal K value. If the average K is a decimal, it is rounded up or down to obtain the optimal K value.

• Sensitivity analysis of clustering results.

K-means clustering is a commonly used unsupervised classification method, but its results are often affected by algorithm settings and data processing methods. First, the K-means algorithm is sensitive to the selection of initial cluster centers, and different initial values may lead to different clustering results³⁸. Second, the standardization method of the input data affects the relative weights among indicators, thereby changing the classification boundaries³⁹. Since the clustering results in this study are directly related to the hierarchical division of cold-chain logistics park site selection and subsequent analysis, it is necessary to conduct a sensitivity analysis of the K-means clustering results to ensure the scientific rigor of the conclusions. By testing variations in initialization methods and standardization methods, the consistency of the study’s conclusions under different conditions can be verified, thereby enhancing the reliability of the model results.

The sensitivity analysis of K-means clustering results is mainly carried out from two aspects: (i) initialization stability: running the clustering algorithm multiple times with random starting points to test whether the classification results are consistent; (ii) impact of standardization methods: processing the original data using both z-score and min–max standardization methods, and comparing the consistency of the clustering partition results.

• Reliability assessment of the site-selection scheme based on a Bayesian model.

In site-selection planning, the uncertainty and incompleteness of historical data sources undermine the reliability of clustering outcomes. Accordingly, the Bayesian discriminant method is applied—building on the K-means clustering results—to assess the robustness of the logistics-park site-selection clusters³². The steps for constructing the Bayesian discriminant model are as follows:

Determination of the prior probabilities $\:{p}_{j}\:$(Eq. 4).

$$\:{p}_{j}=\frac{{n}_{j}}{\sum\:_{j=1}^{k}{n}_{j}}$$

(4)

where $\:{p}_{j}$ is the prior probability of the j-th class (j = 1,2,3,…), $\:{n}_{j}$ is the number of samples in the j-th class, and K is the total number of classes.

Computation of the mean vector $\:{\overline{X}}^{\left(j\right)}\:$(Eq. 5).

$$\:{\overline{X}}^{\left(j\right)}=\frac{1}{{n}_{j}}\sum\:_{l=1}^{{n}_{j}}\:{X}_{l}^{\left(j\right)}$$

(5)

where $\:{\overline{X}}^{\left(j\right)}$ is the mean vector of the j-th class, and $\:{X}_{l}^{\left(j\right)}$​ denotes the ℓ-th sample data vector within the j-th class.

Computation of the entire sample covariance matrix $\:S$ (Eq. 6).

$$\:S=\frac{\sum\:_{j=1}^{k}\:({n}_{j}-1){S}_{j}}{\sum\:_{j=1}^{k}\:{n}_{j}-k}\:$$

(6)

$$\:S_{j} = \frac{1}{{n_{j} - 1}}\sum {\:_{{l = 1}}^{{n_{j} }} } (X_{l}^{{\left( j \right)}} - \overline{{X^{{\left( j \right)}} }} )(X_{l}^{{\left( j \right)}} - \overline{{X^{{\left( j \right)}} }} )^{T} \:$$

(7)

where $\:S$ denotes the covariance matrix of the entire sample, and $\:{S}_{j}$ (Eq. 7) represents the covariance matrix of the j-th class.

Derivation of the Bayesian discriminant function $\:{Y}_{j}$ (Eq. 8) based on prior probabilities.

$$\:{Y}_{j}={C}_{0j}+{C}_{j}^{{\prime\:}}X$$

(8)

$$\:C_{j}^{{\prime \:}} = S^{{ - 1}} \cdot \:\overline{{X^{{\left( j \right)}} }}$$

(9)

$$\:C_{{0j}} = {\text{ln}}\left( {p_{i} } \right) - 0.5\overline{{X^{{\left( j \right)}} }} \cdot \:S^{{ - 1}} \cdot \overline{{X^{{\left( j \right)}} }}$$

(10)

where $\:{Y}_{j}\:$is the Bayesian discriminant function for the j-th class; $\:{C}_{0j}$​ (Eq. 9) and $\:{C}_{j}^{{\prime\:}}$​ (Eq. 10) are the parameter matrices of the function; $\:X$ is the numerical matrix of the samples; and $\:{S}^{-1}$ is the inverse of the entire sample covariance matrix.

Substitute the evaluation index attributes of each sample into the above discriminant function, and according to the magnitude of the function value, classify the sample into the class with the maximum function value.

• Center-distance determination.

K-means algorithm by default uses Euclidean distance to measure the closeness between sample points and cluster centers. Euclidean distance is the most common and also the most appropriate choice. In the calculation of Euclidean distance, each variable is assumed to be independent and equally important. However, in the problem of cold-chain logistics park site selection, there often exist strong correlations among different indicators. If Euclidean distance is still used, the influence of certain variables may be overestimated or underestimated, thereby leading to biased clustering results. Therefore, after clustering is completed, it is necessary to verify whether the samples indeed belong to their respective categories and to evaluate the “statistical distance” between samples and cluster centers. In this study, Bayesian discriminant analysis is introduced to validate the stability of the clustering results, and within the Bayesian discriminant framework the distance in the original measurement scale is re-evaluated. In this process, Mahalanobis distance is more applicable, as it incorporates the covariance matrix in the calculation, which corrects for differences in variable dimensions and accounts for correlations among variables⁴⁰. Compared with Euclidean distance, Mahalanobis distance can more accurately reflect the differences between samples and cluster centers, avoiding repeated weighting caused by inter-variable correlations⁴¹. Conceptually, this makes Mahalanobis distance a more suitable metric in contexts such as cold-chain logistics park site selection, where indicators are strongly correlated. It ensures that the closeness of samples to cluster centroids is measured in a way that reflects both the scale and the correlation structure of the data, thereby improving the robustness of the clustering validation. Essentially, it represents a weighted distance between a sample data vector and the cluster mean; within any given cluster, the member with the smallest Mahalanobis distance is considered the closest to the centroid. The definition of Mahalanobis distance is given as follows in Eq. (11):

$$\:D_{M}^{2} = (X_{i} - \mu \:_{j} )^{{{\text{T}}\:}} S_{j}^{{ - 1}} \left( {X_{i} - \mu \:_{j} } \right)\:$$

(11)

where, $\:{X}_{i}$ is the numerical vector of the i-th sample; $\:{\mu\:}_{j}$ is the mean vector of cluster j; and $\:{S}_{j}^{-1}$ is the inverse of that cluster’s sample covariance matrix $\:{S}_{j}^{\:}$ for cluster j.

After determining the evaluation indicator system and establishing the site-selection model for cold-chain logistics park, one prefecture-level city from the first-class cluster within the province was selected as the study area for GIS-based suitability analysis. A comprehensive suitability evaluation indicator system for cold-chain logistics park locations was then developed at the municipal scale.

Site selection analysis based on GIS suitability evaluation

Construction of the GIS suitability evaluation site selection system

Incorporating the integrated processing, regional distribution, and urban delivery functions of cold chain logistics parks⁴², and considering economic development, transportation conditions, and cold chain facility demand, this study identifies the suitability evaluation indicator layer for the site selection of cold chain logistics parks based on relevant literature. This layer encompasses specific indicators that must be considered to achieve the defined objectives.

Indicators with similar meanings are standardized in naming, and those selected with a frequency of occurrence ≥ 5 in literatures are identified and summarized: ① Market environment^4,5,6,43,44, ② Economic costs^{1,2,3,4,5,8,19,44,45,46,47,48}, ③ Consumption level^{3,4,19,44,45,46,47}, ④ Transportation conditions^{1,2,3,4,5,8,19,44,45,46,47,48}, ⑤ Conditions of three utilities (water, electricity, and natural gas supply)^{1,2,3,4,519,,44,45,46,47}, ⑥ Policy environment^{3,5,819,,44,45,48}, ⑦ Living environment^{1,2,3,8,44,48}, ⑧ Natural environment^{3,5,19,44,47,48}.

After screening the indicator layer, it is necessary to organize and consolidate the indicators to form a criterion layer with strong unity and relevance. By integrating insights from articles and referencing the classification criteria of various scholars, this study provides guidance for selecting the criterion layer indicators for the suitability evaluation of cold chain logistics park site selection. The analysis reveals that most scholars categorize indicators according to dimensions such as natural factors, economic factors, market factors, transportation factors, policy factors, infrastructure factors, and social factors. Overall, there has yet to be a unified standard for suitability evaluation in site selection.

This study, therefore, considers the characteristics necessary for the suitability evaluation of cold chain logistics park site selection, specifically the need for relatively developed economic conditions, well-established infrastructure, and a favorable construction environment. Consequently, the criterion layer is divided into three categories: economic factors, infrastructure factors, and environmental factors. The final organization of the indicator system is summarized in Table 1.

Table 1 Factors influencing the suitability evaluation of cold chain logistics park site selection.

Determination of factor weights using the entropy weight method

A 3000 m × 3000 m fishnet grid was generated in the GIS platform, determined by the analytical scale of the prefecture-level administrative boundary as well as the typical land-use extent and service radius requirements of cold-chain logistics parks. The raster data is subjected to value extraction for point analysis, where attribute values from the raster data are extracted into a table based on specified points. Subsequently, vector data undergoes spatial connection analysis, where attributes are transferred from one vector feature class to another based on the spatial relationships between the two classes. This process results in value tables for the 16 influencing factors across the grid.

Using Excel, the existing data undergoes normalization analysis to produce a standardized matrix (Eqs. 12 to 13). The standardized matrix is then utilized to perform calculations using the entropy weight method (Eqs. 14 to 17), yielding the weights for the 16 influencing factors⁴⁸.

$$\:{x}_{ij}=\frac{{\text{k}}_{\text{i}\text{j}}-\text{m}\text{i}\text{n}\left({\text{k}}_{\text{i}\text{j}}\right)}{max\left({\text{k}}_{\text{i}\text{j}}\right)-\text{m}\text{i}\text{n}\left({\text{k}}_{\text{i}\text{j}}\right)}\:\text{P}\text{o}\text{s}\text{i}\text{t}\text{i}\text{v}\text{e}$$

(12)

$$\:{x}_{ij}=\frac{\text{m}\text{a}\text{x}\left({\text{k}}_{\text{i}\text{j}}\right)-{\text{k}}_{\text{i}\text{j}}}{max\left({\text{k}}_{\text{i}\text{j}}\right)-\text{m}\text{i}\text{n}\left({\text{k}}_{\text{i}\text{j}}\right)}\:\text{N}\text{e}\text{g}\text{a}\text{t}\text{i}\text{v}\text{e}$$

(13)

$$\:{\text{p}}_{\text{i}\text{j}}=\frac{{\text{x}}_{\text{i}\text{j}}}{\sum\:_{\text{i}=1}^{\text{n}}\:{\text{x}}_{\text{i}\text{j}}}(\text{j}=\text{1,2},...,\text{m})$$

(14)

$$\:{e}_{j}=-k\sum\:_{i=1}^{{n}_{\:}}\:{p}_{ij}ln{p}_{ij}$$

(15)

$$\:{g}_{j}=1-{e}_{j}$$

(16)

$$\:{w}_{j}=\frac{{g}_{j}}{\sum\:_{j=1}^{m}{g}_{j}}$$

(17)

In the equations: $\:{K}_{ij}$ represents the initial value of each indicator. $\:{X}_{ij}$ represents the standardized data. $\:{P}_{ij}$ represents the proportion of the indicator value of the i-th scheme under the j-th indicator. $\:{e}_{j}$ represents the information entropy value of the j-th indicator, K = 1/ln(n). $\:{g}_{j}$ represents the information entropy redundancy of the j-th indicator. $\:{w}_{j}$ represents the weight of the j-th indicator.

Single factor suitability evaluation analysis of influencing factors

Relying on the GIS platform, methods such as spatial query, spatial measurement, and buffer analysis⁴⁹ were employed. Except for the “distance” factor, all influencing factors are classified in ArcGIS using the natural breaks method. This method determines classification breakpoints by minimizing intra-class variance and maximizing inter-class differences, thereby reflecting the intrinsic distribution pattern of the data, so the breakpoints are not arbitrarily set. The grading of the “distance” factor, however, refers to logistics accessibility and existing planning standards. Combined with the classification standards of 16 influencing factors (Table 2), the single-factor suitability evaluation results were reclassified and assigned values, dividing them into five zones: optimal zone, suitable zone, moderate zone, less suitable zone, and unsuitable zone. These five zones were assigned values of 5, 4, 3, 2, and 1, respectively.

Table 2 Standard classification table of impact factors.

Comprehensive suitability evaluation analysis

Based on the results of the single-factor suitability evaluation analysis and the factor weights mentioned above, a comprehensive suitability evaluation map for cold chain logistics parks was generated through weighted overlay processing. The higher the comprehensive suitability evaluation score, the stronger the suitability for the location of the cold chain logistics park, indicating greater suitability for construction. Using the reclassification method, the comprehensive suitability evaluation map was divided into five zones: optimal zone, suitable zone, moderate zone, less suitable zone, and unsuitable zone. The exact location of the most suitable zone was identified and marked. Based on the size of the land parcel and the surrounding environment, the optimal site for constructing the cold chain logistics park was selected and determined.

Results

Research area

Jiangsu Province, located in the southern part of China’s Yangtze River Delta region, comprises 13 prefecture-level cities (Fig. 3). As a major province for the production, circulation, and consumption of cold chain products, the cold chain logistics market has been continuously expanding since the 13th Five-Year Plan, with an annual growth rate exceeding 20%. Cities such as Suzhou and Nanjing are included among the national backbone cold chain logistics base cities, with Suzhou’s national backbone cold chain logistics base selected as one of the first construction sites.

Fig. 3

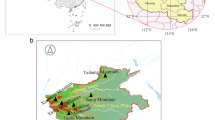
Location analysis map of Jiangsu province. (a) Shows the location of Jiangsu Province in China; (b) shows the administrative divisions of Jiangsu Province. (Base map sources: NASA Blue Marble: NASA Earth Observatory, public domain, URL: https://visibleearth.nasa.gov/. Administrative boundary data source: Tianditu: National Platform for Common Geospatial Information Services, URL: http://www.tianditu.gov.cn/. Cartographic software: ArcGIS 10.5, URL: https://hn.hongria.cn/arcg/hn360.html? source=360a&unitid=3019404834&unit=arcg&e_creative=10122122147&qhclickid=fc779ac3993f5fbf. Adobe Photoshop CC 2022, URL: https://www.adobe.com.)

In response to the requirements outlined in the “14th Five-Year Plan for Cold Chain Logistics Development” issued by the State Council, Jiangsu Province introduced the “Jiangsu Province Cold Chain Logistics Development Plan (2022–2030)” in 2022, which aims to establish a modern cold chain logistics system by 2030. In 2023, Jiangsu Province released the “Three-Year Action Plan for Promoting High-Quality Development of Cold Chain Logistics (2023–2025),” which proposes that by 2025, a network of cold chain logistics facilities in production areas for major agricultural products and regions with advantages in specialty agricultural products will be essentially established.

Given Jiangsu Province’s inherent advantages in developing cold chain logistics and the support of relevant policies, selecting Jiangsu as the case study for this research is conducive to enhancing the core competitiveness of the province’s cold chain logistics and provides technical and practical support for site selection planning of cold chain logistics parks in China.

Construction of a cold-chain logistics park site selection model

Construction of the indicator system

For the Bayesian network analysis to determine the indicator system of cold-chain logistics parks, all continuous indicators need to be discretized into “high” and “low” binary states. Based on the 11 indicators identified in the “Methods” section and the specific indicator values from the Jiangsu Statistical Yearbook 2023, the medians of each indicator across the 13 prefecture-level cities in Jiangsu Province were calculated. For each indicator, the median of all prefecture-level cities was used as the threshold. Values equal to or greater than the median were assigned to the “high” state, while values below the median were assigned to the “low” state. These binary states served as the input dataset for constructing the Bayesian network. Subsequently, the EM (Expectation-Maximization) algorithm in GeNIe software was applied to determine the conditional probability distributions of each node.

As shown in Fig. 4, conditional on a high level for cold-chain logistics park site selection planning, the posterior probabilities that GDP (A₁), fixed-asset investment (A₂), highway freight volume (B₃), total retail sales (B₅), and highway mileage (C₁) are likewise at high levels are 84%, 64%, 82%, 78%, and 73%, respectively. These results highlight GDP and highway freight volume as the principal determinants in the site-selection process for cold-chain logistics parks.

Based on the Bayesian network analysis, eight indicators with a significant influence on cold-chain logistics park site selection were identified: ① GDP; ② Fixed Asset Investment; ③ Per Capita Income of Urban Residents; ④ Proportion of the Tertiary Industry; ⑤ Highway Freight Volume; ⑥ Total Output Value of Agriculture, Forestry, Animal Husbandry, and Fishery; ⑦ Total Retail Sales; ⑧ Highway Mileage.

Fig. 4

Bayesian network model (Cartographic software: GeNIe Modeler. URL: https://download.bayesfusion.com/files.html?category=Academia).

Import the corresponding data of the eight evaluation indicators for cold-chain logistics park site selection into the SPSS statistical software package. Each variable was standardized by converting the raw values to dimension-less standard scores. The significance values for all 8 indicators are ≤ 0.05, demonstrating that every indicator is statistically significant. Accordingly, these 8 indicators were retained to form the final evaluation indicator system for cold-chain logistics park site selection.

Construction of a site selection model

• Determine the optimal number of clusters.

First, the optimal number of clusters is determined using the Elbow Method. All computations are conducted using the specific values of the eight indicators identified above. Before clustering, the variables are standardized to eliminate unit and scale effects, thereby preventing large-magnitude indicators from dominating the analysis. K-means clustering is then applied for a range of K values (1-10), the SSE for each K value is calculated, and the K–SSE curve is plotted (Fig. 5). The calculation results show that when K = 3, the rate of decrease in SSE begins to slow down, presenting a clear “elbow” feature, indicating that further increasing the number of clusters has limited marginal effect on improving the clustering performance.

Secondly, the Silhouette Coefficient method is applied. For different K values (2-10), the dataset is clustered using the K-means algorithm. For each K value, the Silhouette Coefficients of all samples are calculated, and the average Silhouette Coefficient is plotted (Fig. 5). The results show that the highest Silhouette Coefficient occurs at K = 2 (0.464), indicating that, from the perspective of inter-cluster separation alone, K = 2 is optimal. However, the value for K = 3 is also relatively high (0.406). Taking into account the elbow point identified by the Elbow Method, K = 3 is also supported. In the case where the two methods yield different K values, the average of the two is taken as the optimal K value. At this point, the average K value is 2.5. Considering the logical background of the study (the three-level logistics network structure), K is rounded up to the integer 3, making K = 3 the most reasonable choice.

Combining the above two methods, K = 3 not only conforms to the theoretical assumption of the hierarchical structure of the logistics network but is also supported by the statistical test results. Therefore, this paper ultimately selects K = 3 as the optimal number of clusters for the clustering analysis.

Fig. 5

Elbow method and silhouette method for optimal K.

• K-means clustering analysis.

Using SPSS software and the K-means clustering method, the analysis produces the final cluster centers (as shown in Table 3) and cluster members (as shown in Table 4). By comparing the values of the eight indicators in the final cluster centers, the cities are categorized into three classes based on the number of indicators with the highest values.

Table 3 Final cluster centers.

Table 4 Cluster members.

Subsequently, each prefecture-level city in Jiangsu Province is assigned to the appropriate cluster based on the cluster members. This process results in the classification of Jiangsu Province’s thirteen prefecture-level cities into three major categories, yielding the classification results for cold chain logistics parks based on K-means clustering (as summarized in Table 5).

Table 5 Clustering results of cold chain logistics parks in Jiangsu Province based on the K-means clustering method.

• Sensitivity analysis of clustering results.

To verify the robustness of the study’s conclusions, this study conducts a sensitivity analysis of the clustering results on the basis of determining the optimal number of clusters as K = 3.

In the baseline scenario, z-score standardization and K = 3 clustering is applied, with 20 random initializations. The results show that the classification of the 13 prefecture-level cities is completely consistent with Table 5. The consistent results obtained from multiple random starting points indicate that the model is not sensitive to the initial cluster centers. The Silhouette Coefficient of this scheme is 0.406, indicating that the clustering structure has moderate rationality, suggesting that this number of clusters achieves a good balance between classification accuracy and model simplicity.

In the comparison of different standardization methods, the clustering results obtained using min–max standardization are completely consistent with the baseline scheme (Adjusted Rand Index, ARI = 1.00), and the Silhouette Coefficient is 0.408, almost identical to 0.406 for z-score. This indicates that the clustering results do not depend on the choice of standardization method, and the conclusions are robust.

• Multi-method comparative validation.

On this basis, a multi-method comparison is adopted to further validate the clustering results. First, the values of the eight indicators of Jiangsu Province are standardized (including both the z-score and min–max schemes), after which a distance matrix between samples is constructed using Euclidean distance, and Ward’s hierarchical clustering is applied to select, at each step, the merging operation that minimizes the increment of the within-cluster sum of squares (SSE). The final grouping is obtained when K = 3, and this is compared with the results of K-means (Euclidean distance) and reallocation based on Mahalanobis distance. The calculation results show that the classification results obtained under different distance measures, validation methods, and clustering algorithms are consistent with Table 5, indicating that the K-means clustering method is robust and reliable in this study.

• Selection of the central city.

The distance criterion of K-means clustering is to calculate, through iteration, the Euclidean distance from each cluster member to its center. Within a cluster, the smaller the distance, the closer the indicator values are to the cluster center, and the better they represent the characteristics of the preferred cities for cold-chain logistics parks in that cluster.

Based on the distances from each city to the cluster centroids calculated in Table 4, Suzhou has the shortest distance to the centroid of Cluster 1. Consequently, Suzhou is identified as the prefecture-level city in Jiangsu Province most suitable for establishing a cold-chain logistics park and is selected as the study area for the GIS-based suitability evaluation. As shown in Fig. 6, Suzhou administers five urban districts and has jurisdiction over four county-level cities.

Fig. 6

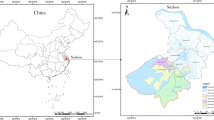
Location analysis map of Suzhou city. (a) Shows the location of Suzhou in Jiangsu Province; (b) Shows the administrative divisions of Suzhou City. (Base map sources: NASA Blue Marble: NASA Earth Observatory, public domain, URL: https://visibleearth.nasa.gov/. Administrative boundary data source: Tianditu: National Platform for Common Geospatial Information Services, URL: http://www.tianditu.gov.cn/. Cartographic software: ArcGIS 10.5, URL: https://hn.hongria.cn/arcg/hn360.html?source=360a&unitid=3019404834&unit=arcg&e_creative=10122122147&qhclickid=fc779ac3993f5fbf. Adobe Photoshop CC 2022, URL: https://www.adobe.com).

Reliability assessment of the site-selection scheme

• Model construction.

Based on the proportions of the three sample classes obtained from the clustering results, the prior probabilities were set to $\:{p}_{1}$=3/13, $\:{p}_{2}$=3/13, and$\:\:{p}_{3}$​=7/13. All sample data were then normalized, as shown in Table 6.

Table 6 Data normalization.

• Calculation of the sample mean vector $\:{\overline{X}}^{\left(j\right)}$, as shown in Table 7.

Table 7 Data mean vector $\:{\overline{X}}^{\left(j\right)}$.

• Determination of discriminant function parameters.

Using MATLAB and the relevant formulas, the inverse of the covariance matrix ($\:{S}^{-1})$ was calculated, and the discriminant function parameters$\:{C}_{0j}$​ and matrix $\:{\:C}_{j}^{{\prime\:}}$​ for each class were subsequently derived, as presented in Tables 8 and 9.

Table 8 Discriminant function matrix $\:{\:C}_{j}^{{\prime\:}}$​.

Table 9 Discriminant function parameters $\:{C}_{0j}$​.

• Reliability assessment of clustering results.

The reliability of the clustering results for the 13 prefecture-level cities in Jiangsu Province was verified using a Bayesian discriminant model. The discriminant rule was defined as follows: each raw-scale sample was substituted into the discriminant function equations, and the resulting values $\:{Y}_{1}$​, $\:{Y}_{2}$​, and $\:{Y}_{3}$​ were compared; the class corresponding to the largest value was assigned as the cluster level of that sample. The final Bayesian discrimination outcomes for the 13 prefecture-level cities are summarized in Table 10.

Table 10 Results of the bayesian discriminant analysis.

• Center-distance determination.

Within the Bayesian discriminant framework, the data of the cities in Cluster 1 were substituted into the model, and their respective Mahalanobis distances were further calculated, which are reported in Table 11. This procedure was employed to verify whether each city truly belongs to its assigned cluster and to quantitatively evaluate the closeness between individual cities and the corresponding cluster centroid. By incorporating the covariance structure of the indicators, Mahalanobis distance provides a more accurate statistical measure than Euclidean distance, thereby ensuring the robustness of the clustering validation.

Table 11 Center-distance of class 1 cluster cities.

• Analysis of the discriminant results.

The K-means clustering method partitioned the 13 prefecture-level cities in Jiangsu Province into three clusters, with Nanjing, Wuxi and Suzhou grouped in Cluster 1. Bayesian discriminant analysis yielded the same classification, confirming the suitability of this combined approach for planning the locations of cold-chain logistics parks.

Both the Euclidean distances iteratively computed by the K-means clustering method and the Mahalanobis distances re-evaluated under the original scale via Bayesian discrimination show that Suzhou lies closest to the centroid of Cluster 1, making it the city that best represents the cluster’s core characteristics. Accordingly, Suzhou city is deemed the most suitable prefecture-level city in Jiangsu Province for establishing a cold-chain logistics park and is selected as the study area for the GIS-based suitability evaluation.

Site selection analysis based on GIS suitability evaluation

Data sources

The data are sourced from the Suzhou Statistical Yearbook, OpenStreetMap, the National Geoinformation Center, and Gaode Map. The collected data include: foreign investment, land prices, per capita GDP, freight volume, water supply capacity, electricity supply capacity, natural gas supply capacity, regional policy support; network data for highway, railway, and waterway; Digital Elevation Model (DEM) data of Suzhou and POIs for logistics parks, agricultural production areas, markets, residential areas.

It should be noted that the statistical periods of these datasets are not the same. The publication year of statistical yearbooks is fixed, and in this study the Suzhou Statistical Yearbook 2023 was used. In contrast, OpenStreetMap is a continuously updated open-source database, and the data used in this study were extracted in October 2024. The data from the National Geomatics Center of China platform are updated annually or every several years; in this study, the “2020 Topographic Map Data,” released on November 24, 2020, was adopted. The POI data from Amap (Gaode Map) are usually updated on a quarterly or monthly basis; in this study, the dataset was extracted in October 2024, as shown in Table 12.

Table 12 Sources of data for the suitability evaluation of cold-chain logistics park site selection.

Determining factor weights using the entropy weight method

Utilizing GIS and Excel platforms, the data undergoes raster and vector analysis. The entropy weight method is then applied to calculate the weights of the 16 influencing factors. The resulting weights are arranged in descending order, as shown in Table 13.

Table 13 Significance analysis.

Single factor suitability evaluation analysis

• Market competition factors.

By examining the suitability evaluation map showing the distance to existing cold chain logistics parks, as show in Fig. 7a, it is evident that the current cold chain logistics parks are predominantly concentrated in areas such as Gusu District, Suzhou Industrial Park, Kunshan, and Taicang. Site selection for new cold chain logistics parks should consider locations that are as far as possible from these existing parks which can help newly established cold chain logistics parks capture more opportunities and ad-vantages in the market, enhancing their competitiveness and sustainability in the industry.

As shown in the foreign investment suitability evaluation map, as show in Fig. 7b, Kunshan City demonstrates strong attractiveness and competitiveness for foreign investment within the Suzhou region. In contrast, Zhangjiagang City, Taicang City, and Wujiang District exhibit relatively low levels of foreign investment, reflecting existing issues in their development environment, policy support, and industrial structure.

Fig. 7

Suitability evaluation analysis map based on market competition factors: (a) Distance to cold chain logistics parks suitability evaluation analysis map; (b) Foreign direct investment suitability evaluation analysis map. (Cartographic software: ArcGIS 10.5. URL: https://hn.hongria.cn/arcg/hn360.html?source=360a&unitid=3019404834&unit=arcg&e_creative=10122122147&qhclickid=fc779ac3993f5fbf.)

• Economic cost factors.

By examining the land cost suitability evaluation analysis map, as show in Fig. 8a, it is evident that Kunshan and Wujiang District have relatively low land prices, while Zhangjiagang has higher prices. Given that the construction of cold chain logistics parks typically requires large areas of land, lower land prices can significantly reduce the overall construction costs for these logistics facilities. This factor is crucial for enhancing the economic viability of new cold chain logistics parks.

By analyzing the distance to agricultural/aquacultural production sites suitability evaluation analysis map, as show in Fig. 8b, it is observed that these production areas are generally evenly distributed. However, there are some areas in Suzhou Industrial Park and Kunshan where agricultural and fishery production sites are lacking. Selecting locations closer to these production sites can enhance the efficiency and effectiveness of logistics operations.

By examining the distance to markets suitability evaluation analysis map, as show in Fig. 8c, it is noted that markets are relatively concentrated in the southern part of Zhangjiagang, Changshu, central Kunshan, Suzhou Industrial Park, and Gusu District. Proximity to markets can reduce transportation and delivery costs, minimize losses, and ensure product freshness, thereby enhancing consumer quality.

Fig. 8

Suitability evaluation analysis map based on economic cost factors: (a) Land cost suitability evaluation analysis map; (b) Distance to agricultural/aquacultural production sites suitability evaluation analysis map; (c) Distance to markets suitability evaluation analysis map. (Cartographic software: ArcGIS 10.5. URL: https://hn.hongria.cn/arcg/hn360.html?source=360a&unitid=3019404834&unit=arcg&e_creative=10122122147&qhclickid=fc779ac3993f5fbf.)

• Consumption level factors.

From the per capita GDP suitability evaluation map, as show in Fig. 9a, it is evident that residents in Suzhou Industrial Park, Zhangjiagang, and Kunshan have higher consumption capabilities. This high consumption level can significantly facilitate the rapid development of cold chain logistics parks.

Additionally, by analyzing the freight volume suitability evaluation map, as show in Fig. 9b, it is found that only Changshu, Taicang, and Wujiang District exhibit relatively low freight volumes, while other regions maintain high levels of freight activity. Freight volume can indirectly reflect a region’s consumption level; therefore, higher freight volumes are more conducive to the growth of the cold chain logistics industry.

Fig. 9

Suitability evaluation analysis map based on consumption level factors: (a) Per capita GDP suitability evaluation analysis map; (b) Freight volume suitability evaluation analysis map. (Cartographic software: ArcGIS 10.5. URL: https://hn.hongria.cn/arcg/hn360.html?source=360a&unitid=3019404834&unit=arcg&e_creative=10122122147&qhclickid=fc779ac3993f5fbf).

• Transportation conditions.

By examining the suitability evaluation maps for distance to highways, railways, and waterways, as show in Fig. 10, it can be concluded that the transportation conditions in Wuzhong District are relatively inadequate in terms of road, railway, and waterway connectivity, while the transportation conditions in other regions are more balanced and capable of supporting the transportation demands of cold chain logistics parks.

Fig. 10

Suitability evaluation analysis map based on transportation conditions: (a) Distance to highways and railways suitability evaluation analysis map; (b) Distance to waterways suitability evaluation analysis map. (Cartographic software: ArcGIS 10.5. URL: https://hn.hongria.cn/arcg/hn360.html?source=360a&unitid=3019404834&unit=arcg&e_creative=10122122147&qhclickid=fc779ac3993f5fbf).

• Water and electricity supply.

By analyzing the suitability evaluation maps of water supply, electricity supply, and natural gas supply, as show in Fig. 11, it is observed that Kunshan City and Wujiang District exhibit higher water supply levels, Kunshan City demonstrates a higher electricity supply level, while Changshu City stands out with a relatively high natural gas supply level. Greater availability of water, electricity, and natural gas pro-vides strong support for the daily operation and maintenance of cold chain logistics parks, contributing to the stable development of cold chain logistics.

Fig. 11

Suitability evaluation analysis map based on water and electricity supply factors: (a) Water supply capacity suitability evaluation analysis map; (b) Electricity supply capacity suitability evaluation analysis map; (c) Natural gas supply capacity suitability evaluation analysis map. (Cartographic software: ArcGIS 10.5. URL: https://hn.hongria.cn/arcg/hn360.html?source=360a&unitid=3019404834&unit=arcg&e_creative=10122122147&qhclickid=fc779ac3993f5fbf).

• Policy environment.

The suitability evaluation map for policy support, as show in Fig. 12 indicates that Taicang, Kunshan, and Wujiang District have high levels of policy support. This suggests that Suzhou is encouraging the development of cold chain logistics in these areas, which is favorable for the establishment of local cold chain logistics parks.

Fig. 12

Policy support level suitability evaluation analysis map. (Cartographic software: ArcGIS 10.5. URL: https://hn.hongria.cn/arcg/hn360.html?source=360a&unitid=3019404834&unit=arcg&e_creative=10122122147&qhclickid=fc779ac3993f5fbf).

• Living environment.

The suitability evaluation map based on the distance from residential areas, as show in Fig. 13, shows that the distribution of residential areas in Zhangjiagang, Wu Zhong District, and Wujiang District is relatively dispersed. Locating cold chain logistics parks away from residential areas can minimize the impact of pollution and noise generated during their construction and operation, thereby reducing disturbances to residents.

Fig. 13

Distance from residential zones suitability evaluation analysis map. (Cartographic software: ArcGIS 10.5. URL: https://hn.hongria.cn/arcg/hn360.html?source=360a&unitid=3019404834&unit=arcg&e_creative=10122122147&qhclickid=fc779ac3993f5fbf).

• Natural environment.

By examining the elevation and slope suitability evaluation maps, as show in Fig. 14, it is evident that Suzhou has a generally flat terrain, with only certain areas in Wu Zhong District being relatively uneven. Therefore, most regions are suitable for the construction of cold chain logistics parks.

Fig. 14

Suitability evaluation analysis map based on natural environment factors: (a) Elevation suitability evaluation analysis map; (b) Slope suitability evaluation analysis map. (Cartographic software: ArcGIS 10.5. URL: https://hn.hongria.cn/arcg/hn360.html?source=360a&unitid=3019404834&unit=arcg&e_creative=10122122147&qhclickid=fc779ac3993f5fbf).

Comprehensive suitability evaluation analysis

Based on the suitability evaluations of the aforementioned single influencing factors, these were converted into raster data. Using the factor weights calculated by the entropy weight method, a weighted sum analysis was conducted to generate the comprehensive suitability evaluation map for cold chain logistics parks in Suzhou, as show in Fig. 15. In the map, the deeper the color, the higher the comprehensive suitability evaluation score, indicating that the site’s suitability for cold chain logistics parks is stronger in those areas.

Fig. 15

Comprehensive suitability evaluation analysis map. (Cartographic software: ArcGIS 10.5. URL: https://hn.hongria.cn/arcg/hn360.html?source=360a&unitid=3019404834&unit=arcg&e_creative=10122122147&qhclickid=fc779ac3993f5fbf).

Site selection results

Based on the results of the comprehensive suitability evaluation, the reclassification method is applied, which involves reclassifying the attribute values of raster data into intervals and assigning new attribute values for qualitative interpretation. Combining this approach with the parcel size of the most suitable areas and the natural break method44, the areas are categorized into five regions according to the site selection classification standards for cold chain logistics parks in Suzhou (Table 14): optimal zone, suitable zone, moderate zone, less suitable zone, and unsuitable zone. The red areas represent the most suitable locations, as show in Fig. 16.

Table 14 Classification standards for cold chain logistics park site selection in Suzhou.

Based on the parcel sizes and surrounding environmental conditions of the red areas, three most suitable areas are selected and identified. These areas are labeled sequentially from top to bottom as Zone 1, Zone 2, and Zone 3. Each of the three zones is introduced in detail below.

By examining the site selection results for cold chain logistics parks in Suzhou, it is evident that the three most suitable areas are all located in Kunshan City. Economically, Kunshan has attracted significant foreign investment, bringing funding and techno-logical support that has driven economic growth and solidified the economic foundation for cold chain logistics parks. The city’s relatively low land costs provide a competitive pricing advantage for constructing these logistics parks. Additionally, Kunshan ranks high in per capita GDP and freight volume within Suzhou, indicating strong consumer purchasing power and offering vast market potential for the cold chain logistics sector.

In terms of infrastructure, Kunshan city has ample water, electricity, and gas sup-ply, ensuring stable daily operations for the logistics parks. Environmentally, the Kunshan government places a high emphasis on the cold chain logistics industry, actively promoting its development by streamlining administrative approval processes and providing tax incentives, creating favorable conditions for establishing logistics parks. Furthermore, Kunshan’s relatively flat terrain is well-suited for building cold chain logistics facilities. Notably, these three optimal areas are situated far from residential zones, ensuring the normal operation of logistics parks while minimizing noise and pollution impacts on nearby residents.

Although all three optimal areas are located in Kunshan City, each has its unique advantages.

The first optimal area is situated in the northwest of Kunshan, covering approximately 9 square kilometers, making it the largest of the three. Its vast area provides ample space and support for future expansion and development of the cold chain logistics park. This area is close to the northern dock of Lianhua Island on Yangcheng Lake and has multiple waterways for easy water transportation. It is also conveniently located near the Huyiy Expressway and X301 Highway, enhancing accessibility. The surrounding region is rich in aquatic resources and features agritourism, providing dining services for nearby residents.

The second optimal area is located in the southwest of Kunshan, with an area of about 4 square kilometers, surrounded by Yangmintian Lake, Bailian Lake, and Shuangyangtan. The Huchang Expressway and Jiangpu Road interchange run through this area, making road traffic quite developed.

The third optimal area is in the southeast of Kunshan, also covering around 4 square kilometers, adjacent to the Huchang Expressway and situated above Dianshan Lake, with proximity to Bailian Lake and Shuangyangtan. The surrounding area has a well-developed tourism industry, a high demand for cold-chain products, and rapid regional economic growth, all of which are conducive to the long-term and stable development of cold-chain logistics.

Fig. 16

Site selection results map for cold chain logistics parks in Suzhou. (Cartographic software: ArcGIS 10.5. URL: https://hn.hongria.cn/arcg/hn360.html?source=360a&unitid=3019404834&unit=arcg&e_creative=10122122147&qhclickid=fc779ac3993f5fbf).

Discussion

The study findings indicate that the site selection model for cold-chain logistics parks based on Bayesian networks and K-means clustering analysis can effectively identify prefecture-level cities within the province that have higher levels of economic development, greater cold-chain market demand, and more complete infrastructure as suitable locations for park construction. This study focuses on applying the Bayesian network method to the field of cold-chain logistics park site selection and planning, serving as an optimization of traditional site selection methods:

When constructing the site selection evaluation indicator system, it allows for quantitative evaluation of the judgments concerning uncertainty factors, which can mitigate the impact of data volatility and fuzziness in traditional research methods on the evaluation results, thereby enhancing the reliability of the evaluation indicator system.

When constructing the logistics park site selection model, the uncertainty and incompleteness of historical data sources make it difficult to ensure the reliability of clustering results. Therefore, based on the K-means clustering results that screen out prefecture-level cities with higher comprehensive development levels, the Bayesian discriminant method is adopted to assess the reliability of the cold-chain logistics park site selection clustering results. After data discrimination, a reliable cold-chain logistics park site selection model is ultimately established.

In addition, the study results also show that further conducting GIS-based suitability evaluation analysis within the range of the selected prefecture-level cities provides practical research on the spatial dimension for cold-chain logistics park planning, realizing visualization of site selection and making the results clearer and more intuitive. Compared with existing studies that are usually limited to the scale of the municipal level and below, or extended to the provincial level and even larger regions, this study achieves an organic combination in research scale, constructing a complete site selection framework from provincial-level clustering division to municipal-level spatial suitability evaluation, thus providing a more reasonable research approach for the scientific site selection of cold-chain logistics parks.

Nevertheless, certain limitations should be acknowledged.

First, this study adopts a single Bayesian network structure to quantify the significance of site selection indicators. Although this choice ensures methodological clarity, it does not fully address the inherent uncertainty in model specification. Future research may adopt Bayesian Model Averaging (BMA)⁵¹, considering a series of candidate Bayesian networks, that is, within the original methodological framework of this study, different choices may occur:

Uncertainty in network structures. Candidate networks may be generated using different structure-learning paradigms. The main categories include three approaches: the first is score-based methods, which assess the goodness of fit and complexity of a network structure by setting a scoring function; the second is constraint-based algorithms, which infer whether variables are conditionally independent through statistical tests and conditional assumptions; and the third is hybrid methods, which combine the advantages of the previous two approaches by first using constraint-based methods to obtain an initial network skeleton, and then using score-based methods within the allowed edges to search for the optimal structure^52,53. These methods may all generate reasonable network structures.

Differences in variable subsets. The choice of variable subsets may also lead to different model results. Rather than relying entirely on the complete indicator system, alternative models may be constructed using different subsets. Filter methods can be used to rank indicators individually according to statistical relevance and select the top items; wrapper-based selection methods can be used to evaluate different combinations of variables through predictive performance and determine the optimal subset; or domain-driven grouping can be applied, where indicators are grouped into logically meaningful subsets based on theoretical or practical considerations⁵⁴, such as economic indicators versus infrastructure indicators. Accordingly, the Bayesian model in this study may include all 11 indicators, only the 8 most relevant indicators, or only economic and infrastructure-related indicators, thereby forming different “variable subsets.”

Differences in prior settings. Variations in priors may also produce different model results. Structural priors are assumptions made about the network structure itself before modeling; parameter priors are assumptions made about conditional probability distributions or parameter settings after the network structure is determined^51,55. These differences will all influence the model results and can therefore be considered part of the family of candidate models.

Differences in data preprocessing. Different data preprocessing methods may likewise lead to different model specifications. Discretization strategies may include equal-interval, quantile-based, or natural breaks methods; treatments of variable types may involve complete discretization or the use of conditional linear Gaussian models to retain partial continuity. For example, when discretizing GDP into “high/low” categories, one model may use the equal-interval method, while another may apply thresholds based on quantiles; these two processing approaches correspond to two different candidate models.

By constructing and evaluating such a family of candidate models, Bayesian Model Averaging can be employed to integrate the results of all models. BMA is a statistical method for handling model uncertainty, which does not rely on a single model but integrates the results of multiple reasonable models^51,55. By weighting different models according to their posterior probabilities and averaging them, BMA can provide more robust parameter estimates and predictive inferences, without relying on a single potentially misspecified model, thereby enhancing the scientific rigor of the site selection framework.

Secondly, the quality of the data used in this study still requires improvement. Differences in the granularity, accessibility, timeliness, and openness of the underlying data may lead to gaps in coverage, and inconsistencies in the time stamps of different indicator datasets. Although statistical yearbooks provide fixed annual data (for example, Jiangsu Statistical Yearbook 2023 and Suzhou Statistical Yearbook 2023), spatial data sources (such as OSM, Tianditu, and Amap) are updated in real time or in batches, with varying update frequencies. Therefore, subtle temporal discrepancies between socio-economic indicators and spatial datasets may affect the accuracy of the results, and should be minimized in future work.

Conclusion

This study integrates Bayesian probability methods with the K-means clustering algorithm and Geographic Information System (GIS) techniques to construct an evaluation indicator system for cold-chain logistics park site selection, develop a corresponding site-selection model, and perform a GIS-based suitability analysis, thereby providing practical value for spatial research in cold-chain logistics park planning. The study establishes a complete framework ranging from provincial-level city clustering to municipal-level spatial suitability evaluation, offering a more rational research approach for the scientific selection of cold-chain logistics park locations.

A Bayesian network model is introduced in this study as a robust framework for decision-making under uncertainty. By constructing the Bayesian network, the key factors influencing site selection for cold-chain logistics parks are identified and quantified, and their statistical significance is assessed. In this way, a scientifically sound and practically feasible evaluation indicator system is established.

At the same time, the K-means clustering method is applied to analyze candidate locations for cold-chain logistics parks, classifying prefecture-level cities into different development tiers to align with the hierarchical structure of logistics networks. Through comparison with Ward’s hierarchical clustering, sensitivity analysis of the K-means results, and Bayesian discriminant analysis of the site-selection clusters, the robustness of the K-means clustering method in this study is further verified. This combined approach provides a novel and scientific solution to the logistics park site-selection problem and significantly improves the reliability of the resulting site-selection scheme.

On the basis of the clustering results, one prefecture-level city from the first-tier cluster was selected as the study area for the GIS-based suitability analysis. Drawing on the specific requirements of cold-chain logistics parks and insights from domestic and international literature, sixteen influencing factors were identified and organized into three dimensions—economic, infrastructural and environmental—thereby establishing a three-tiered suitability-evaluation indicator system. Indicator weights were determined with the entropy-weight method using the GIS platform in conjunction with Microsoft Excel. Single-factor suitability analyses were then carried out in GIS through spatial queries, spatial measurements, buffer analysis and reclassification. Finally, a weighted overlay was applied to generate a composite suitability map for the site-selection evaluation.

Jiangsu Province was selected as the research area to verify the feasibility of the above research method. The results indicate that, within the first major cluster, Suzhou is the most suitable prefecture-level city for establishing a cold-chain logistics park. Subsequent single-factor and composite suitability evaluations divided the entire municipal area into five suitability zones; the optimal site for the cold-chain logistics park was ultimately identified within the highest-suitability zone.

Beyond methodological and empirical contributions, this study also carries several important implications.

At the theoretical level, by combining Bayesian network analysis with K-means clustering and GIS-based suitability evaluation, this research extends the methodological framework of cold-chain logistics park site selection. Unlike traditional approaches that rely on qualitative judgments, the proposed model introduces probabilistic reasoning and uncertainty quantification, thereby enriching theoretical understanding of how to address uncertainty in spatial decision-making. The framework can also serve as a reference for other domains such as urban and regional planning.

At the practical level, the findings provide decision-makers with a more reliable tool for cold-chain logistics park site selection. The results demonstrate that cities with higher levels of economic development, stronger cold-chain demand, and more complete infrastructure are better suited for park construction. This conclusion can assist government agencies and enterprises in resource allocation and investment decisions. Furthermore, the GIS-based suitability evaluation produces visualized outputs that directly support planning practice, ensuring that the site-selection process is both scientifically rigorous and operationally feasible.

At the future research level, a dedicated risk assessment will be required. Introducing a formal risk-assessment component would help mitigate the effects of subjective judgement and data ambiguity, thereby further improving the applicability and scientific rigor of the proposed site-selection model for cold-chain logistics parks. In addition, employing Bayesian model averaging (BMA) could help mitigate model specification uncertainty and further strengthen the robustness of the results.

In summary, this study not only refines the theoretical and methodological system of cold-chain logistics park site selection, but also provides a practical reference for promoting the sustainable development of the cold-chain logistics industry.