Introduction

Supercritical carbon dioxide (scCO₂) has emerged as a key player in green chemistry due to its unique properties, such as zero surface tension, low viscosity, high diffusivity, and tunable solubilization through adjustments in temperature, pressure, or cosolvent addition1,2. Its mild critical temperature (304.1 K) and pressure (7.4 MPa) make it an attractive and sustainable solvent across various industries, from dyeing and extraction to chromatography and cleaning3,4,5,6. In addition to being non-toxic and recyclable, scCO₂ enables efficient separation processes and the dissolution of a wide range of solutes, although its low polarity sometimes requires cosolvent enhancement7,8.

In the pharmaceutical sector, scCO₂ has attracted attention as a green alternative to organic solvents, providing an effective medium for controlling drug solubility, facilitating particle formation, and enabling efficient supercritical fluid processing9,10. Applications include drug extraction, purification, crystal formation, and advanced drug delivery systems (DDSs) such as RESS, SAS, and PGSS methods. These technologies have the potential to reduce drug doses and administration frequency, enhance patient compliance, and support cleaner, safer production processes making scCO₂ a valuable tool for next-generation pharmaceuticals. Understanding the solubility of drugs in scCO₂ is essential because solubility directly affects the efficiency of supercritical processes, the stability and performance of DDSs, and the feasibility of using scCO₂ as a solvent, antisolvent, or solute medium11,12,13. Given that many current and pipeline drugs are poorly soluble (BCS class II and IV), enhancing their solubility in scCO₂ is critical for efficient particle formation, improved processability, controlled release profiles, and stable formulations, all of which are key priorities in pharmaceutical innovation14,15.

While experimental determination of drug solubility in scCO₂ provides vital data for process design, it is often costly, time-consuming, and sometimes impractical under diverse conditions of temperature and pressure. To address these challenges, researchers have developed various simulation models, including correlation models, thermodynamic models, and equations of state (EoSs), which allow for more rapid, cost-effective, and flexible prediction of drug solubility16,17,18,19,20,21,22,23. Thermodynamic models, EoS approaches, and empirical correlations have long been used to predict drug solubility in scCO₂, but they come with notable limitations. These models often rely on simplifying assumptions and idealizations that can compromise accuracy, especially when applied to complex or structurally diverse compounds. Empirical correlations, while simpler to apply, are typically system-specific and struggle to generalize across different datasets. Moreover, many of these traditional models require detailed knowledge of system parameters and involve computationally intensive, iterative calculations, making them less practical for large-scale applications. In contrast, machine learning models can directly learn complex, nonlinear relationships from data without relying on predefined physical equations. This allows them to achieve higher predictive accuracy and better generalization across a wide range of drug-solvent systems. Machine learning approaches enable significantly faster predictions compared to traditional experimental or simulation-based methods. While experimental solubility measurements in scCO₂ can take hours to days per condition, trained ML models can generate predictions in seconds to minutes for thousands of drug solvent condition combinations, depending on dataset size and model complexity. This rapid turnaround, combined with flexibility in handling diverse and heterogeneous datasets and the ability to include critical drug properties as input features, makes ML a powerful tool for efficient solubility estimation and process optimization.

Abdallah El Hadj et al. introduced a hybrid modeling strategy that integrates artificial neural networks (ANN) with particle swarm optimization (PSO) to estimate the solubility of solid drugs in scCO₂. Their ANN–PSO model demonstrated superior predictive capability compared to traditional density-based models and thermodynamic equations of state24. Similarly, Baghban et al. applied a least squares support vector machine (LSSVM) approach to forecast the logarithm of the solubility of 33 pharmaceutical compounds in scCO₂, utilizing key input variables such as temperature, pressure, CO₂ density, molecular weight, and melting point. Employing a radial basis function kernel, their LSSVM model achieved outstanding results with an average absolute relative deviation (AARD) of 5.61% and a coefficient of determination (R²) of 0.9975, outperforming eight established empirical correlations25. Sodeifian et al. examined the solubility behavior of six drugs, including anti-HIV, anti-inflammatory, and anti-cancer agents, using four different modeling paradigms: cubic equations of state (SRK and modified-Pazuki), semi-empirical models (such as those proposed by Chrastil, Mendez-Santiago–Teja, Sparks et al., and Bian et al.), the regular solution theory with Flory–Huggins interaction parameters, and artificial neural networks. Their findings revealed that the ANN model exhibited the highest accuracy across all metrics (AARD, R², F-value), outperforming the other approaches in reproducing the experimental solubility values in arithmetic scale26. In another study, Euldji et al. developed a quantitative structure–property relationship (QSPR) model enhanced with artificial neural networks to estimate drug solubility in scCO₂. The study compiled a comprehensive dataset consisting of 3971 experimental data points from 148 drug-like compounds. Thirteen features comprising eleven molecular descriptors alongside temperature and pressure were used as inputs. The ANN model, structured as 13–10–1 and trained via Bayesian regularization (trainbr) with a log-sigmoid activation function, achieved strong predictive performance with AARD = 3.77%, RMSE = 0.5162, and a correlation coefficient r = 0.976127. Furthermore, Euldji et al. also conducted a comparative assessment of seven meta-heuristic optimization algorithms for tuning the hyperparameters of a hybrid QSPR–Support Vector Regression (SVR) framework. Based on a dataset of 168 drug compounds and 4490 experimental data points, the study found that the hybrid HPSOGWO–SVR model delivered the most accurate solubility predictions, achieving an impressively low AARD of 0.706%, as validated through both statistical indices and graphical analysis28. Makarov et al. investigated the prediction of drug-like compound solubility in scCO₂ using machine learning (ML) approaches and compared them to a theoretical method based on classical density functional theory (cDFT). Two ML models based on the CatBoost algorithm were developed: one using alvaDesc descriptors and another using CDK descriptors plus drug melting points. The CatBoost-alvaDesc model showed strong predictive performance on 187 drugs, achieving an AARD of 1.8% and RMSE of 0.12 log units29.

In this work, we predicted the solubility of 68 different drugs in scCO₂, using newly generated experimental data obtained by the authors and literature, and applied four advanced machine learning models: CatBoost, XGBoost, LightGBM, and Random Forest. Unlike previous studies that primarily relied on molecular descriptors or metaheuristic optimization techniques, our approach integrates critical drug-specific properties including critical temperature (Tc), critical pressure (Pc), acentric factor (ω), molecular weight (MW) and melting point (Tm) alongside commonly used state variables such as temperature (T), pressure (P), and density (ρ). This comprehensive set of input parameters allowed us to capture more nuanced relationships influencing solubility. The workflow involved systematic data preprocessing, hyperparameter tuning using mean square error (MSE) minimization, and performance evaluation through 10-fold cross-validation to ensure model robustness. Furthermore, we employed detailed statistical and graphical error analyses, complemented by outlier detection using William’s plot, to rigorously define the applicability domain of the developed XGBoost model. Overall, this study not only advances predictive modeling for drug solubility in scCO₂ but also provides a practical tool for experimentalists. The developed model is predictive within the range of solubilities and conditions considered in this work, enabling more reliable design and optimization of supercritical fluid processes, and represents a clear improvement over earlier approaches.

Data collection

In this research, a total of 1726 experimental data points detailing the solubility of a set of drugs (Sixty-eight) in scCO2 were compiled from previously published studies. Table 1 lists the names of the drugs used in this study, the number of data points for each, and the sources from which the data were collected Fig. 1 also shows the distribution of the input and output features of the collected database. According to these figures, it can be seen that the amassed measurements cover comprehensive operational conditions. Table 2 provides a detailed statistical summary of the dataset, including parameters such as minimum, maximum, mean, median, skewness, and kurtosis.

Table 1 Names of drugs used in this study, number of data points for each drug, and sources.
Full size table

Statistical assessment of dataset

In this work, we used the input parameters T, P, Tc, Pc, ρ, ω, MW and Tm to predict the solubility of drugs in scCO2.

Fig. 1
figure 1

Histogram plot demonstrating the distribution of the gathered database.

Full size image
Table 2 Summary description of the performed database.
Full size table

Models development

Random forest (RF)

Random Forest (RF) is an influential ensemble-based machine learning technique developed by Leo Breiman in 200192. It operates by constructing a large collection of decision trees during training and combining their outputs to improve predictive accuracy. For regression tasks, RF computes the average of predictions from all trees, while for classification, it selects the most frequent class label. Two central mechanisms underpin its effectiveness: bootstrap sampling where different subsets of the data are randomly drawn with replacement to train each tree, and randomized feature selection, in which only a random subset of features is considered at each split. These strategies help reduce model variance, enhance generalization, and mitigate overfitting, particularly when dealing with high-dimensional or complex datasets.

In regression settings, each tree yields a numeric prediction, and the RF aggregates these outputs by averaging. The trees are typically built using the CART (Classification and Regression Trees) methodology, with optimization often based on minimizing the mean squared error93. One of RF’s advantages is that it functions effectively without the need for scaling or normalizing the input features, making it highly accessible and practical. Additionally, RF can estimate feature importance by analyzing the increase in prediction error when individual features are permuted, using out-of-bag samples for unbiased assessment. However, despite its strengths, RF can face limitations such as reduced performance with noisy datasets, sensitivity to class imbalance, and high computational costs when dealing with many large trees94,95.

Extreme gradient boosting (XGBoost)

Extreme Gradient Boosting (XGBoost) is a high-performance ensemble learning algorithm that extends the gradient boosting technique with several enhancements aimed at increasing both accuracy and efficiency96. It constructs decision trees in sequence, where each new tree is trained to minimize the errors made by the previous ones. Unlike standard gradient boosting, XGBoost incorporates a second-order approximation of the loss function, utilizing both gradients and Hessians to improve the precision of model updates97. This second-order optimization allows the model to better capture complex patterns and nonlinear relationships in the data, making it especially effective for structured datasets. XGBoost stands out due to its scalability, ability to manage missing values natively, and high performance across diverse machine learning applications. The model employs a greedy search strategy to determine optimal splits in each tree and aggregates many shallow decision trees, specifically CARTs (Classification and Regression Trees), to form a strong predictive model. Because its hyperparameters (such as learning rate, regularization strength, and tree depth) interact with one another, careful tuning is critical to achieving reliable results without excessive computation. While XGBoost is renowned for its accuracy and robustness, its reliance on numerous decision trees may hinder interpretability, making the internal decision-making process less transparent than simpler models97,98,99.

Categorical boosting (CatBoost)

CatBoost (Categorical Boosting) is a cutting-edge gradient boosting algorithm developed to natively handle categorical variables with high accuracy and minimal preprocessing100. Unlike traditional models that require techniques such as one-hot encoding to transform categorical data, CatBoost converts these features using target-based statistics while employing a special strategy called ordered boosting to prevent target leakage. This approach ensures that the model uses only past information when computing these statistics, which safeguards the training process against data leakage and helps produce more generalizable results. Built on the gradient boosting principle, CatBoost trains an ensemble of decision trees sequentially, where each new tree corrects the errors of the previous ones. Its use of symmetric trees, combined with optimized depth control and learning rate settings, allows it to strike a balance between flexibility and regularization101.

What makes CatBoost particularly advantageous is its ability to deliver high predictive power on datasets with mixed feature types, including high-cardinality categorical variables and sparse data. It is designed to work effectively with minimal data preprocessing and can accept raw data in various formats. Moreover, its architecture is engineered to mitigate overfitting through mechanisms like depth regulation and refined boosting techniques102,103.

Light gradient boosting machine (LightGBM)

LightGBM (Lightweight Gradient Boosting Machine), introduced by Microsoft in 2017, is a highly efficient gradient boosting framework designed to improve training speed, reduce memory usage, and enhance prediction accuracy104.Unlike traditional GBDT methods such as XGBoost, which rely on pre-sorted algorithms, LightGBM employs a histogram-based algorithm that bins continuous values into discrete intervals, significantly reducing computational complexity and memory requirements. A key innovation of LightGBM is its use of a leaf-wise tree growth strategy, where the algorithm splits the leaf with the highest potential to reduce error, as opposed to growing trees level by level. To control overfitting, LightGBM imposes a maximum depth constraint on trees. Additionally, LightGBM supports distributed training, enabling scalability for large datasets, and it accommodates various objective functions, including those for regression, classification, and ranking. Two core techniques further set LightGBM apart: Gradient-based One-Side Sampling (GOSS) and Exclusive Feature Bundling (EFB). GOSS prioritizes data points with large gradient values, which are more informative for learning, while randomly sampling from the remainder, thus reducing the volume of training data without sacrificing model accuracy. EFB addresses high-dimensional sparse datasets by combining mutually exclusive features those unlikely to be non-zero at the same time into a single bundled feature, thus reducing dimensionality and accelerating computation. LightGBM’s innovations not only lead to faster training and lower memory overhead, but also maintain or even improve model accuracy compared to traditional boosting methods104,105,106,107.

Predictive analytics

Fine-tuning the hyperparameters of each model is essential for achieving high predictive accuracy. Effective hyperparameter optimization enables each model to perform optimally on the given dataset. In this study, we utilize the Mean Squared Error (MSE) as the objective function to guide the hyperparameter tuning process. By minimizing the MSE, we determine the most suitable set of hyperparameters for each model.

Statistical error evaluation

The models’ accuracy was assessed by comparing the predicted drug solubility in scCO₂ (\(\:{y}_{pred}\)) with the corresponding experimental values (\(\:{y}_{exp}\)). To comprehensively evaluate model performance, several statistical error analyses were conducted, as detailed in the following sections:

Mean Square Error (MSE)

$$\:MSE=\frac{1}{n}\sum_{i=1}^{n}{\left({y}_{i,\:pred}-{y}_{i,\:exp}\right)}^{2}$$
(1)

Mean Absolute Error (MAE)

$$\:MAE=\frac{1}{n}\sum_{i=1}^{n}\left|{y}_{i,\:pred}-{y}_{i,\:exp}\right|$$
(2)

Standard Deviation (SD)

$$\:SD=\sqrt{\frac{{\sum}_{i=1}^{n}{\frac{\left({y}_{i,\:exp}-{y}_{i,\:pred}\right)}{{y}_{i,\:exp}}}^{2}}{n-1}}$$
(3)

Coefficient of Determination (R2)

$$\:{\varvec{R}}^{2}=1-\frac{{\sum}_{\varvec{i}=1}^{\varvec{n}}{\left({\varvec{y}}_{\varvec{i},\:\varvec{e}\varvec{x}\varvec{p}}-{\varvec{y}}_{\varvec{i},\:\varvec{p}\varvec{r}\varvec{e}\varvec{d}}\right)}^{2}}{{\sum}_{\varvec{i}=1}^{\varvec{n}}{\left({\varvec{x}}_{\varvec{i},\varvec{e}\varvec{x}\varvec{p}}-{\stackrel{-}{\varvec{x}}}_{\varvec{i},\:\varvec{e}\varvec{x}\varvec{p}}\right)}^{2}}$$
(4)

Results and discussion

To evaluate the models’ ability to predict drug solubility in scCO₂, both statistical indicators and graphical assessments were employed. The outcomes are discussed in the subsequent subsections.

Table 3 summarizes the performance of four machine learning models (CatBoost, RF, LightGBM, and XGBoost) in predicting drug solubility in supercritical CO₂, based on several statistical parameters. Across both training and test datasets, XGBoost and CatBoost consistently achieved the best results, with the lowest MSE and MAE, as well as the highest R². For example, XGBoost showed an almost perfect fit in the training set (MSE ≈ 1 × 10⁻⁴, R² = 0.99999), and it maintained strong generalization ability on the test set (R² = 0.99013), outperforming the other models. CatBoost also delivered highly accurate predictions with test R² = 0.98386 and balanced performance between training and testing. In contrast, LightGBM showed relatively larger errors and wider variability, indicating lower robustness under test conditions.

The inclusion of 95% confidence intervals (CIs) and p-values provides further insight into the reliability and statistical significance of these results. Narrow CIs for XGBoost and CatBoost, particularly in MSE and MAE, confirm that these models produce stable predictions with minimal variability across different subsets of the data. On the other hand, LightGBM exhibited wider CIs, suggesting greater sensitivity to fluctuations in the dataset. The extremely small p-values (close to zero in all cases, often < 1e-300) demonstrate that the observed correlations between input variables and solubility are statistically significant and not due to random chance. Together, these findings show that XGBoost, followed closely by CatBoost, offers the most accurate, consistent, and statistically reliable predictions among the models evaluated.

Table 4 presents the average absolute relative deviation (AARD) for the four evaluated models, providing a measure of their predictive accuracy across the training, test, and total datasets. The XGBoost model exhibited the lowest AARD values (0.01782 for training, 0.30635 for test, and 0.07566 overall), indicating superior accuracy compared to CatBoost, RF, and LightGBM. CatBoost and RF also performed reasonably well, while LightGBM showed the highest deviations, particularly on the test set (AARD = 1.5776), reflecting less reliable predictions. It is important to note that the reported AARD values appear large due to the wide solubility range in the dataset (0.0007 to 13.016), and the deviations generally decrease as the solubility increases, highlighting improved predictive performance for compounds with higher solubility values.

Table 3 Model accuracy evaluation using statistical indicators in the present study.
Full size table
Table 4 Assessing the accuracy of models using AARD.
Full size table

Graphical error analysis

Graphical error analysis is a powerful tool for assessing model performance, especially when comparing the predictive accuracy of multiple models. In this study, several graphical methods were utilized to visualize and demonstrate the effectiveness of the developed models.

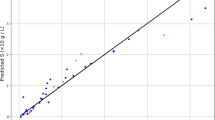
The cross plots provide a visual comparison between the predicted (Pred) and experimental (Exp) values, using the 45° diagonal line as a benchmark for perfect prediction. The predictive power of a model is reflected in how tightly its data points align with this reference line (45° diagonal line). As shown in Fig. 2, both CatBoost and XGBoost display a strong correspondence between predicted and measured solubility values across the training and testing sets. Only a few data points show noticeable deviation from the X = Y line. The dense concentration of points along the 45° line for these two models underscores their excellent performance in capturing the solubility patterns of the system, supporting the statistical findings reported in Table 3.

Fig. 2
figure 2

Cross-plots used to assess model predictions of drug solubility in scCO₂.

Full size image

The error distribution plot provides a visual overview of the residual differences between predicted and experimental values, plotted against the corresponding experimental data points. In this type of plot, a tighter clustering of points near the horizontal axis (Y = 0) indicates lower prediction errors and thus stronger model performance. The x-axis represents the experimental measurements, while the y-axis shows the residuals. As shown in Fig. 3, the XGBoost model exhibits the narrowest spread of error values across both the training and test datasets, highlighting its superior predictive accuracy compared to the other models.

Fig. 3
figure 3

Residual error distribution plots for the models predicting drug solubility in scCO₂.

Full size image

Figure 4 depicts the cumulative frequency versus residual error for each evaluated model. This graphical representation shows the proportion of data points within defined error ranges, providing insight into the predictive reliability of each model. A steeper incline in the cumulative curve indicates that a larger proportion of predictions fall within a narrow error range, suggesting higher model precision. As shown, the XGBoost model outperforms the others, with nearly 90% of its predicted values exhibiting residual errors below 0.05, underscoring its high predictive consistency.

Fig. 4
figure 4

Comparison of cumulative residual frequencies among the developed models.

Full size image

Figure 5 provides a comparative analysis of the prediction errors for the models assessed in this study. These errors reflect the discrepancies between the predicted and experimental solubility values. As illustrated, the XGBoost model demonstrates a narrower error range and superior accuracy in predicting solubility.

Fig. 5
figure 5

Evaluation of model error behavior in solubility prediction tasks.

Full size image

Group error plots are an effective method for evaluating the performance of models across a range of input features. In Fig. 6, these plots are presented for all models in relation to key input parameters: Tc, Pc, ρ, ω, MW, Tm, and the operational conditions of temperature and pressure. A visual comparison reveals that the XGBoost model consistently produces smaller prediction errors, demonstrating its superior accuracy compared to the other models.

Fig. 6
figure 6

Error distribution by input features for all proposed models.

Full size image

Model trend analysis

Trend analysis provides a useful approach to explore how solubility responds to variations in input parameters. In this study, the XGBoost model, identified as the most accurate among the developed models, was employed to predict how solubility evolves with changes in density and temperature. Figure 7 illustrates the solubility behavior of hydroxychloroquine sulfate (HCQS) in scCO₂ as a function of temperature and scCO₂ density. As depicted, solubility rises with both increasing temperature and density trends that the XGBoost model accurately captured. Moreover, the close alignment between the experimental measurements and the model’s predictions, as seen in the figure, further validates the strong predictive capability of the XGBoost model.

Fig. 7
figure 7

HCQS solubility in scCO2 versus density. Symbols are experimental data points. Solid lines are calculated from the XGBoost model.

Full size image

External validation and generalization assessment of drug solubility predictions in scCO₂

We collected gliclazide solubility data from Wang et al.108 and performed an external validation using gliclazide as an independent drug, which was removed from the training dataset. The solubility was predicted at three temperatures (308, 318, and 328 K) across a pressure range of 100–180 bar. The results showed that the XGBoost model achieved the lowest MSE of 0.00022 and an MAE of 0.01282, demonstrating excellent accuracy in capturing the solubility behavior of a completely unseen drug. These findings confirm that the proposed model is highly generalizable, and its performance aligns with the objectives of one-drug-out cross-validation, validating the robustness and practical applicability of our approach.

Sensitivity analysis

Figure 8 displays SHAP summary plots that clarify how each input variable influences the XGBoost model’s estimation of drug solubility in scCO2. The plot on the right ranks features by their mean absolute SHAP values, reflecting their overall contribution to the model’s predictions irrespective of whether the effect is positive or negative. A higher mean SHAP value signifies a greater influence on the model’s output. The left-hand plot offers a pointwise breakdown of SHAP values, mapping how variations in individual feature values impact the predicted solubility. Feature values are color-coded, transitioning from green (low values) to purple (high values), allowing for intuitive visualization of value-dependent effects.

Among all features analyzed, Tm, P, andPc stand out with the most substantial influence on solubility predictions. The model identifies a strong positive relationship between pressure and solubility, aligning with fundamental thermodynamic laws such as Henry’s law, which indicates that higher pressure generally increases gas solubility in liquids. Likewise, higher melting points are associated with greater solubility estimates, likely due to their role in modulating solid-state properties that affect dissolution behavior in supercritical media.

Other variables like Tc and the ω also exhibit non-negligible effects. The acentric factor, which captures molecular shape and polarity deviations from ideal behavior, plays a role in how well drug molecules interact with scCO₂. Conversely, MW and ρ appear to have a comparatively limited impact under the studied conditions, implying their influence on solubility is either indirect or less significant in this modeling context. Notably, T contributes positively to solubility, indicating that as temperature rises, so does the predicted solubility. This trend is characteristic of scCO₂ systems in the most ranges, where higher temperatures enhance solute volatility and diffusivity, often outweighing density-related effects.

In summary, the SHAP results offer clear, model-agnostic explanations of the feature contributions, reinforcing the physical plausibility of the XGBoost model’s internal logic. The dominant features identified by the model correspond well with established thermodynamic expectations, supporting its validity for solubility prediction in supercritical CO₂ systems.

Fig. 8
figure 8

Evaluation of the input parameters’ impact on solubility.

Full size image

Determining outliers and applicability domain of a technique

The ‘Leverage Statistical Approach’ is a widely adopted and efficient method for detecting potential anomalies data points that significantly differ from the rest of the dataset and for determining the validity range of established correlations. This technique generates a graph known as the “Williams Plot,” which is constructed by defining the Hat Matrix (H) and Standardized Residual (SR) (Fig. 9). The critical parameters required to construct this plot are calculated using the following formulas109,110:

• Hat matrix (H):

$$\:H=X{\left({X}^{T}\:X\right)}^{-1}{X}^{T}\:$$
(5)

Here, XT represents the transpose of the matrix X, which is a (y × d) matrix. In this case, y refers to the number of data points, and d refers to the number of input variables used by the model.

• Leverage limit (H*):

$$\:{H}^{*}=\frac{3\times\:(d+1)}{y}$$
(6)

• standardized residuals (SR):

$$\:{R}_{i}=\frac{{z}_{i}}{\sqrt{MSE\left(1-{H}_{ii}\right)}}$$
(7)

The variables zi and Hii represent the error and hat values associated with the i-th data point, respectively111. The region defined by 0 < H < H* and − 3 < SR < 3 indicates the valid domain where the model’s predictions are statistically reliable (valid data region). As shown in Fig. 9, the majority of the data points (97.68%) fall within this range, confirming the strong predictive performance of the XGBoost model. However, points falling outside this domain, specifically in the areas where SR > 3 or SR < −3 and H is within the valid range, are classified as suspicious and are flagged as bad leverage points, accounting for 1.68% of the data. Additionally, points that fall within the range of H* < H and − 3 < SR < 3 are categorized as good high leverage points and represent 0.63% of the data. Given that a significant portion of the data points are valid, it shows that the XGBoost model is very reliable for predicting drug solubility in scCO₂.As a complementary point in optimizing the parameters in the related sections, adjustable parameters in EoSs or semi-empirical models may be obtained by different methods including various algorithms like nonlinear regression methods [112-113].

Fig. 9
figure 9

William’s plan for a leveraged review of the results of the XGBoost modelling.

Full size image

Conclusions

In this study, we employed four machine learning models, CatBoost, XGBoost, LightGBM, and RF, to predict the solubility of a diverse set of drugs in scCO₂. Our dataset, compiled from 68 different drugs, included a total of 1,726 data points. To develop the predictive models, we used key input variables such as T, P, Tc, Pc, ρ, ω, MW, and Tm.

Based on statistical error metrics and graphical analyses, the XGBoost model consistently outperformed the other approaches, exhibiting the lowest prediction errors and highest accuracy in estimating solubility. Residual error analysis across the full range of input parameters further confirmed that XGBoost maintained superior performance regardless of temperature, pressure, or density ranges. Additionally, the model captured expected physical trends such as the increase in solubility with rising density at constant temperature and the enhancement of solubility with increasing temperature, reflecting its robustness and reliability.

SHAP analysis highlighted the Tm as the most influential factor among the input variables. Finally, the application of the Leverage approach for outlier detection showed that the majority of the data points fell within the defined applicability domain on the Williams plot, underscoring the reliability and generalizability of the XGBoost model.