Torsional behaviour of high strength steel (S700) rectangular hollow section stub column

Abstract

This study aims to investigate the torsional behavior of high strength steel (S700) rectangular hollow section stub columns through comprehensive finite element analysis using ABAQUS. The influence of key geometric parameters, including cross-section aspect ratio and wall thickness, on torsional performance is evaluated. The numerical models were validated in two stages: first, the torsional loading scheme was benchmarked against carbon steel rectangular hollow section tests, achieving a strength prediction accuracy of within 3.0%; secondly, the adopted high strength steel material model was verified against axial compression tests with strength predictions within 4.0% of experimental results. The parametric results demonstrate that members with higher aspect ratios (1:1) exhibit superior torsional resistance, with increases up to 32% compared to lower aspect ratio Sect. (1:5), while increasing wall thickness consistently enhances torsional capacity by approximately 9–10 kNm per millimeter increase in thickness across all configurations. Benchmarking against current design specifications, including Eurocode EN 1993-1-5, American code AISC 360 − 10 and the AISI S100 standard with its Direct Strength Method, reveals that existing codes tend to underestimate torsional capacity for high strength steel rectangular hollow section members. These findings emphasize the potential for improved accuracy through FE-based analysis and support calibrated modifications to current design provisions. The study provides critical insights for structural optimization and the refinement of torsion design guidelines for high strength steel rectangular hollow section under pure torsional loading.

Introduction

Construction sector has experienced tremendous development in the last couple of years, mainly due to the emergence of new materials and technologies. The introduction of structural steel sections is considered a game changing material in the construction industry, as it enables safety in manufacturing, quicker construction, improves quality, and reduces environmental impacts¹. Although ordinary structural steel sections have their own benefits, inclusion of high strength steel (HSS) makes the structural members even more reliable since it possesses greater strength-to-weight ratio, high torsional strength, enhanced durability, material efficiency and economy^2,3. HSS typically refers to steel that has a yield strength of 460 MPa or more making it suitable for different applications in structural engineering including bridges, high risk buildings and the design of earthquake-resistant buildings^4,5,6,7. High strength steel has significantly evolved over the years and trends have been adopted in the manufacturing of HSS hollow sections. A wide range of HSS hollow cross-sections are available, such as rectangular hollow sections (RHS), circular hollow sections (CHS), square hollow sections (SHS). Among these RHS plays an important role in hollow steel sections as they provide a combination of strength, aesthetic appeal, and efficiency, which makes them a better choice in different engineering and construction applications⁸. Their versatility and user friendliness make them even more attractive than the other cross-sectional shapes. Growing interests in HSS as a construction material is evident from its applications in construction. Active research works have been carried out on HSS materials in the last few decades^{9,10,11,12,13,14}.

Recent advancements in structural steel research have emphasized the need to evaluate HSS tubular members, particularly under torsional loading. Studies have increasingly focused on cross-sectional geometry, residual stresses, and material nonlinearity to improve the reliability of design standards for RHS and other tubular forms. Meng and Gardner¹⁵ experimentally investigated CHS made from S700 high strength steel with various diameters and thicknesses, validating finite element (FE) models that enhanced design accuracy through bending, tensile, and beam-column tests. Liu et al.¹⁶ studied residual stress and material properties in Q690 grade hexagonal hollow sections, finding welding had minimal impact while press-barking improved strength. Chen and Young¹⁷ examined tensile behavior of cold-formed HSS tubular sections, including RHS, SHS, and CHS, noting that tubular specimens exhibited slightly higher proof stresses than tensile coupons. Liu et al.¹⁸ analyzed residual stresses and tensile strength in irregular octagonal HSS sections, reporting an 8.4% strength increase at welded corners compared to flat coupons. Huang and Zhang¹⁹ focused on lateral-torsional buckling (LTB) of HSS-RHS beam-columns, developing strain energy formulations and validating finite element results, confirming Eurocode 3 provisions effectively predict LTB behavior.

Devi and Singh²⁰ studied torsional characteristics of stainless steel semi-elliptical hollow sections, finding larger aspect ratios and thicknesses increased torque capacity, with existing design equations providing stable predictions. Singh and Sachidananda²¹ experimentally compared RHS and SHS under torsion, concluding unperforated sections have superior torsional resistance. Lu et al.²² validated finite element models of square and rectangular concrete-filled double skin steel tubular members under cyclic torsion and proposed accurate design formulas. Jůza et al.²³ investigated material nonlinearity effects on rectangular and square stainless steel frames, highlighting significant second-order effects on buckling behavior. Poursadrollah et al.²⁴ combined experiments and finite element analysis to study buckling in cold-formed rectangular and square hollow columns, finding results consistent with EN1993-1-1²⁵ standards. Hu et al.²⁶ assessed torsion in cold-formed and hot-finished RHS within steel framing systems, observing higher torsional rotations in thinner sections. Liu et al.²⁷ demonstrated that cold-working via tip-to-tip welding improved corner strength in RHS. Liu et al.²⁸ numerically studied local buckling in high strength hexagonal hollow stub columns, advocating the Continuous Strength Method (CSM) over existing code slenderness limits. Devi and Singh²⁹ further confirmed CSM’s superior accuracy for CHS strength prediction across multiple steel grades through parametric finite element analyses. Finally, Devi et. al³⁰ used validated finite element models to examine torsional behavior of HSS-CHS with varying thicknesses and grades (S700, S900), revealing new torsional slenderness limits.

Despite the increasing utilization of HSS in structural applications, significant gaps remain regarding the torsional behavior of HSS-RHS members. Extensive research has explored axial, flexural, and combined loading scenarios of HSS members, yet limited studies focus on pure torsional loading—particularly involving RHS configurations. Previous torsional investigations have largely concentrated on stainless steel or other steel types rather than HSS, or on circular hollow sections. Earlier works on torsion in RHS mainly address conventional steel grades rather than HSS. Existing design codes predominantly provide guidance for flexural and axial loadings and lack specific torsion provisions for HSS sections. Moreover, available torsion design guidelines mainly target steel grades with yield strengths below 460 MPa, whereas this study focuses on HSS with a yield strength of approximately 700 MPa, addressing an important shortcoming in available design standards.

Though prior experimental and numerical research has advanced understanding of residual stresses, fire behavior, and cold-formed steel responses, comprehensive studies examining the influence of torsion as well as parametric variations in aspect ratios and wall thicknesses are scarce. In this context, a higher aspect ratio refers to RHS cross sections where breadth and height are equal (i.e., square sections). Conversely, as the cross section becomes more rectangular, the aspect ratio decreases, indicating a lower value. The impact of such geometric variations on torsional behavior remains insufficiently quantified or benchmarked against modern design codes.

This study aims to fill these gaps by investigating the torsional behavior of HSS-RHS stub columns subjected to pure torsion across a wide range of aspect ratios and thicknesses. Finite element models validated in ABAQUS version 6.14³¹ are employed for accurate simulation of torsional response. Parametric results will be benchmarked against major design codes, including AISC 360 − 10³², Eurocode 3³³ and modified Direct Strength Method along with established torsion models, to assess their applicability and limitations for RHS-HSS. These findings are expected to provide fundamental data to aid further experimental validation and support the development of improved torsion design provisions for HSS-RHS members.

Finite element modelling

The present study aims to investigate the torsional behavior of HSS-RHS stub columns subjected to pure torsional loading using finite element analysis. Due to the limited availability of experimental data and laboratory facilities for torsional testing of HSS-RHS members, the study is primarily based on numerical simulations conducted using ABAQUS software.

Stress-strain data for S700 provided by Ma³⁴ was adopted for the present study. Specifically, the coupon test result of S700 cold-formed HSS hollow sections. Table 1; Fig. 1 show the standardised material property of S700 as recommended by Ma et al.³⁵ and Ma³⁴.

Table 1 H-Series standardised material properties by Ma³⁵.

Fig. 1

Proposed standadised material property of S700.

This standardized materials property for S700 grade has been adopted in the current study as it allows us to represents the overall behavior of the steel grade, ensuring the results are applicable across different sections and thicknesses within the grade, rather than being specific to an individual cross section or thickness. For materials input in Abaqus³¹, the give stress-strain data³⁵ was converted into true stress (σ_true) and true plastic strain ($\:{\epsilon\:}_{true}^{pl}$) using Eqs. (1) & (2).

$$\:{\sigma\:}_{true}=\:{\sigma\:}_{engg}(1+{\epsilon\:}_{engg})$$

(1)

$$\:{\epsilon\:}_{true}^{pl}={ln}\left(1+{\epsilon\:}_{engg}\right)-\:\frac{{\sigma\:}_{true}}{{E}_{0}}$$

(2)

where, $\:{\sigma\:}_{engg}$ = engineering stress, $\:{\epsilon\:}_{engg}\:$= engineering strain and $\:{E}_{0}$ = initial Young’s modulus.

Finite element simulations were performed using ABAQUS. The cold-formed rectangular hollow section (RHS) has a cross-sectional width ‘b’ and depth ‘h’ and thickness ‘t’ and a member length ‘L’ equal to three times of its depth. Geometric imperfections were incorporated by first conducting an eigen buckling analysis, with the first mode shape employed to introduce the imperfections. Residual stresses were not included in the model, following Ma³⁴, who reported their negligible effect on the performance of high-strength steel stub columns. Previous research conducted by Singh and Singh³⁶, demonstrates that material imperfections occurring at weld joints have a negligible effect. Consequently, the present study does not account for imperfections induced by welding. Nonlinear analysis was conducted using the Static General step solver Nonlinear analysis was conducted using the Static, General step solver in ABAQUS Version 6.14. The step was configured with a time period of 1033 (corresponding to a rotation rate of 9.68 × 10^{− 4} rad/sec). The analysis employed a maximum of 10,000 increments, with an initial increment size of 0.001, a maximum increment size of 10, and a minimum increment size of 0.001. Automatic stabilization was applied to enhance solution convergence. These parameters were chosen to ensure accurate and stable simulation of the nonlinear torsional response. The sensitivity of imperfection amplitudes on the torsional response was investigated by applying various imperfection magnitudes, including t/10, t/50, t/100 and also imperfection value given by Ma³⁴. No significant differences in overall behavior were observed; therefore, an imperfection amplitude of t/100 was adopted throughout the study.

For spatial discretization, the general-purpose shell element S4R available in ABAQUS was employed. Boundary conditions were applied to simulate pure torsional loading, with one end fixed and the other subjected to a twisting moment as shown in Fig. 2. To ensure numerical accuracy, a mesh sensitivity study was performed, confirming that the mesh size recommended by Ma³⁴ (i.e., (b + h) /30) was sufficient. To implement boundary conditions, two reference points (RP) were defined at the centroid of the RHS cross-section: one at the bottom (RP-1) and one at the top (RP-2). These reference points were coupled kinematically with the nodes at the ends of the section, ensuring all degrees of freedom were constrained accordingly. Loads were applied via displacement control at RP-2, while RP-1 was fully constrained following the same procedure as³⁷.

Fig. 2

Typical cross section of rectangular hollow section (RHS).

To maintain consistency across samples, the enclosed midline cross-sectional area was approximately constant for all aspect ratios. The thickness was uniformly protruded both inward and outward from the centerline. Figure 2 depicts the typical RHS cross-section with boundary condition. Specimen length was set to three times the larger width dimension of the section. Furthermore, the outer corner radius was defined as twice the member thickness, and following the recommendation of³⁸, the corner properties were extended by twice the thickness into the flat regions on all faces.

Validation approach

The accurate simulation of structural behavior, particularly for HSS- RHS subjected to torsion, requires rigorous validation of the adopted FE modeling strategy. Given the limited experimental data available on the torsional response of HSS members, a comprehensive two-stage validation procedure was implemented. This approach separately addresses the fidelity of the loading scheme (torsional action) and the representation of material properties (HSS), thereby ensuring the robustness of subsequent parametric studies.

Validation of loading scheme (Torsional loading)

The first stage of validation focused on the accuracy of the FE model in capturing the torsional response of cold-formed carbon steel RHS members. Experimental results from Devi et al.³⁹ and Ridley⁴⁰ were selected due to their relevance to the present study. These experiments involved cold-formed carbon steel of lower grade RHS subjected to pure torsion. Figures 3 and 4 present a direct comparison between the experimental and FE-derived torque-twist curves, demonstrating acceptable agreement in both the elastic and plastic ranges. Quantitative validation is provided in Tables 2 and 3, which summarize the ratios of experimental to FE-predicted ultimate torque T_{u, exp}/T_{u, FE} and normalized torque capacities. For the specimens reported by Devi et al.³⁹, the mean ratio is 1.003 with a coefficient of variation (COV) of 3.06%. Similarly, the results for the lipped channel sections tested by Ridley⁴⁰ yield a mean ratio of 1.011 and a remarkably low COV of 0.22% respectively. These findings confirm the satisfactory accuracy and consistency achieved by the FE modeling approach under torsional loading.

Fig. 3

Validation of FEM with test result from³⁹.

Fig. 4

Validation of FEM with test result from⁴⁰.

Table 2 Comparision of Test³⁹ and FE.

Table 3 Comparision of Test⁴⁰ and FE.

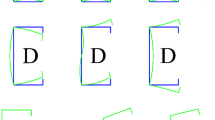
In addition to global response metrics, the FE model’s ability to replicate local deformation phenomena was assessed. Figures 5 and 6 compare the deformed shapes at failure from both experimental observations and FE simulations. The characteristic buckling patterns are faithfully reproduced in the numerical results, validating the model’s capability to capture complex instability mechanisms inherent to thin-walled closed sections under torsion.

Fig. 5

Deformed shaped of FE model by comparison with test result from³⁹.

Fig. 6

Deformed shaped of FE model by comparison with test result from⁴⁰.

Validation of material property (HSS)

The second stage of validation addressed the representation of high-strength steel material behavior within the FE framework. Experimental data from Ma³⁴ involving HSS-RHS stub columns subjected to axial compression, were utilized for this purpose. The FE models incorporated the same material parameters as given in Table 1; Fig. 1. Figure 7 illustrates the comparison between experimental and FE-predicted load vrs end shortening curves for the H-series HSS-RHS material. The comparison shows an acceptable agreement between the FE and experimental results, the slight discrepancy in the curve may be attributed due to the used of standadised material property instead of material specific data. Table 4 presents the comparison of ultimate load capacities between the experimental tests and FE simulations. The mean ratio of T_{u, exp}/T_{u, FE} is 0.964, with a COV of only 1.04%, indicating excellent agreement. The ability of the FE model to replicate observed failure modes was further verified through comparison of deformed shapes at ultimate load, as shown in Fig. 8. The numerical simulations accurately reproduce the localized wrinkling and overall shortening observed in the experiments, confirming the model’s suitability for investigating material-dominated failure mechanisms in HSS stub columns.

Fig. 7

Validation of FEM with HSS test result from³⁴.

Table 4 Comparison of Test³⁴ and FE.

Fig. 8

Deformed shaped of FE model by comparison with test result from³⁴. (a) Typical deform shape of stub column under Axial compression loading (b) FE 80 × 80 × 4.0 (c) FE 100 × 100 × 4.0 (d) FE 120 × 120 × 4.0.

The finite element models demonstrate a good agreement with experimental results, validating its accuracy in predicting the torsional response of HSS-RHS. Following this confirmation, the study employs the verified modeling approach for parametric analysis, incorporating local geometric imperfections as recommended by Ma et al.⁴¹ for HSS members while justifiably omitting residual stresses based on Ma³⁴ findings of their negligible effect on HSS stub column behavior. This validated framework enables reliable investigation of key parameters influencing torsional performance, including cross-section slenderness, material nonlinearity, geometric imperfections, and boundary conditions.

Parametric study

A comprehensive parametric investigation was conducted to evaluate the torsional response of HSS-RHS stub columns, focusing on variations in cross-sectional aspect ratio (b/h) and wall thickness (t). The geometric characteristics of the studied members are summarized in Table 1. The nomenclature for each cross-section follows the format: ‘the cross-section type-b-h-t’. For instance, RHS-80-120-1.6 denotes a rectangular hollow section with a width (b) of 80 mm, height (h) of 120 mm, and wall thickness (t) of 1.6 mm. The study encompassed four distinct cross-sections with (b/h) ratios of 1.0 (1:1), 0.67 (1:1.5), 0.4 (1:2.5), and 0.20 (1:5). To isolate the effect of aspect ratio, the area enclosed by the midline of each section was held constant for all (b/h) ratios at a given thickness. This was achieved by symmetrically adjusting the wall thickness about the cross-sectional centroid, ensuring a consistent enclosed area while varying (t). For each aspect ratio, wall thickness was incremented from 1.6 mm to 10 mm. Details of the stub columns adopted for this parametric study are provided in Table 5.

Table 5 Summary of adopted cross-sectional dimension.

Results and discussion

The findings of this parametric study are consistent with previous experimental and numerical research on torsion of closed hollow sections. The decrease in torsional resistance with decreasing aspect ratio is attributed to geometric asymmetry and stress concentrations, as commonly reported. Similarly, increasing wall thickness enhances torsional capacity and delays local buckling by improving rigidity and promoting smoother elastic-plastic transitions, in agreement with prior studies. The superior performance of square sections (aspect ratio 1:1) compared to rectangular profiles also aligns with existing theoretical and experimental analyses. This validation confirms the reliability of the FE models and the relevance of the results to extending torsion design understanding for high-strength RHS steel members.

The torsional performance of HSS-RHS stub columns is strongly influenced by their cross-sectional aspect ratio and wall thickness. Figure 9 presents representative torsional responses for various aspect ratios and thicknesses, revealing distinct behavioral trends. In general, square sections (aspect ratio 1:1) demonstrate balanced stiffness in both principal directions, leading to uniform buckling patterns and higher torsional resistance. As the aspect ratio decreases, the sections become more elongated rectangles, and their torsional behavior is characterized by increasing geometric asymmetry. This asymmetry causes stress concentrations along the longer faces and corners, which reduce torsional stiffness and ultimate strength, particularly in thin-walled specimens.

Fig. 9

Torsional behavior of RHS-HSS Stub Column with different aspect ratio.

Wall thickness is another critical factor that markedly enhances torsional capacity and stiffness by providing additional material to resist deformation and delay local buckling. Thicker walls enable smoother transitions from elastic to plastic behavior, allowing more efficient stress redistribution. Conversely, thinner walls tend to exhibit premature localized buckling, manifesting in abrupt stiffness reductions after peak torque.

The detailed effects of aspect ratio and wall thickness on torsional behavior are discussed in the following subsections. Section 4.1 analyzes the variation in torsional resistance with changing cross-sectional proportions, supported by torque-rotation responses, stress distributions, and deformation shapes. Section 4.2 focuses on the role of wall thickness in improving torsional strength, stiffness, and overall structural stability. Together, these insights provide a comprehensive understanding of the geometric and material parameters controlling torsional performance in HSS-RHS members.

Effect of aspect ratio

The aspect ratio of HSS-RHS stub columns plays a pivotal role in governing their torsional performance. Figure 10 displays representative torque-rotation curves for different aspect ratios at constant wall thickness, clearly indicating a reduction in torsional resistance as the aspect ratio decreases from 1:1 (square) to more elongated rectangular forms. The combined influence of aspect ratio and cross-sectional geometry is further elucidated in Fig. 11, while Figs. 12a-d present deformed shapes with superimposed Von Mises stress contours for various aspect ratios at peak load.

Fig. 10

Effect of cross sectional aspect ratio for same thickness.

Fig. 11

Comparative analysis of torsional response for different aspect ratios.

Fig. 12

Deformed shape for each specimen at their respective peak load.

A clear trend emerges from Fig. 11, torsional strength diminishes as the section transitions from compact (1:1) to slender (1:5) geometries. In square sections, the uniform slenderness of all four faces ensures a uniform contribution to torsional resistance and facilitates uniform stress flow, resulting in higher torsional efficiency across all thicknesses. The initial elastic response is robust, with gradual yielding and superior peak torque values compared to rectangular sections that exhibit gradual yielding.

Conversely, rectangular sections with lower aspect ratios exhibit geometric asymmetry, complicating their torsional behavior. Stress concentrations become prominent along the longer faces, especially in thinner-walled specimens, increasing susceptibility to local buckling and reducing both torsional stiffness and ultimate capacity. However, as wall thickness increases, the rigidity of these faces improves, enhancing their contribution to torsional resistance. The increment in torsional capacity with increasing thickness is more pronounced in rectangular profiles, due to the initially underutilized broader faces. Nevertheless, square sections consistently outperform rectangular ones due to their geometric balance that helps maintain uniform stress distribution and mitigates stress concentrations, predominantly near corners and edges. The qualitative differences in torsional deformation and stress patterns are vividly illustrated in Fig. 12:

• 1:1 - Symmetrical and uniform stress distribution with moderate warping and minimal stress concentration.

• 1:1.5 and 1:2.5 - Increased stress concentration along longer faces and corners, with more pronounced deformation.

• 1:5 - Significant distortion, high stress concentrations at corners and wide faces, and deformation patterns resembling thin plates under torsion, indicating substantial loss in torsional capacity and stiffness.

Quantitatively, for constant wall thickness, torsional capacity decreases by approximately 32% as the aspect ratio increases from 1:1 to 1:5, by about 15% from 1:1 to 1:2.5, and by roughly 5% from 1:1 to 1:1.5. The reduction in torsional capacity with increasing aspect ratio is more pronounced in slender sections due to their heightened susceptibility to buckling and localized deformations. These results provide clear visual and quantitative evidence that lowering the aspect ratio disrupts uniform stress distribution, leading to earlier yielding and reduced torsional effectiveness.

Effect of wall thickness

Wall thickness is a critical parameter influencing the torsional behavior of HSS-RHS stub columns. Regardless of aspect ratio, increasing wall thickness substantially enhances both torsional strength and stiffness, primarily due to the additional material available to resist buckling and enable a more uniform distribution of shear stresses. Figure 13 compares torque-twist responses for various wall thicknesses across different aspect ratios, showing that torsional capacity increases at an approximate rate of 9–10 kNm per millimeter increase in thickness, largely independent of section geometry. Thicker-walled members exhibit greater initial stiffness, which delays the onset of yielding and allows the section to sustain higher torsional moments before transitioning to nonlinear behavior. The transition from elastic to plastic deformation is smoother in thick-walled specimens, indicating more effective internal stress redistribution and reduced susceptibility to local instability or buckling. In contrast, thin-walled sections are prone to premature local buckling under elevated torsional loads. Such deformation result in earlier yielding and sharper drop in stiffness after peak torque, mainly due to slenderness of the wall and stress concentrations in critical regions.

Fig. 13

Comparative analysis of torsional response for different thickness.

Figure 14 illustrates deformed FE model shapes at peak torsional capacity for various wall thicknesses and aspect ratios. Increased thickness correlates with reduced deformation, delayed localized failure, and improved structural integrity. Thin sections display more pronounced distortions and stress concentrations near corners and wide faces, while thicker specimens maintain more uniform deformation patterns, confirming their superior torsional resistance.

Fig. 14

Deformed shape for each specimen at their respective peak load.

From a design standpoint, increasing wall thickness is an effective strategy to enhance torsional performance, offering improved ductility, strength, and stability under torsion. However, these benefits must be weighed against increased material costs, weight, and fabrication considerations.

Design guidelines for torsion in HSS-RHS

The design for torsional resistance in HSS-RHS, is not comprehensively addressed in various design guidelines. However, the American Standard ANSI/AISC 360 − 16³² provides design guideline for circular and rectangular hollow section applicable for various steel grade mainly upto 460 MPa. This section delineates the available design equations from the American code for HSS-RHS and references adopted formulations from the Eurocode. Additionally, it presents Direct Strength Method (DSM) equations proposed by various researchers^39,42,43.

ANSI/AISC 360 − 16

The AISC 360 − 16³² Specification for Structural Steel Buildings offers a methodology for determining ‘The nominal torsional strength (T_n)’ of rectangular hollow sections. The nominal torsional strength is expressed as:

$$\:{T}_{n}\:=\:{F}_{cr}\:\times\:C$$

(3)

Where:

• F_cr = critical stress, accounting for material and geometric properties.

• C = torsional constant, reflecting the section’s resistance to torsion.

For a rectangular hollow section, the torsional constant (C) can be approximated using the following equation:

$$\:C\:=2\left(B-t\right)\left(H-t\right)t-4.5\left(4-\pi\:\right){t}^{3}$$

(4)

Where:

• B = breadth of the shorter side of the section.

• H = height (or width) of the longer side of the section.

• t = thickness of the section walls.

The critical stress (F_cr) is determined based on the material properties and the section’s susceptibility to buckling under torsional loads. F_cr can be calculated as:

$$\:{F}_{cr}=\left\{\begin{array}{c}0.6{F}_{y},\:\:h/t\le\:2.45\sqrt{E/{F}_{y}}\\\:\frac{0.6{F}_{y}(2.45\sqrt{E/{F}_{y}}}{\left(\frac{h}{t}\right)},\:\:2.45\sqrt{E/{F}_{y}}\:<h/t\le\:3.07\sqrt{E/{F}_{y}}\\\:\frac{0.458{\pi\:}^{2}E}{\left(\frac{h}{t}\right)},\:\:3.07\sqrt{E/{F}_{y}}<h/t\le\:260\end{array}\right.$$

(5)

By calculating both F_cr and C, the nominal torsional strength (T_n) of a given HSS-RHS can be calculated.

EN 1993-1-5:2012

The torsional capacity (T_u) of RHS can be evaluated based on Eurocode 1993-1-5:2006³³ which accounts for both yield torque and the shear resistance of the web plate. The design torsional resistance is given by Eq. (6).

$$\:{T}_{u}={\chi\:}_{w}{T}_{y}$$

(6)

where:

$\:{\chi\:}_{w}\:$is the reduction factor representing the contribution of the web plate to shear buckling resistance.

T_y is the yield torque, calculated as Eq. (7).

$$\:{T}_{y}=2{A}_{e}{\tau\:}_{y}$$

(7)

Here, A_e is the area enclosed by the midline of the section and $\:{\tau\:}_{y}=\frac{{f}_{y}}{\sqrt{3}}$ is the shear yield stress for a material yield with strength f_y.

The value of $\:{\chi\:}_{w}$ depends on the torsional slenderness parameter $\:{\lambda\:}_{w}$ and is defined by the expressions given in Eq. 8 as given in Table 5.1 of³³

$$\:{\chi\:}_{w}=\left\{\begin{array}{c}\eta\:,\:\:{\lambda\:}_{w}<0.83/\eta\:\\\:\frac{0.83}{\eta\:},\:\:0.83/\eta\:\:\le\:\:{\lambda\:}_{w}<1.08\\\:\frac{1.35}{0.7+{\lambda\:}_{w}},\:\:{\lambda\:}_{w}>1.08\end{array}\right.$$

(8)

For steels with yield strength exceeding 460 MPa, the value of η is taken as 1.0 as recommended in³³.

Direct strength method for torsional loading

DSM, initially developed by Schafer and Pekoz⁴⁴, has become a pivotal approach in the design of cold-formed steel structures. Unlike traditional methods that rely on effective width calculations, DSM utilizes elastic buckling analyses to predict the strength of members, considering local, distortional, and global buckling modes. Building upon this foundation, Bian et al.⁴³ introduced DSM equations specifically addressing torsional loading in cold-formed lipped channel sections. Further advancements were made by Devi et al.³⁹, who proposed a modified DSM equation tailored for SHS fabricated from carbon steel grade YSt-310 under torsional loading. This model introduced a torsional slenderness limit of 0.776 to distinguish between stocky and slender sections. For stocky sections, a two-stage linear expression was proposed, while slender sections were addressed using a conventional format, as delineated in Eq. 9.

$$\:\left({T}_{u,DSM}/{T}_{y}\right)=\left\{\begin{array}{c}1+\left(3.43-5.67{\lambda\:}_{T}\right)\left(\frac{{\sigma\:}_{u}}{{\sigma\:}_{y}}-1\right),\:\:{\lambda\:}_{T}\le\:0.358\\\:1+\left(2.6-3.35{\lambda\:}_{T}\right)\left(\frac{{\sigma\:}_{u}}{{\sigma\:}_{y}}-1\right),\:\:{0.358\:<\lambda\:}_{T}\le\:0.776\\\:\frac{2.66}{{{\lambda\:}_{T}}^{0.49}}-\frac{1.84}{{{\lambda\:}_{T}}^{0.35}},\:\:{\lambda\:}_{T}>0.776\end{array}\right.$$

(9)

Expanding the applicability of proposed DSM, Devi et al.⁴⁵ further developed a three-stage expression based on non-linear regression analysis employing the least squares method. This formulation aimed to predict the torsional strength of lean duplex stainless steel semi-elliptical hollow sections, establishing a torsional slenderness limit of 0.68 to differentiate between stocky and slender sections, as presented in Eq. 10.

$$\:\left({T}_{u,DSM}/{T}_{y}\right)=\left\{\begin{array}{c}1+\left(0.13-0.27{\lambda\:}_{T}\right)\left(\frac{{\sigma\:}_{u}}{{\sigma\:}_{y}}-1\right),\:\:{\lambda\:}_{T}\le\:0.548\\\:\left(1.18-3.35{\lambda\:}_{T}\right),\:\:{0.548\:<\lambda\:}_{T}\le\:0.91\\\:\frac{3.42}{{{\lambda\:}_{T}}^{0.38}}-\frac{2.61}{{{\lambda\:}_{T}}^{0.27}},\:\:{\lambda\:}_{T}>0.91\end{array}\right.$$

(10)

Subsequently, Devi et al.⁴² extended this methodology to encompass HSS-CHS of varying grades, including S700, S900, and S1100. A revised torsional slenderness limit of 0.726 was proposed to distinguish between stocky and slender sections. The modified DSM equation, formulated through least squares regression analysis, is encapsulated in Eq. 11.

$$\:\left({T}_{u,DSM}/{T}_{y}\right)=\left\{\begin{array}{c}1+\left(0.27-3.19{{\lambda\:}_{T}}^{3}\right)\left(\frac{{f}_{u}}{{f}_{y}}-1\right),\:\:{\lambda\:}_{T}\le\:0.726\\\:1+\left(0.54-0.73{\lambda\:}_{T}\right),\:\:{0.726\:<\lambda\:}_{T}\le\:1\\\:\frac{2}{{{\lambda\:}_{T}}^{0.52}}-1.18,\:\:{\lambda\:}_{T}>1\end{array}\right.$$

(11)

These progressive developments in DSM for torsional loading underscore the method’s adaptability and precision in addressing the complexities of cold-formed steel design.

Reliability analysis

The reliability of prevailing design standards, including EN 1993-1-1, AISC 360 − 16, and DSM, was evaluated through statistical methods aligned with the guidelines of⁴⁶. The same method was utilized by various researchers^39,42,47. This assessment aimed to determine the applicability and safety margins of existing design methodologies.

The reliability index (β) for each design equation was computed using a statistical expression that incorporates several key parameters. Specifically, Pm represents the mean ratio of experimental results to design predictions, Mm denotes the mean ratio of measured yield stress to nominal yield stress, and Fm signifies the mean ratio of actual section modulus to the specified value. The corresponding coefficients of variation are denoted as V_P, V_M and V_F respectively. Additionally, V_Q represents the coefficient of variation for loading. To account for the effect of data size, a correction factor (C_P) as recommended in AISI S100 was applied. For the analysis, the following values were adopted: M_m = 1.10, F_m = 1.00, V_M = 0.10, V_F = 0.05, and V_Q = 0.228. The correction factor C_P was applied as recommended in AISI S100 to account for the effect of data size. Calibration coefficients (C_Φ) and resistance factors (Φ) were set based on the design method under consideration. For the CSM, C_Φ = 1.521 and Φ = 0.85 were adopted. Load combinations were selected in accordance with the respective design standards. For AISC 360 − 16, a combination of 1.2 × DL + 1.6 x LL was utilized, with a deal load (DL) to live load (LL) ratio of 1:5. In contrast, EN 1993-1-1 employed a load combination of 1.35 × DL + 1.5 × LL.

A design rule is deemed reliable if the computed reliability index (β) as given in Eq. 12 exceeds 2.5, indicating an acceptable level of safety.

$$\:\beta\:=\frac{ln\left[{C}_{{\Phi\:}}{M}_{m}{F}_{m}{P}_{m}/{\Phi\:}\right]}{\sqrt{{C}_{P}{V}_{P}+{{V}_{M}}^{2}+{{V}_{F}}^{2}+{{V}_{Q}}^{2}}}$$

(12)

Evaluation of existing design approaches

This section critically evaluates established methodologies for predicting the torsional capacity of RHS members. The assessment covers international codes—ANSI/AISC 360 − 16 and EN 1993-1-5—as well as DSM approaches by Devi et al.³⁹ and Devi et al.⁴². While these DSM formulations were originally developed for square hollow section of steel grade Yst 310 and circular hollow sections made of high strength steel of Grade S900 and S1100, their suitability for high-strength steel RHS under pure torsion is examined here. The increasing use of high-strength steel in structural engineering is attributed to its superior mechanical properties, which facilitate significant weight reduction without compromising structural performance. However, conventional design models, primarily calibrated for mild steel or standard geometries, may not adequately capture the complex torsional response of high-strength steel closed hollow section members. This raises important concerns regarding the reliability and safety of employing unmodified design equations in contemporary practice. To rigorously assess the predictive accuracy of the selected design approaches, FE analyses were conducted to determine the ultimate torsional capacity (T_u) of various RHS geometries. These capacities were normalized by the predicted torsional resistance (T_u/T_{u, pred}.) from each design method. The results are graphically presented in Fig. 15, where this ratio is plotted against the torsional slenderness.

Fig. 15

Comparision of FE results and design prediction.

As illustrated in Fig. 15, both the ANSI/AISC 360 − 16 and EN 1993-1-5 codes tend to underestimate the torsional capacity, particularly for stocky sections, the underestimation is especially pronounced in ANSI/AISC 360 − 16, for slender section, indicating a significant unconservative bias. The EN 1993-1-5 predictions, while also generally above unity for stocky sections, show a gradual decline as slenderness increases, which tends to overestimate the torsional capacity. In contrast, the DSM formulations by Devi et al.^39,42 demonstrate improved accuracy and consistency. The DSM approach by Devi et. al³⁹ yields (T_u/T_pred.) values tightly clustered around unity across the slenderness range, particularly for intermediate and higher slenderness ratios, indicating a high level of predictive reliability and minimal scatter. Notably, as section slenderness increases, the DSM approach by Devi et. al⁴² exhibits a trend toward conservatism, with (T_u/T_{u, pred}.) values falling above unity for more slender sections. This suggests that the method tends to underpredict the torsional capacity as slenderness increases - a behavior that, while enhancing safety, may result in overly conservative and potentially uneconomical designs for slender RHS members. A statistical data of the predictive performance of each method is provided in Table 6.

Table 6 Comparison of FE result with design prediction.

The ANSI/AISC 360 − 16 method exhibits the highest mean value (1.34) and the largest coefficient of variation (COV = 0.28), indicating a systematic underestimation and significant scatter in predictions. The EN 1993-1-5 approach is somewhat more conservative, with a mean of 1.14 and lower scatter (COV = 0.11), but still tends to underestimate the torsional capacity, especially for stocky sections. Both methods fall short of the minimum reliability index (β = 2.5) required for codal compliance. The DSM method by Devi et al. 2023 closely aligns with the FE results (mean = 0.96), but its (COV = 0.14) and reliability index (β = 2.03) indicate some variability and insufficient reliability. However, the DSM method by Devi et al. 2020 approach stands out for its exceptional consistency (COV = 0.04) and a mean value very close to unity (1.02), though its reliability index (β = 2.44) still marginally falls short of the codal requirement.

Overall, Fig. 15 and the statistical analysis demonstrate that while code-based methods (EN 1993-1-5 and ANSI/AISC 360 − 16) are prone to conservative underestimation—especially for stocky sections—DSM-based approaches provide more accurate and consistent predictions for high-strength steel RHS under torsion. However, even the best-performing DSM method (Devi et al. 2020) does not fully satisfy the reliability threshold stipulated by current codes. Furthermore, the increasing conservatism of DSM method (Devi et al. 2023) with higher slenderness, as evidenced by increasing (T_u/T_{u, pred}.), shows that the method underpredict for slender section. These findings highlight a critical gap in current design frameworks, none of the existing models simultaneously achieve the necessary levels of accuracy and statistical reliability for the torsional design of high-strength steel RHS members. The consistent inability to meet the prescribed reliability index underscores the need for further research and the development of refined design methodologies specifically tailored to HSS-RHS applications.

Need for modification

The comprehensive evaluation of existing design methodologies underscores a critical need for modification in the context of high-strength steel RHS members subjected to torsion. Both ANSI/AISC 360 − 16 and EN 1993-1-5, despite their widespread adoption, consistently underestimate the torsional capacity of these members, particularly for stocky sections, as evidenced by their elevated mean (T_u/T_{u, pred.}) values and substantial prediction scatter. Moreover, neither approach meets the minimum reliability index stipulated for codal compliance, thereby raising concerns regarding structural safety and efficiency. While the DSM proposed by Devi et al. (2020, 2023)^39,42 demonstrate improved predictive accuracy and reduced variability—most notably the prediction 2020 formulation—these methods still fail to achieve the requisite reliability threshold, with the 2023 formulation exhibiting excessive conservatism for slender sections. These limitations can be attributed to the fact that current models are predominantly calibrated for mild steel or conventional section geometries and do not adequately capture the unique mechanical behavior and slenderness effects inherent to HSS-RHS under torsional loading. Consequently, none of the evaluated approaches concurrently satisfy the demands for accuracy and statistical reliability mandated by contemporary design standards. This persistent gap highlights the necessity for the development of refined or new design formulations that explicitly address the material-specific and geometric complexities of HSS-RHS members, thereby ensuring both safety and structural economy in advanced engineering applications.

Modified design equations

Following the evaluation presented in the previous section, it is evident that none of the existing design methodologies, including the European Code (EN) and the DSM proposed by S.V. Devi, fully meet the reliability requirements specified by AISI S100 for HSS-RHS under torsional loading. While these methods demonstrate relatively high accuracy and consistency, their reliability indices fall marginally below the required threshold of 2.5. As a result, modifications to these models are necessary to enhance their predictive performance and ensure codal compliance.

This section outlines the development of modified design equations based on the refinement of the EN and DSM Devi et al. 2020³⁹ approaches. The proposed modifications are grounded in a detailed examination of FE analysis results and statistical calibration procedures, aiming to improve the accuracy, consistency, and reliability of torsional strength predictions for HSS-RHS members.

Modified EN 1993 1–5

In light of the limitations of the design curve from EN 1993 1–5 in predicting torsional buckling resistance for HSS-RHS members, a modified design approach is proposed. This modification is based on the analysis of a comprehensive set of FE simulations covering a wide range of section geometries for S700 series. The results revealed systematic deviations between Eurocode predictions and actual torsional capacities, particularly for sections with higher slenderness. To rectify this, a revised torsional buckling reduction factor χ_{w, modified} was developed to improve prediction accuracy across all slenderness regimes. The proposed reduction factor is defined by a piecewise function that varies depending on the non-dimensional slenderness λ_w as represented in Eq. 13.

$$\:{\chi\:}_{w,\:\text{m}\text{o}\text{d}\text{i}\text{f}\text{i}\text{e}\text{d}}=\left\{\begin{array}{c}\eta\:,\:\:{\lambda\:}_{w}<0.726/\eta\:\\\:\frac{0.69}{{\lambda\:}_{w}^{1.1}},\:\:0.726/\eta\:\:\le\:\:{\lambda\:}_{w}<1.08\\\:\frac{1.585}{1.42+{\lambda\:}_{w}},\:\:{\lambda\:}_{w}>1.08\end{array}\right.$$

(13)

To distinguish between stocky and slender section in high strength steel, the limiting value of λ_T = 0.726, as proposed by Devi et al. 2023⁴² has been adopted in this study. This criterion has demonstrated a high degree of accuracy in categorizing section slenderness. The proposed curve was plotted alongside the Eurocode design curve and FE data (Fig. 16), showing significantly improved agreement, especially, in the transitional and slender regimes.

Fig. 16

Eurocode design curves for HSS-RHS.

To validate the proposed modification, a statistical comparison is presented in Table 7 between the predicted and FE-derived torsional strengths. The ratio T_u/T_{u, EN, Modified} yielded a mean of 1.22 and a COV of 0.08, indicating consistent and conservative predictions. Furthermore, a reliability index (β) of 2.81 was obtained, surpassing the codal threshold proposed in AISI S100-16⁴⁶ of 2.5 for structural safety. This confirms that the modified design rule not only aligns closely with observed behavior but also maintains an acceptable level of reliability for practical use. Overall, the proposed modification offers a more accurate and safer approach to torsional design in HSS-RHS members, making it a viable enhancement to existing design standards.

Table 7 Comparision of FE and proposed modified design rules.

Modified DSM

As highlighted in the previous sections, the existing DSM formulations exhibit significant limitations when applied to HSS-RHS, particularly for stocky cross-sections. Among the various DSM-based approaches evaluated, the formulation proposed by Devi et al. 2020³⁹ demonstrated the closest alignment with FE analysis results. This closeness is attributed to the fact that the original method was developed for a similar geometric profile; however, it was calibrated using a low-strength material of (Yst 310), which differ from high strength Grade S700 material considered in this study. Recognizing the material specific discrepancies and aiming to improve predictive performance, a modified DSM equation was developed based on regression analysis of FE-derived torsional capacities. Specifically, a least squares regression approach was employed to refine the relationship between torsional resistance and slenderness of HSS-RHS members. The objective of this modification was to improve the accuracy and reliability of the DSM when applied to modern, high-performance materials used in structural applications.

The proposed modified DSM equation is provided in Eq. 14, and it represents a recalibrated design expression that accounts for the nonlinear strength degradation observed in FE simulations across varying slenderness levels. This adjustment is particularly effective in addressing the under or over-prediction of torsional capacity in the stocky and transitional slenderness regimes.

$$\:\left({T}_{u,DSM}/{T}_{y}\right)=\left\{\begin{array}{c}1+\left(3-5.67{\lambda\:}_{T}\right)\left(\frac{{\sigma\:}_{u}}{{\sigma\:}_{y}}-1\right),\:\:{\lambda\:}_{T}\le\:0.726\\\:1+\left(1.63-3.2{\lambda\:}_{T}\right)\left(\frac{{\sigma\:}_{u}}{{\sigma\:}_{y}}-1\right),\:\:{0.726\:<\lambda\:}_{T}\le\:1.08\\\:\frac{2.58}{{{\lambda\:}_{T}}^{0.49}}-\frac{1.84}{{{\lambda\:}_{T}}^{0.43}},\:\:{\lambda\:}_{T}>1.08\end{array}\right.$$

(14)

The effectiveness of the modified DSM was validated through graphical and statistical comparisons against the FE results. Figure 17 presents the design curve generated by the modified DSM alongside FE-derived data points, illustrating a significantly improved alignment. Additionally, the statistical performance of the new formulation is summarized in Table 7. The normalized torsional capacity ratio (T_u/T_{u, DSM Modified}) yielded a mean of 1.07, indicating a conservative but close prediction to the FE results. The COV was found to be 0.05, reflecting high consistency across all examined geometries. Most importantly, the reliability index (β) for the modified DSM was computed to be 2.60, thereby exceeding the minimum requirement of 2.5 prescribed in AISI S100-16⁴⁶ for structural safety. This improvement affirms the statistical soundness and codal compliance of the modified formulation.

Fig. 17

DSM design curves for HSS-RHS.

Conclusion

This study presented a comprehensive numerical investigation into the torsional behavior HSS-RHS stub columns under pure torsional loading. A finite element analysis based approach was adopted using ABAQUS to simulate and evaluate the torsional performance of cold-formed HSS-RHS members. Special focus was placed on identifying the influence of geometric parameters particularly aspect ratio and cross sectional wall thickness on torsional resistance, and assessing the applicability of current design provisions, including EN 1993 1–5²⁵ and ANSI/AISC 360 − 16³², as well as several DSM formulations.

The parametric study revealed that geometric configuration significantly impacts torsional behavior. Sections with higher aspect ratios (square) displayed superior torsional strength and stiffness with up to 32% higher torsional capacity compared to more slender sections due to balanced geometry and uniform buckling resistance. In contrast, elongated (lower aspect ratio) sections experienced more pronounced deformation and stress concentration, especially along wider faces, leading to reduced torsional capacity. Similarly, increasing cross sectional wall thickness consistently improve both strength and stiffness across all aspect ratios, confirming the vital role of thickness in resisting torsional loads and minimizing local instability. An increase in thickness was found to enhance torsional capacity by approximately 9–10 kNm per millimeter.

The FE analysis results were validated through a two-tiered methodology involving comparison against experimental data on both torsional loading schemes and material properties. The validation confirmed the model’s capability to accurately simulate torsional behavior in HSS-RHS members. Following validation, the FE analysis outcomes were benchmarked against predictions from established design codes and DSM-based formulations. This comparison highlighted systematic discrepancies, particularly the consistent underestimation of torsional resistance by conventional design methods such as American and European codes, especially in stocky cross-sections. The original DSM approaches, while more aligned with FE data, still failed to meet the reliability index threshold of 2.5 as stipulated in AISI S100-16⁴⁶, particularly due to material specific limitations and lack of calibration for high-strength steel.

To bridge this gap, the study proposed modified design equations based on enhanced interpretations of FEA data. The Eurocode-based modification introduced a revised torsional buckling reduction factor, showing significant improvements in prediction accuracy, especially in the slender section regime. The mean torque ratio (T_u/T_{u_EN_modified}) improved to 1.22 with a COV of 0.08 and a reliability index (β) of 2.81, surpassing the codal benchmark. A modified DSM equation was also developed using least squares regression, yielding a (T_u/T_{u_DSM_modified}) mean of 1.07, COV of 0.05, and (β) of 2.60-thus achieving both accuracy and codal compliance.

In summary, this study makes substantive contributions by filling critical gaps in understanding pure torsional behavior of HSS-RHS members, particularly for steel grades above 460 MPa. The validated numerical models and statistically calibrated design modifications provide accurate, reliable tools that enhance the prediction of torsion capacity and structural safety. These advances support the design of modern high-strength steel structures by enabling safer, more efficient, and code-compliant torsional design. The findings also lay a foundation for future experimental work and updated design provisions tailored to HSS-RHS members under torsion.