An efficient aggregation algorithm based on synchronous-asynchronous mechanism for federated learning

Abstract

With the widespread application of Federated Learning (FL) in distributed data environments, enhancing system communication efficiency while maintaining model performance has become a critical challenge in this field. In this paper, we propose SaAS-FL, an innovative FL algorithm that aims to balance model accuracy and communication efficiency. First, it employs a synchronous training mode to obtain a relatively stable baseline global model. Then, it adopts an asynchronous update approach to achieve efficient aggregation, while introducing a delay factor based on client staleness to dynamically adjust aggregation weights, thereby mitigating the adverse effects of stale clients on model performance. Finally, an accuracy-based decision mechanism is employed to determine whether to update the global model, which avoids the distribution of ineffective models and effectively prevents model degradation. Experimental results demonstrate that SaAS-FL achieves high communication efficiency while maintaining high model accuracy, exhibiting strong robustness and adaptability across diverse heterogeneous data environments. This approach offers novel insights for enhancing FL efficiency.

Introduction

Federated Learning (FL), as a novel distributed machine learning (ML) technique, was first proposed by Google in 2017¹. Its typical architecture comprises a central server and multiple clients. With the FL framework, the central server initializes the global model and distributes it to the participating clients. Upon receiving the model from the server, each client performs local training using its own data and then transmits the updated model parameters back to the server. The server subsequently aggregates these parameters to update the global model and shares the revised global model with all clients. This iterative process continues until predetermined training termination criteria are met. Compared to traditional ML, FL enables collaborative model training without requiring the sharing of raw data, effectively addressing the “data silos” issue while safeguarding user privacy and enabling secure cross-domain data sharing. FL has been widely applied in various domains, including the Internet of Things (IoT), vehicular networks, healthcare, finance, and aviation^2,3,4,5.

However, due to variations in hardware deployment among clients, such as disparities in computational power, storage capacity, and energy consumption, coupled with the ata heterogeneity exhibited by Non-Independent Distributed(Non-IID) data, alongside factors such as communication delays caused by unstable network conditions and bandwidth disparities, all exert a significant impact on the communication efficiency of FL^6,7,8. This, in turn, affects the convergence speed, accuracy, and robustness of the global model. Traditional FL algorithms (such as the classic FedAvg algorithm) typically adopt a synchronous training mechanism, where the central server must wait for all clients to upload their local models before performing aggregation and updates. Clients with poorer computational and communication capabilities can severely hinder communication efficiency. Algorithms such as FedAsync⁹, FedSA¹⁰, and FedBuff¹¹ adopt an asynchronous training mechanism based on “first-come, first-aggregated”, allowing the server to perform federated aggregation without having received all client models, which significantly enhances training efficiency. However, in such methods, stale model updates provided by “straggler clients” may lead to catastrophic gradient staleness, causing a sharp deterioration in model performance¹². Particularly in Non-IID, this negative effect is further amplified, resulting in significant fluctuations in model accuracy¹³. This compromises the robustness of FL systems and constitutes a critical bottleneck constraining the practical application of asynchronous FL.

In this paper, we focus on communication efficiency and model performance in FL, proposing an innovative algorithm named SaAS-FL. By refining aggregation strategies and optimizing communication mechanisms, SaAS-FL effectively integrates synchronous and asynchronous FL training paradigms.This approach effectively mitigates the negative impact of stale gradients on model accuracy and training stability, thereby enabling efficient and robust FL in heterogeneous environments. The main contributions of our paper are listed as follows:

• First, we propose a FL training framework (SaAS-FL) that follows “synchronous aggregation first, asynchronous updates later”. During the initial training phase, synchronous FL mechanisms are employed to conduct model training, effectively mitigating convergence challenges caused by data heterogeneity and ensuring rapid and stable convergence of the initial global model. Subsequently, asynchronous update mode allows flexible participation from each client, significantly reducing system waiting time and enhancing algorithm communication efficiency.

• Second, we introduce an accuracy-based model update mechanism. Upon receiving local model updates from clients, the central server first verifies whether their aggregated accuracy surpasses the current global model. Only when model accuracy improves does the server distribute the updated global model to relevant clients; otherwise, clients retain their original models without updating. This design not only suppresses issues like model oscillation, convergence difficulties, and accuracy degradation caused by stale updates, but also avoids the update and distribution of invalid models. Consequently, it reduces computational and communication overhead, minimizes channel occupancy, and further enhances overall training efficiency.

• Third, we introduce an adaptive aggregation strategy based on a delay factor. During model aggregation, the central server dynamically adjusts the aggregation weights of each client according to its delay level—the greater the delay, the smaller the assigned weight—to prevent stale clients from excessively influencing the global model. This mechanism effectively prevents model accuracy degradation and convergence oscillations caused by stale updates, enhancing the robustness and stability of the global model.

The subsequent sections of this paper are organized as follows: Section “Related work” systematically introduces the classic FL algorithm FedAvg and current mainstream efficiency optimization algorithms for FL. Then, Section “SaAS-FL” details SaAS-FL at three levels: system architecture, design approach, and algorithmic steps. Following this, Section “Experimental simulation and results analysis” conducts performance comparisons and ablation studies on SaAS-FL through experimental simulations, followed by analyses of the results. Finally, Section “Conclusions” summarizes the entire paper and presents the conclusions.

Related work

FedAvg algorithm

FedAvg is a foundational algorithm in FL, originally proposed by McMahan et al.¹. Assume that we have one central server and $K$ distributed clients. Let $\omega_{0}$ denote the initial global model,$T$ represent the total number of global communication rounds,$C$ be the client selection ratio per round, $E$ stand for the number of local training epochs on each client, and $\eta$ denote the learning rate. The FedAvg algorithm operates as follows:

First, Client Selection and Model Distribution. At the start of each round $t\left( {t \in T} \right)$, the central server randomly selects $m = \max \left( {C \cdot K,1} \right)$ clients to form a participant set $S_{t}$, and distributes the current global model $\omega_{t}$ (initialized as $\omega_{0}$) to each client in $S_{t}$.

Second, Local Training. Each client $k$ in $S_{t}$ employs stochastic gradient descent (SGD) to train the distributed model $\omega_{t}$ locally using its own datasets $D_{k}$ for $E$ rounds, obtaining the model $\omega_{t + 1}^{k}$, which is then uploaded to the central server.

Third, Model Aggregation. The server collects the sample sizes $|D_{k} |$ of each participating client and the total sample size $|m_{k} | = \sum\nolimits_{{k \in S_{t} }} {|D_{k} |}$, and performs a weighted average to obtain the new global model $\omega_{t + 1} \, \leftarrow \, \sum\nolimits_{{k \in S_{t} }} {\frac{{|D_{k} |}}{{|m_{k} |}}\omega_{t + 1}^{k} }$.

Finally, Model Distribution. The server distributes the updated global model $\omega_{t + 1}$ back to all clients in $S_{t}$. This process repeats iteratively until the specified number of global epochs $T$ is completed. The entire process is summarized in Algorithm 1.

Algorithm 1

FedAvg.

Furthermore, McMahan et al. demonstrated that appropriately increasing the number of local training rounds on clients can accelerate overall model convergence while reducing communication overhead. However, the classic FedAvg algorithm only performs well when client data satisfies the Independent and Identically Distributed (IID) assumption. When data exhibits Non-IID characteristics, its model accuracy significantly deteriorates. Additionally, FedAvg employs a synchronous aggregation strategy, meaning the server must wait for all selected clients to complete local training and upload their updates before performing model averaging. This approach causes computationally or communicationally constrained “straggler clients” to become a performance bottleneck, thereby slowing down the overall training process and reducing system efficiency.

Efficiency optimization algorithms for FL

To enhance the communication efficiency of FL, researchers have proposed a series of optimization algorithms based on strategies such as model pruning, gradient quantization, knowledge distillation, client selection, and asynchronous/semi-asynchronous updates, and have compared and analyzed model aggregation techniques such as synchronous aggregation, asynchronous aggregation, hierarchical aggregation, and robust aggregation, along with their applicable scenarios¹⁴. Reference¹⁵ proposes the FedProx algorithm to address device and data heterogeneity. It allows clients to perform varying numbers of local model training rounds based on their computational capabilities, which improves model accuracy compared to the FedAvg algorithm to some extent. However, the introduction of the proximal term increases computational overhead and complicates parameter tuning. Literature¹⁶ proposed FedOpt, an adaptive optimization algorithm designed for Non-IID data. By incorporating momentum and adaptive learning rates on the server side, it better accommodates data heterogeneity, thereby improving model accuracy and convergence speed. However, maintaining the adaptive optimizer raises computational complexity and memory usage. In¹⁷, the FjORD algorithm is proposed to address heterogeneity in FL. Servers allocate locally trained models of varying sizes based on clients’ computational capabilities, effectively improving system adaptability and communication efficiency. However, aggregating sub-models of different sizes increases algorithmic complexity. Moreover, model pruning strategies that solely adjust width may result in excessively deep sub-models, compromising training accuracy. Similarly, reference¹⁸ proposed the FedRolex algorithm based on sub-model extraction. Unlike FjORD’s static extraction approach, FedRolex employs a rolling window with adjustable strides to ensure thorough training of all layers in the global model. However, in practice, client models are not uniformly distributed, and the rolling window mechanism introduced additional complexity and computational cost in each communication round.

Considering the inadequacy of global model training caused by sub-model segmentation based solely on width, reference¹⁹ proposed the Scale-FL algorithm. By inserting an early-exit classifier, it achieves depth-based two-dimensional model splitting on top of traditional width-based partitioning, enhancing the model’s generalization capability. However, the algorithm performs poorly when handling extremely Non-IID data, requiring further optimization. Moreover, the two-dimensional model splitting significantly increases the algorithm’s complexity and aggregation difficulty, potentially introducing additional computational overhead. FedDF²⁰ allows local models on clients to vary in architecture size and integrates their knowledge into a single global model on the server through knowledge distillation and ensemble learning. This approach reduces communication rounds and improves efficiency to some extent. However, its heavy reliance on unlabeled data for distillation limits its applicability in scenarios where such data is unavailable or difficult to obtain. Building upon this, Fed-ET²¹ introduces regularization terms and confidence measures to better preserve the diversity of client data and enhance the generalization capability of the global model. Nevertheless, it similarly faces challenges related to dependence on unlabeled data and incurs significant computational overhead due to increased algorithmic complexity. FedAsync⁹, a classical asynchronous optimization algorithm, addresses communication efficiency by allowing the server to aggregate and update the global model immediately upon receiving a client update, without waiting for all clients. While this significantly improves communication efficiency compared to traditional FedAvg, the algorithm exhibits reduced stability under highly heterogeneous data conditions. ASO-FL²² builds upon this foundation by introducing dynamic learning rates and a feature learning module. It extracts device features through attention mechanisms and weight normalization, thereby enhancing the model’s generalization capabilities to some extent and demonstrating robust performance against device disconnections and network latency. However, for datasets with complex features, the feature extraction process increases training time, impacting overall efficiency. Unlike traditional purely asynchronous optimization methods, FedBuff¹¹ proposes a semi-asynchronous federated optimization approach. In this algorithm, the server accumulates a certain number of client updates in a buffer before performing global model aggregation. This design enhances system scalability to a considerable extent. However, the algorithm’s performance depends on the choice of buffer size. Furthermore, fluctuations in buffer filling speed caused by the instability of dynamic client updates can also affect model performance. To address the issue of unfairness in client scheduling, Libra¹² introduces another semi-asynchronous federated optimization algorithm. By limiting the training speed of fast devices and selectively aggregating outdated local models, it ensures that both resource-rich and resource-constrained clients participate fairly in training. This approach mitigates performance degradation due to device heterogeneity to some degree. However, the complex selective aggregation and client selection strategies significantly increase computational and communication overhead, which in turn hinders improvements in communication efficiency. Reference²³ addresses the catastrophic forgetting problem and annotation scarcity issues in FL medical segmentation by proposing the FedCSL method. Through the cross-incremental collaborative distillation (CCD) mechanism, it achieves continuous knowledge accumulation among clients under privacy protection, while utilizing the federated cross-incremental self-supervised pre-training paradigm to effectively reduce dependence on labeled data. However, secure computation increases computational and communication overhead to some extent, and its serialized training mode faces scalability challenges when the number of clients increases. Reference²⁴ proposes the FedBDT algorithm, which combines knowledge distillation with split learning and designs a bidirectional knowledge transfer module and knowledge retrospection mechanism, effectively alleviating the catastrophic forgetting problem in FL under non-independently and identically distributed data. However, the algorithm has strong dependencies on CNN feature extractors. Reference²⁵ focuses on medical image segmentation problems and proposes the FedATA algorithm. This method combines the technical advantages of masked self-distillation and adaptive attention, effectively improving the model’s descriptive capability and adaptability to heterogeneous data. However, the introduction of learnable aggregation weights increases client-side computational overhead and algorithmic complexity to some extent. Reference²⁶ addresses the time series data heterogeneity problem in FL by proposing the Fed-TREND framework, which enhances training consensus through synthetic data augmentation on both clients and servers to improve model performance. However, the algorithm fails to systematically quantify the performance under different degrees of heterogeneity.

SaAS-FL

This section details the system architecture, design scheme, and algorithmic steps of SaAS-FL, as described in Sections “System architecture”, “Design scheme”, and “Algorithmic steps”, respectively.

System architecture

SaAS-FL adopts a centralized FL architecture consisting of one central server and $N$ clients. Each client $k\left( {k = 1,2 \cdots N} \right)$ possesses its own independent datasets $D_{k}$, where the data may be either IID or Non-IID. The specific functions of the central server and clients within the algorithm are as follows.

Central server: Responsible for generating the initial training model and distributing it to all participating clients. During the initial phase of training, it performs synchronous aggregation based on the FedAvg algorithm, coordinating clients to collaboratively generate a stable global model and saving it. In the asynchronous training phase, it receives client model updates in real time and immediately performs federated aggregation. In the model update decision phase, it evaluates model accuracy to determine whether performance has improved and decides whether to update and distribute the new global model.

Clients: Receive the global model from the central server, train it locally using their own dataset, and upload the updated model parameters to the server. They participate in optimizing the global model by continuously receiving and deploying new global models sent from the server, followed by local training. In the initial training phase, all clients participate in synchronous optimization according to the aggregation rules of the server. Once entering the asynchronous phase, clients, depending on their computational and communication capabilities, submit updated models to the server in real time, completing dynamic updates.

Design scheme

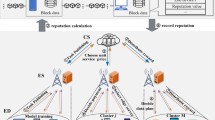
Figure 1 illustrates the system architecture and overall design of SaAS-FL, which consists of three main phases: initial synchronous aggregation training, asynchronous federated training, and accuracy validation and model update. A detailed description is provided below.

Fig. 1

Schemes of SaAS-FL.

Initial synchronous aggregation training

SaAS-FL adopts a “synchronous first, then asynchronous” training paradigm. During the initial phase, the central server coordinates all participating clients to jointly establish a stable baseline model. The detailed procedure is described as follows:

• The central server generates an initial global model and distributes it to all clients participating in FL.

• Each client performs local training using its own datasets, generates a local model update, and uploads it to the central server.

• The central server aggregates all the locally uploaded models using the FedAvg algorithm, updates the global model accordingly, and redistributes the new global model to each client. Clients then conduct a new round of local model training. This process is repeated for $T_{0}$ rounds, ultimately producing a global model $\omega_{{T_{0} }}$ to be used in subsequent asynchronous training. This initial synchronous phase ensures the stability of the model’s baseline performance. The specific implementation is detailed in Algorithm 2.

Asynchronous federated training

SaAS-FL After completing $T_{0}$ rounds of synchronous training, the model enters the asynchronous training stage. Clients with stronger computation or communication capabilities will prioritize uploading their local updates to the central server. Upon receiving these updates, the central server immediately performs federated aggregation based on the global model $\omega_{{T_{0} }}$ without waiting for other clients’ uploads, thereby avoiding idle waiting time inherent in synchronous settings.

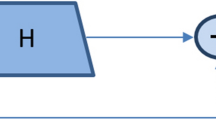
Furthermore, considering that the delay of “straggler clients” may impact model accuracy to varying degrees, SaAS-FL introduces a delay factor $\alpha$ to dynamically adjust the aggregation weights between client models and the global model, as specified in Eqs. (1) and (2):

$$\alpha = \delta \cdot \left( {\tau + 4} \right)^{{ - {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}}$$

(1)

$$\omega_{t + 1} \, \leftarrow \, (1 - \alpha )\omega_{t} + \alpha \omega_{t + 1}^{k}$$

(2)

Here, Eq. (1) defines the delay factor $\alpha$, and Eq. (2) specifies the aggregation strategy for the central server during the asynchronous training phase. The variable $\tau$ represents the delay of client model updates relative to the global model update. A larger $\tau$ indicates a heavier client delay, introducing greater error during global model updates and thus warranting a smaller aggregation weight—corresponding to a smaller value for the delay factor $\alpha$. The hyperparameter $\delta$ is set to $\delta = 0.9$, following the exploration of perturbation settings in reference⁹. The specific steps of this phase are outlined below:

• As shown in Fig. 1, assume that at time $t$, client 2 is the first to complete local training and uploads its model update $\omega_{t}^{2}$ to the central server.

• Upon receiving $\omega_{t}^{2}$, the server immediately initiates asynchronous aggregation. Based on the global model $\omega_{{T_{0} }}$ and using Eq. (2), it computes the updated global model $\omega_{t + 1}$:

  $$\omega_{t} \, \leftarrow \, (1 - \alpha )\omega_{{T_{0} }} + \alpha \omega_{t}^{2}$$

  (3)

Accuracy validation and model update

To mitigate the negative impact of severely delayed clients on model accuracy and training stability, SaAS-FL incorporates an accuracy-based model update mechanism. Specific details are as follows:

• Accuracy Verification: For the globally aggregated model $\omega_{t + 1}$ generated asynchronously, the central server temporarily holds it as a candidate model without immediate distribution. Instead, it first compares the relative magnitudes of model accuracies $ACC_{{\omega_{t + 1} }}$ and $ACC_{{\omega_{t} }}$.

• Model Update Decision: If $ACC_{{\omega_{t + 1} }} > ACC_{{\omega_{t} }}$, the central server distributes $\omega_{t + 1}$ to the corresponding clients. Otherwise, clients retain the original model $\omega_{t}$ without updating.

Algorithmic steps

Based on the above analysis and design, this section outlines the specific algorithm steps.

Model Initialization

Assume FL system consists of $N$ clients and undergoes $T$ training rounds, comprising $T_{0}$ rounds of synchronous training and $T_{{{\text{Async}}}}$ rounds of asynchronous training, where $T = T_{0} + T_{{{\text{Async}}}}$. During the synchronous training phase, $m = \max \left( {C \cdot N,1} \right)$ clients are selected per round to participate in the training, where $C = \left[ {0,1} \right]$ denotes the selection ratio per round. Each client $k\left( {k = 1,2 \cdots N} \right)$ possesses its own independent datasets $D_{k}$, and the initial global model is denoted as $\omega_{0}$.

Synchronous federated training

During synchronous training, the central server and clients execute the following steps based on the FedAvg algorithm (see Algorithm 1).

• The central server distributes the global model $\omega_{t} \left( {t \in T_{0} } \right)$ (initial global model $\omega_{0}$) to the $m$ clients participating in FL.

• Upon receiving the global model $\omega_{t}$ from the central server, client $k\left( {k \in m} \right)$ independently trains locally for $E$ rounds using the SGD algorithm and its own datasets $D_{k}$, generating the local model parameters $\omega_{t + 1}^{k}$ and uploading them to the central server.

• After receiving updates from all $m$ clients, the central server performs federated aggregation to obtain the new global model:$\omega_{t + 1} \leftarrow {\text{FedAvg}}\left( {\omega_{t + 1}^{1} ,\omega_{t + 1}^{2} , \cdots \omega_{t + 1}^{k} , \cdots \omega_{t + 1}^{m} } \right)$, and distributes it to all clients.

The above steps are repeated iteratively for $T_{0}$ rounds, ultimately producing and saving the final global model $\omega_{{T_{0} }}$.

Asynchronous federated training

During asynchronous training, the central server performs model aggregation based on the initial global model $\omega_{{T_{0} }}$ according to Eq. (2). The specific steps are as follows:

• For the first round of asynchronous training, the updated global model is computed as:$\omega_{1} \, \leftarrow \, (1 - \alpha )\omega_{{T_{0} }} + \alpha \omega_{1}^{k} \, \left( {k \in N} \right)$

• Similarly, in the $t - th$ round of asynchronous training, the updated global model is computed as:$\omega_{t + 1} \, \leftarrow \, (1 - \alpha )\omega_{t} + \alpha \omega_{t + 1}^{k}$. Here, $\alpha$ denotes the delay factor, as defined in Eq. (1).

After each round of model aggregation, the central server executes the procedures described in Sections “Model Accuracy Assessment” and “Global Model Update” until completing $T_{{{\text{Async}}}}$ rounds of asynchronous training.

Model accuracy assessment

After completing asynchronous aggregation, the central server calculates and compares the accuracy values of the global models $ACC_{{\omega_{t + 1} }}$ and $ACC_{{\omega_{t} }}$ to provide a quantitative basis for the subsequent model update decision.

Global model update

If $ACC_{{\omega_{t + 1} }} > ACC_{{\omega_{t} }}$, the central server distributes the updated global model $\omega_{t + 1}$ to the corresponding clients. Otherwise, clients retain the current model $\omega_{t}$ without updating.

The detailed implementation of the above training process is shown in Algorithm 2, and the symbols involved are summarized in Table 1.

Table 1 Symbol description.

Algorithm 2

Schemes of SaAS-FL.

Experimental simulation and results analysis

To validate the effectiveness and robustness of SaAS-FL in improving communication efficiency, experimental simulations were conducted under the environment described in Section “Experimental environment setup”. Through comparative analysis with traditional baseline algorithms FedAvg, the classical asynchronous FL algorithm FedAsync, and mainstream methods like Libra, the significant advantages of SaAS-FL in jointly optimizing model performance and communication efficiency were thoroughly demonstrated. Additionally, ablation studies on the synchronous training duration and data heterogeneity degree, presented in Sections “Performance analysis of ablation experiments on synchronous training cycle” and “Performance analysis of ablation experiments on data heterogeneity degree”, respectively, further confirmed the strong adaptability and robustness of SaAS-FL across multiple dimensions.

Experimental environment setup

System configuration

The experiment was conducted on the Hengyuan Cloud training platform, with an FL simulation system built on the PyTorch 2.0.0 framework. An asynchronous training mechanism was implemented through multi-threaded programming: the main thread simulated the central server, responsible for distributing and aggregating the global model and making model update decisions, while worker threads handled local training tasks of clients in parallel. The hardware environment utilized an NVIDIA RTX 3090 GPU (24GB VRAM) to accelerate computations, paired with an Intel Xeon E5-2682 v4 CPU (30GB RAM) to ensure efficient data processing. A total of $N = 100$ clients were set up. During the synchronous training, the client selection ratio was set to $C = 0.2$, the total number of global training rounds was $T = 100$, each client performed $E = 3$ local training epochs, and the learning rate was $\eta = 0.01$. Network communication was simulated using rate limiting (240 Mbps upload / 800 Mbps download), and an SSD storage system was employed to ensure efficient read and write operations of training logs. Detailed configurations are summarized in Table 2.

Table 2 Experimental environment configuration.

Datasets and training models

Experiments were conducted on both MNIST and CIFAR10 public datasets. MNIST serves as a classic handwritten image dataset, comprising 60,000 training samples and 10,000 test samples. Each sample is a 28 × 28 pixel grayscale image representing one of ten digit categories from 0 to 9. The CIFAR10 dataset comprises 60,000 32 × 32 RGB color images, encompassing ten distinct categories: airplanes, cars, birds, cats, deer, dogs, frogs, horses, ships, and trucks. During the FL process, we maintain a global held-out validation set at the server side, which is independent of all clients’ local training data. After each training round, the server evaluates the aggregated global model using this global validation set, and the measured accuracy is used to drive the accuracy-based update mechanism.

For model selection, a lightweight CNN architecture was employed for the MNIST dataset, while the more complex CIFAR-10 dataset utilized the PyTorch official baseline ResNet-18 model²⁷ to leverage its stronger feature extraction capabilities.

Furthermore, to simulate different data distribution scenarios, we set up two data forms: IID and Non-IID based on the Dirichlet distribution²⁸.

Evaluation metrics

To comprehensively evaluate the superiority of SaAS-FL, both model accuracy and training time two metrics were adopted.

• Model accuracy

The test accuracy (ACC) of the global model is used as the metric for evaluating model precision, as defined in Eq. (4). The effectiveness of SaAS-FL is assessed by comparing its global accuracy with that of other algorithms across different datasets. A higher global accuracy indicates better algorithm performance.

$$ACC = \frac{Number \, of \, correctly \, predicted \, samples}{{Total \, number \, of \, samples}}*100\%$$

(4)

Additionally, by observing the trend of accuracy curves during training, we can compare the algorithm’s training stability and evaluation of robustness.

• Training time

Define training time as an evaluation metric for model efficiency. It refers to the total duration required for an algorithm to complete the entire FL training process, including local model training on clients, model aggregation on the central server, and communication overhead for model uploads and downloads. The overall efficiency of the algorithm is assessed by directly comparing the total training time across different algorithms. A shorter training time indicates better computational and communication performance, making the algorithm more suitable for practical deployment.

Compared algorithms

We compare the SaAS-FL against classical FL algorithms such as FedAvg¹, FedAsync⁹, and Libra¹². At the same time, simulation results from reference¹² are also adopted, with relevant algorithms therein serving as benchmarks for further comparative analysis with SaAS-FL. Additionally, In addition, to provide deeper insight into the characteristics of SaAS-FL, ablation studies are conducted from two perspectives: synchronous training cycles and data heterogeneity, as described in Section “Ablation Experiments”.

Ablation Experiments

To further validate the effectiveness of SaAS-FL, ablation experiments were designed from two perspectives: the synchronous training cycle and the degree of data heterogeneity.

• Ablation on synchronous training cycles

Considering the impact of the synchronous training cycles on both model accuracy and training efficiency, experiments were conducted with varying numbers of synchronous epochs on different datasets. By comparing model performance across different training cycles, the optimal synchronization strategy was determined. This ensures the algorithm achieves a superior baseline global model $\omega_{{T_{0}}}$ while minimizing training time, thereby enhancing overall training efficiency.

• Ablation on data heterogeneity degree

In Non-IID scenarios, the concentration parameter $alpha$ of the Dirichlet distribution is used to control the degree of data heterogeneity among clients. Specifically, a smaller $alpha$ value indicates higher skewness in client data distributions, simulating extreme Non-IID scenarios with strong heterogeneity. Conversely, a larger $alpha$ value makes client data distributions approach IID. In ablation experiments, we set four distinct $alpha$ values: 0.1, 0.5, 1, and 5, corresponding to strong Non-IID, moderate Non-IID, weak Non-IID, and near-IID data distributions, respectively. By comparing the algorithm’s performance across these $alpha$ values, we systematically evaluate its robustness and adaptability under varying degrees of heterogeneity.

Performance analysis of SaAS-FL

In this section, we compare the SaAS-FL with baseline algorithms such as FedAvg, FedAsync, and Libra across different datasets and data distributions. We demonstrate the effectiveness and superiority of SaAS-FL across three dimensions: accuracy, communication efficiency, and training stability. Specifically, Figs. 2 and 3 demonstrate the effectiveness, stability, and accuracy advantages of SaAS-FL. Figures 4 and 5 illustrate its superior communication efficiency through training time comparisons.

Fig. 2

Comparison of accuracy and stability of different algorithms on various datasets under IID conditions.

Fig. 3

Comparison of accuracy and stability of different algorithms on various datasets under Non-IID conditions.

Fig. 4

Comparison of model accuracy and training time of different algorithms on various datasets under IID conditions.

Fig. 5

Comparison of model accuracy and training time of different algorithms on various datasets under Non-IID conditions.

Figure 2 (a) displays the accuracy curves of different algorithms on the MNIST dataset under IID conditions, with the vertical axis representing algorithm accuracy (%) and the horizontal axis denoting total training iterations. From the curves, it can be observed that as training rounds increase, SaAS-FL achieves accuracy comparable to FedAvg fast. In contrast, FedAsync shows slower accuracy growth and reaches only about 81% accuracy, significantly lower than SaAS-FL. Furthermore, the curve trends reveal that SaAS-FL exhibits smoother trajectories and superior stability, whereas FedAsync demonstrates significant fluctuations throughout training, indicating poorer stability.

Figure 2 (b) presents accuracy comparisons of different algorithms on the CIFAR10 dataset under IID conditions. It can be clearly seen that SaAS-FL converges around the 15th round with accuracy close to 72%. As training rounds increase, its accuracy peaks at 74%, significantly outperforming FedAsync with a smoother curve, demonstrating SaAS-FL’s superiority in accuracy and robustness.

Figure 3 displays the accuracy curves of various algorithms on the MNIST and CIFAR10 datasets under Non-IID. Comparing the curves reveals that the SaAS-FL algorithm still achieves high accuracy in Non-IID environments, with smooth and stable curves, demonstrating strong robustness and convergence stability.

Figure 4 (a) compares model accuracy and training time of different algorithms on the MNIST dataset under IID conditions. The blue bar represents the average global accuracy over the final three iterations for each algorithm, while the brown line graph depicts the total training time required for each algorithm to complete the entire training process. The results show that SaAS-FL achieves nearly 20% higher accuracy than FedAsync, with only about 40% of FedAsync’s training time. Simultaneously, under comparable accuracy levels, SaAS-FL’s training time is significantly shorter than FedAvg’s total time. This demonstrates that SaAS-FL substantially reduces model training time while maintaining accuracy, fully validating its superiority in communication efficiency.

Figure 4 (b) compares algorithms on the CIFAR10 dataset under IID conditions. Clearly, SaAS-FL outperforms FedAsync in both accuracy and training time. Although FedAvg achieves slightly higher accuracy than SaAS-FL, its training time is seven times longer, resulting in low communication efficiency and high training costs, making it unsuitable for practical deployment.

Figure 5 presents the model accuracy and training time comparison of each algorithm on the MNIST and CIFAR10 datasets under Non-IID conditions. Comparative analysis reveals that SaAS-FL achieves more efficient communication.

Additionally, we adopted the simulation results shown in Fig. 10 of reference¹² as the baseline for comparison and compared the accuracy performance on the CIFAR10 dataset. The experimental results demonstrate that SaAS-FL achieves higher accuracy within a shorter training time, proving its superiority over algorithms such as Libra, StandAlone, FedCS, and SAFA.

To further demonstrate the statistical significance of the performance advantages of SaAS-FL, we conducted ten independent repeated experiments of the SaAS-FL with baseline algorithms under different datasets and data distribution conditions. Independent sample t-tests were performed on the average accuracy and training time of each algorithm with a significance level of $\lambda = 0.05$. The detailed results are presented in Table 3.

Table 3 Algorithm performance comparison and statistical significance test results.

The comparison with FedAvg shows that on the MNIST dataset, there is no significant difference in accuracy between SaAS-FL and FedAvg, both achieving approximately 98%. However, in terms of training time, SaAS-FL requires approximately 850 s, whereas FedAvg takes over 4400 s. The absolute t-values are in the tens, and all p-values are less than 0.001, reaching a highly significant difference level, which fully validates the superiority of SaAS-FL over FedAvg in communication efficiency. On the CIFAR10 dataset, although FedAvg’s average accuracy is approximately 10 percentage points higher than SaAS-FL, its training time exceeds 12000s, approximately 7 times that of SaAS-FL, with p-values less than 10^–5, indicating that SaAS-FL can significantly improve communication efficiency with only a minor sacrifice in accuracy.

Comparing with FedAsync, on the MNIST dataset, SaAS-FL’s average accuracy is significantly superior to FedAsync, with p-values less than 0.001, showing highly significant differences. Meanwhile, SaAS-FL’s training time is approximately 40% of FedAsync’s, and the t-test results show that the p-value is less than 0.001, indicating that SaAS-FL significantly outperforms FedAsync in both accuracy and communication efficiency. On the CIFAR10 dataset, SaAS-FL also demonstrates consistent advantages in both accuracy and communication efficiency.

In summary, the statistical significance analysis further confirms that the proposed SaAS-FL algorithm can significantly reduce training time while maintaining accuracy and stability, demonstrating clear superiority in communication efficiency.

Performance analysis of ablation experiments on synchronous training cycle

This section compares the convergence characteristics of model accuracy under different datasets and data distribution conditions during synchronous training, and explores the impact of the synchronous training period $T_{0}$ on the performance of the SaAS-FL algorithm. The experimental results are shown in Figs. 6 and 7, and the detailed analysis is as follows.

Fig. 6

Convergence curves of ACC under synchronous training on different datasets and data distributions.

Fig. 7

Ablation study of SaAS-FL with different synchronous training cycles on various datasets.

First, to reasonably determine the setting of the synchronous training period $T_{0}$, this study conducts a preliminary analysis of the convergence patterns of different datasets. Figure 6 shows the accuracy variation curves of the MNIST and CIFAR10 datasets over the first 30 global iterations. As shown in the figure, for the MNIST dataset, regardless of IID or Non-IID distribution, the model accuracy rises rapidly within the first 5 rounds and tends to converge around the 5th round, after which the curve becomes relatively stable. In contrast, for the CIFAR10 dataset, the convergence rate is slower, and the accuracy curve continues to increase during the first 10 rounds. This difference indicates that MNIST, as a relatively simple dataset, allows the model to reach stable accuracy with fewer training cycles, whereas CIFAR10, being more complex, requires a longer training period.

Based on this observation, in subsequent experiments, the synchronous training period for the MNIST dataset is set starting from $T_{0} = 5$, while for the CIFAR10 dataset it starts from $T_{0} = 10$, with an incremental step of $\Delta T = 10$. This setup is used to explore the effect of different synchronous training periods on the performance of the SaAS-FL algorithm.

Figure 7 (a) illustrates the impact of different synchronization training periods $T_{0}$ on model accuracy and training efficiency under both IID and Non-IID data distributions on the MNIST dataset, where the green bar chart represents model accuracy (ACC) and the orange line chart represents the corresponding training time. The experimental results show that in the IID case, as the synchronization period increases from 5 to 30, the model accuracy gradually improves from 98.06% to 98.78%, while the training time also increases significantly from 862 to 1951s. Specifically, when $T_{0}$ increases from 5 to 10, the accuracy improves by 0.44 percentage points while the training time increases by 226 s; further increasing $T_{0}$ to 20, the accuracy only improves by 0.13 percentage points but the training time increases by an additional 441 s; when $T_{0}$ continues to increase to 30, the accuracy only improves by 0.15%, yet the training time increases by an additional 422 s. The time increment in this process far exceeds the accuracy gain, showing a diminishing marginal benefit trend. Similarly, in the Non-IID environment, when $T_{0} = 5$, relatively high training accuracy can be achieved within a short training time, and further increasing the synchronization period does not significantly improve model accuracy while being accompanied by a substantial increase in time cost. Based on the above experimental results, to balance model accuracy and training efficiency, this paper sets the synchronization training period on the MNIST dataset to $T_{0} = 5$, aiming to effectively control training costs while maintaining high accuracy.

Figure 7(b) shows the impact of synchronization training periods on model accuracy and training time under both IID and Non-IID data distribution conditions on the CIFAR10 dataset. The experimental results indicate that under the IID setting, when the synchronization training period $T_{0}$ increases from 10 to 20 and 30, the accuracy improves by 3.23% and 1.87%, respectively, but the training time correspondingly increases by 762 s and 671 s. Clearly, as training costs increase, the improvement in model performance is limited. Similarly, in the Non-IID environment, the marginal effect exhibits an obvious diminishing trend. Therefore, when using the CIFAR10 dataset, this paper sets the synchronization training period to $T_{0} = 10$, to avoid the growth in time overhead resulting from model performance improvements..

Performance analysis of ablation experiments on data heterogeneity degree

To evaluate the robustness and adaptability of SaAS-FL under varying Non-IID, ablation studies were conducted by setting $alpha = \left\{ {0.1, \, 0.5, \, 1, \, 5} \right\}$ to simulate four heterogeneity scenarios. The corresponding algorithm variants were named SaAS-FL_high-noniid, SaAS-FL_median-noniid, SaAS-FL_low-noniid, and SaAS-FL_near-iid, respectively, and were evaluated on both the MNIST and CIFAR-10 datasets.

Figure 8(a) illustrates the performance comparison of SaAS-FL under different data heterogeneity levels on the MNIST dataset. The horizontal axis represents the number of training iterations, while the vertical axis denotes model accuracy. The figure reveals that when $alpha = 0.1$ (strong Non-IID), SaAS-FL exhibits slower accuracy improvement during early training. However, as training iterations increase, model accuracy gradually rises and eventually stabilizes around 93%. At $alpha = 0.5$ (moderate Non-IID), SaAS-FL rapidly achieves a high accuracy early in training and maintains stable performance throughout, reaching a final accuracy close to 97%. For $alpha = 1$(weak Non-IID), SaAS-FL demonstrates rapid accuracy improvement early on and ultimately stabilizes around 97%. Under $alpha = 5$(near IID), SaAS-FL rapidly achieved nearly 98% accuracy in the early training phase and maintained stable performance throughout the training process. In summary, SaAS-FL converged quickly under all four $alpha$ values and stabilized at high accuracy levels, demonstrating strong robustness and adaptability.

Fig. 8

Ablation study of SaAS-FL under different degrees of data heterogeneity on various datasets.

Figure 8(b) presents the ablation results of SaAS-FL under varying degrees of data heterogeneity on the CIFAR-10 dataset. Analysis of the curves clearly demonstrates that SaAS-FL exhibits favorable convergence, robustness, and adaptability across different $alpha$ values.

Conclusions

Based on previous research on privacy and security, in this paper, we focus on addressing the challenge of balancing communication efficiency and model performance in federated learning by proposing an innovative algorithm named SaAS-FL. By integrating the stability of synchronous training with the efficiency of asynchronous aggregation, SaAS-FL not only ensures rapid and stable convergence during the initial training phase but also enhances overall training efficiency. Additionally, the algorithm incorporates an accuracy-based model update mechanism that avoids frequent distribution of ineffective models, significantly reducing communication and computational overhead. Experimental results on the MNIST and CIFAR10 datasets show that SaAS-FL achieves substantial improvements in communication efficiency while maintaining high model accuracy. It also exhibits robust adaptability across diverse datasets and varying degrees of data heterogeneity. The current research has primarily conducted comprehensive simulations based on CNN models for image classification tasks. In the next phase, further exploratory studies will be carried out to evaluate the algorithm’s performance on other data types and within large-scale deep network environments, aiming to enhance its generalization capability across more complex models and datasets. Meanwhile, future work will integrate privacy protection and security mechanisms to develop a more secure and efficient FL algorithm.