Optimized design and experiment of a controllable rotary tube strip fertilizer spreader for hilly mountainous terrain

Abstract

The existing fertilizer spreader has suboptimal performance in terms of fertilizer uniformity, lack of controllability of fertilizer spreading width, low utilization rate, and inability to meet the requirements of hills, mountains, and other complex terrains. In response to these shortcomings, we have developed a rotary tube fertilizer spreader for mountainous terrain. This device uses a fertilizer trajectory based on the drop distribution of overlapping prolate cycloids, which enables uniform fertilizer application in both the transversal and longitudinal directions. Based on an analysis of the structure and operating principles of the device, Table L₉ (3⁴) was selected for orthogonal array testing, and the results showed that the transversal fertilizer distribution uniformity (Y₁) and the longitudinal fertilizer distribution uniformity (Y₂) were 14.24% and 12.75%, respectively, when the number of rotating tubes was Z = 3, the angle θ of the rotating tubes with respect to the vertical was 50°, and the length of the rotating tubes was L = 100. The results of the simulation experiments were validated through bench experiments, and the relative errors of the coefficients of variation of traversal and longitudinal fertilizer distribution uniformity in the bench verification experiments were 11.45% and 2.8%, respectively. This demonstrated that the results of the simulation experiments were reliable. A mathematical model was constructed through bench experiments, in which the width of transversal fertilizer spreading (y) was regulated by operating parameters such as the rotational speed of the rotary tube (n) and the height of the tube mouth from the ground (h). The fitting results showed a corrected coefficient of determination of 0.9906. The experimental results were in agreement with the fitted results, thus adapting to crops with 40 cm to 160 cm spacing between rows. This study offers a theoretical foundation for the design of a rotary tube strip fertilizer spreader.

Introduction

In China, hilly and mountainous regions encompass approximately one-third of the country’s total arable land, representing a significant contributor to the nation’s food production¹. The productivity and mass of crops are inextricably linked to the use of fertilizers, which are a crucial component of agricultural output and can optimize agricultural production and ensure global food security^2,3. As indicated by the Food and Agriculture Organization of the United Nations, fertilizers account for a significant portion of crop yield, with a range of 40–60%⁴. However, the excessive application of fertilizers increases the cost of cultivation, causes environmental pollution, and simultaneously results in soil compaction, which in turn affects the growth of crop roots^5,6. The introduction and implementation of fertilizer spreaders have the potential to reduce the quantity of chemical fertilizers utilized, thereby enhancing their efficiency and minimizing environmental contamination. This approach offers a cost-effective and environmentally conscious strategy for enhancing crop yield while promoting sustainable agricultural development⁷. However, the mechanization rate of crop fertilizer spreaders in hilly mountainous regions is less than 50%, which is more than 20% points lower than the national average⁸. This also constrains the growth of grain production in these areas. Therefore, enhancing the mechanization rate of crop fertilizer spreaders in hilly mountainous regions is a crucial step in ensuring grain production.

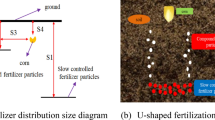
Currently, from the perspective of the type of fertilizer used, Chemical fertilizer spreaders come in two types: solid and liquid. This research focuses on solid particle fertilizer spreaders, which may be categorized into three main groups based on the various methods of fertilizer application: The first is the pneumatic spreader⁹, which expels fertilizer or other materials from the hopper onto the ground using compressed air. But they are typically used for large-scale commercial applications and are costly. The other type is utilized for the comprehensive spreading of the centrifugal fertilizer spreader¹⁰, however, the centrifugal fertilizer spreader equipment is larger in size and has a wider operating width. This results in an uneven distribution of fertilizers, low fertilizer utilization, and other issues¹¹. Therefore, it is not a suitable option for some of the hills in China, such as small pieces of land with a challenging operating environment. The last type is the strip fertilizer spreader¹², which has the advantage of being able to be limited in the horizontal fertilizer application range. Furthermore, it can maintain a high degree of longitudinal uniformity in fertilizer operations. It also has a high utilization rate. In comparison to the centrifugal fertilizer spreader, it is more suitable for hilly and mountainous areas. However, the traditional strip fertilizer spreader has several disadvantages, including the difficulty of trenching, the inability to adjust the width of the fertilizer spread, and other problems.

It is therefore imperative to develop a bespoke fertilizer spreader for the specific topography of hilly mountainous regions. This should be capable of accurately controlling the width of fertilizer spreading and improving the uniformity coefficient of fertilizer spreading, which will have a significant impact on the acceleration of agricultural development in hilly mountainous areas, the enhancement of land resource utilization, and the revitalization of rural communities. Therefore, for the hilly and mountainous areas in southern China, Chen¹³ designed a small Vertical Spiral Ditching-fertilizing Machine. it is suitable for hilly areas with 25°slope terrain and combines the three functions of ditching, fertilizer application and mulching into one; Sun¹⁴ designed a potato mid-tillage fertilizer applicator. The machine has small volume, light weight, sufficient power, compact structure and adjustable fertilizer discharge position.The above design of fertilizer spreaders for hilly areas has some adaptability but the uniformity of fertilizer spreading in their spreaders needs to be further optimized.

In recent years, scholars in both domestic and foreign countries have conducted extensive research on fertilizer spreaders with the aim of improving the uniformity of fertilizer spread^15,16. To enhance the utilization rate of fertilizer, Coetzee¹⁷ examined the impact of disc rotation speed, blade inclination, and other parameters on the uniformity coefficient of fertilizer through EDEM on a centrifugal fertilizer spreading machine. He conducted a discrete element simulation experiment and found that the experimental results could be predicted through the discrete element simulation approach. To enhance the performance and distribution uniformity of a self-developed centrifugal variable-speed fertilizer spreader, Shi¹⁸ constructed a model that depicts the relationship between the fertilizer particle distribution pattern and the operating parameters through EDEM discrete element simulation. Field validation tests were conducted using the optimal parameters to verify the accuracy and validity of the simulation model. Wang¹⁹ devised an unmanned aerial drone-based horizontal auger disc fertilizer spreader and developed a combination design of curved and straight blades and a cover plate with projections. This modification alters the fertilizer distribution from curved to non-hollow circular, thereby enhancing the fertilizer uniformity coefficient.

Extensive testing is done in testing halls of the different fertilizer spreader manufacturers or institutions like INRAE or in Bygholm, Denmark. Villette²⁰ designed a hybrid centrifugal application model by combining theoretical fertilizer equations of motion with statistical information. Gyldengren²¹ assess the effects of uneven fertilizer application by disc spreaders as affected by size and shape of fields and the size of the disc spreader. Piron²² investigated the overall spread patterns uniformity on non-flat fields through simulation. However, there is a paucity of research on the theoretical analysis of the drop distribution trajectory of fertilizer spreading and the control of the width of transversal fertilizer spreading (y) by fertilizer spreader operating parameters to adapt to the spacing of different crop ridges. In response to the aforementioned issues, we have devised a rotary tube strip fertilizer spreader with a controllable width of transversal fertilizer spreading (y), rendering it well-suited for hilly and mountainous regions. A simulation experiment was conducted to analyze the influence of the parameters of the rotary tube on the fertilizer uniformity coefficient. The orthogonal array testing was employed to identify the optimal parameters for the number of rotary tubes (Z), the angle (θ) between the rotary tubes and the vertical direction, and the length of rotary tubes (L). The processing prototype was integrated with the experimental apparatus to conduct a bench test, thereby validating the actual fertilizer spreading performance of the fertilizer spreader. A mathematical model for regulating the width of transversal fertilizer spreading (y) by the operating parameters, including the rotational speed of the rotary tube and the height of the tube mouth from the ground, was developed through bench experimentation. This constitutes the fundamental core research content of this study. The findings of this study are of considerable importance for the design and enhancement of fertilizer spreaders in hilly and mountainous regions.

Materials and methods

Structure composition

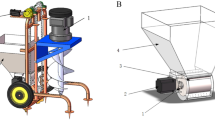
When operating in hilly and mountainous terrain, the rotary tube strip fertilizer spreader can be installed behind the tractor. By changing the relevant operating parameters, the width of fertilizer application can be adjusted to adapt to different spacing of ridges, thus allowing for the efficient and precise application of fertilizer in challenging terrain. As illustrated in Fig. 1, the rotary tube strip fertilizer spreader is designed for use in hilly mountainous terrain. It comprises a double-gear fertilizer discharger¹⁷, a fertilizer controller, a screw lifting mechanism, a rotary tube, a gear drive, a support plate, a connecting tube, a bearing, and a motor.

The rotary tube strip fertilizer spreader is integrated with the driven gear, which is the main working part of the rotary tube strip fertilizer spreader, and the main control part of the rotary tube strip fertilizer spreader is to change the relevant operating parameters to adjust the fertilizer application width.

Accordingly, the fundamental research objectives of this study are divided into two categories: the rotary tube and the establishment of the rotary rotational tube speed, the height of the tube mouth from the ground, and other operating parameters to regulate the width of fertilizer spreading mathematical model.

Fig. 1

Structural composition and working principle of rotary tube strip fertilizer spreader (use solidworks2022 and Microsoft Visio Professional 2021 together for drawing).

Theory of operation

The process of fertilizer spreading operation by the rotary tube strip fertilizer spreader is shown in Fig. 2 Its overall structure mainly consists of primarily comprises implements, a lifting mechanism, a rotary tube strip fertilizer spreader, fertilizer spreading motors, a power supply device, a double-gear fertilizer discharger, and a fertilizer controller, through the dual-gear fertilizer discharger to control the amount of fertilizer discharged. The rotary tube strip fertilizer spreader is operated in a forward direction along the ridge. The action of gravity causes the fertilizer discharger to release the fertilizer from the fertilizer tank into the rotary tube. The motor drives the gear mechanism, which in turn drives the rotary tube to disperse the fertilizer particles. In this process, the movement mechanism of the fertilizer particles can be delineated into three components: uniform circular motion while also in the horizontal direction of uniform linear motion, and to do the vertical direction of free-fall motion. Eventually the fertilizer is spread uniformly in the form of overlapping prolate cycloids.

Fig. 2

Fertilizer application operation process (use solidworks2022 and Microsoft Visio Professional 2021 together for drawing).

Kinematic characterization of fertilizer particles

The fertilizer particles are discharged from the fertilizer tank via the fertilizer discharger, whereupon they fall under the influence of gravity into the rotary tube. Following a period of descent, the particles are thrown into the air and subsequently fall to the ground. The entire process of fertilizer spreading can be divided into two distinct stages: the movement of fertilizer particles within the rotary tube and the movement of fertilizer particles in the atmosphere.

Kinematic analysis of fertilizer in a rotary tube

In the process of fertilizer throwing, the rotational angular velocity (ω) of the rotary tube is maintained at a constant value. The fertilizer discharger then discharges the fertilizer from the fertilizer tank into the rotary tube, after which the rotary tube is driven to rotate by the gear mechanism in order to throw the fertilizer particles. In the absence of rebound between the fertilizer and the rotary tube, as well as the interaction force between the fertilizers, the fertilizer falling within the rotary tube is solely subjected to the forces of gravity, centrifugal force, Kohl’s force (generated by the rotation of the rotary tube), and friction force¹⁸. As illustrated in Fig. 3, the rotary tube is distributed uniformly around the center tube. The mass of the fertilizer particle, which serves as the research object, is designated as m. Under the influence of centrifugal force and gravity, the particle moves along the rotary tube from the fertilizer inlet A to the fertilizer outlet B and subsequently ejects from the rotary tube at a specific velocity, resulting in a conical helix trajectory.

Fig. 3

Motion and force analysis of fertilizer particles in a tube: (a) OYZ Main view; (b) OXY Top view.

The rotary tube’s central axis is designated as the coordinate origin. The main view establishes the OYZ Cartesian coordinate system, while the top view establishes the OXY Cartesian coordinate system. The distance of the fertilizer particles’ movement at the moment t is designated as dr, and the movement time is designated as dt. Subsequently, the balanced equation is as follows:

$${F_1}\cos \theta - G\sin \theta - f=F$$

(1)

$$F=ma$$

(2)

Where F is the combined force on the fertilizer particles in the direction of the rotary tube, N; m is the mass of the fertilizer particles, kg; a is the relative acceleration of the fertilizer in the movement of the fertilizer spreading disc, m/s².

The centrifugal force on the fertilizer particles is:

$${F_1}=mr{\omega ^2}$$

(3)

The gravity of the fertilizer particles is:

$$G=mg$$

(4)

The friction between the fertilizer particles and the wall of the tube during the movement is:

$$f=\mu \left( {{F_c}+{F_1}\sin \theta - G\cos \theta } \right)$$

(5)

where F_c is Kohl’s force on the fertilizer particles as

$${F_c}=2m\omega v$$

(6)

Where v is the relative velocity of fertilizer particles moving on the rotary tube, mm/s.

The organizing equation is

$$ma=mr{\omega ^2}\cos \theta - mg\sin \theta - \mu \left( {2m\omega v+mr{\omega ^2}\sin \theta - mg\cos \theta } \right)$$

(7)

Simplification gives the differential equation as:

$$\frac{{{d^2}r}}{{d{t_2}}}{\text{ }}=r{\omega ^2}\cos \theta - g\sin \theta - \mu \left( {2\omega \frac{{dr}}{{dt}}{\text{+}}r{\omega ^2}\sin \theta - g\cos \theta {\text{ }}} \right)$$

(8)

Equation (8) is solved by setting its initial conditions as r = r₀, dr/dt = 0.

When r = R, the fertilizer particles leave and the velocity of the fertilizer particles as they leave the rotary tube is

$${v^2}{\text{ }}={\text{ }}{\left( {\frac{{dr}}{{dt}}} \right)^2}{\text{ }}+{\left( {\omega R} \right)^2}={\left( {\frac{{d\left( {l\cos \theta } \right)}}{{dt}}} \right)^2}{\text{ }}+{\left( {\omega \left( {L\cos \theta } \right)} \right)^2}$$

(9)

It can be observed that the speed of fertilizer particles exiting the rotary tube is contingent upon three primary factors: the angle θ between the rotary tubes and the vertical direction, the length of the rotary tubes L, and the instantaneous angular velocity of the rotary tube ω. The latter in particular affects the movement of the fertilizer in the subsequent stage of the airflow. Based on the design experience, it can be observed that when the angle θ is less than 20°, the vertical outflow of fertilizer does not have the effect of spreading the fertilizer. Conversely, when θ is greater than 80°, the spreading width of fertilizer is too large, resulting in a significant change in the movement trajectory. To maintain the trajectory of the conical helix, it is necessary to determine the optimal range of θ, which is between 20° and 80°. when L is less than 50 mm when the fertilizer directly out of the spreading effect does not have the effect of spreading fertilizer, and when L is greater than 150 mm, the spreading fertilizer trajectory gap between the too large impact on the fertilizer uniformity coefficient. The effect of fertilizer spreading is not uniform. In consideration of the dimensions of the frame and the width of fertilizer distribution in hilly and mountainous regions, the speed of the rotary tube has been determined to be 60 r/min.

Force analysis of fertilizer in air

The center of the rotary tube was taken as the coordinate origin and the OYZ right-angle coordinate system was established in order to demonstrate the force exerted by fertilizer particles in the air, as illustrated in Fig. 4.

Fig. 4

Force analysis of fertilizer particles in air.

From Fig. 4, it can be seen that the velocity (y) and vertical (z) of the particle’s motion in the horizontal direction can be described by the following Eq. 

$$\frac{{dy}}{{dt}}{\text{ }}=v\cos \theta$$

(10)

$$\frac{{d{\text{z}}}}{{dt}}{\text{ }}=v\sin \theta$$

(11)

Assuming that the wind speed and the rotational effect of the fertilizer particles themselves are neglected, according to the aerodynamic principle, the air resistance F_w acting on the fertilizer particles moving in the air is

$${F_w}{\text{ }}=\frac{{{C_a} \cdot {S_f} \cdot {\rho _d}}}{2}{v^2}$$

(12)

Where C_a is the air resistance coefficient; ρ_d is the air density, kg/m³; S_f is the windward area of the particles, m²; v is the relative velocity of the particles relative to the air, m/s.

According to Newton’s Second Theorem, the force balance equations for the particle’s motion in the air in the y and z directions are, respectively

$$\left\{ \begin{gathered} m\frac{{{d^2}y}}{{d{t^2}}}= - {F_w}\cos \theta \hfill \\ m\frac{{{d^2}z}}{{d{t^2}}}= - {F_w}\sin \theta - mg \hfill \\ \end{gathered} \right.$$

(13)

Where$m{\text{ }}=\frac{\pi }{6}{\rho _a}{d^3}$, ${S_f}=\frac{{\pi {d^2}}}{4}$then let $k{\text{ }}=\frac{3}{4} \cdot \frac{{{C_a}{\rho _a}}}{{d{\rho _d}}}$.

The differential equation is established as

$$\left\{ \begin{gathered} \frac{{{d^2}y}}{{d{t^2}}}= - k\frac{{dy}}{{dt}}\sqrt {{{\left( {\frac{{dy}}{{dt}}} \right)}^2}+{{\left( {\frac{{dz}}{{dt}}} \right)}^2}} \hfill \\ \frac{{{d^2}z}}{{d{t^2}}}= - g - k\frac{{dz}}{{dt}}\sqrt {{{\left( {\frac{{dy}}{{dt}}} \right)}^2}+{{\left( {\frac{{dz}}{{dt}}} \right)}^2}} \hfill \\ \end{gathered} \right.$$

(14)

$$\left\{ \begin{gathered} y=\frac{m}{k}\left( {\sqrt {{{\left( {\frac{{dy}}{{dt}}} \right)}^2}+{{\left( {\frac{{dz}}{{dt}}} \right)}^2}} \cdot v\cos \theta } \right)\left( {1 - {e^{ - \frac{k}{m}t}}} \right) \hfill \\ z=\frac{m}{k}\left( {\sqrt {{{\left( {\frac{{dy}}{{dt}}} \right)}^2}+{{\left( {\frac{{dz}}{{dt}}} \right)}^2}} \cdot v\sin \theta +\frac{{mg}}{k}} \right)\left( {1 - {e^{ - \frac{k}{m}}}} \right) - \frac{{mg}}{k}t \hfill \\ \end{gathered} \right.$$

(15)

Substitution gives the trajectory equation of the fertilizer spreading process as

$${\text{y}}=\frac{{\left( {z+\frac{{mg}}{k}t} \right) \cdot \sqrt {{{\left( {\frac{{dy}}{{dt}}} \right)}^2}+{{\left( {\frac{{dz}}{{dt}}} \right)}^2}} \cdot v\cos \theta }}{{\sqrt {{{\left( {\frac{{dy}}{{dt}}} \right)}^2}+{{\left( {\frac{{dz}}{{dt}}} \right)}^2}} \cdot v\sin \theta +\frac{{mg}}{k}}}$$

(16)

From Eqs. (15) and (16), it can be observed that when the proportion coefficient k is fixed, the fertilizer spreading height z directly influences the spreading width y, which then affects the uniformity coefficient of the fertilizer. In addition to the agronomic requirements of the crops commonly used in fertilizer spreaders and related experience, the height of the tube mouth from the ground h is designed to be 400 mm.

Analysis of fertilizer movement in air

When the rotary tube is in operation, it performs uniform circular motion around the center axis while also exhibiting uniform linear motion in the horizontal direction (x-axis) due to tractor traction. The fertilizer particles, dispersed under the influence of gravity, undergo free-fall motion in the vertical direction (z-axis). Consequently, the spatial drop distribution of the fertilizer particles is the result of a combination of uniform circular motion, uniform linear motion, and free-fall motion. The spatial distribution of the fertilizer particles is illustrated in Fig. 5.

Fig. 5

Spatial drop distribution of fertilizer particle population.

With the center of the rotary tube as the origin to establish a coordinate system, the x-axis for the forward direction of the machine, the z-axis for the vertical direction, with the vertical direction and the vertical direction and the forward direction of the machine perpendicular to the y-axis, the rotary tube threw fertilizer particles as the object of study, the fertilizer particles of the group of spatial drop distribution equations as follows:

$$\left\{ \begin{gathered} x={v_1}t+R\cos (\omega t) \hfill \\ y= - R\sin (\omega t) \hfill \\ z= - \frac{1}{2}g{t^2} \hfill \\ \end{gathered} \right.$$

(17)

Where: v₁ is the forward speed of the machine (m/s); ɷ is the angular velocity of the rotary tube rotation (rad/s); t is the time of movement of fertilizer particles in the air (s); R is the radius of the center of the rotary tube rotary center (m); x is the value of the x-coordinate of the spatial drop distribution of the fertilizer particle group (m); y is the value of the y-coordinate of the spatial drop distribution of the fertilizer particle group (m). z is the value of the z-coordinate of the spatial drop distribution of the fertilizer particle group, up to h (m).

where the distribution trajectory of the fertilizer particle population after falling to the ground is mainly determined by the equations of x and y, while the z equation determines the movement time of fertilizer particles in the air t, $t=\sqrt {\frac{{2h}}{{\text{g}}}}$Bringing t into the trajectory equation of the drop distribution shows that

$$\left\{ \begin{gathered} x={v_1}\sqrt {\frac{{2h}}{{\text{g}}}} +R\cos (\omega \sqrt {\frac{{2h}}{{\text{g}}}} ) \hfill \\ y= - R\sin (\omega \sqrt {\frac{{2h}}{{\text{g}}}} ) \hfill \\ \end{gathered} \right.$$

(18)

From the formula (18) can be seen: that when the rotary tube rotary center radius R is fixed, the tube mouth from the ground height h and the rotary tube rotating angular velocity ɷ directly affect the spreading of fertilizer width y, which in turn affects the fertilizer uniformity coefficient. The spatial drop distribution equation of the fertilizer particles group takes the derivative of time to get the motion velocity equation of fertilizer particles:

$$\left\{ \begin{gathered} {v_x}=\frac{{dx}}{{dt}}={v_1} - R\sin (\omega t) \hfill \\ {v_y}=\frac{{dy}}{{dt}}= - R\cos (\omega t) \hfill \\ {v_z}=\frac{{dz}}{{dt}}= - gt \hfill \\ \end{gathered} \right.$$

(19)

Then the sum velocity v is:

$$v=\sqrt {{v_x}^{2}+{v_y}^{2}+{v_z}^{2}} =\sqrt {{v_1}^{2}+{R^2}{\omega ^2}+2{v_1}R\omega \sin (\omega t)+{g^2}{t^2}}$$

(20)

Since Rω = v₂, v₂ is the tangential velocity of the particles leaving the orifice.

So let

$$\lambda =\frac{{{v_2}}}{{{v_1}}}=\frac{{R\omega }}{{{v_1}}}$$

(21)

λ is the ratio of tangential velocity and forward velocity of the particles when leaving the mouth of the tube, and the size of λ has an important influence on the distribution trajectory and working condition of the fertilizer particle group after falling to the ground.

Bringing Eq. (21) into Eq. (20), one obtains:

$${v_x}={v_1} - R\omega \sin (\omega t)={v_1}(1 - \lambda \sin (\omega t))$$

(22)

When λ < 1, it can be demonstrated that v₂ < v₁. Consequently, regardless of the position in which the rotary tube is situated, it can be shown that v_x > 0. This indicates that the horizontal partial velocity of the endpoint is always identical to the forward direction of the unit. Furthermore, its drop distribution trajectory can be described as a curtate cycloid, as illustrated in Fig. 6a. When λ is equal to 1, the horizontal partial velocity v_x is equal to zero when the endpoint is oriented towards the bottom. In this case, the drop distribution trajectory is a cycloid, as illustrated in Fig. 6b. When λ > 1, it signifies that v₂ > v₁. Consequently, when the rotary tube reaches a specific position, a scenario emerges wherein v_x<0, indicating that the horizontal partial velocity of the endpoint is contrary to the forward direction of the unit. This results in a prolate cycloid-shaped drop distribution trajectory, as illustrated in Fig. 6c.

Fig. 6

Fertilizer particles community drop distribution: (a) curtate cycloid; (b) cycloid; (c) prolate cycloid.

In order to ascertain the advantages and disadvantages of three distinct drop distribution trajectories of fertilizer particle groups following the application of fertilizer, a comparative analysis was conducted using the Adams software, which simulates the aforementioned trajectories.

Given that the rotary tube model is more complex, we simplify the unnecessary parts to ensure that the simulation conditions are realistic. This allows us to improve the calculation speed, as the current simulation only analyzes the rotary tube and its fixed support parts, while other devices are ignored. The SolidWorks 3D modeling software was utilized to construct the model, which was then saved in the X_T format and imported into Adams.

A rotary vice was created for the rotary tube and a rotary drive was added. A fixed vice was also created for the rotary tube and its supporting parts, as well as a moving vice for the aforementioned support parts on the ground, and a moving drive was also set up. The forward speed is set to a fixed value of 0.5 m/s, and the rotary drive derives the rotational speed of the rotary tube from the transmission ratio. A marker point should be created at the upper edge of the rotating tube. Once the simulation has been completed, a trajectory curve should be created under the “Review” tab. The resulting trajectory curve is illustrated in Fig. 7.

Fig. 7

Comparison of the three trochoids.

With the increase of angular velocity, the drop distribution trajectory of fertilizer particles from the prolate cycloid to the cycloid and then to the curtate cycloid changes, the trajectory period at the same time with the increase, the trajectory density is reduced, the longitudinal uniformity is reduced. When the drop distribution trajectory of fertilizer particles is a prolate cycloid, the fertilizer rotary tube rotates to the junction of the upper half cycle and the lower half cycle, and the direction of v_x is superimposed on the trajectory in the opposite direction of the forward direction of the machine, which enhances the width of fertilizer uniformity coefficient, and increases the transversal uniformity coefficient.

When the drop distribution trajectories of fertilizer particles are prolate cycloids, we overlap the prolate cycloid to improve the fertilizer uniformity coefficient. With the overlapping of the fertilizer drop distribution trajectories, the specific situation is shown in Fig. 8. Spreading fertilizer rotary tube for a tube, the drop distribution trajectory is a single prolate cycloid, the middle part of no track, spreading fertilizer is not uniform. To improve the fertilizer uniformity of the drop distribution of fertilizer is superimposed, the rotary tube is increased to two tubes, the drop distribution is two 180 ° difference in the phase of the prolate cycloid, the middle part of the trajectory of the complementary, and the fertilizer is then uniform. The rotary tube is increased to three tubes, the drop distribution trajectory is three 120° difference prolate cycloids, the middle part of the trajectory complements each other, and the fertilizer uniformity coefficient is significantly improved.

Fig. 8

Comparison of overlapping prolate cycloids.

Accordingly, the number of rotary tubes represents a significant variable influencing the efficacy of fertilizer distribution. In light of the inherent limitations associated with 3D printing, the optimal number of rotary tubes Z was identified as 1 ~ 3.

Fertilizer parameter setting

In this study, we selected the small granular urea fertilizer produced by China Agricultural Capital Group in Shandong Province, which has a water content of 0.89% and an actual density of 1.471 g/cm³. A total of 100 urea particles were randomly selected for the test, with an average length of 2.30 mm, width of 2.28 mm, and height of 2.28 mm. The Urea particle is presented in Fig. 9a. The equivalent diameter (D)¹⁹and sphericity (S_P)²⁰ were calculated according to Eqs. (23) and (24), respectively.

$$D=\sqrt[3]{{VWH}}$$

(23)

$${S_p}=\frac{D}{V} \times 100\%$$

(24)

Where: V is the length of the particle, mm; W is the width of the particle, mm; H is the thickness of the particle, mm.

Fig. 9

Urea particle: (a) the real urea particle; (b) derived particle for modelling work.

The calculated equivalent diameter of fertilizer particles (D) is 2.29 mm, with a sphericity (S_P) of 99.5%. As S_P is greater than 90%, the equivalent diameter of 2.29 mm sphere particles is selected as the EDEM simulation experiment particle model in Fig. 9b. The radius standard deviation is 0.168 mm, obeying a normal distribution, in order to achieve the maximum proximity to the real size of particles and thus reduce the simulation error.

Simulation experiment model

As mentioned earlier, in order to meet the agronomic needs of maize fertilizer application in hilly and mountainous areas, a standard maize planting agronomic model with a spacing of 600 mm (the rest of the inter-row spacing is not analyzed) was constructed to simulate the fertilizer application machinery for different crops under the same planting pattern, which is still applicable. The model was constructed using SolidWorks software, as illustrated in Fig. 10, and primarily comprises ground, corn seedlings, soil particle factory, and a rotary tube fertilizer spreader.

To improve the efficiency of EDEM simulation, the SolidWorks model constructed in Fig. 10 was simplified. We retained only the core mechanism at the bottom of the rotary tube strip fertilizer spreader—the rotary tube—and simplified the fertilizer discharger at the top into a fertilizer particle factory.The fertilizer particle factory was constructed as a cylinder with a diameter of 40 mm and a height of 50 mm. Fertilizer particle factory at the inlet of the fertilizer spreading rotary tube to match the outlet of the fertilizer discharger²¹ to ensure the continuity of fertilizer during operation. Therefore, all subsequent EDEM simulation models are composed of a single algorithm.

By changing the structural parameters of the core component of the fertilizer spreader—the rotary tube, namely the number of rotary tubes (Z), the angle (θ) between the rotary tubes and the vertical direction, and the length of the rotary tubes (L),while keeping other structures unchanged, models of rotary tube with different structures were constructed for EDEM simulation.

Fig. 10

SolidWorks model of the experiment.

EDEM simulation process

The SolidWorks software is employed to streamline the moel and subsequently save it as an STL file, which is then imported into the EDEM software. In conjunction with related studies, we select suitable contact models for different simulation objects^22,23. In this study, the Hertz-Mindlin (no-slip)^24,25 model in EDEM is selected as the contact model. The simulation-related parameters are also determined from relevant literature and investigations²⁶, as illustrated in Table 1. The material of the fertilizer spreader was set as PLA for the purpose of facilitating the optimization of prototype processing and manufacturing using 3D printing technology.

Table 1 Parameter settings for discrete element simulation.

In order to simulate the real field operation environment and prevent the fertilizer particles from bouncing, a layer of soil needs to be spread on the ground before the rotary tube strip fertilizer spreader starts its operation, simplify the soil particles into spherical particles with a diameter of 7 mm, and add material properties to them, as shown in Table 1. The soil particles were generated at a rate of 200,000 particles/s, and a total of 400,000 particles were generated, as shown in the purple part of Fig. 11.

Subsequently, a fertilizer particle factory is created, and the radius of the fertilizer particles is set to 1.145 mm, which corresponds to a spherical particle model. Material attributes are then added, as illustrated in Table 1, resulting in a total of 40,000 particles and a generation rate of 5,000 particles/s. Given that the fertilizer particles within the fertilizer spreader are in motion with the advancement of the device, it is necessary to generate the fertilizer particles instantaneously and in synchrony with the advancement of the fertilizer spreader. Furthermore, the advancement speed of the fertilizer particles must align with that of the fertilizer spreader. Therefore, the positive x-axis velocity of the fertilizer particles is set to 0.5 m/s, which corresponds to the forward speed of the fertilizer spreader.

In order to simulate the transmission of the gear mechanism to add linear rotation, the fertilizer spreader is located in the leftmost starting position of the soil model. The fertilizer particles are set to a rotational speed of 60 r/min, a running speed of 60 r/min, and a synchronization of 0.5 m/s in the x-axis direction. The simulation step size is set to 2.0 × 10^− 5 s, the data logging interval is 0.01 s, and the total simulation time is 10 s. The simulation process is illustrated in Fig. 11.

Fig. 11

Fertilizer spreading process in the simulation experiment (use EDEM2022 and Microsoft Visio Professional 2021 together for drawing).

Simulation experiment design and experiment metrics

In reference to the static experiment method, a two-dimensional matrix collection method^27,28 was employed for the collection of fertilizer and the calculation of spreading uniformity. In accordance with the agronomic requirements for corn planting, the distance between ridges is 600 mm. This is done to ensure that the monitoring area can effectively monitor the fertilizer spread by the rotary tube with varying structural parameters. Consequently, the total transverse monitoring area for fertilizer application is 1,210 mm. Given that the fertilizer spreader exhibits a consistent movement pattern across each fertilizer spreading cycle, it can be inferred that the longitudinal width of fertilizer applied in a single cycle is 500 mm. This estimation is based on the forward speed of the device (0.5 m/s) and the rotating speed of the rotary tube (60r/min). Consequently, EDEM post-processing is employed to define the Grid Bin Group within the Selection module. In light of the operational characteristics of the fertilizer spreader, a comprehensive assessment was undertaken to determine the optimal grid configuration. The transversal area was set to a range of -550 mm to 550 mm, while the longitudinal area was set to a range of -220 mm to 220 mm. Each grid was sized at 110 mm × 55.55 mm, resulting in a total grid area of 1210 mm×500 mm collection rectangle can be divided into 11 rows and 9 columns of 99 collection grids, as illustrated in Fig. 12. The mass of the fertilizer that falls into the center of this 550 mm grid (in the forward direction of the machine) is averaged by superimposing it on the grid. A single-row fertilizer uniformity calculation matrix (1 × 5) is formed by superimposing the mass of fertilizer falling into each row of the grid (perpendicular to the forward direction of the machine) at a distance of 500 mm. This process is repeated for all rows to create a single-column 9 × 1 uniformity calculation matrix. The total area of fertilizer spread by the rotary tube in one cycle, which is 550 mm x 500 mm, can be divided into five rows and nine columns, comprising a total of 45 calculation grids. The rotary tube strip spreader, which has a large spreading width, is not sufficiently accurate to measure fertilizer uniformity using the fertilizer transversal uniformity coefficient alone. Therefore, based on a comprehensive evaluation of the relevant factors, both the transversal fertilizer distribution uniformity and the longitudinal fertilizer distribution uniformity were selected as the experimental indexes of fertilizer uniformity²⁹, which were expressed as Y₁ and Y₂, respectively. A lower uniformity coefficient indicates a more uniform distribution of fertilizer, whereas a higher uniformity coefficient indicates a more uneven distribution^30,31. The uniformity coefficient was calculated according to Eq. (13).

Fig. 12

Schematic diagram of fertilizer monitoring area.

$$\overline {m} =\frac{{\sum\nolimits_{{i=1}}^{n} {{m_i}} }}{i}$$

(25)

$$S=\sqrt {\frac{{\sum\nolimits_{{i=1}}^{j} {{{\left( {{m_i} - \overline {m} } \right)}^2}} }}{{i - 1}}}$$

(26)

$${U_C}=\frac{S}{{\overline {m} }} \times 100\%$$

(27)

In Eq. (25): m_i is the mass of fertilizer in the i-th monitoring area, g; i = (1.2.3…5) for calculating transversal uniformity, i = (1.2.3…9) for longitudinal uniformity; Eq. (26): j is the number of statistical cells required, j = 5 for horizontal grid, j = 9 for longitudinal grid; Eq. (27): U_C is the uniformity coefficient of fertilizer spreading, %. When j = 9; Eq. (27) in U_C for fertilizer distribution uniformity, %. For ease of expression, the transversal fertilizer distribution uniformity is Y₁, and the longitudinal fertilizer distribution uniformity is Y₂.‾m is the average mass in the grid of statistical cells, g. S is the standard deviation between the statistical grid cells of a single experiment, g.

Results

Single-factor test

The theoretical analysis of the kinematics and dynamics of fertilizer-spreading particles revealed that the number of rotary tubes (Z), the angle between the rotary tubes and the vertical direction (θ), and the length of the tubes (L) are the parameters that most significantly affect the trajectory of the particles. These parameters were therefore selected for study to determine their influence on the distribution of fertilizer.

Effect of the length of rotary tubes L on transversal distribution regularity of fertilizer

When Z = 2 and θ = 50°, the length of rotary tubes L increases from 50 mm to 150 mm, representing a 25 mm growth. Figure 13 illustrates the regularity of fertilizer distribution in the transversal width direction. As the tube length L increases from 50 mm to 150 mm, the fertilizer in the central area gradually decreases, while the fertilizer in the peaks on both sides gradually rises. The difference between the mass of the fertilizer in the peaks on both sides and that in the central valley initially decreases and then increases. The transversal fertilizer distribution uniformity Y₁ initially exhibits a decline, followed by an uptick.

Fig. 13

Effect of length of rotary tubes L on transversal distribution regularity of fertilizer.

Effect of the length of rotary tubes L on longitudinal distribution regularity of fertilizer

When Z = 2 and θ = 50°, the length of the rotary tubes L increases from 50 mm to 150 mm, representing a 25 mm growth. Figure 14 illustrates the longitudinal width direction fertilizer distribution regularity. As the length of the rotary tubes L increases, the graph demonstrates a trend of steepness on both sides, with a flat middle. The longitudinal fertilizer distribution uniformity Y₂ initially decreases and then increases.

Fig. 14

Effect of length of rotary tubes L on longitudinal distribution regularity of fertilizer.

Effect of the angle θ between the rotary tubes and the vertical direction on transversal distribution regularity of fertilizer

When Z = 2, L = 100 mm, and θ grows from 20° to 80° with an increase of 15°, the fertilizer distribution law in the direction of the transversal width is illustrated in Fig. 15. In the range of 20°~50°, with the angle of θ increasing, the middle peak fertilizer gradually decreases, while the fertilizer of the two side peaks gradually rises. In the range of 50°~80°, with θ increasing, the middle peak fertilizer is gradually insufficient, and the fertilizer of the two side peaks is gradually excessive. The transversal fertilizer distribution uniformity Y₁ initially decreases and then increases.

Fig. 15

Effect of the angle θ between the rotary tubes and the vertical direction on transversal distribution regularity of fertilizer.

Effect of the angle θ between the rotary tubes and the vertical direction on longitudinal distribution regularity of fertilizer

When Z = 2, L = 100 mm, and θ grows from 20° to 80° with an increase of 15°, the distribution regularity of fertilizer in the direction of longitudinal width is illustrated in Fig. 16. As the angle of θ increases from 20° to 80°, the graph demonstrates a general trend of increasing steepness on both sides and decreasing flatness in the middle. Additionally, the longitudinal fertilizer distribution uniformity Y₂ exhibits an initial decline followed in turn by an increase.

Fig. 16

Effect of the angle θ between the rotary tubes and the vertical direction on longitudinal distribution regularity of fertilizer.

Orthogonal array testing

Experimental design

The comprehensive results of the aforementioned analyses and single-factor tests demonstrated that the number of rotary tubes (Z = 1 ~ 3), the angle (θ = 40°~60°) between the rotary tubes and the vertical direction, and the length of tubes (L = 90 mm ~ 110 mm) had a notable impact on both the transversal fertilizer distribution uniformity and the longitudinal fertilizer distribution uniformity. To further optimize the fertilizer application performance, the influence degree of the aforementioned factors and their interaction terms were investigated. Subsequently, a three-factor, three-level orthogonal experiment was conducted using the number of rotary tubes (Z), the angle (θ) between the rotary tubes and the vertical direction, and the length of tubes (L) as the experimental factors, represented as A, B, and C, respectively. The transversal fertilizer distribution uniformity (Y₁) and the longitudinal fertilizer distribution uniformity (Y₂) were employed as the experimental indices. The factor level table is presented in Table 2.

Table 2 Factor levels.

Simulation test scheme and results

The orthogonal array testing was conducted using the L₉ (3⁴) orthogonal Table³², which was selected for its suitability for this purpose. The test factors were the number of rotary tubes (A), the angle between the rotary tubes and the vertical direction (B), the length of the tubes (C), and the test indexes were the transversal fertilizer distribution uniformity (Y₁) and the longitudinal fertilizer distribution uniformity (Y₂). The results of the test were subjected to both an analysis of extreme variance³³ and an analysis of variance (ANOVA)³⁴ in order to ascertain the significance of the observed effects. The analysis was conducted using the Design-Expert 8.0.6 software, and the results are presented in Tables 3, 4, 5 and 6.

Table 3 Results of orthogonal array testing and extreme variance analysis of the transversal fertilization uniformity coefficient.

Table 4 Results of the orthogonal array testing and ANOVA of the transversal fertilization uniformity coefficient.

As illustrated in Table 3, the primary and secondary relationships influencing the transversal fertilizer distribution uniformity are the number of rotary tubes (Z), the angle (θ) between the rotary tubes and the vertical direction, and the length of tubes (L). The A₃B₂C₂ parameter scheme represents the optimal combination, with Z = 3, θ = 50°, and L = 100 mm.

As evidenced in Table 4, the number of rotary tubes Z, the angle θ between the rotary tubes and the vertical direction, and the length of tubes L all had highly significant effects on the transversal fertilizer distribution uniformity (p < 0.01).

Table 5 Results of orthogonal array testing and extreme variance analysis of the longitudinal fertilization uniformity coefficient.

Table 6 Results of the orthogonal array testing and ANOVA of the longitudinal uniformity coefficient.

As evidenced in Table 5, the primary and secondary relationships influencing the longitudinal fertilizer distribution uniformity are the number of rotary tubes (Z), the angle (θ) between the rotary tubes and the vertical direction, and the length of tubes (L). The A₃B₂C₂ parameter scheme represents the optimal combination, with Z = 3, θ = 50°, and L = 100 mm.

As can be seen from Table 6, the number of rotary tubes Z, the angle θ between the rotary tubes and the vertical direction, and the length of tubes L all had highly significant effects on the longitudinal fertilizer distribution uniformity (p < 0.01).

A comprehensive extreme variance analysis table and ANOVA table are employed to ascertain the optimal parameter combination scheme for achieving uniformity in both the transversal and longitudinal axes. The analysis reveals that the optimal combination is Z = 3, θ = 50°, and L = 100 mm.

To validate the precision of the extreme variance analysis and ANOVA, we selected the number of rotary tubes (Z = 3), the angle (θ = 50°) between the rotary tubes and the vertical direction, and the length of tubes (L = 100) within the optimization range, which was employed to conduct the simulation verification test. The results of the test demonstrate that the transversal fertilizer distribution uniformity (Y₁) is 14.24%, while the longitudinal fertilizer distribution uniformity (Y₂) is 12.75%. These values align with the optimization results, substantiating the accuracy of the optimization of the simulation parameters.

Bench test

Validation test

To ascertain the accuracy of the optimized rotary tube parameters and the viability of the EDEM simulation verification experiment, a prototype of a rotary tube strip fertilizer spreader was constructed and integrated with a double-gear fertilizer spreader capable of uniform fertilizer discharge, as illustrated in Fig. 17 On May 1, 2024, the fertilizer spreader was installed on the self-developed experimental bench outside the Intelligent Agricultural Equipment Engineering Laboratory of Harbin Cambridge University to conduct the verification experiment. The rotary tube’s center of projection at the initial position on the ground is taken as the coordinate origin to establish the O₂ × ₂Y₂Z₂ spatial right-angled coordinate system. In this system, the forward direction of the fertilizer spreader is in the direction of the Y₂ axis, the vertical direction is in the direction of the Z₂ axis, and the perpendicular direction to the direction of the Y₂ axis and the direction of the Z₂ axis is in the direction of the X₂ axis. In the rotary tube strip fertilizer spreader, 90 collection boxes were positioned at a distance of 1500 mm from each other in the Y₂ axis direction, with 10 columns in the X₂ axis direction and 9 rows in the Y₂ axis direction. The overall dimensions of a collection box were 55 mm × 55 mm × 55 mm. Due to the lack of a 110 mm × 55 mm collection box, in order to ensure that the collection unit is consistent with the EDEM simulation test, the weight of fertilizer in the two collection boxes was counted in the X₂ axis direction to form a 110 mm × 55 mm collection unit consistent with the EDEM simulation test, which also improves the accuracy of the measurement of the width of the fertilizer spreading, and all the collection boxes on the ground formed a 5 × 9 collection matrix to select the urea that is consistent with the simulation conditions, and the process of validation test is as Fig. 17 Shown.

Fig. 17

Validation test.

The weight of fertilizer particles in the cell was collected and weighed, and the transversal and longitudinal fertilizer distribution uniformity, designated as Y₁ and Y₂, were calculated. Three replicated experiments were conducted, and the mean values were taken as the results of the validation experiments, which yielded Y₁ = 15.87% and Y₂ = 13.11%, respectively.

Upon analysis of the validation test results, it becomes evident that the absolute error between the transversal fertilizer distribution uniformity (Y₁) and the simulation validation result of the rotary tube strip fertilizer spreader in the actual test is 11.45%. Similarly, the longitudinal fertilizer distribution uniformity (Y₂) and the simulation validation result of the absolute error of the simulation validation result is 2.8%.

The results of the validation test demonstrate that the absolute errors associated with the transversal fertilizer distribution uniformity (Y₁) and the longitudinal fertilizer distribution uniformity (Y₂) are within the normal range of fluctuations and are relatively low. These findings indicate that the rotary tube strip fertilizer spreader has been designed to achieve its intended purpose.

Influence of operating parameters on the width of transversal fertilizer spreading

The operating parameters, specifically the rotational speed of the rotary tube (n) and the height of the tube mouth from the ground (h), exert an influence on the width of transversal fertilizer spreading (y) of the rotary tube strip fertilizer spreader, as determined by the trajectory analysis of the drop distribution of the prolate cycloid. To investigate the influence of the operating parameters on the width of transversal fertilizer spreading (y) and adapt to the spacing of the ridges of different crops, a single-factor test was designed. The objective of this study was to examine the effect of the operating parameters on the width of transversal fertilizer spreading (y) of the rotary tube strip fertilizer spreader. The rotational speed (n) of the rotary tube and the height of the tube mouth from the ground (h) were selected as the test factors, and the width of transversal fertilizer spreading (y) was calculated as the test index. All tests were conducted in triplicate, and the resulting data were averaged.

Effect of the rotational speed of the rotary tube n on the width of transversal fertilizer spreading (y)

Based on the relevant research and the motors used in our laboratory, the fastest speed of the rotary tube is determined to be 150 rpm. From the definition of the prolate cycloid, it follows that

$$\lambda =\frac{{R\omega }}{{{v_1}}} \geqslant {\text{1}}$$

(28)

Bringing v₁ = 0.5 m/s, R = 0.4 m into Eq. (28) yields n = 30ω/π > 50 rpm, indicating that the rotational speed of the rotary tube range is 50 rpm ~ 150 rpm. A single-factor test was conducted using this range, which was set up in five levels, each with an interval of 25 rpm, resulting in a total of five groups of tests, each group repeated three times. The tube mouth was positioned at a height of 500 mm above the ground, and the test scheme is presented in Table 7.

The drop distribution trajectories observed in the bench test were found to be consistent with those simulated for the drop distribution trajectories. Figure 18a illustrates the variation of the width of the transversal fertilizer spreading(y) with the rotational speed (n) of the rotary tube. The experiment involved the removal of small squares with extremely sparse fertilizer at the transversal boundaries, while the remaining squares, where the fertilizer is mainly gathered, were used to determine the width of transversal fertilizer spreading (y).

Table 7 Effect of rotational speed n of the rotary tube on the width of transversal fertilizer spreading (y).

The drop distribution trajectory of fertilizer spreading shows prolate cycloid as the device advances. As shown in Fig. 18b, when the rotational speed n of the rotary tube is 50 rpm, the prolate cycloid is just formed, and the trajectory itself has a small amount of overlapping transversal uniformity; as the rotational speed n increases to 75 rpm, the trajectory itself gradually increases the amount of overlapping transversal uniformity becomes better. When the rotational speed n increases to 125 rpm, the fertilizer in the intermediate trajectory interlocking part accumulates a lot after superposition, but it does not affect the middle hollow part, so the transversal uniformity gradually becomes worse; when the rotational speed n increases to more than 150 rpm, the three fully interlocking transversal uniformity subsequently becomes better.

With the change of rotational speed of the rotary tube n, there is a clear distinction between the change curves of the width of transversal fertilizer spreading (y), which demonstrates that the rotary tube strip fertilizer spreader can regulate the width of transversal fertilizer spreading (y) by the rotational speed of the rotary tube n.

Fig. 18

Effect of the rotational speed n of the rotary tube on width of transversal fertilizer spreading (y): (a) 2-dimensional figure; (b) 3-dimensional figure.

Influence of the height of the mouth of the rotary tube from the ground h on the width of transversal fertilizer spreading (y)

The range of h-height of the mouth of the rotary tube from the ground was determined to be 300 mm to 700 mm based on relevant studies and the growth height of the crop during the fertilizer application period³⁵. A single-factor test was conducted using this range. The test factors were set at five levels, each with an interval of 100 mm, resulting in a total of five groups of tests. Each group of tests was repeated three times to obtain the average value. The speed of the rotary tube was set at 100 rpm, and the test scheme is presented in Table 8.

Observing the drop distribution trajectory of fertilizer spreading, is basically the same as the simulated drop distribution trajectory. The width of the transversal fertilizer spread (y) is dependent upon the height of the rotary tube’s mouth above the ground (h), as illustrated in Fig. 19a. We remove the small squares with extremely sparse fertilizer at the transversal boundaries and the remaining squares where fertilizer is mainly gathered serve as the transversal spreading width y,as shown in Fig. 19b.

Table 8 Effect of the height of the mouth of rotary tubes from the ground h on the width of transversal fertilizer spreading (y).

From the previous analysis, it can be seen that the height of the mouth of the rotary tube from the ground h determines the movement time of fertilizer particles in the air t

$$t=\sqrt {\frac{{2h}}{g}}$$

(29)

When the height (h) of the tube mouth from the ground is insufficient, the complete prolate cycloid cannot be formed. Conversely, as the height of the tube mouth from the ground of the rotary tube increases, the movement time of the fertilizer particles in the air increases, resulting in a gradual formation of the prolate cycloid and a gradual uniformity of the fertilizer spreading effect. When the height of the tube mouth from the ground (h) is excessive, the drop cycle of the prolate cycloid line is considerable. The gap in the middle of the drop distribution trajectory of three prolate cycloids superimposed on each other increases, and the fertilizer at the boundary of the trajectory is superimposed on the formation of the peak, which results in the destruction of the spreading of fertilizer uniformity. As the height (h) of the tube mouth from the ground continues to increase, the prolate cycloid drop cycle also increases. This results in the continuous dropping of multiple prolate cycloids in a single drop cycle. After the fertilizer particles have dispersed, the transversal fertilizer distribution uniformity shows a trend of initially decreasing, then increasing, and then decreasing again.

Fig. 19

Effect of the height h of the mouth of the rotary tube from the ground on width of transversal fertilizer spreading (y): (a) 2-dimensional figure; (b) 3-dimensional figure.

Fitted mathematical model of the rotational speed of the rotary tube n and height of tube mouth from the ground on the width of transversal fertilizer spreading (y)

From the above analysis, it can be seen that the transversal spreading width y of the rotary tube strip fertilizer spreader changes significantly when the operational parameters such as the rotational speed of the rotary tube n, and the height of the tube mouth from the ground h, are changed, which demonstrates that the rotary tube strip fertilizer spreader can be adjusted by changing the operating parameters to adjust the width of transversal fertilizer spreading (y), as shown in Table 9.

Table 9 Comprehensive effects of n and h on the width of transversal fertilizer spreading (y).

In order to derive a mathematical model of the rotational speed n and the height of the tube mouth from the ground h for regulating the width of transversal fertilizer spreading (y) of the rotary tube strip fertilizer spreader, the data from the above study were fitted as shown in Fig. 20. The fitted Eq. (30) is:

$$\begin{aligned} y & = {\text{2}}0{\text{54}}.{\text{32857}} - {\text{21}}.{\text{5}}0{\text{762}} \times n - {\text{8}}.{\text{62243}} \times h + 0.0{\text{23289}} \times n \times h + 0.{\text{22691}} \times n^{{\text{2}}} + 0.0{\text{19446}} \times h^{{\text{2}}} \\ & \quad - 0.0000{\text{942857}} \times n^{{\text{2}}} \times h - 0.00000{\text{157143}} \times n \times h^{{\text{2}}} - 0.000{\text{586667}} \times n^{{\text{3}}} - 0.0000{\text{1375}}00 \times h^{{\text{3}}} \\ \end{aligned}$$

(30)

Where R² = 0.9906, the fit is good, which demonstrates that the width of transversal fertilizer spreading (y) can be adjusted by the mathematical model of the rotational speed n and the height of the tube mouth from the ground h to apply to the spacing of the ridges of different crops.

Fig. 20

The fitted effects of n and h adjusting the width of transversal fertilizer spreading (y).

Conclusions

• 1. A rotary tube strip fertilizer spreader has been designed based on a gear mechanism drive, which is installed at the rear of a tractor with a three-point suspension. During operation, the rotary tube strip fertilizer spreader exhibits a uniform circular motion around the central axis, while also demonstrating uniform linear motion in the horizontal direction due to the tractor’s traction force. The drop distribution trajectory of the device is in the form of three complementary prolate cycloids, which enhances the mass of fertilizer spreading. A theoretical analysis of the movement and force of fertilizer particles in the fertilizer spreading rotary tube and air was conducted, resulting in the establishment of the equation of motion of fertilizer particles in the process of fertilizer spreading. The main factors affecting the fertilizer uniformity coefficient were identified as the number of rotary tubes Z, the angle θ between the rotary tubes and the vertical direction, and the length of rotary tubes L.

• 2. A discrete element simulation model of the fertilizer rotary tube was constructed using EDEM to simulate the process. The optimal structural parameter combinations affecting the transversal and longitudinal fertilizer distribution uniformity were obtained through the application of Design-Expert 8.0.6 to the single-factor and orthogonal array testing. The number of rotary tubes Z = 3, the angle θ between the rotary tubes and the vertical direction θ = 50°, and the length of the rotary tubes L = 100 mm were identified as the optimal structural parameter combinations through extreme analysis of variance and analysis of variance.

• 3. To ascertain the veracity of the optimization outcomes, the rotary tube strip fertilizer spreader was subjected to a validation test. The results demonstrated that the rotary tube strip fertilizer spreader, designed in accordance with the optimization parameters, exhibited a transversal and longitudinal fertilizer distribution uniformity of fertilizer spreading. The measured values were 15.87% and 13.11%, respectively, with a relative error of 11.45% and 2.8% with the simulation value. This demonstrates that the measured value has a smaller error and is essentially identical to that of the optimization value, thereby substantiating the assertion that the device meets the operational requirements of the fertilizer spreader.

• 4. A mathematical model was developed through bench experiments to regulate the spreading width of a rotary tube strip fertilizer applicator based on operational parameters such as rotational speed of the rotary tube (n) and height of the tube opening from the ground (h), with the aim of facilitating the application of the fertilizer spreader on crops with different spacing between ridges.

Discussion

In this study, we designed a rotary tube fertilizer spreader for mountainous terrain. Compared to similar technologies developed in France, Germany, or Denmark, this fertilizer spreader uses a fertilizer trajectory based on the drop distribution of overlapping prolate cycloids, which enables uniform fertilizer application in both the transversal and longitudinal directions. At the same time, we developed a mathematical model to adjust the spreading width of a rotary tube strip fertilizer spreader based on operating parameters.Through tests, we found that as n and y increase, the transversal fertilizer distribution uniformity Y₁ first decreases, then increases, and finally tends to stabilize.

Unfortunately, the fertilizer spreader’s uniformity did not meet ISO standards, possibly because we limited the testing range to a narrow scope during the design process, considering the application in narrow hilly areas, and therefore did not use ISO testing methods.Another regrettable point is that although it is applied to mountainous and hilly areas, we have overlooked the impact of inclination on the machinery.Consequently, future investigations must encompass comprehensive experimental research on the fertilizer spreader from several perspectives.