Introduction

The availability of nutrients in the soil is a key factor influencing agricultural productivity, long-term sustainability, and environmental quality. Macronutrients, including total nitrogen (TN), available phosphorus (AP), and available potassium (AK), are essential elements that directly control fundamental plant physiological processes such as cell division, photosynthesis, nutrient uptake, and energy transfer. These nutrients have a significant impact on biomass accumulation and yield formation by supporting the metabolic functions and structural development of plants1,2. Due to the high requirements of plants, maintaining optimal levels of these macronutrients through continuous monitoring, accurate soil testing, and appropriate fertilization strategies is crucial for maintaining soil fertility, avoiding nutrient depletion, and improving plant performance. In addition, balanced nutrient management also mitigates negative environmental impacts such as nutrient leaching, greenhouse gas emissions, and soil degradation3.

Accurate determination of soil macronutrient content is fundamental to precision agriculture as it enables site-specific fertilization and minimize the overuse of agrochemicals that can affect soil and water quality4. Conventional soil testing methods, such as field sampling followed by chemical analysis in laboratory, are widely used but have several limitations, including high cost, high labor intensity, and limited spatial coverage5,6. These limitations are particularly important in large-scale or heterogeneous agricultural regions where nutrient variability is high and timely decision-making is essential7,8.

With the advancement of Earth observation technologies, remote sensing has become a powerful tool for characterizing the spatial variability of soil properties. Satellite-based multispectral data, especially from the Sentinel-2 platform, has proven to be an effective tool for mapping soil properties due to its high temporal frequency, spectral richness, and spatial resolution (10–20 m)2,9,10,11. Various soil properties, such as texture, moisture, organic matter, and nutrient content, can influence the reflectance captured in specific spectral bands12. Therefore, remote sensing offers the opportunity to indirectly estimate soil macronutrients on a broad scale, with lower costs and improved temporal monitoring13.

Previous studies have applied various machine learning and statistical techniques to model soil nutrient distribution using satellite imagery7,14. However, most studies focused on individual nutrients or used simple vegetation or soil indices, often neglecting the interdependencies among soil attributes or the full spectral potential of the Sentinel-2 data. In addition, the presence of noise, redundancy, and multicollinearity in raw spectral bands can affect model performance and reduce generalizability4. To overcome these challenges, dimensionality reduction techniques such as principal component analysis (PCA) have become increasingly important in soil and environmental modeling8. PCA enables the transformation of correlated spectral bands into uncorrelated principal components, preserving the most important spectral variance and reducing noise and redundancy. In combination with appropriate standardization techniques, spectral indices derived from PCA can increase the robustness and interpretability of remote sensing models and improve their predictive performance in complex landscapes1.

In this study, a standardized spectral index called Principal Component Analysis–Standardized Spectral index (PCA-SSI) was developed based on PCA and standardization to accurately estimate the spatial variability of soil macronutrients—TN, AP, and AK—using Sentinel-2 imagery. The Miandoab plain in northwestern Iran was selected as the study area because it is an important agricultural region characterized by high soil heterogeneity, variable fertility levels, and diverse cropping systems. Challenges such as nutrient deficiency and soil salinization in this region highlight the need for accurate, data-driven methods to monitor macronutrient status, as improved soil management here can significantly increase productivity and enhance food security. Therefore, the main objectives of this research are: (1) extract the main spectral components from Sentinel-2 images using PCA, (2) develop a PCA-SSI that integrates the most informative bands for macronutrient prediction, (3) model and map the spatial distribution of TN, AP, and AK using this index, and (4) evaluate the performance of the proposed index in capturing soil fertility variability across the study area. By combining multivariate spectral transformation, statistical standardization, and high-resolution remote sensing data, this work provides a robust and practical framework for precise soil nutrients that can be used for digital soil mapping and optimized nutrient management programs in semi-arid agricultural systems.

Materials and methods

Geographical, climatic, and soil characteristics of the study region

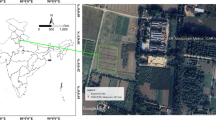
The study area encompasses approximately 8.3 × 104 km2 of agricultural land in the northwest of Iran, located between 45° 50′ 00″ and 46° 20′ 00″ east longitude and 37° 10′ 00″ and 38°50′00″ north latitude (Fig. 1). The region is characterized by a semi-arid climate according to the Köppen climate classification, with an average annual temperature of around 9 °C. Rainfall patterns are bimodal, with a wet season that lasts from early autumn to mid-spring and a dry season that lasts from mid-spring to early autumn. The average annual rainfall during the wet period is about 289 mm. The lithological composition of the region is diverse and consists of igneous, sedimentary, and metamorphic formations such as diorite, marble, andesitic volcanic rocks, marl, limestone, sandstone, shale, conglomerate, and Precambrian granite to granodiorite. These parent materials have contributed to the development of different soil types, which are mainly classified as Entisols and Inceptisols and show a low to moderate levels of pedogenic development. The main land use is agriculture with the main crops being winter wheat, barley, peas, sugar beets, alfalfa, oilseeds, corn, and various fruit crops. Although furrow irrigation was the predominant irrigation practice in the past, increasing water scarcity in recent years has led to a gradual transition to more water-efficient systems, in particular center pivot irrigation (https://www.swri.ir).

Fig. 1
figure 1

Study area boundary and sampling locations in Miandoab plain, West Azerbaijan Province.

Full size image

Soil sampling and macronutrient analysis

After delimiting and defining the boundaries of the study area, soil sampling was conducted randomly at 181 precise geographical locations distributed in the region (Fig. 1). The main objective of sampling strategy was to obtain a comprehensive representation of the chemical properties of the surface soils in the plain. At each sampling point, composite soil samples were collected from the 0 to 30 cm depth interval. More specifically, five subsamples (Fig. 2) were taken at a specific radius around each point and thoroughly mixed into a single composite sample Faramarzi et al.15. This depth range was chosen because it encompasses the zone of highest biological activity, nutrient exchange, and root development for cultivated plants. After collection, the samples were transported to the laboratory where they were air-dried at room temperature, gently ground, and passed through a 2 mm mesh sieve to prepare them for chemical analyzes. The concentrations of the key macronutrients were then determined according to established standard protocols. Total nitrogen (TN) was quantified using the classical Kjeldahl digestion method16. The available phosphorus (AP) was determined using the Olsen procedure17, and soil available potassium (AK) concentration was measured using a flame photometric technique18. These methods were selected due to their proven suitability for the analysis of calcareous soils, which are prevalent in the study region.

Fig. 2
figure 2

Soil sampling locations using the 5-point sampling method.

Full size image

Remote sensing data preparation and preprocessing

In this study, Sentinel-2 satellite images—including Band 2 (Blue, 0.458–0.523 μm), Band 3 (Green, 0.53–0.59 μm), Band 4 (Red, 0.64–0.67 μm), Band 8 (NIR, 0.85–0.88 μm), Band 11 (SWIR1, 1.57–1.65 μm) and Band 12 (SWIR2, 2.11–2.25 μm)—were used to extract the relevant indices. The data was obtained via the Google Earth Engine platform, a robust cloud-based computing environment designed for large-scale remote sensing and geospatial data processing. A specific time window was selected to minimize cloud cover, restricting it to less than 10% to ensure data quality. To enhance spectral fidelity and reduce atmospheric interference, an atmospheric correction was applied to the images. This process used the physically based SEN2COR algorithm, which was developed specifically for Sentinel-2 datasets. SEN2COR uses atmospheric parameters such as water vapor, aerosols, and surface pressure to remove scattering and absorption effects, and convert the data from top-of-atmosphere (TOA) reflectance to bottom-of-atmosphere (BOA) reflectance. For validation purposes, complementary atmospheric correction methods based on empirical models, including dark object subtraction (DOS), were also implemented and cross-compared with the SEN2COR outputs. After atmospheric correction, all images were subjected to geometric co-registration, and the spectral bands were resampled to a uniform spatial resolution of 20 m using bilinear interpolation. This resampling technique was chosen to avoid spatial discontinuities and distortions. It is noteworthy that the Sentinel-2 bands (e.g. blue, green, red, and near-infrared bands) originally recorded at a resolution of 10 m and those recorded at a resolution of 60 m (typically in conjunction with atmospheric correction bands) were rescaled accordingly to the targeted spatial resolution of 20 m. This harmonization was essential for the subsequent integrated data analysis19.

Standardized spectral reflectance index calculation

To determine the standardized spectral reflectance index (SSRI), all relevant reflectance bands from the Sentinel-2 images were first atmospherically corrected and spatially resampled to a common resolution. Each band was then normalized to a range of [0,1] to eliminate scale disparities among them, according to the Eq. 120,21.

$$Rt=\frac{{R}_{i}-{R}_{i-min}}{{R}_{i-max}-{R}_{i-min}}$$
(1)

where, \({R}_{i}\) denotes the reflectance value of band i and \(Rt\) is the normalized reflectance.

PCA was then applied to the matrix of normalized reflectance values. This dimensionality reduction technique enabled the extraction of principal spectral patterns by transforming the correlated spectral bands into a series of uncorrelated components. The first principal component (PC1), which has the highest variance in the spectral data, was selected as the core component of the SSRI. To standardize PC1, a Z-score normalization was performed as follows (Eq. 2).

$$SSRI=\frac{(PC1-\mu )}{\sigma }$$
(2)

where, μ and σ represent the mean and standard deviation of PC1 values across the entire image, respectively.

The SSRI enhances spectral contrast and enables effective discrimination of surface features such as vegetation, bare soil, water bodies, and urban areas. By integrating spectral information from all relevant bands into a single index, the SSRI provides a robust metric for analyzing land cover and assessing spectral variability. Importantly, this ensures that the SSRI is not just another spectral index but rather a generalized and standardized framework that can be consistently applied across different regions and time periods.

Development of predictive models for spatial distribution of soil macronutrients using the SSRI

In this study, prediction models for macronutrient concentrations in soil were developed based on the SSRI. First, the point data obtained from chemical soil analyzes were divided into two different subsets. To ensure the robustness of the model, a random sampling approach was employed, which 70% of the data used for model train and the remaining 30% for test and performance evaluation. After calculating the SSRI values for the entire study area, simple linear regression analyzes were performed to investigate the relationships between spectral reflectance (expressed by SSRI) and soil chemical properties. Separate regression models were established for each macronutrient element, with SSRI as the independent variable and measured nutrient concentration as the dependent variable. Using these regression equations and the spatial SSRI map, predictions of nutrient concentration were made for each image pixel, resulting in spatial distribution maps of soil macronutrients21.

Model evaluation

To assess the spatial accuracy and reliability of the predictive maps, the estimated nutrient concentrations were extracted at the geographic locations corresponding to the points in the test dataset and then compared with the actual measured values. The quality of the predictions was assessed using various statistical metrics, including the coefficient of determination (R2), root mean square error (RMSE), mean squared error (MSE), and the ratio of performance to interquartile distance (RPIQ). While R2, RMSE, and MSE provide information on the overall fit and error magnitude, RPIQ offers a scale-independent measure of predictive performance by relating the model error to the interquartile range of observed values. This combination of metrics provided a more comprehensive understanding of the model’s performance in capturing the spatial variability of soil macronutrients22,23. The statistical metrics were calculated as follows (Eqs. 3–6).

$${R}^{2}=1-\frac{{\sum }_{n=1}^{n}{({y}_{i}-{y}_{j})}^{n}}{{\sum }_{n=1}^{n}{(\overline{y }-{y}_{j})}^{n}}$$
(3)
$$RMSE = \sqrt {\frac{1}{n}\sum\limits_{{n = 1}}^{n} {(y_{i} - y_{j} )^{n} } }$$
(4)
$$MSE = \frac{1}{n}\sum\limits_{{n = 1}}^{n} {(y_{i} - y_{j} )^{n} }$$
(5)
$$RPIQ=\frac{{Q}_{3}-{Q}_{1}}{RMSE}=\frac{IQR (y)}{RMSE}$$
(6)

where, yi and yj are the observed and predicted values, respectively; \(\overline{y }\) is the mean of the observed values; Q1 and Q3 represent the first and third quartiles of the observed values; and IQR (y) denotes the interquartile range, which is defined as the difference between the third and first quartiles. A higher RPIQ value indicates better model performance. Typically, RPIQ values are interpreted as follows: RPIQ > 2 indicates a good model; 1.5 ≤ RPIQ ≤ 2 indicates an acceptable model; and RPIQ < 1.5 indicates a weak model.

Results

Descriptive statistical analysis of soil macronutrients

The mean TN content in the soil was found to be 0.092%. The minimum and maximum values were recorded at 0.010% and 0.80%, respectively. A coefficient of variation (CV) of 75.2% indicates a relatively high variability of nitrogen concentrations across the studied soils (Table 1). This heterogeneity may be due to differences in agricultural practices, vegetation cover, and the rate of organic matter decomposition at different sites24. Among the analyzed macronutrients, AP showed the greatest variability, with a CV of 164.9%, indicating considerable variation in its concentration. AP levels ranged from 1.8 to 361.0 ppm, with a mean value of 20.78 ppm (Table 1). This pronounced variability can be attributed to the dynamic behavior of AP in soils, its particular chemical properties, and anthropogenic influences. In contrast to other macronutrients, P is relatively immobile in soil, as it frequently becomes fixed in insoluble forms such as calcium, iron, and aluminum phosphates. As a result, despite repeated applications of phosphate fertilizers by farmers in each growing season, AP tends to accumulate in localized and non-uniform patterns within the soil profile. In addition, many farmers routinely apply phosphorus fertilizers each year without conducting soil tests. This practice often leads to excessive phosphorus loading in certain areas, and exacerbates spatial heterogeneity. The problem is particularly evident in agricultural lands with a long history of chemical fertilizer usage25. The mean AK content was 377.42 ppm, with values ranging from 52 to 1321 ppm. The CV for K was 49.3%, indicating moderate variability compared to nitrogen and phosphorus (Table 1). This variability can be influenced by factors such as the mineralogical composition of the parent material, cropping pattern, irrigation management, and site-specific potassium fertilization practices26,27.

Table 1 Summary of descriptive statistics for soil macronutrient concentrations.
Full size table

Correlation between spectral bands and soil macronutrients

The Pearson correlation matrix between selected Sentinel-2 spectral bands and three soil macronutrients showed that TN had the strongest correlation with spectral reflectance. The correlation coefficients for TN were consistently high across all bands and statistically significant a confidence level of 99% (α = 0.01). The highest correlation was observed in the green band (Band 3) with a coefficient of 0.878, closely followed by the red band (Band 4) with a value of 0.876 (Table 2). These strong associations are likely due to the direct influence of nitrogen on chlorophyll content in plants, which significantly affects reflectance in the visible and near-infrared (NIR) regions of the spectrum. In contrast, AP showed the weakest correlation with the spectral bands. Its correlation coefficients were generally low, ranging from 0.22 to 0.24, and none reached statistical significance (Table 2). This weak correlation may reflect relatively low mobility of phosphorus in soil and its indirect influence on plant spectral characteristics. AK showed moderate correlations with several spectral bands, with the highest correlation observed at Band 11 (SWIR 1), at 0.591 (Table 2). Considering the role of potassium in stomatal regulation and plant water balance mechanisms, this relationship is biologically plausible, although it is significantly weaker than that observed for nitrogen. Overall, the results indicate that nitrogen is more strongly associated with spectral reflectance in the visible, NIR, and SWIR regions, while phosphorus exerts a comparatively smaller influence on spectral responses. These results indicate that the nitrogen content in soil can be estimated more accurately and reliably by remote sensing data than the other two macronutrients investigated.

Table 2 Pearson correlation coefficients between Sentinel-2 spectral bands and soil macronutrients.
Full size table

Correlation analysis between the SSRI and soil macronutrients

PCA was performed to reduce the dimensionality of the spectral data and to extract the most important features from selected Sentinel-2 bands. The results showed that the first principal component alone explained 96.31% of the total variance in spectral reflectance values (Fig. 3). This high percentage indicates that most of the useful information contained in the spectral bands is actually concentrated in the first component. Consequently, this component was standardized and referred to as SSRI to be used in the subsequent correlation analyzes with soil macronutrients.

Fig. 3
figure 3

PCA of various spectral bands from Sentinel-2 satellite imagery.

Full size image

Pearson correlation analysis revealed a strong and statistically significant positive correlation between SSRI and TN in soil (r = 0.875), significant at the 99% confidence level (Fig. 4). This finding indicates that nitrogen, which directly influences chlorophyll concentration and plant greenness, plays a dominant role in controlling spectral reflectance variations. A moderate and statistically significant correlation was also observed between SSRI and AK (r = 0.560) (Fig. 4). This relationship may reflect the involvement of potassium in important physiological processes such as water regulation, photosynthesis efficiency, and cellular structural stability. In contrast, the correlation between SSRI and AP was relatively weak (r = 0.230) and not statistically significant at a 99% confidence level (Fig. 4). This result is consistent with the limited mobility of phosphorus in the soil and its indirect influence on the reflectance properties of plants.

Fig. 4
figure 4

Correlation between spectral SSRI and soil macronutrient concentrations.

Full size image

Regression analysis of SSRI for estimating soil macronutrient concentrations

To evaluate the potential of the SSRI, derived from Sentinel-2 satellite data, in estimating soil macronutrient concentrations, regression analyses were performed for TN, AK, and AP. The results revealed that SSRI had a statistically significant linear relationship with TN and AK concentrations, whereas no such relationship was observed for AP; consequently, no regression model was developed for phosphorus.

For TN (%), the regression equation (Eq. 7) showed high predictive performance during the training phase, with an R2 of 0.77, RMSE of 0.04%, and MSE of 0.01. The corresponding RPIQ of 2.43 indicates that the model is good in terms of predictive capability during training (Table 3 and Fig. 5a). When applied to the testing dataset (55 samples), the R2 decreased to 0.34, indicating lower explanatory power. Nevertheless, RMSE and MSE remained low at 0.02% and 0.001%, respectively, suggesting limited numerical error. The RPIQ for testing was 1.25, reflecting weak predictive performance, which indicates that while the model maintains reasonable accuracy, its generalization ability is somewhat limited (Table 3 and Fig. 5c).

Table 3 Model validation results for soil macronutrient prediction.
Full size table
Fig. 5
figure 5

Measured versus predicted values of soil macronutrient concentrations for: (a) TN (%) training data, (b) TN (%) test data, (c) AK (ppm) training data, and (d) AK (ppm) test data.

Full size image

For AK, the regression model (Eq. 8) also performed satisfactorily. During training, R2 reached 0.72, with RMSE = 166.49 (ppm) and MSE = 0.27, and an RPIQ of 2.21, indicating good predictive performance (Table 3 and Fig. 5b). In the testing phase, numerical accuracy improved, with RMSE decreasing to 110.37 (ppm) and MSE to 0.12, although R2 decreased to 0.46 (Table 3 and Fig. 5d). The RPIQ of 1.66 suggests acceptable predictive performance, demonstrating that the AK model retains relatively stable predictive ability across both datasets despite a slight decline in explanatory power. Also, regression analysis for AP did not show a statistically significant relationship with SSRI, and thus no predictive model was developed for this nutrient.

$${\text{TN}} = - 1.73{\text{E}} - 02 + 0.65 \times {\text{SSRI}}\left( {0 - 1} \right)$$
(7)
$${\text{AK}} = 194.75 + 1090.86 \times {\text{SSRI}}\left( {0 - 1} \right)$$
(8)

Spatial analysis of soil macronutrient levels across the study area

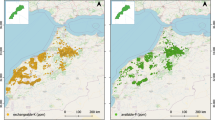
Figure 6a illustrates the spatial distribution of TN in the soils of the study area, which varies between 0.01 and 0.80%. It is evident that nitrogen concentrations are predominantly in a medium to high range in most parts of the region, especially in the western and central zones where the colors change from yellow to pink, indicating elevated levels. This pattern can be attributed to agricultural activities, the use of nitrogen-based fertilizers, and favorable climatic conditions that enhance nitrogen retention in the soil. Conversely, Fig. 6b shows the spatial distribution of AK throughout the area, with values ranging from 52 to 1321 ppm. The color gradients show that large parts of the study region—especially the southern, southeastern, and central areas—marked by yellow to orange hues, corresponding to low to moderate potassium availability. Only limited sections in the northern and eastern parts show higher potassium concentrations, represented by purple and pink shades. This uneven distribution indicates a widespread potassium deficiency throughout the study area. Given the important role of AK in regulating osmotic pressure, enzymatic activities, and nutrient transport in plants, such deficiency can significantly affect crop yields and soil health28. Therefore, it is crucial to include potassium supplementation as a priority in soil management and fertilization strategies in these affected zones. Overall, these results highlight the need for site-specific nutrient management to optimize the distribution and application of essential elements across the region.

Fig. 6
figure 6

Spatial patterns of TN (a) and AK (b) across the study area.

Full size image

Discussion

The results of the present study show that the SSRI models the spatial variability of certain macronutrients in soil with satisfactory accuracy. The descriptive statistical analysis (Table 1) revealed that AP had the highest spatial variability within the study area, with a CV of 164.94%. In contrast, TN and AK showed moderate to high variability, with CV values of 75.23% and 49.27%, respectively. The pronounced heterogeneity observed, particularly for AP, may be attributed to the improper and untested application of phosphate fertilizers, the low stability of phosphorus in soil, and the formation of insoluble compounds29,30,31. Conversely, the relatively lower variability of AK could be related to the mineralogical origin of the soil, cropping patterns, and irrigation practices32,33,34.

Correlation analysis between the Sentinel-2 spectral bands and the soil nutrient elements (Table 2) showed that TN had the strongest significant correlations in all bands, especially with the green band (Band 3, r = 0.878) and the red band (Band 4, r = 0.876). These results are in good agreement with the direct involvement of nitrogen in chlorophyll synthesis and its influence on the spectral reflectance properties of vegetation35. In contrast, AP showed weak correlations with the spectral bands (r ≈ 0.22–0.24), none of which reached statistical significance. This probably reflects the limited mobility of phosphorus in the soil and its indirect effects on plant cover. AK showed moderate correlations, especially with the SWIR1 band (Band 11, r = 0.591), which may be attributed to role of potassium in regulating water balance, stomatal function, and stabilizing cell structure21.

PCA revealed that PC1 accounted for more than 96.31% of the total variance in the spectral data (Fig. 3). This substantial proportion indicates that the most important and dominant information contained in the selected bands is encapsulated in this component. After standardization of PC1 using the Z-score method, the SSRI was derived and subsequently used as a composite spectral reflectance index in further analyzes. The relationship between the SSRI and the macronutrient elements (Fig. 4) showed significant positive correlations with TN (r = 0.875) and AK (r = 0.560), while AP continued to show a weak and statistically insignificant correlation (r = 0.230). This pattern confirms the superior ability of SSRI in modeling nitrogen content compared to other nutrients, especially considering that nitrogen is more strongly associated with plant growth and spectral reflectance Faramarzi et al.15, Cheng36.

The regression analysis between the SSRI and the macronutrient elements (Fig. 5 and Table 3) confirmed the previous results. The TN model showed high accuracy in the training phase with a R2 of 0.77, RMSE of 0.04%, MSE of 0.01, and RPIQ = 2.43 (good predictive performance); however, its performance decreased in the test phase (R2 = 0.34, RMSE = 0.02%, MSE = 0.001, RPIQ = 1.25 (weak predictive performance)). The pronounced decrease in R2 during validation, particularly for TN, is likely attributable to the high mobility and dynamic behavior of nitrogen in soils. Nitrogen is among the most labile soil nutrients, subject to continuous transformations through mineralization, immobilization, leaching, denitrification, and rapid plant uptake. These pronounced spatiotemporal variations result in considerable heterogeneity in nitrogen distribution, thereby constraining the predictive capacity of the model during validation. Consequently, the observed decline in model performance for TN reflects the inherent variability and complexity of the soil nitrogen cycle rather than limitations of the modeling approach. Notably, despite this decline, the low RMSE during testing indicates that the model retains strong practical applicability and reliability for field-scale predictions28,37.

The AK model exhibited a similar trend, with R2 values of 0.72 and 0.46, RMSE values of 166.49 ppm and 110.37 ppm, MSE values of 0.27 and 0.12, and RPIQ values of 2.21 (good predictive performance) and 1.66 (acceptable predictive performance) in the training and testing phases, respectively (Fig. 5 and Table 3). Compared with the TN model, the AK model showed relatively greater stability during the testing phase. This behavior can be explained by the chemical characteristics of potassium in soils. AK is predominantly present in ionic form (K+) in the soil solution and, unlike phosphorus, it is not readily immobilized through fixation reactions. Consequently, it is more mobile within the soil profile and less likely to be bound in insoluble forms such as calcium precipitates or iron and aluminum oxides. This higher mobility and availability in the soil solution means that variations in AK are more strongly reflected in plant nutritional status and, indirectly, in canopy spectral reflectance, thereby allowing more accurate estimation from remote sensing data38,39,40,41.

In contrast, the results showed no significant relationship between AP and the SSRI index, and thus no predictive model for AP could be developed. This limitation is closely tied to the inherent characteristics of phosphorus in soils. Phosphorus is a nutrient with extremely low mobility; it is often concentrated in subsurface soil layers and is rapidly fixed through reactions with Ca2+ in alkaline soils or Fe3+ and Al3+ in acidic soils, resulting in the formation of insoluble compounds. As a result, the fraction of phosphorus that remains available in the soil solution is minimal and its direct influence on plant reflectance signals is weak21,42,43.

From a remote sensing perspective, spectral indices primarily capture signals from the soil surface and vegetation canopy. Consequently, nutrients with low solubility and limited translocation, such as phosphorus, exert little to no direct effect on spectral reflectance. This suggests that the lack of predictability for AP is not only a limitation of the SSRI approach but also reflects the broader constraints of spectral indices for estimating low-mobility nutrients. In other words, while SSRI proved effective for more mobile nutrients such as TN and AK, the prediction of phosphorus content remains challenging due to its low mobility, subsurface distribution, and weak spectral activity44,45,46.

The spatial analysis (Fig. 6a and b) further supports the statistical findings. TN concentrations predominantly range from moderate to high across most parts of the study area, especially in the western and central regions, probably due to repeated applications of nitrogenous fertilizers as well as more favorable climatic conditions for nitrogen retention. Conversely, the spatial distribution of AK shows a widespread deficiency in the southern, southeastern, and central parts of the region. This heterogeneous pattern emphasizes the need for site-specific nutrient management, especially for potassium, to increase crop productivity. In addition, the use of high-resolution maps generated through this approach can play a crucial role in optimizing the use of nutrients47,48. In summary, the results of this study show that the SSRI-based approach in combination with simple statistical models offers significant potential for predicting the spatial variability of nitrogen and potassium in soil. However, elements with lower mobility, such as AP, still require direct measurement methods or more sophisticated modeling approaches that integrate remote sensing data, soil properties, and land management history.

Conclusion

The results of this study demonstrated that the Sentinel-2 satellite data and the spectral indices derived from them—in particular the novel SSRI based on principal component analysis—have considerable capabilities in the spatial modeling of certain soil macronutrients, especially TN and AP. The observed significant correlations between the spectral indices and TN content reflect the indirect but reliable influence of vegetation cover on spectral reflectance, allowing inference of plant nutritional status from remote sensing data. The model performance for AK was also acceptable, although with lower accuracy compared to nitrogen. Conversely, AP modeling faced limitations mainly due to its limited mobility, subsurface concealment in the soil layers, and lack of direct impact on the spectral indices. These results suggest that the integration of soil science knowledge with remote sensing technologies can provide an effective, non-destructive, rapid, and cost-efficient approach for monitoring soil nutrient status at agricultural and regional scales. Based on these results, it is recommended that future research aiming to improve the modeling accuracy of low-mobility or spectrally inactive elements include a combination of remote sensing data with ground-truth information, soil physicochemical properties, and topographic parameters. In addition, the use of multi-temporal Sentinel-2 imagery throughout the growing season and the derivation of spectral reflectance indices from these time-series images can better capture nutrient dynamics, enabling dynamic monitoring and timely management recommendations. The expansion of such integrated approaches in the context of precision agriculture has the potential to optimize fertilizer use, increase productivity, and reduce environmental impacts in agricultural systems. Moreover, the SSRI index could serve as a valuable environmental variable for integration into nonlinear and machine learning models, potentially enhancing predictive accuracy and providing deeper insights in future studies.