Introduction

The first theoretical explanation and study of the self-synchronization effect in exciters was reported by Blekhman I.I. in 19531,2. In the following thirty years, the self-synchronization theory of two identical exciters in a vibrating system has been rapidly developed and widely applied, a new class of vibro-machines, such as sizing screens, conveyors, feeders, shakers and so on, had been developed in various industries2. Later Wen expanded on Blekhman’s work and developed an integral average method to address self-synchronization problems in vibrating machine3. According to wen’s theory, the synchronization problem of two vibrators in a vibration system was transformed into an analysis of the existence and stability of the zero-solution considering small parameters by Zhao4.

Zhang et al. used the average method to study the vibratory synchronization transmission (VST) of a cylindrical roller in a vibrating mechanical system excited by two exciters, and achieved the criterion of implementing synchronization of two exciters and that of ensuring VST of a roller5.They also studied the synchronization of two exciters in a nonlinear vibrating system using the average method, in which, the spring has a non-linear restoring force with segmented linear characteristics6.

Although the vibration system with two exciters is widely used, sometimes in order to obtain greater exciting force or achieve new vibration machine functions, three or more exciters are required. Yan studied the synchronization and stability of self-synchronization vibration system with three parallel exciters by Hamiltons Principle, and verified its electromechanical coupling mechanism by Simulink, it was found that the phase difference angle of the two homodromy exciters in this vibration system is always around 180°7. When studying the synchronization and dynamic characteristics of multipe eccentric rotors in a vibration system by theoretical analysis and experiments, Zhang and Chen et al. also obtained the similar results8,9,10.The exciting forces of two homodromy exciters are almost opposite, and the two forces almost counteract each other. Multiple exciters not only do not increase the vibration amplitude of the system, but also make the amplitude smaller than that of the two exciters.

Controlled synchronization proposed by Blekhman I.I.11 can effectively solve this problem. Blekhman I.I.et al. provided the definition of controlled synchronization and an example of two vibroactuators based on a speed-gradient method12. Wen systematically elaborated the controlled synchronization of multi-motor vibration systems based on the traditional control methods and the intelligent methods3. To implement the in-phase controlled synchronization between the two co‑rotating eccentric rotors, Fang et al. systematically designed the controllers based on master–slave control structure and sliding mode control algorithm13. Jia et al. investigated controlled synchronization of three co-rotating exciters based on a circular distribution in a vibratory system, and found that the stability of the vibrating system depends on the controlling method and suitable controlling strategy in the controlled synchronization motion14. Kong et al. investigated controlled synchronizations of three co-rotating eccentric rotors in line driven by induction motors in a vibrating system, the controllers by an adaptive sliding mode control algorithm based on a modified master–slave control strategy were designed, and the stability of the controllers was verified by using Lyapunov theorem15. Kong used the same control algorithm and strategy to study the phase and speed synchronization control of four eccentric rotors driven by induction motors in a linear vibratory feeder, the designed controller achieves four eccentric rotors operating synchronously with zero phase difference16. The composite synchronization, which is a combination of self-synchronization and controlled synchronization, of four eccentric rotors driven by induction motors in a vibration system with a mass-spring rigid base was researched by Kong and Wen 17, the results showed that the composite synchronization method provides a possible energy-saving way to address the synchronization problem.

Through literature research, it was found that the existing dual-exciter vibration system of the vibration device generates relatively small excitation forces in the working conditions, and cannot adequately meet the large excitation force requirements in most engineering operations. The existing multi-stimulator vibration systems mostly adopt electronic control synchronization. Although the above controlled synchronization methods are effective, they have significant limitations in practical applications. The controlled synchronization requires configuring corresponding hardware, software, and appropriate control algorithms and strategies, which leads to complex systems and high costs, especially in the vibration system of multi exciters, this limitation is extremely prominent. The monitoring sensors for the working state parameters of the exciters operate under severe vibration conditions, which results in low system reliability. All exciters must be powered on during operation, which is disadvantageous from an energy-saving perspective.

Elastic coupling mechanical synchronization of two or three co-rotating rotors in a plane vibration system was studied by Hou and Du, which can achieve zero phase difference synchronization between two homodromy exciters, and maximize the combined excitation force of two or three co-rotating exciters. The elastic coupling mechanical synchronization does not have the aforementioned limitations of controlled synchronization, but can also avoid the rigid starting impact between multiple exciters in mechanical forced synchronization. They established synchronization and stability conditions for this vibration system, and conducted simulation and experimental research on the system. The research results are of great significance for reducing the energy consumption of vibration machines18,19,20,21,22,23. Hou D Y. proposed the elastic coupling mechanical synchronization of two coaxial co-rotating exciters coupling with a torsion spring in far-resonance system, established the synchronization and stability conditions, and explored the influence of torsional stiffness of coupling components on the phase difference angle24. The composite synchronization of three exciters, which is a combination of the elastic coupling mechanical synchronization of two coaxial co-rotating exciters and the self-synchronization between these two-exciter and another, was studied by Hou D Y. et al., and a double-layer elliptical shale shaker with this composite synchronization of three exciters was developed25.

In this paper, the elastic coupling mechanical synchronization of three coaxial co-rotating exciters coupling with two torsional springs in a far-resonance system is introduced, and the synchronization characteristics of the system is comprehensively investigated through theoretical analysis, numerical calculations, simulations, and testing. The research results provide a contribution to the development of more energy-saving vibration machines.

Material and methods

Mechanical model

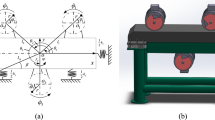
The dynamic model of the coaxial co‑rotating tri-exciter far-resonance system is shown as Fig. 1. In this system, the three coaxial exciting motors are coupled by two torsional springs with torsional stiffness \(k_{\vartheta 1}\),\(k_{\vartheta 2}\) and damping \(f_{\vartheta 1}\),\(f_{\vartheta 2}\). The rigid frame is symmetrically supported by springs with stiffness \(k_{j}\) and damping \(f_{j}\) in \(j\)-direction \(\left( {j = x,y,z,\psi ,\delta ,\theta } \right)\).The mass of the rigid frame is expressed as \(m_{{0}}\), which consists of the mass of the vibrating box and the mass of three exciting motors. The masses of the three ERs mounted on the exciting motor shaft are represented by \(m_{i} \left( {i = {1,2,3}} \right)\), respectively. The distances from the rotation centers of the three ERs to their own mass.

Fig. 1
figure 1

Dynamical model of the vibration system.

Full size image

centers are represented by \(r\). The distance from the rotating center of the ERs to YOZ plane is \(l_{X}\).The coordinates of eccentric rotos in the Z direction are \(l_{Zi}\). The vertical distance from the rotating centers of the three ERs to plane XOZ is \(l_{y}\). The centroid of the vibrating body is coincided with the origin of coordinate system \(o\,x\,y\,z\) when the vibrating system in static equilibrium. The transforming law of the reference coordinates is shown in Fig. 1. And the conversion sequence of the reference coordinates is followed by \(o^{\prime\prime}x^{\prime\prime}y^{\prime\prime}z^{\prime\prime} \to o^{\prime}x^{\prime}y^{\prime}z^{\prime} \to oxyz\). The rigid frame is translated in \(x\)- , \(y\)-and \(z\)- axes, and rotated in \(\psi\)- ,\(\delta\)- and \(\theta \;\)-axes. The phase angles of the ERs are represented by \(\varphi_{{1}}\), \(\varphi_{2}\) and \(\varphi_{3}\) respectively.

In coordinate \(o^{\prime\prime}x^{\prime\prime}y^{\prime\prime}z^{\prime\prime}\), the centroid coordinates \({\mathbf{I^{\prime\prime}}}_{1}\),\({\mathbf{I^{\prime\prime}}}_{2}\) and \({\mathbf{I^{\prime\prime}}}_{3}\) of the three ERs can be expressed as:

$${\mathbf{I^{\prime\prime}}}_{i} = \left[ {\begin{array}{*{20}c} {l_{X} + r{\text{cos}}\varphi_{i} } \\ {l_{Y} + r{\text{sin}}\varphi_{i} } \\ {l_{Zi} } \\ \end{array} } \right]\quad \quad \left( {i = 1,2,3} \right)$$
(1)

The centroid of the rigid frame is \({\mathbf{I}}_{0} = \left[ {\begin{array}{*{20}c} {x,} & {y,} & 0 \\ \end{array} } \right]^{T}\) in fixed coordinate \(oxyz\), the centroid coordinate of the ERs regarding coordinate \(oxyz\) can be converted through rotation matrix A, ie.,

$${\mathbf{I}}_{i} = {\mathbf{I}}_{0} + {\mathbf{AI^{\prime\prime}}}_{i} \begin{array}{*{20}c} , & {} \\ \end{array} {\mathbf{I}}_{0} = \left[ {\begin{array}{*{20}c} {x,} & {y,} & 0 \\ \end{array} } \right]^{T} \begin{array}{*{20}c} , & {} \\ \end{array} {\mathbf{A}} = \left[ {\begin{array}{*{20}c} {1} & { - \theta } & \psi \\ \theta & {1} & { - \delta } \\ { - \psi } & \delta & {1} \\ \end{array} } \right],\left( {i = {1,2,3}} \right)$$
(2)

Due to the lack of force in the z-direction, the movement in this direction is very small, so the movement and its influence are ignored. In the synchronous state, the kinetic energy of the whole system should be calculated as:

$$T = \frac{1}{2}m_{0} \left( {\dot{x}^{2} + \dot{y}^{2} } \right) + \frac{1}{2}J_{\psi } \dot{\psi }^{2} + \frac{1}{2}J_{\delta } \dot{\delta }^{2} + \frac{1}{2}J_{\theta } \dot{\theta }^{2} + \frac{1}{2}\sum\limits_{{i = 1}}^{3} {m_{i} \dot{I}_{i}^{{\prime T}} } I_{i}^{\prime } + \frac{1}{2}\sum\limits_{{i = 1}}^{3} {J_{{0i}} \dot{\varphi }_{i}^{2} }$$
(3)

where, the symbols of \(\left( \cdot \right)\) and \(\left( { \cdot \cdot } \right)\) are represented \(d/dt\) and \(d^{2} /dt^{2}\) respectively, and the rotational inertia of the rigid framework around \(x\)-, \(y\)- and \(z\)-axis are defined as \(J_{\psi }\),\(J_{\delta }\) and \(J_{\theta }\), respectively. In addition, the moment of inertia of the i-th eccentric rotor related to the motor axis can be expressed as \(J_{0i} \left( {i = 1,2,3} \right)\).

The total potential energy of the vibrating system can be expressed by:

$$V = \frac{{1}}{{2}}k_{x} x^{2} + \frac{{1}}{{2}}k_{y} y^{2} + \frac{{1}}{{2}}k_{\psi } \psi^{2} + \frac{{1}}{{2}}k_{\delta } \delta^{2} + \frac{{1}}{{2}}k_{\theta } \theta^{2} + \frac{{1}}{{2}}k_{\vartheta 1} \left( {\varphi_{1} - \varphi_{2} } \right)^{2} + \frac{{1}}{{2}}k_{\vartheta 2} \left( {\varphi_{2} - \varphi_{3} } \right)^{2}$$
(4)

Meanwhile, the dissipated energy of this system can be calculated as:

$$D = \frac{1}{2}f_{x} \dot{x}^{2} + \frac{1}{2}f_{y} \dot{y}^{2} + \frac{1}{2}f_{\psi } \dot{\psi }^{2} + \frac{1}{2}f_{\delta } \dot{\delta }^{2} + \frac{1}{2}f_{\theta } \dot{\theta }^{2} + \frac{1}{2}f_{1} \dot{\varphi }_{1}^{2} + \frac{1}{2}f_{2} \dot{\varphi }_{2}^{2} + \frac{1}{2}f_{3} \dot{\varphi }_{3}^{2} + \frac{1}{2}f_{\vartheta 1} {(}\dot{\varphi }_{1} - \dot{\varphi }_{2} {)}^{2} + \frac{1}{2}f_{\vartheta 2} {(}\dot{\varphi }_{2} - \dot{\varphi }_{3} {)}^{2}$$
(5)

The Lagrange’s equation can be written as:

$$\frac{d}{dt}\frac{\partial T}{{\partial \dot{q}_{i} }} - \frac{{\partial \left( {T - V} \right)}}{{\partial q_{i} }} + \frac{\partial D}{{\partial \dot{q}_{i} }} = Q_{i}$$
(6)

where, \(q_{i}\) is an element of generalized coordinate matrix \({\mathbf{q}}\) of the system, which can be expressed as \(q = \left[ {\begin{array}{*{20}c} {x,} & {y,} & {\psi ,} & {\begin{array}{*{20}c} {\delta ,} & {\theta ,} & {\begin{array}{*{20}c} {\varphi _{1} ,} & {\begin{array}{*{20}c} {\varphi _{2} ,} & {\varphi _{3} ,} \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]\) Meanwhile, \({\text{Q}}_{{\;{\text{i}}}}\) is an element of generalized force matrix Q, which should be expressed as:

$${\mathbf{Q}} = \left[ {\begin{array}{*{20}c} {0,} & {0,} & {0,} & {\begin{array}{*{20}c} {0,} & {0,} & {M_{{e{1}}} - R_{{e{1}}} ,} & {\begin{array}{*{20}c} {M_{{e{2}}} - R_{{e{2}}} ,} & {M_{{e{3}}} - R_{{e{3}}} ,} \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]$$
(7)

where, \(M_{ei}\) is electromagnetic torque in the motors, and \(R_{ei}\) is the damping torque in the motors \(\left( {i ={1,2,3}} \right)\). Substituting Eqs. (3), (4), (5), and (7) into Eq. (6), meanwhile, the parameters with following relationships \(m_{i} \ll m_{0} \left( {i ={1,2,3}} \right)\), \(\psi \ll {1}\), \(\delta \ll{1}\), \(\theta \ll {1}\) are satisfied when the vibrating system operated in synchronous state. Therefore, the dynamic equations of this system are written as:

$$\begin{gathered} \left( {m_{0} + m_{1} + m_{2} + m_{3} } \right)\ddot{x} + f_{x} \dot{x} + k_{x} x = \sum\limits_{i = 1}^{3} {m_{i} r(\ddot{\varphi }_{i} \sin \varphi_{i} + \dot{\varphi }_{i}^{2} \cos \varphi_{i} )} \hfill \\ \left( {m_{0} + m_{1} + m_{2} + m_{3} } \right)\ddot{y} + f_{y} \dot{y} + k_{y} y = \sum\limits_{i = 1}^{3} {m_{i} r( - \ddot{\varphi }_{i} \cos \varphi_{i} + \dot{\varphi }_{i}^{2} \sin \varphi_{i} )} \hfill \\ J_{\delta } \ddot{\delta } + f_{\delta } \dot{\delta } + k_{\delta } \delta = \sum\limits_{i = 1}^{3} {l_{zi} m_{i} r(\ddot{\varphi }_{i} \cos \varphi_{i} - \dot{\varphi }_{i}^{2} \sin \varphi_{i} )} \hfill \\ J_{\psi } \ddot{\psi } + f_{\psi } \dot{\psi } + k_{\psi } \psi = \sum\limits_{i = 1}^{3} {l_{zi} m_{i} r(\ddot{\varphi }_{i} \sin \varphi_{i} + \dot{\varphi }_{i}^{2} \cos \varphi_{i} )} \hfill \\ J_{\theta } \ddot{\theta } + f_{\theta } \dot{\theta } + k_{\theta } \theta = - \sum\limits_{i = 1}^{3} {m_{i} rl_{y} (\ddot{\varphi }_{i} \sin \varphi_{i} + \dot{\varphi }_{i}^{2} \cos \varphi_{i} ) + \sum\limits_{i = 1}^{3} {m_{i} rl_{x} ( - \ddot{\varphi }_{i} \cos \varphi_{i} + \dot{\varphi }_{i}^{2} \sin \varphi_{i} )} } \hfill \\ J_{01} \ddot{\varphi }_{1} + f_{1} \dot{\varphi }_{1} = T_{e1} - k_{\vartheta 1} (\varphi_{1} - \varphi_{2} ) + m_{1} r(\ddot{x} - l_{y} \ddot{\theta } + l_{z1} \ddot{\psi })\sin \varphi_{1} - m_{1} r(\ddot{y} + l_{x} \ddot{\theta } - l_{z1} \ddot{\delta })\cos \varphi_{1} \hfill \\ J_{02} \ddot{\varphi }_{2} + f_{2} \dot{\varphi }_{2} = T_{e2} + k_{\vartheta 1} (\varphi_{1} - \varphi_{2} ) - k_{\vartheta 2} (\varphi_{2} - \varphi_{3} ) + m_{2} r(\ddot{x} - l_{y} \ddot{\theta } + l_{z2} \ddot{\psi })\sin \varphi_{2} \hfill \\ \quad - m_{2} r(\ddot{y} + l_{x} \ddot{\theta } - l_{z2} \ddot{\delta })\cos \varphi_{2} \hfill \\ J_{03} \ddot{\varphi }_{3} + f_{3} \dot{\varphi }_{3} = T_{e3} + k_{\vartheta 2} (\varphi_{2} - \varphi_{3} ) + m_{3} r(\ddot{x} - l_{y} \ddot{\theta } + l_{z3} \ddot{\psi })\sin \varphi_{3} - m_{3} r\cos \varphi_{3} (\ddot{y} + l_{x} \ddot{\theta } - l_{z3} \ddot{\delta }) \hfill \\ \end{gathered}$$
(8)

The phase difference between ER 1 and 2 is defined by \(\alpha_{1}\), and the phase difference between the ER 2 and 3 is assumed as \(\alpha_{2}\). That is

$$\begin{gathered} \varphi_{1} - \varphi_{2} = \alpha_{1} \hfill \\ \varphi_{{2}} - \varphi_{3} = \alpha_{2} \hfill \\ \end{gathered}$$
(9)

Let the phase angle of ER 2 \(\varphi_{2} = \varphi\), according to Eq. (9), the phase angles of the three ERs can be expressed as:

$$\begin{gathered} \varphi_{1} = \varphi + \alpha_{1} \hfill \\ \varphi_{2} = \varphi \hfill \\ \varphi_{3} = \varphi - \alpha_{2} \hfill \\ \end{gathered}$$
(10)

The motion of the vibration system in the synchronous process is periodic, and the motion of the rotors also is periodic. Therefore, the average value of the rotational velocity of the ERs should be constant. The minimum positive period of rotation of the rotors is defined as \(T_{P\min }\), the average angular velocity of the ERs during \(T_{P\min }\) is a constant.

$$\omega_{m0} = \frac{1}{{T_{P\min } }}\int\limits_{t}^{{t + T_{P\min } }} {\dot{\varphi }dt} = {\text{const}}ant$$
(11)

where,\(\omega_{{m{0}}}\) is average value of rotational velocity of the eccentric rotor in a single period. In this case, when the middle ER is on the XOY plane, and the distance from the other two ERs to the XOY plane is equal and represented by \(L_{Z}\), the approximate steady state responses of the system in \(x\)-,\(y\)-,\(\delta\)-,\(\psi\)-and \(\theta\)- direction can be expressed as:

$$\begin{gathered} x = E_{x} \left[ {m_{1} {\text{cos}}\left( {\varphi + \alpha_{1} - \gamma_{x} } \right) + m_{2} {\text{cos}}\left( {\varphi - \gamma_{x} } \right) + m_{3} {\text{cos}}\left( {\varphi - \alpha_{2} - \gamma_{x} } \right)} \right] \hfill \\ y = E_{y} \left[ {m_{1} {\text{sin}}\left( {\varphi { + }\alpha_{1} - \gamma_{y} } \right) + m_{2} {\text{sin}}\left( {\varphi - \gamma_{y} } \right) + m_{3} {\text{sin}}\left( {\varphi - \alpha_{2} - \gamma_{y} } \right)} \right] \hfill \\ \delta = E_{\delta } \left[ {m_{1} {\text{sin}}\left( {\varphi { + }\alpha_{1} - \gamma_{\delta } } \right) - m_{3} {\text{sin}}\left( {\varphi - \alpha_{2} - \gamma_{\delta } } \right)} \right] \hfill \\ \psi = E_{\psi } \left[ {m_{1} {\text{cos}}\left( {\varphi { + }\alpha_{1} - \gamma_{\psi } } \right) - m_{3} {\text{cos}}\left( {\varphi - \alpha_{2} - \gamma_{\psi } } \right)} \right] \hfill \\ \theta = E_{\theta } \left[ {m_{1} {\text{sin}}\left( {\varphi + \alpha_{1} + \gamma_{XY} - \gamma_{\theta } } \right) + m_{2} {\text{sin}}\left( {\varphi + \gamma_{XY} - \gamma_{\theta } } \right) + m_{3} {\text{sin}}\left( {\varphi - \alpha_{2} + \gamma_{XY} - \gamma_{\theta } } \right)} \right] \hfill \\ \end{gathered}$$
(12)

where,

\(E_{x} = \frac{{r\omega_{m0}^{2} }}{{M\mu_{x} }}\), \(E_{y} = \frac{{r\omega_{m0}^{2} }}{{\mu_{y} M}}\), \({\rm E}_{\delta } = \frac{{rl_{Z} \omega_{m0}^{2} }}{{J_{\delta } \mu_{\delta } }}\),\(E_{\psi } = - \frac{{rl_{Z} \omega_{m0}^{2} }}{{J_{\psi } \mu_{\psi } }}\), \(E_{\theta } = \frac{{rl_{XY} \omega_{m0}^{2} }}{{J_{\theta } \mu_{\theta } }}\)\(l_{XY} = \sqrt {l_{X}^{2} + l_{Y}^{2} }\),

\(M = {(}m_{{0}} { + }m_{{1}} { + }m_{{2}} { + }m_{{3}} {)}\),\(\gamma_{XY} = \arctan \left( {\frac{{l_{Y} }}{{l_{X} }}} \right)\),\(\mu_{i} = \sqrt {\left( {\frac{{k_{i} }}{M} - \omega_{m0}^{2} } \right)^{2} + \left( {\frac{{f_{i} \omega_{m0} }}{M}} \right)^{2} }\),

\(\gamma_{i} = \arctan \left( {\frac{{f_{i} \omega_{m0} }}{{k_{i} - M\omega_{m0}^{2} }}} \right)\),\(\left( {i = x,y,\psi ,\delta ,\theta } \right)\).

Synchronization analysis and stability analysis

Synchronization analysis

According to the modified averaging small parameter method, when the average angular velocity of the three rotors is satisfied by the condition of \(\dot{\varphi } \approx \omega_{m0}\), and the transient coefficients \(\zeta {\kern 1pt}_{0}\), \(\zeta {\kern 1pt}_{1}\) and \(\zeta {\kern 1pt}_{2}\)(\(\zeta {\kern 1pt}_{0}\), \(\zeta {\kern 1pt}_{1}\) and \(\zeta {\kern 1pt}_{2}\) are small parameters changed with time) are introduced to describe \(\dot{\varphi }\), \(\dot{\alpha }_{1}\),\(\dot{\alpha }_{2}\). \(\dot{\varphi }\), \(\dot{\alpha }_{1}\),\(\dot{\alpha }_{2}\) are written as

$$\begin{gathered} \dot{\varphi } = \left( {1 + \zeta_{0} } \right)\omega_{m0} \hfill \\ \dot{\alpha }_{1} = \zeta_{1} \omega_{m0} \hfill \\ \dot{\alpha }_{2} = \zeta_{2} \omega_{m0} \hfill \\ \end{gathered}$$
(13)

The first derivation of Eq. (10) with respect to time t can be calculated. Then combining the results of differentiation with the Eq. (13), the formulas can be defined as:

$$\begin{gathered} \dot{\varphi }_{1} = \dot{\varphi } + \dot{\alpha }_{1} = \left( {1 + \zeta_{0} } \right)\omega_{m0} + \zeta_{1} \omega_{m0} \hfill \\ \dot{\varphi }_{2} = \dot{\varphi } = \left( {1 + \zeta_{0} } \right)\omega_{m0} \hfill \\ \dot{\varphi }_{3} = \dot{\varphi } - \dot{\alpha }_{2} = \left( {1 + \zeta_{0} } \right)\omega_{m0} - \zeta_{2} \omega_{m0} \hfill \\ \ddot{\varphi }_{1} = \left( {\dot{\zeta }_{0} + \dot{\zeta }_{1} } \right)\omega_{m0} \hfill \\ \ddot{\varphi }_{2} = \dot{\zeta }_{0} \omega_{m0} \hfill \\ \ddot{\varphi }_{3} = \left( {\dot{\zeta }_{0} - \dot{\zeta }_{2} } \right)\omega_{m0} \hfill \\ \end{gathered}$$
(14)

Substitute Eqs. (12) and (14) into the last three equations of formula (8), and integrating the equations over single period T, averaged in the interval \(\left( {0,2\pi } \right)\),the corresponding moment equilibrium equation can be obtained.

$$\begin{gathered} J_{01} \left( {\dot{\zeta }_{0} + \dot{\zeta }_{1} } \right)\omega_{m0} + f_{1} \left( {\left( {1 + \zeta_{0} } \right)\omega_{m0} + \zeta_{1} \omega_{m0} } \right) + k_{{\vartheta {1}}} \alpha_{1} { + }f_{\vartheta 1} \zeta_{1} \omega_{m0} \hfill \\ = M_{e1} - R_{e1} - \frac{{m_{1} r\omega_{m0}^{2} }}{2}\left[ \begin{gathered} \left( {W_{1} + W_{{3}} } \right)m_{1} + W_{2} m_{2} \sin \alpha_{1} + W_{1} m_{2} \cos \alpha_{1} \hfill \\ + \left( {W_{2} - W_{4} } \right)m_{3} \sin (\alpha_{1} + \alpha_{2} ) + \left( {W_{1} - W_{{3}} } \right)m_{3} \cos (\alpha_{1} + \alpha_{2} ) \hfill \\ \end{gathered} \right] \hfill \\ J_{02} \dot{\zeta }_{0} \omega_{m0} + f_{2} \left( {1 + \zeta_{0} } \right)\omega_{m0} - k_{{\vartheta {1}}} \alpha_{1} + k_{{\vartheta {2}}} \alpha_{2} - f_{\vartheta 1} \zeta_{1} \omega_{m0} + f_{\vartheta 2} \zeta_{2} \omega_{m0} \hfill \\ = M_{e2} - R_{e2} - \frac{{m_{2} r\omega_{m0}^{2} }}{2}\left( \begin{gathered} W_{1} m_{2} - W_{2} m_{1} {\text{sin}}\alpha_{1} + W_{1} m_{1} \cos \alpha_{1} \hfill \\ + W_{2} m_{3} {\text{sin}}\alpha_{2} + W_{1} m_{3} \cos \alpha_{2} \hfill \\ \end{gathered} \right) \hfill \\ J_{03} \left( {\dot{\zeta }_{0} - \dot{\zeta }_{2} } \right)\omega_{m0} + f_{3} \left( {1 + \zeta_{0} - \zeta_{2} } \right)\omega_{m0} - k_{{\vartheta {2}}} \alpha_{2} - f_{\vartheta 2} \zeta_{2} \omega_{m0} \hfill \\ = M_{e3} - R_{e3} - \frac{{m_{3} r\omega_{m0}^{2} }}{2}\left[ \begin{gathered} \left( {W_{1} + W_{{3}} } \right)m_{3} - W_{2} m_{2} {\text{sin}}\alpha_{2} + W_{1} m_{2} \cos \alpha_{2} \hfill \\ + \left( {W_{4} - W_{2} } \right)m_{1} {\text{sin}}\left( {\alpha_{1} + \alpha_{2} } \right) + \left( {W_{1} - W_{{3}} } \right)m_{1} \cos \left( {\alpha_{1} + \alpha_{2} } \right) \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered}$$
(15)

where,

$$\begin{gathered} W_{1} = - E_{x} {\text{sin}}\gamma_{x} + E_{y} {\text{sin}}\gamma_{y} { + }l_{XY} E_{\theta } {\text{sin}}\gamma_{\theta } \hfill \\ W_{2} = - E_{x} {\text{cos}}\gamma_{x} + E_{y} {\text{cos}}\gamma_{y} + l_{XY} E_{\theta } {\text{cos}}\gamma_{\theta } \hfill \\ W_{{3}} = l_{Z} E_{\psi } {\text{sin}}\gamma_{\psi } + l_{Z} E_{\delta } {\text{sin}}\gamma_{\delta } \hfill \\ W_{4} = l_{Z} E_{\psi } {\text{cos}}\gamma_{\psi } + l_{Z} E_{\delta } {\text{cos}}\gamma_{\delta } \hfill \\ \end{gathered}$$
(16)

As \(\zeta_{0} ,\zeta_{1} ,\zeta_{2}\) are small parameters, and so \(\zeta_{i} \approx 0\),\(\dot{\zeta }_{i} \approx 0\), (\(i \approx 0,1,3\))are considered in the calculated process. The rotational damping coefficients of three rotors are identical as the same type of motor is selected, i.e.,\(f_{1} = f_{2} = f_{3} = f\). Subtracting formula 2 from formula 1 and formula 3 from formula 2 in Eq. (15), then it can be obtained:

$$\begin{gathered} { + 2}k_{{\vartheta {1}}} \alpha_{1} - k_{{\vartheta {2}}} \alpha_{2} = T_{e12} \hfill \\ + \frac{{r\omega_{m0}^{2} }}{2}\left[ \begin{gathered} W_{1} m_{2}^{2} - \left( {W_{1} + W_{{3}} } \right)m_{1}^{2} - 2W_{2} m_{1} m_{2} {\text{sin}}\alpha_{1} + W_{2} m_{2} m_{3} {\text{sin}}\alpha_{2} + W_{1} m_{2} m_{3} \cos \alpha_{2} \hfill \\ - \left( {W_{2} - W_{4} } \right)m_{1} m_{3} \sin (\alpha_{1} + \alpha_{2} ) - \left( {W_{1} - W_{{3}} } \right)m_{1} m_{3} \cos (\alpha_{1} + \alpha_{2} ) \hfill \\ \end{gathered} \right] \hfill \\ - k_{{\vartheta {1}}} \alpha_{1} + 2k_{{\vartheta {2}}} \alpha_{2} = T_{e23} \hfill \\ + \frac{{r\omega_{m0}^{2} }}{2}\left[ \begin{gathered} \left( {W_{1} + W_{{3}} } \right)m_{3}^{2} - W_{1} m_{2}^{2} + W_{2} m_{1} m_{2} {\text{sin}}\alpha_{1} - W_{1} m_{1} m_{2} \cos \alpha_{1} - 2W_{2} m_{2} m_{3} {\text{sin}}\alpha_{2} \hfill \\ + \left( {W_{4} - W_{2} } \right)m_{1} m_{3} {\text{sin}}\left( {\alpha_{1} + \alpha_{2} } \right) + \left( {W_{1} - W_{{3}} } \right)m_{1} m_{3} \cos \left( {\alpha_{1} + \alpha_{2} } \right) \hfill \\ \end{gathered} \right] \hfill \\ \end{gathered}$$
(17)

where,\(T_{e12} = \left( {M_{e1} - M_{e2} } \right) - \left( {R_{e1} - R_{e2} } \right);\quad T_{e23} = \left( {M_{e2} - M_{e3} } \right) - \left( {R_{e2} - R_{e3} } \right)\).

Let \(x_{1} = {\text{sin}}\alpha_{1}\),\(\dot{x}_{1} = {\text{cos}}\alpha_{1}\),\(x_{2} = {\text{sin}}\alpha_{2}\),\(\dot{x}_{2} = {\text{cos}}\alpha_{2}\),then there is, \(\alpha_{{1}} = \arcsin x_{1}\), \(\alpha_{2} = \arcsin x_{2}\). Then Eq. (17) can be converted to:

$$\begin{gathered} P_{1} (x_{1} ,x_{2} ) = T_{e12} - {2}k_{{\vartheta {1}}} \arcsin x_{1} + k_{{\vartheta {2}}} \arcsin x_{2} \hfill \\ + \frac{{r\omega_{m0}^{2} }}{2}\left[ \begin{gathered} W_{1} m_{2}^{2} - \left( {W_{1} + W_{{3}} } \right)m_{1}^{2} - 2W_{2} m_{1} m_{2} x_{1} + W_{2} m_{2} m_{3} x_{2} + W_{1} m_{2} m_{3} \dot{x}_{2} \hfill \\ - \left( {W_{2} - W_{4} } \right)m_{1} m_{3} \left( {x_{1} \dot{x}_{2} + \dot{x}_{1} x_{2} } \right) - \left( {W_{1} - W_{{3}} } \right)m_{1} m_{3} \left( {\dot{x}_{1} \dot{x}_{2} - x_{1} x_{2} } \right) \hfill \\ \end{gathered} \right] = 0 \hfill \\ P_{2} (x_{1} ,x_{2} ) = T_{e23} + k_{{\vartheta {1}}} \arcsin x_{1} - 2k_{{\vartheta {2}}} \arcsin x_{2} \hfill \\ + \frac{{r\omega_{m0}^{2} }}{2}\left[ \begin{gathered} \left( {W_{1} + W_{{3}} } \right)m_{3}^{2} - W_{1} m_{2}^{2} + W_{2} m_{1} m_{2} x_{1} - W_{1} m_{1} m_{2} \dot{x}_{1} - 2W_{2} m_{2} m_{3} x_{2} \hfill \\ + \left( {W_{4} - W_{2} } \right)m_{1} m_{3} \left( {x_{1} \dot{x}_{2} + \dot{x}_{1} x_{2} } \right) + \left( {W_{1} - W_{{3}} } \right)m_{1} m_{3} \left( {\dot{x}_{1} \dot{x}_{2} - x_{1} x_{2} } \right) \hfill \\ \end{gathered} \right] = 0 \hfill \\ \end{gathered}$$
(18)

As can be seen from the above formula, there are \(- 1 \le x_{1} \le 1\) and \(- 1 \le x_{2} \le 1\).Under normal conditions, exciters 1 and 3 will select the same type, that is \(m_{1} = m_{3} = m\). The two coupled torsional springs are selected with the same stiffness, that is \(k_{{\vartheta {1}}} = k_{{\vartheta {2}}} = k_{\vartheta }\).

If \(P_{1} \left( { - 1, - 1} \right) - P_{1} \left( {1,1} \right) \ge 0\) and \(P_{2} \left( { - 1, - 1} \right) - P_{2} \left( {1,1} \right) \ge 0\), then,

$$W_{2} \ge - \frac{{\pi k_{\vartheta } }}{{mm_{2} r\omega_{m0}^{2} }}$$
(19)

When the formula (19) is satisfied, if the following equation come into existence, then Eq. (9) must have a solution.

$$\begin{gathered} P_{1} ( - 1, - 1) = T_{e12} + \frac{\pi }{2}k_{\vartheta } + \frac{{r\omega_{m0}^{2} }}{2}\left( {N + W_{2} mm_{2} } \right) \ge 0 \hfill \\ P_{2} ( - 1, - 1) = T_{e23} + \frac{\pi }{2}k_{\vartheta } + \frac{{r\omega_{m0}^{2} }}{2}\left[ { - N + W_{2} mm_{2} } \right] \ge 0 \hfill \\ P_{1} (1,1) = T_{e12} - \frac{\pi }{2}k_{\vartheta } + \frac{{r\omega_{m0}^{2} }}{2}\left[ {N - W_{2} mm_{2} } \right] \le 0 \hfill \\ P_{2} (1,1) = T_{e23} - \frac{\pi }{2}k_{\vartheta } + \frac{{r\omega_{m0}^{2} }}{2}\left[ { - N - W_{2} m_{2} m} \right] \le 0 \hfill \\ \end{gathered}$$

where, \(N = W_{1} m_{2}^{2} - 2W_{{3}} m_{{}}^{2}\).Based on the above analysis, it can be obtained,

$$\begin{gathered} - \frac{{2T_{e12} + k_{\vartheta } \pi }}{{r\omega_{m0}^{2} }} - W_{2} mm_{2} \le N \le \frac{{2T_{e23} + k_{\vartheta } \pi }}{{r\omega_{m0}^{2} }} + W_{2} mm_{2} \hfill \\ \frac{{2T_{e23} - k_{\vartheta } \pi }}{{r\omega_{m0}^{2} }} - W_{2} mm_{2} \le N \le - \frac{{2T_{e12} - k_{\vartheta } \pi }}{{r\omega_{m0}^{2} }} + W_{2} mm_{2} \hfill \\ \end{gathered}$$
(20)

Besides, exciter 1, 3 select the same type of motors. The torque difference of motor 1 and 2 is equal to that of motor 2 and 3. And the direction of them is opposite, that is \(T_{e12} = - T_{e23}\). Plugging this result into the previous two equations, it can be obtained.

$$\frac{{2T_{e23} - k_{\vartheta } \pi }}{{r\omega_{m0}^{2} }} - W_{2} mm_{2} \le N \le \frac{{2T_{e23} + k_{\vartheta } \pi }}{{r\omega_{m0}^{2} }} + W_{2} mm_{2}$$
(21)

In the same way, when \(W_{2} \le - \frac{{k_{\vartheta } \pi }}{{mm_{2} r\omega_{m0}^{2} }}\), the equation can be obtained.

$$\frac{{2T_{e23} + k_{\vartheta } \pi }}{{r\omega_{m0}^{2} }} + W_{2} mm_{2} \le N \le \frac{{2T_{e23} - k_{\vartheta } \pi }}{{r\omega_{m0}^{2} }} - W_{2} mm_{2}$$
(22)

According to the above derivation, Eqs. (21) and (22) constitute the synchronization conditions of the coaxial co-rotating elastic coupling tri-exciter vibration system. It can be arranged as,

$$\begin{gathered} \frac{{2T_{e23} - k_{\vartheta } \pi }}{{r\omega_{m0}^{2} }} - W_{2} mm_{2} \le N \le \frac{{2T_{e23} + k_{\vartheta } \pi }}{{r\omega_{m0}^{2} }} + W_{2} mm_{2} \quad \quad \left( {W_{2} \ge - \frac{{k_{\vartheta } \pi }}{{mm_{2} r\omega_{m0}^{2} }}} \right) \hfill \\ {\text{or}} \hfill \\ \frac{{2T_{e23} + k_{\vartheta } \pi }}{{r\omega_{m0}^{2} }} + W_{2} mm_{2} \le N \le \frac{{2T_{e23} - k_{\vartheta } \pi }}{{r\omega_{m0}^{2} }} - W_{2} mm_{2} \quad \quad \left( {W_{2} < - \frac{{k_{\vartheta } \pi }}{{mm_{2} r\omega_{m0}^{2} }}} \right) \hfill \\ \end{gathered}$$
(23)

The absolute value form of the above equation can be arranged as,

$$\begin{gathered} \left| N \right| \le \left| {\frac{{2T_{e23} + k_{\vartheta } \pi }}{{r\omega_{m0}^{2} }} + W_{2} mm_{2} } \right| \hfill \\ {\text{or}} \hfill \\ \left| N \right| \le \left| {\frac{{2T_{e23} - k_{\vartheta } \pi }}{{r\omega_{m0}^{2} }} - W_{2} mm_{2} } \right| \hfill \\ \end{gathered}$$
(24)

Equation (24) can also be rewritten as,

$$\begin{gathered} C_{s1} = \frac{{\left| {\frac{{2T_{e23} + k_{\vartheta } \pi }}{{r\omega_{m0}^{2} }} + W_{2} mm_{2} } \right|}}{\left| N \right|} \ge 1 \hfill \\ C_{s2} = \frac{{\left| {\frac{{2T_{e23} - k_{\vartheta } \pi }}{{r\omega_{m0}^{2} }} - W_{2} mm_{2} } \right|}}{\left| N \right|} \ge 1 \hfill \\ \end{gathered}$$
(25)

\(C_{s1}\) and \(C_{s2}\) can be defined as synchronization index, and 1 is defined as the limiting synchronization index. The larger the value of the synchronization index \(C_{s1}\),\(C_{s2}\), the easier the inequality of Eq. (28) is to satisfy, and the better the synchronization performance of the system is.

When the moment difference between the two motors is zero, that is \(T_{e23} = 0\) and \(C_{s1} = C_{s2} = C_{s}\), the synchronization condition of the system can be rewritten as,

$$C_{s} = \frac{{\left| {\frac{{k_{\vartheta } \pi }}{{r\omega_{m0}^{2} }} + W_{2} mm_{2} } \right|}}{\left| N \right|} \ge 1$$
(26)

Stability analysis

In order to simplify the analysis, in the study of system stability, the same and symmetrical arrangement of excitation motors 1 and 3 is also considered, that is \(m_{1} { = }m_{3} { = }m\).Add and subtract the two formulas of the Eq. (18) respectively,

$$\begin{gathered} T_{e12} + T_{e23} - k_{{\vartheta {1}}} \arcsin x_{1} - k_{{\vartheta {2}}} \arcsin x_{2} \hfill \\ + \frac{{r\omega_{m0}^{2} }}{2}\left[ { - W_{2} mm_{2} x_{1} - W_{2} mm_{2} x_{2} - W_{1} mm_{2} \dot{x}_{1} + W_{1} mm_{2} \dot{x}_{2} + 2\left( {W_{4} - W_{2} } \right)m^{2} \left( {x_{1} \dot{x}_{2} + \dot{x}_{1} x_{2} } \right)} \right] = 0 \hfill \\ T_{e12} - T_{e23} - {3}k_{{\vartheta {1}}} \arcsin x_{1} + 3k_{{\vartheta {2}}} \arcsin x_{2} \hfill \\ + \frac{{r\omega_{m0}^{2} }}{2}\left[ \begin{gathered} 2W_{1} m_{2}^{2} - 2\left( {W_{1} + W_{{3}} } \right)m^{2} - 3W_{2} mm_{2} x_{1} + 3W_{2} mm_{2} x_{2} \hfill \\ + W_{1} mm_{2} \dot{x}_{1} + W_{1} mm_{2} \dot{x}_{2} - 2\left( {W_{1} - W_{{3}} } \right)m^{2} \left( {\dot{x}_{1} \dot{x}_{2} - x_{1} x_{2} } \right) \hfill \\ \end{gathered} \right] = 0 \hfill \\ \end{gathered}$$
(27)

When \(x_{1} = 0,\,x_{2} = 0\), if Eq. (27) could hold, it indicates that the equation has zero solutions, the stability of the system can be directly judged by the stability of the zero solution of equation. Otherwise a coordinate transformation of Eq. (27) is required, the non-zero solutions of \(x_{1}\) and \(x_{2}\) in Eq. (27) are transformed into zero solutions in new coordinates, and then the stability of the system can be analyzed in the new coordinate system.

Let the solution of formula (27) be \(x_{{\alpha 1}} ,\,x_{{\alpha 2}}\), and,

$$\begin{gathered} y_{1} = x_{1} - x_{\alpha 1} \hfill \\ y_{2} = x_{2} - x_{\alpha 2} \hfill \\ \end{gathered}$$
(28)

If the solution of Eq. (27) (i.e. synchronous phase difference Angle) is \(\alpha _{{10}} ,\alpha _{{20}}\).Then in Eq. (28),

$$\begin{gathered} x_{\alpha 1} = \sin \alpha_{10} \hfill \\ x_{\alpha 2} = \sin \alpha_{20} \hfill \\ \end{gathered}$$
(29)

Equation (28) to find the first derivative with respect to the time variable, then.

$$\begin{gathered} \dot{y}_{1} = \dot{x}_{1} \hfill \\ \dot{y}_{2} = \dot{x}_{2} \hfill \\ \end{gathered}$$
(30)

Substituting the Eq. (28) ~ (30)into Eq. (27), the Eq. (27) can be transformed into,

$$\begin{gathered} T_{e12} + T_{e23} - k_{{\vartheta {1}}} \arcsin \left( {y_{1} + x_{\alpha 1} } \right) - k_{{\vartheta {2}}} \arcsin \left( {y_{2} + x_{\alpha 2} } \right) \hfill \\ + \frac{{r\omega_{m0}^{2} }}{2}\left[ \begin{gathered} - W_{2} mm_{2} \left( {y_{1} + x_{\alpha 1} } \right) - W_{2} mm_{2} \left( {y_{2} + x_{\alpha 2} } \right) - W_{1} mm_{2} \dot{y}_{1} + W_{1} mm_{2} \dot{y}_{2} \hfill \\ + 2\left( {W_{4} - W_{2} } \right)m^{2} \left( {\left( {y_{1} + x_{\alpha 1} } \right)\dot{y}_{2} + \dot{y}_{1} \left( {y_{2} + x_{\alpha 2} } \right)} \right) \hfill \\ \end{gathered} \right] = 0 \hfill \\ T_{e12} - T_{e23} - {3}k_{{\vartheta {1}}} \arcsin \left( {y_{1} + x_{\alpha 1} } \right) + 3k_{{\vartheta {2}}} \arcsin \left( {y_{2} + x_{\alpha 2} } \right) \hfill \\ + \frac{{r\omega_{m0}^{2} }}{2}\left[ \begin{gathered} 2W_{1} m_{2}^{2} - 2\left( {W_{1} + W_{{3}} } \right)m^{2} - 3W_{2} mm_{2} \left( {y_{1} + x_{\alpha 1} } \right) + 3W_{2} mm_{2} \left( {y_{2} + x_{\alpha 2} } \right) \hfill \\ + W_{1} mm_{2} \dot{y}_{1} + W_{1} mm_{2} \dot{y}_{2} - 2\left( {W_{1} - W_{{3}} } \right)m^{2} \left( {\dot{y}_{1} \dot{y}_{2} - \left( {y_{1} + x_{\alpha 1} } \right)\left( {y_{2} + x_{\alpha 2} } \right)} \right) \hfill \\ \end{gathered} \right] = 0 \hfill \\ \end{gathered}$$
(31)

The standard matrix form of the above equation can be rewritten as,

$${\dot{\mathbf{y}}} = {\mathbf{F}}({\mathbf{y}})$$
(32)

\({\mathbf{F}}({\mathbf{y}})\) has a continuous second partial derivative in the neighborhood of \({\mathbf{y}} = 0\). From the multivariate Taylor formula, \({\mathbf{F}}({\mathbf{y}})\) can be expanded to,

$${\mathbf{F}}({\mathbf{y}}) = {\mathbf{D}}_{f} {\mathbf{y}}_{0} + {\mathbf{g}}({\mathbf{y}})$$
(33)

\({\mathbf{D}}_{f}\) is the Jacobian matrix of the function \({\mathbf{F}}({\mathbf{y}})\),

$${\mathbf{D}}_{f} = \left[ \begin{gathered} \frac{{\partial \dot{y}_{1} }}{{\partial y_{1} }}\quad \frac{{\partial \dot{y}_{1} }}{{\partial y_{2} }} \hfill \\ \frac{{\partial \dot{y}_{2} }}{{\partial y_{1} }}\quad \frac{{\partial \dot{y}_{2} }}{{\partial y_{2} }} \hfill \\ \end{gathered} \right]_{{{\mathbf{y}} = 0}}$$
(34)

The nonlinear term in Eq. (33) is satisfied,

$$\mathop {\lim }\limits_{{\left\| {\mathbf{y}} \right\| \to 0}} \frac{{\left\| {{\mathbf{g}}({\mathbf{y}})} \right\|}}{{\left\| {\mathbf{y}} \right\|}} = 0$$
(35)

Then the first-order approximation system of formula (32) can be written as,

$${\dot{\mathbf{y}}}{ = }{\mathbf{D}}_{{f{\kern 1pt} }} {\mathbf{y}}$$
(36)

Equation (31) takes the partial derivative of \(y_{1}\) and \(y_{2}\) respectively. At zero solution \(y_{1} { = }0,y_{2} { = }0\), let,

$$\begin{gathered} \left. {a_{11} = \frac{{\partial \dot{y}_{1} }}{{\partial y_{1} }}} \right|_{{y_{1} = y_{2} = 0}} ;\quad \left. {a_{12} = \frac{{\partial \dot{y}_{1} }}{{\partial y_{2} }}} \right|_{{y_{1} = y_{2} = 0}} \hfill \\ \left. {a_{21} = \frac{{\partial \dot{y}_{2} }}{{\partial y_{1} }}} \right|_{{y_{1} = y_{2} = 0}} ;\quad \left. {a_{22} = \frac{{\partial \dot{y}_{2} }}{{\partial y_{2} }}} \right|_{{y_{1} = y_{2} = 0}} \hfill \\ \dot{y}_{10} = \left. {\dot{y}_{1} } \right|_{{y_{1} = y_{2} = 0}} ;\quad \dot{y}_{20} = \left. {\dot{y}_{2} } \right|_{{y_{1} = y_{2} = 0}} \hfill \\ \end{gathered}$$
(37)

By substituting \(y_{1} { = }0,y_{2} { = }0\) and into Eq. (37), the following conclusion can be can be sorted out:

$$\begin{gathered} A_{1} a_{11} + B_{1} a_{21} + C_{1} = 0 \hfill \\ A_{2} a_{11} + B_{2} a_{21} + C_{2} = 0 \hfill \\ A_{3} a_{12} + B_{3} a_{22} + C_{3} = 0 \hfill \\ A_{4} a_{12} + B_{4} a_{22} + C_{4} = 0 \hfill \\ \end{gathered}$$
(38)

where,

$$\begin{gathered} A_{1} = 2\left( {W_{4} - W_{2} } \right)m^{2} x_{\alpha 2} - W_{1} mm_{2} ;B_{1} = 2\left( {W_{4} - W_{2} } \right)m^{2} x_{\alpha 1} + W_{1} mm_{2} \hfill \\ C_{1} = - \frac{{2k_{{\vartheta {1}}} }}{{r\omega_{m0}^{2} \sqrt {1 - \left( {x_{\alpha 1} } \right)^{2} } }} - W_{2} mm_{2} + 2\left( {W_{4} - W_{2} } \right)m^{2} \dot{y}_{20} \hfill \\ A_{2} = W_{1} mm_{2} - 2\left( {W_{1} - W_{{3}} } \right)m^{2} \dot{y}_{20} ,\quad B_{2} = W_{1} mm_{2} - 2\left( {W_{1} - W_{{3}} } \right)m^{2} \dot{y}_{10} \hfill \\ C_{2} = - \frac{{6k_{{\vartheta {1}}} }}{{r\omega_{m0}^{2} \sqrt {1 - \left( {x_{\alpha 1} } \right)^{2} } }} - 3W_{2} mm_{2} + 2\left( {W_{1} - W_{{3}} } \right)m^{2} x_{\alpha 2} \hfill \\ A_{3} = 2\left( {W_{4} - W_{2} } \right)m^{2} x_{\alpha 2} - W_{1} mm_{2} ,\quad B_{3} = W_{1} mm_{2} + 2\left( {W_{4} - W_{2} } \right)m^{2} x_{\alpha 1} \hfill \\ C_{3} = - \frac{{2k_{{\vartheta {2}}} }}{{r\omega_{m0}^{2} \sqrt {1 - \left( {x_{\alpha 2} } \right)^{2} } }} - W_{2} mm_{2} + 2\left( {W_{4} - W_{2} } \right)m^{2} \dot{y}_{10} \hfill \\ \end{gathered}$$
$$\begin{gathered} A_{4} = W_{1} mm_{2} - 2\left( {W_{1} - W_{{3}} } \right)m^{2} \dot{y}_{20} ,\quad B_{4} = W_{1} mm_{2} - 2\left( {W_{1} - W_{{3}} } \right)m^{2} \dot{y}_{10} \hfill \\ C_{4} = \frac{{6k_{{\vartheta {2}}} }}{{r\omega_{m0}^{2} \sqrt {1 - \left( {x_{\alpha 2} } \right)^{2} } }} + 3W_{2} mm_{2} + 2\left( {W_{1} - W_{{3}} } \right)m^{2} x_{\alpha 1} \hfill \\ \end{gathered}$$

Solve the Eq. (38),

$$\begin{gathered} \begin{array}{*{20}c} {a_{{11}} = \frac{{B_{1} C_{2} - B_{2} C_{1} }}{{A_{1} B_{2} - A_{2} B_{1} }},} & {a_{{21}} = \frac{{A_{1} C_{2} - A_{2} C_{1} }}{{A_{2} B_{1} - A_{1} B_{2} }}} \\ \end{array} , \hfill \\ \begin{array}{*{20}c} {a_{{12}} = \frac{{B_{3} C_{4} - B_{4} C_{3} }}{{A_{3} B_{4} - A_{4} B_{3} }},} & {a_{{22}} = \frac{{A_{3} C_{4} - A_{4} C_{3} }}{{A_{4} B_{3} - A_{3} B_{4} }}} \\ \end{array} , \hfill \\ \end{gathered}$$
(39)

The Jacobian matrix of the first-order approximation system of Eq. (33) can be written as,

$${\mathbf{D}}_{f} = \left[ \begin{gathered} a_{{{11}}} \quad a_{{{12}}} \hfill \\ a_{{{21}}} \quad a_{{{22}}} \hfill \\ \end{gathered} \right]$$
(40)

The characteristic equation of the first-order approximate system can be written as,

$$\left| {{\mathbf{D}}_{f} - \lambda {\mathbf{I}}} \right| = \left| \begin{gathered} a_{{{11}}} - \lambda \quad a_{{{12}}} \hfill \\ a_{{{21}}} \quad a_{{{22}}} - \lambda \hfill \\ \end{gathered} \right| = 0$$

That is,

$$\lambda^{2} - \left( {a_{{{11}}} + a_{{{22}}} } \right)\lambda + a_{{{11}}} a_{{{22}}} - a_{{{21}}} a_{{{12}}} = 0$$
(41)

The necessary and sufficient conditions for the root of Eq. (23) to have negative real parts are,

$$\begin{gathered} - \left( {a_{{{11}}} + a_{{{22}}} } \right) > 0 \hfill \\ a_{{{11}}} a_{{{22}}} - a_{{{21}}} a_{{{12}}} > 0 \hfill \\ \end{gathered}$$
(42)

Assuming that,

$$\begin{gathered} C_{W1} = - \left( {a_{{{11}}} + a_{{{22}}} } \right) \hfill \\ C_{W2} = a_{{{11}}} a_{{{22}}} - a_{{{21}}} a_{{{12}}} \hfill \\ \end{gathered}$$
(43)

Then the synchronous stability condition of the system can be determined as,

$$\begin{gathered} C_{W1} > 0 \hfill \\ C_{W2} > 0 \hfill \\ \end{gathered}$$
(44)

\(C_{W1}\) and \(C_{W2}\) are referred to as the synchronous stability index of the system. When the value of synchronous stability index is positive, the greater the value, the better the stability of the system.

Discussion and results

Numerical analysis

The data used in numerical analysis

In order to further verify the validity and accuracy of the above synchronization theoretical analysis and numerical calculation results of the self-synchronous vibration system of the coaxial triple-excited motor in the same direction rotation, and thus to find out the synchronization behavior and electromechanical coupling dynamic characteristics of the eccentric rotor and screen box of the coaxial triple-excited motor in the case of self-synchronization, this section is based on the multi-degree of freedom motion differential equation of the system. The electromechanical coupling model of the system is established by using Simulink module of MATLAB. The parameters used in numerical analysis are shown in Table 1.

Table 1 Parameters of the vibration system of a coaxial tri-exciter elastic coupling shaker.
Full size table

Computational analysis of synchronization

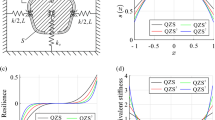
Assuming that the performance of the motors of the three exciters is identical, that is \(T_{{{\text{e12}}}} = T_{{{\text{e23}}}} = 0\). At this point, the synchronization index \(C_{{{\text{S1}}}} = C_{{{\text{S2}}}}\). Figure 2 shows the variation curve of synchronization index \(C_{S}\) with torsional stiffness \(k_{\vartheta }\) that calculated according to parameters in Table 1. When torsional stiffness \(k_{\vartheta }\) is zero, Synchronicity index \(C_{S0} =\) 554.82. At this point, the value of the synchronization index is much greater than 1, indicating that the vibration system with the parameters in Table 1 has good self-synchronization performance.

Fig. 2
figure 2

Change curve of synchrony index with torsional stiffness.

Full size image

The synchronization index \(C_{S}\) decreased linearly with the increase of torsional stiffness \(k_{\vartheta }\),and \(C_{S0}\) = 0 until \(k_{\vartheta }\) = 1.0532N·m/rad. Then, the synchronization index \(C_{S0}\) increases linearly with the increase of torsional stiffness \(k_{\vartheta }\). When the torsional stiffness of the coupling torsion spring reaches the condition \(k_{\vartheta }\) < 1.0513N·m/rad(region \({\rm I}\) in Fig. 2), the synchronization index is still > 1 and the system is still in the synchronization state with the increase of torsional stiffness. Under this condition, the synchronization index value is getting lower and lower, indicating that the synchronization performance of the system is getting worse and worse. When the torsional stiffness of the coupling torsion spring reaches the condition \(k_{\vartheta }\) > 1.055N·m/rad(region \({\rm I}{\rm I}{\rm I}\) in Fig. 2), the synchronization index \(C_{S}\) > 1. Under this condition, with the increase of torsional stiffness, the synchronization index increases linearly, and the synchronization performance of the system becomes better. However, when the torsional stiffness of the coupling torsion spring reaches the condition 1.0513 < \(k_{\vartheta }\) < 1.055N·m/rad(region \({\rm I}\) in Fig. 2), the synchronization index \(C_{S} < 1\), the system cannot be synchronized.

The above numerical law shows that, the synchronous performance of the coaxial tri-exciter vibration system with elastic coupling elements is lower than that of its’ self-synchronous system when the torsional stiffness of the coupling elements is small. When the torsional stiffness is greater than a certain value, the system will have better synchronization performance than its self-synchronization system. Therefore, the synchronization performance of the system is closer to the self-synchronization state in region \({\rm I}\), which is called the near-self-synchronization region. In region \({\rm I}{\rm I}{\rm I}\), the synchronization performance of the system mainly depends on the stiffness of the coupling element, which is called the coupling synchronization region. The system in zone \({\rm I}{\rm I}\) is out of synchronization, which is called the asynchronous zone. The torsional stiffness range of the corresponding coupling element in the asynchronous region is very small.

When conducting the analysis of the influence of the parameters involved in Fig. 3, except for the parameters being discussed, all other parameters were set according to the values in Table 1 and remained constant. Figure 3a shows the relationship between the synchronization index CS and torsional stiffness \(k_{\vartheta }\) of the system when other parameters remain unchanged and the mass of the eccentric rotor changes. It can be seen that, the change trend of the synchronization index and torsional stiffness is first linear decline, and then linear increase while the mass of the eccentric rotor increases. The greater the mass of the eccentric rotor, the greater the torsional stiffness \(k_{\vartheta }\) of the coupling element corresponding to the non-synchronous state of the system. In other words, the range of the near-self-synchronous region of the system increases, the near self-synchronization capability of the system is increased. In the coupling synchronization region, when the torsion stiffness of the coupling element is the same, the larger the mass of the eccentric rotor, the smaller the synchronization index CS, that is, the coupling synchronization ability of the system decreases. For asynchronous region \({\rm I}{\rm I}\) of the system, the larger the mass of the eccentric rotor, the gentler the synchrony index curve, and the wider the asynchronous region.

Fig. 3
figure 3

The curve of synchronization index changes with torsional stiffness when 4 important parameters change separately. (a) Change curve of synchrony index with torsional stiffness for different eccentric masses. (b) Change curve of synchrony index with torsional stiffness for different eccentricity radius. (c) Change curve of synchronization index with torsional stiffness at different rotate speed. (d) Change curve of the synchronization index with torsional stiffness for different screen mass.

Full size image

Figure 3b shows the relationship between the synchronization index and torsional stiffness CS of the system when other parameters remain unchanged and the eccentricity radius changes. As can be seen from Fig. 4, the change between synchronization index CS and torsional stiffness kg is similar to that of the eccentricity mass while the eccentricity radius increases. That is, The greater the eccentricity radius, the greater the near-self-synchronization region. In the coupling synchronization region, the larger the mass of the eccentric rotor, the smaller the synchronization index CS and the lower the coupling synchronization ability of the system when the torsional stiffness of the coupling element is the same. Therefore, the larger the eccentricity radius, the gentler the synchrony index curve, and the wider the asynchronous region \({\rm I}{\rm I}\) of the system.

Fig. 4
figure 4

The relationship between stability index and torsional stiffness in synchronous state (a)\(\alpha_{1} = 0\),\(\alpha_{2} = \pi\)(b)\(\alpha_{1} = 0\),\(\alpha_{2} = 0\)(c)\(\alpha_{1} = \pi\),\(\alpha_{2} = 0\) (d)\(\alpha_{1} = \pi\),\(\alpha_{2} = \pi\).

Full size image

Figure 3c shows the relationship between the synchronization index CS and torsional stiffness kg of the system when other parameters remain unchanged and the rotate speed changes. It can be seen that, the relationship between the synchronization index CS and torsional stiffness kg is similar to that of the eccentric mass and eccentric radius while the rotate speed of the eccentric rotor increases. The greater the rotational speed of the eccentric rotor, the larger the near-self-synchronization region. In the coupling synchronization region, the higher the rotational speed of the eccentric rotor, the smaller the synchronization index, and the lower the coupling synchronization ability of the system. Thus, the higher the speed of the eccentric rotor, the gentler the synchrony index curve, and the wider the non-synchronous region \({\rm I}{\rm I}\) of the system.

Figure 3d shows the relationship between the synchronization index CS and torsional stiffness kg of the system while other parameters remain unchanged and the mass of the screen frame changes. It can be seen that in the state of self-synchronization, the bigger the quality of the screen frame, the larger synchronization index of the system. That is, the self-synchronization performance of the system is better. In the near self-synchronization region, the greater the mass of the screen frame, the faster the linear decline of the synchronization index and torsional stiffness, and the smaller the near self-synchronization region of the system. In the coupling synchronization region, the larger the mass of the screen frame, the faster the synchronization index increases, and the better the coupling synchronization performance of the system. The larger the mass of the screen frame, the gentler the synchrony index curve, and the wider the non-synchronous region II of the system. In other words, this is mainly due to the increase of the system vibration mass when the screen frame mass increases. Thus, the vibration acceleration is reduced, the vibration torque acting on the eccentric rotor is reduced, and the torsional stiffness required by the coupling element is also reduced.

Computational analysis of stability

The analysis of the influence of system parameters on stability is carried out under the synchronous state of system stability in Table 1.

According to the parameters in Table 1 and considering Te12=Te23=0, the stability coefficient of the system is calculated by Eq. (44). It can be considered as a self-synchronous vibration system of the triple-excited motor when the vibration system meets the condition  kg = 0N·m/rad. Through synchronization analysis, it can be known that the system has four synchronization states, those are, \(\alpha_{1} = 0\),\(\alpha_{2} = \pi\);\(\alpha_{1} = 0\),\(\alpha_{2} = 0\);\(\alpha_{1} = \pi\),\(\alpha_{2} = 0\) and \(\alpha_{1} = \pi\), \(\alpha_{2} = \pi\). The system is stable only when \(\alpha_{1} = 0\),\(\alpha_{2} = \pi\), and this kind of synchronization state is the true motion state of the system.

Figure 4a shows the relationship curve between stability index and torsional stiffness in synchronous state \(\alpha_{1} = 0\),\(\alpha_{2} = \pi\). It can be seen that the stability index CW1 and CW2 are linearly decreased with the increase of torsional stiffness kg of the coupled elements. The stability index CW1 and CW2 both are greater than zero when the torsional stiffness \(k_{\vartheta } \le\) 0.585N·m/rad. In this stiffness interval, the synchronization state of the system is stable, but the stability becomes worse and worse. The stability index CW2<0 when torsional stiffness kg >0.585 N·m/rad. In this stiffness interval, the corresponding synchronization state is unstable, and the system cannot work stably in this synchronization state.

Figure 4b shows the relationship curve between stability index and torsional stiffness in synchronous state \(\alpha_{1} = 0\),\(\alpha_{2} = 0\). It can be concluded that the stability index CW1 and CW2 of the system in this synchronous state both increase linearly with the increase of the torsional stiffness of the coupled elements, and the stability of the system gradually becomes better. The values of stability index are both greater than zero when the torsional stiffness kg N·m/rad. Therefore, the synchronization state of the system is stable when \(\alpha_{1} = 0\),\(\alpha_{2} = 0\).

Figure 4c and d show the relationship curve between stability index and torsional stiffness in synchronous states \(\alpha_{1} = \pi\),\(\alpha_{2} = 0\) and \(\alpha_{1} = \pi\),\(\alpha_{2} = \pi\). Comparing these two figures, it can be seen that these two synchronization states are unstable in this system. These two synchronous states are not true motion states in a self-synchronous system. Similarly, it is not the true motion state in a triaxial motor system coupled by a torsion spring.

By comparing Fig. 4a and b, it can be seen that the elastic coupling elements are coupled between the coaxial triple excitation motors, even if the coupling elements adopt a small torsional stiffness, the real synchronization state \(\alpha_{1} = 0\),\(\alpha_{2} = \pi\) of the synchronous system will lose stability. In order to change the unstable synchronization state into the real stable synchronization state, the torsional stiffness of the coupling element must be large enough.

Simulations

In order to verify the validity and accuracy of the numerical analysis results above, it is necessary to simulate the electromechanical dynamics based on the electromechanical coupling model of the system. Therefore, after the numerical analysis yields the results, some of these values are randomly selected to be used in the mechanical–electrical coupling simulation analysis. If the results of the mechanical–electrical coupling simulation analysis are consistent with those of the numerical analysis, it can indicate the correctness of the numerical analysis. As a result, the arrangement of the research process can achieve a logical flow. The electromechanical coupling model of this vibration system is established by the Simulink of MATLAB. In the practical engineering, three identical types of asynchronous induction motor are applied to actuate exciters. The electromagnetic parameters of the induction motors are shown in Table 2. The schematic diagram of the vibration system model in this paper, presented in the Simulink flowchart of MATLAB, is shown in Fig. 5. In the simulation model, the parameters of the system are \(M = 100\) kg,\(m_{1} = m_{2} = m_{3} = 2\) kg, \(f_{1} = f_{2} = f_{3} = 0\) N·m·s/rad, \(J_{\psi } = J_{\delta } = J_{\theta } = 10\) kg·m2, \(f_{x} = f_{y} = 125\) N·s/m,\(f_{\psi } = f_{\delta } = f_{\theta } = 15\) N·m·s/rad, \(\omega_{m0} = 157\) rad/s, \(k_{x} = k_{y} = 10037\) N/m, \(k_{\psi } = k_{\delta } = k_{\theta } = 1500\) N·m/rad , \(l_{X} = 0.1\) m,\(l_{Y} = 0.25\) m and \(l_{Z} = 0.1\) m, respectively.

Table 2 The parameter values of motors.
Full size table
Fig. 5
figure 5

Simulink flowchart of MATLAB of the vibration system.

Full size image

Figure 6 shows the synchronization of the ERs as \(k_{\vartheta } = 4\) N·m/rad,\(l_{Z} = 0.1\) m, when the three asynchronous exciters started at the same time, the angle acceleration of the two coaxial exciters is different in the initial stage. In the steady phase, the two rotors are synchronously rotated with average speed of 157 rad/s, the phase difference \(\alpha_{{1}}\) between rotor 1 and 2 is approached to 1.756 rad, and the phase difference \(\alpha_{{2}}\) between rotor 2 and non-coaxial rotor 3 is stable around 1.748 rad. As can be seen from Fig. 6c, the synchronous torque of the three rotors is stable around 0 N.m. when the rotors are steadily and synchronously rotated. From Fig. 6d–h, in this synchronous state, the rigid frame is vibrated with amplitudes 1.8 × 10-3 m and 1.8 × 10–3 m in x- and y- directions, respectively. Meanwhile, the amplitudes of twisting vibration of rigid frame in the \(\psi\)-,\(\delta\)- and \(\theta\)- directions are 5.5 × 10–3 rad ,6.3 × 10–3 rad and 2.1 × 10–1 rad, respectively. By comparing the simulation results with the numerical analysis, it can be seen that the simulation results are consistent with the theoretical values.

Fig. 6
figure 6

Synchronization for \(k_{\vartheta } = 4\).67N·m/rad,\(l_{Z} = 0.1\) m. (a) Velocities. (b) Phase difference. (c) Electromagnetic torque. (d) Displacement in x- direction. (e) Displacement in y- direction. (f) Pitching vibration in \(\psi\)- direction. (g) Pitching vibration in \(\delta\)- direction. (h) Pitching vibration in \(\theta\)- direction.

Full size image

Experiment

Utilizing the findings from the aforementioned study, a elastic coupling mechanical synchronization laboratory experimental device illustrated in Fig. 7 is devised. This device consists of three coaxial exciters, interconnected by two torsional springs of equal stiffness with rated value of \(k_{\vartheta }\).

Fig. 7
figure 7

Schematic diagram of the device for vibration testing. (a) Complete vibration test system. (b) Experimental instrument.

Full size image

In order to compare with the self-synchronization system, the torsion spring between the coaxial three exciters was removed, and the self-synchronization state of the system was also tested. To analyze the effect of torsional stiffness \(k_{\vartheta }\) on the synchronization state of the system, the experiments were conducted on coaxial tri-motors with several pairs of identical torsional springs of the different stiffness. HX-6E high-speed imaging system was employed to achieve visual measurements of the phase angles of the exciters. The structural parameters involved in this experiment are as follows:\(l_{Z} = 0.1\) m,\(l_{X} = 0.1\) m,\(l_{Y} = 0.25\) m.

In the experiments of self-synchronization and elastic coupling mechanical synchronization, the phase difference angle between three exciters was tested in two situations. One of them is that all three exciters are powered, and the other is that exciters 1 and 3 are powered, while exciter 2 is powered off. The rated power of each exciter is 0.12kw.

The previous part conducted a comparative experiment on the full-power startup of the motor and the interruption of the intermediate motor power supply during operation. This comparative experiment to some extent validates that the coupled synchronous system studied in this paper has a more energy-efficient working mode. In order to further verify that the indoor experimental model of the tri-exciter-coupled vibration system studied in this paper has the advantage of energy saving, an additional experimental section was specially added to measure the working current of each working motor.

In the test of the working current of the excitation motor, a BM803A + digital DC/AC type clamp meter was selected. To achieve more accurate measurement, the selected range is 10A and the measurement accuracy is 10 mA. Under the condition where all three excitation motors are powered on, the working currents of motor 1, motor 2 and motor 3 are 0.39A, 0.33A and 0.34A respectively. Furthermore, in the operating condition where all three excites are powered on first and then the middle exciter is turned off, the working currents of motors 1, 2 and 3 are 0.39A, 0A and 0.34A respectively. Based on the working current of each motor under two working conditions, the corresponding actual power of each motor can be obtained. Under the two working conditions, the actual power of motors 1 and 3 is basically the same. Motor 2 has no current flowing through when it is disconnected from power. That is, when the coaxial three-exciter vibration synchronization system is operating, if the power supply of one of the working motors is suddenly cut off, the other two working motors can still operate at the same actual power as when all three motors were powered on simultaneously. Therefore, it can be concluded that the coaxial tri-exciter synchronous system has a running mode that can achieve higher energy efficiency during operation.

Based on the vibration test platform shown in Fig. 7, the dynamic response of the vibration system under the state of self-synchronization and mechanical synchronization coupled by torsional spring are shown in Fig. 8.

Fig. 8
figure 8

Dynamic response under self-synchronization and coupling synchronization state. (a) Dynamic response of the self-synchronization system when all motors are in. (b) Dynamic response of the self-synchronization system when the intermediate motor is power off. (c) 15 Dynamic response of the synchronization system coupled by torsion spring when all motors are in operation. (d) Dynamic response of the synchronization system coupled by torsion spring when the intermediate motor is power off.

Full size image

It can be seen from Fig. 8a and b that the system can operate stably under two self-synchronous states of three motors in a fully energized state and the intermediate motor in a state of power off, respectively. The acceleration amplitudes in the x and y directions of the system are stable at about 8.1, 6.8 and 7.9, 4.6 m/s2, respectively. In the same way, it can be seen from Fig. 8c and d that the system can operate stably under two coupling synchronization states of three motors in a fully energized state and the intermediate motor in a state of power off, respectively. The acceleration amplitudes in the x and y directions of the system are stable at about 23, 22 and 15, 11 m/s2, respectively.

It is worth noting that, despite the inevitable errors, the stable values of the dynamic response of the system in degrees of freedom x-, y- and z- are consistent with the values obtained from the theoretical analysis and numerical calculation above.

The experimental results of synchronous phase difference obtained by vibration test with indoor prototype are shown in the Figs. 9, 10 and the Table 3.

Fig. 9
figure 9

Experimental results of self-synchronization. (a) Experimental results for three motors are all energized. (b) Experimental results for motor 2 is powered off.

Full size image
Fig. 10
figure 10

Experimental results for coupling synchronization with torsion spring when \(k_{\vartheta } = 4.67,8.33,16.67\) N·m/rad. (a) Experimental results for three motors are all energized. (b) Experimental results for motor 2 are powered off. (c) Experimental results for three motors are all energized. (d) Experimental results for motor 2 are powered off. (e) Experimental results for three motors are all energized. (f) Experimental results for motor 2 are powered off.

Full size image
Table 3 The phase difference angle of experimental results.
Full size table

The self-synchronization experimental results show that, the synchronous phase difference \(\alpha_{1}\) between rotor 1 and rotor 2 is -164°, rotors 1 and 2 are in anti-phase synchronization state; the synchronous phase difference \(\alpha_{2}\) realize between rotor 2 and rotor 3 is -49°, which is far greater than zero. The coaxial rotors 1, 2and 3 of the system cannot zero-phase synchronization in the self-synchronization state.

The torsion springs used in the experimental scheme have been measured and their torsional stiffness are \(k_{\vartheta }\) = 4.67, 8.33, 16.67 N·m/rad. The experiment results of elastic coupling mechanical synchronization show that, when the torsional stiffness \(k_{\vartheta }\) = 4.67, 8.33, 16.67 N·m/rad, the synchronous phase difference \(\alpha_{1} = 4^\circ ,3^\circ ,2^\circ\) and \(\alpha_{2} = - 1^\circ , - 2^\circ , - 3^\circ\) under three motors energized, the synchronous phase difference \(\alpha_{1} = - 4^\circ ,4^\circ , - 1^\circ\) and \(\alpha_{2} = - 3^\circ , - 6^\circ ,2^\circ\) under motor 1 and 3 energized. The experimental results have verified that elastic coupled mechanical synchronization can effectively achieve in-phase synchronization of coaxial three exciters, and the phase difference angle is close to 0°. When only two of the three motors are powered on, there is no significant change in the synchronization phase difference angle between the three exciters, the power consumption of the experimental device has been reduced by one-third.

Conclusions

Through researching the synchronous mechanism of the coaxial co–rotating tri-exciter with two torsional springs, several key conclusions can be highlighted.

  1. (a)

    It is mentioned that the theoretical analysis, simulation analysis, and experimental results of the system’s synchronization characteristics are in good agreement. This suggests that the findings obtained from these three different approaches closely match and support each other.

  2. (b)

    By selecting the right torsion spring stiffness and ensuring the system meets the synchronization and stability criteria, the three elastic coupling coaxial exciters can operate in a nearly zero-phase synchronized and stable manner.

  3. (c)

    The research results show that, when the torsional stiffness of the coupling element changes, the synchronization state of the system is divided into near self-synchronization zone, asynchronous zone, and coupled synchronization zone. In the near self- synchronization zone, the synchronization performance of the system decreases with the increase of torsional stiffness, while in the coupled synchronization zone, the synchronization performance increases with the increase of torsional stiffness. The larger the mass, eccentricity radius, and rotational speed of an eccentric rotor, the greater the torsional stiffness corresponding to the asynchronous zone, and the wider the variation range of torsional stiffness of the asynchronous zone. As the mass participating in vibration increases, the torsional stiffness and variation range corresponding to the asynchronous zone become smaller.

  4. (d)

    When the system is in self-synchronization, the theoretical synchronization state \(\alpha_{1} = 0\), \(\alpha_{2} = \pi\) is stable. Due to differences in electromagnetic parameters and mechanical structural errors of the actual motor, the self-synchronization stable state is \(\alpha_{1} = { - }49\)°,\(\alpha_{2} = { - }164\)°. Although there is a certain difference from the theoretical synchronization state, it also reflects that exciters 1 and 2 are in-phase synchronization, and exciters 2 and 3 are in anti-synchronization. In the near self-synchronization zone, as the torsional stiffness increases, the stability of the system’s anti-phase synchronization decreases; In the coupled synchronization zone, as the torsional stiffness increases, the stability of the system in-phase synchronization increases.

  5. (e)

    When only two of the three motors are powered on, the synchronization phase difference angles are almost the same as when all three motors are powered on. This means that, for a multi-exciter vibration system with elastic coupling mechanical synchronization, energy saving can be achieved by reducing the number of energized motors during stable operation, and the energy-saving effect is significant.