Introduction

Pre-diabetes is a condition where an individual’s blood glucose levels are elevated above normal but not high enough to be diagnosed as diabetes1. This state indicates an increased risk of developing type 2 diabetes and other diseases, such as cardiovascular diseases, if not addressed2. Prediabetes has become a worldwide epidemic3, characterized by various associated complications, and its prevalence is on the rise, notwithstanding its treatable nature4,5. The Expert Committee on Diagnosis and Classification of DM in 1997 initially recognized prediabetes as an intermediate stage, signifying a relatively elevated risk for future diabetes development6. It has been documented that around 5–10% of individuals with untreated prediabetes subsequently progress to develop diabetes. With prolonged observation, there is a potential for an increase in this progression rate7. This statistic is especially concerning, given the high prevalence of prediabetes among Iranian adults (18.2%)8. In Iran, it is predicted that the prevalence of diabetes will increase by 91% by 2035, and the associated economic burden is expected to increase significantly by 20359,10. Therefore, identifying people with prediabetes provides an opportunity for intervention through lifestyle modification and pharmacological treatments aimed at preventing the progression of diabetes11,12. The primary aim of the present study is to investigate the determinants of prediabetes within an urban population in Tehran, Iran.

Existing prediabetes screening tools, which rely on a limited selection of established risk factors, reportedly failed to identify a significant proportion of undetected individuals with prediabetes13. In addition to clinical tools for the diagnosis of pre-diabetes, the scientific community has increasingly focused on the use of powerful statistical models for early and accurate prediction of pre-diabetes. These models can contribute to identifying predisposing factors for pre-diabetes in various communities, particularly in Iranian society, and aid in delaying or preventing diabetes. As a result, they can help reduce mortality and associated complications in the studied population.

This study analyzes longitudinal data from the Tehran Lipid and Glucose Study (TLGS) using advanced statistical models. Traditional methods, such as generalized linear mixed models (GLMM), are commonly applied to such data but have certain limitations14,15,16. A key limitation of GLMMs is the need for users to pre-specify interactions between predictors and nonlinear relationships with the outcome, features that are often unknown beforehand and difficult to identify in high-dimensional datasets17. To address these challenges, machine learning (ML) models have been increasingly utilized. Although ML techniques are more complex than conventional statistical methods, they do not rely on assumptions such as linear relationships or normally distributed residuals18. This flexibility enables data analysts to explore large datasets with many variables more thoroughly and efficiently19.

Currently, ML methods are being employed for the detection and prediction of pre-diabetes, complications, and disease progression20,21,22,23,24. One of the advanced ML methods used for developing predictive models is the Random Forest (RF) algorithm. The standard RF algorithm, like other ML methods, assumes that observations are independently sampled from the population. Ignoring the dependencies among observations collected over time in longitudinal data can result in biased inferences, such as underestimated standard errors in linear models25. To date, research studies have not adequately emphasized the examination and understanding of the correlations within the data learning methods that have recently been proposed. One advanced technique is generalized mixed effects random forests (GMERF)26. The main concept of integrating random forests into mixed linear models is to replace the fixed effect component with a tree or forest while using random effects to model the dependence structure26. This comprehensive approach enables scientists, especially in areas like healthcare, to investigate intricate questions about treatment efficacy while considering the diverse responses of individual subjects27.

The objective of this research is to utilize a more advanced statistical model to determine the most efficient ML approaches for examining interrelated data. Additionally, it seeks to rigorously evaluate the predictive capabilities of the selected model in accurately classifying new patients at risk of prediabetes. For the first time, we incorporate the longitudinal nature of the Tehran Lipid and Glucose Study (TLGS) data into the RF models. Our objective is to predict prediabetes based on key indicators utilizing the GMERF method. The results will be compared with those obtained from GLMM and a standard RF model. The investigators aim for these findings to help identify individuals at risk of developing prediabetes, thereby contributing to a reduction in the disease’s burden on the population.

Materials and methods

Data source

The Tehran Lipid and Glucose Study (TLGS) is the first prospective population-based study in Iran, initiated in 1998, aimed at determining risk factors for non-communicable diseases, including glucose and lipid disorders, obesity, smoking, low physical activity, and hypertension, with the goal of improving lifestyle to prevent these risk factors. This study was conducted on a group of residents aged 3–69 years in District 13 of Tehran. District 13 was chosen as the sampling framework due to the greater stability of its residents, the presence of healthcare centers affiliated with the University of Medical Sciences, and the demographic similarities (age and gender distribution) of its population to that of the broader Tehran population. The participants were invited to the Lipid and Glucose Research Unit through face-to-face contact, where their data were collected through interviews, physical examinations, serum tests, and anthropometry measurements. This study consists of seven phases, with measurements repeated every three years. The design and methodology of the TLGS have been thoroughly detailed in previously published works28.

Initially, 15,011 subjects participated in the Tehran Lipid and Glucose Study. Due to dropouts during the first phase and enrolling new subjects in the second phase, the combined data from both phases were treated as the initial phase of the study. In other words, this combined phase included participants from both phases. Ultimately, the total study population consisted of 12,240 subjects.

Inclusion criteria

The inclusion criteria for this study were: age over 20 years, participants who were healthy in phase one (i.e., without prediabetes, diabetes, or cancer), and individuals who participated in at least two phases of the study. After applying these criteria, 5361 participants remained eligible for the study. Since participants might develop pre-diabetes between phases, the independent risk factors from the previous phase were considered for each outcome phase. For example, the risk factors from the second phase were used for the third phase outcome, and similarly, up to the seventh phase, where the independent variables from the sixth phase were considered. According to this definition, five phases were identified in total. The next scenario in the study was the possibility that individuals might progress directly from being healthy to developing diabetes without passing through a pre-diabetes stage. This could be due to unrecorded pre-diabetes in previous phases, non-attendance, or developing pre-diabetes in the time interval between phases. Therefore, the initial phase of diabetes onset for these individuals was classified as prediabetes, and any subsequent records for those individuals were removed from the study.

Main outcome and potential predictors

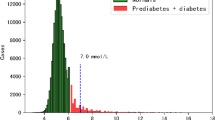
In this study, the primary outcome variable was prediabetes, defined as a binary variable based on fasting blood sugar (FBS) between 100 and 125.9 mg/dL or 2-h post-load blood sugar (BS2HR) between 140 and 199.9 mg/dL, with no use of anti-diabetic medication. In addition, 31 variables were initially treated as the potential factors influencing pre-diabetes. These variables included demographic factors (such as age, gender, marital status, occupation, and education), medical history (including the use of thyroid drugs, antihyperlipidemic drugs, antihypertensive drugs, cardiac drugs, corticosteroids, aspirin, family history of diabetes, family history of cardiovascular diseases (CVD), and history of CVD, as well as smoking and the metabolic equivalent of task (MET). Additionally, medical examination data including pulse rate, systolic blood pressure (SBP), diastolic blood pressure (DBP), and anthropometric measurements such as body mass index (BMI), waist circumference (WC), wrist circumference, hip circumference, waist-to-height ratio (WHtR), and waist-to-hip ratio (WHR) were considered. Blood biomarkers including HDL, total cholesterol (TC), creatinine, triglycerides (TG), Glomerular Filtration Rate (GFR), TC-to-HDL ratio, and TG-to-HDL ratio were also analyzed. In this study, individuals (ID) were used as a clustering variable, or, in other words, as a random effect. Comprehensive information regarding anthropometric and laboratory measurements, along with the techniques used, can be found in earlier published studies29.

Statistical analysis

For each variable in the dataset, the proportion of missing data was below 20%. We assessed the missing data patterns and found no evidence of systematic bias, suggesting that the data were missing at random (MAR). Missing values were imputed using the Multiple Imputation by Chained Equations (MICE) package in R, employing the weighted predictive mean matching (WPMM) method. Five imputed datasets were generated and combined using Rubin’s rules to account for imputation uncertainty30. In the quantitative analysis, central tendency and variability measures were computed for numerical variables, while qualitative factors were summarized using frequency distributions. To evaluate model performance, the data was randomly split into 80% training and 20% test sets, ensuring that the outcome variable’s distribution remained consistent across both data sets. The data splitting method ensured that all occurrences of a given ID were assigned to either the training or test dataset, not split between them.

In the second step, we employed the ‘varSelRF’ and ‘VSURF’ R packages to address the problem of feature multicollinearity. This step focused on identifying a definitive set of features most pertinent to predictive modeling, aiming to enhance the effectiveness of our ML techniques. The varSelRF method, developed by Diaz-Uriarte et. al., employs a backward elimination approach for the feature selection. This technique systematically removes the least important features while preserving a comparable error rate to that of the full model (including all features)31. The VSURF is a method that utilizes a stepwise procedure introduced by Genuer et al. This approach also ensures that the error rate remains similar to that of the full model32. We selected these two algorithms because they are robust to multicollinearity, widely validated in biomedical studies, and well-suited to high-dimensional data. Their ensemble nature reduces variance and overfitting, thus improving the generalizability of the models31,33.

Then, the predictor variables were utilized to fit a multivariable random intercept mixed-effects logistic regression (LR) model using the glmer package. The model parameters were estimated using the restricted maximum likelihood (REML) method and Z-normalization was finally applied to the numerical variables.

The GMERF is based on a GLMM, where the fixed effects are estimated using an RF, while the dependence structure is preserved through random effects. The RF aims to handle interactions among covariates and addresses highly nonlinear effects.

The severe class imbalance in our longitudinal data, with only 25% of cases belonging to the positive class (those with prediabetes), posed a significant challenge. This imbalance can hinder the model’s ability to accurately classify cases, leading to low sensitivity (true positive rate) and potentially low specificity (true negative rate). To address this issue, we adjusted the decision threshold, lowering it to improve sensitivity, though at the expense of specificity. The cutoff point was chosen to ensure that the proportion of instances assigned to the positive class in the training set closely matched the true proportion of the positive class34. Finally, we compared the performance of the GMERF model with the GLMM and RF models in predicting prediabetes. The evaluation was based on various metrics, including accuracy, sensitivity, specificity, and the area under the ROC curve (AUC).

It is crucial to note that the validation parameters were determined using the ten-fold cross-validation technique, tailored to each algorithm type. For the RF algorithm specifically, we fine-tuned several parameters: the total quantity of decision trees in the RF35, the maximum depth of trees (deeper trees can capture more intricate patterns but risk overfitting36 and the number of features considered at each node split35. Other parameters were left at their default settings. The prediction error was quantified as the average absolute difference between predicted and observed values, corresponding to the predictive misclassification rate (PMCR).

Prediction models based on ML were developed using the variables obtained from comparing two feature selection methods. To ensure robust performance and avoid overfitting, we employed the K-fold cross-validation procedure. This approach helps prevent artificially inflated validation metrics by providing a more reliable estimate of model performance37. Figure 1 presents a detailed overview of the study design framework. All statistical analyses were conducted using the R version 4.4.1, with P values less than 0.05 considered statistically significant.

Fig. 1
figure 1

Flowchart of the study design.

Full size image

Ethical approval

The research was carried out in alignment with ethical guidelines and national standards for medical research in Iran. All procedures involving human participants in the Tehran Lipid and Glucose Study (TLGS) were approved by the National Research Council of the Islamic Republic of Iran, and written informed consent was obtained from each participant.

Additionally, the study received approval from the Ethics Committee of Shahid Beheshti University of Medical Sciences under approval number IR.SBMU.RETECH.REC.1402.593.

Results

This study analyzed data from a cohort of 5361 individuals. Table 1 presents the distribution of participants by gender, along with the mean (SD) age and the percentage of prediabetes for each phase of the study. In addition, Table 2 displays the general characteristics of the population under study. Based on the varSelRF and VSURF packages, we included the variables identified as important by both methods in the modeling process. Regarding this, 21 variables (features) were selected to include the described models (Fig. 2). The selected features were: age, gender, education, antihyperlipidemic drugs, antihypertensive drugs, SBP, DBP, BMI, WC, wrist circumference, hip circumference, HDL, TC, creatinine, TG, GFR, WHtR, WHR, TC-to-HDL ratio, TG-to-HDL ratio, and Time (Phase).

Table 1 Percentage of prediabetes for each phase of the study.
Full size table
Table 2 General characteristics of the population under study.
Full size table
Fig. 2
figure 2

Feature selection of variables using: (A) VSURF algorithm, (B) varSelRF algorithm.

Full size image

In the next step, a multivariate mixed-effects LR model was utilized to identify the risk factors for prediabetes within the study population. Table 3 presents the estimated values obtained from the analysis. The results indicate that the variables age, education, antihyperlipidemic drugs, antihypertensive drugs, SBP, BMI, Waist circumference, Hip circumference, HDL, TC, TG, WHR, TC-to-HDL were significantly linked to the presence of prediabetes in the cohort under investigation (P < 0.05).

Table 3 Results of mixed-effects logistic regression analysis of risk factors for prediabetes in the TLGS.
Full size table

Additionally, we applied a conventional RF model to the dataset. The variable importance indices obtained from the fitted RF model are displayed in Fig. 3. Based on these findings, it can be inferred that five variables emerged as the most significant predictors of prediabetes: WHR, TG-to-HDL, WHtR, BMI, and TC-to-HDL. Conversely, the five variables with the lowest importance scores were: time, education, antihypertensive drugs, antihyperlipidemic drugs, and gender.

Fig. 3
figure 3

Importance index of variables in RF. TG_HDL, TG-to-HDL ratio; TC_HDL, TC to HDL ratio.

Full size image

In the third stage of data analysis, we fitted the GMERF model to the data. The most influential predictors identified by the GMERF model were: WHR, age, WC, time (phase), and TG. The least important variables were creatinine, education, antihypertensive drugs, antihyperlipidemic drugs, and gender (Fig. 4).

Fig. 4
figure 4

Importance index of variables in GMERF. TG_HDL, TG-to-HDL ratio; TC_HDL, TC to HDL ratio.

Full size image

Figure 6 presents the ranked importance of all 21 predictor variables in both the RF and GMERF models. The figure highlights shifts in variable importance between models using connecting lines, allowing for visual comparison of their relative rankings.

Lastly, we calculated the predictive power indices for the conventional RF, GLMM, and GMERF models (Table 4). The results indicate that the GMERF model outperforms the other models in terms of predictive capability. The RF model exhibited the lowest sensitivity (0.62) and specificity (0.63) values among the fitted models. To visually compare the estimated predictive criteria of these models, we assessed their effectiveness in predicting prediabetes using the ROC curve. In this context, the RF and GMERF models showed, respectively, the lowest and highest area under the ROC curve, with AUC of 0.65 and 0.75. Additionally, the GLMM model demonstrated better performance than the RF model, with an estimated AUC of 0.73 (Fig. 5).

Table 4 Comparison of predictive power indices for GLMM, RF, and GMERF.
Full size table
Fig. 5
figure 5

Receiver operating characteristic (ROC) curve for different machine learning models and GLMM.

Full size image

Discussion

Early identification of individuals at risk for prediabetes is crucial for preventing the onset of type 2 diabetes38,39. Despite the benefits of early intervention, no effective strategy currently exists for large-scale prediabetes screening40,41. Our research explored the use of ML approaches to create robust predictive models for diseases. An analysis of predictive power indices showed that the GMERF model outperformed other evaluated models. The GLMM ranked second in performance, yielding results very similar to those of the GMERF model. The RF model demonstrated lower accuracy compared to both. This is in agreement with the results of the study conducted by Asadi et al. to diagnose cardiovascular disease (CVD) in clustered data. Among the four statistical models—Generalized Linear Mixed Model tree (GLMMtree), decision tree (DT), GMERF, and RF—the GMERF model showed the best performance, while the RF model had the lowest accuracy42 (Fig. 6).

Fig. 6
figure 6

Variable importance comparison between RF and GMERF models for all 21 predictors.

Full size image

According to the findings from the GMERF model in our study, waist-to-hip ratio and age have the greatest impact on predicting prediabetes. Similarly, in the GLMM model, these variables also had a significant effect on the outcome. A cross-sectional study conducted in Vietnam, which included 2142 individuals aged 30–72 years, found that waist-to-hip ratio and systolic blood pressure are significant predictors of type 2 diabetes risk. The area under the ROC curve for these two risk factors was 0.73 for men and 0.69 for women43. Numerous studies have explored the use of ML for predicting and diagnosing diabetes, presenting various prediction models and comparing their sensitivity and ROC curves44,45,46,47. In a cross-sectional study conducted in 2024, a total of 3376 individuals over the age of 30 in Iran, who participated in a diabetes screening program across 16 comprehensive health service centers, were included. Five different ML algorithms—CatBoost, RF, XGBoost, logistic regression (LR), and artificial neural networks (ANN)—were used to model the dataset. Among these models, CatBoost performed slightly better, achieving an overall AUC of 0.737. Age, WHR, BMI, and SBP were identified as the most important factors for predicting diabetes48. A cohort of 36,652 individuals from a rural population in China was analyzed to predict the risk of T2DM using six machine learning algorithms: logistic regression (LR), classification and regression tree (CART), artificial neural network (ANN), support vector machine (SVM), random forest (RF), and gradient boosting machine (GBM). Model performance was evaluated using 30 variables in each algorithm, except for the CART model49. In that study, a high urinary glucose level was identified as the most significant variable by all algorithms. However, urinary glucose was not measured in our study, which limits direct comparison. Despite this, obesity indicators such as WHR and WHtR consistently ranked among the most important variables across all ML models in both studies, aligning with our findings. Other significant risk factors identified in the Chinese cohort included gender, age, family history of diabetes, WC, BMI, and SBP. In our analysis, however, gender and family history of diabetes were not among the top predictive variables50.

Our study demonstrated that WC is an important additional factor in the prediabetes prediction model. In a study conducted by Hu et al. in 2020 on 22,945 prediabetic individuals who were followed for eight years, it was concluded that those who later developed diabetes experienced a greater annual increase in BMI and WC compared to those who did not develop diabetes51. Additionally, Alperet et al. demonstrated that for diagnosing diabetes mellitus, central obesity criteria such as WC and WHtR are more effective than BMI in three major Asian ethnic groups (Chinese, Malay, and Asian-Indian)52. In Europe, WC has been identified as a stronger predictor of diabetes risk compared to BMI53. Prospective analyses in the Iranian population also revealed comparable associations between BMI and WC in predicting diabetes progression54.

In an analytical cross-sectional study conducted in Mashhad, the statistical population was selected using a stratified-cluster sampling method, comprising 8810 individuals aged 35–64 years. LR models were utilized to identify determinants of prediabetes, revealing significant statistical associations between age (OR = 1.055), WC (OR = 1.02), and TG (OR = 1.002) with prediabetes. Furthermore, gender, marital status, and tobacco use did not show significant relationships with prediabetes. The prevalence of prediabetes in this study was 10.2% (885 cases)55. In a study conducted in South Africa involving 6442 individuals aged over 15, it was shown that gender and WC have significant relationships with prediabetes56, whereas, in our study, the gender variable was not significantly important.

Interestingly, gender did not emerge as a significant predictor of prediabetes in our study, which contrasts with some previous research reporting gender-related differences in metabolic risk57,58,59. This discrepancy could stem from population-specific factors, such as genetic background, lifestyle behaviors, or cultural influences unique to the TLGS cohort. Additionally, our modeling approach, which adjusted for a comprehensive set of covariates and considered repeated measures, may have reduced residual confounding that could otherwise amplify gender effects. Another possible explanation is that the interaction between gender and other predictors (e.g., age, waist circumference, or lipid profiles) may have moderated the direct effect of gender itself. Further studies are warranted to explore potential gender interactions or to validate this finding in different populations and using alternative modeling strategies.

In our analysis, both triglyceride (TG) levels and time (i.e., study phase) emerged as important predictors of prediabetes, particularly in the GMERF model. The significant role of TG is consistent with previous epidemiological studies demonstrating its association with insulin resistance and impaired glucose metabolism. For instance, a large-scale longitudinal study by Guo et al. in 2024 showed that elevated TG levels were independently associated with increased risk of type 2 diabetes, even after adjusting for other metabolic risk factors60. Our findings align with this evidence, as TG was significantly associated with prediabetes across all three modeling approaches (GLMM, RF, GMERF). Similarly, “time” was identified as an important variable in the GMERF model. This reflects the dynamic nature of prediabetes risk, which can evolve over different phases of follow-up due to aging, lifestyle changes, and cumulative exposure to risk factors. In longitudinal or multi-phase cohort studies, time functions as a proxy for these evolving influences. Its predictive importance in our model suggests that incorporating temporal dynamics may improve risk stratification, particularly in settings where data are collected across multiple time points or phases61,62.

This study represents the first application of an ML model that accounts for the correlation structure of the data to the TLGS dataset. A key aspect of our approach is the comprehensive feature selection and model development process. We utilized the power of ML algorithms to systematically assess the significance of these features in predicting prediabetes. Interestingly, our results indicated that the RF model exhibited the lowest accuracy compared to GMERF and GLMM. This discrepancy may arise from the inherent assumptions of the RF algorithm. Like many other machine learning methods, RF assumes that observations are sampled independently from the population, which may not hold true in longitudinal settings. Although RF assumes independent observations and is therefore suboptimal in this context, its widespread use in clinical prediction tasks and decision-support systems makes it a relevant comparator in real-world healthcare applications. In longitudinal data, however, this assumption is often violated due to the inherent dependence between observations collected over time. Despite this limitation, RF was included as a benchmark model in our study to highlight the potential drawbacks of neglecting intra-individual correlations. Its inclusion allowed us to contrast traditional ML methods with those designed to handle clustered or repeated measures data. Ignoring this dependence can result in biased inferences, such as underestimated standard errors in linear models63. This bias may help explain the subpar accuracy observed in the RF model. In contrast, classification methods that properly account for the data structure and effectively handle the correlations from repeated measurements generally exhibit better predictive performance64,65. By incorporating these considerations, GMERF and GLMM models are better equipped to handle the complexities of longitudinal data, leading to more reliable and accurate predictions with direct relevance to clinical risk stratification and early intervention. Conversely, the GLMM model exhibited accuracy that was nearly comparable to, but slightly lower than, that of GMERF. This difference may arise from the GLMM’s reliance on certain assumptions, including a linear relationship between the response and the predictors, as well as a normal distribution of the residuals. Departures from these assumptions may result in inaccurate interpretations, especially in mixed-effects models. In contrast, the GMERF method does not impose these assumptions, allowing for greater flexibility in modeling.

Therefore, the GMERF model holds promise for integration into clinical screening protocols, particularly for identifying individuals at elevated risk of prediabetes in longitudinal cohort settings, where capturing intra-individual variation is essential. Beyond the statistical performance of the models, the clinical implications of our findings are of significant importance. The identification of waist-to-hip ratio (WHR), age, and triglyceride (TG) levels as key predictive factors offers a practical advantage, as these are non-invasive, low-cost, and routinely collected measures in primary care. WHR, in particular, emerged as a dominant predictor, supporting its integration into prediabetes risk assessment tools, especially in resource-limited settings. Age is an easily obtainable demographic factor that can help stratify individuals into risk categories, while TG levels represent a modifiable metabolic risk factor that can guide early lifestyle or pharmacological interventions. By translating these findings into clinical screening protocols and public health strategies, healthcare providers can identify at-risk individuals earlier and more effectively, enabling timely preventive interventions and potentially reducing the burden of diabetes.

Finally, we acknowledge that the TLGS data are based on a Tehran-specific urban population, which may raise concerns regarding the generalizability of the findings to other geographic or ethnic groups. However, previous studies have shown that the TLGS cohort is demographically representative of both the city of Tehran and the broader Iranian population in terms of age and sex distribution66,67. Nevertheless, external validation using independent datasets from other populations is necessary.

Conclusion

This study acknowledges the inherent dependence between observations collected over time, and we account for this data structure in our models. In the current work, we utilized approaches for feature selection and model development. The integrated application of feature selection and machine learning offers a broad array of potential risk factors—such as demographic details, medical history, medical examinations, anthropometric measurements, and blood biomarkers—enabling more accurate predictions of prediabetes. This approach enhances our understanding of potential prediabetes risk ratios at the public health level, facilitating the implementation of more effective diabetes prevention and control strategies. These findings can guide targeted screening and early intervention efforts to delay or prevent progression to type 2 diabetes. In addition, future research should focus on validating these models on external datasets, testing additional machine learning algorithms, and incorporating time-varying predictors to enhance model performance and generalizability.

Study’s limitations

This study has some limitations that should be addressed in future research. Although the longitudinal design of the Tehran Lipid and Glucose Study (TLGS) is a key strength, we did not explore whether the importance of predictors changes over time. Analyzing time-dependent variable importance could provide valuable insights into how risk factors evolve, and we suggest that this could be an important direction for future research.

Regarding the GMERF model, while it demonstrated the best predictive performance with an AUC of 0.75, this accuracy is still moderate. There is potential to improve predictive power by exploring more advanced machine learning models, such as XGBoost or neural networks. However, these models do not naturally account for the inherent dependencies in longitudinal data and would require additional adaptations, which were beyond the scope of this study. Future studies could address this limitation by incorporating more complex models designed specifically for longitudinal data, and by considering additional predictors, such as dietary or genetic factors, to further enhance performance.

Although we addressed class imbalance by adjusting the decision threshold, we acknowledge that this approach has limitations. Methods like SMOTE, commonly used for cross-sectional data, are not suitable for longitudinal datasets due to the inherent correlation within subjects over time. Applying SMOTE would violate these dependencies and potentially introduce bias. Therefore, while threshold adjustment helped mitigate imbalance, this approach remains a limitation. Future research could explore imbalance-handling techniques specifically designed for longitudinal data, such as subject-level resampling or model-based.