Introduction

SNMR was first proposed for groundwater detection by Varian in 19621 and realised in 1978, when Semenov’s team built the first prototype2. A decade of technical refinement produced the Hydroscope, the first instrument capable of recording subsurface-water NMR signals in the Earth’s field. Inversion research soon followed: Mueller et al. introduced QT schemes3, Mohnke et al. applied simulated annealing4, and subsequent work extended SNMR to 2-D5,6 and 3-D7,8 imaging of karst conduits and cave volumes. In parallel, TEM sounding matured into a deep-penetrating, high-resolution resistivity method that performs well in arid terrain9. SNMR is directly sensitive to hydrogen in pore water, whereas TEM excels at mapping conductive structures—making the two techniques strongly complementary10.

Although SNMR is highly effective for shallow aquifers, its signal attenuates rapidly below roughly 100 m11, and TEM alone can be masked by conductive overburden12. Integrating both methods therefore offers a practical route to greater depth and accuracy13,14. Early field studies that combined SNMR and TEM demonstrated clear gains in aquifer delineation and water-quality assessment15, and laterally constrained joint inversion further improved interpretation9. Yet a flexible, uncertainty-driven framework that fully exploits the strengths of each data set has remained elusive16.

Bayesian inference—originating with Bayes and Laplace and introduced to geophysical inversion by Tarantola & Valette17—casts inversion as the estimation of posterior probability density functions, naturally quantifying parameter uncertainty. Monte-Carlo sampling was first applied to SNMR data by Guillen18 and later extended to 3-D imaging19; for TEM, fast Markov-chain algorithms enabled efficient 2-D inversion20, while adaptive Voronoi parameterisation achieved quasi-2-D loop-centred models with high precision21. Most recently, Hamiltonian Markov Chain Monte Carlo (MCMC) has yielded robust joint SNMR–TEM inversion under complex geological conditions22. Meanwhile, the trans-dimensional Bayesian inversion has also been validated in the joint TEM–DCR inversion12. These advances confirm Bayesian inversion’s ability to fuse heterogeneous data and propagate uncertainty rigorously23.

To fully integrate the complementary strengths of SNMR and TEM in groundwater exploration, this study proposes and implements a probabilistic SNMR–TEM Bayesian joint inversion method24. The approach employs reversible-jump (variable-dimension) MCMC sampling to adaptively balance the data weights of SNMR and TEM during inversion and to optimize model structural complexity, thereby overcoming the limitations of conventional gradient-based deterministic inversions that are sensitive to initial conditions and model assumptions. Numerical experiments on synthetic data derived from multiple aquifer conceptual models demonstrate that, compared with SNMR-only inversion, the Bayesian joint inversion more effectively combines the strong sensitivity of SNMR to water content with the high-resolution capability of TEM for subsurface resistivity and stratigraphic structure. As a result, it better recovers water content distributions at varying depths and quantifies uncertainty through posterior probability distributions, significantly enhancing the reliability of the inversion.

For the field application, the proposed Bayesian joint inversion method was applied to groundwater prospecting in the Beishan area of Ejin Banner, Inner Mongolia. By processing and jointly interpreting SNMR and TEM field data, we delineated favorable groundwater targets, and subsequent drilling verified the accuracy of the results. The findings indicate that the method effectively integrates the direct sensitivity of SNMR to water content with the high-resolution imaging capability of TEM for resistivity structures, substantially improving the inversion accuracy of aquifer location and water content. This work provides a scientific basis for groundwater exploration in arid regions and offers robust technical support for investigations under complex geological conditions.

Theory and methods

Surface nuclear magnetic resonance theory

SNMR is a geophysical technique that exploits the nuclear magnetic resonance phenomenon exhibited by hydrogen nuclei (protons) in water molecules25. By analyzing the characteristics of the NMR signals originating from subsurface water, SNMR enables the quantitative determination of groundwater content and distribution26. The process begins with a pulsed excitation current transmitted at the local Larmor frequency (the resonance frequency of nuclear spins precessing in an external magnetic field, proportional to the local field strength) through a wire loop deployed on the ground surface. This excitation disturbs the equilibrium of hydrogen nuclei within the groundwater, generating a measurable nuclear magnetic resonance response. Once the excitation pulse is terminated, the same loop functions as a receiver, capturing the NMR signals emitted as the protons return to equilibrium. Key groundwater information, such as volumetric water content and its spatial distribution, is extracted by interpreting the initial amplitude and decay behavior of the received signal27.

Transient electromagnetic theory

The TEM method28, also referred to as Time-Domain Electromagnetics, is based on the fundamental principles depicted. Initially, a direct current is applied to a transmitter loop to generate a primary pulsed magnetic field that propagates into the subsurface. According to Faraday’s law of induction, this primary field induces an electromotive force within conductive geological bodies, generating secondary eddy currents underground. During the off-time, when the transmitter current is turned off, the secondary magnetic field produced by these eddy currents is detected by a receiver loop. The decay rate of this secondary field is governed by the electrical conductivity of the subsurface materials. By analyzing the temporal response of the induced Electromagnetic Force, valuable geoelectrical information about the underground formations can be obtained.

Bayesian inversion theory

From a statistical perspective, the goal of geophysical inversion is not to recover a single, perfectly accurate model, but rather to robustly estimate model parameters and rigorously quantify their associated uncertainties. Thus, geophysical inversion aims not only to determine specific physical properties of the subsurface, but also to provide a credible range of possible parameter values. As a quantitative framework for incorporating prior information and handling uncertainty, Bayesian theory offers a powerful approach to addressing these challenges in geophysical inversion29.

According to Bayesian inversion theory, the posterior probability distribution of the model parameters, \(p\left( \mathbf {m|d} \right)\), given the observed data, \(\textbf{d}\), is obtained by updating the prior probability distribution, \(p\left( \textbf{m} \right)\), with the information extracted from the data:

$$\begin{aligned} p\left( \textbf{m}\mid \textbf{d} \right) =\frac{p\left( \textbf{d}\mid \textbf{m} \right) p\left( \textbf{m} \right) }{p\left( \textbf{d} \right) }\propto p\left( \textbf{d}\mid \textbf{m} \right) p\left( \textbf{m} \right) \end{aligned}$$
(1)

The posterior probability density function (PDF) of the model parameters depends on the prior information, \(p\left( \textbf{m} \right)\), and the likelihood function, \(p\left( \mathbf {d|m} \right)\).

Transdimensional Bayesian joint inversion

In early applications of geophysical inversion, Bayesian theory was typically implemented within a fixed-dimensional framework, where the number of unknown model parameters remained constant. This limited the method’s adaptability to complex geological structures, as the model complexity is often unknown in practice. Therefore, fixed-dimensional approaches frequently struggle to resolve key subsurface features with both completeness and accuracy30.

Transdimensional Bayesian inversion addresses these limitations by allowing the inversion process to traverse model spaces of varying dimensions. This approach dynamically adjusts model complexity to match the data, leading to more accurate uncertainty quantification and improved adaptability to geological heterogeneity.

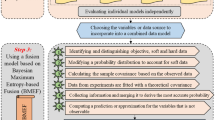
For nonlinear and non-Gaussian problems, deriving an explicit analytical form of the posterior PDF is often infeasible. In such cases, transdimensional Markov Chain Monte Carlo (MCMC) methods31, most notably those based on the Metropolis-Hastings algorithm, offer a robust solution. These methods iteratively generate Markov chain samples, treating the number of model parameters as an unknown and allowing direct exploration of model spaces with variable dimensions. As a result, a comprehensive suite of plausible models can be identified, each consistent with the observed data and the associated uncertainties. The flowchart of trans-dimensional Bayesian Joint version is shown in Fig. 1.

Model parameterization

The first step in Bayesian inversion is to select a suitable parameterization method. In this study, the subsurface is assumed to be a horizontally layered model composed of n homogeneous and isotropic layers. The number of layers (n), interface depths (z), water content (w), and resistivity (\(\rho\)) are treated as the inversion parameters. Therefore, the inversion model space, \(\textbf{m}\), is defined as:

$$\begin{aligned} \textbf{m}=\left[ n,z,\rho ,w \right] \end{aligned}$$
(2)

where n is the number of layers, \(z = \left[ z_1, z_2, \dots , z_{n-1} \right]\) is the depth vector for the top interface of each layer, \(w = \left[ w_1, w_2, \dots , w_{n-1} \right]\) represents the water content of each layer, and \(\rho = \left[ \rho _1, \rho _2, \dots , \rho _{n-1} \right]\) denotes the resistivity of each layer. The number of layers, interface depths, water content, and resistivity are uniformly sampled within their respective bounded ranges.

Prior distribution

According to Bayes’ theorem, the choice of prior distribution has a significant influence on the resulting posterior distribution. In this study, all model parameters are assigned a uniform prior over a sufficiently broad range to minimize any undue influence on the posterior. The prior serves a similar role to the regularization term in deterministic inversion methods. To ensure credibility, the prior should be wide enough to encompass all plausible parameter values, yet as simple as possible, commonly taken to be a uniform or Gaussian distribution. Assuming that observational errors are Gaussian distributed, the likelihood function can be expressed as follows:

$$\begin{aligned} p\left( \textbf{d}\mid \textbf{m} \right) =\prod _{j=1}^{\widehat{M}}{\frac{1}{\sqrt{\left( 2\pi \right) ^{N_j}\left| \textbf{C}_{d_j} \right| }}}\times \exp \left\{ -\frac{\left[ \textbf{d}_j-F_j\left( \textbf{m} \right) \right] ^T\textbf{C}_{d_j}^{-1}\left[ \textbf{d}_j-F_j\left( \textbf{m} \right) \right] ^2}{2} \right\} \end{aligned}$$
(3)

where \(\widehat{M}\) is the number of data types included in the inversion (in this study, \(\widehat{M} = 1\) for single-method inversion and \(\widehat{M} = 2\) for joint inversion). \(N_j\) denotes the number of observed data points for the j-th data type; \(\textbf{C}_{d_j}\) is the data covariance matrix of the j-th data type; \(\textbf{d}_j\) represents the observed data of the j-th data type; and \(F_j\left( \textbf{m} \right)\) is the forward response operator mapping the model space to data space for the j-th data type.

Proposal distribution

During the sampling process, the posterior distribution of the Markov chain is independent of the choice of proposal distribution. The proposal distribution only affects the rate of convergence, not the quality of the convergence itself. This proposal distribution is composed of the following four types of perturbations:

  1. 1.

    Move: A ”Move” step changes the position of an interface. The new position is drawn from a Gaussian distribution centered on the current interface position.

  2. 2.

    Update: The ”Update” step does not change the dimensionality of the model. It only perturbs the water content of each layer by drawing a new value from a Gaussian distribution centered on the layer’s current mean water content.

  3. 3.

    Birth: A ”Birth” step adds a new interface at a random position within the domain. The water content for the new layer is drawn from a Gaussian distribution centered on the water content of the original layer being split.

  4. 4.

    Death: A ”Death” step randomly removes an interface, thereby merging two adjacent layers. The water content for the new, larger layer is assigned by randomly choosing the water content value from one of the two original layers.

Each perturbation type is assigned a fixed probability of being selected. While the choice of these probabilities is largely subjective, in this study, the four perturbation types were assigned equal probabilities of [1/4, 1/4, 1/4, 1/4]. The number of layers, interface depths, and water content values are all drawn from uniform prior distributions. The ranges for these priors were set to be sufficiently wide to minimize their influence on the posterior distribution.

Fig. 1
figure 1

Flowchart of the trans-dimensional Bayesian Joint inversion.

Full size image

Bayesian joint inversion of SNMR and TEM synthetic data

Fig. 2
figure 2

(a) Synthetic Geoelectric Model 1 (b) SNMR response curves (c) TEM response curves.

Full size image
Fig. 3
figure 3

Posterior probability distributions of the inversion results for Model 1. The distributions shown are from: (a, b) the standalone SNMR inversion, (c,d) the standalone TEM inversion, (e,f) the sequentially constrained SNMR-TEM inversion, and (g,h) the Bayesian joint SNMR-TEM inversion. The black solid line is the posterior mean model, while the magenta dashed lines denote the 5th and 95th percentiles of the posterior PDF. The true models to generate the synthetic data are indicated by the green solid line.

Full size image

In this section, two multilayer synthetic models are designed to demonstrate the advantages of SNMR-TEM Bayesian joint inversion algorithm. The objective is to show how combining SNMR and TEM data can enhance the accuracy of the inversion results and effectively reduce the inherent uncertainty associated with each method when applied individually within a Bayesian framework.

Model 1, shown in Fig. 2a, represents a typical aquifer structure located between two aquitards, where the relationship between water content and resistivity is established by Archie’s law. The synthetic SNMR and TEM data were generated using a 100 \(\times\) 100 \(m^2\) square transmitter-receiver loop. To simulate field conditions, 3% random Gaussian noise was added to the data. The resulting synthetic datasets are shown in Fig. 2b and c.

We tested three inversion strategies using the synthetic data. First, a standalone SNMR Bayesian inversion was run with a 100 \(\Omega \cdot m\) uniform half-space as the initial model, assuming no prior resistivity information (Fig. 3a, b). Second, a standalone TEM Bayesian inversion was performed (Fig. 3c, d). The resulting mean resistivity model was then used as a fixed prior to constrain a subsequent SNMR inversion (Fig. 3e, f). Finally, our proposed SNMR-TEM Bayesian joint inversion was applied (Fig. 3g, h).

In all scenarios, we used wide, non-informative prior bounds for the parameters (\(n = [2], [20]\), \(z = [0, 120] m\), \(w = [0, 0.3]\), and \(\rho = [10^0, 10^4] \Omega \cdot m\)) to minimize their influence on the final solution. Each method was run for 300,000 MCMC iterations, with the first 150,000 discarded for burn-in phase. The standalone SNMR, standalone TEM, and joint SNMR-TEM inversion took approximately 10, 30, and 90 minutes to run, respectively.

The results of the standalone SNMR inversion are shown in Fig. 3a and b. When a 100 \(\Omega \cdot m\) uniform half-space was used as the background resistivity model, the resulting credible interval deviates significantly from the true water content profile. A spurious anomaly of approximately 5% appears in the 30–50 m depth range, and there are substantial errors in identifying the position and estimating the water content of the aquifer between 50 m and 70 m. Furthermore, the posterior probability for the interface depth fails to converge on the true interface location. As shown in Fig. 3c and d, the standalone TEM inversion accurately resolves the high-resistivity layer in the 0–50 m depth range and also identifies the low-resistivity aquifer at 50–70 m with reasonable accuracy. However, significant uncertainty exists in defining the boundary of the deep high-resistivity layer from 70–120 m. This is primarily because the TEM method is highly sensitive to low-resistivity targets and is subject to a shielding effect from overlying conductive structures, which masks deeper high-resistivity features.

Overall, the credible interval of the TEM Bayesian inversion aligns well with the true model’s distribution, indicating that its results can provide reliable a priori resistivity information for the SNMR inversion. In comparison, the results of the sequentially constrained SNMR-TEM inversion (Fig. 3e and f) show that by incorporating the TEM-derived prior resistivity information, the inversion accuracy is significantly improved. The credible interval now shows excellent agreement with the true water content curve. The delineation of the aquifer’s position (50–70 m) and the estimation of its water content are both substantially enhanced, and the interface probability is now sharply focused on the true depth. Finally, as seen in Fig. 3g and h, the Bayesian joint SNMR-TEM inversion not only further narrows the uncertainty interval but also provides a more precise identification of the aquifer’s location and water content. The recovered model shows a high-fidelity match to the true curve. A comprehensive comparison of these three strategies clearly demonstrates the significant advantages of the SNMR-TEM joint inversion in enhancing parameter resolution and improving the reliability of the inversion.

To further demonstrate the effectiveness of the SNMR-TEM joint inversion algorithm under more complex geological conditions, we designed Model 2, shown in Fig. 4a. This model represents a typical multi-layer aquifer structure, where the relationship between water content and resistivity is again established using Archie’s law. As with the previous experiment, the synthetic SNMR and TEM data were generated for a 100 \(\times\) 100 \(m^2\) loop and contaminated with 3% random Gaussian noise; the resulting datasets are shown in Fig. 4b and c. Subsequently, we applied the same three inversion strategies described previously, with the results presented in Fig. 5a–h. All inversion parameters were kept identical to those used for Model 1.

Fig. 4
figure 4

(a) Synthetic Geoelectric Model 2 (b) SNMR response curves (c) TEM response curves.

Full size image

As shown in Fig. 5a and b, the standalone SNMR inversion, which used a 100 \(\Omega \cdot m\) uniform half-space as the initial background model, yields a credible interval that differs substantially from the true water content profile. Although it accurately identifies the position and water content of the shallow aquifer in the 20–40 m depth range, the delineation of the deep aquifer (80–100 m) and its estimated water content are significantly biased. Consequently, the inversion result fails to accurately reflect the true subsurface water distribution. Figure 5c and d show that the standalone TEM inversion exhibits high accuracy in resolving the low-resistivity layers at 20–40 m and 80–100 m, as well as the near-surface high-resistivity layer at 0–20 m. However, for the high-resistivity layers at 40–80 m and 100–120 m, the credible intervals are wide, indicating poor accuracy. This is primarily due to the shielding effect of the overlying low-resistivity layers in the TEM method. Overall, the credible interval from the standalone TEM inversion is largely consistent with the true model distribution, confirming that it can provide reliable a priori resistivity information for the SNMR inversion.

In comparison, the sequentially constrained SNMR-TEM inversion (Fig. 5e, f) shows a marked improvement. Its credible interval aligns closely with the true water content curve. It not only accurately delineates the position and water content of the shallow aquifer (20–40 m) but also correctly identifies the position of the deep aquifer (80–100 m), with an estimated water content that closely matches the true values. Finally, the results of the SNMR-TEM joint inversion, shown in Fig. 5g and h, are even more precise. This approach achieves high-accuracy identification of both the location and water content of the aquifers, with an uncertainty interval that is tightly focused around the true model curve. Furthermore, the posterior probability distribution for the interface depths is precisely centered on the true aquifer locations. These results further confirm that SNMR-TEM joint inversion algorithm maintains high accuracy and reliability even under complex geological conditions.

Fig. 5
figure 5

Posterior probability distributions of the inversion results for Model 2. The distributions shown are from: (a, b) the standalone SNMR inversion, (c, d) the standalone TEM inversion, (e, f) the sequentially constrained SNMR-TEM inversion, and (g, h) the Bayesian joint SNMR-TEM inversion. The black solid line is the posterior mean model, while the magenta dashed lines denote the 5th and 95th percentiles of the posterior PDF. The true models to generate the synthetic data are indicated by the green solid line.

Full size image

Application of SNMR-TEM Bayesian joint inversion for groundwater exploration in the Beishan area, Inner Mongolia

Geological background of the study area

Fig. 6
figure 6

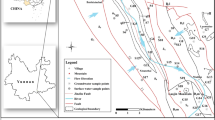
Location map of the study area. The map is generated using the Generic Mapping tool v6.0.0 .32, and the digital elevation model (DEM) data is obtained from https://www.ngdc.noaa.gov/mgg/global/.

Full size image

As shown in Fig. 6, the study area is located in Beishan, within the Hei Ying Shan (Black Hawk Mountain) region. It lies in the heart of the arid Beishan region of Inner Mongolia, bordered to the east by Dalaihubu Town (the seat of Ejina Banner) and to the north by the national border with Mongolia, making its geographical location relatively remote. The Hei Ying Shan region itself is situated in the northwestern part of Ejina Banner, Alxa League, Inner Mongolia, adjacent to the Sino-Mongolian border, and is a typical temperate continental arid desert zone.

The topography of the study area is dominated by low mountains, hills, and Gobi desert, with a general trend of being higher in the southwest and lower in the northeast. The elevation ranges from 972 to 1637 meters. The landscape is complex, characterized by widespread Gobi, gravel plains (bajada), paleochannels, and aeolian sand dunes, with significant wind erosion. The area has a mean annual temperature of 9.9 °C and a mean annual precipitation of only 37 mm, while potential annual evaporation is extremely high at 3842 mm. Consequently, the area suffers from chronic water scarcity. There is no perennial surface runoff; seasonal floods occur only briefly during the rainy season, making groundwater the primary water source.

The geological structure is controlled by NNW-trending faults and folds. The area features Mesozoic and Cenozoic sedimentary strata, along with some Paleozoic rocks, and abundant mineral resources. Vegetation coverage is extremely low, and the ecosystem is fragile. These complex geomorphological structures, arid conditions, and challenging hydrogeological settings pose significant challenges for groundwater exploration in this region, underscoring the practical significance of the present study.

Building on the foundation of prior hydrogeological surveys and geophysical exploration, this study conducted SNMR data acquisition in seven priority exploration zones (ZK1 to ZK7), identified by the hydrogeological investigation33. Due to challenging field conditions, TEM soundings were performed only in zones ZK1 and ZK4. The specific distribution of all measurement points is shown in Fig. 6. To establish a baseline for interpreting the SNMR data in the work area, two additional SNMR measurements were conducted for calibration: one at the SK01 water well in Ejina Beishan and another at an abandoned dry well near the wind farm. The SNMR data were acquired using a GMR SNMR instrument, while the TEM data were collected with a GDP-32 Transient Electromagnetic system. The quality of the collected data was high and met the requirements for subsequent data processing and interpretation.

Establishment of benchmarks

Fig. 7
figure 7

(a) SNMR response curve for the water-producing well (b) Deterministic inversion result for the water-producing well (c) SNMR response curve for the dry well (d) Deterministic inversion result for the dry well.

Full size image
Fig. 8
figure 8

(a,b) Posterior probability distribution for the water-producing well (c,d) Posterior probability distribution for the dry well. The black solid line is the posterior mean model, while the magenta dashed lines denote the 5th and 95th percentiles of the posterior PDF.

Full size image

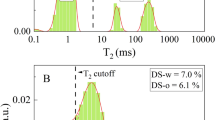
Due to the arid nature of the study area, the subsurface water content is generally extremely low. Consequently, conventional water content thresholds for defining an aquifer (e.g., >15%) are not applicable. It was therefore necessary to establish a specific interpretation criterion tailored to this region.34 To define this benchmark, the SNMR data acquired at the SK01 water well were processed using both deterministic inversion (Fig. 7) and Bayesian inversion (Fig. 8). The deterministic inversion results indicated a water-bearing layer from 0–20 m depth with a water content of approximately 3%, and another from 20–30 m depth, also with a water content of about 3%. Below 40 m, the water content gradually decreased. The Bayesian inversion results similarly identified a water-bearing layer from 0–20 m with a water content of about 3%, and another from 30–40 m with a water content of approximately 5%. While the results from both inversion methods were largely consistent, the Bayesian approach provided a more sensitive and focused delineation of the water-bearing layers.

Subsequently, the data collected at the abandoned dry well near the wind farm were also processed using both deterministic (Fig. 7) and Bayesian (Fig. 8) inversion for comparison. The deterministic results showed a 1% water content variation in the 0–10 m depth interval and a 0.5% variation from 20–30 m. Although the water content at greater depths exceeded 1%, this was primarily bound water, with the free water content remaining below 1%. The Bayesian results indicated a 1% water content variation from 0–10 m and another 1% variation from 10–20 m, with a slight change noted at the 80–100 m depth, though the overall water content remained extremely low.

The consistent outcomes from both wells validated the accuracy of Bayesian SNMR inversion algorithm. By synthesizing the interpretation results from both the productive water well and the dry well, a definitive criterion for identifying aquifers in the study area was established: a water content exceeding 3% indicates a promising zone for water exploration, whereas a water content below 1% suggests an unfavorable zone. Based on this benchmark, all measured SNMR data were interpreted to identify promising targets for groundwater exploration.

Constraining geophysical data using borehole data

The SNMR and TEM response curves for the ZK1 key exploration area, as obtained from field measurements, are shown in Fig. 9a and b. Deterministic inversion was performed on the ZK1 data, and the results are presented in Fig. 9c. Bayesian inversion of the SNMR field data for the ZK1 exploration area was also conducted, utilizing a homogeneous half-space resistivity model of 100 \(\Omega \cdot m\) as prior information. The Markov chain was sampled 300,000 times, with a burn-in period of 150,000 steps; the inversion results are shown in Fig. 10a and b. Additionally, Bayesian joint inversion of the SNMR and TEM data for ZK1 was performed under the same sampling conditions (300,000 samples, 150,000 burn-in), and the results are illustrated in Fig. 10c and d. By comparing the results from the single-method Bayesian inversion, the Bayesian joint inversion, and the deterministic inversion, a more comprehensive understanding of the aquifer distribution and water content variations can be achieved.

The individual Bayesian inversion results indicate an aquifer at a shallow depth of 0–5 m with a water content of approximately 8%, which is inferred to be surface water. Another aquifer is identified at a depth of 20 m with a water content of about 3%. A third aquifer is also recognized within the 50–70 m depth range, with a water content of approximately 2%. In comparison, the Bayesian joint inversion results also show an aquifer in the 0–5 m depth range with a water content of about 8%. The aquifer at 20 m is also present, but its water content increases to 4%. A third aquifer is identified in the 60–70 m depth range, where its water content significantly increases to 9%. The deterministic inversion results, on the other hand, show one aquifer in the 0–20 m depth range with a water content of about 4%, and a second aquifer is identified in the 40–80 m depth range, with a maximum water content reaching 7%. A comparison of the three methods reveals that the individual Bayesian inversion and the joint Bayesian inversion are largely consistent in identifying the positions of the aquifers, though they differ in the estimated water content values. Conversely, the results from the Bayesian joint inversion and the deterministic inversion show greater consistency in both the aquifer locations and their corresponding water contents.

Overall, the Bayesian joint inversion provides a more precise delineation of aquifer positions and demonstrates higher accuracy in estimating water content. The inversion results for ZK1 collectively indicate the presence of aquifers at both shallow and deep levels, with water content in both exceeding the 3% threshold for a viable target. This suggests that the ZK1 location is a promising target for water exploration. This conclusion not only offers a crucial reference for water resource exploration in the study area but also validates the reliability and accuracy of the Bayesian inversion method for aquifer identification.

Fig. 9
figure 9

(a) SNMR and (b) TEM response curves for ZK1 (c) The deterministic inversion result for ZK1.

Full size image
Fig. 10
figure 10

Posterior probability distributions for the ZK1 data (a,b) Results from the individual SNMR Bayesian inversion (c,d) Results from the joint SNMR-TEM Bayesian inversion. The black solid line is the posterior mean model, while the magenta dashed lines denote the 5th and 95th percentiles of the posterior PDF.

Full size image
Fig. 11
figure 11

(a) SNMR and (bjoint inversion for groundwater exploration in the) TEM response curves for ZK4 (c) The deterministic inversion result for ZK4.

Full size image
Fig. 12
figure 12

Posterior probability distributions for the ZK4 data (a,b) Results from the individual SNMR Bayesian inversion (c,d) Results from the joint SNMR-TEM Bayesian inversion. The balck solid line is the posterior meanmodel, while the magenta dashed lines denote the 5th and 95th percentiles of the posterior PDF.

Full size image

The measured data from the ZK4 exploration area were processed using three different inversion strategies. The corresponding SNMR and TEM response curves are displayed in Fig. 11a and b, and the deterministic inversion results are shown in Fig. 11c. The individual SNMR Bayesian inversion results are shown in Fig. 12a and b, while the SNMR-TEM joint inversion results are presented in Fig. 12c and d. According to the individual Bayesian inversion results, an aquifer is present at a shallow depth of 10 m with a water content of approximately 4%. A second aquifer is identified in the 80–100 m depth range with a water content of about 1%, which gradually increases to 4% within the 100–120 m depth range. In comparison, the Bayesian joint inversion results also show an aquifer at 10 m with a water content of about 5%. A second aquifer is identified in the 60–80 m depth range with a water content of about 1%, which gradually increases to 4% in the 80–100 m depth range. The deterministic inversion results, on the other hand, indicate an aquifer in the 0–20 m depth range with a maximum water content of approximately 7%. A second aquifer is also present in the 40–120 m depth range, with a maximum water content of about 5%. A comparison of the three sets of results reveals a discrepancy between the individual Bayesian inversion and the joint Bayesian inversion in the delineation of the deep aquifer. In contrast, the Bayesian joint inversion and the deterministic inversion show greater consistency in both aquifer location and water content estimation. The Bayesian joint inversion provides a more precise delineation of aquifer positions and a more accurate estimation of water content, better reflecting the distribution characteristics of the subsurface aquifers.

Across the seven priority exploration areas, SNMR soundings produced high-quality data with minimal interference. Analysis of productive and dry-well measurements allowed us to establish an SNMR interpretation baseline for the Beishan region: intervals with water content> 3%, combined with appreciable aquifer thickness, are deemed promising groundwater targets.

Applying this criterion, together with the inversion results and local topography, identifies the vicinities of ZK1 and ZK4 as favourable targets: each shows water contents exceeding 3% and well-defined aquifer geometries. In the remaining areas, the likelihood of abundant groundwater above 150 m depth is low; domestic and industrial supply will probably require drilling deeper than 150 m.

These findings furnish a valuable reference for future groundwater exploration and development in the Beishan region and provide clear guidance for subsequent drilling operations.

Results and analysis

Fig. 13
figure 13

Borehole Lithology for (a) ZK1 and (b) ZK4.

Full size image

Based on the interpretation of the SNMR data, sites ZK1 and ZK4 were identified as promising targets for water exploration, and drilling was conducted at these locations for validation. According to the drilling results, water was successfully encountered at all three sites (ZK1 and ZK4), further confirming the accuracy and reliability of SNMR inversion algorithm. This demonstrates the high practical value of SNMR-based inversion and interpretation methods for aquifer identification and the delineation of promising exploration targets.

The borehole logs and drilling curves for ZK1 and ZK4 are shown in Fig. 13, respectively.35These figures provide a direct visual representation of the aquifer distribution characteristics and the variations in water content.

An analysis of the borehole log for ZK1 reveals that it is fundamentally consistent with the inversion results for the same site, showing a high degree of correlation in both stratigraphic structure and hydrogeological properties?. Specifically, the borehole log indicates that the formation shallower than 20 meters consists primarily of a relatively loose gravel and sand layer. Due to its coarse grains and large pores, this layer exhibits good permeability and storage capacity, allowing it to readily accumulate groundwater (as an unconfined aquifer with a high proportion of free water), resulting in high water content. This characteristic makes the shallow zone the primary area for groundwater accumulation. Below 20 meters, the formation gradually transitions to gravelly sandstone. Although this layer retains some porosity and permeability, these properties are significantly reduced due to cementation, leading to diminished water storage capacity and lower free water content, which manifests as a weak aquifer. This change corresponds well with the decrease in water content at greater depths shown in the SNMR inversion results. The excellent consistency between the measured water content and the drilling results further validates the applicability of surface NMR technology and the reliability of its measurements in the Beishan area.

An analysis of the borehole log for ZK4 shows that the geological formation within the shallow 30-meter depth range is primarily composed of gravel/sand, mudstone, and gravelly sandstone. Within this structure, the mudstone layer acts as an intermediate aquitard; due to its fine particles, low porosity, and poor permeability, it functions as a barrier to groundwater flow. In contrast, the overlying and underlying layers of gravel/sand and gravelly sandstone exhibit higher porosity and better permeability, thus behaving as aquifers. This stratigraphic structure shows a high degree of correlation with the distribution of the two shallow aquifers identified in the ZK4 inversion results, further validating their accuracy. In the deeper 60–100 meter range, the formation consists mainly of gravelly sandstone. Although cementation has reduced its porosity and permeability to some extent, it retains a certain water storage capacity, manifesting as a deep aquifer. This characteristic corresponds to the trend of increasing water content at depth shown in the ZK4-1 results, indicating that the deep formation has strong hydrogeological properties and can effectively store groundwater. Overall, the excellent consistency between the ZK4 borehole log and the ZK4 inversion results, in terms of both stratigraphic structure and hydrogeological properties, provides a reliable basis for studying the regional distribution patterns of groundwater.

Conclusion

This study presents a trans-dimensional Bayesian joint-inversion framework that integrates surface nuclear magnetic resonance and transient electromagnetics to explicitly quantify uncertainty while simultaneously inferring model complexity. By leveraging SNMR’s direct sensitivity to water content alongside TEM’s high-resolution constraints on subsurface resistivity and structure, the framework enables a more comprehensive and reliable characterization of hydrogeological conditions. Its feasibility and effectiveness are demonstrated through synthetic experiments, which indicate clear gains in resolution, stability, and parameter recovery relative to conventional approaches.

The feasibility and effectiveness of the SNMR–TEM joint inversion were first validated using synthetic data, which showed markedly improved resolution, stability, and parameter estimation compared with conventional methods. The algorithm was subsequently applied to field data from the Beishan area (Ejina Banner, Inner Mongolia). The joint-inversion results were consistent with deterministic inversion while delivering superior stratigraphic resolution—particularly at depth. Aquifer positions were accurately predicted, and follow-up drilling at sites ZK1 and ZK4 confirmed these predictions, underscoring the practical value of the approach.

In conclusion, the proposed SNMR–TEM Bayesian joint-inversion method substantially enhances the delineation of groundwater distribution in complex geological settings. The workflow provides a robust technical reference for integrating SNMR and TEM in groundwater exploration and represents a promising strategy for water-resource detection in arid environments.

Future work will advance along three fronts. First, we will extend the inversion dimensionality from the current one-dimensional framework to two- and three-dimensional formulations to achieve higher spatial resolution and more detailed subsurface characterization. Second, we will pursue multimethod joint inversion: building on SNMR and TEM, we will incorporate additional resistivity-sensitive techniques (e.g., high-density electrical resistivity and induced polarization) to strengthen multi-source constraints and improve the delineation of subsurface structures and aquifers. Third, we will optimize the inversion algorithms to address the increased computational burden associated with higher-dimensional problems; specifically, for 2D/3D Bayesian inversions, we will employ multi-GPU and multi-chain parallelization to accelerate sampling and convergence, thereby achieving a more favorable balance between accuracy and efficiency.