Introduction

Whole Slide Images (WSIs) scanned from histopathological images provide critical information for computer-aided cancer diagnosis and prognosis evaluation1,2,3,4,5,6,7,8. WSIs are of large size (100,000 \(\times\) 100,000 pixels) and cannot be directly processed by deep learning models9,10,11. Therefore, it is typically essential to tile a WSI into numerous patches to ensure that deep learning models can process them effectively. In this context, WSI classification is often formulated as a multiple instance learning (MIL) problem12,13,14,15,16,17, which is a weakly supervised learning paradigm.

Fig. 1
figure 1

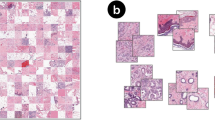
Illustration of the different ways to obtain instance scores. A: Conventional attention-based WSI classification frameworks usually model the interrelationship between instances to obtain instance scores. B: CAMCSA introduces CAM on WSIs to obtain the accurate instance scores to represent the contribution of each instance to the bag classifications.

Full size image

In MIL, each patch crop from a WSI image is defined as an instance, and thus, a WSI is considered a bag that includes many patches (instances). In cancer diagnosis, if at least one patch (positive instance) contains tumor tissue, the corresponding WSI is labeled as tumor (positive bag). In other words, a positive bag contains at least one positive instance, while a negative bag contains no positive instances. The goal of MIL methods is to predict the labels of bags or instances based on the datasets that only provided bag labels.

Among the various MIL methods, attention-based approaches are the most promising. Some MIL methods use Transformer to extract instance features, such as FDTs18 and MamlFormer19, A ViT-AMC network with adaptive model fusion and multiobjective optimization for interpretable laryngeal tumor grading from histopathological images. Some other MIL methods focus on using attention mechanisms to obtain instance relationships. That is, they can obtain attention-based instance scores by modeling the instance interrelations (as shown in Fig. 1(A)), which is beneficial to improving bag classification performance. However, they face two significant challenges: (1) The attention-based instance scores cannot accurately represent the contribution of the instances to the bag-level classification, as they mostly indicate the degree of the morphological similarity, semantic correlation, or distance between instances, which makes it difficult to identify the discriminative regions in WSIs. (2) Whole-slide pathological image analysis frequently suffers from model overfitting and insufficient representation of positive samples for training caused by a small number of samples and class imbalance of WSI datasets.

To address the above challenges, we propose a framework named Class Activation Map with Cross-Slide Augmentation (CAMCSA), which consists of two WSICAM modules and a Cross-Slide Augmentation (CSA) module. For the first challenge, we design the WSICAM modules, which introduce Class Activation Map (CAM)20 into the conventional MIL framework to generate instance scores. Compared to other methods, our approach yields instance scores that benefit from the theoretical underpinnings of CAM, thereby accurately indicating the contribution weights of individual instances to a bag classifications (as shown in Fig. 1(B)). To solve the problem of model overfitting and insufficient representation of positive samples, inspired by RankMix21, we extend the application of Mixup22 (commonly used in natural images) to WSI datasets. Specifically, we construct a CSA module that selects significant instances from each bag based on instance scores provided by WSICAMs and proportionally mixes significant instance features of two slides. It effectively alleviates the poor generalization performance caused by imbalanced WSI datasets with limited samples.

The contributions are summarized as follows:

  1. (1).

    Based on CAM, we propose the WSICAM module to acquire accurate instance scores. These scores indicate the contribution weight of each instance in a WSI to the bag classifications. Additionally, WSICAM is beneficial to identify the discriminative regions in WSIs. This serves as an effective basis for physicians to make subsequent diagnoses.

  2. (2).

    Inspired by RankMix, we design a Cross-Slide Augmentation module (CSA). Based on the accurate instance scores provided by WSICAM, CSA creates mixed bags by introducing Mixup (commonly used in natural images) to mix significant instances from two WSIs. It addresses the common issue of class imbalance in WSI datasets, which enhances the representation learning and generalization capabilities of our framework significantly.

  3. (3).

    Extensive experiments on widely used datasets demonstrate the effectiveness of CAMCSA, reaching new SOTA in bag classification performance. Moreover, the visualizations and instance classification results on Camelyon16 show the powerful lesion localization capacity of CAMCSA.

Related work

Attention-based MIL methods

Recently, numerous embedding-based MIL methods have employed attention-based instance scores to elucidate the importance of instances and improve classification performance. Attention scores can be achieved through attention-based spatial or feature distances23,24,25,26,27,28 or autonomous learning by neural networks such as capsule networks29, transformers30, or graph neural networks31. AB-MIL23 predicted the attention score of each patch using a multi-layer perceptron (MLP) without explicit patch relation modeling. DSMIL26 used the cosine distance between an instance and a key instance to represent the attention score of the current instance. An adaptive attention mechanism was used in C2C27 to construct instance scores. In TransMIL30, the instance scores came from the output of the Multi-head Self-Attention blocks in the transformer.

Although the above attention-based MIL models can effectively improve classification performance, instance attention scores in these methods are achieved through the similarity of morphological features, spatial distance, etc., between instances. They mostly indicate the degree of intrinsic correlation or potential connection among instances and cannot represent the accurate contribution weight of an individual instance to the bag classification prediction.

Class activation map

Class Activation Map (CAM) is an effective visualization tool in computer vision, and it also shows great potential in Weakly Supervised learning. Specifically, it and its variants (Grad-CAM)32 are often used as embedded components in various weakly supervised tasks that only provide image-level labels, such as weakly supervised object detection and weakly supervised semantic segmentation. The emergence of CAM has led to a consistent approach in these weakly supervised tasks, proposing CAM-based weakly supervised frameworks33,34,35,36. The proposal of CAM has promoted the development of the weakly supervised learning field and refreshed new records on multiple weakly supervised datasets.

The procedure for obtaining CAM is as follows: Firstly, extract the feature layers that require visualization. For instance, an input image with dimensions of \(H \times W \times C\) can yield a feature map with dimensions of \(H_f \times W_f \times C_f\) by convolutions. Secondly, generate the weight of each channel in the feature map under a specific class, i.e., a vector of length \(C_f\); Thirdly, weight and sum the vector of length \(C_f\) along the channel dimension of the feature map to acquire a map of size \(H \times W\) through linear fusion. Finally, normalize the map of size \(H \times W\) under a specific class and resize it to the original image size through interpolation to get the CAM map of this class.

Assuming the CAM map for class c is \(M_{c}(x,y)\), \(M_{c}(x,y)\) directly indicating the importance of the activation at the spatial grid (x, y) leads to the classification of an image to class c20. Inspired by this theory, we propose WSICAM modules to map each instance contribution to a pixel in the CAM of our proposed CAMCSA, which indicates the magnitude of the contribution of the corresponding instance to a bag classification. In other words, the pixel values of the CAM in the WSICAM modules represent the instance scores. This method corrects the mistake of the previous AB-MIL series methods, which used the similarity between instances as instance scores. It is a new instance score generation method improved based on CAM and can accurately indicate the contribution of instances within a bag.

Data augmentation

As we know, data augmentation can improve the generalization ability of neural networks and has been widely applied in the training of neural networks. CutMix37 drew masked areas (produced by random occlusion) with the content of another image at the same location. ReMix38 proposed using latent-space data augmentation to deal with WSI classification. These data augmentation methods effectively improve the neural network performance in both natural and medical images. Chen et al. introduced Flow-Mixup39 as a method to regulate medical images that have inaccurate multilabels, since annotating medical images is expensive and automatic annotation frequently results in corrupted labels. Gazda et al.40 made use of the mixup technique with the aim of improving model performance in medical image segmentation. The RankMix21 fused the information from two images through convex combinations.

RankMix is a data augmentation method for mixing ranked features of two WSI images. After obtaining all instance embeddings of a WSI, it uses a simple score function to generate pseudo-labels. These pseudo-labels are then ranked in descending order to select m significant patches that can represent the WSI. The m significant patches from two WSIs respectively, are then fused in proportions to construct mixed features. Similarly, the mixed labels are generated in the same way. Finally, the mixed features and mixed labels are used for training the MIL model. RankMix draws on the idea of Mixup commonly used in natural images, linearly combining both inputs and outputs, and ensures that the mapping of mixed inputs and mixed outputs maintains linear constraints to improve the generalization and robustness of neural network models when encountering class imbalance issues. However, the pseudo-labels in RankMix are generated through a simple fully connected layer. As discussed in previous sections, this method is incorrect for describing instance contributions.

Inspired by RankMix, we construct a Cross-Slide Augmentation (CSA) module. This module selects significant instances based on instance scores provided by WSICAM and mixes significant instances from a pair of WSIs and finally uses mixed labels to guide the classification process of the mixed feature. This approach significantly enhances the representation learning and generalization capabilities of our framework.

Methods

MIL formulation

WSIs are of high resolution, often reaching billions of pixels. Due to the limitations of current computer hardware, researchers cannot directly input digital pathology images to computers for analysis and processing. Therefore, special preprocessing is usually required, i.e., tiling a WSI into many patches of the same size. The method of representing a WSI as a bag composed of multiple patches (instances) and achieving classification prediction of the bag or instances with a slide-level label is called Multiple Instance Learning (MIL). Given a dataset \(W = \{W_ 1, W_2, \ldots , W_N\}\) consisting of \(N\) WSIs, each WSI \(W_i\) is tiled into non-overlapping small patches \(\{p_ {i,j}, j=1,2,\ldots ,n_i\}\), where \(n_i\) is the number of patches cropped from \(W_i\). All patches \(p_ {i,j}\) in \(W_i\) form a bag, where each patch is an instance. The bag labels \(\{ Y_i, i=1,2,\ldots ,N\}\) and the instance labels \(\{y_ {i,j}, j=1,2,\ldots ,n_i\}\) have the following relationship:

$$\begin{aligned} Y_i = {\left\{ \begin{array}{ll} 0, & \text {if } \sum _j y_{i,j} = 0 \\ 1, & \text {else} \end{array}\right. } \end{aligned}$$
(1)

That is, each bag is given a class label, either positive or negative. If there is at least one positive instance in a bag, the bag label is positive; otherwise, it is negative.

Overall framework

Fig. 2
figure 2

The architecture of the proposed CAMCSA framework.

Full size image

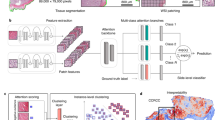
The overall architecture of our proposed method, Class Activation Map with Cross-Slide Augmentation (CAMCSA), is shown in Fig. 2. It consists of basic classification modules WSICAM in branches (b) and (d) and a Cross-Slide Augmentation module (CSA) in branch (c). Inspired by CAM, WSICAM is proposed to adapt to the enormous size of WSIs to obtain discriminative instances in WSIs. The CSA module uses discriminative instances from different bags to construct new samples with mixed labels for model training. The MIL modules in branches (b), (c), and (d) share weights, and the MIL module in this framework can be any attention-based MIL model. Branch (a) shows the visualization calculation process of generating the CAM for a WSI using the WSICAM module.

Class activation map suitable for WSI (WSICAM)

In the field of pathological images, many researchers use the attention mechanism23,24,25,26,27,28 to obtain the instance score for representing the contribution of each instance to the bag classification prediction. However, these attention scores are achieved based on the relationships between instances using MLP, Transformer, GCN, etc., which actually reflect the intercorrelations among instances and cannot correctly indicate the contribution of instances to the bag-level prediction.

We will demonstrate through theoretical analysis the limitations of traditional attention scoring mechanisms. There are essential differences in the optimization objectives.

  1. (1)

    The Core Optimization Goal of The Attention Mechanism The instance score for traditional attention is generated by the following formula:

    $$\begin{aligned} \alpha _i = \frac{\exp (\textbf{w}^T \tanh (\textbf{V} \textbf{h}_i))}{\sum _j \exp (\textbf{w}^T \tanh (\textbf{V} \textbf{h}_j))} \end{aligned}$$
    (2)

There exist the following two key deficiencies:

Firstly, the trainable parameters \(\textbf{w}\) and \(\textbf{V}\) in Eq.(2) can only model inter-instance relationships while it calculates instance similarity via \(\tanh (\textbf{V}\textbf{h}_i)\). Secondly, supervised signals (bag labels) can only indirectly influence weighted summation \(\mathbf {z = \sum \alpha _i h_i}\).

\(h_i\) or \(h_j\) represents the feature vector of an individual instance within the bag. z denotes the aggregated bag-level representation obtained by performing a weighted sum of all instance feature vectors using the attention scores (\(\alpha _i\)) as weights. This composite representation integrates information from all instances in the bag and is subsequently used for making the final bag-level prediction.

  1. (2)

    Decision-Correlation Mechanism in WSICAM The instance score is calculated directly from the classification layer weights:

    $$\begin{aligned} {s}_i = \sum _{k=1}^{d} w_k^c \cdot f_k(x_i, y_i) \end{aligned}$$
    (3)

In Eq.(3), \(w_k^c\) is the weight of the fully connected classification layer and \(f_k\) is the instance feature. d denotes the number of channels in \(I_{cam}\) While the variable k serves as an iterative index traversing the channel dimension d, it explicitly denotes the ordinal position of the currently accessed channel within the Icam tensor. The variables x and y correspond to the horizontal and vertical coordinates, respectively, specifying the spatial position of a specific instance within the Icam structure.

$$\begin{aligned} \frac{\partial {L}_{cls}}{\partial s_i} = \frac{\partial {L}_{cls}}{\partial {y}} \cdot \frac{\partial {y}}{\partial w_k^c} \cdot \frac{\partial w_k^c}{\partial s_i} \end{aligned}$$
(4)

Compared to the above attention mechanism, the core advantages of the decision-correlation mechanism in WSICAM is that the gradient is directly backpropagated to \(s_i\) through the classification loss. Thus, it can achieve end-to-end optimization of instance contribution and classification decision.

In natural images, methods such as CAM and Grad-CAM can be used to obtain the contribution of different regions in the original image to the prediction of image classification, as described in Section 2.2. Unfortunately, because of the enormous size of WSIs, it is difficult to directly apply CAM series methods to WSIs.

Inspired by CAM, for accurately capturing the contribution of each instance to the bag prediction, we construct WSICAM modules according to the characteristics of WSIs. They include preprocessing, patch feature extraction, feature aggregation using MIL, patch rearrangement and bag prediction. In the preprocessing stage, we tile each WSI into non-overlapping patches (\(p\in \mathbb {R}^{h\times w\times c}\)). In patch feature extraction, we use the self-supervised contrastive learning method SimCLR41 to pre-train the feature extractor, mapping each patch into a one-dimensional feature vector \(f_p \in \mathbb {R}^{1 \times d}\), facilitating subsequent processing. In the MIL feature aggregation, for each WSI, we select \(n\) patch feature vectors \(I_{mil} \in \mathbb {R}^{n \times d}\) randomly and input them into MIL, obtaining the output \(O_{mil} \in \mathbb {R}^{n \times d}\) of the MIL module. During the patch rearrangement, we utilize the position information of each patch from the original image to reshape and pad \(O_{mil}\), so that we can achieve \(I_{cam} \in \mathbb {R}^{(H_{wsi}/h) \times (W_{wsi}/w) \times d}\).

To be specific, we initialize a matrix M of size \({(H_{wsi}/h) \times (W_{wsi}/w) \times d}\) with all values set to 0, i.e., each patch in a WSI is compressed into a vector at the corresponding position in the matrix M. Thus, the height of M is equal to the height of the WSI divided by the height of patch, i.e., \((H_{wsi}/h)\). Similarly, its width is \((W_{wsi}/w)\) and the number of channels is d. For the output \(O_{mil} \in \mathbb {R}^{n \times d}\) of the MIL module, it comes from n patches mapping of the WSI. Each patch feature in \(O_{mil}\) is placed into the matrix M, with its location in the matrix coinciding with the position in the WSI. If a patch is not selected, the corresponding position in the matrix M is filled with a zero vector. The updated matrix M is the input of CAM, \(I_{cam} \in \mathbb {R}^{(H_{wsi}/h) \times (W_{wsi}/w) \times d}\). Therefore, if an instance in a bag is selected, it will be mapped to a non-zero vector at the corresponding position in \(I_{cam}\). Otherwise, the corresponding position in \(I_{cam}\) will be filled with a zero vector. In the procedure of bag prediction, through Global Average Pooling (GAP) on \(I_{cam}\), we can obtain \(O_{gap} \in \mathbb {R}^{1 \times d}\). Input the \(O_{gap}\) into the fully connected layer (\(MLP \in \mathbb {R}^{d \times 2}\)) and finally achieve the bag classification prediction \(y_i \in \mathbb {R}^{1 \times 2}\). Algorithm 1 clearly summarizes the whole pipeline of the WSACAM modules.

Algorithm 1
figure a

WSICAM.

Full size image
$$\begin{aligned} O_{cam}^c(x, y) = \sum _k w_k^c \cdot I_{\text {cam}\underline{\ }{k}}(x, y) \end{aligned}$$
(5)

\(I_{\text {cam}\underline{\ }{k}} \in \mathbb {R}^ {(H_{wsi}/h) \times (W_{wsi}/w)}\) represents the feature of the k-th channel in \(I_{cam}\) and \(w_{k}^{c}\) indicates the weight of the k-th channel in class c. Noted that \(k\in \{1,\ldots ,d\}\). As mentioned by CAM, ’\(M_c(x,y)\) directly indicates the importance of the activation at the spatial grid (x, y) leading to the classification of an image to class c.’ Thus, the value in \(O_{cam}\), in the range of (0, 1), which represents the instance score. A higher instance score in \(O_{cam}\) suggests that the instance at the corresponding position in the WSI makes a more substantial contribution to the classification of the bag into class c. We use cross-entropy loss to train the two branches (b) and (d), with the loss functions defined as follows:

$$\begin{aligned} L_{cls} = -\frac{1}{N} \sum _{i = 1}^{N} \left[ y_i \log (\hat{y}_i) + (1 - y_i) \log (1 - \hat{y}_i) \right] \end{aligned}$$
(6)

Cross-slide augmentation

Due to the difficulty in achieving pathology images and the common issue of imbalance between positive and negative samples, RankMix explores weakly supervised learning from the perspective of data augmentation to address the problems of insufficient training data and class imbalance in WSI classification. RankMix processes two WSIs at a time and for each WSI, obtains pseudo-labels for each instance through a simple fully connected layer at first. Then, it sorts the pseudo-label scores and selects the top m instances with the highest pseudo-label scores from the bag. Construct a mixed subset of m significant instances selected respectively from two WSIs for training. However, RankMix cannot generate accurate instance scores through a simple fully connected layer, and the instances selected based on inaccurate pseudo-label scores may not include those that have a decisive impact on the result. In contrast, WSICAM can accurately capture the contribution of each instance to the bag prediction, effectively addressing the shortcomings of RankMix.

Building on WSICAM, we further propose a Cross-Slide Augmentation (CSA) module. It constructs new samples with mixed labels by selecting discriminative instances from different bags for model training to improve the feature learning capability and generalization of the model. As shown in branch (c) of Fig. 2, we select m instances, \(H'_a\) and \(H'_b\), corresponding to the m positions with the largest pixel values in \(O_{cam}\) from (b) and (d) respectively. Their mixing process is as follows:

$$\begin{aligned} H_ {mxp} = \lambda H'_a + (1 - \lambda ) H'_b \end{aligned}$$
(7)

Where \(\lambda \in [0, 1]\). We construct a mixed bag \(H_ {mxp}\) by mixing the m instances from the two WSIs in proportions of \(\lambda\) and \(1 - \lambda\). The label \(Y_ {mxp}\) is also obtained in the same way as the instance mixing. The loss functions \(L_ {mxp}\) for the CSA module and \(L_ {CAMCSA}\) for the CAMCSA framework are expressed as follows:

$$\begin{aligned} L_{mxp}&= -\frac{1}{2k} \sum _{i = 1}^{2k} \left[ y_i \log (\hat{y}_i) + (1 - y_i) \log (1 - \hat{y}_i) \right] \end{aligned}$$
(8)
$$\begin{aligned} L_ {CAMCSA}&= L_ {cls-b} + L_ {cls-d} + L_ {mxp} \end{aligned}$$
(9)

\(L_{cls-b}\) and \(L_{cls-d}\) are the cross-entropy loss respectively in branch (b) and branch (d).

CSA is a data augmentation module based on accurate instance scores providing by WSICAM. It enhances the classification performance of branch (c) while inducing the branches (b) and (d) to produce more accurate instance scores, achieving mutual improvement among the three branches.

Results

Datasets & evaluation metrics

We evaluate CAMCSA on two public clinical WSI datasets: CAMELYON-1642 and The Caner Genome Atlas (TCGA) lung cancer. We crop each WSI into various \(224 \times 224\) patches at a magnification of \(20 \times\) without overlap and discard background patches with tissue entropy less than 10% of a WSI.

Camelyon16 is a public dataset utilized for metastasis detection in breast cancer. It comprises 271 training images and 129 test images, resulting in approximately 3.2 million patches with an average of about 8,000 per bag. Tumor lesion regions are fully labeled with pixel-level annotations on each slide. In the training stage, we disregard the pixel-level annotations and only consider slide-level labels. Due to the availability of pixel-level annotations on Camelyon16, we are allowed to test the localization capability of CAMCSA, and the localization performance illustrates its ability to represent positive instances. We use the FROC score to evaluate the localization performance.

Besides, we show the performance of CAMCSA on TCGA lung cancer dataset. It has two types of lung cancer, Lung Adenocarcinoma (TCGA-LUAD) and Lung Squamous Cell Carcinoma (TCGA-LUSC), which can be obtained from https://portal.gdc.cancer.gov/ with 1054 diagnostic WSIs. We divided the WSIs randomly into 840 slides for training and 210 slides for testing, excluding 4 slides that were of low quality and corrupted. It is cropped into a total of 5.2 million patches at \(20 \times\) magnification. For this dataset, only slide labels are accessible.

We evaluate CAMCSA for the task of WSI classification on the above both datasets by accuracy and area under the curve (AUC) scores. The performances of the bag-level classification can serve as evidence of the effectiveness of CAMCSA in generating high-quality bag embeddings. The FROC and visualization results (Fig. 3) illustrate the ability of CAMCSA to accurately delineate the contributions of positive instances to the classification of a bag as positive.

Experimental settings

The Adam optimizer with a fixed learning rate of 0.0001 is employed to iteratively update the framework weights throughout the training phase. For training CAMCSA, the mini-batches size is 256 (bags). All patch features from WSIs are extracted by a feature extractor pre-trained by SimCLR. For SimCLR, we use Adam optimizer with an initial learning rate of 0.0001, a cosine annealing (without warm restarts) scheme for learning rate scheduling, and a min-batch size of 512. Both the MIL module of CAMCSA and SimCLR employ ResNet18 as their CNN backbones.

Performance comparison with existing works

Table 1 and Table 2 show the strong classification ability of our proposed framework CAMCSA on the Camelyon16 and TCGA lung cancer datasets. It can be found that our method outperforms all the other baselines in WSI classification performance by a great margin, which fully indicates the significance of our WSICAM and CSA modules in improving bag-level representations. We remove the CAM and CSA modules and directly connect a simple fully connected layer after the MIL module in Figure 2 as the classification head for ablation experiments, i.e., CAMCSA/without CAM and CSA in Table 1 and Table 2. CAMCSA/without CAM indicates the removal of the CAM module, meaning that instances are no longer selected based on the instance scores provided by the WSICAM module. Instead, the top k instances are selected from the features before the MIL module through an MLP. CAMCSA/without CSA means that k instances are not selected separately on the two branches for cross-slice MIX data augmentation.

In terms of localization performance, as shown in Table 1, when comparing CAMCSA/without CAM and CSA with CAMCSA/without CSA, the introduction of CAM results in an FROC improvement of over 3%. This demonstrates that WSICAM significantly enhances the delineation of positive patches in detection localization. In summary, WSICAM improves the ability to localize lesion areas by accurately inferring instance scores/contributions within the bag. This not only enhances the interpretability of CAMCSA but also provides a reliable basis for clinical diagnosis. The detection maps of representative samples from the Camelyon16 testing set are shown in Fig. 3. As observed, using only slide-level labels, our method can precisely predict nearly all positive instances–regardless of whether the proportion of positive areas in the WSIs is large or small. This visually confirms the robust performance of CAMCSA and its significant potential for clinical applications.

In terms of classification performance, CAMCSA/without CAM achieves significantly higher ACC and AUC compared to CAMCSA/without CAM and CSA, as evidenced in Tables 1 and 2. These results demonstrate that our proposed CSA is a highly effective data augmentation method, substantially improving the model’s feature extraction capability.

Compared with the previous state-of-the-art framework MHIM-MIL, CAMCSA demonstrates significant improvements in both classification and localization performance across both datasets. The overall results illustrate that our method not only visibly improves WSI classification performance on multiple datasets but also possesses powerful tumor lesions localization abilities, which fully testify the generality and effectiveness of CAMCSA.

Table 1 Comparison of WSI classification and location performance between CAMCSA and other methods on the Camelyon16 dataset. CAMCSA/without CSA denotes the experimental results on Camelyon16 of CAMCSA before introducing the CSA module.
Full size table
Table 2 Comparison of WSI classification between CAMCSA and other methods on the TCGA Lung Cancer dataset. CAMCSA/without CSA denotes the experimental results of CAMCSA on TCGA Lung Cancer before introducing the CSA module.
Full size table
Table 3 Comparison of CAMCSA performance with different kinds of Mixed Labels on Camelyon16.
Full size table
Table 4 Comparison of CAMCSA performance with different kinds of Mixed Labels on the TCGA Lung Cancer.
Full size table

Table 3 and Table 4 show the advantages of utilizing soft labels instead of hard labels within the CSA module. The labels of the mixed bags are generated by mixing the labels of two WSIs in varying proportions; that is, a probability is employed as the soft label of a mixed bag. In comparison to directly employing the original labels of WSIs as the hard labels of the mixed bags (if both WSI labels are 0, the mixed bag label is 0; otherwise, it is 1.), using a probability to guide the training of the CSA module is obviously more effective.

Ablation study

It should be noted that our WSICAM is a plug-and-play module, and the MIL component can be seamlessly integrated with any existing MIL model architecture. To prove this, we conducted ablation experiments using different MIL backbones in WSICAM. Tables 5 and 6 respectively represent the performance of AUC improvement after replacing the MIL module in WSICAM with ABMIL, DSMIL, and TransMIL on the Camelyon16 and TCGA Lung Cancer datasets. The experiments show that in our CAMCSA, WSICAM is a plug-and-play module that can effectively improve performance.

Table 5 Ablation Study on Camelyon16 with Different MIL Backbones.
Full size table
Table 6 Ablation Study on TCGA Lung Cancer with Different MIL Backbones.
Full size table

Visualization on the Camelyon16 and TCGA lung testing set

As shown in Fig. 3, the warmer-colored subregions imply a higher probability of abnormal tissues. Through comparisons with methods like Max-pooling, ABMIL, and DSMIL, it visually demonstrates our superior localization performance even for tiny lesions. In other words, CAMCSA has the ability to learn more diverse and abundant features of positive instances and perform precise localization of positive instances within WSIs. The visualization results demonstrate that the proposed CAMCSA generates more reliable instance scores. Based on these reliable instance scores, more precise tumor localization can be obtained, which is beneficial to improve the interpretability of CAMCSA. In order to further illustrate the generalization and versatility of our method, we invited lung cancer experts in hospital to annotate the WSIs of the TCGA-Lung testing set, and the visualizations are presented in Fig. 4.

Fig. 3
figure 3

Comparison of tumor localization under different methods. (a) A WSI derived from the Camelyon16 testing set with tumor masks. (c)-(f) are the magnified regions within the yellow box of (b). (c) Max-pooling. (d) ABMIL. (e) DSMIL. (f) CAMCSA.

Full size image
Fig. 4
figure 4

Comparison of tumor localization under different methods. (a) A WSI derived from the TCGA Lung Cancer testing set with tumor masks. (c)-(e) are the magnified images of ROI region (b). (c) Max-pooling. (d) ABMIL. (e) CAMCSA.

Full size image

Discussion & conclusions

The proposed CAMCSA framework addresses two critical limitations in attention-based MIL approaches for WSI classification: inaccurate instance contribution estimation and insufficient representation learning under data scarcity. By integrating WSICAM and CSA modules, our method achieves state-of-the-art performance on the most representative WSI datasets, demonstrating its substantial potential in automated WSI classification while providing interpretable lesion localization–a crucial requirement for clinical adoption.

Traditional attention mechanisms in MIL often prioritize morphological similarity between instances, which may misalign with actual diagnostic relevance. Our WSICAM module resolves this by grounding instance scores in class-specific activation patterns, ensuring that contributions directly correlate with pathological features (e.g., tumor nuclei or stromal patterns). This aligns with recent calls for explainable AI in digital pathology, as evidenced by the improved lesion localization accuracy on Camelyon16. The ablation studies further validate that WSICAM’s spatial weighting mechanism enhances feature discriminability, outperforming conventional attention mechanisms that may overemphasize redundant tissue regions.

The CSA module introduces a biologically plausible augmentation strategy by mixing discriminative instances across slides–a significant advancement over conventional patch-level augmentation. Unlike natural image Mixup, which risks creating unrealistic tissue transitions, our instance selection via WSICAM ensures that mixed features preserve diagnostically critical patterns while expanding feature diversity.

The framework’s dual capability–accurate classification coupled with precise lesion localization–addresses two fundamental needs in computational pathology: diagnostic reliability and interpretability. By highlighting WSICAM-derived discriminative regions, pathologists can efficiently validate model decisions against known histopathological criteria, potentially accelerating the integration of AI into clinical workflows. Furthermore, the method’s robustness to dataset imbalance suggests broader applicability to resource-constrained settings where comprehensive data collection remains challenging.

While CAMCSA demonstrates strong performance on benchmark datasets, its computational overhead for large-scale WSI analysis warrants optimization for real-time applications. Future work should investigate dynamic instance sampling strategies and adaptive mixing ratios in CSA. Additionally, validating the framework on multi-class scenarios and metastatic cancer detection could further demonstrate its generalizability. Integrating patient-level clinical data with WSICAM’s spatial weighting may enable more comprehensive prognostic models.