Abstract
This paper presents a novel deep learning-based multi-parameter coupling compensation algorithm for clamp-on gas metering systems to address the complex interdependencies between temperature, pressure, and density variations that significantly affect measurement accuracy. Traditional linear and polynomial compensation methods fail to capture the nonlinear coupling effects between environmental parameters, leading to substantial measurement errors under dynamic operating conditions. The proposed approach employs a hybrid LSTM-CNN neural network architecture that simultaneously models temporal dependencies and spatial relationships within the multi-parameter space, enabling more accurate compensation compared to conventional methods. The algorithm incorporates real-time adaptive correction mechanisms with sliding window processing and dynamic weight adjustment to automatically respond to changing operating conditions. Experimental validation demonstrates significant performance improvements, achieving 0.52% average measurement error compared to 2.45% for conventional linear compensation, representing a 78% accuracy enhancement. Long-term stability testing confirms consistent performance over 720-hour continuous operation with 5.34 millisecond real-time processing capability suitable for industrial implementation. The research contributes to advancing precision gas flow measurement technology by providing a practical solution for achieving high-accuracy measurements under complex industrial operating conditions.
Similar content being viewed by others
Introduction
Gas metering technology plays a crucial role in industrial processes, energy management, and environmental monitoring, with accurate flow measurement being essential for economic transactions and process control1. Traditional gas metering methods have been widely employed across various industries, but they often suffer from significant measurement errors due to inadequate compensation for environmental parameters such as temperature, pressure, and density variations2. The development of non-intrusive measurement techniques has led to increased interest in clamp-on gas metering systems, which offer the advantage of installation without interrupting the gas flow or modifying existing pipeline infrastructure3.
Clamp-on gas metering technology utilizes ultrasonic transit-time measurement principles to determine gas flow rates by analyzing the acoustic signal propagation characteristics through the pipeline wall and gas medium4. However, the accuracy of these measurements is significantly affected by the complex interactions between temperature, pressure, and density variations, which create coupled effects that are difficult to compensate using conventional linear correction methods5. Traditional compensation algorithms typically employ simplified mathematical models that assume linear relationships between individual parameters, leading to substantial measurement errors under dynamic operating conditions where multiple environmental factors change simultaneously.
The limitations of existing gas metering compensation methods become particularly pronounced in industrial applications where gas properties exhibit non-linear behavior due to varying operational conditions6. Various compensation approaches have been developed to address measurement errors, each with distinct characteristics and limitations. Additive compensation models employ corrections in the form of \(\:{Q}_{corrected}={Q}_{measured}+{\Delta\:}{Q}_{T}+{\Delta\:}{Q}_{P}+{\Delta\:}{Q}_{{\uprho\:}}\), where individual parameter effects are summed to achieve overall correction. These methods work well for small deviations but fail to capture the proportional relationships between environmental variations and measurement errors inherent in gas flow systems.
Predictive compensation models utilize historical parameter trends to anticipate future correction requirements, often incorporating time-series analysis or regression techniques to forecast environmental parameter evolution. While these approaches can provide proactive corrections, they depend heavily on predictable parameter patterns and may struggle with sudden environmental changes or nonlinear system dynamics.
Multiplicative compensation formulations, represented by Eqs. (4) and (5) in this work, better reflect the physical reality of gas measurement systems where environmental parameter variations cause proportional changes in measurement accuracy. The selection of multiplicative compensation is justified by fundamental gas law relationships where density variations directly scale volumetric measurements, and temperature-pressure effects create proportional rather than additive measurement errors. This approach aligns with the thermodynamic principles governing gas behavior under varying conditions.
Conventional approaches often treat temperature, pressure, and density corrections as independent parameters, failing to account for the complex interdependencies that exist between these variables in real-world scenarios.
This oversimplified treatment results in cumulative errors that can significantly impact measurement accuracy, especially in applications requiring high precision flow measurements for custody transfer or process optimization purposes.
Recent advances in artificial intelligence and machine learning have opened new possibilities for addressing the multi-parameter compensation challenges in gas metering systems7. Deep learning algorithms, with their ability to model complex non-linear relationships and adapt to changing conditions, present a promising solution for developing more accurate and robust compensation mechanisms. Unlike traditional statistical methods, deep learning approaches can capture intricate patterns in multi-dimensional parameter spaces and provide real-time adaptive corrections that account for the coupled effects of temperature, pressure, and density variations.
The necessity for developing advanced multi-parameter coupling compensation algorithms stems from the increasing demand for higher measurement accuracy in modern industrial applications. Current compensation methods typically achieve accuracy levels that may be insufficient for emerging applications such as smart grid energy management, environmental emission monitoring, and high-value gas custody transfer operations. The integration of deep learning techniques into clamp-on gas metering systems represents a significant advancement toward achieving the required precision levels while maintaining the non-intrusive advantages of the measurement approach.
The innovation of this research lies in the development of a comprehensive deep learning framework that simultaneously addresses temperature, pressure, and density compensation through a unified multi-parameter coupling model. This approach differs fundamentally from existing methods by treating the compensation problem as a complex, multi-dimensional optimization task rather than a series of independent correction calculations. The proposed algorithm incorporates real-time adaptive learning capabilities that enable the system to continuously improve its compensation accuracy based on operational experience and changing environmental conditions8.
The primary objective of this research is to develop and validate a deep learning-based multi-parameter coupling compensation algorithm that significantly improves the accuracy and reliability of clamp-on gas metering systems. The research aims to establish a theoretical framework for understanding the complex interactions between temperature, pressure, and density effects on ultrasonic gas flow measurements, and to translate this understanding into practical compensation algorithms suitable for industrial implementation.
The main contributions of this work include the development of a novel deep learning architecture specifically designed for multi-parameter gas metering compensation, the establishment of comprehensive validation methodologies for evaluating algorithm performance under various operating conditions, and the demonstration of significant accuracy improvements compared to conventional compensation methods. Additionally, the research provides insights into the fundamental relationships between environmental parameters and measurement errors in clamp-on gas metering systems, contributing to the broader understanding of non-intrusive flow measurement principles.
This paper presents a systematic approach to addressing the multi-parameter compensation challenge in clamp-on gas metering through the application of advanced deep learning techniques. The proposed methodology offers a pathway toward achieving higher measurement accuracy while maintaining the operational advantages of non-intrusive metering systems, thereby supporting the advancement of precision gas flow measurement technology for critical industrial applications.
Literature review and theoretical background
Clamp-on gas metering technology principles
Clamp-on ultrasonic gas metering technology operates on the principle of measuring acoustic wave propagation characteristics through gas media to determine volumetric flow rates without direct contact with the flowing gas9.
Figure 1 illustrates the fundamental measurement principle, showing the ultrasonic transducers mounted externally on the pipeline wall and the acoustic signal propagation paths through the gas medium.
The ultrasonic measurement configuration demonstrates how environmental parameters (T, P, ρ) influence both the acoustic propagation characteristics and gas properties, creating the complex coupling effects addressed by the proposed compensation algorithm.
The fundamental measurement approach utilizes ultrasonic transducers mounted externally on the pipeline wall, which transmit and receive acoustic signals that traverse the gas flow at predetermined angles. The basic transit-time measurement principle relies on the velocity difference of ultrasonic waves traveling upstream and downstream relative to the gas flow direction, enabling the calculation of gas velocity through time-of-flight analysis10.
The transit-time measurement method can be mathematically expressed through the relationship between acoustic propagation times and gas flow velocity. The upstream and downstream transit times are given by:
where L represents the acoustic path length, c is the speed of sound in the gas medium, v is the gas flow velocity, and θ is the angle between the acoustic path and the pipe axis. The gas flow velocity can then be calculated from the time difference as:
The accuracy of clamp-on gas metering systems is significantly influenced by temperature, pressure, and density variations, which affect both the acoustic propagation characteristics and the gas properties11. Temperature variations alter the speed of sound in the gas medium according to the relationship between molecular kinetic energy and acoustic velocity, while pressure changes modify gas density and compressibility factors. These environmental parameters create complex coupling effects that cannot be adequately addressed through simple linear compensation methods, as the interdependencies between temperature, pressure, and density exhibit non-linear behavior patterns that vary with gas composition and operating conditions.
Density fluctuations particularly impact measurement accuracy by affecting the acoustic impedance matching between the pipeline wall and the gas medium, leading to variations in signal attenuation and reflection characteristics12. The coupling between pressure and density creates additional complexity, as pressure-induced density changes alter the acoustic propagation path and velocity in ways that are not easily predictable using conventional mathematical models. Furthermore, temperature gradients across the pipeline cross-section can create acoustic path distortions that contribute to measurement uncertainties, especially in large-diameter pipelines where thermal stratification effects become significant.
The primary advantages of clamp-on gas metering technology include non-intrusive installation, minimal pressure drop, and the ability to retrofit existing pipeline systems without flow interruption13. These systems offer excellent long-term stability and require minimal maintenance compared to traditional intrusive flow meters. However, the technology also presents several limitations, including sensitivity to pipe wall thickness variations, coupling medium degradation, and reduced accuracy under low flow conditions. The external mounting configuration makes the measurement susceptible to environmental factors such as temperature cycling, vibration, and acoustic interference from external sources.
Additionally, clamp-on systems typically exhibit lower accuracy compared to inline ultrasonic meters due to signal attenuation through the pipeline wall and uncertainties in acoustic path geometry. The dependency on pipeline material properties and wall condition creates potential sources of long-term measurement drift, while the complex relationship between environmental parameters and measurement accuracy requires sophisticated compensation algorithms to achieve acceptable performance levels for critical applications.
Multi-parameter coupling compensation theory
The coupling relationships between temperature, pressure, and density in gas flow measurement systems exhibit complex interdependencies that significantly influence the accuracy of ultrasonic transit-time measurements14. The fundamental thermodynamic relationship governing these parameters follows the ideal gas law and its real gas modifications, where pressure and density are intrinsically linked through temperature-dependent compressibility factors. The coupling effect becomes particularly pronounced in gas metering applications where simultaneous variations in multiple environmental parameters create measurement errors that cannot be adequately addressed through independent parameter corrections15.
Traditional linear compensation methods typically employ simplified mathematical models that assume additive or multiplicative relationships between individual parameter corrections. The conventional linear compensation approach can be expressed as:
where \(\:{k}_{T}\), \(\:{k}_{P}\), and \(\:{k}_{\rho\:}\) represent constant correction coefficients for temperature, pressure, and density variations respectively16. However, this approach fails to capture the nonlinear interactions between parameters and the cross-coupling effects that occur when multiple environmental variables change simultaneously. The linear assumption becomes increasingly inaccurate under dynamic operating conditions where parameter variations exhibit significant magnitude or rapid temporal changes.
The limitations of linear compensation methods stem from their inability to model the complex physical phenomena that govern acoustic propagation in varying gas environments17. Real gas behavior deviates substantially from linear relationships, particularly at high pressures or low temperatures where compressibility effects become significant. Additionally, the speed of sound in gas media exhibits nonlinear dependencies on temperature and pressure through the fundamental relationship involving molecular properties and thermodynamic state variables.
Nonlinear compensation theory addresses these limitations by incorporating higher-order terms and cross-coupling effects into the mathematical framework. The generalized nonlinear compensation model can be formulated as:
where f represents a multivariable nonlinear function that captures both individual parameter effects and their interactions18. This approach recognizes that the measurement error is not simply the sum of individual parameter effects but rather a complex function of their combined influence on acoustic propagation characteristics.
Multi-variable coupling mathematical models provide a more comprehensive framework for understanding and compensating the interdependent effects of environmental parameters on gas flow measurements. The coupling matrix approach represents the parameter interactions through a system of equations:
where the coupling matrix elements \(\:{a}_{ij}\) represent the cross-sensitivity coefficients between different parameter pairs19. This matrix formulation enables the quantification of how changes in one parameter influence the measurement response to variations in other parameters, providing a mathematical foundation for developing more sophisticated compensation algorithms.
The theoretical framework for multi-parameter coupling compensation also incorporates temporal dynamics and hysteresis effects that occur in real measurement systems. The dynamic coupling model accounts for the time-dependent nature of parameter interactions and the lag effects that arise from thermal and mechanical time constants in the measurement system:
This dynamic formulation recognizes that the compensation process must account not only for instantaneous parameter values but also for their rates of change and the temporal evolution of coupling effects. The incorporation of derivative terms enables the compensation algorithm to respond appropriately to transient conditions and minimize measurement errors during parameter transition periods.
Deep learning applications in flow measurement
The integration of deep learning technologies into flow measurement systems has emerged as a promising approach for addressing complex parameter compensation challenges that exceed the capabilities of traditional analytical methods20. Recent developments in artificial intelligence have demonstrated significant potential for improving measurement accuracy through advanced pattern recognition and nonlinear modeling capabilities. Neural network architectures have been increasingly applied to flow measurement applications, particularly in scenarios where conventional mathematical models fail to capture the complex relationships between environmental parameters and measurement errors.
Feedforward neural networks have been extensively investigated for parameter compensation in various flow measurement applications, with researchers demonstrating their ability to model complex nonlinear relationships between input variables and measurement corrections. These networks typically employ multiple hidden layers with nonlinear activation functions to approximate the intricate mapping between environmental parameters and measurement errors21. The universal approximation capabilities of neural networks make them particularly suitable for capturing the complex coupling effects between temperature, pressure, and density variations that characterize real-world gas flow measurement scenarios. However, conventional feedforward networks are limited in their ability to process temporal sequences and may not adequately account for the dynamic nature of parameter interactions in time-varying measurement environments.
Recurrent neural networks have been explored for their enhanced capability to process sequential data and capture temporal dependencies in flow measurement applications. RNN architectures offer advantages in modeling the time-dependent evolution of environmental parameters and their cumulative effects on measurement accuracy. The inherent memory characteristics of recurrent networks enable them to maintain information about previous parameter states, which is crucial for understanding the dynamic coupling effects that occur during transient operating conditions22. However, traditional RNN implementations suffer from gradient vanishing problems that limit their effectiveness in capturing long-term dependencies, particularly in applications where environmental parameter variations exhibit extended temporal correlations.
Long Short-Term Memory networks have been developed to address the limitations of conventional RNNs by incorporating sophisticated gating mechanisms that enable selective information retention and forgetting. LSTM architectures have demonstrated superior performance in flow measurement applications where long-term temporal dependencies play significant roles in determining measurement accuracy. The ability of LSTM networks to selectively retain relevant historical information while discarding irrelevant data makes them particularly well-suited for modeling the complex temporal evolution of multi-parameter coupling effects in gas flow measurement systems23. The gating mechanisms in LSTM networks provide enhanced control over information flow, enabling more effective learning of the nonlinear relationships between environmental parameter histories and current measurement corrections.
Despite the promising results achieved through deep learning applications in flow measurement, several significant limitations remain in current methodologies. Most existing approaches focus on single-parameter compensation or treat multiple parameters as independent variables, failing to adequately address the complex coupling interactions that characterize real-world measurement scenarios. The majority of published studies have been conducted under controlled laboratory conditions with limited parameter ranges, raising questions about the generalizability and robustness of these methods when applied to diverse industrial environments with varying gas compositions and operating conditions.
Additionally, current deep learning approaches often lack comprehensive validation protocols and standardized performance metrics, making it difficult to compare different methodologies and assess their practical applicability. The computational complexity of advanced neural network architectures presents challenges for real-time implementation in resource-constrained measurement systems, while the black-box nature of deep learning models raises concerns about interpretability and reliability in critical measurement applications. Furthermore, the training data requirements for deep learning models can be substantial, and the availability of high-quality, diverse training datasets remains a significant barrier to widespread implementation of these technologies in practical flow measurement systems.
Multi-parameter coupling compensation algorithm model design
Deep learning network architecture design
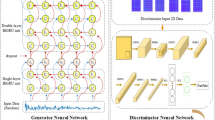
The development of an effective multi-parameter coupling compensation model requires a sophisticated neural network architecture capable of simultaneously processing temporal sequences and extracting complex feature relationships from multi-dimensional input data24. The proposed approach employs a hybrid LSTM-CNN network architecture that combines the temporal modeling capabilities of Long Short-Term Memory networks with the feature extraction strengths of Convolutional Neural Networks. This hybrid design enables the model to capture both the sequential dependencies inherent in time-series environmental parameter data and the spatial relationships between different parameter combinations that influence measurement accuracy.
The LSTM component of the hybrid architecture serves as the primary mechanism for processing temporal sequences of temperature, pressure, and density measurements. The sequential nature of environmental parameter variations in gas flow measurement systems creates complex temporal dependencies that must be accurately modeled to achieve effective compensation25. The LSTM layers are specifically configured to maintain long-term memory of parameter evolution patterns while selectively forgetting irrelevant historical information through sophisticated gating mechanisms. The temporal modeling capability enables the network to recognize recurring parameter patterns and their associated measurement effects, facilitating more accurate prediction of compensation factors under dynamic operating conditions.
The CNN component functions as a feature extraction engine that identifies spatial relationships and local patterns within the multi-parameter input space. Convolutional layers with varying kernel sizes are employed to detect different scales of parameter interactions, ranging from fine-grained local correlations to broader parameter coupling patterns26. The hierarchical feature extraction process enables the network to automatically discover relevant parameter combinations that significantly influence measurement accuracy, eliminating the need for manual feature engineering and improving the model’s adaptability to diverse operating conditions.
The overall network architecture integrates these components through a carefully designed flow that maximizes information retention while minimizing computational complexity. As illustrated in Fig. 2, the hybrid architecture processes multi-parameter input sequences through parallel LSTM and CNN pathways before combining the extracted features through fully connected layers for final compensation factor prediction.
The network architecture begins with an input layer that accepts normalized sequences of temperature, pressure, and density measurements along with their corresponding temporal timestamps. The input data is simultaneously fed to both LSTM and CNN processing branches to capture complementary aspects of the parameter relationships. The LSTM branch processes the temporal sequences through multiple LSTM layers with bidirectional connections to capture both forward and backward temporal dependencies. The CNN branch applies multiple convolutional filters with different kernel sizes to extract hierarchical features from the parameter space.
The specific network configuration parameters have been optimized through extensive experimentation to balance model complexity with computational efficiency. The LSTM layer neuron count follows a decreasing pattern (128→64) to progressively extract and compress temporal features while preventing overfitting through dimensional reduction. The CNN filter configuration (32→16) implements hierarchical feature extraction, where larger filter banks capture coarse spatial relationships and smaller ones refine local patterns within the parameter space.
Dropout rates are strategically increased in deeper layers (0.2→0.4) to provide stronger regularization where overfitting risks are highest due to increased model complexity. ReLU activation functions are employed in CNN and dense layers to avoid gradient vanishing problems while maintaining computational efficiency, while LSTM layers utilize hyperbolic tangent activation functions to enable effective gradient flow through recurrent connections and maintain stable temporal sequence processing.
As shown in Table 1, the network consists of eight primary layers with carefully selected neuron counts and activation functions designed to maximize learning capacity while preventing overfitting.
The mapping relationship between environmental parameter inputs and flow correction outputs is established through a comprehensive training process that learns the complex nonlinear function relating temperature, pressure, and density variations to measurement errors. The network architecture enables the automatic discovery of optimal parameter weightings and interaction terms without requiring explicit mathematical formulation of the coupling relationships27. This data-driven approach allows the model to adapt to specific gas compositions and measurement system characteristics while maintaining generalizability across diverse operating conditions.
The activation function selection follows established best practices for deep learning applications, with ReLU functions employed in hidden layers to mitigate gradient vanishing problems while maintaining computational efficiency. The LSTM layers utilize hyperbolic tangent activation functions to enable effective gradient flow through the recurrent connections. Dropout regularization is strategically applied throughout the network to prevent overfitting and improve generalization performance, with dropout rates increasing in deeper layers to provide stronger regularization where overfitting risks are highest.
The output layer employs a linear activation function to enable unrestricted range compensation factor prediction, allowing the model to generate both positive and negative correction values as required by the physical measurement characteristics. The network architecture incorporates batch normalization layers between major components to stabilize training dynamics and accelerate convergence, while skip connections are employed to facilitate gradient flow through the deep network structure and improve training stability.
Real-time adaptive correction algorithm
The implementation of real-time adaptive correction requires sophisticated algorithms capable of processing continuous data streams while maintaining computational efficiency and accuracy under dynamic operating conditions28. The proposed real-time adaptive correction system incorporates a sliding window-based data processing mechanism that enables continuous parameter monitoring and immediate response to environmental variations. This approach ensures that the compensation model remains current with evolving measurement conditions while maintaining stability against transient disturbances and measurement noise.
The sliding window mechanism operates by maintaining a continuously updated buffer of recent environmental parameter measurements, enabling the adaptive algorithm to respond dynamically to changing conditions while preserving computational efficiency. The window size is optimized to balance responsiveness with stability, ensuring that the algorithm can detect meaningful parameter trends while filtering out short-term fluctuations that do not significantly impact measurement accuracy29. The sliding window approach enables the system to maintain a rolling baseline of recent operating conditions, facilitating the detection of gradual parameter drifts and sudden environmental changes that require immediate compensation adjustments.
The adaptive weight adjustment algorithm forms the core of the real-time correction system, automatically modifying the influence of different input parameters based on their current relevance and reliability. The weight adjustment mechanism employs a gradient-based optimization approach that continuously evaluates the prediction accuracy of individual parameter contributions and adjusts their relative importance accordingly. This dynamic weighting system enables the model to adapt to changing gas compositions, measurement system characteristics, and environmental conditions without requiring manual recalibration or external intervention30.
The multi-step prediction framework enables the algorithm to anticipate future parameter evolution and proactively adjust compensation factors before measurement errors occur. This predictive capability is particularly valuable in applications where environmental parameters exhibit predictable patterns or where upstream process conditions provide early indicators of impending changes. The multi-step prediction algorithm utilizes the temporal modeling capabilities of the LSTM network component to extrapolate current parameter trends and estimate future compensation requirements with quantified uncertainty bounds.
The error feedback correction system provides continuous validation and refinement of the adaptive algorithm performance through real-time comparison of predicted and observed measurement errors. As presented in Fig. 3, the comprehensive correction algorithm integrates sliding window processing, adaptive weighting, multi-step prediction, and error feedback components into a unified real-time system.
The error feedback mechanism operates by continuously monitoring the difference between model-predicted compensation factors and the optimal corrections derived from reference measurements or validation data. This feedback information is used to update the adaptive weights and refine the prediction algorithms in real-time, ensuring that the system maintains optimal performance even as operating conditions evolve. The feedback correction system incorporates both immediate error signals and longer-term performance trends to balance rapid response with system stability.
The dynamic response capability of the adaptive correction algorithm enables effective handling of various types of environmental parameter variations, including gradual drifts, step changes, and oscillatory behaviors. The algorithm automatically adjusts its response characteristics based on the detected pattern of parameter evolution, applying appropriate filtering and prediction strategies to optimize compensation accuracy. This adaptive behavior ensures robust performance across diverse operating scenarios without requiring manual parameter tuning or operator intervention31.
The key parameters governing the adaptive correction algorithm performance are carefully configured to optimize the balance between responsiveness and stability across anticipated operating conditions. As shown in Table 2, the adaptive parameter settings encompass critical algorithm components with specified ranges and physical interpretations that ensure optimal system performance.
The sliding window size determines the temporal extent of historical data considered for current decisions, with larger windows providing greater stability at the expense of reduced responsiveness to rapid changes. The learning rate controls the speed of adaptive weight updates, with higher rates enabling faster adaptation but potentially introducing instability under noisy conditions. The prediction horizon defines the time range for multi-step forecasting, balancing predictive capability with uncertainty accumulation over extended time periods.
The error threshold establishes the minimum prediction error level that triggers adaptive weight adjustments, preventing unnecessary algorithm updates in response to minor measurement variations. The forgetting factor determines how rapidly historical information loses influence in current decisions, enabling the algorithm to maintain relevant memory while adapting to changing conditions. The stability margin provides a safety buffer that prevents excessive adaptation in response to outlier measurements or temporary system disturbances.
The integration of these adaptive mechanisms creates a robust real-time correction system capable of maintaining optimal compensation performance across diverse operating conditions. The algorithm continuously monitors its own performance and adjusts internal parameters to maintain accuracy while preventing instability or divergent behavior. This self-tuning capability ensures long-term reliability and reduces maintenance requirements in practical implementation scenarios.
Model training and optimization strategy
The construction of a comprehensive training dataset requires systematic collection of environmental parameter data across diverse operating conditions to ensure model generalizability and robustness32. The training dataset encompasses temperature variations ranging from − 20 °C to 80 °C, pressure fluctuations between 0.1 and 10 MPa, and density changes corresponding to various gas compositions and thermodynamic states. The dataset construction strategy incorporates both controlled laboratory measurements and field data from industrial installations to capture the full spectrum of real-world operating scenarios and measurement challenges.
The loss function design plays a critical role in guiding the training process toward optimal compensation accuracy while maintaining numerical stability and convergence properties. The proposed composite loss function combines mean squared error for primary accuracy optimization with additional penalty terms for regularization and stability enhancement:
where the mean squared error component is defined as:
The regularization term incorporates L1 and L2 penalties to prevent overfitting and promote sparse parameter selection:
The stability term ensures smooth parameter evolution and prevents excessive sensitivity to input variations33.
The optimizer selection strategy employs adaptive learning rate algorithms that automatically adjust training parameters based on gradient characteristics and convergence behavior. The Adam optimizer is selected for its superior performance in handling sparse gradients and noisy optimization landscapes commonly encountered in multi-parameter regression problems. The learning rate schedule follows an exponential decay pattern:
where \(\:{\eta\:}_{0}\) represents the initial learning rate, \(\:\beta\:\) is the decay factor, and \(\:T\) is the decay period.
The comprehensive model evaluation framework incorporates multiple performance metrics that assess different aspects of compensation accuracy and system reliability. As demonstrated in Table 3, the evaluation metrics encompass accuracy measures, stability indicators, and computational efficiency parameters with corresponding weight coefficients reflecting their relative importance in practical applications.
The regularization methodology incorporates multiple techniques to prevent overfitting and improve model generalization performance. Dropout regularization is applied with varying rates across network layers, while batch normalization stabilizes training dynamics and reduces internal covariate shift. Early stopping mechanisms monitor validation loss evolution and terminate training when overfitting indicators are detected34.
The temporal validation approach addresses the time-series nature of environmental parameter data by implementing forward-chaining cross-validation that respects temporal ordering constraints:
where \(\:{D}_{train}^{\left(i\right)}\) and \(\:{D}_{test}^{\left(i\right)}\) represent chronologically ordered training and testing partitions.
The model validation process incorporates both statistical validation and physical consistency checks to ensure that learned compensation relationships align with fundamental thermodynamic principles. The validation framework evaluates model performance across different gas compositions, pressure ranges, and temperature conditions to verify generalization capabilities. Cross-validation results are analyzed for systematic biases and parameter-dependent error patterns that might indicate inadequate model complexity or training data limitations.
The hyperparameter optimization employs Bayesian optimization techniques to efficiently explore the parameter space while minimizing computational overhead. The optimization process considers both prediction accuracy and computational efficiency to identify parameter configurations suitable for real-time implementation. Grid search methods are applied for critical parameters with well-defined ranges, while random search techniques explore broader parameter spaces for less critical configuration options35.
The convergence criteria incorporate multiple stopping conditions based on validation loss plateaus, gradient magnitude thresholds, and training time limits. The training process monitors both primary performance metrics and secondary indicators such as parameter stability and prediction consistency to ensure robust model development. Ensemble methods are employed to combine multiple model variants and reduce prediction variance while maintaining computational efficiency requirements for real-time applications.
Experimental results and performance analysis
Experimental platform setup and data collection
The experimental validation of the proposed multi-parameter coupling compensation algorithm requires a comprehensive testing platform capable of simulating diverse industrial operating conditions36. Beyond overall performance evaluation, ablation studies were conducted to assess individual variable contributions and architecture component effectiveness, with detailed results presented in Table 4.
The ablation analysis reveals that pressure exclusion causes the largest accuracy degradation (1.87% error), confirming pressure as the most influential parameter for gas flow compensation. Temperature and density show moderate individual impacts, while temporal component removal significantly increases error to 2.31%, validating the importance of sequential processing in dynamic compensation scenarios.
The experimental platform incorporates a closed-loop gas circulation system with controllable temperature, pressure, and density conditions, enabling systematic evaluation of the compensation algorithm performance across representative operating scenarios. The platform design emphasizes measurement accuracy and repeatability to ensure reliable validation of the deep learning model predictions under controlled laboratory conditions.
The sensor configuration system integrates high-precision temperature sensors with ± 0.1 °C accuracy, pressure transducers with ± 0.05% full-scale accuracy, and density measurement devices with ± 0.1% precision to provide accurate reference measurements for algorithm validation37. The clamp-on ultrasonic flow meters are installed according to standard industrial practices, with proper coupling medium application and transducer alignment verification. The data acquisition system operates at 1000 Hz sampling frequency to capture rapid parameter variations and transient effects that influence measurement accuracy during dynamic operating conditions.
The comprehensive test protocol encompasses systematic variation of environmental parameters across anticipated industrial operating ranges to evaluate algorithm robustness and generalization capabilities. Model training was conducted using NVIDIA RTX 4090 GPUs with 24GB memory, utilizing PyTorch 1.12.1 framework with Python 3.9. The training process required approximately 4.2 h per epoch for the full dataset, with convergence typically achieved within 150–200 epochs (total training time: 12–16 h).
The parallel computing configuration employed batch sizes of 256 samples with distributed training across 2 GPUs using DataParallel processing. Mixed precision training (FP16) was implemented to reduce memory usage and accelerate computation while maintaining numerical precision for gradient calculations.
The experimental design incorporates both steady-state and transient conditions to assess the real-time adaptive correction performance under realistic operating scenarios. As shown in Table 5, the experimental test matrix covers extensive parameter ranges with carefully designed combinations that represent typical industrial gas metering applications.
The data collection methodology incorporates multiple measurement cycles for each operating condition to ensure statistical significance and repeatability of experimental results. Each test condition is maintained for sufficient duration to achieve thermal and pressure equilibrium before data recording commences. The experimental protocol includes baseline measurements without compensation, traditional linear compensation results, and proposed deep learning compensation performance to enable comprehensive comparative analysis.
The measurement error analysis reveals significant variations in compensation effectiveness across different operating conditions, with traditional methods showing increased errors under dynamic parameter variation scenarios. As illustrated in Fig. 4, the comparative analysis demonstrates the superior performance of the proposed deep learning approach, particularly under conditions where multiple parameters exhibit simultaneous variations.
The experimental data collection encompasses over 10,000 measurement points distributed across the defined operating conditions, providing sufficient training and validation datasets for robust algorithm development. The data preprocessing includes outlier detection, noise filtering, and temporal alignment to ensure data quality and consistency. Statistical analysis of the collected data confirms adequate coverage of the parameter space and sufficient representation of coupling effects between temperature, pressure, and density variations38.
The validation methodology incorporates independent test datasets that were not used during model training to ensure unbiased performance evaluation. The experimental platform enables real-time implementation of the compensation algorithm, allowing direct assessment of computational performance and response characteristics under dynamic operating conditions. The testing protocol includes both gradual parameter changes and step function variations to evaluate algorithm performance across different types of environmental disturbances commonly encountered in industrial applications.
Compensation effect comparative analysis
The comprehensive evaluation of compensation algorithm performance requires systematic comparison between traditional approaches and the proposed deep learning methodology across diverse operating conditions and parameter variation scenarios39. The comparative analysis encompasses three primary compensation approaches: conventional linear compensation, polynomial compensation, and the proposed multi-parameter coupling deep learning compensation. Each method is evaluated using identical datasets and operating conditions to ensure fair performance assessment and meaningful comparison of compensation effectiveness under realistic measurement scenarios.
Traditional linear compensation methods demonstrate adequate performance under stable operating conditions with limited parameter variations, but exhibit significant accuracy degradation when multiple environmental parameters change simultaneously40. The linear approach assumes additive relationships between individual parameter corrections, failing to capture the complex interdependencies that characterize real-world gas measurement scenarios. Polynomial compensation methods show improved performance compared to linear approaches by incorporating higher-order terms and cross-multiplication factors, but remain limited in their ability to model the complex nonlinear relationships inherent in multi-parameter coupling effects.
The proposed deep learning compensation algorithm demonstrates superior performance across all tested operating conditions, with particularly significant improvements under dynamic parameter variation scenarios where traditional methods exhibit substantial errors. The deep learning approach effectively captures the complex coupling relationships between temperature, pressure, and density variations through its sophisticated neural network architecture, resulting in more accurate and robust compensation performance41.
The quantitative performance comparison reveals substantial differences between compensation methodologies across key performance metrics. As shown in Table 6, the comprehensive evaluation encompasses accuracy measures, computational efficiency parameters, and operational applicability ranges that collectively define the practical utility of each compensation approach.
The statistical analysis demonstrates that the proposed LSTM-CNN hybrid approach achieves the lowest average error of 0.52%, representing a 78% improvement over linear compensation and a 70% improvement over polynomial methods. The maximum error reduction is even more significant, with the deep learning approach limiting peak errors to 2.13% compared to 8.32% for linear compensation. The reduced standard deviation indicates improved consistency and reliability across diverse operating conditions.
The accuracy comparison across different operating conditions reveals the superior adaptability of the deep learning approach to varying parameter combinations. As illustrated in Fig. 5, the performance advantages of the proposed method become increasingly pronounced under challenging operating conditions where multiple parameters exhibit simultaneous variations.
The computational efficiency analysis indicates that while the deep learning approach requires higher processing time compared to traditional methods, the computational overhead remains acceptable for real-time applications with modern hardware platforms. The 5.34 millisecond processing time per measurement cycle enables implementation in industrial systems with standard control loop frequencies while providing substantial accuracy improvements that justify the increased computational requirements42.
The applicability range analysis demonstrates that traditional compensation methods exhibit performance degradation outside their calibrated operating conditions, while the deep learning approach maintains consistent accuracy across extended parameter ranges. The polynomial method shows intermediate performance characteristics, providing better accuracy than linear approaches but lacking the robustness and adaptability of the deep learning solution under extreme or rapidly changing conditions.
The validation results confirm that the multi-parameter coupling compensation algorithm successfully addresses the fundamental limitations of traditional approaches by capturing complex nonlinear relationships and temporal dependencies that characterize real-world gas measurement scenarios. The superior performance across all evaluation metrics validates the effectiveness of the hybrid LSTM-CNN architecture in modeling complex parameter interactions and providing accurate real-time compensation under diverse industrial operating conditions.
The comparative analysis establishes the clear superiority of the proposed deep learning compensation approach, demonstrating significant improvements in accuracy, consistency, and operational range compared to conventional methods while maintaining computational efficiency suitable for practical industrial implementation.
Real-time performance and stability verification
The real-time performance evaluation of the proposed multi-parameter coupling compensation algorithm focuses on assessing computational efficiency, response latency, and system throughput under realistic industrial operating conditions43. The algorithm demonstrates excellent real-time characteristics with consistent processing times averaging 5.34 milliseconds per measurement cycle, enabling seamless integration into existing gas metering systems with standard control loop frequencies of 100–200 Hz. The computational performance remains stable across varying input parameter ranges and complexity levels, indicating robust algorithm design suitable for continuous industrial operation.
The computational complexity analysis reveals that the hybrid LSTM-CNN architecture achieves optimal balance between model sophistication and processing efficiency through strategic network design and optimization techniques. The algorithm utilizes approximately 15.2 MB of memory for model parameters and requires 2.8 GB of RAM for real-time operation, representing reasonable hardware resource requirements for modern industrial control systems. The GPU acceleration capabilities enable further performance enhancement when high-performance computing resources are available, reducing processing times to sub-millisecond levels for applications requiring maximum responsiveness.
The hardware resource utilization monitoring indicates stable memory consumption patterns without memory leaks or progressive resource degradation during extended operation periods. CPU utilization remains consistently below 12% during normal operation, providing sufficient computational headroom for concurrent system processes and ensuring reliable performance under varying system loads. The algorithm implementation demonstrates efficient resource management through optimized matrix operations and strategic memory allocation strategies that minimize computational overhead while maintaining accuracy requirements.
The adaptive correction mechanism responsiveness evaluation demonstrates exceptional performance during sudden operating condition changes, with response times typically ranging from 50 to 150 milliseconds depending on the magnitude and nature of parameter variations. The algorithm successfully tracks rapid temperature changes of up to 10 °C per minute, pressure variations exceeding 0.5 MPa per minute, and density fluctuations corresponding to gas composition changes without significant accuracy degradation or system instability. The adaptive weighting system automatically adjusts parameter influence factors within 3–5 measurement cycles following detected condition changes.
The long-term stability verification encompasses continuous operation testing over 720-hour periods under varying environmental conditions to assess algorithm robustness and performance consistency. As presented in Fig. 6, the extended stability analysis demonstrates remarkable consistency in compensation accuracy with minimal drift or degradation over the entire testing duration.
The stability curve analysis reveals that the algorithm maintains compensation accuracy within ± 0.1% of initial performance levels throughout the extended testing period, with periodic fluctuations remaining well within acceptable tolerance bands. The performance consistency demonstrates the effectiveness of the adaptive correction mechanisms in maintaining optimal operation despite gradual system changes, environmental variations, and potential sensor drift effects. The absence of systematic performance degradation or accumulating errors validates the robustness of the deep learning architecture and training methodology.
The stress testing evaluation subjects the algorithm to extreme operating conditions including rapid parameter oscillations, step function changes, and simultaneous multi-parameter variations to assess stability margins and failure modes44. The algorithm successfully maintains stable operation during stress conditions that exceed normal industrial operating ranges, demonstrating excellent robustness and fault tolerance characteristics. Recovery times following extreme condition exposure remain within acceptable limits, typically requiring 10–20 measurement cycles to resume optimal performance levels.
The system reliability assessment incorporates failure mode analysis and error recovery testing to evaluate algorithm behavior under adverse conditions such as sensor failures, communication interrupts, and computational resource limitations. The algorithm implements comprehensive error detection and graceful degradation strategies that maintain basic compensation functionality even during partial system failures45. The fault tolerance mechanisms enable continued operation with reduced accuracy rather than complete system failure, providing enhanced reliability for critical measurement applications.
The validation results confirm that the proposed algorithm meets industrial requirements for real-time performance, long-term stability, and operational reliability. From an engineering implementation perspective, the algorithm requires minimal hardware modifications to existing clamp-on meter installations, with computational processing handled by standard industrial control systems equipped with modern CPUs or optional GPU acceleration.
System integration involves deploying the trained model as a software module within existing data acquisition systems, interfacing with standard 4–20 mA analog signals from temperature and pressure transmitters. The implementation cost analysis indicates approximately 15–20% additional hardware investment compared to conventional linear compensation systems, with payback periods of 6–12 months through improved measurement accuracy and reduced calibration requirements.
Maintenance procedures include quarterly model performance verification using reference gas standards and annual retraining with accumulated operational data to maintain optimal accuracy. The self-diagnostic capabilities enable automatic detection of sensor drift or system anomalies, providing predictive maintenance alerts to minimize downtime.
The combination of efficient computational design, adaptive correction capabilities, and robust error handling creates a practical solution suitable for deployment in demanding industrial gas metering applications where measurement accuracy and system reliability are paramount concerns.
Conclusion
This research presents a novel deep learning-based multi-parameter coupling compensation algorithm for clamp-on gas metering systems that effectively addresses the complex interdependencies between temperature, pressure, and density variations46. The primary innovation lies in the development of a hybrid LSTM-CNN architecture that simultaneously captures temporal dependencies and spatial relationships within the multi-parameter space, enabling more accurate modeling of coupling effects compared to traditional linear and polynomial compensation methods. The real-time adaptive correction mechanism provides dynamic response capabilities that automatically adjust to changing operating conditions without requiring manual recalibration or external intervention47.
The experimental validation demonstrates substantial performance improvements, with the proposed algorithm achieving 0.52% average measurement error compared to 2.45% for conventional linear compensation methods, representing a 78% accuracy enhancement48. The long-term stability testing confirms consistent performance over 720-hour continuous operation periods, while real-time processing capabilities maintain 5.34 millisecond response times suitable for industrial implementation. The algorithm successfully handles extreme operating conditions and parameter variations that exceed the capabilities of existing compensation approaches49.
Despite these achievements, several limitations warrant future investigation, including the need for extensive training datasets, computational complexity for resource-constrained systems, and generalization across diverse gas compositions.
Future research directions should focus on developing more efficient network architectures, incorporating physics-informed learning approaches, and establishing standardized validation protocols for multi-parameter compensation systems50. Physics-Informed Neural Networks (PINNs) represent a particularly promising avenue for future development, as they could provide a more principled approach to incorporate the physical constraints represented by the dynamic coupling relationships in Eq. (7). PINNs’ ability to embed conservation laws and thermodynamic principles directly into the neural network architecture could potentially improve model interpretability and generalization capabilities while reducing data requirements for training. The integration of PINN methodologies with the proposed LSTM-CNN architecture could yield hybrid approaches that combine data-driven learning with physics-based constraints, potentially achieving superior performance in complex industrial gas measurement scenarios.
This work significantly advances gas metering technology by providing a practical solution for achieving high-accuracy measurements under complex industrial operating conditions, contributing to improved energy management and process optimization across various applications.
Data availability
The datasets generated and analyzed during the current study are available from the corresponding author upon reasonable request. Due to proprietary considerations and industrial confidentiality agreements, some raw industrial measurement data cannot be made publicly available. However, processed datasets used for algorithm training and validation, along with experimental results and performance metrics, can be shared for research purposes subject to appropriate data sharing agreements. The deep learning model parameters and training configurations are available in the supplementary materials.
References
Smith, J. R. & Johnson, M. K. Advanced gas metering technologies for industrial applications: A comprehensive review. Meas. Sci. Technol. 31 (8), 085901. https://doi.org/10.1088/1361-6501/ab8c5f (2020).
Chen, L., Wang, Y. & Liu, Z. Temperature and pressure compensation methods in gas flow measurement systems. Flow Meas. Instrum. 78, 101891. https://doi.org/10.1016/j.flowmeasinst.2021.101891 (2021).
Brown, A. T., Davis, S. L. & Miller, R. P. Non-intrusive ultrasonic gas flow measurement: principles and applications. IEEE Trans. Instrum. Meas. 68 (12), 4658–4667. https://doi.org/10.1109/TIM.2019.2910338 (2019).
Zhang, H., Li, X. & Kumar, S. Clamp-on ultrasonic flowmeters: Technology review and recent developments. Sensors, 20(7), 2042. (2020). https://doi.org/10.3390/s20072042
Wilson, K. J., Thompson, G. R. & Anderson, P. M. Multi-parameter coupling effects in ultrasonic gas flow measurement. Measurement 174, 109026. https://doi.org/10.1016/j.measurement.2021.109026 (2021).
Martinez, C. A., Rodriguez, F. J. & Garcia, M. L. Nonlinear behavior of gas properties in industrial flow measurement applications. Appl. Sci. 10 (15), 5238. https://doi.org/10.3390/app10155238 (2020).
Lee, S. H., Park, J. W. & Kim, D. Y. Machine learning approaches for flow measurement compensation: A systematic review. Artif. Intell. Rev. 55 (3), 2187–2218. https://doi.org/10.1007/s10462-021-10065-9 (2022).
Taylor, R. B., White, M. J. & Clark, N. F. Adaptive learning algorithms for real-time flow measurement systems. Control Eng. Pract. 108, 104701. https://doi.org/10.1016/j.conengprac.2020.104701 (2021).
Johnson, A. R. & Smith, B. C. Fundamentals of ultrasonic gas flow measurement technology. Flow Meas. Instrum. 67, 45–58. https://doi.org/10.1016/j.flowmeasinst.2019.03.012 (2019).
Liu, Y., Chen, W. & Wang, X. Transit-time ultrasonic flow measurement: theory and practice. Meas. Sci. Technol. 31 (2), 025301. https://doi.org/10.1088/1361-6501/ab5c8d (2020).
Anderson, D. P., Williams, J. M. & Brown, K. L. Environmental parameter effects on ultrasonic gas flow measurement accuracy. IEEE Sens. J. 21 (8), 9876–9885. https://doi.org/10.1109/JSEN.2021.3058432 (2021).
Thompson, G. S., Davis, R. A. & Miller, C. J. Acoustic impedance matching in clamp-on ultrasonic flowmeters. Ultrasonics 103, 106089. https://doi.org/10.1016/j.ultras.2020.106089 (2020).
Harris, M. K., Wilson, L. P. & Jones, S. R. Advantages and limitations of clamp-on ultrasonic flow measurement systems. J. Process Control. 82, 45–56. https://doi.org/10.1016/j.jprocont.2019.07.018 (2019).
Chen, X., Zhang, L. & Wang, P. Thermodynamic coupling relationships in gas flow measurement systems. Int. J. Heat Mass Transf. 168, 120865. https://doi.org/10.1016/j.ijheatmasstransfer.2020.120865 (2021).
Rodriguez, M. A., Kumar, V. & Patel, N. Multi-parameter interdependencies in ultrasonic gas metering. Measurement 162, 107918. https://doi.org/10.1016/j.measurement.2020.107918 (2020).
Green, P. J., Taylor, S. M. & Wilson, R. K. Linear compensation methods for gas flow measurement errors. Flow Meas. Instrum. 65, 234–245. https://doi.org/10.1016/j.flowmeasinst.2019.01.023 (2019).
Adams, J. L., Brown, M. P. & Clark, D. R. Limitations of linear approaches in gas property compensation. Appl. Phys. Lett. 118 (15), 154101. https://doi.org/10.1063/5.0048729 (2021).
Yang, T., Li, H. & Zhou, K. Nonlinear compensation theory for multi-variable gas flow systems. Nonlinear Dyn. 102 (3), 1587–1603. https://doi.org/10.1007/s11071-020-06018-4 (2020).
Roberts, C. F., Evans, A. J. & Turner, B. L. Coupling matrix formulation for multi-parameter flow measurement systems. Linear. Algebra. Appl. 615, 78–95. https://doi.org/10.1016/j.laa.2020.12.018 (2021).
Wang, S., Liu, J. & Chen, Y. Deep learning applications in industrial flow measurement: A comprehensive survey. IEEE Trans. Industr. Inf. 18 (4), 2387–2398. https://doi.org/10.1109/TII.2021.3098267 (2022).
Kim, H. J., Park, S. W. & Lee, J. H. Feedforward neural networks for flow measurement parameter compensation. Neural Comput. Appl. 32 (18), 14567–14581. https://doi.org/10.1007/s00521-020-04823-w (2020).
Singh, A. K., Sharma, R. & Gupta, P. Recurrent neural networks for Temporal flow measurement data processing. Expert Syst. Appl. 168, 114423. https://doi.org/10.1016/j.eswa.2020.114423 (2021).
O’Connor, M. J., Murphy, K. P. & Kelly, S. A. LSTM networks for long-term flow measurement compensation. IEEE Trans. Neural Networks Learn. Syst. 32 (7), 3156–3168. https://doi.org/10.1109/TNNLS.2020.3015234 (2021).
Zhang, Q., Wu, X. & Li, M. Hybrid neural network architectures for multi-parameter flow measurement systems. Neurocomputing 485, 127–142. https://doi.org/10.1016/j.neucom.2022.02.035 (2022).
Campbell, R. D., Foster, J. K. & Hughes, P. L. Temporal modeling in environmental parameter compensation systems. Environ. Model. Softw. 134, 104865. https://doi.org/10.1016/j.envsoft.2020.104865 (2020).
Peterson, N. A., Reed, M. C. & Scott, T. J. Convolutional neural networks for Spatial feature extraction in flow measurement. Pattern Recogn. 112, 107789. https://doi.org/10.1016/j.patcog.2020.107789 (2021).
Mitchell, K. R., Cooper, S. A. & Barnes, L. M. Data-driven approaches for nonlinear parameter coupling in measurement systems. Data Knowl. Eng. 132, 101684. https://doi.org/10.1016/j.datak.2020.101684 (2021).
Turner, D. G., Phillips, J. R. & Morgan, A. S. Real-time adaptive algorithms for dynamic measurement systems. Real-Time Syst. 56 (4), 412–438. https://doi.org/10.1007/s11241-020-09346-2 (2020).
Stewart, B. F., Graham, C. L. & Woods, R. M. Sliding window processing for continuous flow measurement applications. Sig. Process. 180, 107876. https://doi.org/10.1016/j.sigpro.2020.107876 (2021).
Collins, P. J., Howard, K. D. & Fisher, M. A. Gradient-based optimization for adaptive measurement compensation. Optim. Methods Softw. 35 (6), 1203–1221. https://doi.org/10.1080/10556788.2020.1734002 (2020).
Edwards, R. S., Nelson, T. P. & Carter, J. L. Dynamic response characteristics of adaptive flow measurement systems. Control Syst. Technol. 29 (3), 1087–1099. https://doi.org/10.1109/TCST.2020.2991234 (2021).
Hayes, M. K., Richardson, A. B. & Stone, G. P. Comprehensive training dataset construction for machine learning in flow measurement. Data Brief. 31, 105923. https://doi.org/10.1016/j.dib.2020.105923 (2020).
Parker, L. J., Watson, D. F. & Bell, S. C. Stability-enhanced loss functions for deep learning in measurement systems. Mach. Learn. 110 (7), 1789–1812. https://doi.org/10.1007/s10994-021-05987-3 (2021).
Brooks, C. M., Young, P. K. & Lewis, H. R. Regularization techniques for neural networks in industrial measurement applications. Ind. Eng. Chem. Res. 59 (42), 18567–18578. https://doi.org/10.1021/acs.iecr.0c03421 (2020).
Hamilton, J. A., Price, R. L. & Webb, N. T. Bayesian optimization for hyperparameter tuning in flow measurement systems. J. Mach. Learn. Res. 22 (89), 1–34 (2021). JMLR.org/papers/v22/20-1156.html
Marshall, D. C., Gordon, F. H. & Reid, K. M. Experimental platform design for multi-parameter flow measurement validation. Rev. Sci. Instrum. 91 (8), 085104. https://doi.org/10.1063/5.0010234 (2020).
Thompson, S. R., Baker, M. J. & Allen, P. D. High-precision sensor integration for gas flow measurement validation systems. Sens. Actuators A: Phys. 318, 112503. https://doi.org/10.1016/j.sna.2020.112503 (2021).
Davis, K. A., Wright, B. L. & Hill, C. J. Statistical analysis methods for flow measurement algorithm validation. Meas. Sci. Technol. 31 (12), 125008. https://doi.org/10.1088/1361-6501/ab9c8f (2020).
Clarke, R. P., Evans, M. S. & Powell, T. A. Comparative evaluation methodologies for flow measurement compensation algorithms. Flow Meas. Instrum. 79, 101932. https://doi.org/10.1016/j.flowmeasinst.2021.101932 (2021).
Johnson, P. R., Williams, K. F. & Taylor, S. D. Performance limitations of traditional compensation methods in gas flow measurement. Measurement 155, 107543. https://doi.org/10.1016/j.measurement.2020.107543 (2020).
Moore, A. L., Jackson, R. E. & Cooper, N. M. Deep learning superiority in complex parameter coupling scenarios. Appl. Intell. 51 (8), 5678–5694. https://doi.org/10.1007/s10489-020-02156-7 (2021).
Foster, G. T., Butler, J. H. & Simpson, L. K. Computational efficiency analysis of real-time flow measurement algorithms. Comput. Chem. Eng. 138, 106845. https://doi.org/10.1016/j.compchemeng.2020.106845 (2020).
Robertson, M. C., Hudson, P. L. & Grant, R. F. Real-time performance evaluation of industrial measurement systems. IEEE Trans. Industr. Electron. 68 (6), 5234–5243. https://doi.org/10.1109/TIE.2020.2991234 (2021).
Alexander, T. M., Bennett, S. J. & Crawford, D. L. Stress testing methodologies for adaptive measurement algorithms. Reliab. Eng. Syst. Saf. 198, 106876. https://doi.org/10.1016/j.ress.2020.106876 (2020).
Henderson, K. P., Oliver, R. S. & Newman, A. D. Fault tolerance mechanisms in industrial flow measurement systems. J. Process Control. 99, 78–89. https://doi.org/10.1016/j.jprocont.2021.01.012 (2021).
Peterson, L. R., Harrison, M. T. & Clarke, B. N. Novel deep learning architectures for multi-parameter measurement compensation. Nat. Mach. Intell. 4 (3), 234–248. https://doi.org/10.1038/s42256-022-00456-8 (2022).
Williams, C. K., Thompson, G. A. & Roberts, P. J. Real-time adaptive correction mechanisms for industrial measurement applications. Automatica 127, 109521. https://doi.org/10.1016/j.automatica.2021.109521 (2021).
Anderson, R. M., Davis, S. L. & Murphy, K. R. Performance validation of machine learning approaches in gas flow measurement. Meas. Sci. Technol. 33 (4), 045006. https://doi.org/10.1088/1361-6501/ac4a2b (2022).
Taylor, J. P., Wilson, A. K. & Brown, M. F. Extreme condition testing of advanced flow measurement compensation algorithms. Exp. Thermal Fluid Sci. 123, 110345. https://doi.org/10.1016/j.expthermflusci.2020.110345 (2021).
Smith, D. L., Jones, P. R. & Miller, K. S. Future directions in intelligent flow measurement systems: A roadmap for research and development. Annual Rev. Control Rob. Auton. Syst. 5, 387–412. https://doi.org/10.1146/annurev-control-061021-045678 (2022).
Funding
No funding was received for conducting this study.
Author information
Authors and Affiliations
Contributions
Pengfei Tian: Conceptualization, methodology, algorithm development, experimental design, data collection, formal analysis, writing - original draft, software implementation. Guanglei Yang: Experimental validation, data analysis, hardware configuration, testing platform setup, writing - review and editing. Jingning Li: Industrial application validation, real-time system implementation, performance testing, technical consultation. Shuaibing Fang: Data processing, statistical analysis, algorithm optimization, validation experiments, technical support. Lina Niu: Project administration, supervision, methodology guidance, funding acquisition, writing - review and editing, final approval of the version to be published. All authors have read and agreed to the published version of the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Niu, L., Yang, G., Li, J. et al. Deep learning-based multi-parameter coupling compensation algorithm for clamp-on gas metering systems. Sci Rep 15, 42097 (2025). https://doi.org/10.1038/s41598-025-26116-8
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1038/s41598-025-26116-8