Introduction

As the critical component of Vehicle-Road-Cloud Integration Systems (VRCIS)1,2, roadside perception offers a broader view field compared to vehicle sensors. It can compensates the limitations of autonomous vehicles to promote the development of full driverlessness3,4, and provide foundations for intelligent city transportation. Camera and millimeter-wave(MMW) radar are the main sensors in the roadside perception system. MMW radar has a wide-range sensing capability and can operate in various weather and lighting conditions. However, it also suffers from low angular resolution, poor target classification ability, and high false-detection rate5. Camera data effectively compensates for these shortcomings. The roadside perception system mostly adopts the multi-sensors distributed installation, leading to disadvantages like hardware complexity and insufficient real-time data processing. Therefore, the integrated devices which combine MMW radars and cameras have attract a great attention.

For integrated roadside radar-camera devices, the quality of calibration directly determines the precision of subsequent data fusion. The calibration requires associating the radar-camera pairs belonging to the same targets. However, there are significant modal differences between radar and camera data. Radar provides relative coordinates, azimuth and velocity information6, while cameras provide descriptive features like object type, color, or dimensions. This fundamental heterogeneity creates substantial difficulties for reliable radar-camera association.

The existing radar-camera calibration algorithms can be categorized into target-based and target-less methods. Target-based methods require special calibration targets, such as chess board and radar corner reflectors. Oh et al.7 manually marked pixel coordinates of corner reflectors and recorded the corresponding radar coordinates, and then calculated transformation matrix with the camera-radar pairs. Du et al.8 manually annotated four lane marking corner points in images, and estimated the coordinates of these points through standard highway lane dimensions for calibration. However, manual measurement increases labor costs and make it hard to apply in practical sensor fusion, especially for continuous decalibrations that frequently occur in the real-time scenarios applications.

For target-less calibration methods, mutual information calibration are purposed by maximizing the mutual information, eliminating the need for specific calibration targets and manual steps. Cheng et al.9 used deep learning to extract a common feature from raw radar data (i.e., range doppler-angle data) and camera images. Then, the common features of radar and camera were utilized to achieve target-less calibration. The feature extraction from radar was inaccurate, it only selected two targets with obvious feature like people and vehicle. However, the online complex scenarios contain multi-targets, the difficulty of feature extraction will greatly decrease the continuous calibration accuracy.

Another target-less calibration requires prior knowledge such as a initial extrinsic matrix. It needs to preset an initial external matrix and then maps camera and radar data to the same coordinate for correlation. Schöller et al.6 estimated the initial rotation matrix with the camera vanishing point and projected radar data onto the pixel plane, then constructed a two-stream Convolutional Neural Network (CNN) for automatic radar-camera calibration. It improves adaptability to different scenarios, but it requires manual acquisition of the initial matrix and high annotation costs. X. Li et al.10 purposed a edge feature calibration based on the Segment Anything Model (SAM), a mean rotation error of 0.069° on the KITTI dataset was achieved. However, these methods need to preset the initial extrinsic parameters. If the prior extrinsic matrix differs from the actual situation, resulting in a decrease in the calibration. In addition, when sensor is installed in different locations, the network needs to be retrained, manual annotation costs are high. Thus, the adaptability to different online scenarios should be improved.

More target-less methods are based on trajectories. Jin et al.11 proposed an automatic traffic volume-based calibration, it matched three dimensional(3D) trajectories based on the Euclidean distance in low traffic volume scenarios. However, 3D object detection in camera consumes significant computational resources on embedded devices, and the coarse trajectories association must be conducted in scenarios with few targets, the adaptability for online scenario should be enhanced. Deng et al.12 adopted a bidirectional selection association method to match radar and camera trajectories, and then reconstructed the road plane for extrinsic parameters calibration. Peršić et al.13,14 proposed a multi-sensor trajectories calibration method based on Gaussian processes. It utilized the characteristic that the speed magnitude is in-variance in different coordinate system. Different targets in multi-target scenarios can be separated by the velocity. However, it requires velocity changes in the calibration. If the target moves at a constant velocity, the accuracy of calibration will decrease. Trajectory-based calibration methods achieve some results, yet demanding excessive storage and computational resources, which makes it difficult in continuous online application, especial in the online traffic scenario.

To address the challenges arising from the roadside integrated radar-camera calibration in the real-time scenario, this paper proposes a continuous online calibration method based on azimuth angle and multi frame tracking. This method does not require the initial extrinsic parameter matrix or excessive computational resources, and can easily embedded into hardware to meets the online requirements in real-world scenarios. A multistage calibration approach is developed to obtain the transformation matrix. Firstly, azimuth angle and azimuth angle rate is used to establish radar-camera correspondences, and complete the coarse calibration. Subsequently, we project radar data from the Bird’s-Eye View(BEV) coordinate system onto the pixel coordinate system with the coarse transformation matrix, and use the Hungarian algorithm for multi-frame data association, identifying correspondences in a broader range for fine calibration. The key contributions of our work include:

  1. 1)

    The coarse calibration of integrated radar-camera don’t need initial extrinsic matrix. It only needs the the camera’s intrinsic parameters such as focal length and pixel size. It utilizes target azimuth angle and its change rate to establish radar-camera corresponding pairs. And then achieves coarse calibration.

  2. 2)

    Continuously calibration without longtime storage. This method can reduce storage and computational resources and can be directly embedded into the radar-camera system rather than running in a separate calibration program.

  3. 3)

    Valid criterion were established, which ensures the fine calibration can operate continuously and timely adjust when the device pose changes.

The structure of this paper is organized as follows. Section 2 introduces the study scenario and the calibration theory. Section 3 describes the proposed automatic calibration method. Section 4 analyzes and discusses the results of real-world experiments. Finally, Sect. 5 summarizes the conclusions and expands on future research directions.

Preliminary knowledge

This paper focuses on the real-time roadside scenario. The integrated MMW radar-camera device is installed on a traffic monitoring pole at the crossroads. The coordinate systems are shown in Fig. 1, including radar coordinate system (RCS), camera coordinate system (CCS), pixel coordinate system(PCS) and Bird’s-Eye View (BEV) coordinate system(BCS). In the BCS, the projection of the device on the road surface is the origin, the lane direction is the y-axis, the vertical to road plane is the z-axis, and the direction perpendicular to the lane is the x-axis. For the integrated radar-camera system, the detection directions of the radar and the camera are consistent in the horizon, the horizontal angles of RCS is the same as CCS.

The calibration is performed on the BCS. The camera and radar points are both projected onto the BCS. The camera target point is projected from PCS onto the BCS, the radar target point is projected from the RCS onto the BCS. And then the projected camera points and radar points on the BCS are aligned. In this paper, the radar and camera data on the BCS are aligned for its fusion performance and calibration accuracy15. The BEV projecting camera data can maintain geometric consistency on the BCS and enable reliable trajectory reconstruction, which can effectively compensate for the missing radar track.

Fig. 1
figure 1

Coordinate system of the integrated radar-camera device.

Full size image

The projection of radar points on the BCS can be represented as:

$$\left\{ \begin{gathered} {x_r}=\sqrt {{r^2} - h_{{dev}}^{2}} \times \sin (\theta +\beta ) \hfill \\ {y_r}=\sqrt {{r^2} - h_{{dev}}^{2}} \times \cos (\theta +\beta ) \hfill \\ {z_r}=0 \hfill \\ \end{gathered} \right.$$
(1)

Where \({x_r},{y_r},{z_r}\) is the coordinates of the radar target on the BCS, \(r,\theta\)is the coordinates of the radar target on the RCS, \({h_{dev}}\) is device installation height, \(\beta\) is the angle between the ground projection of the radar \({{\text{Y}}_r}\)-axis and the Y-axis, obtained by vehicles travelling direction along the lane markings on the BCS, which ensures that the tracked velocity represents the vehicle’s true velocity. We adopt the 3D millimeter-wave radar in this paper. There is no height information of the target, all monitored targets are on the road surface, so \({z_r}\)is 0.

The radar and camera data are aligned on the BCS, so the transformation between radar points on the BCS and camera point on the PCS can be derived as:

$${z_c}\left[ \begin{gathered} {u_c} \hfill \\ {v_c} \hfill \\ 1 \hfill \\ \end{gathered} \right]=\left[ {\begin{array}{*{20}{c}} {{f_u}}&0&{{c_u}}&0 \\ 0&{{f_v}}&{{c_v}}&0 \\ 0&0&1&0 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {\mathbf{R}}&{\mathbf{t}} \\ 0&{\mathbf{1}} \end{array}} \right]\left[ \begin{gathered} {x_{\text{r}}} \hfill \\ {y_{\text{r}}} \hfill \\ 0 \hfill \\ 1 \hfill \\ \end{gathered} \right]$$
(2)

Where \({f_u}\), \({f_v}\), \({c_u}\), \({c_v}\) are camera’s intrinsic parameters, which is usually expressed as K and can be obtained in the laboratory, R and t respectively represent the rotation and translation matrix, \({u_c},{v_c}\) are the pixel coordinates of the target bounding boxes detected by the camera on the PCS, \({x_r},{y_r}\) is the coordinates of the target detected by the radar on the BCS, \({Z_c}\) is the camera depth.

With more than 6 pairs of radar points \(\{ ({x_{r1}},{y_{r1}},0),{\text{ }}({x_{r2}},{y_{r2}},0),{\text{ }} \cdots {\text{ }}({x_{rn}},{y_{rn}},0)\}\)and their associated camera points \(\{ ({u_1},{v_1}),{\text{ }}({u_2},{v_2}),{\text{ }} \cdots {\text{ }}({u_n},{v_n})\}\), the pose transformation\(\{ {\mathbf{R}}\left| {\mathbf{t}} \right.\}\)can be solved as classic Perspective-n-Point (PnP) problem. Common solutions include DLT(Direct Linear Transform), P3P16, AP3P17, EPnP18, UPnP19, etc. The DLT is adopted for the extrinsic matrix calculation in this paper.

Proposed calibration and association algorithm

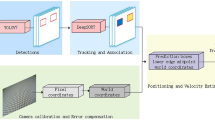
The radar-camera calibration is the process of solving PnP problem with radar-camera corresponding pairs. As the PnP problem has been maturely resolved, the primary challenge lies in automatically acquiring the corresponding point pairs. This paper purposes an automatically point pairs associating method. The overall architecture of purposed method is illustrated in Fig. 2, which mainly consists of three parts: vehicle detection, coarse calibration, fine calibration.

Fig. 2
figure 2

Overall architecture of the proposed calibration method.

Full size image

Coarse calibration

The coarse extrinsic transformation calculation

When only the camera intrinsic parameters (camera focal length, sensor pixel size, etc.) are known, camera data cannot be projected onto the BCS, so it is hard to use coordinate correlation to match radar-camera corresponding pairs. The paper utilizes the directional consistency between radar and camera in integrated radar camera devices. The target azimuth angles on the RCS and CCS is used to identify corresponding pairs, as shown in Fig. 3.

Fig. 3
figure 3

The alignment of target azimuth angles in the RCS and CCS.

Full size image

As shown in Fig. 3, the camera’s optical axis and the radar’s boresight axis lie on the same plane, this alignment is guaranteed in the factory assembly of the integrated device. Even accounting for installation errors, the difference in their horizontal yaw angles can be constrained within a limited range, denoted as \({\theta _\varepsilon }\). The target azimuth angles detected by the camera \({\theta _c}\) and radar \({\theta _r}\) should satisfy \(|{\theta _c} - {\theta _r}| \leqslant {\theta _\varepsilon }\). Where \({\theta _r}\) can be directly obtained from the radar’s raw detection data\({[r,v,\theta ]^T}\), \({\theta _r}=\theta\). \({\theta _c}\) can be obtained through Eq. (3):

$${\theta _c}=\arctan (\frac{{({u_c} - {c_u}){d_{pixel}}}}{{\sqrt {{f^2}+{{({v_c} - {c_v})}^2}d_{{pixel}}^{2}} }})$$
(3)

Where \({c_u}\), \({c_v}\) are camera’s intrinsic parameters, \({[{u_c},{v_c}]^T}\) is the bottom center point of bounding box, \(f\) is camera’s focal length, \({d_{pixel}}\) is pixel size. The geometrical configuration is shown in Fig. 4.

Fig. 4
figure 4

Azimuth angle computation of targets by the camera.

Full size image

Targets at varying distances may share identical azimuth angles in the dense traffic scenarios, as shown in Fig. 5. It will complicate the association and decrease the calibration accuracy. So in this paper we introduce the azimuth angular rate as an additional associate criterion.

Fig. 5
figure 5

Targets at varying distances share identical azimuth angles.

Full size image

The azimuth angle changing rate of the radar\(\omega _{t}^{k}\) and the camera \(\omega _{c}^{k}\) are calculated with the follow equation:

$$\left\{ \begin{gathered} \omega _{t}^{k}=q\omega _{t}^{{k - 1}}+({\text{1}} - q \frac{{\theta _{r}^{k} - \theta _{r}^{{k - 1}}}}{T} \hfill \\ \omega _{c}^{k}=q\omega _{c}^{{k - 1}}+({\text{1}} - q \frac{{\theta _{c}^{k} - \theta _{c}^{{k - 1}}}}{T} \hfill \\ \end{gathered} \right.$$
(4)

Where, the superscript k denotes time, T is the frame interval,\({\theta _c}\)denotes the camera target azimuth angles, \({\theta _r}\) denotes the radar target azimuth angles, and \(q\) is the weight used to smooth the angular rate of change.

In each frame of radar and camera data, the corresponding radar-camera pairs should satisfy:

$$\left\{ \begin{gathered} \left| {\theta _{r}^{k} - \theta _{c}^{k}} \right| \leqslant {\theta _{thres}} \hfill \\ \left| {\omega _{r}^{k} - \omega _{c}^{k}} \right| \leqslant {\omega _{thres}} \hfill \\ \end{gathered} \right.$$
(5)

Where, \({\theta _{thres}}\) and \({\omega _{thres}}\) are the thresholds. When the difference of azimuth angle and azimuth angle rate between the radar point and camera point are both less than the threshold, they are marked as the corresponding point pair. These thresholds account for the inherent misalignment between the radar and camera due to factory assembly deviations (e.g., horizontal angular offset \({\theta _\varepsilon }\)) and the limited angular resolution of the radar.

In the coarse calibration, at least six qualified radar-camera pairs are required for the calculation of the transformation matrix \(\{ {\mathbf{R}}_{c}^{\prime }\left| {\mathbf{t}} \right._{c}^{\prime }\}\)20. In this paper, we enforce an additional constraint that radar points must be separated more than 10 m apart.

Coarse calibration evaluation criteria

To enable automatic transition from coarse calibration to fine calibration, the coarse calibration evaluation criteria is proposed. Firstly, extract the k-th frame of data after, project the radar target onto the PCS with the obtained coarse transition matrix \(\{ {{\mathbf{R^{\prime}}}_c}\left| {{{{\mathbf{t^{\prime}}}}_c}} \right.\}\), count the number of valid projected radar target points \(m\) and camera target points \(n\) , if it satisfies: \(m \approx n{\text{ }}(m,{\text{ }}n>5)\), the Hungarian algorithm is applied for matching.

Secondly, associate point pairs on the PCS with the Hungarian tracking algorithm21, the cost function is designed as:

$${\text{cost\_funtion}}=\sqrt {{{(\frac{{\left| {{u_c} - {u_r}} \right|}}{w})}^2}+{{(\frac{{\left| {{v_c} - {v_r}} \right|}}{h})}^2}}$$
(6)

Where \(w\) and \(h\) represent the width and height of the camera detection bounding box respectively.\(({u_r},{v_r})\)is projected radar points on the PCS, \(({u_c},{v_c})\)is camera points on the PCS.

As the number of successful associating pairs N satisfies:\(N/n>90\%\), the system will proceed to fine calibration, and update the best coarse transformation matrix\(\{ {\mathbf{R}}_{c}^{*}\left| {\mathbf{t}} \right._{c}^{*}\}\).

The flowchart for coarse calibration is shown in Fig. 6.

Fig. 6
figure 6

The flowchart for coarse calibration.

Full size image

Fine calibration

The fine extrinsic transformation calculation

In the real multi-target scenarios, coarse calibration can only identify a limited number of corresponding radar-camera pairs. These point pairs mostly concentrated at large angles or short distances, the calculated transformation matrix can only guarantee local optimal. In order to maintain high accuracy across the entire detection range, fine calibration is conducted for achieving global optimal.

Point pairs are associated on the PCS with the Hungarian tracking algorithm. When the radar-camera trajectories maintain continuous association over 25 cycles, the point pairs are considered successfully matched, and the 1 st, 12th, and 25th frames of point data are recorded as the corresponding pairs, as shown in Fig. 7. This calibration process only record 3 frames data, which is different from the traditional longtime trajectories storage method. This method can operate in a dedicated thread with negligible processing, easily integrated into the main radar-camera fusion thread to enhance its online performance.

Fig. 7
figure 7

Radar-camera pairs matching in fine calibration.

Full size image

As more than six valid corresponding pairs (with minimum 10-meter distance in radar coordinates) are identified, calculate the fine calibration matrix \(\left\{ {{\mathbf{R}}_{{fn}}^{\prime }\left| {{\mathbf{t}}_{{fn}}^{\prime }} \right.} \right\}\). To obtain accurate calibration results, the fine calibration process will be conducted continuously.

Fine calibration evaluation criteria

To ensure progressive improvement in continuous fine calibration, the fine calibration evaluation criterion is proposed. As the new fine calibration matrix \(\left\{ {{\mathbf{R}}_{{fn}}^{\prime }\left| {{\mathbf{t}}_{{fn}}^{\prime }} \right.} \right\}\) is calculated, it must be validate for twice before updating it as the best calibration matrix \(\{ {\mathbf{R}}_{f}^{*}\left| {{\mathbf{t}}_{f}^{*}} \right.\}\). The evaluation steps including:

Step 1, Generate new validation dataset V with the previous best calibration matrix \(\{ {\mathbf{R}}_{f}^{*}\left| {{\mathbf{t}}_{f}^{*}} \right.\}\).

Accumulate the new identified radar-camera point pairs \(\{ {p_{rn}},{p_{cn}}\}\)into the calibration dataset V, where \(n\) denotes the number of radar-camera pairs, \({p_{rn}}={[{x_{rn}},{y_{rn}},0]^T}\)denotes the radar point coordinates in the BCS, and \({p_{cn}}={[{u_{cn}},{v_{cn}}]^T}\) denotes the camera point coordinates in the PCS.

Step 2, Verified the new matrix\(\left\{ {{\mathbf{R}}_{{fn}}^{\prime }\left| {{\mathbf{t}}_{{fn}}^{\prime }} \right.} \right\}\) with verification dataset V ..

Project the camera point onto the BCS with the new matrix\(\left\{ {{\mathbf{R}}_{{fn}}^{\prime }\left| {{\mathbf{t}}_{{fn}}^{\prime }} \right.} \right\}\)and previous best matrix\(\{ {\mathbf{R}}_{f}^{*}\left| {{\mathbf{t}}_{f}^{*}} \right.\}\), denoted as \({[{x_{cn}},{y_{cn}},0]^T}\) and \({[x_{{{\text{cn}}}}^{*},y_{{cn}}^{*},0]^T}\). The reprojection errors are computed as:

$$\varepsilon =\left( {\sum\limits_{{i=1}}^{n} {\sqrt {{{\left( {{x_{ri}} - {x_{ci}}} \right)}^2}+{{\left( {{y_{ri}} - {y_{ci}}} \right)}^2}} } } \right)/n{\text{, }}n \geqslant 20{\text{ }}$$
(7)
$${\varepsilon ^*}=\left( {\sum\limits_{{i=1}}^{n} {\sqrt {{{\left( {{x_{ri}} - x_{{ci}}^{*}} \right)}^2}+{{\left( {{y_{ri}} - y_{{ci}}^{*}} \right)}^2}} } } \right)/n{\text{ }},{\text{ }}n \geqslant 20$$
(8)

if \(\varepsilon <{\varepsilon ^*}\), clear the current verification dataset V for the second validation.

Step 3, Repeat steps 2 ~ 3. If all two rounds of validations both have the superior performance, update the best transition matrix\(\{ {\mathbf{R}}_{f}^{*}\left| {{\mathbf{t}}_{f}^{*}} \right.\}\).

The fine calibration process continuously updates the extrinsic matrix, progressively improving calibration accuracy. This enables online adaptation to maintain optimal performance when the device undergoes minor pose changes.

The flowchart for fine calibration is shown in Fig. 8.

Fig. 8
figure 8

The flowchart for fine calibration.

Full size image

Experiment results

Data collection

The integrated radar-camera device LR-T13 made by Shanghai Limradar Electronic Technology Co., Ltd is used to evaluate the calibration performance. The device is installed on the traffic pole at the crossroad, providing an overview of the opposite lanes, shown in Fig. 10. Table 1 shows the specifications of the sensors in the integrated device. The MMW radar in this paper is an 80 GHz frequency-modulated continuous wave (FMCW) 3D radar. The camera’s sensor is Sony IMX334, with a resolution of 3840 × 2160 and a sensor size of 1/1.8’’. The intrinsic camera parameters are obtained in the laboratory. To validate the performance of the purposed method, the experiments in the challenge traffic dense scenario are conducted.

The YOLOv5 and ByteTrack22 are used for the vehicle recognition in camera data samples, we obtain the bounding box of each vehicle, and select the bottom center of bounding box to represent the object’s location. The DBSCAN (Density-Based Spatial Clustering of Applications with Noise) and EKF (Extended Kalman Filter) are used to process the radar cloud point and obtain the radar object’s location. Table 2 contains part of the data from the video and radar detection of one frame, including the coordinates of the camera target in the PCS and the radar target in the BCS, which are strictly time-synchronized.

Fig. 9
figure 9

The integrated radar-camera device and its installation.

Full size image
Table 1 The specifications of the sensors in the integrated device.
Full size table
Table 2 The partial data (one frame) of video and MMW radar detection.
Full size table

Coarse and fine calibration performance evaluation

To validate the proposed coarse calibration algorithm, the experimental verification in the traffic dense scenario are conducted. The coarse calibration method is used to match the corresponding radar-camera point pairs. The azimuth and azimuth change rate are adopted for point pairs matching. As the azimuth and the azimuth rate difference between points are less than the threshold, they are marked as corresponding point pairs. In addition, the radar points also must be separated more than 10 m apart. The matching moments of the 1 st to 6th point pairs are shown in Fig. 10. It can been seen that the six corresponding pairsis identified within 8 s (from 15:47:57 to 15:48:05), the red ellipse in Fig. 10 a&f indicate the corresponding camera points. Figure 10 g show the corresponding radar points on the BCS, the radar points distribute at the distance of 23 m ~ 57 m on the vertical direction, concentrated within 60 m distance. This contribution point pairs can only ensure accuracy at the short distance, no guarantee for long-distance precision.

Fig. 10
figure 10

The matched radar-camera pairs in the coarse calibration.

Full size image

In order to improve calibration accuracy at the different distances, six iterative rounds of fine calibration algorithm is performed. The radar data are projected to the PCS with the coarse or previous fine calibration matrix, and then associate point pairs with the Hungarian tracking algorithm. When the radar-camera trajectories maintain continuous association over 25 cycles, then are considered to match successfully.

Figure 11 shows the spatial distributions of corresponding point pairs in the calibration. The corresponding point pairs in the coarse calibration are concentrated at the short distance. The point pairs in the 1 st fine calibration are distributed at various distances, but bad symmetrical, with no point pairs in the upper left part. The point pairs in the 6 st fine calibration showed good performance in both distance and symmetry.

Fig. 11
figure 11

Spatial distribution of corresponding radar points.

Full size image

The performance of different rounds of calibration is shown in Fig. 12. In the coarse calibration, the blue radar point and the red camera projection point overlap well within the distance less than 50 m, having a larger deviation at the long distance, as shown in Fig. 12 a. The deviation between the corresponding point pairs reduces after the 1 st fine calibration, as shown in Fig. 12 b. The corresponding point pairs basically aligned within a 100 m area in the 6 st fine calibration, as shown in Fig. 12 c. The content of green ellipse in the figure obviously indicate this changes. The dashed arrow lines represents the reprojection error between the blue radar and the red camera projection point. In addition, part of radar and camera points cannot be matched, such as the red camera points at the short distance and the blue radar points at the long distance. The sensor detection limitation blame for this phenomenon. The vehicles that park on the roadside can’t be detected by the radar, so only the red camera projection points appears without associate blue radar point.The long distant targets can’t be recognized by camera, so there are only the blue radar at the long distance. The results demonstrate that the reprojection errors of the point pairs are optimized after several rounds of calibration, the calibration accuracy is significantly improved.

Fig. 12
figure 12

The performance comparison between coarse and fine calibration.

Full size image

The reprojection errors are employed to evaluate the calibration performance. One frame data is extracted for the quantitative evaluation. The partial data of the test frame is shown in Table 2, the targets points distributed from − 4.2 m to 19.9 m at the x-axis, 19.5 to 156.8 m at the y-axis, effectively covers the entire detection range.

The manual calibration for the reprojection error comparison is conducted, and the manual transformation matrix is obtained by the visual projection calibration. We project the radar points onto the PCS, and then fine-tune the three Euler angle for minimizing the visual projection error between the corresponding pairs. The reprojection error comparison is shown in Fig. 13. Coarse calibration exhibits significant average reprojection error. Fine calibration progressively reduces errors. At the end of the 6th fine calibration, the average reprojection error is 1.5 m within the distance range of 200 m. Compared with the manual calibration, the average reprojection error is reduced from 2 m to 1.5 m, reduced by 25%. Figure 14 show the variation of reprojection error with distance. The coarse calibration exhibits significant error variation, with an exponential increase in error as the distance increased. The maxim error occurs at the distance of 156.8 m, with an 39.2 m, as shown in Fig. 14b. After several rounds of fine calibration, the long-distance error has been reduced. At the end of 6th fine calibration, the reprojection error at 156.8 m is reduced from 39.2 m to 3.4 m, reduced by 91%. The results demonstrate that the proposed calibration method automatically optimize the reprojection error, greatly reducing the debugging costs and improve accuracy.

Fig. 13
figure 13

Reprojection errors of manual calibration, coarse calibration and fine calibration.

Full size image
Fig. 14
figure 14

The variation of reprojection error with distance using different calibration methods.

Full size image

The radar-camera calibration is the process of solving the PnP problem with radar-camera corresponding pairs. The accuracy of the point pairs association is crucial to the calibration accuracy. The comparative analysis is conducted with other automatic trajectory correlation method, including Euclidean distance11, angle distance and bidirectional selection association12. The data for the association accuracy experiment is 82 s road traffic, with a total of 1,600 frames. The required initially transformation matrix is generated for the comparison method. This article adopts the manual calibration matrix as a reference and changes the three Euler Angles to generate the different decalibration initial matrix. It preset the initial matrix with deviation of 5 degrees, 2 degrees, and 0 degrees. The comparative results are illustrated in Table 3. As can be seen from the table, the association accuracy of the three comparison methods is related to the preset initial matrix. The greater the deviation of the preset initial matrix, the lower the association accuracy. When the deviation angle is 5 degrees, the association accuracy rates of the three comparison methods are 31%, 19%, and 10% respectively. When the deviation angle decreases, the association accuracy increases, reaching a maximum of 82%. By contrast, the method proposed in this paper is independent of the preset matrix, and its association accuracy reaches 93%.

Table 3 Association accuracy comparison with other methods.
Full size table

The method in reference23 performs well in the association accuracy experiment. Thus, a comparative calibration accuracy experiment is conducted between this method and the proposed method. The initial matrix are set with deviation of 5 degrees, 2 degrees, and 0 degrees, and then calibrate with the method mentioned in reference23. The accuracy evaluation merit adopts the reprojection error in the image plane mentioned in reference23. At the 5-degree deviation matrix, more than half of the radar projection points fall outside the image plane, resulting in calibration failure. The initial matrix has a significant impact on calibration accuracy in this method. At the 2-degree deviation and 0-degree deviation, the calibration accuracy is improved, the calibration accuracy comparisons with the proposed method are shown in Fig. 15, A and B represent 2-degrees and 0-degrees with method mentioned in reference23, C represents the method proposed in this paper. The average reprojection error is 2.38 cm, 2.37 cm and 1.05 cm respectively. The method proposed in this paper has the lowest error, reduced by 55%. These results indicate that the purposed method outperform the compared method. It doesn’t rely on initial assumptions, it has high association accuracy and calibration accuracy. These findings emphasize the potential of the proposed method to reduce the manual costs of roadside radar-camera calibration required for other methods. and then conduct a comparative calibration accuracy experiment with the method proposed in this paper.

Fig. 15
figure 15

Reprojection errors comparisons with other automatic calibration.

Full size image

Conclusions

To address the challenges arising from the roadside integrated radar-camera calibration in the real-time scenario, this paper proposes an continuous online calibration method based on azimuth angle and multi frame tracking. A multistage initialization approach is first developed to obtain coarse transformation matrix. It leverages the azimuth angle and azimuth angle rate to match the radar-camera correspondences. Subsequently, the Hungarian tracking algorithm was used for multi-frame data association.This method does not require the manual initial extrinsic parameter matrix. The association accuracy is 93%, which emphasized the potential of the proposed method to reduce the manual costs of roadside radar-camera calibration. This method don’t demand excessive computational resources and can be easily embedded into hardware to meets the online requirements in real-world scenarios. The experimental results show that it can automatically optimize the reprojection error with rounds of calibration. Compared with the manual calibration, the average reprojection error is reduced from 2 m to 1.5 m within the distance range of 200 m, reduced by 25%. Compared with the other automatic calibration method, the average reprojection error on is reduced by 55%. This approach significantly enhances calibration accuracy and robustness in complex environments, which provides reliable technical support for intelligent transportation systems. The proposed method is inadequate for scenarios involving undulating terrains with significant elevation variations. To address this limitation, our subsequent work will focus on developing an adaptive multi-parameter calibration framework.