Abstract
Since traffic congestion is a major issue worldwide, particularly in urban areas due to the increasing population on a daily basis, it negatively impacts human life, leading to time wastage, health problems, and economic repercussions. Therefore, establishing a sustainable transportation system in densely populated urban areas is crucial. To overcome this challenge, various factors on which a sustainable transportation system depends must be deeply analyzed. However, this analysis may involve fuzziness and vagueness due to imprecise data and incomplete information. In this regard, a mathematical framework called the Complex Intuitionistic Fuzzy Hypersoft Set (CIFHSS) is introduced in this research. This article presents and thoroughly investigates essential set-theoretical operations based on the complex intuitionistic fuzzy hypersoft set, using appropriate examples. Furthermore a novel Multi-Attribute Decision Making approach, based on the CIFHSS is developed. This approach incorporates decision-valued matrices (both maximum and minimum), a scoring framework for CIFHSS, and matrix-based aggregations, such as the core matrix. Moreover, the algorithm is implemented in a real-world scenario to solve traffic congestion in urban areas, demonstrating the versatility of the proposed algorithm. The model assigns scores of 0.6161 to the Electric Bus Rapid Transit system, 0.6089 to the Expanded Bicycle Lane Network, 0.6571 to Light Rail Transit, and 0.7627 to the Hybrid Car-Sharing Program, identifying the latter as the most suitable option. A sensitivity analysis of the proposed model is also presented using statistical tools. Finally, a detailed conclusion and future directions for the application of this research are provided.
Similar content being viewed by others
Introduction
In different real-life decision-making problems, experts (decision-makers) usually deal with complex problems that involve multiple, often conflicting information and criteria. Selecting the best option from a set of available choices based on different depending factors is not always straightforward. Multi-Criteria Decision Making (MCDM)1,2,3 provides a structured and systematic approach for dealing with such decision making problems by providing the analysis and ranking of alternatives in the presence of various criteria. MCDM is a branch of operations research and decision science that deals with decision making problems in the presence of conflicting and vague criteria. Unlike single-criterion decision-making, which optimizes one objective, MCDM focuses on optimizing a balance among competing objectives. This makes it highly suitable for problems in which trade-offs among multiple criteria are necessary.
MCDM models have been broadly used across different fields, especially where decision-making scenarios involves balancing performance, risk, values and other effecting parameters. Some notable application areas include as Transportation and Urban Planning (Choosing the most suitable transport model for providing the secure and fast system to the public), Energy Management (Selecting the best energy source with respect to the different factors that are helpful for long term and safe environmental system), Healthcare and Medical Decision-Making (Deciding the accurate disease in a patient with respect to the condition of the different symptoms), Supply Chain Management (Selecting the best supplier by considering the different factors to increase benefit and decrease the risk) and many others.
The global population is increasing daily, presenting numerous challenges to maintaining stable human life. One of the major global issues arising from this population growth is the provision of a sustainable transportation system. This problem is particularly prevalent in urban areas worldwide. Traffic congestion is a common issue in many cities, especially in rapidly growing regions. In addition, a sustainable transportation system is a core component of smart cities, aiming to reduce environmental impact while enhancing mobility through efficient, data-driven solutions. In smart transportation system, sustainability is obtained by combining technologies and multimodal transit systems to support eco-friendly urban growth. In this regard, several factors contribute to traffic congestion, including population growth, increased private transportation, inadequate public transportation infrastructure, and poor traffic planning. This issue negatively impacts human life, leading to time wastage, health problems, and economic repercussions. Therefore, establishing a sustainable transportation system in densely populated urban areas is crucial. Many researchers4,5,6 have discussed the issue of traffic congestion and proposed suitable solutions to address it. However, all the studies mentioned, as well as many others in the literature, have primarily provided a theoretical framework for resolving this issue. Furthermore, various state organizations are putting efforts into managing sustainable development in the transportation sector. Since traffic congestion involves different parameters such as traffic volume, traffic density, signal cycle time, and peak hour traffic, these must be thoroughly analyzed to make well-informed decisions. The analysis of these parameters may involve uncertainty and ambiguity due to incomplete data and information, which must be minimized to facilitate informed decision-making. In this context, several criterion- and attribute-based models have been proposed in the literature7,8,9. However, these models are primarily focused on parametric analysis and do not delve deeply into the sub-parameters associated with each parameter. To address this gap, a comprehensive mathematical and theoretical framework is required to handle both data and the parameters and associated sub-parameters.
Fuzzy set theory is particularly useful for addressing data uncertainty and reducing fuzziness in decision-making processes. It allows for more flexible and robust models that can account for imprecision and incomplete information, providing a better foundation for sustainable transportation planning. Zadeh10 pioneered fuzzy set theory in 1965, which has grown into one of the most widely recognized approaches in modern mathematics. Zadeh emphasized that classical set theory and its mathematical tools frequently fail to illustrate the underlying uncertainty and ambiguity present in practical problems. Fuzzy set theory developed as a groundbreaking solution, but with its own set of challenges. Specifically, the theory depends on membership functions to establish fuzzy sets, but Molodtsov claimed that establishing these functions is a highly personalised process, making it difficult to design a general strategy for all scenarios.
In 1999, Molodtsov11 proposed the soft set theory as a more practical alternative. This idea is a more recent technique for dealing with decision-making and ambiguity. The main advantage of soft set theory over fuzzy set and other theories is that it is devoid of complications. Soft set theory has quickly gained popularity among academics, with several scientific studies conducted periodically12,13,14,15. Maji et al.16,17 presented a soft set implementation that reduces parameters while preserving optimum selection antiques in decision-making problems. Chen18 presented a novel definition and practical applications for reducing soft sets to parameters. Pei and Miao19 later demonstrated that soft sets represent a unique category of information systems. Kong et al.20 introduced a technique for transforming soft sets into normal parameters, whereas Zou and Xiao21 proposed a method for analyzing soft data. Aktas and Cagman22 made significant contributions to the establishment of the algebraic structure of soft set theory. In an associated milestone, the intuitionistic fuzzy set (IFS) theory23,24 was developed by including a non-membership function into the fuzzy set framework, which considerably improved decision-making skills. Maji et al.25,26 expanded on this by combining soft set theory and fuzzy set theory, resulting in the intuitionistic fuzzy soft set (IFSS). The parameterization and hesitancy obtained by IFSS from this combination allow for an extremely precise depiction of real-world events. IFSS is an effective strategy for handling data ambiguity and vagueness. Many research articles have proved the appropriateness of IFSS for making decisions27,28.
Smarandache29 suggested a revolutionary technique for managing uncertainty by transforming soft sets into hypersoft sets. This generalization involves breaking the function into numerous decision functions, resulting in considerable research on hypersoft set structures30,31,32,33,34,35,36,37. Multi-criteria decision-making (MCDM) is concerned with organizing and addressing issues, including preferences, as well as planning based on multiple criteria. Traditional intuitionistic fuzzy soft sets are insufficient for tackling specific sorts of problems, particularly when dealing with multiple attributes that are further subdivided. To resolve this limitation, Yolcu et al.38 created intuitionistic fuzzy hypersoft sets (IFHSS), providing an effective way to address such difficulties.
Ramot et al.39 proposed the notion of complex fuzzy sets, in which each element has a complex-valued membership function rather than a real-valued one. Alkouri and Salleh40 extended the concept of intuitionistic fuzzy sets to complex intuitionistic fuzzy sets by defining all functions in the complex plane. They provided an illustration of this notion using distance measurements for complex intuitionistic fuzzy sets. Later, Thirunavukarasu41 combined fuzzy sets with soft sets to develop complex fuzzy soft sets, which alleviated deficiencies in prior models. The aim was to create a unified framework that could better handle data characterised by uncertainty and complexity. Kumar and Bajaj42 advanced the field by introducing complex intuitionistic fuzzy soft sets, which extend the principles of intuitionistic fuzzy sets and soft sets through the integration of complex numbers. Later, Rahman et al.43 expanded this idea further with the development hybrid structure of intuitionistic fuzzy set and hypersoft sets. This approach aimed to address uncertainty, ambiguity, and complex interactions in a more precise and complete manner. These frameworks were developed in response to the requirement to solve complicated, multi-faceted decision-making problems, including uncertainty, imprecision, and multidimensional attributes.
Research gap and limitations
Traditional fuzzy sets and their extensions, such as Intuitionistic Fuzzy Sets (IFS), fail to deal with cases in which both membership and non-membership degrees are not known or when data has hierarchical or complicated structures. Hypersoft Sets improved on this by splitting attributes into sub-attributes, leading to a more detailed representation of multidimensional data, but they still lacked the capacity to handle complicated uncertainty, including magnitude and phase information. Complex Fuzzy Sets (CFS) introduced complex-valued membership functions to reflect magnitude and phase uncertainty, which is valuable in domains such as signal processing and quantum mechanics. By combining IFS and CFS, complex Intuitionistic Fuzzy Sets (CIFS) were established, which can handle membership/non-membership degrees as well as complicated uncertainty. However, CIFS alone cannot handle hierarchical or multi-granular data structures, which are prevalent in real-world applications such as supply chain management, environmental modeling, and financial analysis.
While CIFS and IFSS are effective in dealing with uncertainty and incomplete information, they lack the capacity to deal with multi-attribute parameterization and sub parametrization, which are crucial in real-world multi-attribute decision-making problems where parameters are not always independent or single-valued. IFHSS extends the hypersoft concept to intuitionistic fuzzy environments, but it does not incorporate the complex-valued membership and non-membership degrees, which are beneficial in modeling periodic, bipolar, or phase-based uncertainties. In addition, IFHSS combines the intuitionistic fuzzy set with the structure hypersoft set, it deals with the parameters, sub-parameters and degrees of the universal set, but it does not deal with the phase terms of the membership and non-membership functions. The hybrid structure CIFSS handles both amplitude and phase terms. However, it also faces limitations when dealing with sub-parameters, as many real-world decision-making problems depend on both parameters and sub-parameters. CIFHSS integrates the intuitionistic fuzzy set, complex number system and hypersoft framework, offering a more effective and useful robust model capable of handling the multi-parameter, ambiguous, and dynamically fluctuating decision scenarios. This is particularly useful in urban traffic systems, where factors often exhibit vague, time-dependent, or phase-shifted behavior (e.g., morning/evening traffic patterns, public sentiment shifts, etc.).
Motivation behind the structure CIFHSS
Based on the research as discussed above, each of these frameworks offers valuable structures for modeling incomplete and vague information, they exhibit key limitations and drawbacks when applied to MADM problems, especially in real-world problems involving hierarchical parameters. In this regard, a new type of hypersoft set, known as a complex intuitionistic fuzzy hypersoft set, is proposed, along with its basics and theoretical operations. This study is new and more generalized than previous relevant studies for more accurate findings. As in CIFHSS, the hypersoft parameterization allows for the handling of both parameters and sub-parameters simultaneously, which is useful in more detailed and structured decision-making scenarios. The intuitionistic fuzzy values in this structure capture both the membership and non-membership degrees, which accommodate the hesitation degree (uncertainty) more accurately than classical fuzzy sets. Finally, the complex plane in CIFHSS enables the modeling of periodicity, phase term and multidimensional uncertainty. CIFHSS arose from merging the competencies of hypersoft sets and CIFS, providing the modeling of complicated, hierarchical, and multidimensional data with magnitude and phase uncertainty. This framework has increased expressiveness and versatility, making it appropriate for usage in artificial intelligence, pattern recognition, and multi-criteria decision-making. For example, in medical diagnosis, CIFHSSs can represent symptoms and sub-symptoms with complicated linkages, but in financial analysis, they can manage uncertain interdependent data. In theoretical terms, CIFHSS unifies and extends existing notions, expanding fuzzy mathematics and soft computing. Practically, it gives an effective tool for making accurate decisions in difficult situations, which benefits academics and practitioners from a variety of sectors. In this context, a comparative table (see Table 1) illustrates the structural differences and capabilities of CIFHSS compared to CIFS, IFHSS, and IFSS. The comparison focuses on key features such as the representation of uncertainty, the handling of parameter hierarchies, and the ability to encode phase-based or complex-valued information.
This study introduces the notion of complex intuitionistic fuzzy hypersoft set theory, a hybrid of complex intuitionistic fuzzy set theory and hypersoft set theory. We define various operations such as complement, subset, equality, “AND”, “OR”, intersection, and union within the framework of CIFHSSs. Moreover, the paper includes various illustrative examples to support the theoretical framework. Furthermore, a reliable decision support system is established by introducing a MADM-based algorithm that utilizes novel matrix-based CIFHSS aggregations. The algorithm is then discussed in detail, employing a decision-making example to demonstrate its efficacy.
Characterization of complex intuitionistic fuzzy hypersoft sets
To understand the core concept of this article, recall some basic definitions.
Fundamental knowledge
Definition 1
Suppose10 that \(\breve{\mathcal {D}}\) is an initial universe and \(\grave{\mathfrak {J}} \widehat{\subseteq } \breve{\mathcal {D}}\) is a fuzzy set. The set \(\grave{\mathfrak {J}}\) will be written as \(\grave{\mathfrak {J}} = \{({\grave{\breve{\varrho }}}, \zeta ^{T}_{\grave{\mathfrak {J}}}({\grave{\breve{\varrho }}}))|{\grave{\breve{\varrho }}} \in \breve{\mathcal {D}}\}\) such that
where \(\zeta ^{T}_{\grave{\mathfrak {J}}}({\grave{\breve{\varrho }}})\) denotes the membership function of \({\grave{\breve{\varrho }}} \in \breve{\mathcal {D}}\).
Definition 2
A complex39 fuzzy set \(\grave{\mathfrak {J}}\) is defined as
where \(\zeta ^{T}_{\grave{\mathfrak {J}}}({\grave{\breve{\varrho }}})\) is a membership function of \(\grave{\mathfrak {J}}\) with \(r^{T}_{\grave{\mathfrak {J}}}({\grave{\breve{\varrho }}}) \in [0,1]\) and \(\omega ^{T}_{\grave{\mathfrak {J}}}({\grave{\breve{\varrho }}}) \in [0,2\pi ]\) as amplitude and phase terms respectively and \(\iota = \sqrt{-1}\).
Definition 3
A soft11 set \(\grave{\mathfrak {J}}\) over \(\breve{\mathcal {D}}\), is defined as
where \(\zeta ^{T}_{\grave{\mathfrak {J}}} : {\mathfrak {Q}} \rightarrow P(\breve{\mathcal {D}})\), and \({\mathfrak {Q}}\) is the set of all parameters.
Definition 4
A complex46 fuzzy soft set \(\grave{\mathfrak {J}}\) over \(\breve{\mathcal {D}}\), is defined as
where \(\zeta ^{T}_{\grave{\mathfrak {J}}}: {\mathfrak {Q}} \rightarrow CP(\breve{\mathcal {D}})\) such that \(\zeta ^{T}_{\grave{\mathfrak {J}}}(\grave{\breve{\varrho }}) = \emptyset\).
Definition 5
An intuitionistic23 fuzzy set \(\grave{\mathfrak {J}}\) over \(\breve{\mathcal {D}}\) is \(\grave{\mathfrak {J}}=\{({\grave{\breve{\varrho }}},\zeta ^{T}_{\grave{\mathfrak {J}}}({\grave{\breve{\varrho }}}),\zeta ^{F}_{\grave{\mathfrak {J}}}({\grave{\breve{\varrho }}})):{\grave{\breve{\varrho }}}\in \breve{\mathcal {D}}\}\), where \(\zeta ^{T}_{\grave{\mathfrak {J}}}, \zeta ^{F}_{\grave{\mathfrak {J}}} :\breve{\mathcal {D}}\rightarrow [0,1]\), with the condition \(0\le \zeta ^{T}_{\grave{\mathfrak {J}}}({\grave{\breve{\varrho }}})+\zeta ^{F}_{\grave{\mathfrak {J}}}({\grave{\breve{\varrho }}})\le 1\), \(\forall {\grave{\breve{\varrho }}}\in \breve{\mathcal {D}}\). \(\zeta ^{T}_{\grave{\mathfrak {J}}},\zeta ^{F}_{\grave{\mathfrak {J}}}\in [0,1]\) indicate the membership and non-membership values of \({\grave{\breve{\varrho }}}\) to \(\grave{\mathfrak {J}}\), respectively. \(IFP(\breve{\mathcal {D}})\) refers to the set of all IFSs in \(\breve{\mathcal {D}}\).
Definition 6
Consider26 an initial universe of discourse \(\breve{\mathcal {D}}\) and a set of attributes \({\mathfrak {Q}}\). A pair \((\grave{\mathfrak {J}},{\mathfrak {Q}})\) is referred to as an IFSS over \(\breve{\mathcal {D}}\), where \(\grave{\mathfrak {J}}\) is a function defined as, \(\grave{\mathfrak {J}}:{\mathfrak {Q}}\rightarrow IFP(\breve{\mathcal {D}})\) such that \(\grave{\mathfrak {J}}(\grave{\breve{\varrho }})=\{({\grave{\breve{\varrho }}},\zeta ^{T}_{\grave{\mathfrak {J}}}({\grave{\breve{\varrho }}}),\zeta ^{F}_{\grave{\mathfrak {J}}}({\grave{\breve{\varrho }}})):{\grave{\breve{\varrho }}}\in \breve{\mathcal {D}}\}\).
Definition 7
Suppose29 that \(\breve{\mathcal {D}}\) is the universal set and \({\mathfrak {Q}}(\breve{\mathcal {D}})\) is the power set of \(\breve{\mathcal {D}}\). Suppose \(\varrho _{1},\varrho _{2},\varrho _{3},...,\varrho _{n}\) for \(n\ge 1\), are \(n\) distinct attributes with associated attribute value sets \({\mathfrak {Q}}_{1},{\mathfrak {Q}}_{2},...,{\mathfrak {Q}}_{n}\) satisfying \({\mathfrak {Q}}_{i}\widehat{\cap } {\mathfrak {Q}}_{j}=\emptyset\), for all \(i\ne j\) and \(i,j\in \{1,2,...,n\}\). A Hypersoft set in \(\breve{\mathcal {D}}\) is represented by the pair \((\grave{\mathfrak {J}},{\mathfrak {Q}}_{1}\times {\mathfrak {Q}}_{2}\times ...\times {\mathfrak {Q}}_{n})\), where \(\grave{\mathfrak {J}}:{\mathfrak {Q}}_{1}\times {\mathfrak {Q}}_{2}\times ...\times {\mathfrak {Q}}_{n}\rightarrow P(\breve{\mathcal {D}})\).
Definition 8
Consider38 \(\breve{\mathcal {D}}\) is an initial universe and \(IFP(\breve{\mathcal {D}})\) denote the IF power set of \(\breve{\mathcal {D}}\). Suppose \(\varrho _{1},\varrho _{2},\varrho _{3},...,\varrho _{n}\) for \(n\ge 1\) are \(n\) distinct attributes with associated attribute value sets \({\mathfrak {Q}}_{1},{\mathfrak {Q}}_{2},...,{\mathfrak {Q}}_{n}\) such that \({\mathfrak {Q}}_{i}\widehat{\cap } {\mathfrak {Q}}_{j}=\emptyset\), for all \(i\ne j\) and \(i,j\in \{1,2,...,n\}\). For each \(i=1,2,...,n\), let \(\mathfrak {B}_{i}\) be a nonempty subset of \({\mathfrak {Q}}_{i}\). An Intuitionistic Fuzzy Hypersoft set is a pair \((\grave{\mathfrak {J}},\mathfrak {B}_{1}\times \mathfrak {B}_{2}\times ...\times \mathfrak {B}_{n})\), where: \(\grave{\mathfrak {J}}:\mathfrak {B}_{1}\times \mathfrak {B}_{2}\times ...\times \mathfrak {B}_{n}\rightarrow IFP(\breve{\mathcal {D}})\) and
where \(\zeta ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}\) and \(\zeta ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}\) are the membership and non-membership degrees, respectively, satisfying \(0\le \zeta ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})+\zeta ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\le 1\) with \(\zeta ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}}),\zeta ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\in [0,1]\).
Complex intuitionistic fuzzy hypersoft sets and its set theoretical properties
Definition 9
Consider \({\breve{\mathcal {D}}}\) is an initial universe and \(CIFP({\breve{\mathcal {D}}})\) denote the CIF power set of \({\breve{\mathcal {D}}}\). Suppose \(\varrho _{1},\varrho _{2},\varrho _{3},...,\varrho _{n}\) for \(n\ge 1\) are \(n\) distinct attributes with associated attribute value sets \({\mathfrak {Q}}_{1},{\mathfrak {Q}}_{2},...,{\mathfrak {Q}}_{n}\) such that \({\mathfrak {Q}}_{i}\widehat{\cap } {\mathfrak {Q}}_{j}=\emptyset\), for all \(i\ne j\) and \(i,j\in \{1,2,...,n\}\). For each \(i=1,2,...,n\), suppose that \(\mathfrak {B}_{i}\) is the nonempty subset of \({\mathfrak {Q}}_{i}\). A Complex Intuitionistic Fuzzy Hypersoft set is a pair \((\grave{\mathfrak {J}},\mathfrak {B}_{1}\times \mathfrak {B}_{2}\times ...\times \mathfrak {B}_{n})\), where \(\grave{\mathfrak {J}}:\mathfrak {B}_{1}\times \mathfrak {B}_{2}\times ...\times \mathfrak {B}_{n}\rightarrow CIFP(\breve{\mathcal {D}})\) and
where \(\zeta ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}\) and \(\zeta ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}\) are the complex-valued membership and non-membership degrees, respectively, satisfying \(\zeta ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})=r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}}) e^{\iota \omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})}\) and \(\zeta ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})=r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}}) e^{\iota \omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})}\) with \(0\le r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})+ r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\le 1\),\(0 \le \omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})+\omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\le 2\pi\), \(r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}}),r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\in [0,1]\), and \(\omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}}),\omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\in [0,2\pi ]\).
We use the symbols \(\nabla\) for \({\mathfrak {Q}}_{1}\times {\mathfrak {Q}}_{2}\times ...\times {\mathfrak {Q}}_{n}\), \({{\widehat{\Psi }}}\) for \(\mathfrak {B}_{1}\times \mathfrak {B}_{2}\times ...\times \mathfrak {B}_{n}\) and \({\grave{\breve{\mathfrak {z}}}}\) for an element of the set \({{\widehat{\Psi }}}\).
Definition 10
Assume that \((\grave{\mathfrak {J}},\nabla )\) is a \(CIFHSS\) over \(\breve{\mathcal {D}}\), then
i) \((\grave{\mathfrak {J}},\nabla )\) is called a null \(CIFHSS\), denoted by \(0_{\{ \breve{\mathcal {D}}_{CIFH},\nabla \}}\) if \(r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})=r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})=0\) and \(\omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})=\omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})=0 \pi\) \(\forall {\grave{\breve{\varrho }}} \in \breve{\mathcal {D}}\).
ii) \((\grave{\mathfrak {J}},\nabla )\) is called an absolute \(CIFHSS\), denoted by \(1_{\{ \breve{\mathcal {D}}_{CIFH},\nabla \}}\) if \(r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})=r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})=1\) and \(\omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})=\omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})=2 \pi\) \(\forall {\grave{\breve{\varrho }}} \in \breve{\mathcal {D}}\).
Example 1
Suppose that a university admissions committee evaluating students based on multiple criteria. The “set of discourse” consists of prospective students applying for admission. Consider the set of prospective students is \(\breve{\mathcal {D}}=\{{\grave{\breve{\varrho }}}_{1},{\grave{\breve{\varrho }}}_{2},{\grave{\breve{\varrho }}}_{3}\}\). The university evaluates students based on three main parameters as \({\mathfrak {Q}}_{1}\)= Academics, \({\mathfrak {Q}}_{2}\)= Extracurricular Activities, \({\mathfrak {Q}}_{3}\)= Social Skills and their respective sub-attributes are given as:
\({\mathfrak {Q}}_{1}\) = Academics = {GPA\((\breve{\varsigma }_{1})\), Standardized Test Scores\((\breve{\varsigma }_{2})\), Research Work\((\breve{\varsigma }_{3})\)}
\({\mathfrak {Q}}_{2}\) = Extracurricular Activities = {Sports\(({\breve{\varpi }}_{1})\), Volunteering\(({\breve{\varpi }}_{2})\), Arts and Creativity\(({\breve{\varpi }}_{3})\)}
\({\mathfrak {Q}}_{3}\) = Social Skills = {Communication\(({\breve{\delta }}_{1})\), Leadership\(({\breve{\delta }}_{2})\), Teamwork\(({\breve{\delta }}_{3})\)}.
Suppose that
and
are subsets of \({\mathfrak {Q}}_{i}\), for each \(i=1,2,3\). Then, the CIFHSS \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\) and \((\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\) are defined as follows:
and
Tabular representations of these sets are given in Tables 2 and 3.
Corollary 1
Each CIFHSS is evidently a CIFSS. Following is an example of this scenario.
Example 2
We look at Example 1. The CIFSS is the outcome of developing the CIFHSS with parameters chosen from a single attribute set, such as \({\mathfrak {Q}}_{1}\). Therefore, we can say that each CIFHSS is also a CIFSS. In other words, the structure of CIFHSS is a generalized variant of the CIFSS.
Definition 11
Suppose that \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\) and \((\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\) are two CIFHSS in \(\breve{\mathcal {D}}\). The set \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\) is termed as a subset of \((\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\), if
-
i)
\({{\widehat{\Psi }}}_{1}\widehat{\subseteq }{{\widehat{\Psi }}}_{2}\)
-
ii)
\(\forall\) \({\grave{\breve{\mathfrak {z}}}}\in {{\widehat{\Psi }}}_{1}\), \(\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})\widehat{\subseteq } \grave{\mathfrak {K}}({\grave{\breve{\mathfrak {z}}}})\) implies \(\zeta ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\widehat{\subseteq } \zeta ^{T}_{\grave{\mathfrak {K}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\) and \(\zeta ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\widehat{\subseteq } \zeta ^{F}_{\grave{\mathfrak {K}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\) i.e. \(r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}}) \le r^{T}_{\grave{\mathfrak {K}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}}), r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}}) \le r^{F}_{\grave{\mathfrak {K}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}}),\omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}}) \le \omega ^{T}_{\grave{\mathfrak {K}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\) and \(\omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\le \omega ^{F}_{\grave{\mathfrak {K}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\).
Example 3
Assume that attributes in Example 1. Consider \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\) and \((\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\) are two CIFHSSs in \(\breve{\mathcal {D}}=\{{\grave{\breve{\varrho }}}_{1},{\grave{\breve{\varrho }}}_{2},{\grave{\breve{\varrho }}}_{3}\}\) as given in Tables 2 and 3, respectively. It is evident that \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}) {\widehat{\subseteq }}(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\), we may write it as:
Definition 12
Two CIFHSSs \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\) and \((\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\) over the same \(\breve{\mathcal {D}}\) are called equal if \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\widehat{\subseteq }(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\) and \((\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\widehat{\subseteq }(\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\).
Theorem 1
Assume that \(\breve{\mathcal {D}}\) is an initial universe, \({{\widehat{\Psi }}}_{1},{{\widehat{\Psi }}}_{2},{{\widehat{\Psi }}}_{3}\widehat{\subseteq }\nabla\) and \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}),(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\), \((\mathfrak {L},{{\widehat{\Psi }}}_{3})\) are CIFHSSs in \(\breve{\mathcal {D}}\). Then,
-
i)
\((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}) {\widehat{\subseteq }} {1}_{\{ \breve{\mathcal {D}}_{CIFH},\nabla \}}\),
-
ii)
\(0_{\{ \breve{\mathcal {D}}_{CIFH},\nabla \}}\widehat{\subseteq }(\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\),
-
iii)
\((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}){\widehat{\subseteq }}(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\) and \((\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2}){\widehat{\subseteq }}(\mathfrak {L},{{\widehat{\Psi }}}_{3})\Rightarrow (\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}) {\widehat{\subseteq }}(\mathfrak {L},{{\widehat{\Psi }}}_{3}).\)
Proof
-
i)
\((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}) \widehat{\subseteq } 1_{\{\breve{\mathcal {D}}_{CIFH},\nabla \}}\), since \(\zeta ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\le \zeta ^{T}_{\grave{\mathfrak {J}}(\nabla )}({\grave{\breve{\varrho }}})=1\) and \(\zeta ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\ge \zeta ^{F}_{\grave{\mathfrak {J}}(\nabla )}({\grave{\breve{\varrho }}})=0\) \(\forall\) \({\grave{\breve{\mathfrak {z}}}}\in \nabla\), \({\grave{\breve{\varrho }}}\in \breve{\mathcal {D}}\),
-
ii)
\(0_{\{\breve{\mathcal {D}}_{CIFH},\nabla \}} \widehat{\subseteq }(\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\), since \(0=\zeta ^{T}_{\grave{\mathfrak {J}}(\nabla )}({\grave{\breve{\varrho }}})\le \zeta ^{T}_{\grave{\mathfrak {J}}(\varepsilon )}({\grave{\breve{\varrho }}})\) and \(1=\zeta ^{F}_{\grave{\mathfrak {J}}(\nabla )}({\grave{\breve{\varrho }}})\ge \zeta ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\) \(\forall\) \({\grave{\breve{\mathfrak {z}}}}\in \nabla\), \({\grave{\breve{\varrho }}}\in \breve{\mathcal {D}}\),
-
iii)
\((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}) \widehat{\subseteq }(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\Rightarrow \zeta ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\le \zeta ^{T}_{\grave{\mathfrak {K}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\) and \(\zeta ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\ge \zeta ^{F}_{\grave{\mathfrak {K}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\) \(\forall\) \({\grave{\breve{\mathfrak {z}}}}\in \nabla\), \({\grave{\breve{\varrho }}}\in \breve{\mathcal {D}}\). Also \((\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\widehat{\subseteq }(\mathfrak {L},{{\widehat{\Psi }}}_{3})\Rightarrow \zeta ^{T}_{\grave{\mathfrak {K}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\le \zeta ^{T}_ {\mathfrak {L}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\) and \(\zeta ^{F}_{\grave{\mathfrak {K}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\ge \zeta ^{F}_{\mathfrak {L}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\) \(\forall\) \({\grave{\breve{\mathfrak {z}}}}\in \nabla\), \({\grave{\breve{\varrho }}}\in \breve{\mathcal {D}}\). Therefore, \(\zeta ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\le \zeta ^{T}_{\mathfrak {L}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\) and \(\zeta ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\ge \zeta ^{F}_{\mathfrak {L}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\). Thus, we obtain \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\widehat{\subseteq }(\mathfrak {L},{{\widehat{\Psi }}}_{3})\).
\(\square\)
Definition 13
The complement of CIFHSS \((\grave{\mathfrak {J}},{{\widehat{\Psi }}})\) in \(\breve{\mathcal {D}}\) is denoted by \((\grave{\mathfrak {J}},{{\widehat{\Psi }}})^{c}\) and defined as \((\grave{\mathfrak {J}},{{\widehat{\Psi }}})^{c}=(\grave{\mathfrak {J}}^{c},{{\widehat{\Psi }}})\), where \(\grave{\mathfrak {J}}^{c}:({\mathfrak {Q}}_{1}\times {\mathfrak {Q}}_{2}\times ...\times {\mathfrak {Q}}_{n})=\nabla \rightarrow CIFP(\breve{\mathcal {D}})\) and \(\grave{\mathfrak {J}}^{c}({{\widehat{\Psi }}})=(\grave{\mathfrak {J}}({{\widehat{\Psi }}}))^{c}\) \(\forall\) \({{\widehat{\Psi }}}\widehat{\subseteq }\nabla\). Thus, if \((\grave{\mathfrak {J}},{{\widehat{\Psi }}})=\{\langle {\grave{\breve{\mathfrak {z}}}},(\frac{{\grave{\breve{\varrho }}}}{\zeta ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}}),\zeta ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})})\rangle :{\grave{\breve{\varrho }}}\in \breve{\mathcal {D}},{\grave{\breve{\mathfrak {z}}}} \in {{\widehat{\Psi }}})\}\), then
\((\grave{\mathfrak {J}},{{\widehat{\Psi }}})^{c}=\{\langle {\grave{\breve{\mathfrak {z}}}},(\frac{{\grave{\breve{\varrho }}}}{\zeta ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}}),\zeta ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})})\rangle :{\grave{\breve{\varrho }}}\in \breve{\mathcal {D}} ,{\grave{\breve{\mathfrak {z}}}}\in {{\widehat{\Psi }}}\}\).
Example 4
According to Example 1, consider a CIFHSS \((\grave{\mathfrak {J}},{{\widehat{\Psi }}})\) in \(\breve{\mathcal {D}}=\{{\grave{\breve{\varrho }}}_{1},{\grave{\breve{\varrho }}}_{2},{\grave{\breve{\varrho }}}_{3},{\grave{\breve{\varrho }}}_{4}\}\).
Then, the complement of \((\grave{\mathfrak {J}},{{\widehat{\Psi }}})\) is written as:
Theorem 2
Let \((\grave{\mathfrak {J}},{{\widehat{\Psi }}})\) be any CIFHSS over \(\breve{\mathcal {D}}\). Then,
-
i)
\(((\grave{\mathfrak {J}},{{\widehat{\Psi }}})^{c})^{c}=(\grave{\mathfrak {J}},{{\widehat{\Psi }}})\)
-
ii)
\(0^{c}_{( \breve{\mathcal {D}}_{CIFH},\nabla )}=1_{(\breve{\mathcal {D}}_{CIFH},\nabla )}\)
-
iii)
\(1^{c}_{( \breve{\mathcal {D}}_{CIFH},\nabla )}=0_{(\breve{\mathcal {D}}_{CIFH},\nabla )}\)
Proof
Straightforward.\(\square\)
Definition 14
Assume that \(\breve{\mathcal {D}}\) is a universal discourse, \({{\widehat{\Psi }}}_{1},{{\widehat{\Psi }}}_{2}\widehat{\subseteq }\nabla\) and \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}),(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\) are two CIFHSSs in \(\breve{\mathcal {D}}\). The union of \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\) and \((\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\) is denoted as; \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}) \widehat{\cup } (\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})=(\mathfrak {L},{{\widehat{\Psi }}}_{3})\), where \({{\widehat{\Psi }}}_{3}={{\widehat{\Psi }}}_{1}\widehat{\cup }{{\widehat{\Psi }}}_{2}\) and
Theorem 3
Assume that \(\breve{\mathcal {D}}\) is a universal set, \({{\widehat{\Psi }}}_{1},{{\widehat{\Psi }}}_{2},{{\widehat{\Psi }}}_{3}\widehat{\subseteq }\nabla\) and \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}),(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\), \((\mathfrak {L},{{\widehat{\Psi }}}_{3})\) are CIFHSSs in \(\breve{\mathcal {D}}\). Then,
- i):
-
\((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}){\widehat{\cup }}(\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})=(\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\)
- ii):
-
\(0_{(\breve{\mathcal {D}}_{IFH},\nabla )}\) \({\widehat{\cup }}(\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})=(\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\)
- iii):
-
\((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}){\widehat{\cup }}\) \(1_{(\breve{\mathcal {D}}_{CIFH},\nabla )}=1_{(\breve{\mathcal {D}}_{CIFH},\nabla )}\)
- iv):
-
\((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}){\widehat{\cup }}(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})=(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2}){\widehat{\cup }}(\grave{\mathfrak {J}},{{\widehat{\Psi }}} _{1})\)
- v):
-
\(((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}){\widehat{\cup }}(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2}))\,{\widehat{\cup }}(\mathfrak {L},{{\widehat{\Psi }}}_{3})=(\grave{\mathfrak {J}}, {{\widehat{\Psi }}}_{1}){\widehat{\cup }}\,((\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2}){\widehat{\cup }}(\mathfrak {L},{{\widehat{\Psi }}}_{3}))\)
Proof
Proofs are trivial.\(\square\)
Definition 15
Suppose that \(\breve{\mathcal {D}}\) is an initial universe, \({{\widehat{\Psi }}}_{1},{{\widehat{\Psi }}}_{2}\widehat{\subseteq }\nabla\) and \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}),(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\) are two CIFHSSs in \(\breve{\mathcal {D}}.\) The intersection of \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\) and \((\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\) is denoted as: \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}){\widehat{\cap }}(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})=(\mathfrak {L},{{\widehat{\Psi }}}_{3})\), where \({{\widehat{\Psi }}}_{3}={{\widehat{\Psi }}}_{1}\widehat{\cap }{{\widehat{\Psi }}}_{2},\)
Theorem 4
Consider an initial universe \(\breve{\mathcal {D}}\), \({{\widehat{\Psi }}}_{1},{{\widehat{\Psi }}}_{2},{{\widehat{\Psi }}}_{3}\widehat{\subseteq }\nabla\) and \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}),(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2}),\) \((\mathfrak {L},{{\widehat{\Psi }}}_{3})\) are CIFHSSs in \(\breve{\mathcal {D}}\). Then,
- i):
-
\((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}){\widehat{\cap }}(\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})=(\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\)
- ii):
-
\(0_{(\breve{\mathcal {D}}_{CIFH},\nabla )}\) \({\widehat{\cap }}(\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})=0_{(\breve{\mathcal {D}}_{CIFH},\nabla )}\)
- iii):
-
\((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}){\widehat{\cap }}1_{(\breve{\mathcal {D}}_{CIFH},\nabla )}=(\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\)
- iv):
-
\((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}){\widehat{\cap }}(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})=(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2}){\widehat{\cap }}(\grave{\mathfrak {J}},{{\widehat{\Psi }}} _{1})\)
- v):
-
\(((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}){\widehat{\cap }}(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2}))\,{\widehat{\cap }}(\mathfrak {L},{{\widehat{\Psi }}}_{3})=(\grave{\mathfrak {J}}, {{\widehat{\Psi }}}_{1}){\widehat{\cap }}\,((\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2}){\widehat{\cap }}(\mathfrak {L},{{\widehat{\Psi }}}_{3}))\)
Proof
Straightforward. \(\square\)
Definition 16
Assume that \(\breve{\mathcal {D}}\) is a universal set, \({{\widehat{\Psi }}}_{1},{{\widehat{\Psi }}}_{2}\widehat{\subseteq }\nabla\) and \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}),(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\) are two CIFHSSs in \(\breve{\mathcal {D}}.\) The difference of \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\) and \((\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\) is denoted as \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}){\tilde{\backslash }}(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})=(\mathfrak {L},{{\widehat{\Psi }}}_{3})\), where
\((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}){\widehat{\cap }}(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})^{c}=(\mathfrak {L},{{\widehat{\Psi }}}_{3}).\)
Example 5
Assume the attributes of Example 1 and consider \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\), \((\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\) are two CIFHSSs in \(\breve{\mathcal {D}}=\{{\grave{\breve{\varrho }}}_{1},{\grave{\breve{\varrho }}}_{2},{\grave{\breve{\varrho }}}_{3}\}.\) The CIFHSS \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\) and \((\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\) defined by:
The union, intersection, and difference operators for the aforementioned CIFHSSs are expressed as:
and
Theorem 5
Consider an initial universe \(\breve{\mathcal {D}}\), \({{\widehat{\Psi }}}_{1},{{\widehat{\Psi }}}_{2}\widehat{\subseteq }\nabla\) and \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}),(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\) are two CIFHSSs in \(\breve{\mathcal {D}}\). Then, De-Morgan Laws are valid.
-
i)
\(((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\widehat{\cup }(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2}))^{c}=(\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})^{c}\widehat{\cap }(\grave{\mathfrak {K}}, {{\widehat{\Psi }}}_{2})^{c}\)
-
ii)
\(((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\widehat{\cap }(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2}))^{c}=(\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})^{c}\widehat{\cup }(\grave{\mathfrak {K}}, {{\widehat{\Psi }}}_{2})^{c}\)
Proof
We just prove \(((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\widehat{\cup }(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2}))^{c}=(\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})^{c}\widehat{\cap }(\grave{\mathfrak {K}}, {{\widehat{\Psi }}}_{2})^{c}\). The other property can be shown in a similar manner.
Consider \(((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\widehat{\cup }(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2}))^{c}=(\mathfrak {L},{{\widehat{\Psi }}}_{1}\widehat{\cup }{{\widehat{\Psi }}}_{2})\) and \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})^{c}\widehat{\cap }(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})^{c}=(\mathfrak {O},{{\widehat{\Psi }}}_{1}\widehat{\cup }{{\widehat{\Psi }}}_{2})\).
We examine the following possibilities for every \({\grave{\breve{\mathfrak {z}}}}\in {{\widehat{\Psi }}}_{1}\widehat{\cup }{{\widehat{\Psi }}}_{2}\).
Case 1: \({\grave{\breve{\mathfrak {z}}}}\in {{\widehat{\Psi }}}_{1}-{{\widehat{\Psi }}}_{2}\). Then \(\mathfrak {L}({\grave{\breve{\mathfrak {z}}}})=\grave{\mathfrak {J}}^{c}({\grave{\breve{\mathfrak {z}}}})=\mathfrak {O}({\grave{\breve{\mathfrak {z}}}})\).
Case 2: \({\grave{\breve{\mathfrak {z}}}}\in {{\widehat{\Psi }}}_{2}-{{\widehat{\Psi }}}_{1}\). Then \(\mathfrak {L}({\grave{\breve{\mathfrak {z}}}})=\grave{\mathfrak {K}}^{c}({\grave{\breve{\mathfrak {z}}}})=\mathfrak {O}({\grave{\breve{\mathfrak {z}}}})\).
Case 3: \({\grave{\breve{\mathfrak {z}}}}\in {{\widehat{\Psi }}}_{1}\widehat{\cap }{{\widehat{\Psi }}}_{2}\). Then \(\mathfrak {L}({\grave{\breve{\mathfrak {z}}}})=(\zeta ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\widehat{\cap }\zeta ^{F}_{\grave{\mathfrak {K}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}}),\zeta ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})\widehat{\cup }\zeta ^{T}_{ \grave{\mathfrak {K}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}}))=\grave{\mathfrak {J}}^{c}({\grave{\breve{\mathfrak {z}}}})\widehat{\cap } \grave{\mathfrak {K}}^{c}({\grave{\breve{\mathfrak {z}}}})=\mathfrak {O}({\grave{\breve{\mathfrak {z}}}})\).
Therefore, \(\mathfrak {L}\) and \(\mathfrak {O}\) are same operators, so
\(\square\)
Definition 17
Assume that \(\breve{\mathcal {D}}\) is a universal set, \({{\widehat{\Psi }}}_{1},{{\widehat{\Psi }}}_{2}\widehat{\subseteq }\nabla\) and \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}),(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\) are two CIFHSSs in \(\breve{\mathcal {D}}\). The “AND” operation on them expressed by \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\widehat{\wedge }(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})=(\mathfrak {L},{{\widehat{\Psi }}}_{1}\times {{\widehat{\Psi }}}_{2})\) is presented as:
where
Definition 18
Suppose that \(\breve{\mathcal {D}}\) is a universal discourse, \({{\widehat{\Psi }}}_{1},{{\widehat{\Psi }}}_{2}\widehat{\subseteq }\nabla\) and \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}),(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\) are two CIFHSSs in \(\breve{\mathcal {D}}\). The “OR” operation on them expressed by \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\widehat{\vee }(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})=(\mathfrak {L},{{\widehat{\Psi }}}_{1}\times {{\widehat{\Psi }}}_{2})\) is written as:
where
Theorem 6
Consider an initial universe \(\breve{\mathcal {D}}\), \({{\widehat{\Psi }}}_{1},{{\widehat{\Psi }}}_{2},{{\widehat{\Psi }}}_{3}\widehat{\subseteq }\nabla\) and \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}),(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\), \((\mathfrak {L},{{\widehat{\Psi }}}_{3})\) are CIFHSSs in \(\breve{\mathcal {D}}\). Then,
-
i)
\((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\widehat{\vee }[(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\widehat{\vee }(\mathfrak {L},{{\widehat{\Psi }}}_{3})]=[(\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\widehat{\vee }(\grave{\mathfrak {K}}, {{\widehat{\Psi }}}_{2})]\widehat{\vee }(\mathfrak {L},{{\widehat{\Psi }}}_{3})\)
-
ii)
\((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\widehat{\wedge }[(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\widehat{\wedge }(\mathfrak {L},{{\widehat{\Psi }}}_{3})]=[(\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\widehat{\wedge } (\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})]\widehat{\wedge }(\mathfrak {L},{{\widehat{\Psi }}}_{3})\)
Proof
Proofs are trivial. \(\square\)
Theorem 7
Assume that \(\breve{\mathcal {D}}\) is an initial universe, \({{\widehat{\Psi }}}_{1},{{\widehat{\Psi }}}_{2}\widehat{\subseteq }\nabla\) and \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1}),(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\) are two CIFHSSs in \(\breve{\mathcal {D}}\). Then,
-
i)
\([(\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\widehat{\vee }(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})]^{c}=(\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})^{c}\widehat{\wedge }(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})^{c}\)
-
ii)
\([(\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\widehat{\wedge }(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})]^{c}=(\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})^{c}\widehat{\vee }(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})^{c}.\)
Proof
We merely show (i). The other properties can be shown in a similar way.
For all \(({\grave{\breve{\mathfrak {z}}}}_{1},{\grave{\breve{\mathfrak {z}}}}_{2})\in {{\widehat{\Psi }}}_{1}\times {{\widehat{\Psi }}}_{2}\) and \({\grave{\breve{\varrho }}}\in \breve{\mathcal {D}},\)
However,
Then,
Thus, \([(\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\widehat{\vee }(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})]^{c}=(\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})^{c}\widehat{\wedge }(\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})^{c}\) is proved. \(\square\)
Example 6
Assume the attributes of Example 1. Then, the CIFHSSs \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\) and \((\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\) are defined as:
Suppose \((\breve{\varsigma }_{2},{\breve{\varpi }}_{2},{\breve{\delta }}_{1})=\mathfrak {x}_{1}\), \((\breve{\varsigma }_{2},{\breve{\varpi }}_{2},{\breve{\delta }}_{2})=\mathfrak {x}_{2}\), \((\breve{\varsigma }_{2},{\breve{\varpi }}_{3},{\breve{\delta }}_{1})=\mathfrak {x}_{3}\), \((\breve{\varsigma }_{2},{\breve{\varpi }}_{3},{\breve{\delta }}_{2})=\mathfrak {x}_{4}\) in \((\grave{\mathfrak {J}},{{\widehat{\Psi }}}_{1})\) and \((\breve{\varsigma }_{1},{\breve{\varpi }}_{3},{\breve{\delta }}_{2})=\mathfrak {z}_{1}\), \((\breve{\varsigma }_{1},{\breve{\varpi }}_{3},{\breve{\delta }}_{3})=\mathfrak {z}_{2}\), \((\breve{\varsigma }_{2},{\breve{\varpi }}_{3},{\breve{\delta }}_{2})=\mathfrak {z}_{3},(\breve{\varsigma }_{2},{\breve{\varpi }}_{3},{\breve{\delta }}_{3})=\mathfrak {z}_{4}\) in \((\grave{\mathfrak {K}},{{\widehat{\Psi }}}_{2})\) for simplifications. Then, the “AND” and “OR” operations of these sets are given in Tables 4 and 5, respectively.
Applications of CIFHSS in decision-making
Traffic congestion is a common issue in many cities, especially in rapidly growing regions. This issue negatively impacts human life, leading to time wastage, health problems, and economic repercussions. Therefore, establishing a sustainable transportation system in densely populated urban areas is crucial. As traffic congestion involves different parameters such as traffic volume, traffic density, signal cycle time, and peak hour traffic, these must be thoroughly analyzed to make well-informed decisions. However, this analysis may involve fuzziness and vagueness due to imprecise data and incomplete information. In this regard, this section proposed a Multi-Attribute Decision-Making (MADM) model based on the complex intuitionistic fuzzy hypersoft set and used for a real-world scenario to demonstrate its application. The scenario focuses on selecting the most sustainable urban transit solutions by aggregating CIFHSSs. This strategy makes the complex decision-making process more understandable and applicable to daily life scenarios.
Algorithmic approach based on CIFHSS
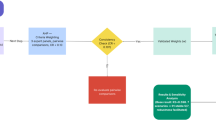
This algorithm includes the following steps:
-
1.
Considering the substantial sets and perspectives of decision makers, design CIFHSS: \(\breve{\Gamma }=(\grave{\mathfrak {J}},{\nabla })\) i.e. \(\breve{\Gamma }= \left\{ \langle {\grave{\breve{\mathfrak {z}}}}, (\frac{{\grave{\breve{\varrho }}}}{\zeta ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}}),\zeta ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}})}({\grave{\breve{\varrho }}})})\rangle :{\grave{\breve{\varrho }}}\in \breve{\mathcal {D}},{\grave{\breve{\mathfrak {z}}}}\in {\widehat{\Psi }} \widehat{\subseteq } \nabla \right\}\).
-
2.
The matrix form of CIFHSS is represented as \(\breve{\Theta }_{h \times k}\), where h and k are natural values representing the number of attributes and dimension of the initial object space, respectively.
$$\breve{\Theta }_{h \times k} = \left( {\begin{array}{*{20}{c}} \breve{\tau }_{11}& \breve{\tau }_{12}& \cdots & \breve{\tau }_{1k}\\ \breve{\tau }_{21}& \breve{\tau }_{22}& \cdots & \breve{\tau }_{2k}\\ \breve{\tau }_{31}& \breve{\tau }_{32}& \cdots & \breve{\tau }_{3k}\\ \vdots & \vdots & \ddots & \vdots \\ \breve{\tau }_{h1}& \breve{\tau }_{h2}& \cdots & \breve{\tau }_{hk} \end{array}} \right)$$where,
$$\begin{aligned} \breve{\tau }_{11}= \left\langle r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_1)}({{\grave{\breve{\varrho }}}}_1) e^{\iota \omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_1)}({{\grave{\breve{\varrho }}}}_1)}, r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_1)}({{\grave{\breve{\varrho }}}}_1) e^{\iota \omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_1)}({{\grave{\breve{\varrho }}}}_1)} \right\rangle \end{aligned}$$$$\begin{aligned} \breve{\tau }_{12}= \left\langle r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_1)}({{\grave{\breve{\varrho }}}}_2) e^{\iota \omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_1)}({{\grave{\breve{\varrho }}}}_2)}, r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_1)}({{\grave{\breve{\varrho }}}}_2) e^{\iota \omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_1)}({{\grave{\breve{\varrho }}}}_2)}\right\rangle \end{aligned}$$$$\begin{aligned} .......................................................................... \end{aligned}$$$$\begin{aligned} .......................................................................... \end{aligned}$$$$\begin{aligned} .......................................................................... \end{aligned}$$$$\begin{aligned} \breve{\tau }_{1k}= \left\langle r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_1)}({{\grave{\breve{\varrho }}}}_k) e^{\iota \omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_1)}({{\grave{\breve{\varrho }}}}_k)}, r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_1)}({{\grave{\breve{\varrho }}}}_k) e^{\iota \omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_1)}({{\grave{\breve{\varrho }}}}_k)}\right\rangle \end{aligned}$$$$\begin{aligned} \breve{\tau }_{21}= \left\langle r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_2)}({{\grave{\breve{\varrho }}}}_1) e^{\iota \omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_2)}({{\grave{\breve{\varrho }}}}_1)}, r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_2)}({{\grave{\breve{\varrho }}}}_1) e^{\iota \omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_2)}({{\grave{\breve{\varrho }}}}_1)}\right\rangle \end{aligned}$$$$\begin{aligned} \breve{\tau }_{22}= \left\langle r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_2)}({{\grave{\breve{\varrho }}}}_2) e^{\iota \omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_2)}({{\grave{\breve{\varrho }}}}_2)}, r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_2)}({{\grave{\breve{\varrho }}}}_2) e^{\iota \omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_2)}({{\grave{\breve{\varrho }}}}_2)}\right\rangle \end{aligned}$$$$\begin{aligned} .......................................................................... \end{aligned}$$$$\begin{aligned} .......................................................................... \end{aligned}$$$$\begin{aligned} .......................................................................... \end{aligned}$$$$\begin{aligned} \breve{\tau }_{2k}= \left\langle r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_2)}({{\grave{\breve{\varrho }}}}_k) e^{\iota \omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_2)}({{\grave{\breve{\varrho }}}}_k)}, r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_2)}({{\grave{\breve{\varrho }}}}_k) e^{\iota \omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_2)}({{\grave{\breve{\varrho }}}}_k)}\right\rangle \end{aligned}$$$$\begin{aligned} \breve{\tau }_{31}= \left\langle r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_3)}({{\grave{\breve{\varrho }}}}_1) e^{\iota \omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_3)}({{\grave{\breve{\varrho }}}}_1)}, r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_3)}({{\grave{\breve{\varrho }}}}_1) e^{\iota \omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_3)}({{\grave{\breve{\varrho }}}}_1)}\right\rangle \end{aligned}$$$$\begin{aligned} \breve{\tau }_{32}= \left\langle r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_3)}({{\grave{\breve{\varrho }}}}_2) e^{\iota \omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_3)}({{\grave{\breve{\varrho }}}}_2)}, r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_3)}({{\grave{\breve{\varrho }}}}_2) e^{\iota \omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_3)}({{\grave{\breve{\varrho }}}}_2)}\right\rangle \end{aligned}$$$$\begin{aligned} .......................................................................... \end{aligned}$$$$\begin{aligned} .......................................................................... \end{aligned}$$$$\begin{aligned} .......................................................................... \end{aligned}$$$$\begin{aligned} \breve{\tau }_{3k}= \left\langle r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_3)}({{\grave{\breve{\varrho }}}}_k) e^{\iota \omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_3)}({{\grave{\breve{\varrho }}}}_k)}, r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_3)}({{\grave{\breve{\varrho }}}}_k) e^{\iota \omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_3)}({{\grave{\breve{\varrho }}}}_k)}\right\rangle \end{aligned}$$$$\begin{aligned} .......................................................................... \end{aligned}$$$$\begin{aligned} .......................................................................... \end{aligned}$$$$\begin{aligned} .......................................................................... \end{aligned}$$$$\begin{aligned} \breve{\tau }_{h1}= \left\langle r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_h)}({{\grave{\breve{\varrho }}}}_1) e^{\iota \omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_h)}({{\grave{\breve{\varrho }}}}_1)}, r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_h)}({{\grave{\breve{\varrho }}}}_1) e^{\iota \omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_h)}({{\grave{\breve{\varrho }}}}_1)}\right\rangle \end{aligned}$$$$\begin{aligned} \breve{\tau }_{h2}=\left\langle r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_h)}({{\grave{\breve{\varrho }}}}_2) e^{\iota \omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_h)}({{\grave{\breve{\varrho }}}}_2)}, r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_h)}({{\grave{\breve{\varrho }}}}_2) e^{\iota \omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_h)}({{\grave{\breve{\varrho }}}}_2)}\right\rangle \end{aligned}$$$$\begin{aligned} .......................................................................... \end{aligned}$$$$\begin{aligned} .......................................................................... \end{aligned}$$$$\begin{aligned} .......................................................................... \end{aligned}$$$$\begin{aligned} \breve{\tau }_{hk}= \left\langle r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_h)}({{\grave{\breve{\varrho }}}}_k) e^{\iota \omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_h)}({{\grave{\breve{\varrho }}}}_k)}, r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_h)}({{\grave{\breve{\varrho }}}}_k) e^{\iota \omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_h)}({{\grave{\breve{\varrho }}}}_k)}\right\rangle \end{aligned}$$.
-
3.
Convert the original matrix \(\breve{\Theta }_{h \times k}\) into its core form \(\breve{\Theta }^{core}_{h \times k}\) which is represented as:
$$\breve{\Theta }^{core}_{h \times k} = \left( {\begin{array}{*{20}{c}} \breve{\tau }^{'}_{11}& \breve{\tau }^{'}_{12}& \cdots & \breve{\tau }^{'}_{1k}\\ \breve{\tau }^{'}_{21}& \breve{\tau }^{'}_{22}& \cdots & \breve{\tau }^{'}_{2k}\\ \breve{\tau }^{'}_{31}& \breve{\tau }^{'}_{32}& \cdots & \breve{\tau }^{'}_{3k}\\ \vdots & \vdots & \ddots & \vdots \\ \breve{\tau }^{'}_{h1}& \breve{\tau }^{'}_{h2}& \cdots & \breve{\tau }^{'}_{hk} \end{array}} \right)$$where,
$$\begin{aligned} \breve{\tau }^{'}_{11}=\left\langle | r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_1)}({{\grave{\breve{\varrho }}}}_1)- r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_1)}({{\grave{\breve{\varrho }}}}_1)| e^{{\iota }|\omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_1)}({{\grave{\breve{\varrho }}}}_1)-\omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_1)}({{\grave{\breve{\varrho }}}}_1)|} \right\rangle \end{aligned}$$$$\begin{aligned} \breve{\tau }^{'}_{12}= \left\langle | r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_1)}({{\grave{\breve{\varrho }}}}_2)- r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_1)}({{\grave{\breve{\varrho }}}}_2)| e^{{\iota }|\omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_1)}({{\grave{\breve{\varrho }}}}_2)-\omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_1)}({{\grave{\breve{\varrho }}}}_2)|} \right\rangle \end{aligned}$$$$\begin{aligned} ................................................................................ \end{aligned}$$$$\begin{aligned} ................................................................................ \end{aligned}$$$$\begin{aligned} ................................................................................ \end{aligned}$$$$\begin{aligned} \breve{\tau }^{'}_{1k}=\left\langle | r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_1)}({{\grave{\breve{\varrho }}}}_k)- r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_1)}({{\grave{\breve{\varrho }}}}_k)| e^{{\iota }|\omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_1)}({{\grave{\breve{\varrho }}}}_k)-\omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_1)}({{\grave{\breve{\varrho }}}}_k)|} \right\rangle \end{aligned}$$$$\begin{aligned} \breve{\tau }^{'}_{21}= \left\langle | r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_2)}({{\grave{\breve{\varrho }}}}_1)- r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_2)}({{\grave{\breve{\varrho }}}}_1)| e^{{\iota }|\omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_2)}({{\grave{\breve{\varrho }}}}_1)-\omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_2)}({{\grave{\breve{\varrho }}}}_1)|} \right\rangle \end{aligned}$$$$\begin{aligned} \breve{\tau }^{'}_{22}= \left\langle | r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_2)}({{\grave{\breve{\varrho }}}}_2)- r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_2)}({{\grave{\breve{\varrho }}}}_2)| e^{{\iota }|\omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_2)}({{\grave{\breve{\varrho }}}}_2)-\omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_2)}({{\grave{\breve{\varrho }}}}_2)|} \right\rangle \end{aligned}$$$$\begin{aligned} ................................................................................ \end{aligned}$$$$\begin{aligned} ................................................................................ \end{aligned}$$$$\begin{aligned} ................................................................................ \end{aligned}$$$$\begin{aligned} \breve{\tau }^{'}_{2k}= \left\langle | r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_2)}({{\grave{\breve{\varrho }}}}_k)- r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_2)}({{\grave{\breve{\varrho }}}}_k)| e^{{\iota }|\omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_2)}({{\grave{\breve{\varrho }}}}_k)-\omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_2)}({{\grave{\breve{\varrho }}}}_k)|} \right\rangle \end{aligned}$$$$\begin{aligned} \breve{\tau }^{'}_{31}= \left\langle | r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_3)}({{\grave{\breve{\varrho }}}}_1)- r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_3)}({{\grave{\breve{\varrho }}}}_1)| e^{{\iota }|\omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_3)}({{\grave{\breve{\varrho }}}}_1)-\omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_3)}({{\grave{\breve{\varrho }}}}_1)|} \right\rangle \end{aligned}$$$$\begin{aligned} \breve{\tau }^{'}_{32}=\left\langle | r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_3)}({{\grave{\breve{\varrho }}}}_2)- r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_3)}({{\grave{\breve{\varrho }}}}_2)| e^{{\iota }|\omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_3)}({{\grave{\breve{\varrho }}}}_2)-\omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_3)}({{\grave{\breve{\varrho }}}}_2)|} \right\rangle \end{aligned}$$$$\begin{aligned} ................................................................................ \end{aligned}$$$$\begin{aligned} ................................................................................ \end{aligned}$$$$\begin{aligned} ................................................................................ \end{aligned}$$$$\begin{aligned} \breve{\tau }^{'}_{3k}= \left\langle | r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_3)}({{\grave{\breve{\varrho }}}}_k)- r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_3)}({{\grave{\breve{\varrho }}}}_k)| e^{{\iota }|\omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_3)}({{\grave{\breve{\varrho }}}}_k)-\omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_3)}({{\grave{\breve{\varrho }}}}_k)|} \right\rangle \end{aligned}$$$$\begin{aligned} ................................................................................ \end{aligned}$$$$\begin{aligned} ................................................................................ \end{aligned}$$$$\begin{aligned} ................................................................................ \end{aligned}$$$$\begin{aligned} \breve{\tau }^{'}_{h1}= \left\langle | r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_h)}({{\grave{\breve{\varrho }}}}_1)- r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_h)}({{\grave{\breve{\varrho }}}}_1)| e^{{\iota }|\omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_h)}({{\grave{\breve{\varrho }}}}_1)-\omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_h)}({{\grave{\breve{\varrho }}}}_1)|} \right\rangle \end{aligned}$$$$\begin{aligned} \breve{\tau }^{'}_{h2}= \left\langle | r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_h)}({{\grave{\breve{\varrho }}}}_2)- r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_h)}({{\grave{\breve{\varrho }}}}_2)| e^{{\iota }|\omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_h)}({{\grave{\breve{\varrho }}}}_2)-\omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_h)}({{\grave{\breve{\varrho }}}}_2)|} \right\rangle \end{aligned}$$$$\begin{aligned} ................................................................................ \end{aligned}$$$$\begin{aligned} ................................................................................ \end{aligned}$$$$\begin{aligned} ................................................................................ \end{aligned}$$$$\begin{aligned} \breve{\tau }^{'}_{hk}= \left\langle | r^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_h)}({{\grave{\breve{\varrho }}}}_k)- r^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_h)}({{\grave{\breve{\varrho }}}}_k)| e^{{\iota }|\omega ^{T}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_h)}({{\grave{\breve{\varrho }}}}_k)-\omega ^{F}_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_h)}({{\grave{\breve{\varrho }}}}_k)|} \right\rangle \end{aligned}$$.
-
4.
Divide the core matrix into two independent matrices: one for amplitude terms \(\breve{\Theta }^{core}_{amp}\), and another for phase terms \(\breve{\Theta }^{core}_{pha}\) represented as:
$$\breve{\Theta }^{core}_{amp} = \left( {\begin{array}{*{20}{c}} \breve{\tau }^{''}_{11}& \breve{\tau }^{''}_{12}& \cdots & \breve{\tau }^{''}_{1k}\\ \breve{\tau }^{''}_{21}& \breve{\tau }^{''}_{22}& \cdots & \breve{\tau }^{''}_{2k}\\ \breve{\tau }^{''}_{31}& \breve{\tau }^{''}_{32}& \cdots & \breve{\tau }^{''}_{3k}\\ \vdots & \vdots & \ddots & \vdots \\ \breve{\tau }^{''}_{h1}& \breve{\tau }^{''}_{h2}& \cdots & \breve{\tau }^{''}_{hk} \end{array}} \right) _{h \times k}$$where \(\breve{\tau }^{''}_{uv}= r_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_u)}({{\grave{\breve{\varrho }}}}_v), u\,\in \{1,2,...,h\}\, \& \, v\,\in \{1,2,...,k\}\) and
$$\breve{\Theta }^{core}_{pha} = \left( {\begin{array}{*{20}{c}} \breve{\tau }^{'''}_{11}& \breve{\tau }^{'''}_{12}& \cdots & \breve{\tau }^{'''}_{1k}\\ \breve{\tau }^{'''}_{21}& \breve{\tau }^{'''}_{22}& \cdots & \breve{\tau }^{'''}_{2k}\\ \breve{\tau }^{'''}_{31}& \breve{\tau }^{'''}_{32}& \cdots & \breve{\tau }^{'''}_{3k}\\ \vdots & \vdots & \ddots & \vdots \\ \breve{\tau }^{'''}_{h1}& \breve{\tau }^{'''}_{h2}& \cdots & \breve{\tau }^{'''}_{hk} \end{array}} \right) _{h \times k}$$where \(\breve{\tau }^{'''}_{uv}= \omega _{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_u)}({{\grave{\breve{\varrho }}}}_v), u\,\in \{1,2,...,h\}\, \& \, v\,\in \{1,2,...,k\}\).
-
5.
Calculate the maximum decision values \(\breve{\mathfrak {W}}^{max}_{amp}({\grave{\breve{\varrho }}}_v)\), minimum decision values \(\breve{\mathfrak {W}}^{min}_{amp}({\grave{\breve{\varrho }}}_v)\) and score values \(\mathfrak {O}_{amp}({\grave{\breve{\varrho }}}_v)\) for each alternative \({\grave{\breve{\varrho }}}_v\), with \(\, v\,\in \{1,2,...,k\}\) from matrix \(\breve{\Theta }^{core}_{amp}\). Similarly determine the corresponding values \(\breve{\mathfrak {W}}^{max}_{pha}({\grave{\breve{\varrho }}}_v)\), \(\breve{\mathfrak {W}}^{min}_{pha}({\grave{\breve{\varrho }}}_v)\) and \(\mathfrak {O}_{pha}({\grave{\breve{\varrho }}}_v)\) from matrix \(\breve{\Theta }^{core}_{pha}\) by applying the given set of formulas.
$$\begin{aligned} \breve{\mathfrak {W}}^{max}_{amp}({\grave{\breve{\varrho }}}_v)= \sum \limits _{u = 1}^h {{{\left( {1 - r_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_u)}({{\grave{\breve{\varrho }}}}_v)} \right) }^2}}.\end{aligned}$$(1)$$\begin{aligned} \breve{\mathfrak {W}}^{min}_{amp}({\grave{\breve{\varrho }}}_v)= \sum \limits _{u = 1}^h {{{\left( {r_{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_u)}({{\grave{\breve{\varrho }}}}_v)} \right) }^2}}. \end{aligned}$$(2)$$\begin{aligned} \mathfrak {O}_{amp}({\grave{\breve{\varrho }}}_v)= \frac{\breve{\mathfrak {W}}^{max}_{amp}({\grave{\breve{\varrho }}}_v) + \breve{\mathfrak {W}}^{min}_{amp}({\grave{\breve{\varrho }}}_v)}{v}. \end{aligned}$$(3)$$\begin{aligned} \breve{\mathfrak {W}}^{max}_{pha}({\grave{\breve{\varrho }}}_v)= \sum \limits _{u = 1}^h {{{\left( {1 - {\omega _{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_u)}({{\grave{\breve{\varrho }}}}_v)}} \right) }^2}}. \end{aligned}$$(4)$$\begin{aligned} \breve{\mathfrak {W}}^{min}_{pha}({\grave{\breve{\varrho }}}_v)= \sum \limits _{u = 1}^h {{{\left( {\omega _{\grave{\mathfrak {J}}({\grave{\breve{\mathfrak {z}}}}_u)}({{\grave{\breve{\varrho }}}}_v)} \right) }^2}}. \end{aligned}$$(5)$$\begin{aligned} \mathfrak {O}_{pha}({\grave{\breve{\varrho }}}_v)= \frac{\breve{\mathfrak {W}}^{max}_{pha}({\grave{\breve{\varrho }}}_v) + \breve{\mathfrak {W}}^{min}_{pha}({\grave{\breve{\varrho }}}_v)}{v}. \end{aligned}$$(6) -
6.
Calculate the mean \(\mathfrak {O}({\grave{\breve{\varrho }}}_v)\) by utilizing the below mentioned formula.
$$\begin{aligned} \mathfrak {O}({\grave{\breve{\varrho }}}_v)= \frac{ \mathbb {O}_{amp}({\grave{\breve{\varrho }}}_v) + \mathbb {O}_{pha}({\grave{\breve{\varrho }}}_v)}{2}. \end{aligned}$$(7) -
7.
Choose the alternative with highest \(\mathfrak {O}({\grave{\breve{\varrho }}}_v)\) as optimal recommendation.
The progressive graphical analysis of the proposed CIFHSS-based algorithm is depicted in Fig. 1.
Practical implementation of proposed algorithm
This section demonstrates the effectiveness of the proposed algorithm using a practical MADM-based scenario. The following example gives a detailed explanation.
Example 7
To demonstrate the practical applicability of the proposed CIFHSS-based MADM model, we examine a transportation planning scenario using realistic attribute values aligned with publicly available data from municipal transport reports and urban mobility planning studies. While access to raw smart city datasets was limited, parameters such as operational cost, emission levels, coverage, and user satisfaction were constructed based on credible policy documents and transport studies. A city planning authority, “URBANPLAN” (a fictitious name), is entrusted with determining the best sustainable urban transportation option to alleviate the traffic congestion, reduce the environmental impact, and improve the quality of life for its residents. The managing director (MD) of “URBANPLAN” is much concerned about the long-term viability of the available options. In order to ensure a thorough investigation, the MD has decided to establish two internal committees \(\mathfrak {S}_1= \{\hat{Y}_1, \hat{Y}_2\}\) and \(\mathfrak {S}_2= \{\hat{Y}_3, \hat{Y}_4\}\). Committee \(\mathfrak {S}_1\) is responsible for the initial screening of transportation options. They will choose the most promising options based on preliminary criteria. The committee \(\mathfrak {S}_2\) is responsible for further review and ultimate evaluation of the shortlisted options. They will evaluate each alternative based on a more detailed set of attributes and sub-attributes. After the initial screening by Committee \(\mathfrak {S}_1\), four transportation options are shortlisted for further evaluation:
where \({\grave{\breve{\varrho }}}_1\) = Electric Bus Rapid Transit, \({\grave{\breve{\varrho }}}_2\) = Expanded Bicycle Lane Network, \({\grave{\breve{\varrho }}}_3\) = Light Rail Transit and \({\grave{\breve{\varrho }}}_4\) = Hybrid Car-Sharing Program.
Committee \(\mathfrak {S}_2\) has agreed on the following attributes and sub-attributes to evaluate the shortlisted transport alternatives.
\(\mathfrak {Q}_1\) = Environmental Impact = { Air Pollution Reduction \((\breve{\varsigma }_1)\), Noise Pollution Reduction \((\breve{\varsigma }_2)\), Carbon Footprint Reduction \((\breve{\varsigma }_3)\) }
\(\mathfrak {Q}_2\) = Economic Viability = { Initial Investment Cost \((\breve{\varpi }_1)\), Long-Term Operational Costs \((\breve{\varpi }_2)\), Job Creation \((\breve{\varpi }_3)\)}
\(\mathfrak {Q}_3\) = Social Acceptance = { Public Convenience \((\breve{\delta }_1)\), Accessibility for Disabled Individuals \((\breve{\delta }_2)\), Safety Perception \((\breve{\delta }_3)\) }
\(\mathfrak {Q}_4\) = Technological Readiness ={ Infrastructure Maturity \((\breve{ \varrho }_1)\), Maintenance Complexity \((\breve{\varrho }_2)\), Energy Source Reliability \((\breve{\varrho }_3)\) }.
Suppose that
\(\mathfrak {A}_1\) = { Air Pollution Reduction \((\breve{\varsigma }_1)\), Noise Pollution Reduction \((\breve{\varsigma }_2)\) } \(\widehat{\subseteq }\) \(\mathfrak {Q}_1\),
\(\mathfrak {A}_2\) = { Initial Investment Cost \((\breve{\varpi }_1)\), Long-Term Operational Costs \((\breve{\varpi }_2)\) } \(\widehat{\subseteq }\) \(\mathfrak {Q}_2\),
\(\mathfrak {A}_3\) = { Public Convenience \((\breve{\delta }_1)\) } \(\widehat{\subseteq }\) \(\mathfrak {Q}_3\),
\(\mathfrak {A}_4\) = { Energy Source Reliability \((\breve{\varrho }_3)\) } \(\widehat{\subseteq }\) \(\mathfrak {Q}_4\).
Combining these sub-attributes, we have the set \(\breve{\Xi } = \mathfrak {A}_1 \times \mathfrak {A}_2 \times \mathfrak {A}_3 \times \mathfrak {A}_4= \{ \breve{a}_1= (\breve{\varsigma }_1, \breve{\varpi }_1, \breve{\delta }_1, \breve{\varrho }_3 ), \breve{a}_2=(\breve{\varsigma }_1, \breve{\varpi }_2, \breve{\delta }_1, \breve{\varrho }_3), \breve{a}_3=(\breve{\varsigma }_2, \breve{\varpi }_1, \breve{\delta }_1, \breve{\varrho }_3) , \breve{a}_4=(\breve{\varsigma }_2, \breve{\varpi }_2, \breve{\delta }_1, \breve{\varrho }_3)\}\). The experts of Committee \(\mathfrak {S}_2\) will provide their opinions for each alternative in the set \(\breve{\mathcal {D}}\), which is considered as a universal set in terms of CIFHSS. The alternatives considered include Electric Bus Rapid Transit, Expanded Bicycle Lane Network, Light Rail Transit, and Hybrid Car-Sharing Program. Each alternative is evaluated using sub-attributes derived from high-level criteria including cost-efficiency, environmental impact, and feasibility. This ensures that the dataset used, while synthesized, reflects real-world patterns and decision-making conditions.
In the given case study, the hierarchical framework of parameters was developed based on field knowledge and expert consultation in the area of urban transportation planning. Initial criteria such as cost-dependent, sustainability of the environmental, coverage and availability were identified, each further decomposed into relevant sub-parametrs (e.g., cost into initial investment cost, long-term operational costs, and affordability).
To give the weights of these parameters and sub-parameters, an expert-driven approach (judgements, opinions, or estimations of experts) was employed. Two panels of field experts, including transport engineers, urban area field expert and public interest policy consultants, were considered to evaluate the relative importance of each parameter and sub-parameter using expressive terms (high importance and moderate importance, etc.). These linguistic attribute’s evaluations were then converted into intuitionistic fuzzy numbers and normalized to ensure consistency within the CIFHSS-based MADM framework.
Further, formal weighting methods such as Analytic Hierarchy Process (AHP) or entropy-based techniques were not used in this study, the qualitative expert-based method was considered appropriate due to the exploratory nature of the case study and limited availability of statistical datasets. Future research may incorporate AHP, fuzzy AHP, or machine learning-based weighting techniques to enhance the objectivity and scalability of the weight assignment process.
The steps of the proposed algorithm are followed in order to fully evaluate sustainable urban transport choices.
-
(1,2)
A CIFHSS \((\breve{\Gamma })\) is developed which is given in matrix notation \(\breve{\Theta }_{4 \times 4}\), as seen below:
$$\breve{\Theta }_{4 \times 4} = \left( {\begin{array}{*{20}{c}} \breve{\tau }_{11}& \breve{\tau }_{12}& \breve{\tau }_{13}& \breve{\tau }_{14} \\ \breve{\tau }_{21}& \breve{\tau }_{22} & \breve{\tau }_{23}& \breve{\tau }_{24}\\ \breve{\tau }_{31}& \breve{\tau }_{32}& \breve{\tau }_{33}& \breve{\tau }_{34}\\ \breve{\tau }_{41}& \breve{\tau }_{42} & \breve{\tau }_{43}& \breve{\tau }_{44} \end{array}} \right)$$where
$$\begin{aligned} \breve{\tau }_{11}=\left\langle {0.81\,e^{\iota \frac{\pi }{4}},0.13\,e^{\iota \frac{\pi }{8}}}\right\rangle ,\breve{\tau }_{12}=\left\langle {0.43\,e^{\iota \frac{\pi }{2}},0.25\,e^{\iota \frac{\pi }{3}}}\right\rangle , \end{aligned}$$$$\begin{aligned} \breve{\tau }_{13}=\left\langle {0.67\,e^{\iota \frac{\pi }{5}},0.02\,e^{\iota \frac{\pi }{6}}}\right\rangle ,\breve{\tau }_{14}=\left\langle {0.62\,e^{\iota \frac{\pi }{4}},0.01\,e^{\iota \frac{\pi }{5}}}\right\rangle , \end{aligned}$$$$\begin{aligned} \breve{\tau }_{21}=\left\langle {0.91\,e^{\iota \frac{\pi }{3}},0.03\,e^{\iota \frac{\pi }{6}}}\right\rangle ,\breve{\tau }_{22}=\left\langle {0.32\,e^{\iota \frac{\pi }{5}},0.19\,e^{\iota \frac{\pi }{8}}}\right\rangle , \end{aligned}$$$$\begin{aligned} \breve{\tau }_{23}=\left\langle {0.57\,e^{\iota \frac{\pi }{2}},0.31\,e^{\iota \frac{\pi }{3}}}\right\rangle , \breve{\tau }_{24}=\left\langle {0.49\,e^{\iota \frac{\pi }{4}},0.04\,e^{\iota \frac{\pi }{7}}}\right\rangle , \end{aligned}$$$$\begin{aligned} \breve{\tau }_{31}=\left\langle {0.84\,e^{\iota \frac{\pi }{2}},0.06\,e^{\iota \frac{\pi }{4}}}\right\rangle ,\breve{\tau }_{32}=\left\langle {0.29\,e^{\iota \frac{\pi }{3}},0.16\,e^{\iota \frac{\pi }{7}}}\right\rangle , \end{aligned}$$$$\begin{aligned} \breve{\tau }_{33}=\left\langle {0.61\,e^{\iota \frac{\pi }{6}},0.15\,e^{\iota \frac{\pi }{8}}}\right\rangle , \breve{\tau }_{34}=\left\langle {0.33\,e^{\iota \frac{\pi }{4}},0.25\,e^{\iota \frac{\pi }{12}}}\right\rangle , \end{aligned}$$$$\begin{aligned} \breve{\tau }_{41}=\left\langle {0.95\,e^{\iota \frac{\pi }{3}},0.01\,e^{\iota \frac{\pi }{12}}}\right\rangle , \breve{\tau }_{42}=\left\langle {0.17\,e^{\iota \frac{\pi }{12}},0.05\,e^{\iota \frac{\pi }{16}}}\right\rangle , \end{aligned}$$$$\begin{aligned} \breve{\tau }_{43}=\left\langle {0.45\,e^{\iota \frac{\pi }{4}},0.36\,e^{\iota \frac{\pi }{5}}}\right\rangle ,\breve{\tau }_{44}=\left\langle {0.73\,e^{\iota \frac{\pi }{12}},0.22\,e^{\iota \frac{\pi }{19}}}\right\rangle . \end{aligned}$$ -
(3)
The matrix
$$\begin{aligned} \breve{\Theta }_{4 \times 4} \end{aligned}$$is transformed into core matrix \(\breve{\Theta }^{core}_{4 \times 4}\)
$$\breve{\Theta }^{core}_{4 \times 4} = \left( {\begin{array}{*{20}{c}} {\langle 0.68\,e^{\iota (0.39)}\rangle }& {\langle 0.18,\,e^{\iota (0.52)}\rangle }& {\langle 0.65,\,e^{\iota (0.10)}\rangle }& {\langle 0.61,\,e^{\iota (0.15)}\rangle }\\ {\langle 0.88,\,e^{\iota (0.52)}\rangle }& {\langle 0.13,\,e^{\iota (0.24)}\rangle }& {\langle 0.26,\,e^{\iota (0.52)}\rangle }& {\langle 0.45,\,e^{\iota (0.34)}\rangle }\\ {\langle 0.78,\,e^{\iota (0.79)}\rangle }& {\langle 0.13,\,e^{\iota (0.60)}\rangle }& {\langle 0.46,\,e^{\iota (0.13)}\rangle }& {\langle 0.08,\,e^{\iota (0.52)}\rangle }\\ {\langle 0.94,\,e^{\iota (0.79)}\rangle }& {\langle 0.12,\,e^{\iota (0.07)}\rangle }& {\langle 0.09,\,e^{\iota (0.16)}\rangle }& {\langle 0.51,\,e^{\iota (0.10)}\rangle }\\ \end{array}} \right) .$$ -
(4)
The core matrix \(\breve{\Theta }^{core}_{h \times k}\) is divided into two parts: one for amplitude terms \(\breve{\Theta }^{core}_{amp}\) and another for phase terms \(\breve{\Theta }^{core}_{pha}\) as shown below
$$\breve{\Theta }^{core}_{amp} = \left( {\begin{array}{*{20}{c}} {0.68}& {0.18}& {0.65}& {0.61}\\ {0.88}& {0.13}& {0.26}& {0.45}\\ {0.78}& {0.13}& {0.46}& {0.08}\\ {0.94}& {0.12}& {0.09}& {0.51} \end{array}} \right) _{4 \times 4},$$and
$$\breve{\Theta }^{core}_{pha} = \left( {\begin{array}{*{20}{c}} {0.39}& {0.52}& {0.10}& {0.15}\\ {0.52}& {0.24}& {0.52}& {0.34}\\ {0.79}& {0.60}& {0.13}& {0.52}\\ {0.79}& {0.07}& {0.16}& {0.10} \end{array}} \right) _{4 \times 4}.$$ -
(5)
Maximum decision values \(\breve{\mathfrak {W}}^{max}_{amp}({\grave{\breve{\varrho }}}_m)\), minimum decision values \(\breve{\mathfrak {W}}^{min}_{amp}({\grave{\breve{\varrho }}}_v)\) and score values \(\mathfrak {O}_{amp}({\grave{\breve{\varrho }}}_v)\) for each alternative \({\grave{\breve{\varrho }}}_v\), with \(\, v\,\in \{1,2,...,k\}\) are calculated from matrix \(\breve{\Theta }^{core}_{amp}\). Similarly, the corresponding values \(\breve{\mathfrak {W}}^{max}_{pha}({\grave{\breve{\varrho }}}_v)\), \(\breve{\mathfrak {W}}^{min}_{pha}({\grave{\breve{\varrho }}}_v)\) and \(\mathfrak {O}_{pha}({\grave{\breve{\varrho }}}_v)\) are determined from matrix \(\breve{\Theta }^{core}_{pha}\) by utilizing the Equations 1-6 and are presented in Table 6 and Table 7.
-
(6)
The mean score \(\mathfrak {O}({\grave{\breve{\varrho }}}_v)\) is calculated by utilizing Equation 7 and is given in Table 8.
-
(7)
Since \({{{\grave{\breve{\varrho }}}_4}}\) has obtained the maximum value 0.7627, therefore it is recommended for the transportation option. The alternatives are ranked as follows: \({{{\grave{\breve{\varrho }}}_4}}\rangle {{{\grave{\breve{\varrho }}}_3}}\rangle {{{\grave{\breve{\varrho }}}_1}}\rangle {{{\grave{\breve{\varrho }}}_2}}\).
Sensitivity analysis-based discussion
In this section, a sensitivity analysis of score values for transportation choices is performed to determine the stability of the obtained results. For this objective, we used several statistical methods such as Pythagorean means and measures of dispersion to calculate the estimated score values for evaluating transportation choices. Thus, we analyze the following cases:
-
1.
Geometric Mean: By applying the concept of geometric mean for the calculation of mean score, we obtain
$$\begin{aligned} \mathfrak {O}({\grave{\breve{\varrho }}}_v)= \sqrt{\mathbb {O}_{amp}({\grave{\breve{\varrho }}}_v) \times \mathbb {O}_{pha}({\grave{\breve{\varrho }}}_v)}. \end{aligned}$$(8)
-
2.
Harmonic Mean: By applying the concept of harmonic mean for the calculation of mean score, we obtain
$$\begin{aligned} \mathfrak {O}({\grave{\breve{\varrho }}}_v)= \frac{2}{\frac{1}{\mathbb {O}_{amp}({\grave{\breve{\varrho }}}_v)}+\frac{1}{\mathbb {O}_{pha}({\grave{\breve{\varrho }}}_v)}}. \end{aligned}$$(9)
-
3.
Variance: By utilizing the concept of variance, we get Table 11.
-
4.
Standard Deviation: By utilizing the concept of standard deviation, we get Table 12.
By employing Pythagorean means and dispersion measures, the readers will be able to discover how score values impact the evaluation of various transit options. Table 13 provides a clear representation of the computed results as well as the final ranking of these alternatives.
The graphical representation of the statistical analysis is also shown in Fig. 2. As shown in Table 13 and in Fig. 2, the ranking of \({{{\grave{\breve{\varrho }}}_4}}\) remains consistent, while the rankings of \({{{\grave{\breve{\varrho }}}_1}},{{{\grave{\breve{\varrho }}}_2}}\) and \({{{\grave{\breve{\varrho }}}_3}}\) are analogous to each other. Specifically, \({{{\grave{\breve{\varrho }}}_3}}\) is preferred over \({{{\grave{\breve{\varrho }}}_1}}\) and \({{{\grave{\breve{\varrho }}}_2}}\).
Sensitivity analysis and robustness evaluation
To check the robustness of the proposed CIFHSS-based MADM approach, another sensitivity analysis is conducted by changing the weights of the main decision criteria. This analysis determines how small changes in parametric weights effect the final ranking of alternatives, thereby determining the model’s stability in uncertain decision scenario.
A one-at-a-time (OAT) sensitivity analysis is used, in which each parameter weight is independently increased and decreased by 10% and 20% respectively, while maintaining the remaining weights unchanged. After change of each weight, the overall score and ranking of the alternatives is calculated again. The original weight set is denoted as the baseline scenario. Note that the Table 14 summarizes the changes in the ranking of alternatives by changing the weight conditions of each parameter. The most critical parameters and sub-parameters are tested for their effect on the final ranking, specifically for the top-ranked alternative, \({\grave{\breve{\varrho }}}_4\) (Hybrid Car-Sharing Program).
Results and discussions
The sensitivity analysis indicates that the final ranking of the alternatives remains largely stable under moderate perturbations. The Hybrid Car-Sharing Program (\(\grave{\breve{\varrho _4}}\)) remains the top-ranked alternative in most cases, which confirms the models effectiveness and robustness. Only under a 20% increase in the weight of the ‘Coverage‘ parameters does the second-best alternative (\(\grave{\breve{\varrho _3}}\) Light Rail Transit) temporarily become the top-ranked option. This slight change is consistent with practical expectations, different stakeholder preferences can effect decision priorities, but the model still maintains consistent and interpretable results, reinforcing its suitability for complex decision environments.
Comparison
To evaluate the effectiveness and robustness of the proposed CIFHSS-based MADM model, a detailed comparative analysis with existing models is essential. In this regard, several existing fuzzy MADM models are considered from the literature47,48,49,50,51.
The model proposed by Singh et al.47 is based on the intuitionistic fuzzy framework, which accounts for both membership and non-membership values. However, it lacks the ability to handle the phase component of each membership function. Furthermore, it does not support parameterization or sub-parameter structures, which are crucial in many real-world decision-making scenarios. Hadi et al.48 proposed a novel MADM approach under a Fermatean fuzzy environment. While this model provides a broader representation of uncertainty compared to traditional fuzzy sets, it also suffers from limitations in handling sub-parameters, which can significantly influence the decision-making process. Similarly, the method introduced by Rani et al.49 is based on picture fuzzy sets, allowing three degrees of membership. Although this model adds richness in expressing uncertainty, it also fails to address multi-layered parameter structures effectively. The proposed CIFHSS-based model also demonstrates superiority over the models presented by Asghar et al.50 and Xiao et al.51, especially in terms of dealing with complex-valued uncertainty and hierarchical parameterization. For further comparison, we also applied several well-known TOPSIS-based MADM models from the literature52,53,54 to the same real-world case study. The results obtained from these models are presented in Table 15, which highlights the differences in ranking and decision outcomes, thereby supporting the effectiveness of the proposed approach.
As noted from Table 15, the alternative \({\grave{\breve{\varrho }}}_4\), which represents the Hybrid Car-Sharing Program, achieves the highest rank among all considered transportation options. The results are also shown graphically in Fig.3 for visual understanding of the ranking of alternatives. This result demonstrates the consistency and decision-making reliability of the proposed CIFHSS-based MADM model. This comparative analysis shows that the proposed CIFHSS-based approach offers improved decision differentiation, especially in decision-making problem involving uncertainty and sub-parameter interactions, the factors which traditional models do not effectively handle. This supports the relevance and added value of the proposed model over existing methods.
Conclusion
The aim of this study is to deal with the uncertainty problem in a more specific way by combining CIFSs with HS sets. Some operations of the CIFHSS are discussed, including subset, equal set, union, intersection, complement, AND, and OR. By establishing these concepts, the groundwork for the CIFHSS structure was constructed. The correctness and execution of the suggested operations and definitions are validated by giving appropriate instances. In the future, these operations are expected to play an important role in refining decision-making strategies, particularly in applications such as recruiting, management strategies, and other analytical domains, assuring more accuracy and efficiency.
In addition, a robust decision support system is developed employing a MADM-based algorithm that leverages sophisticated matrix-based CIFHSS aggregation approaches. The algorithm is thoroughly explained, and its practicality is demonstrated using a real-life decision-making scenario. This application to a real-life transportation problem demonstrated the model’s ability to effectively rank transportation models which identify that the Hybrid Car-Sharing Program as the most suitable choice. The implications of this research are twofold. First, it provides a flexible and robust tool for decision-makers in urban planning, especially in situations involving uncertain and vague information. Second, the framework can be extended to other sectors such as energy planning, healthcare prioritization, and environmental management, where multi-attribute analysis under uncertainty is difficult to deal. However, the study also has some limitations. A comparison with established methods55,56, highlighted the need for future benchmarking using standard datasets and hybrid approaches that combine traditional and fuzzy-based approaches. Future work will include matrices, similarity measures (single and multi-valued, interval-valued), functions, distance measures, and algorithms such as the score function, VIKOR, TOPSIS, and AHP of CIFHSSs.
Data availability
All data generated or analyzed during this study are included in this article.
Code availability
All algorithmic steps and mathematical formulations used in this study are explicitly described within the manuscript. The proposed Complex Intuitionistic Fuzzy Hypersoft Set (CIFHSS)-based Multi Attribute Decision Making (MADM) algorithm is presented in the manuscript, allowing readers to implement it in any computational environment such as MATLAB, Python, or R. No separate source code or external files are required to reproduce the reported results.
References
Kornyshova, E., & Salinesi, C. MCDM techniques selection approaches: state of the art. In 2007 ieee symposium on computational intelligence in multi-criteria decision-making (pp. 22-29). IEEE (2007).
Zavadskas, E. K. & Turskis, Z. Multiple criteria decision making (MCDM) methods in economics: an overview. Technol. Econ. Dev. Econ. 17(2), 397–427 (2011).
Kumar, R. A comprehensive review of MCDM methods, applications, and emerging trends. Decis. Mak. Adv. 3(1), 185–199 (2025).
Mrad, S., & Mraihi, R. Towards a sustainable transportation system: innovative measures to alleviate road traffic congestion. In Achieving Economic Growth and Welfare Through Green Consumerism (pp. 208-239). IGI Global (2023).
Wei, K., Vaze, V. & Jacquillat, A. Transit planning optimization under ride-hailing competition and traffic congestion. Transp. Sci. 56(3), 725–749 (2022).
Xu, Y. et al. Optimization path design for urban travel system based on CO2-congestion-satisfaction multi-objective synergy: Case study in Suzhou China. Sustain. Cities Soc.81, 103863 (2022).
Ekhlakov, R. & Andriyanov, N. Multicriteria assessment method for network structure congestion based on traffic data using advanced computer vision. Mathematics 12(4), 555 (2024).
Huang, C. N. & Lo, H. W. A hybrid Z-based MADM model for the evaluation of Urban resilience. Math. Probl. Eng. 2021(1), 9474753 (2021).
Jain, S., Jain, V. K. & Mishra, S. Fuzzy-AHP based optimal RSU deployment (Fuzzy-AHP-ORD) approach using road and traffic analysis in VANET. Ad Hoc Netw. 161, 103529 (2024).
Zadeh, L. A. Fuzzy sets. Inform. Control 8(3), 338–353 (1965).
Molodtsov, D. Soft set theory-first results. Comput. Mathe. Appl. 37(4–5), 19–31 (1999).
Zahedi Khameneh, A. & Kiliçman, A. Multi-attribute decision-making based on soft set theory: a systematic review. Soft. Comput. 23, 6899–6920 (2019).
Ozturk, T. Y. & Bayramov, S. Soft mappings space. Sci. World J. 2014(1), 307292 (2014).
Ozturk, T. Y., Aras, C. G. & Bayramov, S. A new approach to operations on neutrosophic soft sets and to neutrosophic soft topological spaces. Commun. Math. Appl. 10(3), 481–493 (2019).
Zhang, X., Park, C. & Wu, S. Soft set theoretical approach to pseudo-BCI algebras. J. Intell. Fuzzy Syst. 34(1), 559–568 (2018).
Maji, P. K., Biswas, R. & Roy, A. R. Soft set theory. Comput. Math. Appl. 45(4–5), 555–562 (2003).
Maji, P. K., Roy, A. R. & Biswas, R. An application of soft sets in a decision making problem. Comput. Math. Appl. 44(8–9), 1077–1083 (2002).
Chen, D., Tsang, E. C. C., Yeung, D. S. & Wang, X. The parameterization reduction of soft sets and its applications. Comput. Math. Appl. 49(5–6), 757–763 (2005).
Pei, D., & Miao, D. From soft sets to information systems. In IEEE international conference on granular computing, 617-621 (2005).
Kong, Z., Gao, L., Wang, L. & Li, S. The normal parameter reduction of soft sets and its algorithm. Comput. Math. Appl. 56(12), 3029–3037 (2008).
Zou, Y. & Xiao, Z. Data analysis approaches of soft sets under incomplete information. Knowl.-Based Syst. 21(8), 941–945 (2008).
Aktas, H. & Çagman, N. Soft sets and soft groups. Inf. Sci. 177(13), 2726–2735 (2007).
Atanassov, K. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 20, 87–96 (1986).
Atanasov, K. Intuitionistic Fuzzy Sets (Physica-Verlag, Heidelberg, Theory and applications, 1999).
Maji, P. K. More on intuitionistic fuzzy soft sets, In: H. Sakai, M.K. Chakraborty, A.E. Hassanien, D. Slezak, W. Zhu (Eds.), Proceedings of the 12th International Conference on Rough Sets, Fuzzy Sets, Data Mining and Granular Computing (RSFDGrC 2009), Lecture Notes in Computer Science, 5908, Springer, 231-240 (2009).
Maji, P. K., Biswas, R., Roy, A. Intuitionistic fuzzy soft sets. J. Fuzzy Math.9(3), 677–692 (2001).
Jiang, Y., Tang, Y. & Chen, Q. An adjustable approach to intuitionistic fuzzy soft sets based decision making. Appl. Math. Model. 35(2), 824–836 (2011).
Maji, P. K. An application of intuitionistic fuzzy soft sets in a decision making problem. In IEEE International Conference on Progress in Informatics and Computing 349-351 (2010).
Smarandache, F. Extension of soft set to hypersoft set, and then to plithogenic hypersoft set. Neutrosophic Sets Syst.: An Int. Book Series Inform. Sci. Eng. 22, 168 (2018).
Abbas, M., Murtaza, G., & Smarandache, F. Basic operations on hypersoft sets and hypersoft point. Neutrosophic sets Syst. 35 (2020).
Gayen, S. et al. Introduction to Plithogenic Hypersoft Subgroup. Neutrosophic Sets Syst. 33(1), 14 (2020).
Ozturk, T. Y. & Yolcu, A. On Neutrosophic Hypersoft Topological Spaces 215–234 (Theory and Application of Hypersoft Set. Pons Publishing House, Brussel, 2021).
Saeed, M., Ahsan, M., Siddique, M. K. & Ahmad, M. R. A study of the fundamentals of hypersoft set theory. Int. J. Sci. Eng. Res. 11(1), 320–329 (2020).
Saqlain, M., Saeed, M., Ahmad, M. R. & Smarandache, F. Generalization of TOPSIS for neutrosophic hypersoft set using accuracy function and its application. Neutrosophic Sets Syst. 27, 131–137 (2019).
Saqlain, M., Jafar, N., Moin, S., Saeed, M. & Broumi, S. Single and multi-valued neutrosophic hypersoft set and tangent similarity measure of single valued neutrosophic hypersoft sets. Neutrosophic Sets Syst. 32, 317–329 (2020).
Saqlain, M., Moin, S., Jafar, M. N., Saeed, M. & Smarandache, F. Aggregate Operators of neutrosophic hypersoft set. Neutrosophic Sets Syst. 32(1), 18 (2020).
Yolcu, A. & Ozturk, T. Y. Fuzzy Hypersoft Sets and Its Application to Decision-Making 50–64 (Theory and Application of Hypersoft Set. Pons Publishing House, Brussel, 2021).
Yolcu, A., Smarandache, F., & Öztürk, T. Y. Intuitionistic fuzzy hypersoft sets. Commun. Fac. Sci. Univ. Ankara Series A1 Math. Stat. 70(1), 443-455 (2021).
Ramot, D., Milo, R., Friedman, M. & Kandel, A. Complex fuzzy sets. IEEE Trans. Fuzzy Syst. 10(2), 171–186 (2002).
Alkouri, A. M. D. J. S. & Salleh, A. R. Complex intuitionistic fuzzy sets. AIP Conf. Proc. Am. Instit. Phys. 1482(1), 464–470 (2012).
Thirunavukarasu, P., Suresh, R. & Thamilmani, P. Applications of complex fuzzy sets. JP J. Appl. Math. 6(1), 5–22 (2013).
Kumar, T. & Bajaj, R. K. On complex intuitionistic fuzzy soft sets with distance measures and entropies. J. Math. 2014(1), 972198 (2014).
Rahman, A. U., Saeed, M., Smarandache, F., & Ahmad, M. R. Development of hybrids of hypersoft set with complex fuzzy set, complex intuitionistic fuzzy set and complex neutrosophic set. Neutrosophic Sets Syst. 38 (2020).
Cagman, N., Enginoglu, S. & Citak, F. Fuzzy soft set theory and its applications. Iran. J. Fuzzy Syst. 8(3), 137–147 (2011).
Thirunavukarasu, P., Suresh, R. & Ashokkumar, V. Theory of complex fuzzy soft set and its applications. Int. J. Innov. Res. Sci. Technol. 3(10), 13–18 (2017).
Nadia, A. Complex fuzzy soft set, Master Thesis, Universiti Kebangsaan Malaysia (2010).
Singh, M., Rathi, R., Antony, J., & Garza-Reyes, J. A. Lean six sigma project selection in a manufacturing environment using hybrid methodology based on intuitionistic fuzzy MADM approach. IEEE Trans. Eng. Manag. (2021).
Hadi, A., Khan, W. & Khan, A. A novel approach to MADM problems using Fermatean fuzzy Hamacher aggregation operators. Int. J. Intell. Syst. 36(7), 3464–3499 (2021).
Rani, P., Chen, S. M. & Mishra, A. R. Multi-attribute decision-making based on similarity measure between picture fuzzy sets and the MARCOS method. Inf. Sci. 658, 119990 (2024).
Asghar, A., Khan, K. A., Albahar, M. A. & Alammari, A. An optimized multi-attribute decision-making approach to construction supply chain management by using complex picture fuzzy soft set. PeerJ Comput. Sci. 9, e1540 (2023).
Xiao, Y., Asghar, A., Niaz, T., & Ali, R. S. Mathematical modeling for precise disease diagnosis: Distance and similarity measures in complex neutrosophic soft structures. Neurocomputing, 130620 (2025).
Mehri, M., Sadeghi, S., & Mehdy Hashemy Shahdany, S. A fuzzy TOPSIS-based approach for prioritizing low-impact development methods in high-density residential areas. Water Sci. Technol.89(2), 484–503 (2024).
Madhavi, S., Santhosh, N. C., Rajkumar, S. & Praveen, R. Pythagorean fuzzy sets-based vikor and topsis-based multi-criteria decision-making model for mitigating resource deletion attacks in wsns. J. Intell. Fuzzy Syst. 44(6), 9441–9459 (2023).
Zulqarnain, R. M., Ma, W. X., Siddique, I., Ahmad, H. & Askar, S. A fair bed allocation during COVID-19 pandemic using TOPSIS technique based on correlation coefficient for interval-valued pythagorean fuzzy hypersoft set. Sci. Rep. 14(1), 7678 (2024).
Kaur, P., & Priya, A. Selection of inventory policy under pythogrean fuzzy environment. Sci. Technol. Asia, 62-71 (2020).
Dutta, V., Haldar, S., Kaur, P. & Gajpal, Y. Comparative analysis of TOPSIS and TODIM for the performance evaluation of foreign players in Indian premier league. Complexity 2022(1), 9986137 (2022).
Acknowledgements
Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R404), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Author information
Authors and Affiliations
Contributions
T. A. conceptualized and designed the experiments, conducted the experiments, analyzed the data, created figures and tables, drafted or reviewed the manuscript, and approved the final version. A. A. conceptualized and designed the experiments, conducted the experiments, analyzed the data, created figures and tables, drafted or reviewed the manuscript, and approved the final version. T. A. conceptualized and designed the experiments, conducted the experiments, analyzed the data, created figures and tables, drafted or reviewed the manuscript, and approved the final version. I. S. conducted the experiments, carried out computational work, prepared figures and tables, contributed to drafting or reviewing the manuscript and approved the final version. H. A. E. W. K. responsible for designing the experiments, conducting data analysis, contributing to manuscript drafting and revision, and approving the final version for submission.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Ethics approval and consent to participate
This article does not contain any studies with human participants or animals performed by any of the authors.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Alballa, T., Asghar, A., Alharbi, T. et al. An advanced multi-attribute decision-making model for Urban transportation planning based on complex intuitionistic fuzzy sets with hierarchical parameters. Sci Rep 15, 43636 (2025). https://doi.org/10.1038/s41598-025-27402-1
Received:
Accepted:
Published:
Version of record:
DOI: https://doi.org/10.1038/s41598-025-27402-1